Abstract
The main objective of this paper is to solve state observation and external disturbances estimation for a class of second-order nonlinear systems. The proposed method relies mainly on the high gain observer as an estimator that tries to estimate the state vector and at the same time identifies the system’s unknown combined structured and unstructured uncertainties. The efficiency of the proposed method is demonstrated by estimating the flux and the speed of the induction motor by simulation.
1. Introduction
Dynamic systems are usually exposed to control signals that can be used to drive them to achieve a given objective and solve regulation and tracking control problems based on reliable models and in the presence of external perturbations and disturbances. These disturbances are, generally speaking, unstructured, i.e., they may depend on internal variables of the system in an either unknown or an ignored manner or else, they may also depend on external phenomena affecting the system [1]. They are unknown, unpredictable, or unmodeled. They can affect the controlled system response, its stability and closed-loop performance if they are ignored in the control synthesis phase. Solving this problem is still an open issue for control systems researchers. In the literature, many control methods that rely on a reliable model that approximates the system to be controlled are proposed feedback linearization and backstepping. In this case, some analytic robust terms are included in the derivation of the controller to guarantee stability and performance in the presence of uncertainties [2,3]. Sliding mode control techniques are among the robustifying methods that derive the control law bead on two combined terms, the equivalent control term based on the system model and a switching robustifying term [4]. High-gain observers are first used in the context of linear feedback as a tool for robust observer design for loop transfer recovery achieved by state feedback and in robust H∞ control in [5]. High-gain observers integration in nonlinear feedback control started in the late 1980 [6,7,8,9], where researchers in these papers have studied a wide range of nonlinear control issues, including stabilization, regulation, tracking, and adaptive control. They also studied time-varying high-gain observers and related problems [5]. In any case, disturbances are classed into two main categories and referred to as internal uncertainties and disturbances [10,11,12,13,14]. The main idea of this short note is to simplify the prediction of disturbances acting on the plant by grouping all external and internal dynamic disturbances into a single disturbance term and proceed to estimate the effects of this disturbance using High-Gain observers. The rest of the paper is organized as follows: in Section 2, we present the problem statement and state observation scheme with active disturbance estimation (ADE) based on the high-gain observer. The resulting ADE observer is applied to the induction motor system in Section 3 followed by the concluding remarks in Section 4.
2. State Observation Scheme with Active Disturbance Estimation (ADE)
2.1. Problem Statement
Active Disturbance Estimation ADE strategy is based on the possibility of online estimating of unknown disturbance inputs affecting the plant. The feedback control law usually requires full knowledge of the state which can be at the same time reconstructed by the same designed observer. In this section, we consider the following endogenously perturbed second-order system:
where & is the state vector and the first element of is only the measured state or output and known linearly parameterized terms and represents the unmodelled unknown uncertain terms. The system defined in (1) can be used to derive an adaptive high-gain observer that reconstructs the state vector with an adaptive law that estimates the unknown parameter vector the observer error is bounded and is ensured to converge given some robustness conditions on the term to be verified. For more information on designing high-gain observers, the readers can refer to reference [5]. In the context of Active Disturbance Estimation ADE disturbances and nonlinearities may be combined in a single term that can be approximated online. This suggests rewriting the second-order uncertain system in the following form:
This is an example of the equation:
where .
The term combines all the unknown exogenous terms. It is assumed that and its first-order time derivative are uniformly absolutely bounded. Note that many mechanical electrically driven systems in robotics and mechatronics can be represented by the system in Equation (1). The objective can then be stated as follows: to design a state observer to estimate the state vector and actively estimates the unknown exogenous terms with converging observation errors.
2.2. High-Gain Observer with Active Disturbance Estimator
Consider the following Extended State Observer (ADE):
where , and are (ADE) observer gains and they are chosen to achieve convergence.
with , , are positive constants and being a small parameter bestowing a high-gain character to the ESO design. Here, the variable is supposed to estimate the total disturbance input to the system , composed of the two terms; the endogenous perturbation input and the exogenous perturbation input .
Defining the estimation error vector as , and , its dynamics evolve according to the linear perturbed dynamics
The derivative term is given by:
It is bounded given that the nonlinear terms are continuous and their derivatives are continuous as well. Another methodology based on adaptive control can be used to estimate the term rather than Defining the error vector as Equation (4) can be written as
3. Ade Observer for the Induction Motor
3.1. Induction Motor System Modeling
The induction motor is one of the most complex dynamical systems due it is difficult to control since this system is considered to be multivariate having properties such as high coupling and high non-linearity. It is generally described by a fifth-order nonlinear differential equation with two inputs. Moreover, the control and the parameters estimation of an induction motor is very complex, because it is subject to unknown disturbances and the variation of motor parameters due to heating and magnetic saturation. We used field-oriented control (FOC) to perform a change of variables to bring the equations into new coordinates that will be simple to work with, where the currents regulating the flux and the speed are decoupled [15,16]. Thus, instead of working with (,), one uses the polar coordinate representation (,) [15,16]. IM is represented by the model [15,16,17].
In the above model, the angular speed of the rotor is denoted by , is the flux in the stator reference frame, and and denote the stator currents and voltages, is the number of pole pairs, and are the stator and rotor resistances, M is the mutual inductance, and are the stator and rotor inductances, and the two mechanical parameters: J is the inertia of the rotor and f is the load torque. The resistances , and the inductances , will be treated as uncertain parameters with , and , as their rated values, respectively. , . Where and are continuous functions of , , , are continuous functions of (, ). The electromagnetic torque is now just proportional to the product of two state variables and . That is the first four equations of (6) may be written as two decoupled subsystems consisting of the flux subsystem model:
and the speed subsystem model:
where
and
and are perturbation terms. The field-oriented control consists of using to force to track the constant flux reference in the flux subsystem, and the control of speed in the subsystem is done through the input . Consequently, the flux dynamics are now decoupled from the speed dynamics. However, the differential equations for and still contain quite complicated nonlinearities in both flux (7) and speed subsystems (8). To solve the problem of unknown variations in plant parameters and structure, in this paper a robust ADE observer will be designed to eliminate the effect of unstructured uncertainties in each subsystem of the decoupled dynamics of flux and speed subsystems of the IM.
3.2. High-Gain Observer with Active Disturbance Estimator
Noting that in applying the feedback (6), there is some uncertainty in the knowledge of the motor parameters and the state variables. Furthermore, the motor parameters and can vary significantly due to Ohmic heating while and can also vary due to magnetic saturation [15]. For that, assuming that all neglected terms for each subsystem as an error signal ( and ) consequently, the dynamics of the output () (). Defined by (7) and (8), respectively, will be expressed as:
Flux expressed:
Speed expressed:
Our objective is to develop a high-gain observer with an active disturbance estimator that is capable of estimating the flux and speed of an induction motor and eliminating the uncertainties effect in the observer law in order to achieve a good estimation of the desired trajectory and to solve the problem of unknown variations in plant parameters and the load torque. In designing an observer law for speed estimation and torque load generation based on a given flux reference signal, for each subsystem, a simpler strategy is followed in this paper where two ADE observers are used to overcome the effects of nonlinear uncertainties and neglected terms in the accuracy of the estimation. The desired torque to be generated with the corresponding reference flux . In order to the flux tracking, we introduce the state variables and the state space model (6) and for the tracking problem of the speed we define the new state vector and the speed subsystem dynamics given in (9) can be written as follows:
where
and
where
and
Note that the objective of the ADE strategy is to obtain proper estimation, minimize the total disturbance and obtain a good estimation of the flux and the speed. The ADE observer law is given by (7) and (8), where are design parameters chosen as described in Section 2. The observer uses the error between the actual measured flux and the estimated flux for correcting the estimated vector.
4. Results
The performance of the high-gain observer with an active disturbance estimator is tested by a differential simulation model under Matlab/Simulink environment. The simulated motor is a six-pole , 1/12 horsepower two-phase IM and the rated parameters of the motor were taken from [15] as , , H, H, H , K·gm2, N·m/rad/s.
The speed and flux estimation performance of ADE is illustrated in graphs (a) and (b) in Figure 1, respectively, which shows that the ADE observer is robust to parametric uncertainties and external disturbance variation. Although the references peed is changed from 100 rad/s to 20 rad/s and the torque load is kept constant with variations. The ADE observer has not encountered a tracking problem to follow the reference speed and flux as illustrated in Figure 1 This result shows the achieved performance of the ADE strategy for the perfect speed and flux esteeming.
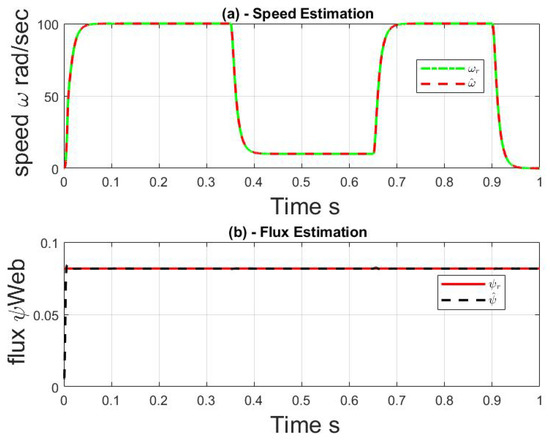
Figure 1.
Simulation results with constant load and variation of parametric uncertainties with ADE Observer.
For the last simulation scenario, a highly varying load torque is applied with parametric uncertainty to show the power of ADE to achieve perfect speed tracking for highly varying load illustrated in the Figure 2. Obviously, the ADE observer can estimate the speed, flux and disturbance despite a change in the torque simulation scenario as demonstrated in Figure 3.
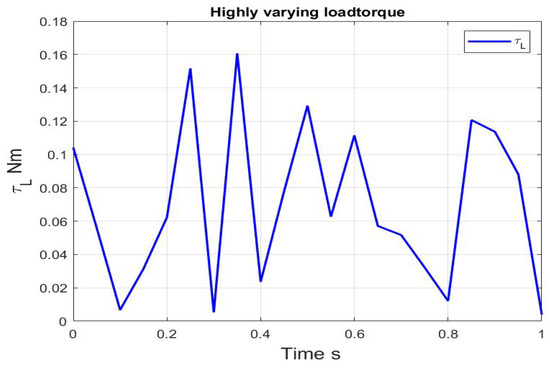
Figure 2.
The applied of varying load.
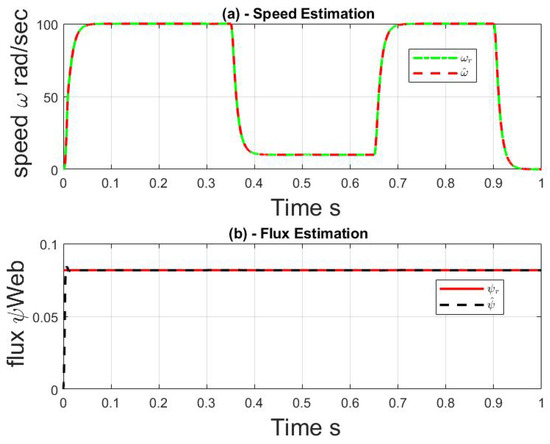
Figure 3.
Simulation results with varying load and parametric uncertainties with ADE Observer.
Figure 4 illustrates the ADE observer system’s and d, q-axes control voltage waveform, respectively.
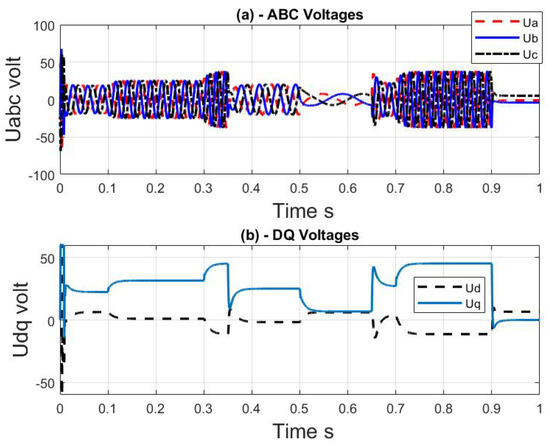
Figure 4.
Simulation results with varying load and parametric uncertainties with ADE Observer.
The external and internal disturbances are grouped in a single term and estimated by the observer it is highlighted in Figure 5. This signal can be usefull in designing feedback controllers for induction motor. The above shows the power and robustness of the observer to estimate the speed and flux in spite of the highly varying load torque and parametric uncertainty.
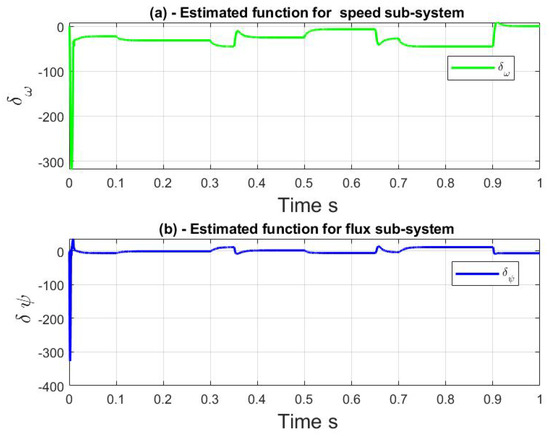
Figure 5.
Simulation results with varying load and parametric uncertainties with ADE Observer.
5. Conclusions
An active disturbance estimator combined with a high gain state observer is presented in this paper to address the problem of unmodelled and external disturbances for a second-order nonlinear system. The convergence of the state estimation disturbances is guaranteed by the right choice of observer gains. We have applied this method to an induction motor to show the design choices and the achieved performance although we have assumed a partly known model of the system to be estimated. In future research, we will try to include the ADE in designing robust observers to compensate for the unknown terms.
Author Contributions
Conceptualization, S.K.; methodology, S.K.; software, S.K., M.C. and M.B.; writing—original draft preparation, S.K.; writing—review and editing, S.K., CH.M., M.B. and M.A.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Directorate-General for Scientific Research and Technological Development/Ministry of High Education and Scientific Research of Algeria (DGRSDT/MESRS).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FOC | Field-Oriented Control |
| IM | Induction motor |
| ADE | Active Disturbance Estimation |
References
- Sira-Ramírez, H.; Luviano-Juárez, A.; Ramírez-Neria, M.; Zurita-Bustamante, E.W. Active Disturbance Rejection Control of Dynamic Systems: A Flatness-Based Approach; Elsevier Ergonomics Book Series; Butterworth-Heinemann: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Ammar, A.; Kheldoun, A.; Metidji, B.; Ameid, T.; Azzoug, Y. Feedback linearization based sensorless direct torque control using stator flux MRAS-sliding mode observer for induction motor drive. ISA Trans. 2020, 98, 382–392. [Google Scholar] [CrossRef] [PubMed]
- Regaya, C.B.; Farhani, F.; Zaafouri, A.; Chaari, A. A novel adaptive control method for induction motor based on Backstepping approach using dSpace DS 1104 control board. Mech. Syst. Signal Process. 2018, 100, 466–481. [Google Scholar] [CrossRef]
- Regaya, C.B.; Farhani, F.; Zaafouri, A.; Chaari, A. An adaptive sliding-mode speed observer for induction motor under backstepping control. Int. J. Innov. Comput. I 2017, 11, 763–771. [Google Scholar]
- Khalil, H.K. High-Gain Observers in Nonlinear Feedback Control; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2017. [Google Scholar]
- Petersen, I.R.; Holot, C.V. High-gain observers applied to problems in disturbance attenuation, H-infinity optimization and the stabilization of uncertain linear systems. In Proceedings of the 1988 American Control Conference, Atlanta, GA, USA, 15–17 June 1988; pp. 2490–2496. [Google Scholar]
- Esfandiari, F.; Khalil, H.K. Observer-based design of uncertain systems: Recovering state feedback robustness under matching conditions. In Proceedings of the 1989 American Control Conference, Pittsburgh, PA, USA, 21–23 June 1989. [Google Scholar]
- Khalil, H.; Saberi, A. Adaptive stabilization of a class of nonlinear systems using high-gain feedback. IEEE Trans. Autom. Contr. 1987, 32, 1031–1035. [Google Scholar] [CrossRef]
- Saberi, A.; Sannuti, P. Observer design for loop transfer recovery and for uncertain dynamical systems. IEEE Trans. Autom. Contr. 1990, 35, 878–897. [Google Scholar] [CrossRef]
- Tornambe, A. Use of asymptotic observers having high-gains in the state and parameter estimation. In Proceedings of the 28th IEEE Conference on Decision and Control, Tampa, FL, USA, 13–15 December 1989; pp. 1792–1794. [Google Scholar]
- Yin, Z.; Zhang, Y.; Du, C.; Liu, J.; Sun, X.; Zhong, Y. Research on Anti-Error Performance of Speed and Flux Estimation for Induction Motors Based on Robust Adaptive State Observer. IEEE Trans. Ind. Electron. 2016, 63, 3499–3510. [Google Scholar] [CrossRef]
- Guo, B.-Z.; Zhao, Z.-L. On convergence of the nonlinear active disturbance rejection control for MIMO systems. SIAM J. Control Optim. 2013, 51, 1727–1757. [Google Scholar] [CrossRef]
- Guo, B.-Z.; Zhao, Z.-L. On the convergence of an extended state observer for nonlinear systems with uncertainty. Syst. Control Lett. 2011, 60, 420–430. [Google Scholar] [CrossRef]
- Zheng, Q.; Gao, L.; Gao, Z. On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 12–14. [Google Scholar]
- Chiasson, J. : Modeling and High Performance Control of Electric Machines; John Wiley and Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Abbas, H.A.; Belkheiri, M.; Zegnini, B. Feedback Linearization Control of an Induction Machine Augmented by Single Hidden Layer Neural Networks. Int. J. Control 2016, 89, 140–155. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Z.; Yu, X. Indirect Field-Oriented Control of Induction Machines Based on Synergetic Control Theory. In Proceedings of the IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–7. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).