Large Landing Trajectory Dataset for Go-Around Analysis †
Abstract
1. Introduction
2. Dataset
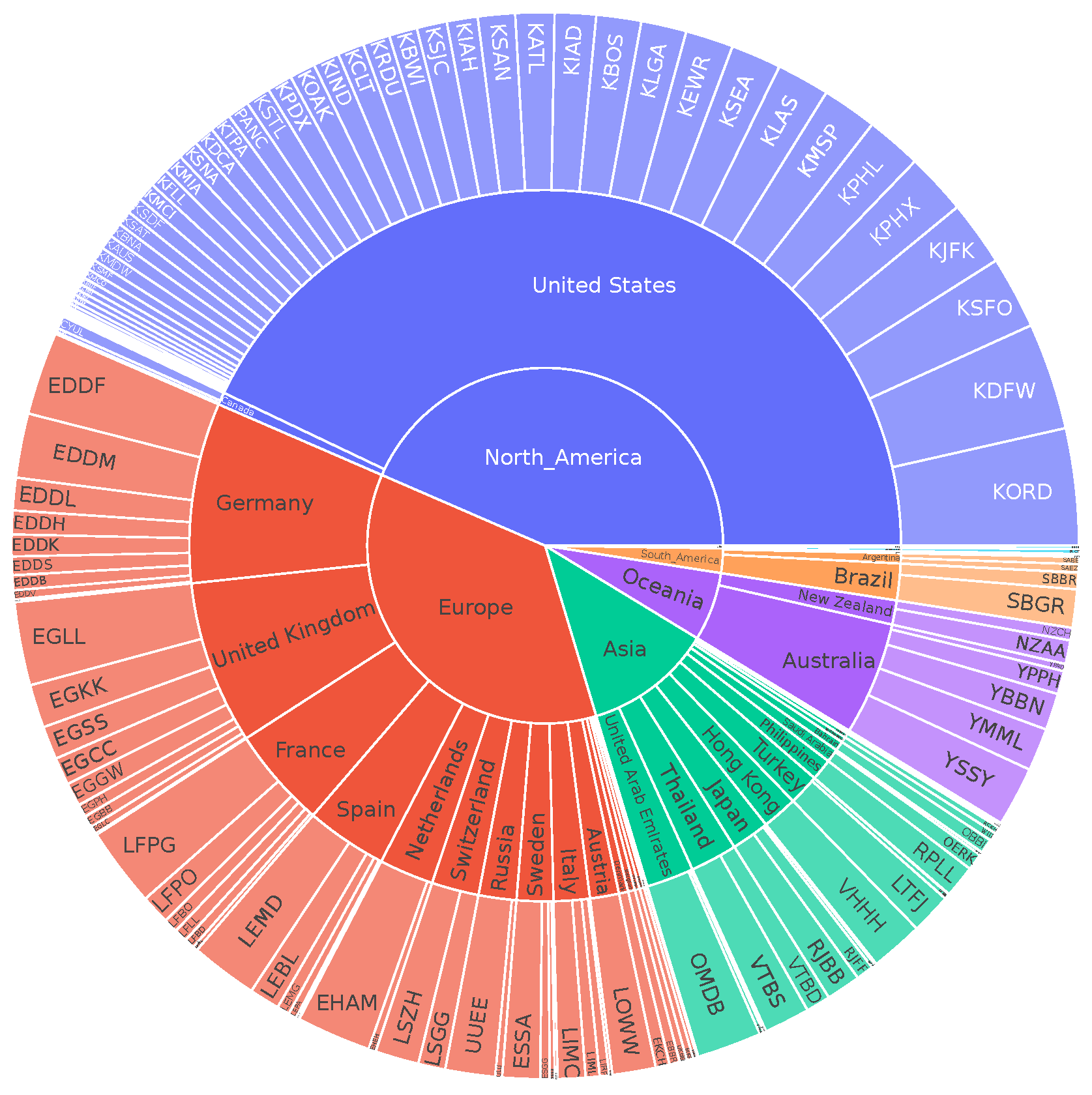
2.1. Description
2.2. Dataset Processing
- Assigns each portion of the trajectory to a flight phase by using the machine learning based algorithms introduced by Sun et al. [25].
- Identifies the portion of the trajectory that is aligned with a runway of the airport.
- Classifies the trajectory as having a GA if two distinct portions that are aligned with a runway are separated by one climb phase.
2.3. Dataset Quality
2.4. Dataset Availability
3. Example Applications
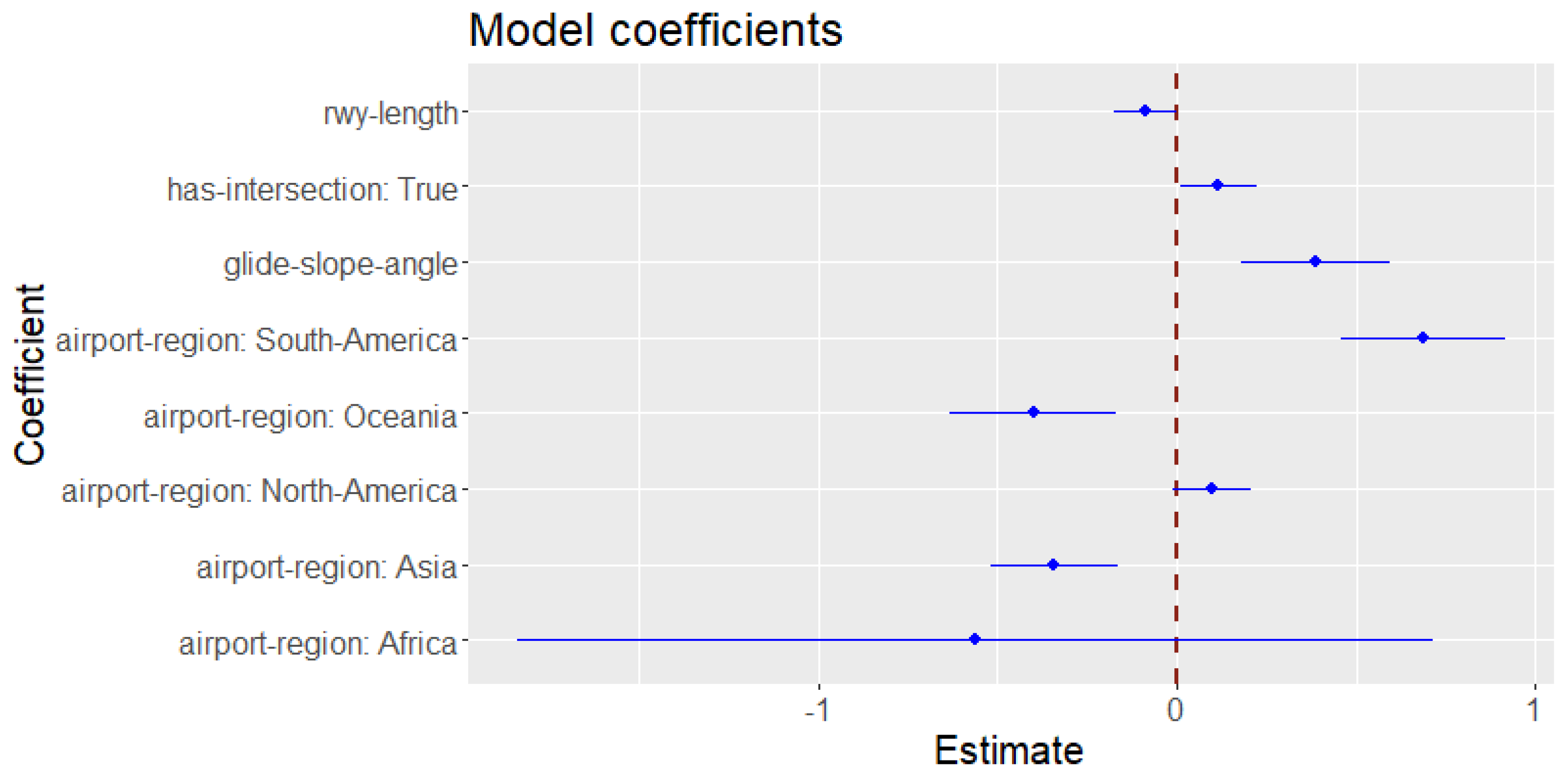
3.1. GA Probability Prediction for Airport–Runway Pairs
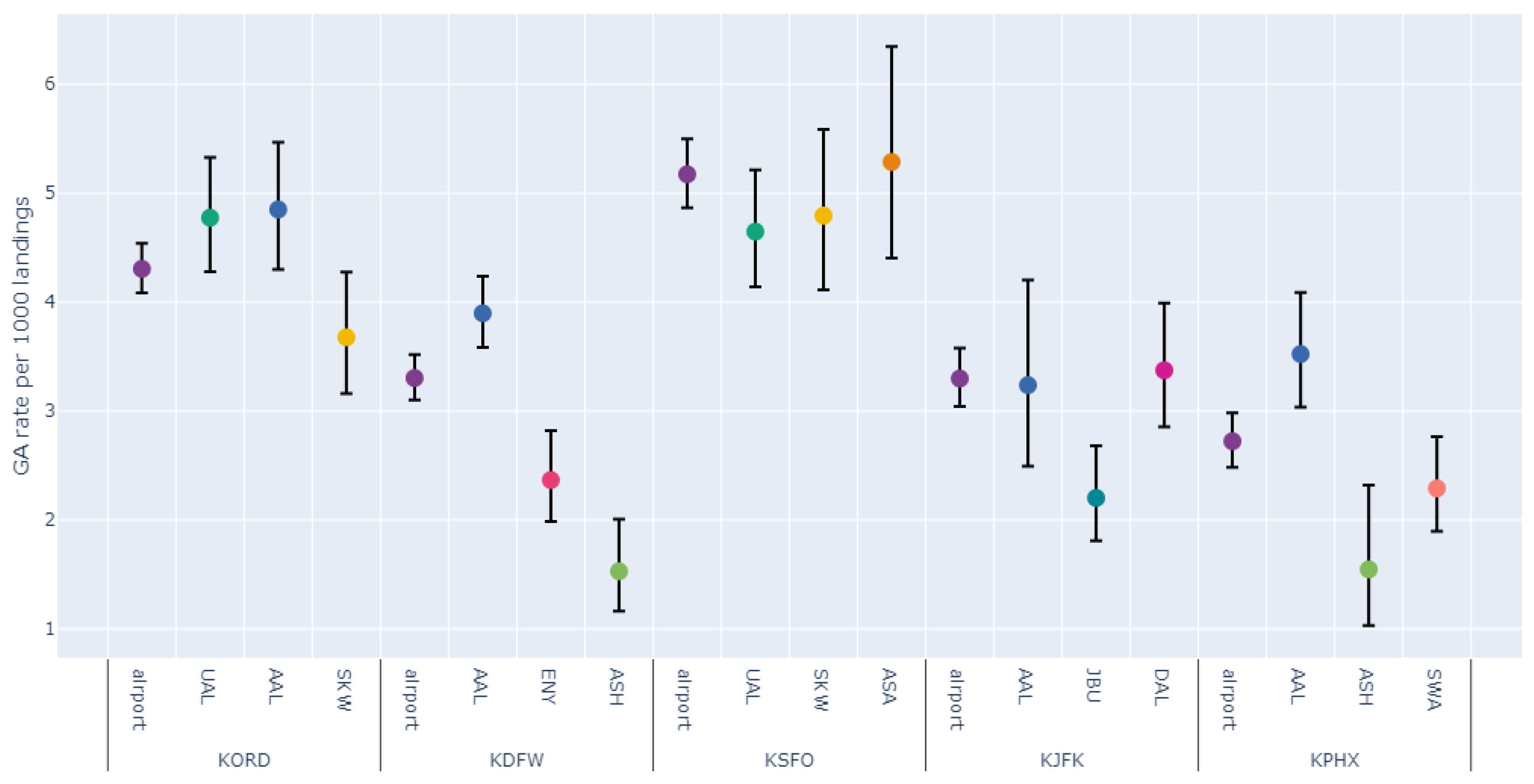
3.2. Comparing GA Rates between Operators
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Coker, M. Why and When to Perform a Go-around Maneuver. Available online: https://www.smartcockpit.com/docs/why-and-when-to-perform-a-go-around-maneuver.pdf (accessed on 2 November 2022).
- Civil Air Navigation Services Organisation. Unstable Approaches: Air Traffic Control Considerations. Available online: https://www.icao.int/APAC/RASG/eDocs/Guidance%20material%20on%20Unstablished%20Approach.pdf (accessed on 2 November 2022).
- Gluck, J.; Tyagi, A.; Grushin, A.; Miller, D.; Voronin, S.; Nanda, J.; Oza, N. Too fast, too low, and too close: Improved real time safety assurance of the national airspace using long short term memory. In AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2019. [Google Scholar] [CrossRef]
- Campbell, A.M.; Zaal, P.M.T.; Shah, S.R.; Schroeder, J.A. Go-around criteria refinement for transport category aircraft. J. Air Transp. 2022, 30, 3–22. [Google Scholar] [CrossRef]
- Gariel, M.; Spieser, K.; Frazzoli, E. On the statistics and predictability of go-arounds. arXiv Prepr. 2011, arXiv:1102.1502. [Google Scholar]
- Proud, S.R. Go-around detection using crowd-sourced ADS-B position data. Aerospace 2020, 7, 16. [Google Scholar] [CrossRef]
- Donavalli, B.; Mattingly, S.P.; Massidda, A. Impact of weather factors on go-around frequency. In Proceedings of the Transportation Research Board 96th Annual Meeting, Washington, DC, USA, 8–12 January 2017. [Google Scholar]
- Schäfer, M.; Strohmeier, M.; Lenders, V.; Martinovic, I.; Wilhelm, M. Bringing up OpenSky: A large-scale ADS-B sensor network for research. In Proceedings of the IPSN-14 Proceedings of the 13th International Symposium on Information Processing in Sensor Networks, Berlin, Germany, 15–17 April 2014; pp. 83–94. [Google Scholar]
- Figuet, B.; Monstein, R.; Waltert, M.; Barry, S. Predicting airplane go-arounds using machine learning and open-source data. Proceedings 2020, 59, 6. [Google Scholar] [CrossRef]
- Xu, Z.; Lu, X.; Zhang, Z. Aircraft go-around detection employing open source ADS-B data. In Proceedings of the 2021 IEEE 3rd International Conference on Civil Aviation Safety and Information Technology (ICCASIT), Changsha, China, 20–22 October 2021; pp. 259–262. [Google Scholar] [CrossRef]
- Kumar, S.G.; Corrado, S.J.; Puranik, T.G.; Mavris, D.N. Classification and analysis of go-arounds in commercial aviation using ADS-B data. Aerospace 2021, 8, 291. [Google Scholar] [CrossRef]
- Dai, L.; Liu, Y.; Hansen, M. Modeling go-around occurrence. In Proceedings of the Thirteenth USA/Europe Air Traffic Management Research and Development Seminar (ATM2019), Vienna, Austria, 18 June 2019; pp. 17–21. [Google Scholar]
- Dhief, I.; Alam, S.; Lilith, N.; Mean, C.C. A machine learned go-around prediction model using pilot-in-the-loop simulations. Transp. Res. Part Emerg. Technol. 2022, 140, 103704. [Google Scholar] [CrossRef]
- Dai, L.; Liu, Y.; Hansen, M. Predicting go-around occurrence with input-output hidden Markov model. In Proceedings of the International Conference on Research in Air Transportation, online, 15 September 2020. [Google Scholar]
- Puranik, T.G.; Rodriguez, N.; Mavris, D.N. Towards online prediction of safety-critical landing metrics in aviation using supervised machine learning. Transp. Res. Part C Emerg. Technol. 2020, 120, 102819. [Google Scholar] [CrossRef]
- Chou, C.S.; Tien, A.; Bateman, H. A machine learning application for predicting and alerting missed approaches for airport management. In Proceedings of the 2021 IEEE/AIAA 40th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 3–7 October 2021; pp. 1–9. [Google Scholar] [CrossRef]
- Dancila, R.; Botez, R.M.; Ford, S. Fuel burn and emissions evaluation for a missed approach procedure performed by a B737-400. Aeronaut. J. 2014, 118, 1329–1348. [Google Scholar] [CrossRef]
- Casado, R.; López-Lago, M.; Serna, J.; Bermúdez, A. Enhanced missed approach procedure based on aircraft reinjection. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 4149–4170. [Google Scholar] [CrossRef]
- Carmona, M.; Casado, R.; Bermúdez, A.; Francisco, M.P.; Boronat, P.; Calafate, C.T. Fuel savings through missed approach maneuvers based on aircraft reinjection. arXiv Prepr. 2022, arXiv:2207.03262. [Google Scholar] [CrossRef]
- Campbell, A.; Zaal, P.; Schroeder, J.A.; Shah, S. Development of possible go-around criteria for transport aircraft. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar] [CrossRef]
- Ross, G.; Tomko, L. Go-around noncompliance during unstabilized approaches and landings in commercial aviation: A human factors analysis. In Proceedings of the 82nd International Symposium on Aviation Psychology, Corvallis, OR, USA, 5 January 2021; pp. 299–302. [Google Scholar]
- de Voogt, A.; Kalagher, H.; Santiago, B.; Lang, J.W. Go-around accidents and general aviation safety. J. Saf. Res. 2022, 82, 323–328. [Google Scholar] [CrossRef] [PubMed]
- Krauth, T.; Morio, J.; Olive, X.; Figuet, B.; Monstein, R. Synthetic Aircraft Trajectories Generated with Multivariate Density Models. Eng. Proc. 2021, 13, 7. [Google Scholar] [CrossRef]
- Olive, X. Traffic, a toolbox for processing and analysing air traffic data. J. Open Source Softw. 2019, 4, 1518. [Google Scholar] [CrossRef]
- Sun, J.; Ellerbroek, J.; Hoekstra, J. Large-scale flight phase identification from ads-b data using machine learning methods. In Proceedings of the 7th International Conference on Research in Air Transportation, Philadelphia, OA, USA, 20–24 June 2016; pp. 1–8. [Google Scholar]
- Monstein, R.; Figuet, B.; Krauth, T.; Waltert, M.; Dettling, M. Large Landing Trajectory Data Set for Go-Around Analysis. open dataset. 1 November 2022. [Google Scholar] [CrossRef]
- Dunn, P.K.; Smyth, G.K. Generalized Linear Models with Examples in R; Springer Texts in Statistics; Springer New York: New York, NY, USA, 2018. [Google Scholar]
- Wilson, E.B. Probable inference, the law of succession, and statistical inference. J. Am. Stat. Assoc. 1927, 22, 209–212. [Google Scholar] [CrossRef]
| Column Name | Type | Description |
|---|---|---|
| time | date time | UTC time of landing or first GA (in the format YYYY-MM-DD). Specifically, it is the timestamp when the flight was last aligned on the runway on its first landing attempt. |
| icao24 | string | Unique 24-bit (hexadecimal number) ICAO identifier of the aircraft concerned. |
| callsign | string | Aircraft identifier in air-ground communications. |
| airport | string | ICAO airport code where the aircraft is landing. |
| runway | string | Designation of the runway on which the aircraft performed its first landing attempt. |
| has_ga | string | “True” if at least one GA was performed, otherwise “False”. |
| n_approaches | integer | Number of approaches identified for this flight. |
| n_rwy_approached | integer | Number of unique runways approached by this flight. |
| Time | icao24 | Callsign | Airport | Runway | has_ga | n_approached | n_rwy_approached |
|---|---|---|---|---|---|---|---|
| 2019-10-12 05:21:20 | 48455a | KLM88J | EHAM | 18C | False | 1 | 1 |
| 2019-06-30 20:53:14 | 4000937 | BAW957L | EGGL | 27L | True | 2 | 1 |
| 2019-10-03 14:38:45 | 070ed4 | 6VONE | GOBD | 01 | True | 6 | 2 |
| Feature | Type | Description |
|---|---|---|
| has_intersection | categorical | True if the runway has another runway intersecting it, otherwise false. |
| rwy_length | continuous | Length of the runway in kilometers. |
| glide_slope_angle | continuous | Angle of the ILS glide slope in degrees. |
| airport_region | categorical | Geographical region of the airport (either Europe, North America, South America, Asia, Africa, or Oceania). |
| Coefficient | Estimate | Std. Error | p-Value |
|---|---|---|---|
| intercept | −6.6 | 0.40 | 0 |
| has_intersection = True | 0.11 | 0.054 | 0.033 |
| rwy_length | −0.086 | 0.044 | 0.055 |
| glide_slope_angle | 0.39 | 0.11 | 0.0003 |
| airport_region = North America | 0.097 | 0.055 | 0.078 |
| airport_region = South America | 0.68 | 0.12 | 0 |
| airport_region = Asia | −0.34 | 0.090 | 0.0001 |
| airport_region = Oceania | −0.4 | 0.12 | 0.0007 |
| airport_region = Africa | −0.56 | 0.65 | 0.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monstein, R.; Figuet, B.; Krauth, T.; Waltert, M.; Dettling, M. Large Landing Trajectory Dataset for Go-Around Analysis. Eng. Proc. 2022, 28, 2. https://doi.org/10.3390/engproc2022028002
Monstein R, Figuet B, Krauth T, Waltert M, Dettling M. Large Landing Trajectory Dataset for Go-Around Analysis. Engineering Proceedings. 2022; 28(1):2. https://doi.org/10.3390/engproc2022028002
Chicago/Turabian StyleMonstein, Raphael, Benoit Figuet, Timothé Krauth, Manuel Waltert, and Marcel Dettling. 2022. "Large Landing Trajectory Dataset for Go-Around Analysis" Engineering Proceedings 28, no. 1: 2. https://doi.org/10.3390/engproc2022028002
APA StyleMonstein, R., Figuet, B., Krauth, T., Waltert, M., & Dettling, M. (2022). Large Landing Trajectory Dataset for Go-Around Analysis. Engineering Proceedings, 28(1), 2. https://doi.org/10.3390/engproc2022028002







