Unsupervised and Computationally Lightweight Spectrum Sensing in IoT Devices ^†

Abstract

Principal component analysis (PCA) is a widespread technique in data analysis. Recently, the L1-norm has been proposed as an alternative criterion to classical L2-norm in PCA due to its greater robustness to outliers. The present work shows that, with a whitening step, L1-PCA can perform spectrum sensing and modulation recognition in IoT applications. Numerical experiments confirm this finding.

1. Introduction

The pressure on the radio spectrum is increasing as more and more Internet of Things (IoT) devices are deployed, as most of them communicate via wireless technology. Spectrum sharing poses serious challenges for stakeholders when massive amounts of data need to be transmitted, as both spectrum availability and bandwidth remain scarce resources, even after the advent of the impressive 5G technology. In the search of efficient solutions, there is a growing interest in incorporating cognitive radio technologies into IoT devices [1]. A cognitive radio is a wireless transceiver that can adapt its behavior to the environment. In particular, among other capabilities, the device must be able to automatically select the best channel in real time. The ultimate goal of cognitive radio is to make optimal and efficient use of the radio spectrum [2].

The key feature of cognitive radio devices is their spectrum-sensing capability: they must be able to detect whether a wireless channel is occupied and, if so, recognize the type of modulation of the radiofrequency signal in the channel. This is necessary, for example, to detect whether it is a primary user or an interferer who occupies the spectrum. To perform this recognition, matched filters or certain properties of the modulated signals, such as cyclostationarity, have been traditionally exploited [3,4]. In addition, deep learning techniques have recently been reported to perform well in classifying radiocommunication signals [5,6,7,8].

However, previous approaches for modulated signal recognition have a high computational complexity, which limits the ability of IoT transceivers to adapt to variations in their radio environment. In this communication, we will present a new method for spectrum sensing and categorization of modulated signals that has two main features (1) it is unsupervised and (2) it is computationally simple, so that it can operate even with IoT devices with limited capabilities and adapt in real time to changes in the channel. The proposed approach exploits properties of the L1 standard that have been explored in our previous work [9]. Experiments demonstrate the feasibility of the proposed approach.

2. Material and Methods

2.1. L1-Norm Principal Component Analysis

This section presents the foundations of the principal component analysis (PCA) based on the L1 norm [10,11,12], which is the theoretical method that underpins the approach presented in this paper.

Consider the observation of N samples ${\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_N$ drawn from a d-dimensional random variable $\mathbf{x}\in {\mathbb{R}}^d$, where it is assumed that the sample mean of the observed dataset is zero. The aim of traditional PCA is to find a direction defined by unit vector $\mathbf{w}\in {\mathbb{R}}^d$, ${\parallel \mathbf{w}\parallel }_2=1$, such that the variance of all points in the set of projected samples

$$y_n={\mathbf{w}}^{\top }{\mathbf{x}}_n$$

(1)

is maximal. By defining vector $\mathbf{y}={[y_1,y_2,\cdots ,y_N]}^{\top }$, the problem can be expressed in mathematical form as follows:

$$\underset{{\parallel \mathbf{w}\parallel }_2=1}{max}{\parallel \mathbf{y}\parallel }_2=\underset{{\parallel \mathbf{w}\parallel }_2=1}{max}\sum _{n=1}^N{\left({\mathbf{w}}^{\top }{\mathbf{x}}_n\right)}^2.$$

(2)

Alternatively, by writing $\mathbf{y}={\mathbf{X}}^{\top }\mathbf{w}$, where $\mathbf{X}=[{\mathbf{x}}_1,\dots ,{\mathbf{x}}_N]\in {\mathbb{R}}^{d\times N}$ is the matrix that collects the observed data points, the problem can be recast as:

$$\underset{{\parallel \mathbf{w}\parallel }_2=1}{max}{\parallel {\mathbf{X}}^{\top }\mathbf{w}\parallel }_2.$$

The main drawback with this method is that the square in (2) magnifies the effects of large outliers and, hence, this approach degrades when there is faulty data. To solve it, Ref. [10] proposed to replace the quadratic function by the absolute value, thus yielding the following optimization problem:

$$\underset{{\parallel \mathbf{w}\parallel }_2=1}{max}{\parallel \mathbf{y}\parallel }_1=\underset{{\parallel \mathbf{w}\parallel }_2=1}{max}{\parallel {\mathbf{X}}^{\top }\mathbf{w}\parallel }_1.$$

(3)

where

$$\begin{array}{cc}\hfill & {\parallel \mathbf{y}\parallel }_1=\sum _{n=1}^N\left|y_n\right|\hfill \end{array}$$

(4)

is the L1-norm of vector $\mathbf{y}$. This new version of PCA has been given the name L1-norm based PCA or, simply, L1-PCA.

The maximization in (3) can be carried out using the low-computational-load-algorithm proposed by Kwak [10], whose main loop consists of the following two steps (observe the algorithm has no parameters to adjust):

• $\mathbf{y}={\mathbf{X}}^{\top }{\mathbf{w}}_i$;
• ${\displaystyle {\mathbf{w}}_{i+1}=\frac{\mathrm{sign}{\left(\mathbf{y}\right)}^{\top }\mathbf{X}}{{\parallel \mathrm{sign}\left(\mathbf{y}\right)}^{\top }{\mathbf{X}\parallel }_2}}$.

where ${\mathbf{w}}_i$ is the value of $\mathbf{w}$ after the ith iteration. It can be shown that this algorithm monotonically increases the objective function ${\parallel \mathbf{y}\parallel }_1$ so that the algorithm converges at least to a local maximum. In case we want to find several optimal directions, say P, the algorithm is run P times with the constraint that the direction obtained after the k-th run, ${\mathbf{w}}_k$, must be orthogonal to ${\mathbf{w}}_1,\dots ,{\mathbf{w}}_{k-1}$.

Discriminative Capabilities of the L1-Norm

Whitening is a common data pre-processing technique. It consists in linearly transforming the data such that the elements of the data vector become uncorrelated and of unit variance. Under a whitening constraint, therefore, the data covariance turns out to be equal to the identity matrix, i.e.,

$$\frac{1}{N}\mathbf{X}{\mathbf{X}}^{\top }=\mathbf{I}.$$

This is actually the generalization of standardizing the variables in the univariate case. Likewise, it can always be carried out without any loss of generality. In fact, there exist many whitening procedures and some of them are cost-effective [13].

It can be shown that, under the whitening assumption, L1-PCA is useful in classification problems. Specifically, close connections with Fisher’s linear discriminant analysis and the Fukunaga–Koontz transform (also known as ‘common spatial patterns’ technique) have been rigorously proven in [9,14]. Furthermore, L1-PCA can emulate these two techniques in a completely unsupervised manner. It is precisely these characteristics that have encouraged the present research.

3. Link to Modulation Recognition

A modulated signal can be expressed in general terms by the following expression [15]:

$$x\left(t\right)=i\left(t\right)cos\left(2\pi f_{c}t\right)-q\left(t\right)sin\left(2\pi f_{c}t\right),$$

(5)

where $i\left(t\right)$ and $q\left(t\right)$ are named in phase and quadrature components, respectively, and $f_c$ is the carrier frequency. Each family of modulations, analog or digital, can be distinguished because it builds $i\left(t\right)$ and $q\left(t\right)$ in a different and characteristic way. For example, in a QAM modulation,

$$\begin{array}{cc}\hfill i\left(t\right)& =\sum _k{I}_{k}r(t-kT)\hfill \\ \hfill q\left(t\right)& =\sum _k{Q}_{k}r(t-kT)\hfill \end{array}$$

where $I_k$ and $Q_k$ represent the coordinates of the k-th transmitted symbol in the QAM constellation diagram, T is the symbol duration time and $r\left(t\right)$ is a pulse-shaped waveform of width T.

The best known approach to modulation recognition consists of two steps. First, distinctive features are extracted from the modulated signals, and second, a pattern recognition system is applied to determine the type of modulation. In the classic reference paper of Nandi and Azzouz [16], nine fundamental features have been proposed, all of which can be used to discriminate one modulation from others. These include the ‘maximum spectral power density of the normalized signal’, i.e.,

$${\gamma }_{max}=max{\left|DFT\left[x_{cn}\left(t\right)\right]\right|}^2$$

where $x_{cn}\left(t\right)=\frac{x\left(t\right)-\overline{x}}{\overline{x}}$, $\overline{x}$ is the average of the instantaneous amplitude of the signal and $DFT$ stands for the discrete fourier transform; the ‘spectrum symmetry’, i.e.,

$$P=\frac{P_L-P_U}{P_L+P_U}$$

where $P_L$ and $P_U$ are the powers in the upper and the lower sidebands, and the ‘kurtosis’, which is defined by:

$$k=\frac{E\left\{x_{cn}^4\left(t\right)\right\}}{{\left\{E\left\{x_{cn}^2\left(t\right)\right\}\right\}}^2}.$$

The computation of these features is computationally intensive, however, which limits the practical application of this approach in IoT devices. As an alternative, we propose a method that only requires projecting the data in the appropriate directions, i.e., performing a reduced number of additions and multiplications. These directions will be precisely those determined by L1-PCA, which, unlike the previous features, can be computed offline and stored on the device. This approach has its theoretical roots in the relationship between the L1 norm and the kurtosis [17], which is one of the classical features proposed by Nandi and Azzouz [16], and the discriminative characteristics of this variant of PCA [9,14]. For reasons of space, a more detailed explanation will be left for future papers. The basics of the algorithm are illustrated by an example in the following Section.

4. Experimental Results

In this experimental demonstration, 64-QAM (Quadrature Amplitude Modulation), AM-DSB (Amplitude Modulated Double-SideBand transmission), and GFSK (Gaussian Frequency Shift Keying o GFSK) modulated signals have been used. These are representative of many real-world applications: 64-QAM is a typical subcarrier modulation in 5G, AM-DSB is a widely used analog modulation and GSFK is used, among others, by Bluetooth transceptors. Raw data are taken from the RADIOML 2016.10A dataset, which is one of the standards for research in this field and is publicly available at the RadioML website https://www.deepsig.ai/datasets (accessed on 1 September 2022). The dataset contains 1000 fragments or frames, all composed of 128 samples, of in-phase and quadrature components for each modulation type, although for simplicity only the in-phase components will be used in the experiments. Figure 1 shows some randomly chosen waveforms.

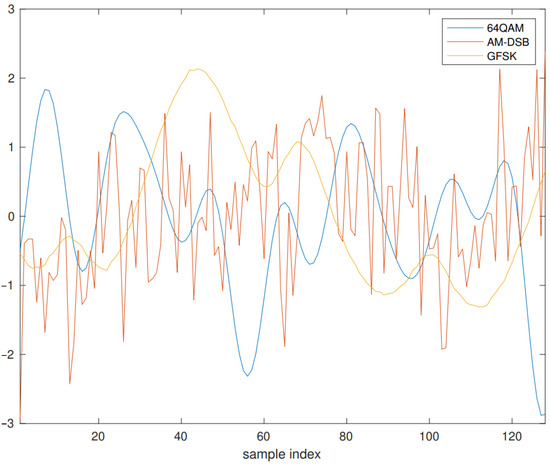
Figure 1. Illustration of typical 64QAM, AM−DSB, and GFSK in−phase waveforms.

Therefore, the experiment considers 1000 samples ${\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_{1000}$ from each modulation type, with ${\mathbf{x}}_k\in {\mathbb{R}}^{128}$ for all k. The signal to noise ratio (SNR), i.e., the ratio of the power of the signal to the power of the noise, is 18 dB. As a pre-processing step, we subtract from each vector ${\mathbf{x}}_k$ the average of its components, which is equivalent to removing the DC value from each in-phase signal. Additionally, to equalize the power of all signals, all vectors ${\mathbf{x}}_k$ are normalized to be of unit-norm. The small number of outliers detected (which actually appear to be mislabeled data) are filtered out and replaced by arbitrary waveforms of the same modulation type. Finally, all vector samples from the three modulations are put together in a matrix $\mathbf{X}\in {\mathbb{R}}^{128\times 3000}$ as columns.

Matrix $\mathbf{X}$ is whitened using the singular value decomposition and then we find orthogonal directions ${\mathbf{w}}_i$, $i=1,\dots ,P$, that maximize the L1-norm of the projected data ${\mathbf{X}}^{\top }{\mathbf{w}}_i$ using a slightly modified variant of the algorithm in [9]. Finally, we linearly transform each data vector ${\mathbf{x}}_k$ by multiplying it with matrix $\mathbf{W}=[{\mathbf{w}}_1,\dots ,{\mathbf{w}}_P]$ as follows:

$${\mathbf{v}}_k={\mathbf{W}}^{\top }{\mathbf{x}}_k.$$

Figure 2 shows the squared norm of the vectors ${\mathbf{v}}_k$ for $P=15$, with different colors for each type of modulation. It is seen that this procedure allows us to distinguish between 64-QAM, AM-DSB, and GFSK. Each type of modulation is amplified differently after the linear transformation (recall that the norm of all raw data was normalized to one in the pre-processing step). Furthermore, the procedure is unsupervised: the algorithm has not required any data label.

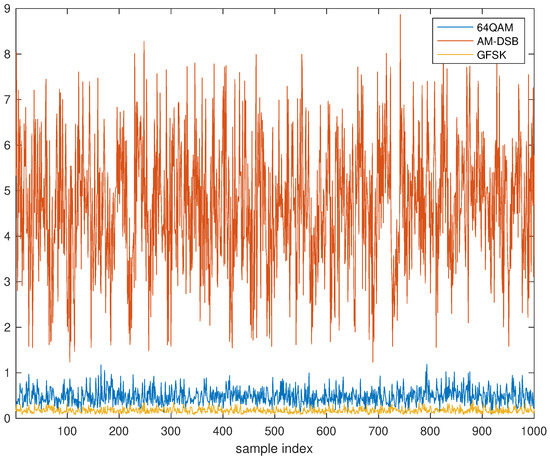
Figure 2. Squared norm of the projected data vectors, separated by the type of modulation. The sample rate refers to the signal frame used.

Note that the calculation of the directions ${\mathbf{w}}_i$ can be done offline. All the IoT device has to do is project the data onto them and compare the result with a reference threshold. In other words, it does not need to calculate any feature, which leads to considerable computational savings.

5. Conclusions

The present work has experimentally shown that L1-PCA can be used for modulation classification. L1-PCA can be carried out using several efficient algorithms recently proposed in the literature. Our future work will be focused on establishing the theoretical foundations of this approach and on developing algorithms for complex environments, including fading and substantial noise.