1. Introduction
Over the recent years, data-driven approaches, including deep learning techniques have played an instrumental role in the way we model, predict, and control dynamical systems [
1]. Thanks to the help of modern mathematical methods, the availability of data and computational resources, Neural Networks have been increasingly used to understand complex systems (non linear and high dimensional systems) [
2]. In 1989, Hornik, Stinchcombe, and White proved through the Universal Approximation theorem that Multi-layer feedforward Networks are Universal Approximators [
3]. The Universal Approximation for RNN is stated in [
2]. Recurrent neural networks (or RNN) are a family of Neural networks designed for processing sequential data. They are increasingly being used to understand, analyze and forecast the evolution of complex dynamical systems due to the explicit modeling of time and memory they offer [
4]. RNN fulfill the universal approximation properties and allow the identification of dynamical systems in form of high dimensional, non-linear state space models [
5]. Simple in architectures with sophisticated learning algorithms, they have emerged as one of the first class candidates for modeling dynamical systems [
6]. The benefits they offer to deal with the typical challenges associated with forecasting in general, make them suitable for learning non-linear dependencies from observed time series data [
7].
Throughout the training process, RNN rely on external inputs, which make them suitable for the modeling of open dynamical systems. However, they assume constant environmental conditions as from present time on, which make them temporarily inconsistent [
7]. HCNN do not have this inconsistency between past and future modeling. Introduced by [
8], HCNN is based upon the assumption that dynamical systems must be seen in a context of large systems in which various (non-linear) dynamics interact with each other in time. HCNN do not only model the individual dynamics of interest, but also the external drivers in the same manner, by embedding them in the dynamics of a large state space [
8].
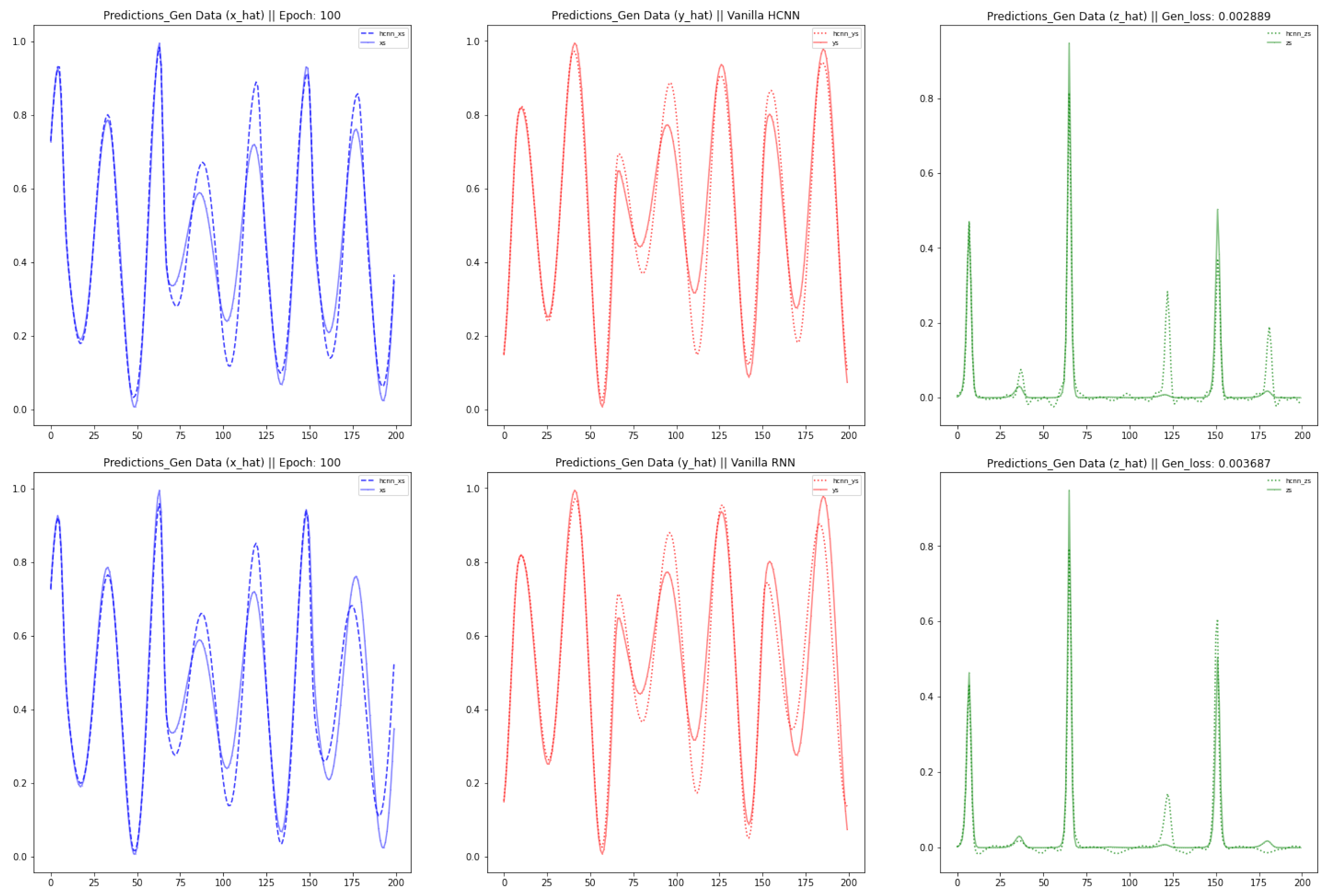
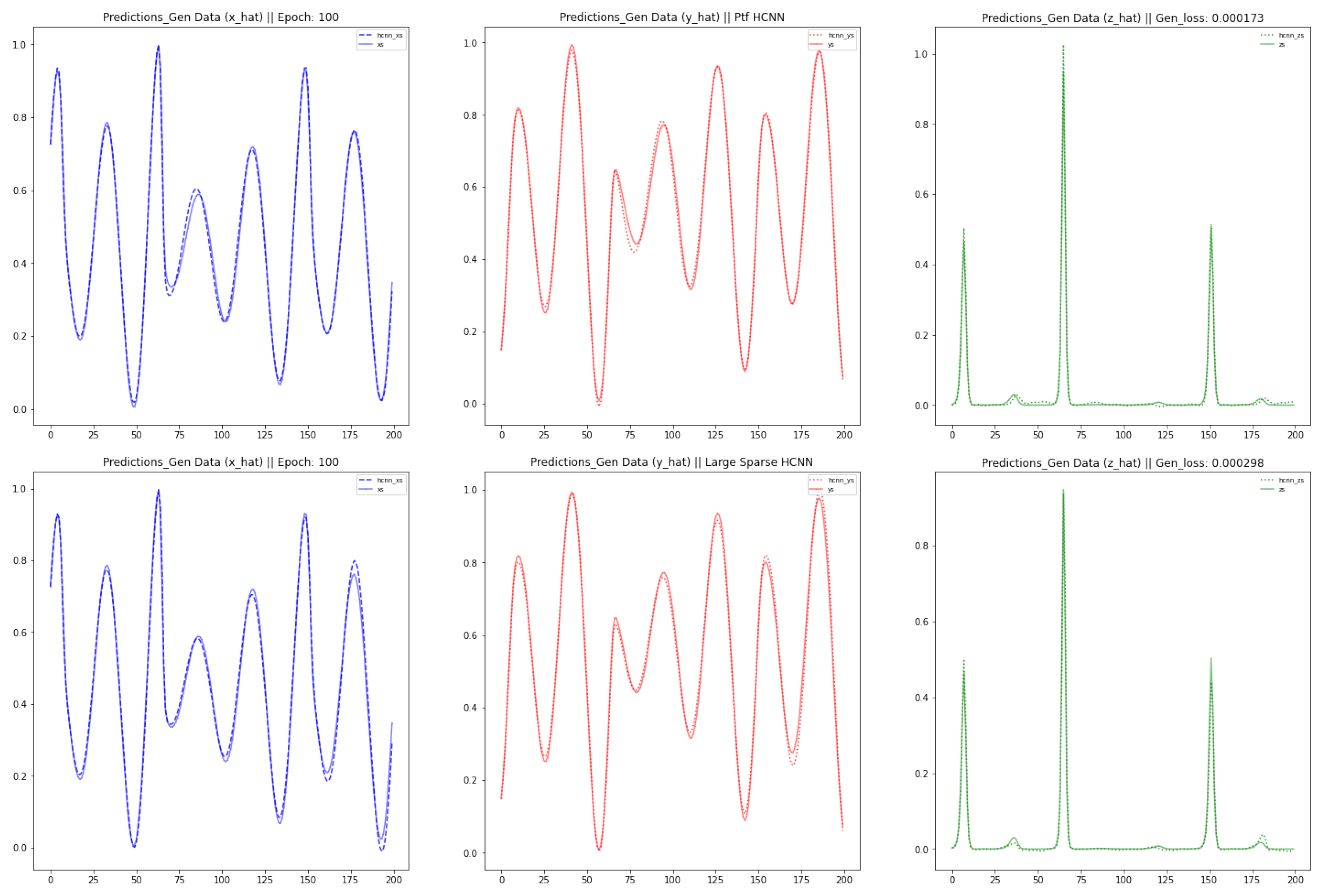
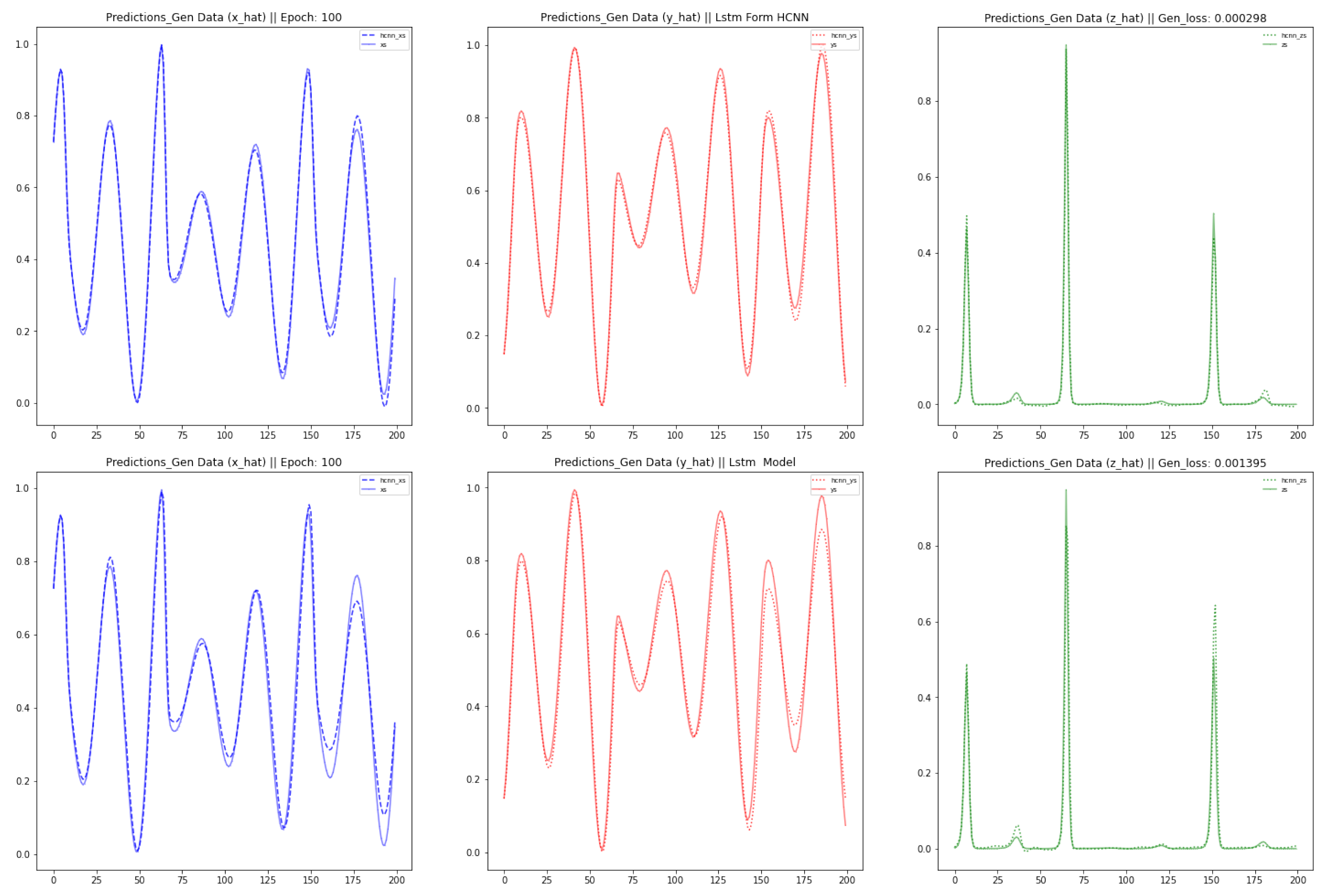
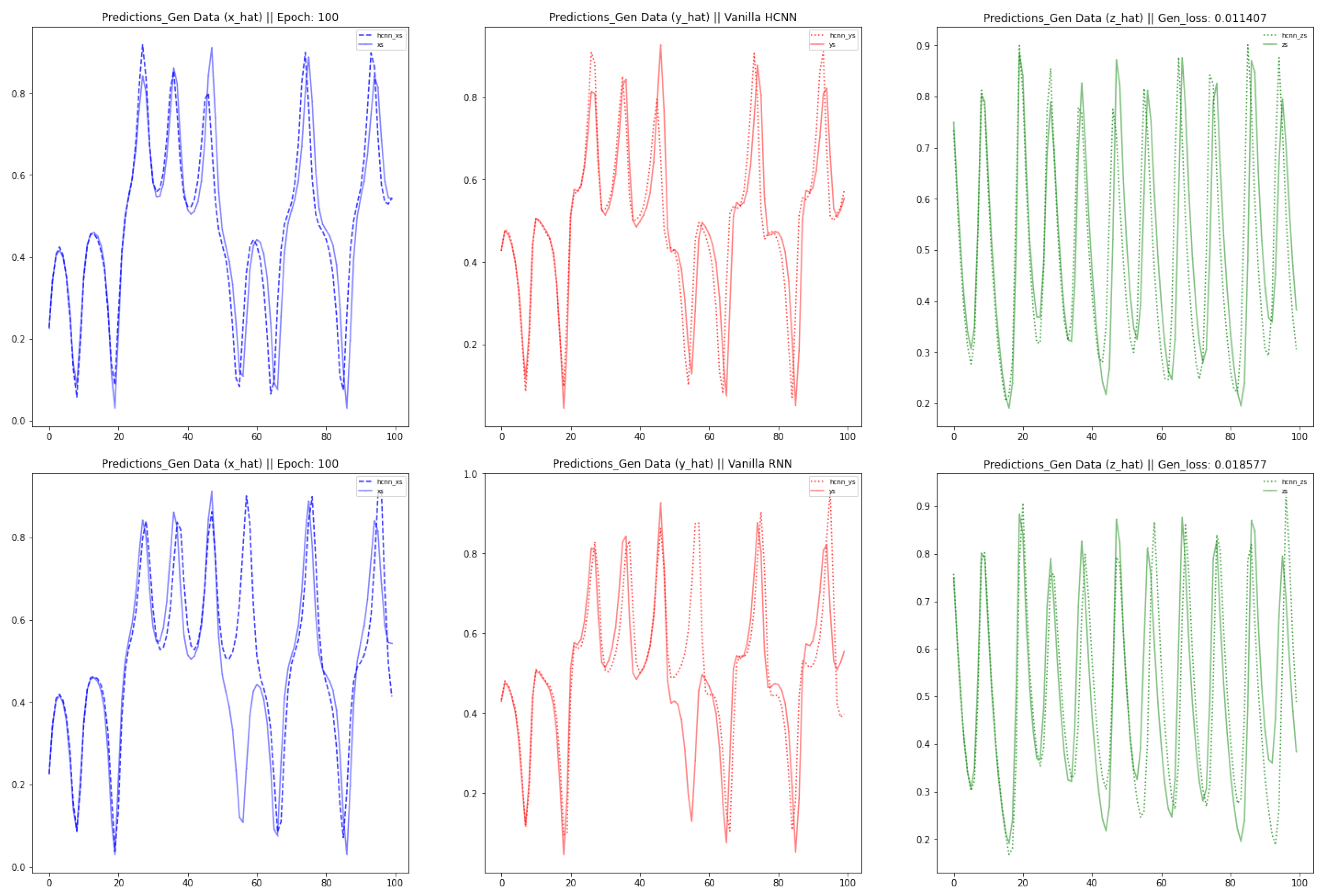
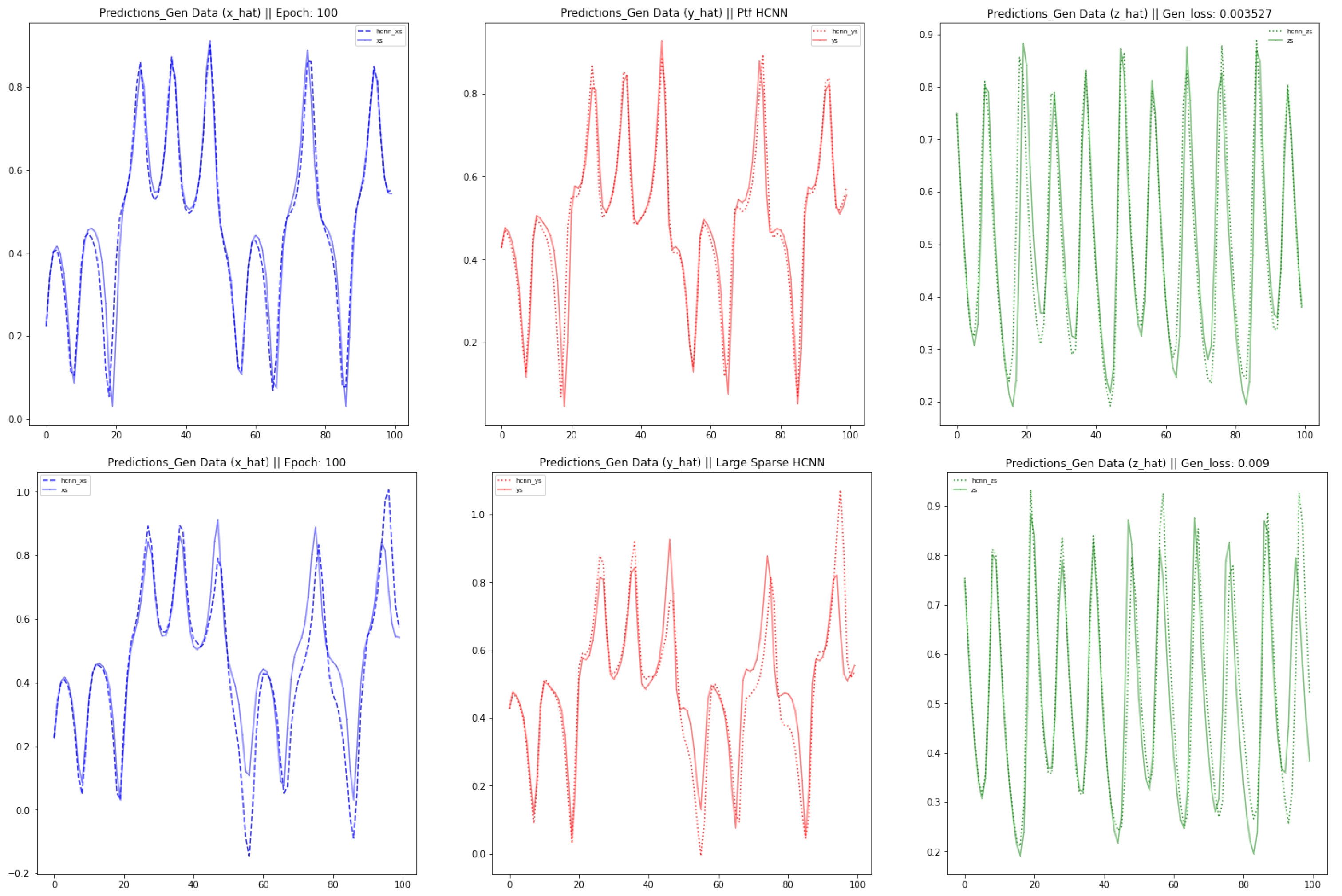
This paper brings about three contributions: Firstly, we modeled three well-known chaotic dynamical systems by the use of Vanilla HCNN: namely the Lorenz, the Rabinovich–Fabrikant and the Rossler Systems. Secondly, we improved the forecast accuracy and the length of the forecast horizon of the Vanilla HCNN using three methods: HCNN with Partial Teacher Forcing, HCNN with Sparse constraint on state transition matrix, and a Long Short Term Memory Formulation of HCNN. Thirdly, we ran a comparative analysis between those different strands of HCNN and well-known deep learning neural network models such as Vanilla Recurrent Neural Networks (RNN) and long-short term memory based model (LSTM). The rest of this paper is organized as follows.
The
Section 2 and
Section 3 provide respectively a review of the mathematical description of RNN and an architectural description of HCNN as well as its learning algorithm. In
Section 4, we discussed the intuition behind and the architecture of the different HCNN improvement methods. The focus of
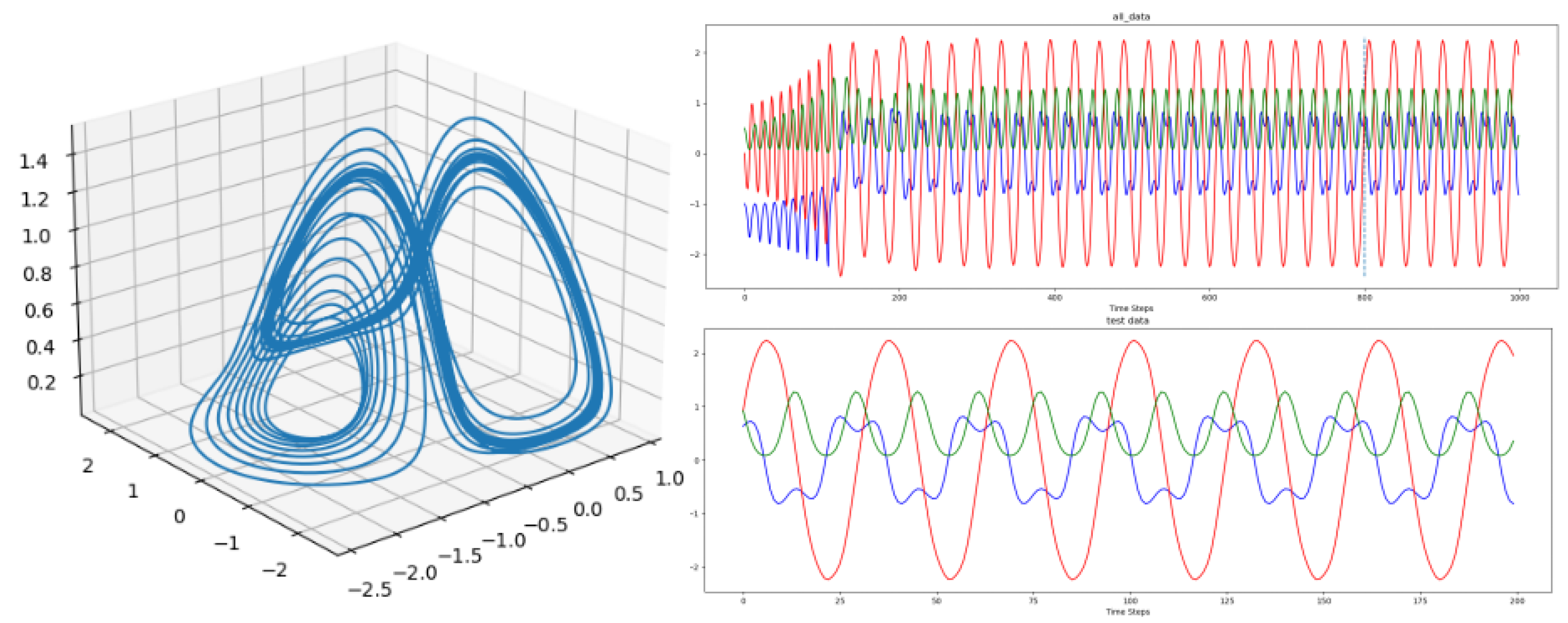
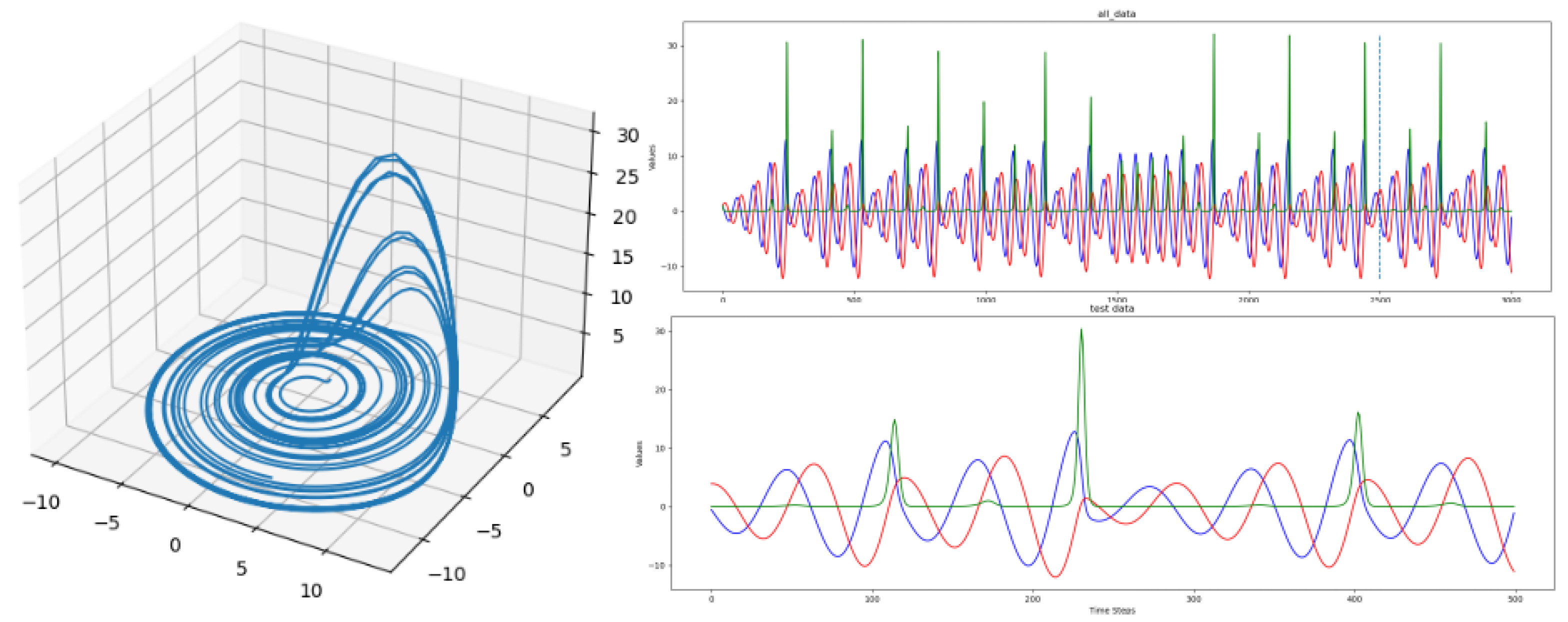
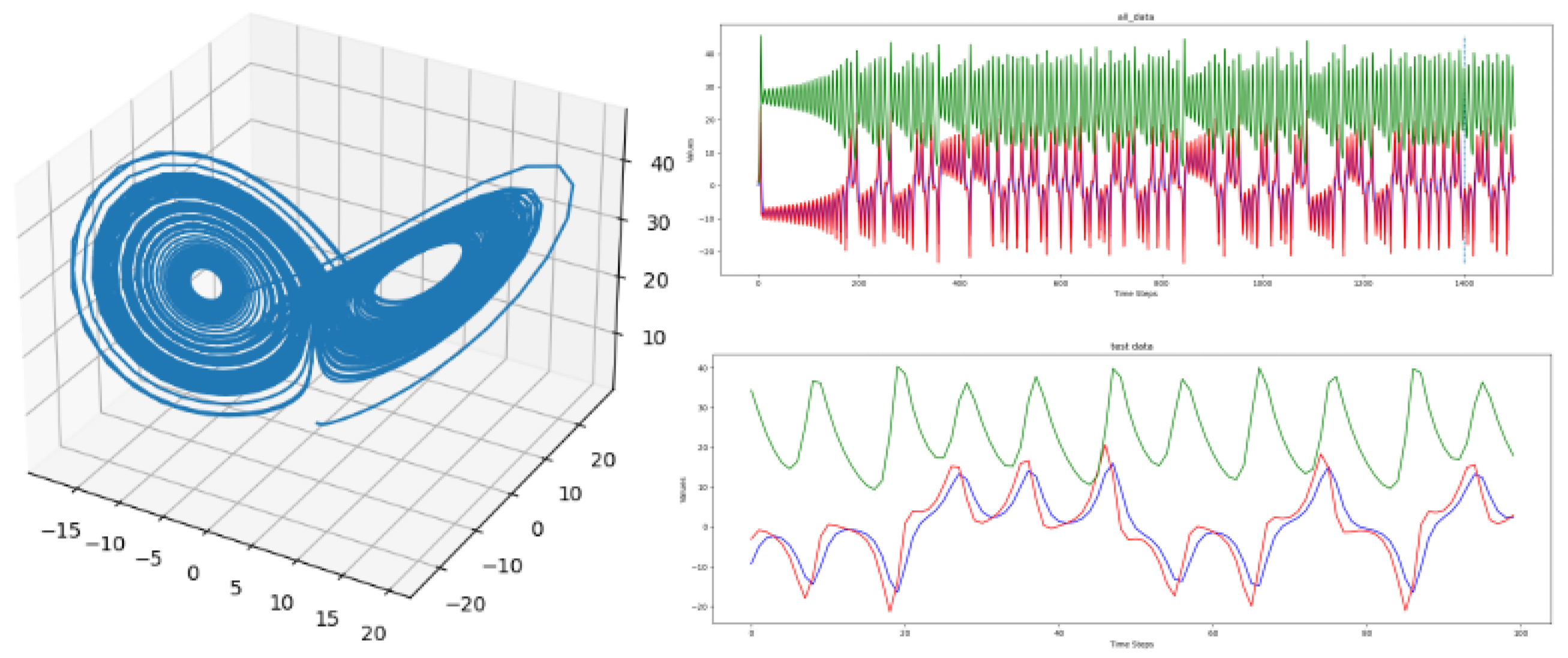
Section 5 is on the data generation of the three chaotic dynamical systems.
Section 6 shows the different results and comparative analysis between the pre-cited methods and the existing well-known recurrent neural networks namely RNN and LSTM. In
Section 7, we demonstrate that our results are reproducible for different HCNN instances. Finally, we present the conclusion and future work in the
Section 8.
2. Reminder of Recurrent Neural Networks for Dynamical Systems
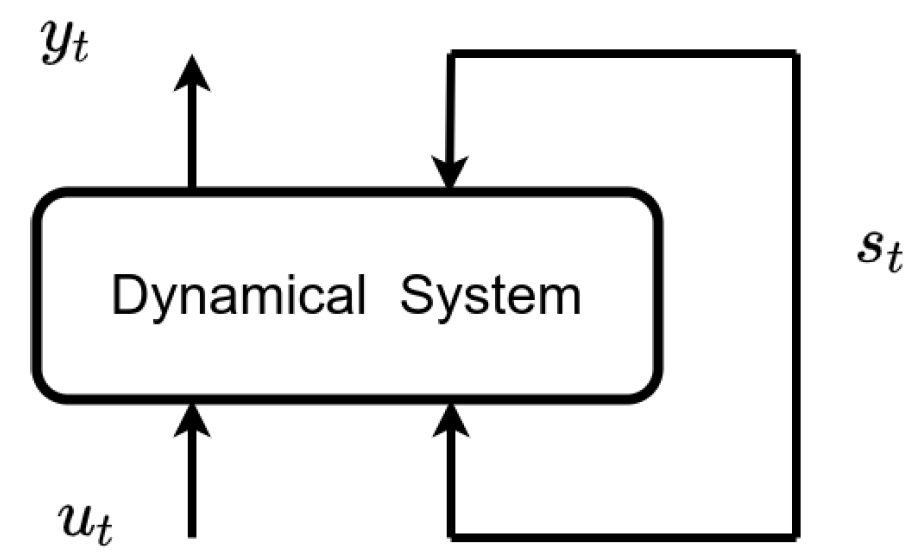
Let us consider, as in
Figure 1, a dynamical system driven by an external signal
.
Let us assume that, at each time
t, an output
is recorded. A dynamical system can be described for discrete time grids by a state space model, consisting respectively of a state transition and an output equation. The recursive Equation (
1) describes the current state of the system
with respect to the previous state of the system
and the external signals
. The expected output
is computed as a function of the current state of the system (
2). Key in the success of RNN, is their ability to generalized well, due to the fact that it is trained using parameter sharing [
9]. Without loss of generality, we can approximate the state space model with the state transition (
3) and the related output Equation (
4):
where
A,
B and
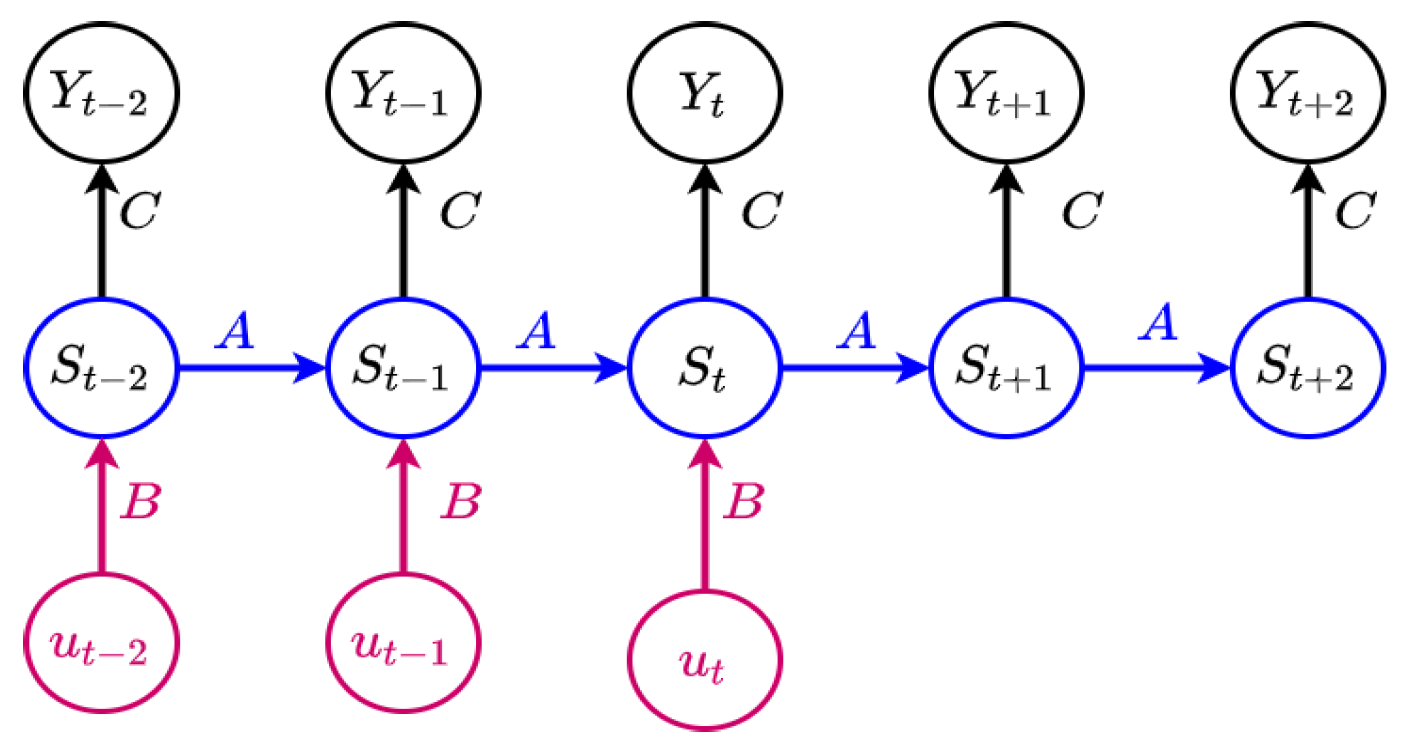
C are the weight matrices, respectively, for hidden-to-hidden, input-to-hidden and hidden-to-output connections. This makes a simple Recurrent Neural Network (RNN) with recurrent connections between hidden units across the whole time range [
4]. By performing a finite unfolding in time, we transform the temporal equations above into the spatial architecture as shown in the
Figure 2 above [
8].
The Vanilla RNN explains the dynamics observed on the
at each time point by splitting its complexity into two parts: the external driven part represented by the external influences
and the autonomous driven part (or hidden dynamics) represented by the internal states
. If the internal states of the system play an important role into understanding the dynamics of the observables, then an overshooting extends the autonomous part of the system several steps in the future and enable a reliable forecast of the
. For a given sequence of
and computed
values, we pair the corresponding observed values
and find the optimal set of shared parameters (the matrices
A,
B and
C) by solving the following optimization problem in the Equation (
5) here after [
7]:
The training of the RNN can be conducted using the error-back-propagation-through-time (BPTT) algorithm. This is a natural extension of standard back-propagation that performs gradient descent on a network unfolded in time. More details on BPTT are given in [
4]. However, despite its success over the past years, and especially on short term forecasts, the missing external inputs
in the future (which can be interpreted as a constant environment, i.e.,
), makes a vanilla RNN temporarily inconsistent [
7].
3. Historical Consistent Neural Networks
The HCNN were designed to address the temporal inconsistency in RNN. A dynamical system is often viewed in the context of large systems in which various (non-linear) dynamics interact with one another in time. However, we can only measure/observe a small subset of those variables. Therefore, HCNN reconstruct (at least part of) the hidden variables in order to understand the dynamics of the whole system [
7,
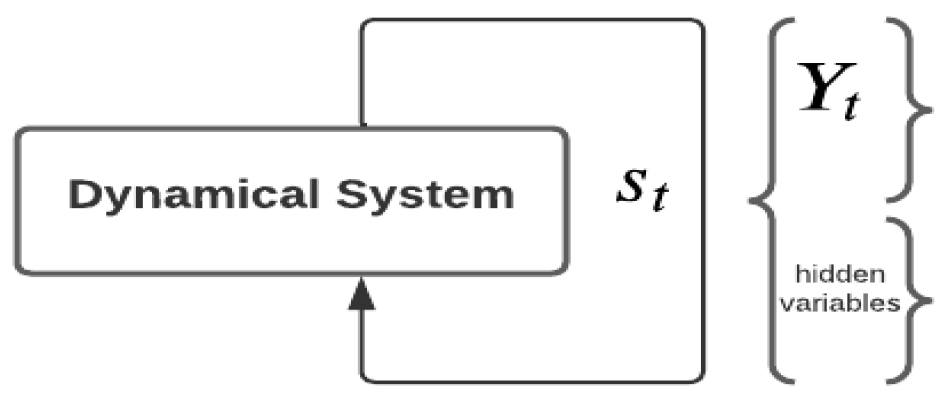
10]. Here the input and output variables are combined and termed as observables (
). Together with the hidden variables, they form the state of the system at each time
(see
Figure 3) and are treated by the model in the same manner. The corresponding state transition Equation (
6) and output Equation (
7) are also provided below.
The joint dynamics for all observables is characterized in the HCNN by the sequence of states
. The observables
are arranged on the first
N state neurons of
and followed by non-observable (hidden) variables as subsequent neurons. The object
is a fixed matrix that reads out the observables from the state vector
[
7]. At the initial time, the state
is described as a bias/random vector and the matrix
A contains the only free parameters [
7].
Similar to a standard RNN, HCNN fulfils the universal approximation theorem, as highlighted in [
7,
10]. However, the lack of any input signals and an unfolding across the complete data makes it difficult to train in practice [
8]. As proposed by [
4], the models that have recurrent connections from their outputs leading back into the model may be trained with teacher forcing.
This is a procedure that emerges from the maximum likelihood criterion. It makes the best possible use of the data from the observables and therefore accelerates the training of the HCNN [
2,
10]. Throughout the fitting procedure, the teacher forcing mechanism introduces a hidden layer
that is a copy of the internal state
, with the exception that its first
N components which correspond to the computed expected values
are replaced with the observed values
as shown in the Equation (
8).
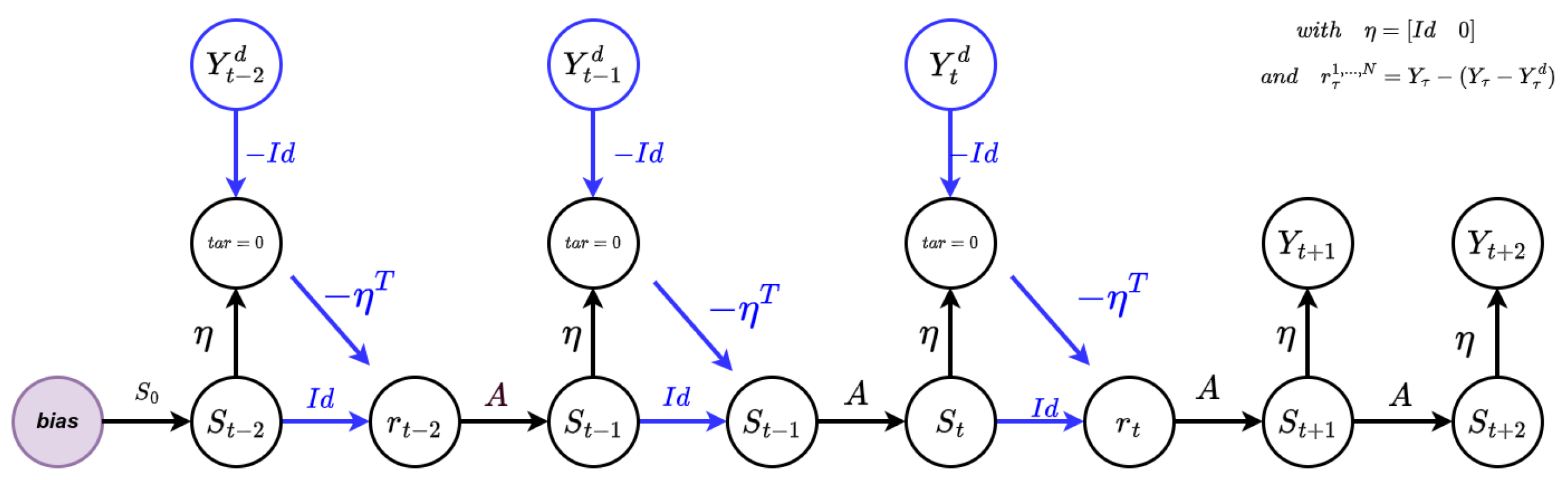
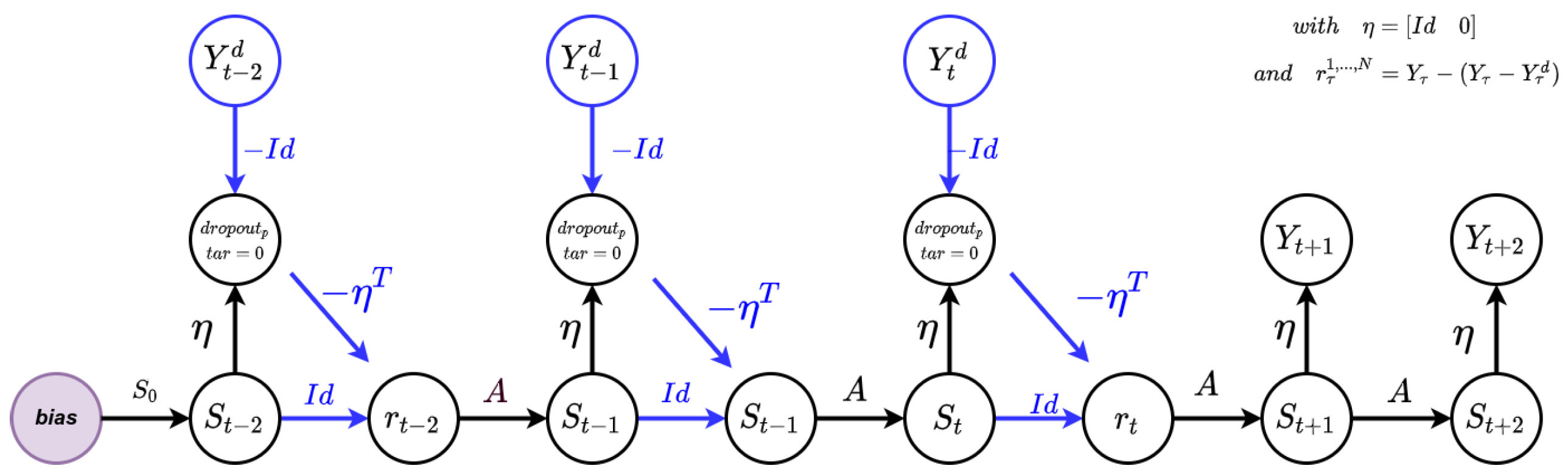
From the temporal equations above, we can also derive its spatial representation, through the resulting network architecture of the HCNN with integrated teacher forcing mechanism as illustrated in the
Figure 4 below.
At each time
t during training, the output layer of the HCNN is replaced by a cluster that is given a fixed target value of zero. This forces the HCNN to create the expected values
at each time
t, to compensate for the negative observed values
coming from the top node [
8]. The content of that cluster, i.e.,
, with a minus symbol is transferred to the upper part (the first
N neurons) of the hidden layer
. Furthermore, a copy of the state
is also transferred to the intermediate hidden layer
on a component-by-component basis. As a result of that, the expected values
on the first
N components of the hidden layer
are replaced by the observed values [
8] and the subsequent state
is computed using the state transition Equation (
9).
4. Long-Term Memory Improvement Methods
To improve the long-term memory of the Vanilla HCNN model, three different improvement methods have been designed: HCNN with Partial Teacher Forcing, with Large Sparse State Transition Matrices and a Long Short-Term Memory Formulation. The intuitions behind each of the methods are shown below.
4.1. HCNN with Partial Teacher Forcing
To enforce the long-term learning of the HCNN, we endow the output layers of the HCNN with a dropout filter, guided by a probability, as illustrated in the Equation (
10).
At time
t, when the filter is activated (which means for a probability
p), the HCNN randomly suppress elements in the time series that come from the cluster containing the difference between expectations and observations
. Thus, in the upper part (the first
N components) of the
vector, the network is enforced to replace the observations with its internal expectations. The architecture is represented in the
Figure 5 below.
4.2. HCNN with Large Sparse State Transition Matrix
HCNN may often use large state vectors to model large dynamical systems (number of observables > 100). During training time, the iteration with a fully connected state transition matrix A could cause an information overload, leading to two risks:
The matrix–vector computation between A and , which includes the addition of randomly generated (and learned) scalar values will likely blow up to infinity (∞).
The superposition of additional information brought in by the large dimensionality of A could destroy the longer memory information acquired throughout.
In order to overcome that, we can choose to set the transition matrix
A sparse to a chosen degree. As a result of that, the spread of the information peak through the network is damped by the sparsity too. Another approach, as proposed by [
7], consists of a heuristic approach that represents the sparsity of
A, as inversely proportional to the state dimensionality of the system, as shown in the Equation (
11) below:
4.3. HCNN with LSTM Formulation
The third approach to improve the long-term memory of the vanilla HCNN is through an exponential smoothing embedding of the HCNN with a learnable diagonal matrix [
11], subject to the following constraints
. The resulting state transition Equation (
12) and output Equation (
13) are provided below:
where
Built upon the ideas of the LSTM formulation of RNN [
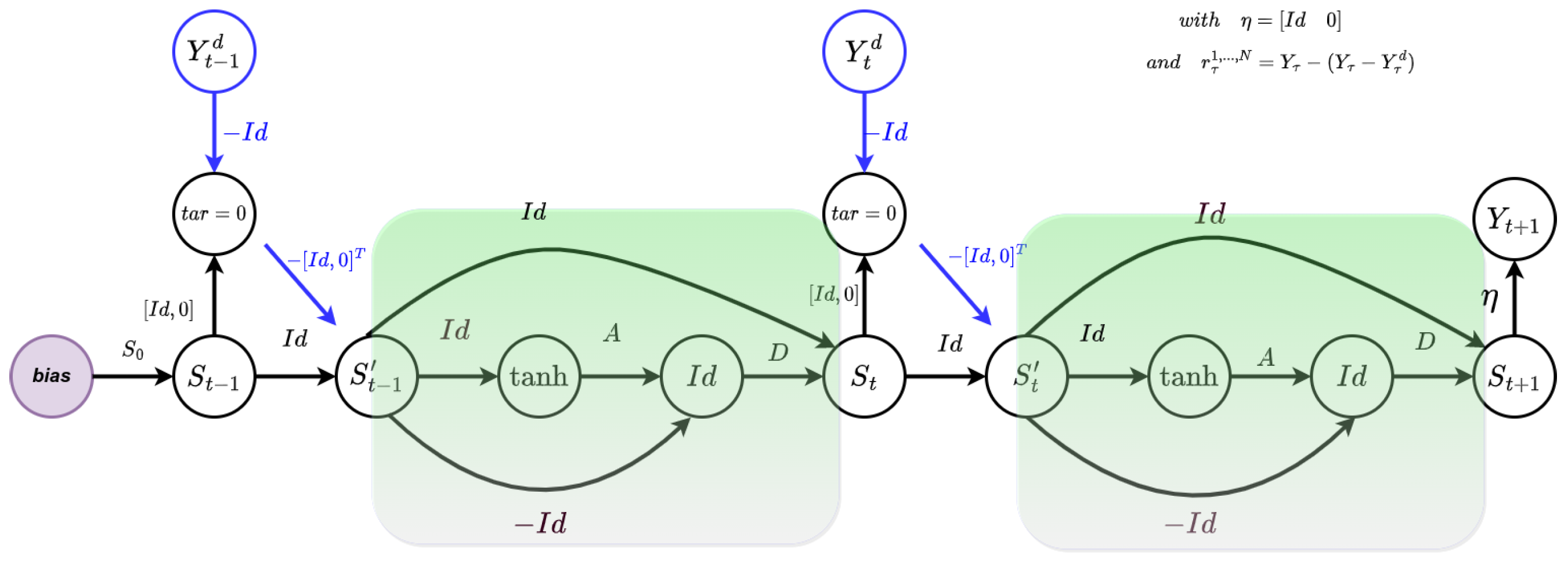
12], the resulting architecture of the LSTM formulation of HCNN is provided in the
Figure 6 below.
The next section will focus on the different dynamical systems that will be used to generate the data for the fitting procedure of the HCNN models.
7. Ensemble Computations
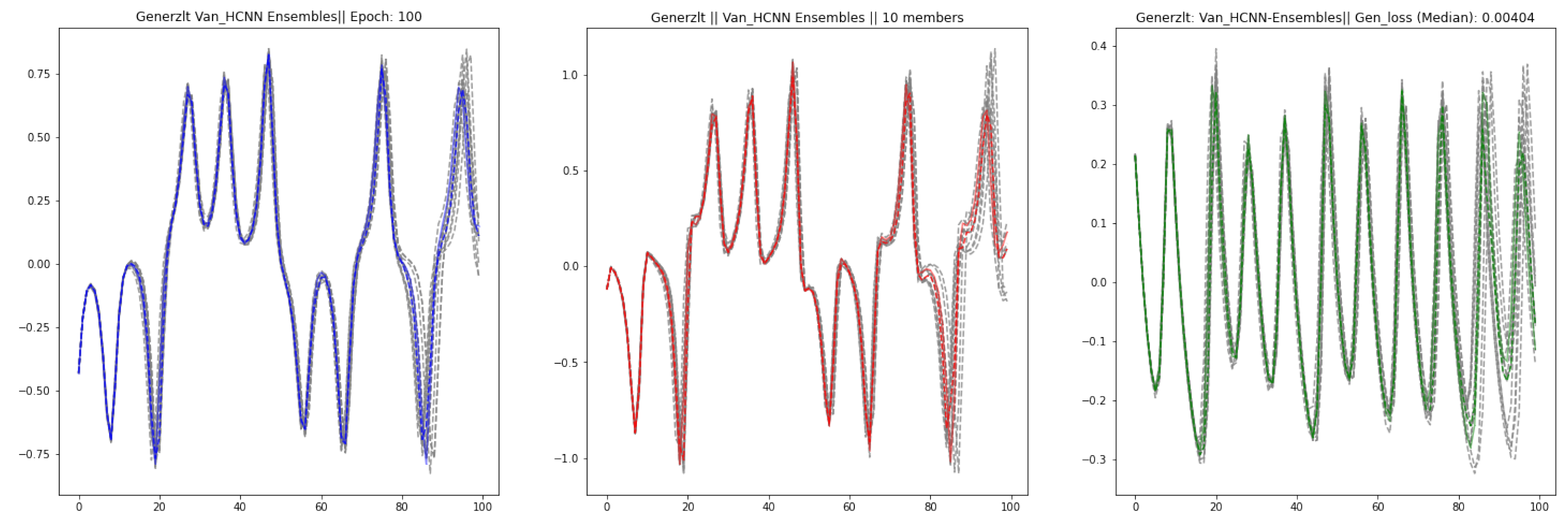
To ensure that our results are reproducible, we instantiate an ensemble of HCNN with 10 members and train them simultaneously to forecast the dynamics of the Lorenz system. The
Figure 19 below consists of both the actual observations and the 10 instances of the HCNN model, and median of the ensembles.
Looking at the picture above, we can see that for the 10 different instances of Vanilla HCNN, the shape of the three time series are preserved. At each time step, we computed the median and average out of each the 10 forecasts. The result we obtained show a balance between both generalization errors with the values being respectively for the ensemble’s median forecast and for the ensemble’s average forecast. This shows that HCNN are able to model High dimensional non linear systems in a consistent way and that both the ensemble’s median and average forecast are also reliable candidates for the forecast the dynamics of such systems.
8. Conclusions
Throughout this paper, we have seen that HCNNs are able to model High dimensional deterministic non linear systems in a consistent way. The different improvement methods have been instrumental in enforcing a long term learning of the dynamics of the multivariate time-series generated from the Lorenz, the Rossler and the Rabinovich-Fabrikant Systems. Among the three improvement methods, measuring by the generalization error, the Partial Teacher Forcing method is the superior way to improve both the long memory and the extent of the forecast horizon. The Large Sparse HCNN method is mostly aligned to biological methods. The LSTM Formulation Method has a linear sub-structure to overcome the vanishing/exploding gradient problems which sometimes creates numerical instability. The results obtained from the ensemble computation graphically show that the shape of the three time series are near each other throughout the whole forecast horizon. Hence, this shows that for different instances of HCNN, the results are ensured to be reproducible. Moving forward, it is worth noting that the datasets were generated mathematically. This gives to those dynamical systems the attribute of fully observables. Since the final goal of this ongoing research is on the analysis of climate data, those are rather high-dimensional and noisy measurements: such kind of system are called partially observables.There is currently a work in progress to extend these techniques to wind forecasting as a basis for wind turbine control. Analysing such systems will require transferring the long memory insights gained from this experiment to that new task. Furthermore, the identification of the optimal HCNN meta-parameters and the formulation of additional improvement techniques for the learning of HCNN will also be probable directions to look at. On another hand, the ensemble forecasts (median and average of the ensemble forecasts) seem to be a promising direction to navigate into, for such forecasting exercise.