Analysis of the Two-Stage Phenomenon and Construction of the Theoretical Model for Metal Hydride Reactors ^†

Abstract

The metal hydride (MH) reactor serves as the core unit of hydrogen storage systems, with its reaction performance limited by heat transfer rates. Effective enhancement of reactor heat transfer performance can only be achieved through a fundamental understanding of the reactor’s hydrogen–thermal coupling mechanism. The reaction process within the reactor typically exhibits two distinct stages, a characteristic frequently disregarded in previous theoretical models. Through numerical simulation and analysis, the two-stage phenomenon and its associated hydrogen–thermal coupling mechanism were first quantitatively investigated. Based on the assumptions of neglecting the first-stage reaction time and maintaining bed thermal equilibrium, a novel two-stage theoretical model (a quantitative analytical model) was developed. This model successfully characterizes the internal hydrogen–thermal coupling and reaction progress. Having been numerically validated, the new model achieves a prediction accuracy of 2% for reaction rates, significantly outperforming the original reaction front model’s 25.5% error margin.

1. Introduction

Theoretical models of metal hydride (MH) reactors can predict the reaction completion time for specific bed thicknesses, serving as practical tools for designing reactor dimensions under given operating conditions [1,2]. Understanding the internal thermal–hydrogen coupling mechanism is crucial for effective thermal management in reactor design. Previous studies have analyzed the reaction front phenomenon and confirmed the existence of a two-stage process in MH reactors [3,4]. Furthermore, the heat transfer rate has been identified as the rate-limiting factor for the reaction kinetics, leading to the development of analytical theoretical models based on this finding. However, the specific mechanisms underlying the bidirectional thermal–hydrogen coupling in MH reactors remain unclear. Existing analytical models, such as the reaction front model [5,6] and thermal diffusion model [7,8], primarily describe the heat transfer controlled second stage of the reaction, while lacking quantitative characterization of the first stage involving uniform reaction and temperature rise. Therefore, it is essential to investigate and quantitatively analyze these stages to develop corresponding quantitative theoretical models for a more systematic understanding of reactor performance.

2. Numerical Model

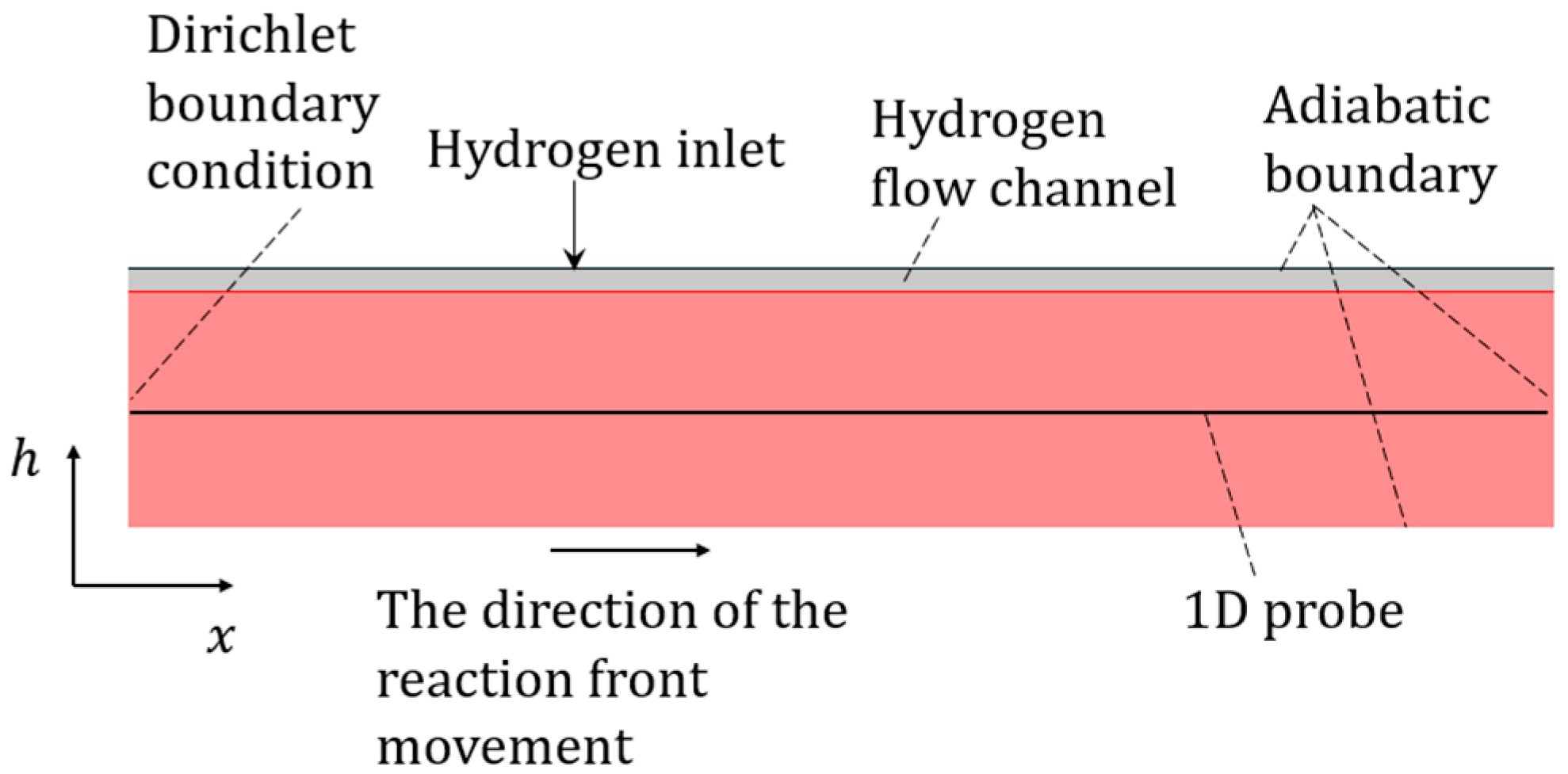
2.1. Geometric Model

To facilitate the analysis of the internal thermal–hydrogen coupling characteristics within the reactor, a numerical model of a simple rectangular MH reactor was constructed. The geometric model of the reactor has a length of 0.06 m and a height of 0.012 m. The reactor is filled with an MH bed layer with a height of 0.02 m, while a free space of 0.005 m in height is maintained at the top to serve as a hydrogen flow channel, as illustrated in Figure 1. The commonly used LaNi5 material was selected as the MH material, and 1060 aluminum alloy was used for the reactor wall. The main parameters used in the simulation can be found in our group’s prior work [9].

2.2. Model Assumptions

• Heat conduction is the dominant mode of thermal transfer in the reactor model, with zero contact thermal resistance between the bed and the wall.
• The thermophysical properties of the metal hydride (MH) and hydrogen remain constant and isotropic.
• Local thermal equilibrium is maintained between hydrogen and the MH bed (porous medium).
• Pressure drop induced by hydrogen flow is neglected.
• Heat dissipation from the outer wall to the environment is ignored.

2.3. Basic Setup

As shown in Figure 1, the thermal boundary conditions for the MH reactor are defined as follows: the left wall is subjected to a Dirichlet boundary condition with a constant temperature of 283 K, while the remaining boundaries are adiabatic. The initial temperature of the MH bed is set to 294 K (ambient temperature), at which the equilibrium reaction pressure is 0.15 MPa. The hydrogen charging pressure of the reactor is 2 MPa.

The numerical model was implemented using the finite element analysis software COMSOL Multiphysics 5.6. The backward differentiation formula (BDF) method was employed for equation discretization, with key equations discretized to second-order accuracy. Experimental data from a water-cooled reactor [10] were used to validate the model’s accuracy, and the results [9] confirmed the reliability of the model.

3. Simulation Results and Discussion

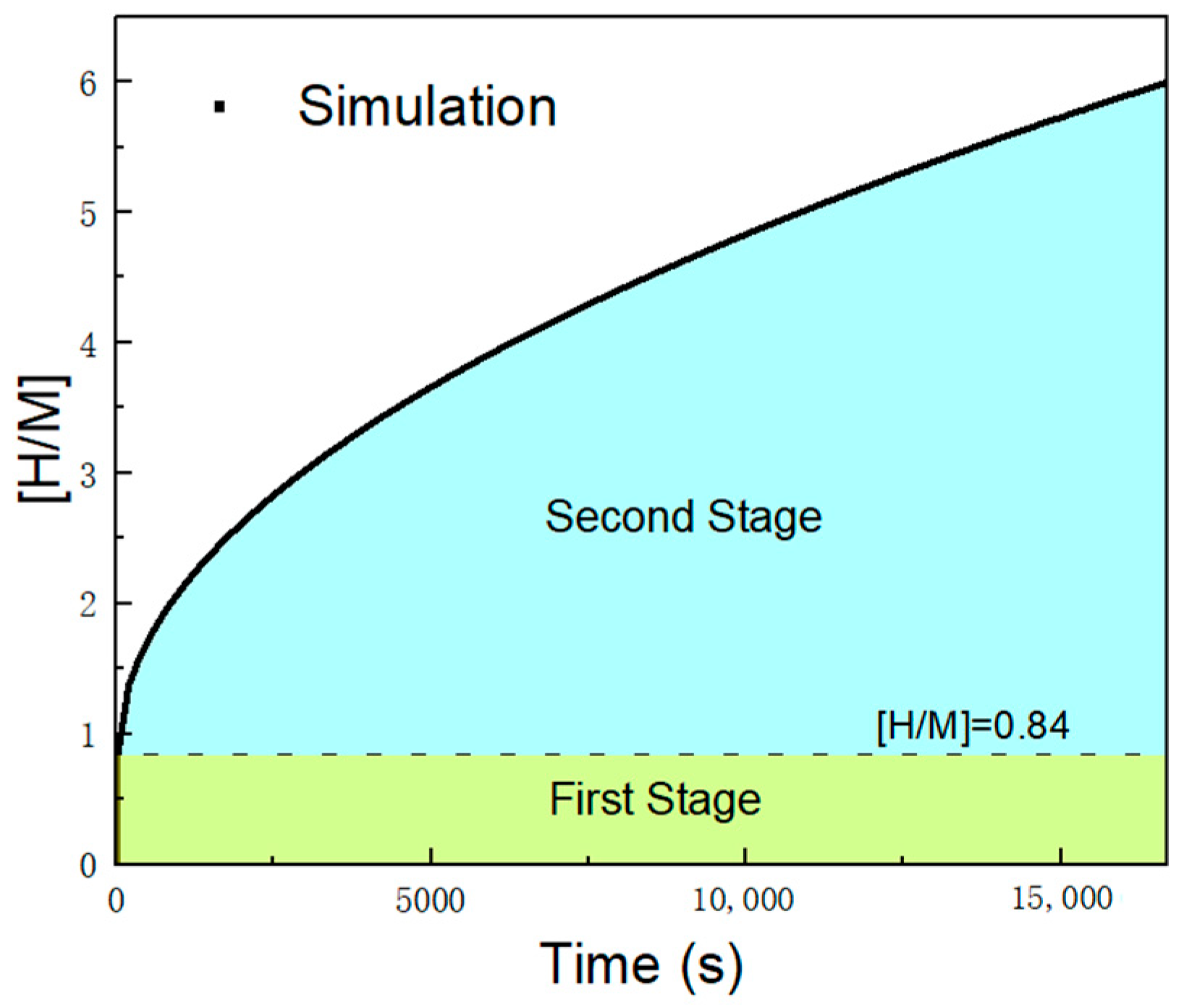
3.1. Variation of the [H/M] Ratio over Time

The key hydrogen absorption characteristics of the MH reactor in practical applications were first considered, with analysis focused on the temporal evolution of the hydrogen-to-metal atom ratio [H/M] (hereinafter referred to as the hydrogen ratio), as shown in Figure 2. Previous studies [4] have found that during the first reaction stage, the [H/M] ratio increases rapidly throughout the reactor, indicating highly efficient hydrogen absorption/desorption in the early reaction period. At this stage, the reaction is governed by the initial temperature and pressure, with heat transfer exhibiting negligible influence on the process. The simulation results in this work also show that in the early reaction phase, the [H/M] ratio in most regions of the bed quickly rises to 0.84 and then stabilizes, corresponding to the first reaction stage. The hydrogen ratio of 0.84 at the end of the first stage is marked in Figure 2, clearly illustrating the two-stage phenomenon reported by researchers [3,11]. The reaction curve exhibits two stages: in the first stage, the MH material reacts rapidly, and the [H/M] ratio increases to approximately 0.84; in the second stage, the reaction rate gradually decreases, and the growth of the [H/M] ratio slows down, following a power-law function with an exponent less than 1.

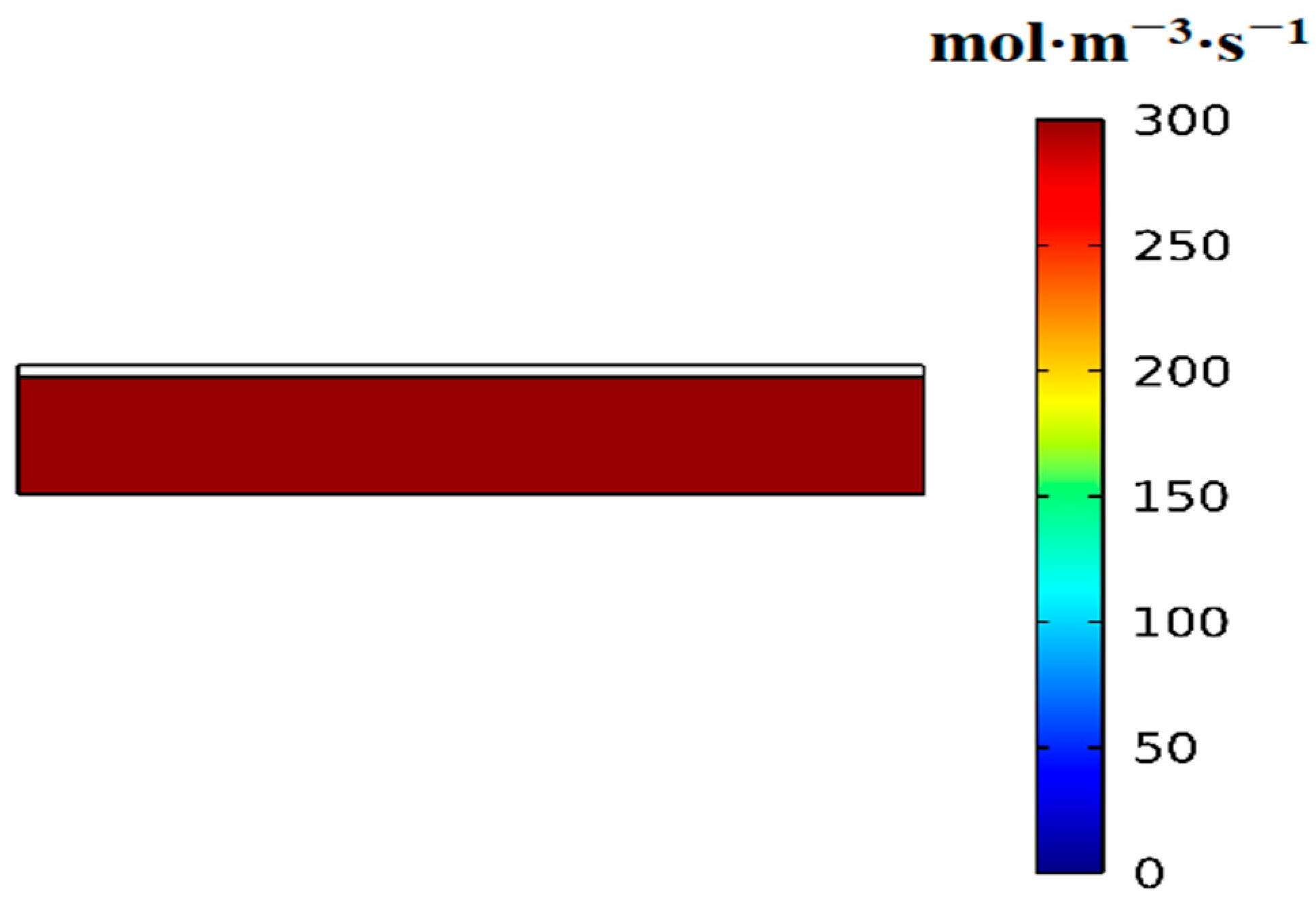
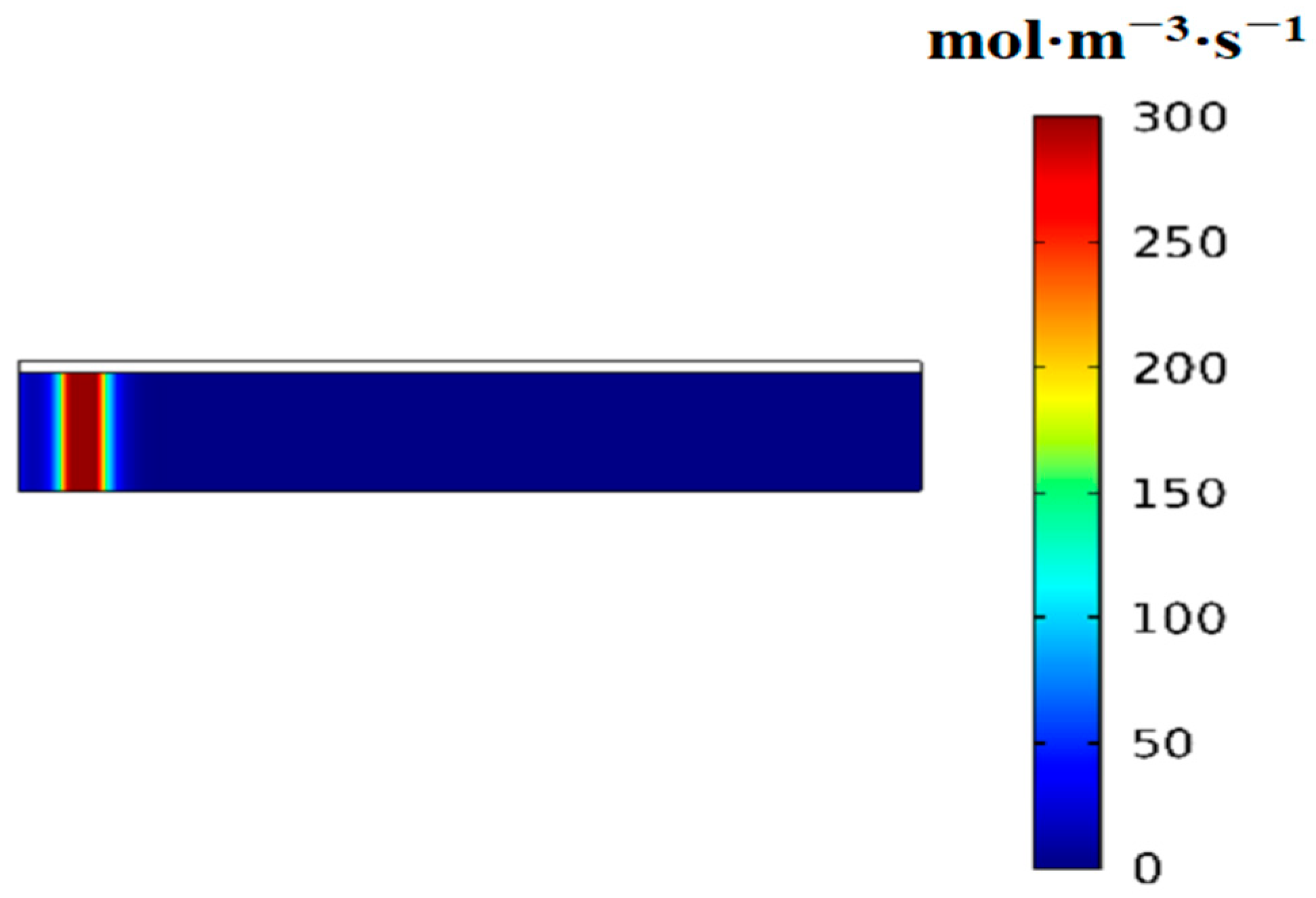
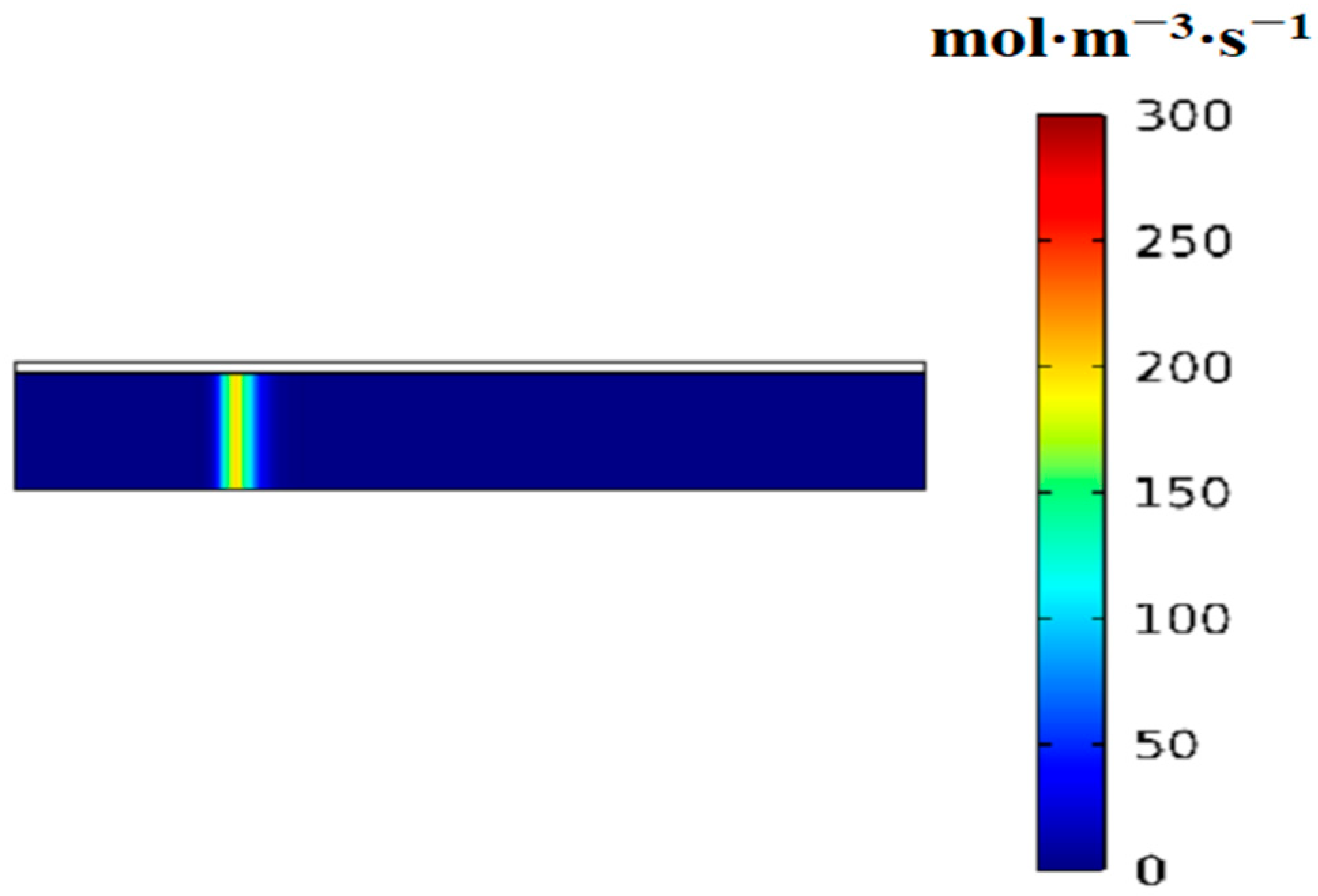
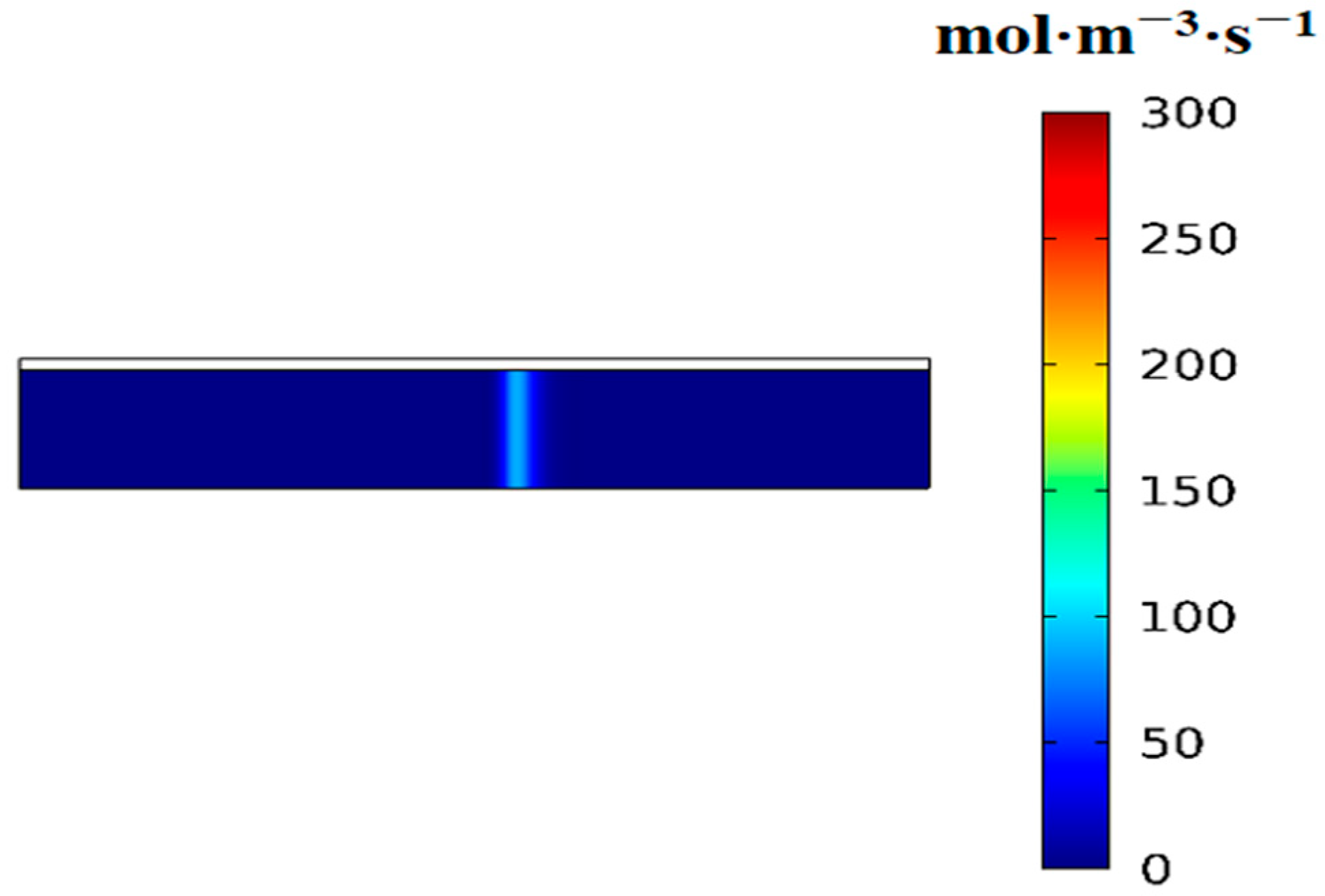
3.2. Variation of the Volumetric Reaction Rate over Time

Figure 3, Figure 4, Figure 5 and Figure 6 show the variation of the volumetric reaction rate within the bed of the MH reactor. At t = 1 s, the bed exhibits a clearly uniform and rapid reaction state, with the reaction occurring throughout the entire bed.

As time increases to 100 s, 1000 s, and 5000 s, the reaction becomes concentrated in a narrow region, which progressively moves toward the adiabatic boundary in the direction perpendicular to the heat exchange boundary. From the variation of the reaction region over time in Figure 4, Figure 5 and Figure 6, the center of the reaction region is located at 0.0045 m, 0.015 m, and 0.033 m at 100 s, 1000 s, and 5000 s, respectively. As the reaction region penetrates deeper into the bed, the bed material gradually undergoes reaction. Analysis of the numerical results indicates that near the end of the reaction at t = 16,000 s, the reaction region is precisely located at the adiabatic boundary (x = 0.06 m). This demonstrates a one-to-one correspondence between the position of the reaction region and the reaction progress. Therefore, theoretically determining the location of the reaction region can indirectly estimate the reaction progress. Given that the reaction region is relatively narrow and exhibits significant changes in reaction states ahead of and behind it, many studies model it as a zero-thickness reaction front. This assumption is also adopted in the present work.

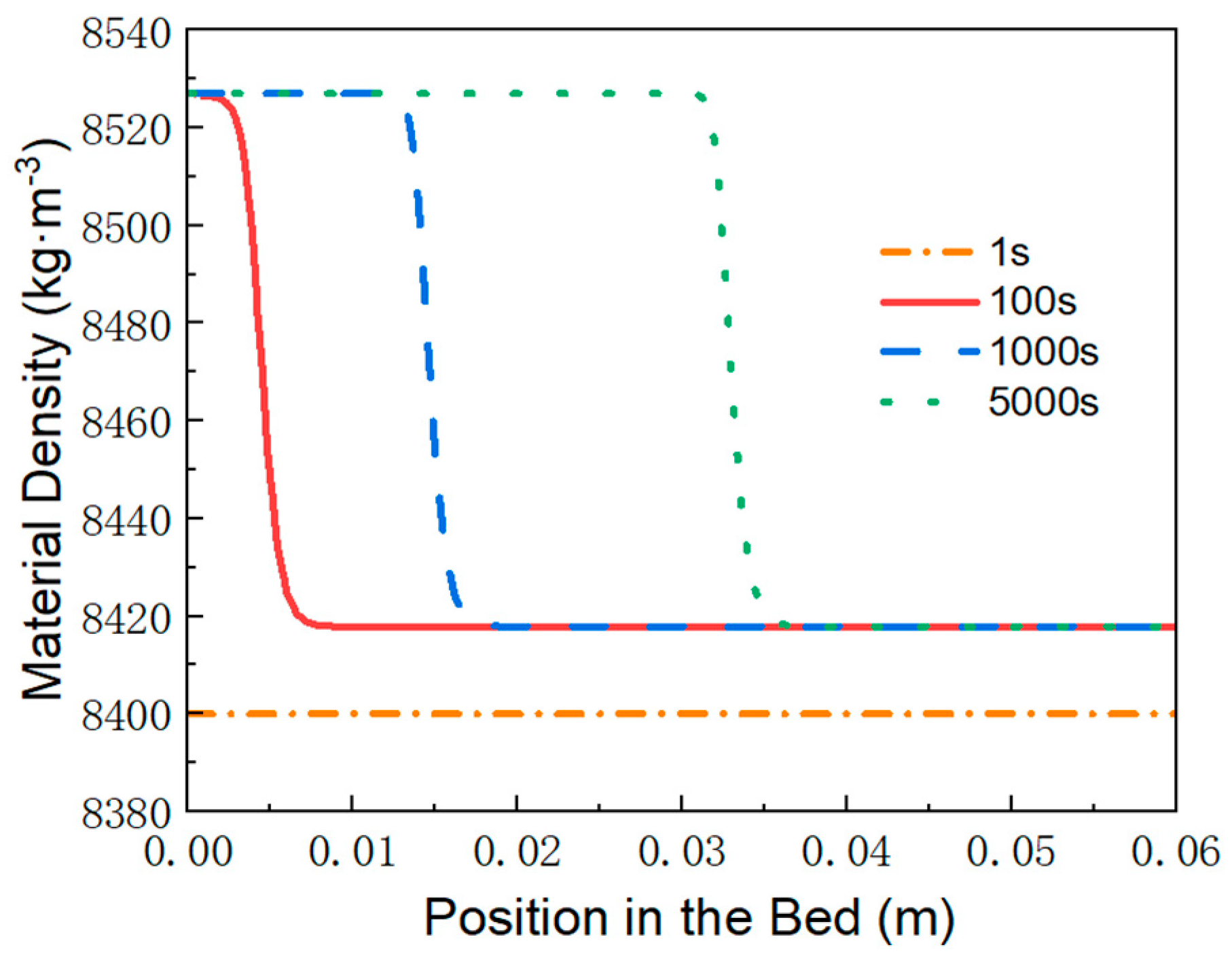
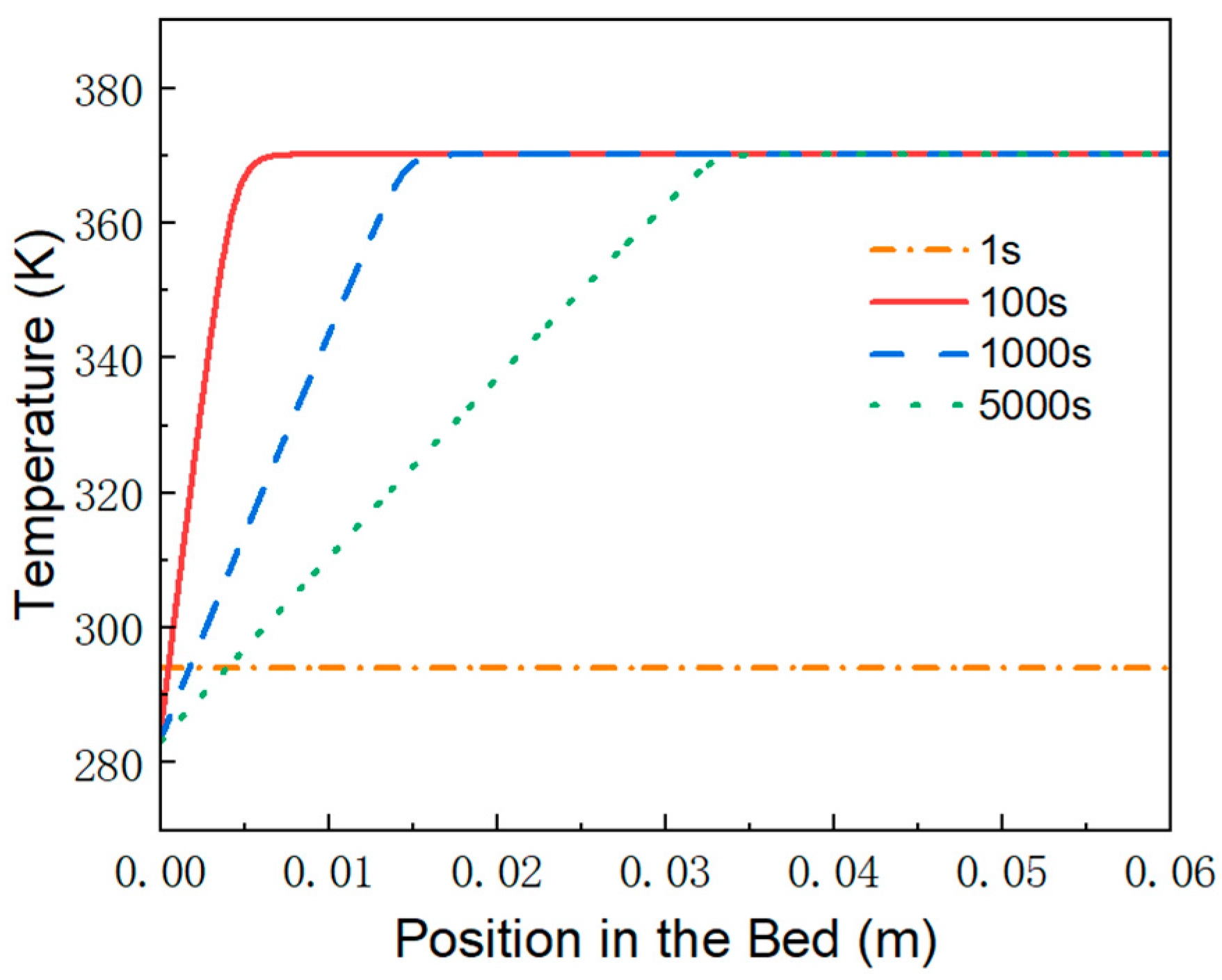
3.3. Variation of Material Density, Temperature and Heat Flux over Time

To facilitate intuitive analysis of the material density, temperature and heat flux variation within the bed, a one-dimensional probe was added along the direction of reaction front propagation, as shown in Figure 1. The temporal variation of the MH material density at various locations along this probe is shown in Figure 7. At 100 s, 1000 s, and 5000 s, an abrupt change in density occurs along the propagation direction of the reaction front, with the location consistent with the previously identified center of the reaction region (i.e., the front position) in Section 3.2.

As observed in Figure 8, which shows the temperature distribution over time at different positions along the one-dimensional probe, the slope of the temperature profile also undergoes a distinct change at the reaction front location in 100 s, 1000 s, and 5000 s, shifting from a positive value to near zero. The fact that both the density and temperature gradient change abruptly at the same position confirms a one-to-one correspondence between the material reaction state and the thermal distribution.

It is worth noting that, at a given time, the temperature profile remains almost linear from the heat exchange boundary to the reaction front, indicating a constant temperature gradient. Since both the cross-sectional area for heat transfer and the effective thermal conductivity remain unchanged, the heat flux should also be nearly constant. As shown in Figure 9, at 100 s, 1000 s, and 5000 s, the heat flux drops rapidly from a positive value to zero at positions of 0.0045 m, 0.015 m, and 0.033 m, respectively. These results corroborate the findings in Figure 8 and demonstrate a significant change in heat transfer state across the reaction front, which can be regarded as a moving thermal boundary.

Notably, the temperature rise caused by the first-stage reaction determines the initial temperature across most of the bed in the second stage. The temperature difference between the bed and the wall represents the maximum thermal driving force throughout the heat transfer process, governing the propagation speed of the reaction front and the overall reaction rate in the second stage.

As shown in Figure 9, the heat flux remains almost constant within the bed from the heat transfer boundary to the reaction front. The heat transferred from the bed to the surroundings is partly consumed by the hydrogen absorption reaction and partly stored as sensible heat due to temperature changes in the bed. Taking the heat flux curve at 5000 s in Figure 9 as an example, the heat flux decreases from 2970 W·m⁻² to 2669 W·m⁻² between 0 m and 0.031 m. This decrease is attributed to changes in the sensible heat of the bed, where the heat flux is defined as positive when transferred from the bed to the external environment. As the reaction front moves, the temperature distribution in the reacted region changes, altering the sensible heat storage and consequently affecting the heat flux distribution within the bed.

Between 0.031 m and 0.035 m, a narrow reaction region is observed, where the heat flux drops rapidly from 2669 W·m⁻² to 0. This sharp decline reflects the influence of the reaction heat at the front, indicating that the heat released by the hydrogen absorption reaction significantly alters the heat flux distribution. The variation in heat flux shown in Figure 9 demonstrates that the impact of reaction heat on the heat flux is far greater than that of sensible heat changes. This justifies the assumption in existing reaction front models [5,6] that neglect the effect of bed heat capacity.

Analysis of the simulation results reveals that most of the bed reaches approximately 370 K by the end of the first stage. Examination of the thermodynamic properties of the MH material (via the Van’t Hoff equation: $\ln (P_{\mathrm{eq}}/P_{\mathrm{ref}})=\mathrm{a}-\mathrm{b}/T$, where $P_{\mathrm{eq}}$ is the equilibrium pressure, $P_{\mathrm{ref}}$ is the reference pressure, T is temperature and both a and b are constants in the formula.) indicates that a hydrogen charging pressure of 2 MPa corresponds to a reaction equilibrium temperature of 370.21 K. This confirms that a uniform hydrogen absorption reaction occurs throughout the bed during the first stage and ceases once the bed temperature rises to the equilibrium temperature corresponding to the charging pressure.

By neglecting heat exchange with the external environment,, an overall heat balance of the bed shows that the sensible heat required to raise the bed temperature is approximately equal to the reaction heat released by the MH material during the first stage, i.e., $\Delta H\cdot X_1=\rho c(T_{\mathrm{eq}}-T_0)$, where $X_1$ represents the average reaction fraction of the MH at the end of the first stage, $\Delta H$ is the reaction enthalpy, $\rho$ is the density, $c$ is the heat capacity, $T_{\mathrm{eq}}$ is the equilibrium temperature, and $T_0$ is the initial bed temperature. This relation demonstrates that calculating the sensible heat required to heat the bed from its initial temperature to the reaction equilibrium temperature allows estimation of the state of the MH material upon completion of the first reaction stage.

3.4. Summary

A distinct reaction front propagation phenomenon is observed inside the MH reactor:

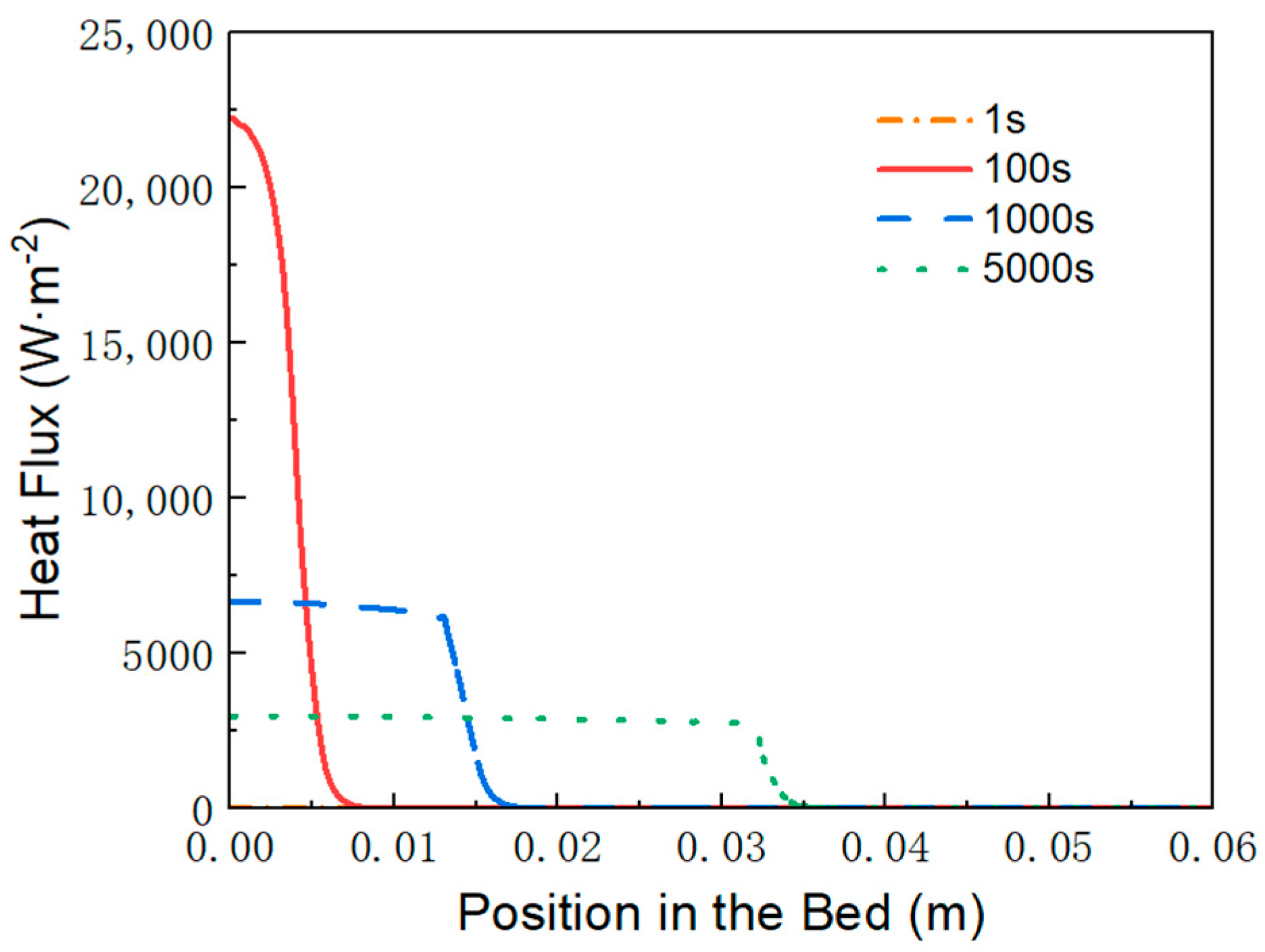
• First item; in regions swept by the reaction front, the hydrogen absorption reaction is complete, and heat transfer occurs with nearly constant heat flux.
• In regions not yet reached by the reaction front, the hydrogen absorption reaction is temporarily stopped, and no heat transfer takes place, resulting in zero heat flux.

Due to differences in heat transfer across the reaction front, the reaction state and temperature distribution exhibit significant distinctions:

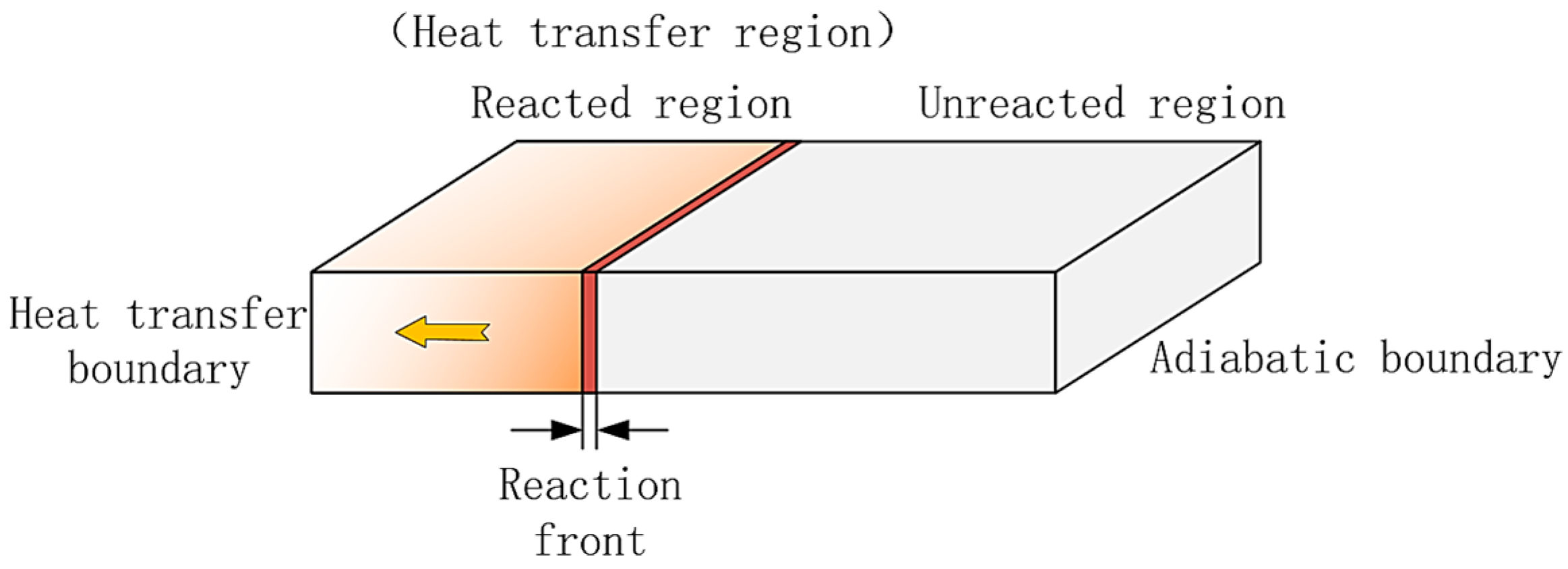
• Behind the reaction front, the reaction is complete, and the MH material reaches saturated hydrogen absorption. At any given time, the temperature distribution increases linearly from the wall temperature to the equilibrium temperature at the reaction front.
• Ahead of the reaction front, the reaction is temporarily paused, and the MH material remains in the hydrogen absorption state achieved at the end of the first stage. The bed temperature remains at the equilibrium temperature until the reaction front sweeps through the region.
• At the reaction front, the bed temperature is slightly lower than the equilibrium temperature, enabling an intense and rapid reaction. Most of the heat (or cooling) transferred from the external environment to the bed is supplied to sustain the reaction at the front.

The two-stage phenomenon is more complex, as the bed temperature rise during the first stage directly determines the reaction rate of the second stage. In the two-stage process, the bed temperature increases and the material undergoes an initial reaction. Once the bed temperature reaches the equilibrium temperature, the difference between the equilibrium temperature and the wall temperature becomes the most critical factor determining the heat transfer rate during the reaction front movement stage (i.e., the second stage). Furthermore, the total reaction fraction throughout the two-stage process remains constant. The reaction rate in the first stage is not governed by the heat transfer rate and therefore proceeds more rapidly. If the reaction fraction of the first stage increases, it will lead to a decrease in the reaction fraction of the second stage, which indirectly enhances the overall reaction rate.

4. MH Reactor Two-Stage Theoretical Model Development

The existing theoretical model for MH reactors is the reaction front model, which idealizes the reaction zone as an infinitely thin front and estimates the reaction progress by calculating the movement of this front, as shown in Figure 10.

This model overlooks the two-stage phenomenon present in the reactor and primarily describes the second stage of the reaction. Therefore, we have developed a new two-stage model by incorporating a quantitative description of the first stage using the Van’t Hoff equation and combining it with the reaction front model for the second stage. The basic assumptions of the two-stage model, in addition to those of the reaction front model, include the following:

• The duration of the first reaction stage is negligible.
• No heat transfer occurs during the first stage, and the reaction process is governed solely by the initial bed temperature and the hydrogen absorption/desorption pressure.
• At the end of the first reaction stage, the bed temperature equals the reaction equilibrium temperature, and no temperature gradient exists.

4.1. Boundary and Initial Conditions

The boundary conditions remain consistent with reaction front model, where the left heat exchange wall is defined as a Dirichlet boundary condition (constant temperature) and the right side is treated as adiabatic.

The initial bed temperature is $T_0$, which is lower than the reaction equilibrium temperature $T_{\mathrm{eq}}$.

4.2. Theoretical Derivation

The bed temperature at the end of the first stage of the metal hydride reaction is $T_{\mathrm{eq}}$. The wall temperature is $T_{\mathrm{wall}}$, hence the temperature difference in the heat transfer is given by:

$$T_{\mathrm{e}}=T_{\mathrm{eq}}-T_{\mathrm{wall}}$$

(1)

The increase in sensible heat of the bed can be calculated based on the temperature difference. According to the heat balance of the bed, this sensible heat is approximately equal to the reaction heat released by the reacted portion. Therefore, the reaction fraction of the metal hydride at the end of the first stage can be calculated as:

$$X_1=\rho c(T_{\mathrm{eq}}-T_0)/\Delta H$$

(2)

Considering the linear relationship between the maximum theoretically attainable temperature of the bed and the reaction enthalpy value,

$$T_{\max }=({\rho }_{\mathrm{sat}}-{\rho }_0)\Delta H/\left(\stackrel{-}{\rho }c{M}_{\mathrm{MH}}\right)$$

(3)

where T_max is the maximum theoretically attainable temperature of the bed under the condition of infinitely high hydrogen charging pressure and constant thermophysical properties, ρ_sat is the saturated density and ρ₀ is the initial density, $\stackrel{-}{\rho }$ is the average density of the bed, M_MH is the molar mass of the MH.

In this case, the equilibrium temperature can be determined by the Van’t Hoff Equation, and (2) can be expressed as:

$$X_1={\displaystyle \frac{b/(a-\ln (P_{\mathrm{eq}}/P_{\mathrm{ref}}\left)\right)-T_0}{({\rho }_{\mathrm{sat}}-{\rho }_0)\Delta H/\left(\stackrel{-}{\rho }c{M}_{\mathrm{MH}}\right)-T_0}}$$

(4)

Therefore, by integrating the reaction front model, the temporal evolution of the reaction fraction X during the two stages can be described as follows:

$$X\left(\tau \right)=X_1+(1-X_1)\delta \left(\tau \right)/{\delta }_{\max }$$

(5)

where τ is time. The heat required for reaction front advancement per unit distance no longer equals the total reaction heat of the MH per unit volume $\dot{q}$ but rather corresponds to the reaction heat of the unreacted MH per unit volume. Therefore, the reaction heat change parameter in conventional reaction front model should be multiplied by (1 − X₁). The reaction front model will be expressed as:

$$\delta (\tau )=\sqrt{2k{T}_{\mathrm{e}}/\left(\right(1-X_1\left)\dot{q}\right)\tau }$$

(6)

Therefore, the two-stage model incorporating the reaction front model is formulated as:

$$X(\tau )={\displaystyle \frac{b/(a-\ln (P_{\mathrm{eq}}/P_{\mathrm{ref}}\left)\right)-T_0}{({\rho }_{\mathrm{sat}}-{\rho }_0)\Delta H/\left(\stackrel{-}{\rho }c{M}_{\mathrm{MH}}\right)-T_0}}+{\displaystyle \frac{1-X_1}{{\delta }_{\mathrm{m}\mathrm{a}\mathrm{x}}}}\sqrt{{\displaystyle \frac{2k{T}_{\mathrm{e}}}{(1-X_1)\dot{q}}}\tau }$$

(7)

Validation was performed using the same numerical model described in Section 2, comparing the predictive performance of various theoretical models on the variation of the hydrogen-to-metal ratio [H/M] over time under different pressures. Hydrogen charging pressures of 0.15 MPa, 2 MPa, and 5 MPa were selected. The prediction curves of reaction progress obtained from the original reaction front model and the two-stage model, were compared with the numerical model results, as shown in Figure 11, Figure 12 and Figure 13.

When the hydrogen charging pressure is 0.15 MPa, the corresponding equilibrium temperature equals the bed temperature, and no first-stage reaction occurs. Therefore, both the reaction front model and the two-stage model demonstrate high prediction accuracy in Figure 11. As can be seen from Figure 12 and Figure 13, the reaction front model deviates significantly from the numerical simulation results, the values predicted by the two-stage method closely match the simulation data. Because, as the hydrogen charging pressure increases, the hydrogen charging pressure deviates from the equilibrium pressure corresponding to the initial bed temperature and the reaction fraction of the first stage increases. The reaction front model gradually diverges from the simulation results due to its failure to account for the first stage. In contrast, the two-stage model maintains excellent predictive accuracy across all operating conditions considered. The prediction results of the two models for the reaction completion time were compared with the numerical simulation results. It was found that the two-stage model had a prediction error of only 2% for the reaction rate, which was drastically lower than the 25.5% error of the original reaction front model.

5. Conclusions

Based on numerical simulation, the hydrogen–thermal coupling mechanism inside the reactor was analyzed, and a new analytical theoretical model for the MH reactor was developed based on this analysis, leading to the following conclusions:

• When the initial bed temperature is lower than the reaction equilibrium temperature corresponding to the hydrogen charging pressure, a uniform and rapid hydrogen absorption reaction accompanied by heat release occurs in the MH reactor bed. The temperature rises to the equilibrium level, after which the reaction ceases in most of the bed region. This process is defined as the first reaction stage. At the end of this stage, the product of the reaction fraction per unit volume of the MH material and the reaction enthalpy equals the sensible heat required for the temperature rise of the bed.
• When the temperature of the reactor’s heat exchange wall is lower than the reaction equilibrium temperature, the reaction region progressively advances from the heat transfer boundary toward the adiabatic boundary within the MH reactor. This process is defined as the second reaction stage. In regions swept by the reaction front, the hydrogen absorption reaction reaches saturation, and heat transfer occurs with an almost constant heat flux along the direction of front propagation. In regions not yet reached by the reaction front, heat transfer is negligible, the heat flux remains zero, the hydrogen absorption reaction is temporarily halted, and the hydrogen absorption saturation level of the material remains at the state achieved at the end of the first stage.
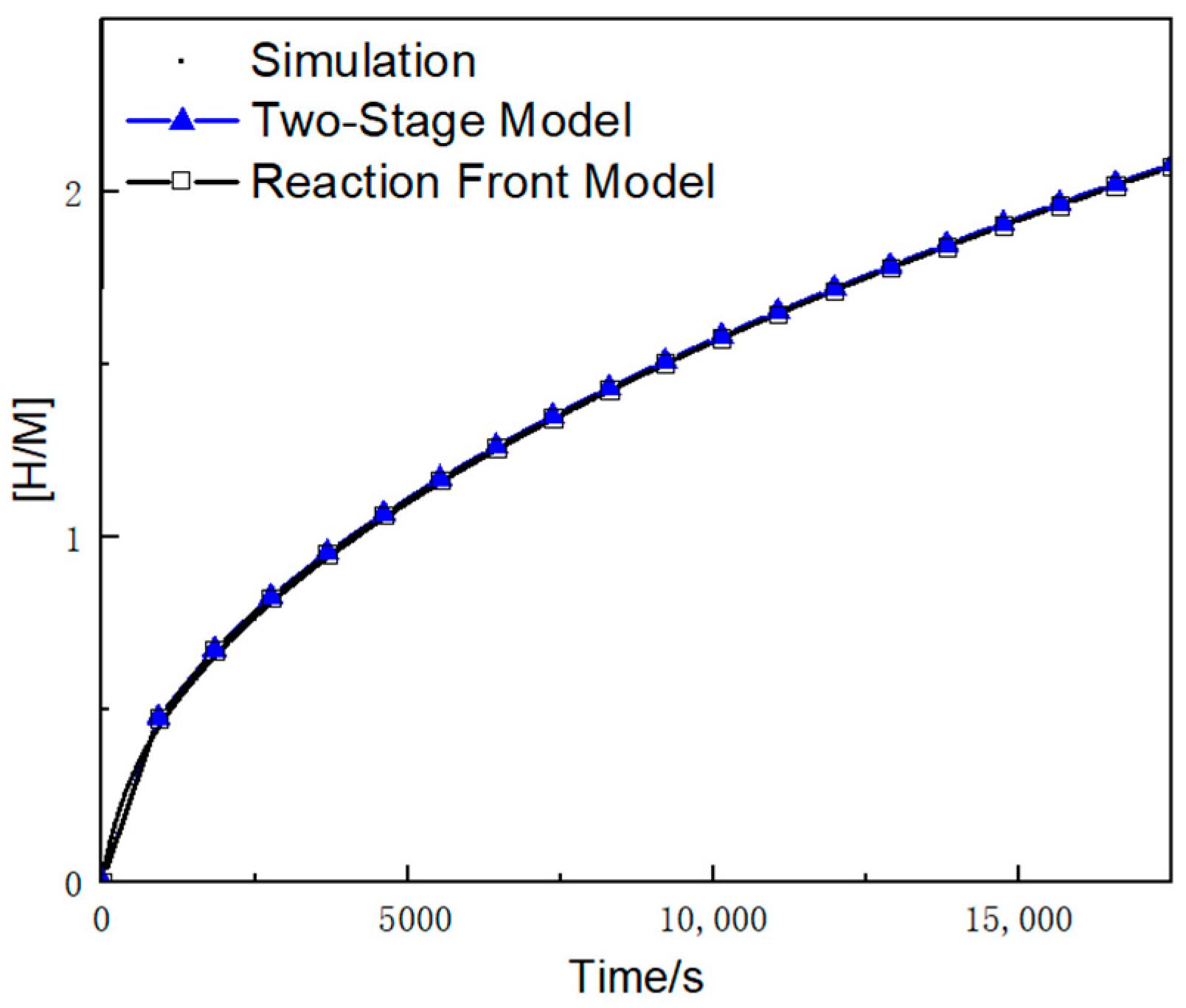
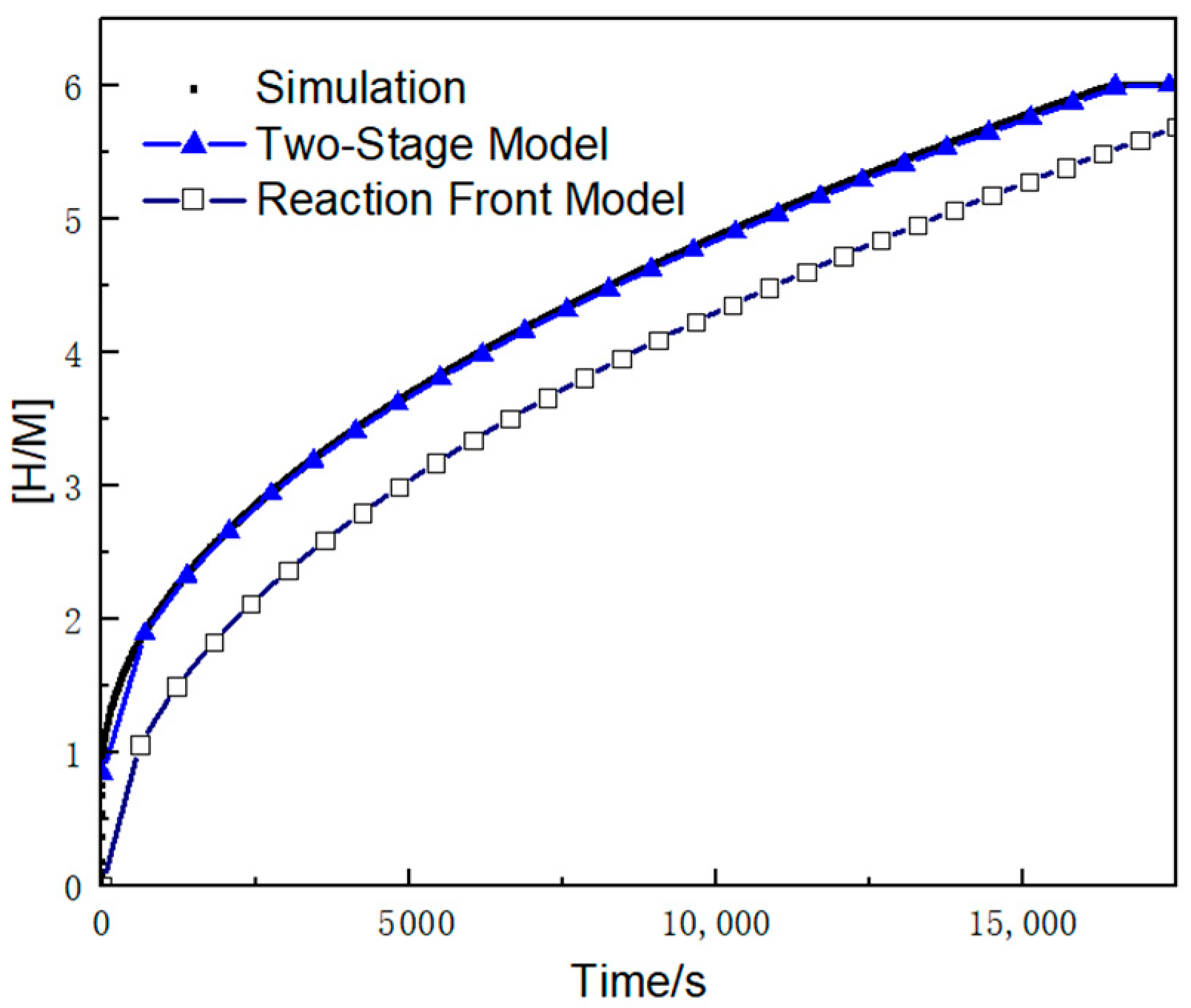
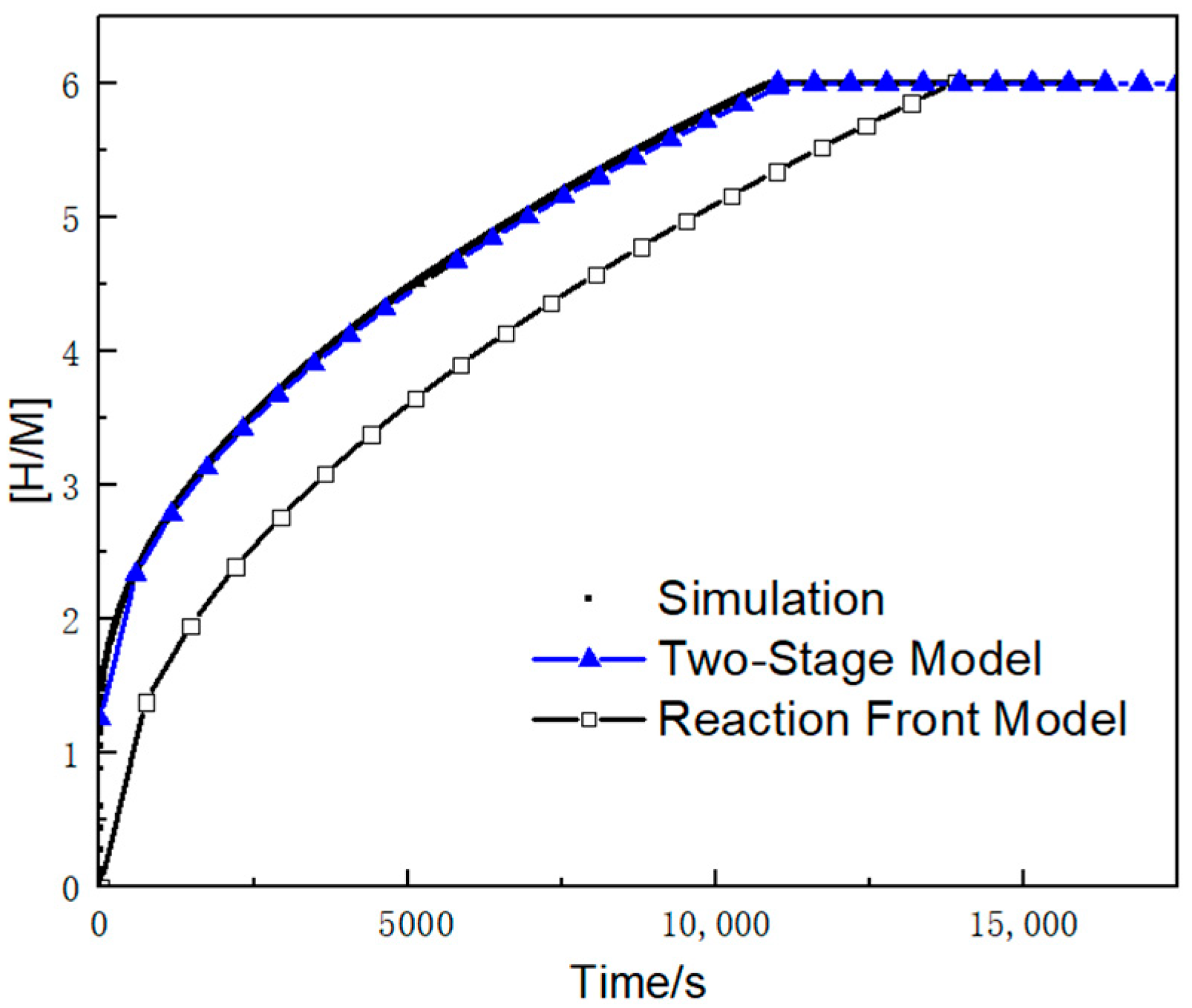
• Based on the assumptions of neglecting the first-stage reaction time and maintaining bed thermal equilibrium, a novel two-stage theoretical model was developed. This model successfully characterizes the internal hydrogen–thermal coupling and reaction progress. Having been numerically validated, the new model achieves a prediction accuracy of 2% for reaction rates, significantly outperforming the original reaction front model’s 25.5% error margin.