Adaptive Extended Kalman Filtering for Online Monitoring of Concrete Structures Subject to Impacts ^†

Abstract

Structures are susceptible to external impacts over the long term, resulting in various types of damage. An online, accurate assessment of the severity of damage is the basis for formulating subsequent maintenance and reinforcement plans. In this work, an online damage identification method based on the Adaptive Extended Kalman Filter (AEKF) is proposed. Initially, the vibration signals of a concrete-filled steel tubular (CFST) test structure subject to multiple lateral impacts are processed, and signals before and after damage inception are spliced to track damage evolution. Subsequently, the natural frequencies extracted from the signals before and after damage inception, along with the amplitude of the damage itself, are integrated into the state vector to build a nonlinear state transfer and observation model, allowing estimation of the dynamic flexural stiffness of the structure. To further improve the problem solution in the presence of signal losses due to sensor detachment or breakage, missing signals are reconstructed using the weighted matrix pencil (MP), thereby ensuring the continuity and stability of the AEKF filtering process. By comparing the results with the actual damage state, the proposed method is shown to effectively track the gradual reduction in flexural stiffness and to verify its feasibility for providing reliable support for online monitoring and damage assessment.

1. Introduction

Concrete-filled steel tubes (CFSTs) combine the properties of steel tubes and concrete to achieve high strength and durability. This type of composite structure is characterized by an extremely high load-bearing capacity and has been widely used as a major structural component in large-scale structures and infrastructures [1].

During their service life, CFST structures are susceptible to various external factors, including loads (which may exceed design levels) and temperature variations, which can lead to a range of issues that gradually worsen over time. Moreover, extreme conditions resulting from impacts or earthquakes [2,3] can cause varying levels of damage, threatening the safety of the entire structure. In practice, damaged CFST structures are not able to attain their ultimate failure level, though they still have a residual bearing capacity. There are several types of damage that may occur in the core concrete, such as core debonding, crushing, or cracking, all of which lead to a significant reduction in the relevant flexural stiffness, affecting safe serviceability. Therefore, an accurate assessment of the damage state is a prerequisite for determining appropriate repair measures, if needed.

The Extended Kalman Filter (EKF) [4,5] has been extensively used for nonlinear state estimation in structural dynamics. It works by linearizing the system equations around the current estimate, and it recursively updates the state vector. However, its accuracy strongly depends on the correct specification of the process and measurement noise covariances, which are often unknown or time-varying in practice. To overcome this limitation, the Adaptive Extended Kalman Filter (AEKF) [6,7] has been developed to adaptively update the noise covariances during the filtering process, thus improving robustness to modeling uncertainties and measurement losses.

In this study, impact tests were conducted on CFST beam–column specimens. Vibration signals were acquired before and after the impacts and artificially spliced to simulate real service conditions. An AEKF [8] was then adopted for real-time damage identification. Finally, to address potential data losses induced by structural damage, a weighted matrix pencil (MP) method was proposed for reconstructing possibly missing data. By comparing the real damage states observed in the laboratory experiments, the effectiveness of the proposed approach is validated.

2. Experimental Modal Testing on CFST Specimens

To understand the influence of damage on the vibration properties of CFST structures, a series of CFST specimens was fabricated, and a modal testing program was conducted before and after lateral impact tests [9].

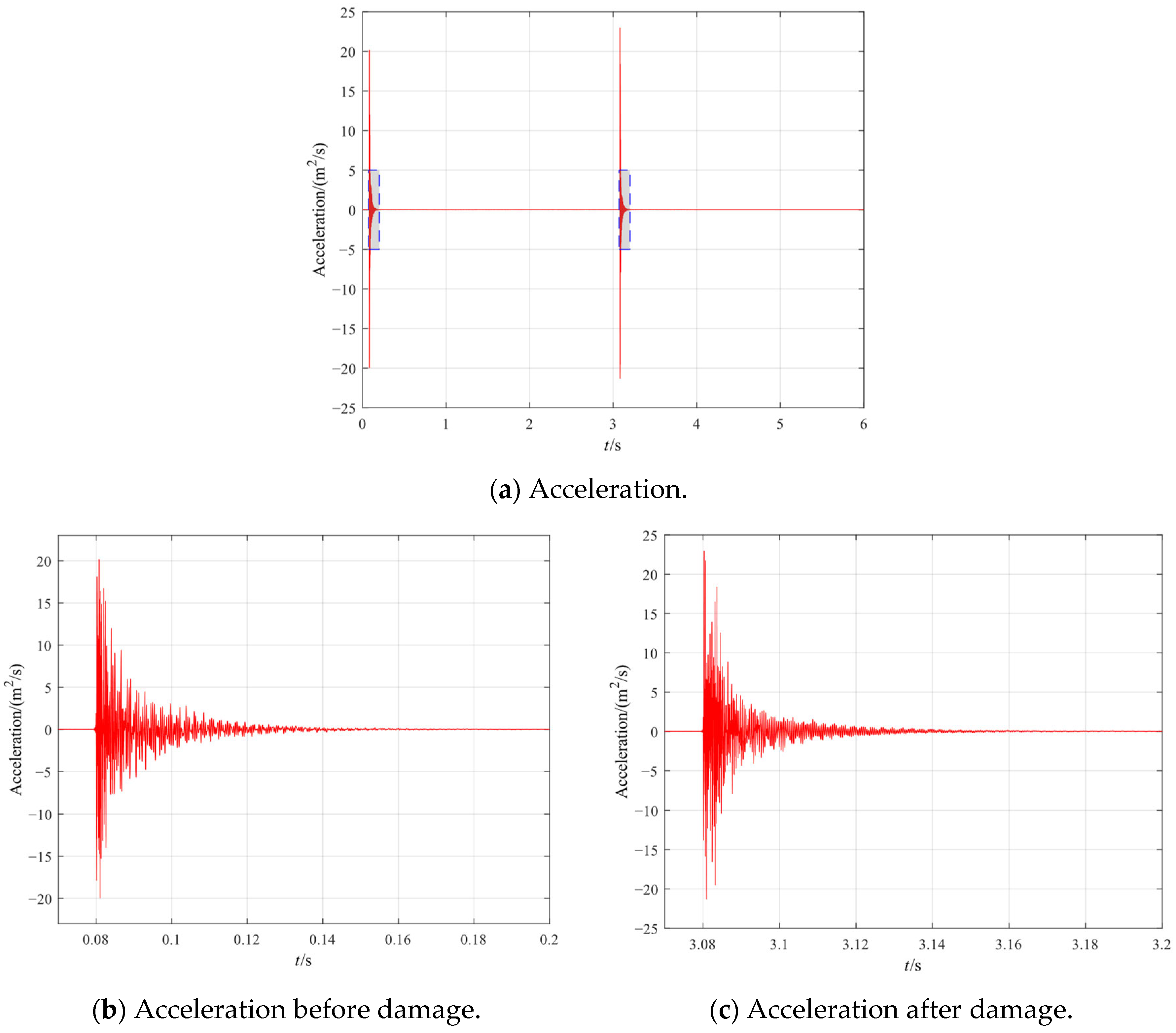
2.1. Modal Testing Setup and Data Splicing

Before and after the lateral impact tests, hammer-induced vibration tests were performed on the instrumented CFST specimens. Each specimen was placed on rubber supports [10], and vibration responses in both the pristine and damaged states were recorded for subsequent analysis. Impacts were sequentially applied with a force hammer at fifteen predefined points marked on the top surface of the steel tube. In modal tests, 7 sensors were installed evenly spaced along the top surface of the specimen, and force and acceleration signals were sampled at 25 kHz. To minimize noise effects, each CFST specimen underwent five full repetitions of the entire impact sequence. The experimental setup is illustrated in Figure 1.

Subsequently, the 1 s vibrations, obtained before and after the impact, were artificially spliced. At the interval between the intact and damaged signals, the frequency spectra of the final 1000 data points of the baseline signals and the initial 1000 data points of the damaged signals were merged to form a 2 s noise segment. Furthermore, by replicating the spectra of the final 1000 data points of the damaged signals, an additional 2 s noise segment was finally added at the end of the dataset. Therefore, the signal used for online updates lasts 6 s. The artificially spliced vibration time history is depicted in Figure 2.

It should be noted that when damage occurs, the installed sensors may detach from the specimen’s outer surface or even break, leading to data loss. In these conditions, reconstructing the missing data is essential to ensure the continuous operation of the online damage identification process. In this paper, an MP method was employed, as referenced in [11,12,13], and a standard Vandermonde matrix [14,15,16,17] was constructed to apply weighting to data regions requiring particular attention, specifically the tail part of the time domain data and the mode highlighted in the frequency domain.

In a discrete time series, data x_k can be represented as a linear superposition of r exponential modes, according to

$$x_k=\sum _{i=1}^r{\alpha }_i{\lambda }_i^k$$

(1)

where λ_i is the i-th mode, α_i is the relevant amplitude, and r is the total number of considered modes.

Subsequently, an L × M Hankel matrix H is constructed [18,19,20], with H₁ and H₂ being the submatrices obtained by deleting the last and first column of H, respectively:

$$H=\left[\begin{array}{cccc}{x}_0& x_1& \dots & x_{M-1}\\ x_1& x_2& \dots & x_M\\ ⋮& ⋮& \ddots & ⋮\\ x_{L-1}& x_L& \dots & x_{L+M-2}\end{array}\right],H_1=\left[\begin{array}{cccc}{x}_0& x_1& \dots & x_{M-2}\\ x_1& x_2& \dots & x_{M-1}\\ ⋮& ⋮& \ddots & ⋮\\ x_{L-1}& x_L& \dots & x_{L+M-2}\end{array}\right],H_2=\left[\begin{array}{cccc}{x}_1& x_2& \dots & x_{M-1}\\ x_2& x_3& \dots & x_M\\ ⋮& ⋮& \ddots & ⋮\\ x_L& x_{L+1}& \dots & x_{L+M-2}\end{array}\right]$$

(2)

At this stage, the MP is defined as

$$\mathrm{P}\left(z\right)=H_2-z{H}_1$$

(3)

where z is a generalized eigenvalue of the matrix pencil H₁ and H₂. If there exists a non-zero vector v that satisfies the following eigenproblem:

$$\left(H_2-z{H}_1\right)v=0$$

(4)

z turns out to be the mode of the signal.

Once the modal parameter identification is completed, the following standard Vandermonde matrix is constructed:

$$V=\left[\begin{array}{cccc}{\lambda }_1^0& {\lambda }_2^0& \dots & {\lambda }_r^0\\ {\lambda }_1^1& {\lambda }_2^1& \dots & {\lambda }_r^1\\ ⋮& ⋮& \ddots & ⋮\\ {\lambda }_1^{N-1}& {\lambda }_2^{N-1}& \dots & {\lambda }_r^{N-1}\end{array}\right]$$

(5)

In this matrix, each column corresponds to a modal parameter λ_i, and each row corresponds to a discrete k-th time point. The obtained Vandermonde matrix can then be used to apply weighting to both the time-domain and frequency-domain modal components.

A comparison between the measured and reconstructed data is shown in Figure 3. From the graphs, it is clear that the reconstructed vibration signal is very similar to the measured data in both the time and frequency domains, verifying the effectiveness of the proposed weighted MP method.

2.2. Adaptive Extended Kalman Filter

Extended Kalman filtering (EKF) [4,21,22] has been extensively applied in real-time system state estimation, demonstrating excellent performance. In what follows, the discrete EKF and AEKF for structural state estimation are briefly recalled.

Several studies have been devoted to enhancing EKF techniques by adaptively estimating unknown or time-varying system parameters. Among these approaches, maximum likelihood (ML)-based methods iteratively update the measurement noise covariance using optimization techniques, such as sequential quadratic programming [23]. Random-weighting-based strategies, including adaptive random-weighted H-infinity filtering and random-weighting Kalman filters, have been proposed to handle process and measurement uncertainties with limited prior knowledge [24,25]. Windowing strategies, such as moving-window adaptive H-infinity filters and moving-horizon estimation-based adaptive unscented Kalman filters, have been applied to capture temporal variations in noise statistics in nonlinear systems [26,27]. In addition, advanced nonlinear Gaussian filters, including the adaptive unscented Kalman filter (UKF) [28] and adaptive cubature Kalman filter (CKF) [29], have been widely investigated in navigation, sensor fusion, and target tracking applications. These filters integrate online noise covariance estimation with nonlinear transformations of the state distribution, yielding improved estimation accuracy in complex systems.

Moving to the problem of interest here in relation to CFST structures, the flexural stiffness EI₀ of each section can be determined as

$${\left(EI\right)}_0=E_{\mathrm{s}}{I}_{\mathrm{s}}+E_{\mathrm{c}}{I}_{\mathrm{c}}$$

(6)

where subscripts s and c, respectively, refer to steel and concrete; E and I represent the Young’s modulus and the moment of inertia of each material. After lateral impacts, a simplified model is adopted to allow for the general influence of concrete damage and steel-concrete debonding on the same flexural stiffness of the CFST specimens. It is assumed that the elastic modulus E_c of concrete is affected by a uniform reduction, so that the stiffness of the beam–columns can be determined as

$${\left(EI\right)}_{\mathrm{d}}=E_{\mathrm{s}}{I}_{\mathrm{s}}+{\alpha E}_{\mathrm{c}}{I}_{\mathrm{c}}$$

(7)

where α is a factor ruling the aforementioned reduction in E_c due to damage.

The equation of motion for a multi-degree-of-freedom (DOFs) CFST structure can be written as

$$Ma\left(t\right)+Cv\left(t\right)+Ku\left(t\right)=F\left(t\right)$$

(8)

where M, C, and K are the mass, damping, and stiffness matrices, respectively; u, v, and a are the displacement, velocity, and acceleration vectors; and F is the external force vector. In this study, the DOF of CFST specimens was set to 63.

In the time-discrete version of the EKF, the nonlinear state transition equation and the observation equation are

$$x_k=\mathbb{f}\left(x_{k-1}\right)+w_k$$

(9)

$${\mathbb{z}}_k=\mathbb{H}{x}_k+v_k$$

(10)

where x_k is the state vector at time instant t_k, which gathers displacement, velocity, and acceleration. In this study, it also includes the damage indicator α and the three lowest natural frequencies f_i of the specimen:

$$x_k=\left[\begin{array}{c}u\\ v\\ a\\ \alpha \\ f_i\end{array}\right]$$

(11)

${\mathbb{z}}_k$ is the observation vector at time t_k, which lists the acceleration and the lowest three natural frequencies f_i obtained from the online updating procedure. In Equation (11), $\mathbb{f}(·)$ is the state transition function, which is derived by discretizing the multi-DOF equation of motion using the Newmark-β method. $\mathbb{H}$ denotes instead the observation matrix, which provides a map between the measurement and the state variables. In this study, $\mathbb{H}$ is a Boolean matrix used to select the measured accelerations in seven channels and the natural frequencies. Finally, w_k and v_k are zero-mean Gaussian processes, with covariance matrices Q_k and R_k, respectively.

In the initial stage of the EKF, the state vector is initialized as follows:

$${\widehat{x}}_{0|0}=\left[\begin{array}{c}0\\ 0\\ 0\\ 1\\ 0\end{array}\right]$$

(12)

In the prediction stage, the estimate of the predicted state is obtained as

$${\widehat{x}}_{k|k-1}=\mathbb{f}\left({\widehat{x}}_{k-1|k-1}\right)$$

(13)

At the same time, the Jacobian matrix is computed as follows:

$${\mathbb{F}}_{k-1}={\displaystyle \frac{\partial \mathbb{f}}{\partial x}}{|}_{{\widehat{x}}_{k-1|k-1}}$$

(14)

Therefore, the predicted error covariance is given by

$$P_{k|k-1}={\mathbb{F}}_{k-1}{P}_{k-1|k-1}{\mathbb{F}}_{k-1}^T+Q_{k-1}$$

(15)

The innovation, defined as the difference between the measurement and the current prediction, is expressed in the following form:

$$y_k={\mathbb{z}}_k-\mathbb{H}{\widehat{x}}_{k|k-1}$$

(16)

The innovation covariance and the Kalman gain are defined as

$$S_k=\mathbb{H}{P}_{k|k-1}{\mathbb{H}}^T+R_k$$

(17)

$$K_k=P_{k|k-1}{\mathbb{H}}^T{S}_k^{-1}$$

(18)

And the updated state estimate and corresponding error covariance are given by the following expressions:

$${\widehat{x}}_{k|k}={\widehat{x}}_{k|k-1}+K_k{y}_k$$

(19)

$$P_{k|k}=\left(1-K_k\mathbb{H}\right)P_{k|k-1}$$

(20)

Practical applications of the EKF still have some limitations. While noise covariance R can typically be determined through repeated experimentation, an incorrectly chosen process noise covariance Q can introduce substantial errors into the structural state estimation. Hence, an accurate selection of Q is critical to ensure a reliable online evaluation of structural state via the EKF. An adaptive, innovation-based method [7,30] for the online estimation of Q is here adopted, according to:

$$Q_k=\left(1-{\beta }_{q,k-1}\right)Q_{k-1}+{\beta }_{q,k-1}{K}_k{y}_k{y}_k^T{K}_k^T$$

(21)

with the initial value of β_q set to 0.25.

A preliminary trial-and-error process revealed that the selection of βq influences online updating performance. Therefore, a real-time updating method for β_q was also defined as follows:

$${\beta }_{q,k}={\beta }_{q, k-1}\times \left(1+\tanh \left({\displaystyle \frac{y_k^T{y}_k}{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left(S_k\right)}}-1\right)\right)$$

(22)

To provide β_q,k through multiplication by a scaling factor. This latter factor is computed as the ratio of the squared norm of the innovation vector and the trace of the innovation covariance, and then mapped to (−1, 1) through the hyperbolic tangent function. If this ratio is larger than 1, the scaling factor becomes greater than 1, indicating that the system uncertainty is underestimated; conversely, if the ratio is less than 1, the estimated uncertainty is too high.

3. Results

The accuracy of the proposed AEKF method for estimating the reduction in the elastic modulus of the core concrete in CFST beam–column specimens subjected to impacts is now investigated. Simultaneously, data loss scenarios caused by sensor detachment or breakage due to damage were also simulated. The proposed weighted MP method was then applied to online reconstruction of the missing data, and the reconstructed data were subsequently used to continue the AEKF update process.

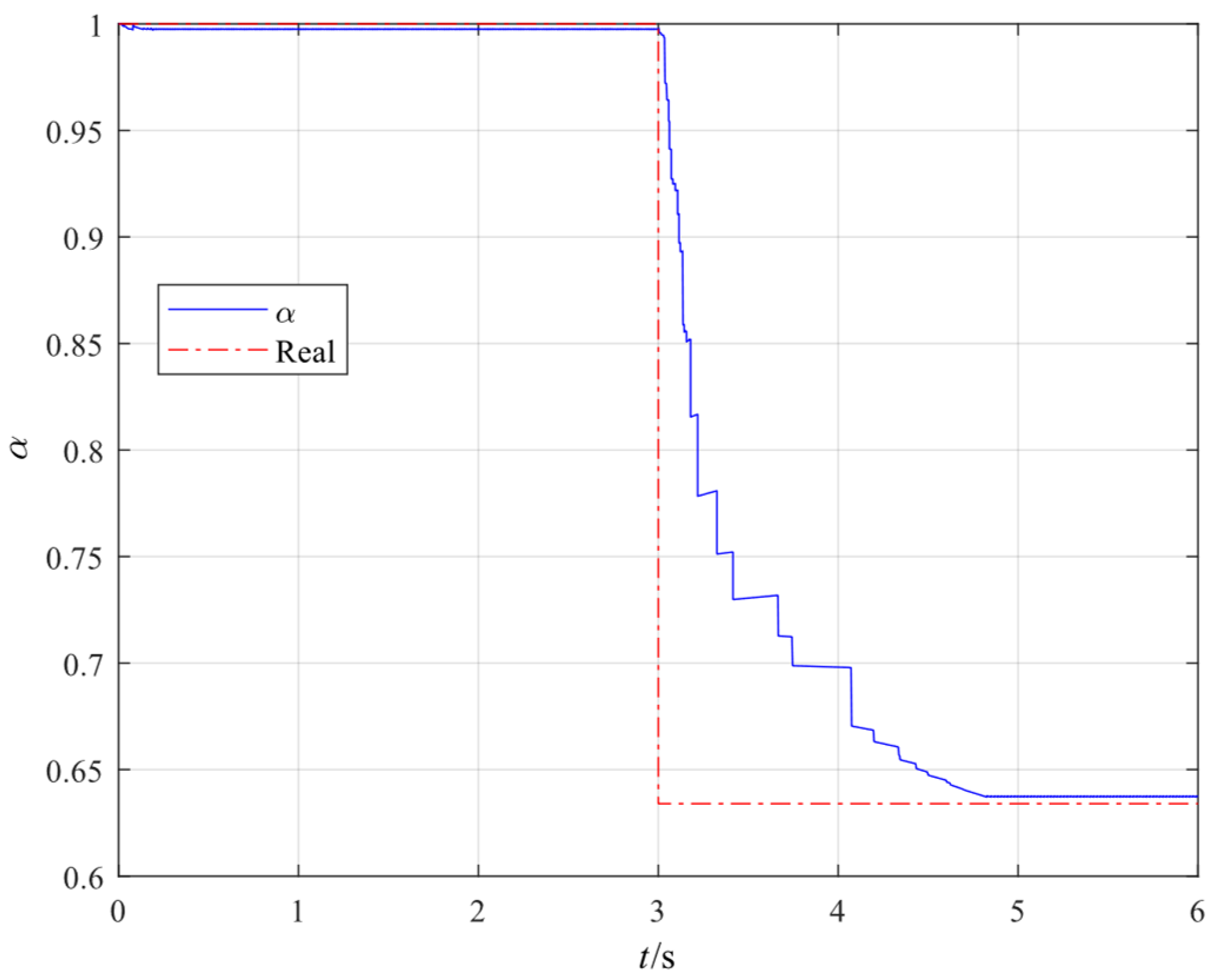
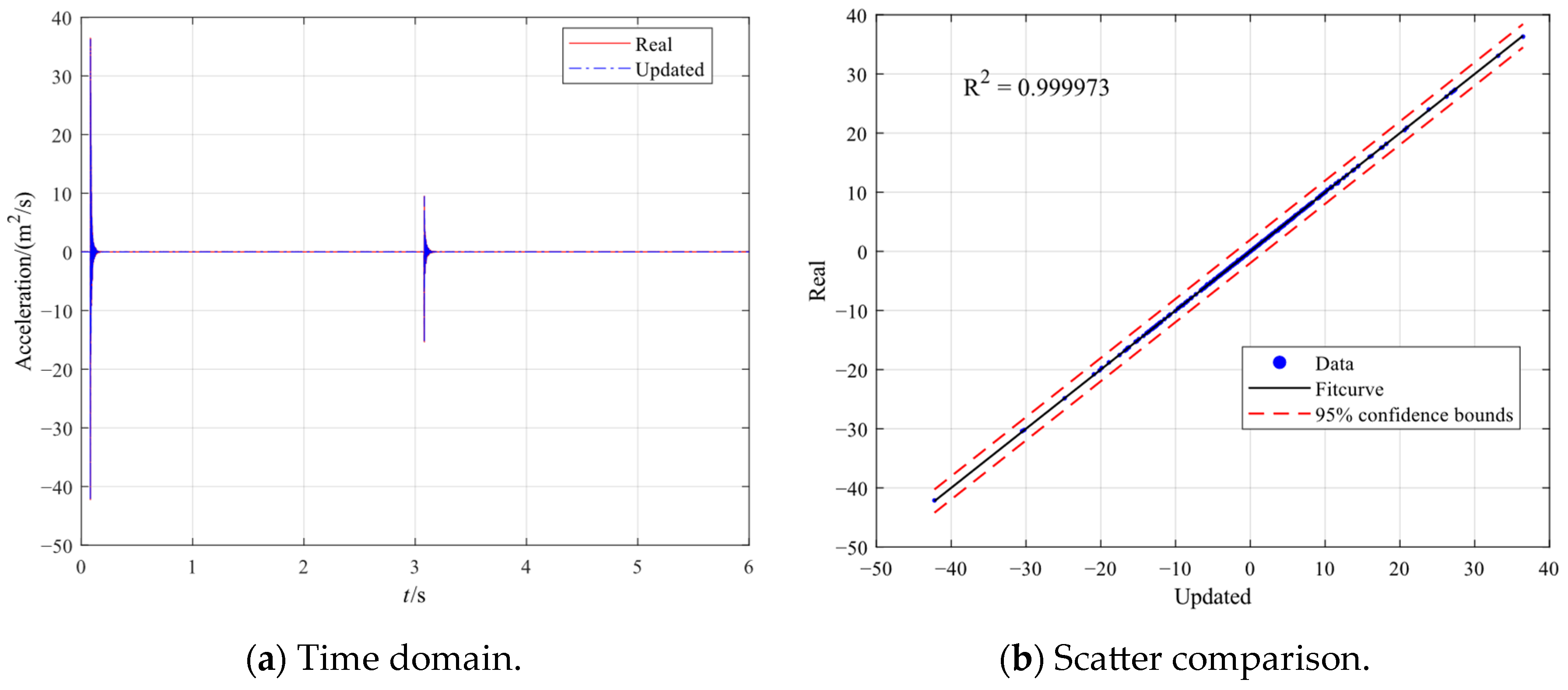
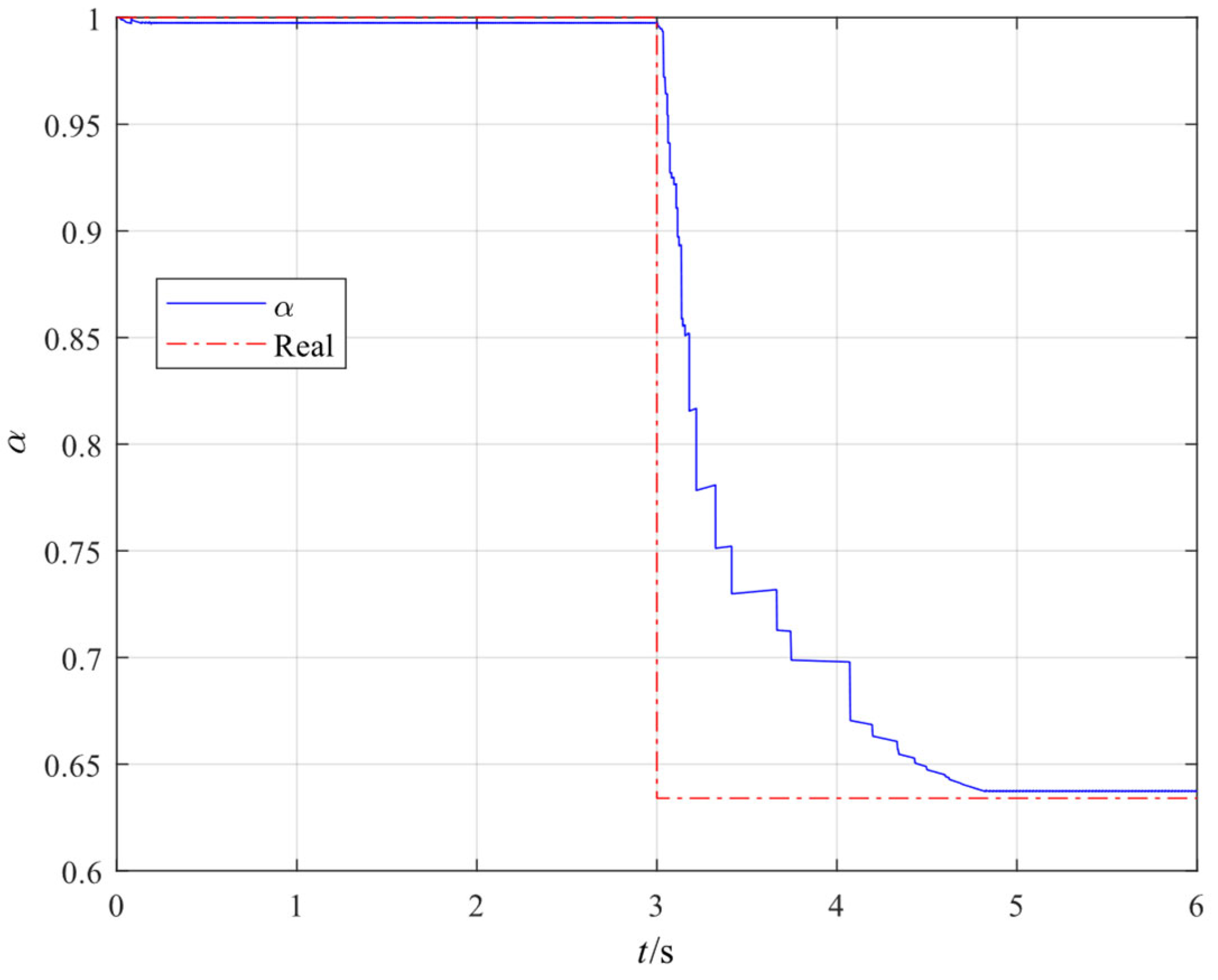
3.1. AEKF Update Results Without Data Loss

In this test case, the initial values of the state vector, error covariance matrix, process noise covariance matrix Q, and observation noise covariance matrix R are defined as follows:

$${\widehat{x}}_{0|0}={\left[\begin{array}{c}0\\ 0\\ 0\\ 1\\ 0\end{array}\right]}_{193\times 1}$$

(23)

$$P_{0|0}={\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(1\times {10}^{-12},1\times {10}^{-12},1\times {10}^{-12},1\times {10}^{-12},1\times {10}^{-12}\right)}_{193\times 193}$$

(24)

$$Q_0={\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(1\times {10}^{-1},1\times {10}^{-1},1\times {10}^{-1},1\times {10}^{-1},1\times {10}^{-1}\right)}_{193\times 193}$$

(25)

$$R_0={\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(1\times {10}^{-1},1\times {10}^{-1}\right)}_{10\times 10}$$

(26)

The real-time results of the AEKF are presented in Figure 4 in terms of the time evolution of the damage factor α. From the plot, it is clear that the proposed AEKF method promptly detects the damage and converges to 0.637 in no more than 2 s. The said damage value is close to the target value of 0.634, with an error of only 0.47%, indicating the effectiveness of the proposed approach.

The time history of the acceleration is shown in Figure 5. The AEKF method shows outstanding performance in online acceleration prediction and further demonstrates its effectiveness.

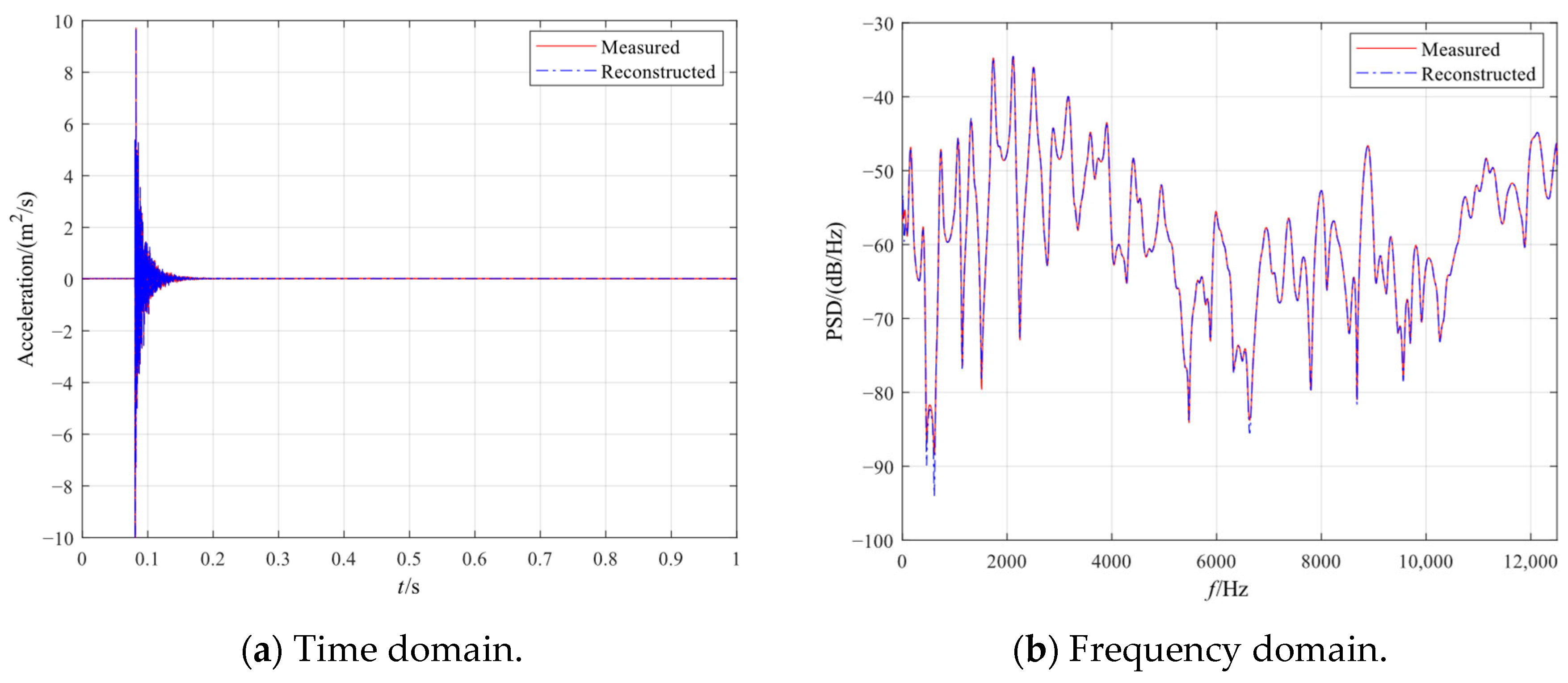
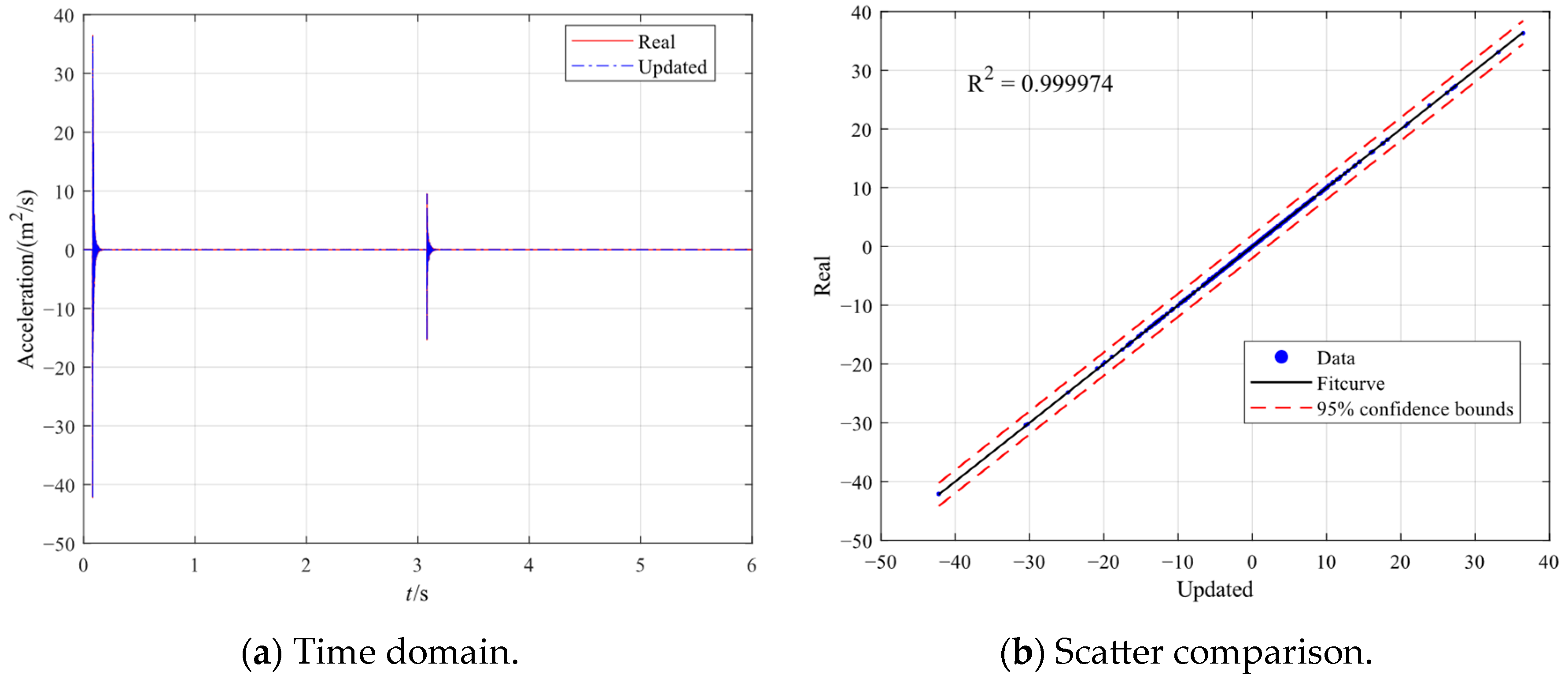
3.2. AEKF Update Results with Data Loss

During the structure’s service life, damage may cause sensors to detach or break, leading to data loss. Under such circumstances, it is necessary to reconstruct missing data online and in real time. In this section, missing damage data are artificially generated and reconstructed using the proposed weighted MP method; thereafter, the AEKF is employed to estimate the damage state. As illustrated in Figure 6, for data reconstructed by the weighted MP method, the proposed AEKF approach still promptly captures the damage features and obtains online estimation of the elastic modulus reduction with high accuracy.

The online acceleration estimation of the reconstructed data is illustrated in Figure 7, which shows that the AEKF method achieves high-accuracy acceleration estimation. This shows that the structural state can be captured in real time by updating the structural parameters.

4. Conclusions

In this study, to obtain an online, real-time estimate of structural damage states, an AEKF-based damage identification method has been proposed. Simultaneously, to address data loss due to damage, a weighted MP method has been proposed to reconstruct missing data. Based on the obtained results, the following conclusions can be drawn.

• By adaptively updating Q and the scale factor β_q, the proposed method avoids the estimation fluctuation problem caused by time-invariant Q, as in the traditional EKF, thereby maintaining stable, accurate filtering at varying damage states.
• This study incorporated the lowest three natural frequencies and the damage parameter α into the state vector and updated them in the nonlinear state transfer and observation model. It can therefore automatically track a gradual degradation process of the structural flexural stiffness, if any.
• When acceleration data are missing, the weighted MP method can be used, and weights were applied to the time domain and the target mode to complete data reconstruction. The reconstructed data were found to be highly consistent with the real measurements in both time and frequency domains, and the subsequent AEKF process yielded an effective stiffness reduction in close agreement with the true value. The proposed methodology has been shown to achieve high accuracy and prompt response to changing states, as well as tolerance to sensor failures in actual operational conditions.

In future research, the focus will be on extending the proposed AEKF-based monitoring strategy to other structural systems and loading conditions. Furthermore, applications to large-scale structures with multi-sensor fusion and operational uncertainty will also be explored. Finally, the combination of adaptive filtering with machine learning-based uncertainty evaluation methods will be pursued to enhance structural health monitoring applications.