An Improved Fruit Fly Optimization Algorithm for Multi-Objective Scheduling in Hybrid Flow Shops ^†

Abstract

This study proposes an improved Fruit Fly Optimization Algorithm integrated with Simulated Annealing (SA-FOA) for hybrid flow shop scheduling problems with dual objectives of minimizing makespan and total tardiness. The algorithm adopts a three-stage integration strategy to generate high-quality initial populations, surpassing random initialization. During olfactory search, insertion-based neighborhood operations expand search scope, while visual search incorporates simulated annealing acceptance criteria to escape local optima. Validation employs three scalable instances, comparing SA-FOA against basic FOA and classical scheduling rules. Experimental results demonstrate significant superiority in Inverted Generational Distance (IGD), Non-dominant rate (NR), and Convergence Matrix (C-matrix metrics), highlighting enhanced convergence, distribution, and diversity. Notably, performance advantages amplify with problem scale growth.

1. Introduction

With the advancement of economic globalization, modern manufacturing systems are facing dual pressures of small-batch customization and rapid delivery [1]. Traditional Flow Shop Scheduling (FSP), characterized by rigid linear process constraints and single-machine configurations, fails to meet the flexible production demands of multi-variety and variable-batch manufacturing [2]. Against this backdrop, Hybrid Flow Shop Scheduling (HFSP) has emerged as a research focus in both industrial and academic communities due to its flexible production capabilities [3]. As an extension of classical FSP, HFSP is distinguished by multiple parallel machines at each processing stage, requiring joint optimization of job sequencing and machine assignment.

In the field of hybrid flow shop scheduling, Cheng et al. [4] investigated single-objective batch scheduling problems in flow shops, designing a simulation-based simulated annealing algorithm. Zhong et al. [5] investigated scheduling algorithm effectiveness within two-stage no-wait hybrid flow shop systems, which are defined by parallel machines at each stage and flexible inter-stage transitions in the production process. Gong et al. [6] explored the impact of worker selection on HFSP, developing a novel variable neighborhood search algorithm alongside a hybrid evolutionary algorithm (Hybrid Evolutionary Algorithm, HEA) incorporating multiple innovative operators to solve this problem. Zeng et al. [7] developed a discrete fruit fly optimization algorithm (DFFO) for the no-idle permutation flow shop scheduling problem, aiming solely at minimizing the makespan.

Many studies have worked on improving metaheuristic algorithms for hybrid flow shop scheduling with unrelated machines. However, most of the updated Fruit Fly Optimization Algorithms (FOAs) only deal with one objective. They often focus only on reducing makespan and ignore how to handle the trade-off with total tardiness. Traditional multi-objective approaches suffer from high computational complexity and lack dynamic weight adjustment mechanisms. To address these gaps, this paper proposes an SA-FOA for solving the HFSP with objectives of minimizing makespan and total tardiness. The SA-FOA adopts a three-stage integration strategy to generate high-quality initial populations, outperforming random initialization. In the olfactory search stage, the algorithm expands the solution space via insertion-based neighborhood searches, and the visual search phase adopts simulated annealing to mitigate local optima trapping.

2. Description of the Problem

The problem can be described as follows: a hybrid flow shop scheduling problem involving $\mathrm{n}$ jobs $J=\{J_1,J_2,\dots ,J_n\}$ to be processed on $\mathrm{m}$ sequential operations. Each job follows an identical routing sequence, and each operation comprises $M_{\left(k\right)}\ge 1$ unrelated parallel machines, with at least one operation having multiple machines available. The processing time of job $i$ on machine j at operation $k$ is represented as $p_{i,j}^{\left(k\right)}$, and the due date for job $i$ is represented as $d_j$. The decision variables involve determining the processing sequence of n jobs and the assignment of each job to machines across m operations. The optimization objectives aim to minimize the makespan (maximum completion time) and total tardiness time. According to the three-field notation [8], the problem is represented as $F_m/prmu,d_j,p_{i,j}^{(k)}/C_{\max },TT$, where ${\mathrm{F}}_{\mathrm{m}}$ represents a hybrid flow shop with $\mathrm{m}$ processing stages,$\mathrm{p}\mathrm{r}\mathrm{m}\mathrm{u}$ denotes the permutation constraint on job processing sequences, $d_j$ denotes the due date of job $J_i$, $p_{i,j}^{\left(k\right)}$ represents the processing time of job $i$ on machine $j$ at stage $k$, $C_{max}$ is the makespan and $\mathrm{T}\mathrm{T}$ is the total tardiness.

The problem is formulated based on the following assumptions:

• Each job is allowed to run on any machine that is ready to handle operation k;
• Processing times vary across different machines within the same operation for the same job;
• All jobs follow an identical routing sequence that requires processing through m sequential operations;
• A machine can process only one job at a time, and the task cannot be interrupted once started.

3. Simulated Annealing—Fruit Fly Optimization Algorithm

Due to the complex combinatorial structure and multi-objective conflicts inherent in hybrid flow shop scheduling problems with unrelated parallel machines (HFSPs), the solution space exhibits exponential growth. To address the optimization objectives of this multi-objective problem, an improved Fruit Fly Optimization Algorithm integrating a three-stage integration strategy and simulated annealing (SA-FOA) is proposed. Compared to the basic FOA, SA-FOA employs a hybrid initialization strategy to generate high-quality initial solutions. In the olfactory search phase, the algorithm explores new regions via insertion-based neighborhood searches, and the visual search phase employs simulated annealing to avoid getting stuck in local optima. The flowchart of the proposed SA-FOA is illustrated in Figure 1.

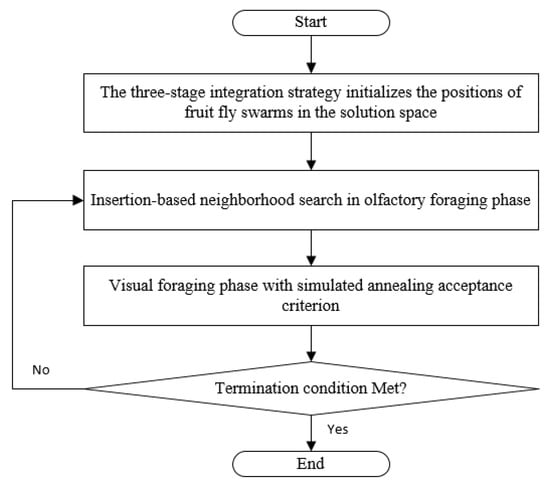
Figure 1. SA-FOA Flowchart.

3.1. Encode Figures

The Hybrid Flow Shop Scheduling Problem (HFSP) requires solving two sub-problems: job sequencing and machine assignment. An $n\times (m+1)$ matrix encoding is adopted, where n denotes the number of jobs. The first row represents the processing sequence of jobs, while rows 2 to m + 1 specify the machine assignments for each job across m operational stages.

To illustrate this encoding scheme, consider a scheduling problem with six jobs and three stages, where Stage 1 comprises 2 machines, Stage 2 consists of 3 machines, and Stage 3 also includes 3 machines. As showed in Figure 2.

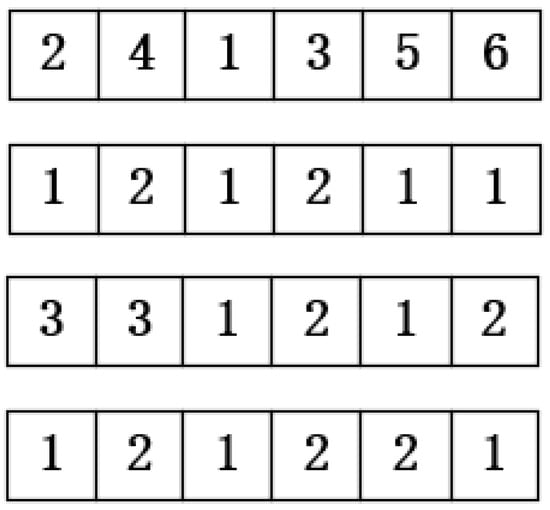
Figure 2. Illustrative Example of Encoding Scheme.

3.2. Initial Solution Generation

High-quality initial populations can significantly enhance algorithmic performance by providing search starting points in proximity to optimal solution regions, thereby effectively reducing the search space and enabling sub-populations to rapidly converge towards potential optima; simultaneously, well-maintained initial diversity serves to prevent premature convergence and diminishes the required number of iterations. The SA-FOA adopts a three-stage integration strategy for generating initial solutions, which sequentially encompasses initial job sequencing, machine assignment, and job re-sequencing, with specific implementation steps as follows.

• Considering the processing times of each job’s operations across different machines and the job due dates, an initial sequencing is generated. Calculate the sum of minimum processing times for each job across all operations, with the following formulation:

  $$P_{\mathrm{i}}={\displaystyle \sum _{k=1}^{\mathrm{m}}\underset{j\in M_k}{\min }(p_{i,j}^{(k)})}$$

  (1)

  where m represents the total number of operations, $M_k$ represents the machine set for the j-th machine at the k-th operation, and $p_{i,j}^{\left(k\right)}$ indicates the processing time of job $i$ on the j-th machine during the k-th operation. Based on these definitions, normalization is performed by incorporating job due dates, followed by a weighted summation of the time-related metrics with due dates to derive priority parameters for each job. Jobs are then sequenced according to these priority parameters to generate an initial job sequence with favorable quality.
• Based on the processing times of jobs across different machines, a roulette wheel selection mechanism is employed to assign machines for each operation. Assume that a job i has $M_{\left(k\right)}$ alternative machines available for operation k, with its processing times on these machines given by $\{p_{i,1}^{\left(k\right)},p_{i,2}^{\left(k\right)},\dots ,p_{i,j}^{\left(k\right)}\}$. The fitness value of each machine is then calculated according to the processing time $p_{i,j}^{\left(k\right)}$

  $$f_i={\displaystyle \frac{1}{p_{i.j}^{(k)}}}$$

  (2)

  The fitness values of machines are normalized into probabilities $p_i$. These probabilities form a distribution where the sum equals 1, ensuring that machines with shorter processing times are assigned higher probabilities $p_i$, thereby increasing their likelihood of being selected. Based on this probability distribution, machine selection is performed using the roulette wheel selection mechanism. Consequently, this probabilistic selection strategy effectively enhances the probability of generating superior solutions.
• An improved NEH [9] algorithm optimizes the initial job sequence by ranking jobs in descending order of total processing time and then inserting each job into the position that minimizes the objective function across all candidate positions in the current partial sequence. A neighborhood perturbation mechanism further refines the sequence by randomly removing and globally reinserting preceding/succeeding jobs (or combinations) to escape local optima.

3.3. Olfactory Foraging Phase

During the odor-based foraging process, each fruit fly examines the central area and generates SN neighboring solutions based on its current position in the solution space. To enhance global search capabilities, an efficient insertion-based neighborhood operator is designed. This operator comprises two subprocesses: destruction and construction (illustrated in Figure 3). By destructing and reconstructing existing solutions, the operator explores novel solution spaces, thereby improving global search performance.

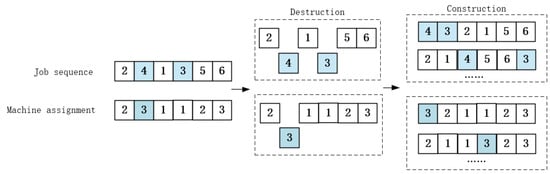
Figure 3. Insertion-based Neighborhood Operator.

During the destruction phase, several jobs are randomly picked and taken out of the current sequence. After that, during reconstruction, these removed jobs are placed back one by one into all possible positions within the partial sequence, following the order in which they were removed. The goal is to rebuild a full job sequence that leads to the shortest possible total completion time. Simultaneously, a mild perturbation mechanism is introduced to the machine assignment: with a 30% probability, the machine allocation for a randomly selected job–operation pair is exchanged with another job’s assignment on the same operation. This joint operation simultaneously modifies both the job sequence and machine configuration, as the machine swap not only alters the processing order of jobs but also adjusts their machining times and subsequent scheduling outcomes, thereby optimizing the overall solution.

3.4. Visual Search Phase

During vision-based foraging, it is essential to not only guide the swarm toward potentially promising locations but also continuously explore the surrounding areas through depth-search operators. To address the optimization requirements of objectives ${\mathrm{C}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and $\mathrm{T}\mathrm{T}$, the neighborhood search operators proposed in Table 1 are specifically designed.

Table 1. Neighborhood search operators.

	Neighborhood Search Scheme
Job sequencing	Select the job with the maximum tardiness time and swap its position with the adjacent preceding job
	Select a sequence of consecutive delayed jobs and insert them as a block into an earlier processing position
Machine selection	Select the job with the longest completion time in the current schedule and reassign machines for all its operations
	Select the machine with the highest current load and reallocate the jobs in the processing queue to other machines.

The simulated annealing acceptance criterion is simultaneously applied during the vision-based foraging phase. Inspired by the physical annealing process in metallurgy, this mechanism addresses local optima trapping in optimization algorithms. It operates by initially permitting suboptimal solutions with higher probability and then gradually reducing this acceptance probability over iterations. The simulated annealing mechanism enables SA-FOA to maintain sufficient exploration capability during global search while progressively refining solution quality in later stages, ultimately converging toward the global optimum.

Specifically, when the best neighboring solution surpasses the current candidate, it becomes the new reference point, prompting all fruit flies in the population to shift toward this position. If not, a random value rand is drawn from the interval [0,1] to decide the next action. Subsequently, if the generated random number falls below the acceptance probability η, the most promising neighboring solution generated from the current candidate is accepted under a certain probability. This acceptance probability, denoted as η, is defined as follows:

$$\eta =e^{-{\displaystyle \frac{C_{max}\left({\Pi }^{\prime }\right)-C_{max}\left(\Pi \right)}{Temp}}}$$

(3)

Here, $\Pi$ represents the candidate solution. Temp denotes the ambient temperature, calculated by the formula $Temp=t·\sum _{i=1}^n\sum _{j=1}^m{\mathrm{p}}_{i,\mathrm{j}}/(10·m·n)$. In this formula, $T$ is a predefined constant, as shown in Equation (3). If $C_{max}\left({\Pi }^{\prime }\right)$ approaches $C_{max}\left(\Pi \right)$, then $\eta \to 1$. Therefore, ${\Pi }^{\prime }$ can be accepted with a high probability. On the other hand, if solution ${\Pi }^{\prime }$ is significantly worse than solution $\Pi$, it will be easily discarded since $\eta \to 0$. The acceptance rule is designed to keep the search focused on promising regions by preventing large deviations from the current solution area.

4. Design of Experiments and Analysis of Outcomes

4.1. Design of Experiments

To assess the performance of SA-FOA, it was compared with the original Fruit Fly Optimization (FOA) algorithm and two classical scheduling heuristics: Shortest Processing Time (SPT) and Earliest Due Date (EDD). The experimental environment was configured on an AMD Ryzen 5 4600H processor with Radeon Graphics (3.00 GHz), and the implementation was developed in Python 3.7.

The specific parameter ranges are configured as follows: the number of jobs (n) takes values of 20, 50, and 100; the number of stages (k) is set to 3; the processing time for each job–operation pair is uniformly distributed in the range [1,99]; the due date for each job is uniformly distributed in the range [250,300]; the number of machines available per stage is uniformly distributed in the range [1,4].

4.2. Experiments and Discussion

In order to measure the algorithm’s effectiveness, three commonly used multi-objective optimization metrics are employed: Inverted Generational Distance (IGD), which quantifies how closely the solution set approximates the true Pareto front, reflecting the convergence and distribution quality of the algorithm; Non-dominant Rate (NR), which indicates the share of non-dominated individuals within the solution set, serving as an indicator of solution set quality; and the Convergence Matrix (C-matrix), a matrix-based comparative metric used to assess the overall dominance relationship between different algorithms. For brevity, these metrics are referred to as IGD, NR, and C(A,*), respectively, in the subsequent sections.

This section compares the proposed SA-FOA with the basic FOA, as well as the SPT and EDD scheduling rules. Each algorithm was independently executed 10 times on problem instances. Specifically, experiments evaluated algorithm effectiveness by comparing the performance of SA-FOA against the basic FOA, SPT, and EDD scheduling rules across problem instances of varying scales. During each run, algorithms were executed multiple times independently to ensure result reliability, with performance measured using average IGD, NR, and C(A,*). Experimental data are presented in Table 2.

Table 2. Comparison of algorithm results.

Size	SA-FOA			FOA			SPT			EDD
	IGD	NR	C(A,*)	IGD	NR	C(A,*)	IGD	NR	C(A,*)	IGD	NR	C(A,*)
n = 20	10.62	0.75	0.64	63.96	0.25	0.53	466.48	0	0.10	366.86	0	0.16
n = 50	55.6	0.82	0.7	291.56	0.18	0.41	5191.12	0	0.07	3323.19	0	0.12
n = 100	3.8	0.89	0.91	5164.02	0.11	0.29	16,907.84	0	0	8739.87	0	0.05

Note: In the figure, C(A,*) represents the average matrix value of algorithm A compared to the other three algorithms *.

For small-scale scheduling problems involving 20 jobs, the SA-FOA demonstrates statistically significant superiority over the basic Fruit Fly Optimization (FOA) algorithm and classical scheduling rules (SPT and EDD) in terms of both IGD and NR metrics, indicating its solution set exhibits closer approximation to the true Pareto front and encompasses a greater number of non-dominated solutions. Furthermore, SA-FOA achieves the optimal performance in the C(A,*) metric, providing additional evidence of its enhanced global exploration capabilities.

For medium-scale scheduling problems involving 50 jobs, the SA-FOA consistently maintains its leading performance across all evaluation metrics, with particularly remarkable advantages in IGD and NR indicators. This demonstrates that SA-FOA not only obtains high-quality multi-objective solution sets but also ensures superior solution set balance and diversity. Under this scale, neither the SPT nor EDD scheduling rules can generate non-dominated solutions, while the basic FOA exhibits significantly inferior performance compared to SA-FOA.

For complex large-scale scheduling problems involving 100 jobs, the SA-FOA consistently demonstrates superior performance across all three evaluation metrics, achieving the lowest IGD value and highest NR value and attaining a C(A,*) metric score of 0.91. These results comprehensively validate SA-FOA’s robustness and optimization superiority in large-scale search spaces. In contrast, the basic FOA exhibits a significantly higher IGD value of 5164.02 under the same scale, indicating substantial deterioration in solution quality and manifesting severe premature convergence issues.

It is worth noting that the NR (non-dominated ratio) values for the SPT and EDD scheduling rules are all zero across all problem sizes. This outcome stems from the inherent limitations of heuristic-based rules, which are designed to generate only a single deterministic solution rather than a diverse set of candidate solutions. Consequently, these methods exhibit extremely low non-dominated rates in multi-objective optimization scenarios, as their outputs rarely contribute to the Pareto front. In contrast, metaheuristic algorithms like SA-FOA are capable of exploring a wide solution space and generating a variety of non-dominated solutions, which explains the significant differences observed in NR values.

In conclusion, the proposed SA-FOA demonstrates robust convergence properties and maintains solution set diversity across the entire spectrum of problem scales, with particularly significant advantages observed in medium- and large-scale instances of hybrid flow shop scheduling problems. These characteristics render the algorithm particularly suitable for complex multi-objective production scheduling environments where both solution quality and diversity are critical requirements.

5. Conclusions

This study addresses the multi-objective optimization requirements in hybrid flow shop scheduling problems (HFSPs) by proposing an improved Fruit Fly Optimization Algorithm integrated with simulated annealing (SA-FOA). The algorithm incorporates a three-stage integration strategy during initial solution generation, employs insertion-based neighborhood operations in the olfactory search phase, and utilizes simulated annealing acceptance criteria in the visual search phase. Comparative experiments across scheduling instances of varying scales demonstrate that SA-FOA consistently outperforms the basic Fruit Fly Optimization Algorithm (FOA) and two classical scheduling rules (SPT and EDD) across all evaluation metrics, including IGD, NR, and C-matrix coverage. Notably, SA-FOA exhibits superior stability and optimization capabilities for large-scale problems. The results validate the algorithm’s capability to tackle hybrid flow shop scheduling problems involving multiple objectives.