An Improved Adaptive Sliding Mode Controller with Dynamic Surface Extension for Uncertain Robotic Manipulators ^†

Abstract

This article presents an improved adaptive sliding mode control (SMC) scheme designed for uncertain robotic manipulators through a novel dynamic surface extension. Unlike conventional SMC approaches, which have scalar sliding surfaces, our proposed approach introduces a two-stage sliding variable along with a dynamic extension, which allows the independent shaping of reaching and sliding dynamics. The controller adaptively estimates unknown disturbances and ensures finite-time convergence of the sliding variable, while chattering and steady-state errors are suppressed by including the integral term in the dynamic extension. Lyapunov-based analysis was carried out to prove the boundedness of the overall control approach and the asymptotic tracking of the desired trajectory. Simulation studies were carried out on a two-link robot manipulator under varying payloads and external disturbances. The results validate its superior tracking accuracy and disturbance rejection compared to traditional SMC controllers. The results confirm that the proposed control scheme achieves fast convergence, low chattering, and robust performance in the presence of modeling uncertainties, making it a promising solution for high-precision robotic applications.

1. Introduction

Robotic manipulators play a key role in automation, manufacturing, and service applications, where precise trajectory tracking under uncertain dynamics and external disturbances is crucial [1,2,3,4]. Traditional control strategies such as proportional–integral–derivative (PID) controllers often cannot maintain high accuracy in the presence of model uncertainties or sudden load changes [5,6,7,8]. An SMC scheme has emerged as an alternative to conventional PID controllers because of its robust properties and the simplicity in handling matched disturbances [9,10]. However, classical SMC typically suffers from chattering and may only guarantee asymptotic convergence, thus leading to unwanted oscillations and steady-state errors in practical implementations [11,12,13].

Adaptive sliding mode control (ASMC) techniques address some of these shortcomings by tuning the switching gain online in order to compensate for unknown disturbances, thereby reducing the chattering mechanism and also improving disturbance rejection [14]. However, most ASMC controllers still utilize first-order sliding surfaces which limit design flexibility, where a single scalar gain must maintain balance between speed of reaching and low chattering, and therefore steady-state errors can exist under constant disturbances. Moreover, existing stability proofs often focus on asymptotic stability without providing explicit bounds on the reaching time or a clear mechanism for eliminating steady-state error. Neural network controllers seek to learn and compensate for unmodeled dynamics offline or online, but they often require extensive training data, risk slow or unstable convergence, and typically guarantee only bounded-error performance rather than strict finite-time stability. Higher-order sliding mode methods, such as the super-twisting algorithm, can reduce the discontinuity of the control signal but introduce additional differential terms and more complex tuning procedures.

To overcome these limitations, an improved adaptive SMC controller is proposed with dynamic surface extension. The main contribution is a two-stage sliding variable where the primary surface incorporates both the proportional and integral terms, while a dynamic extension variable is utilized to shape the reaching phase via a tunable exponent. This proposed control structure decouples sliding-phase convergence from reaching dynamics, thus allowing the controller to independently adjust the speed of convergence, chattering levels, and steady-state accuracy of the overall system. An adaptive law is utilized to estimate the disturbance bound, thus ensuring robustness without overestimation. A three-step Lyapunov analysis is established for the finite-time convergence of the sliding variable and asymptotic tracking of the position error for the robotic manipulator system.

The remainder of this paper is organized as follows. Section 2 formulates the manipulator dynamics. Section 3 details the proposed control design, along with the stability proofs. Section 4 presents the results and comparative analyses. Finally, conclusions are provided in Section 5.

2. Analytical Modeling of the Manipulator

An $n$–degree-of-freedom rigid robotic manipulator is considered whose joint coordinates are collected in the matrix $q\left(t\right)$ given below.

$$q\left(t\right)={\left[q_1\left(t\right), q_2\left(t\right), \dots ,q_n\left(t\right)\right]}^T \in {\mathbb{R}}^n$$

Each link $i$ has mass $m_i$ and inertia tensor $I_i$ about its center of mass. The total kinetic energy is given as follows.

$$\mathrm{T}\left(q,\dot{q}\right) = {\displaystyle \frac{1}{2}}\hspace{0.17em} \dot{q^T} \mathrm{M}\left(q\right) \dot{\mathrm{q}}$$

Assuming gravity acts in the negative $z$-direction, the potential energy is given as follows.

$$V\left(q\right)=\sum _{i=1}^n{m}_i\hspace{0.17em}g\hspace{0.17em}{h}_i\left(q\right)$$

where $h_i\left(q\right)$ is the height of link $i$’s center of mass above a reference plane and $g$ is the gravitational acceleration. Therefore, the Lagrangian is given as follows.

$$\mathcal{L}\left(q,\dot{q}\right)=T\left(q,\dot{q}\right)-V\left(q\right)$$

Applying the Euler–Lagrange equation to each generalized coordinate $q_j$ gives the following result.

$${\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial \mathcal{L}}{\partial {\dot{q}}_j}}\right)-{\displaystyle \frac{\partial \mathcal{L}}{\partial q_j}}={\tau }_j+D_j\left(q,\dot{q}\right),\hspace{1em}j=1,\dots ,n$$

(1)

where ${\tau }_j$ is the actuator torque at joint $j$, and $D_j$ is an external matched disturbance (e.g., unmodeled dynamics or payload variation).

From Equation (1), the standard Euler–Lagrange form of the manipulator equation is given as follows.

$$M\left(q\right)\ddot{q}+C\left(q,\dot{q}\right)\dot{q}+G\left(q\right)+F\left(\dot{q}\right)=\tau +D\left(q,\dot{q}\right)$$

(2)

where

• $M\left(q\right)\in {\mathbb{R}}^{n\times n}$ is the symmetric, positive-definite inertia matrix.
• $C\left(q,\dot{q}\right)\in {\mathbb{R}}^{n\times n}$ collects Coriolis and centrifugal terms (chosen so that $\dot{M}-2C$ is skew-symmetric).
• $G\left(q\right)\in {\mathbb{R}}^n$ is the vector of gravitational torque.
• $F\left(\dot{q}\right)\in {\mathbb{R}}^n$ captures frictional or viscous effects.
• $\tau \in {\mathbb{R}}^n$ is the vector of control torque.
• $D\left(q,\dot{q}\right)\in {\mathbb{R}}^n$ is a lumped matched disturbance (e.g., payload variation and unmodeled dynamics), bounded by $‖D‖\le K$.

The state variables are defined as follows.

$$x_1=q, x_2=\dot{q}$$

Therefore, the state space form can be written from Equation (2) as follows.

$$\left\{\begin{array}{c}{\dot{x}}_1=x_2\\ {\dot{x}}_2=M^{-1}\left(q\right)\left[\tau +D\left(q,\dot{q}\right)-C\left(q,\dot{q}\right)x_2-G\left(q\right)-F\left(x_2\right)\right]\end{array}\right.$$

(3)

where ${\dot{x}}_1=x_2$ represents the velocity and ${\dot{x}}_2$ shows how the control $\tau$ and disturbance $D$ drive the acceleration, counteracted by inertia $M$, Coriolis/centrifugal force $C$, gravity $G$, and friction $F$.

3. Adaptive Controller Design

In this section, a new sliding surface is introduced that incorporates both proportional and integral action to enhance robustness against persistent disturbances. A dynamic extension along with the adaptive law is implemented that together ensure finite-time convergence of the sliding variable and asymptotic tracking of the position error. The tracking error between the actual joint position and the desired trajectory is defined as follows.

$$\begin{gathered} e\left(t\right)=x_1\left(t\right)-q_d\left(t\right) \\ \dot{e}\left(t\right)=x_2\left(t\right)-{\dot{q}}_d\left(t\right) \end{gathered}$$

where $x_1=q$ and $x_2=\dot{q}$ are the state variables, and $q_d\left(t\right)$ is the smooth, twice-differentiable reference trajectory. This error formulation is then utilized for constructing a sliding surface that drives both $e$ and $\dot{e}$ to zero as given below.

$$S\left(t\right)=\dot{e}\left(t\right)+\Lambda e\left(t\right)+\Gamma {\int }_0^{t}e\left(\tau \right)\hspace{0.17em}d\tau$$

(4)

Here, $\Lambda$ and $\Gamma$ are symmetric positive-definite gain matrices. The proportional term $\Lambda e$ shapes the error dynamics, while the integral term $\Gamma {\int }_0^{t}e$ guarantees zero steady-state error by accumulating past deviations. Differentiating $S$ with respect to time yields the following:

$$\dot{S}=\ddot{e}+\Lambda \dot{e}+\Gamma e=\dot{x_2}-\ddot{q_d}+\Lambda \left(x_2-\dot{q_d}\right)+\Gamma e$$

(5)

This equation highlights how the manipulator’s acceleration $\dot{x_2}\left(t\right)$ directly influences the sliding variable’s evolution. Substituting the full Euler–Lagrange dynamics in Equation (5) gives the following result.

$$\dot{S}=M^{-1}\left(q\right)\left[\tau +D-C\left(x_1,x_2\right)x_2-G\left(x_1\right)-F\left(x_2\right)\right]-\ddot{q_d}+\Lambda \left(x_2-\dot{q_d}\right)+\Gamma e$$

(6)

All the model-dependent and reference terms (excluding $\tau$) are combined into a single function denoted by $h\left(x\right)$, given as follows.

$$h\left(x\right)=M^{-1}\left(q\right)\left[C{x}_2+G+F\right]+\ddot{q_d}-\Lambda \left(x_2-\dot{q_d}\right)-\Gamma e$$

In order to achieve finite-time convergence without excessive control gains, the sliding surface is augmented with an auxiliary variable $\chi \left(t\right)$, as follows.

$$\begin{gathered} J\left(t\right)=S\left(t\right)+\chi \left(t\right), \\ \dot{\chi }={\rho }_1{‖S‖}^{\alpha }sgn\left(S\right)-{\rho }_2{‖J‖}^{\alpha }sgn\left(J\right), 0<\alpha <1, { \rho }_1,{\rho }_2>0, { \rho }_1\ne {\rho }_2 \end{gathered}$$

(7)

The exponent $\alpha$ shapes the reaching law in order to tune the convergence speed versus smoothness. Differentiating $J$ and substituting from Equations (6) and (7) gives the following:

$$\dot{J}=\dot{S}+\dot{\chi }$$

(8)

The control input is chosen as shown below.

$$\tau =-M\left(q\right)\left[h\left(x\right)+\dot{\chi }+\Xi J+\widehat{K}{\displaystyle \frac{J}{‖J‖}}\right]$$

(9)

where $\mathsf{\Xi }$ is a positive-definite gain matrix, and $\widehat{K}(t)$ is an online estimate of the unknown disturbance bound. In order to avoid overestimation, the gain $\widehat{K}(t)$ is adaptively tuned online as shown below.

$$\dot{\widehat{K}}=\gamma ‖J‖, \gamma >0$$

(10)

This ensures that $\widehat{K}(t)$ grows only as needed to counteract the measured sliding deviation. The Lyapunov function is chosen as shown below.

$$V_1={\displaystyle \frac{1}{2}}{J}^{T}J+{\displaystyle \frac{1}{2\gamma }}{\left(K-\widehat{K}\right)}^2$$

(11)

where $K$ is the bound on the true disturbance. By taking the time derivative of $V_1$,

$$\dot{V_1}=J^T\dot{J}-{\displaystyle \frac{1}{\gamma }}\left(K-\widehat{K}\right)\dot{\widehat{K}}$$

(12)

$$\begin{gathered} =J^T\left(-\Xi J-\widehat{K}{\displaystyle \frac{J}{‖J‖}}+D\right)-\left(K-\widehat{K}\right)‖J‖ \\ \le -J^T\mathsf{\Xi }J-\widehat{K}‖J‖+‖J‖K-\left(K-\widehat{K}\right)‖J‖ \\ \le -{\lambda }_{min}\left(\Xi \right)|J{|}^2 \end{gathered}$$

Therefore, $V_1\left(t\right)$ is non-increasing and hence guarantees boundedness of $J$ and $\widehat{K}$, with $J\to 0$. By Barbalat’s lemma, $J\left(t\right)\to 0$ as $t\to \infty$. Therefore, once $J\left(t\right)=S\left(t\right)+\chi \left(t\right)$ becomes zero, then Equation (7) simplifies to the following:

$$\dot{S}=-{\rho }_1{‖S‖}^{\alpha }sgn\left(S\right)$$

(13)

The second Lyapunov function is selected as follows.

$$V_2={\displaystyle \frac{1}{2}}{S}^{T}S$$

Therefore,

$$\dot{V_2}=-{\rho }_1{‖S‖}^{(1+\alpha )}$$

(14)

Hence the finite reaching time bound is obtained as below.

$$T_S\le {\displaystyle \frac{{‖S\left(0\right)‖}^{(1-\alpha )}}{\left(1-\alpha \right){\rho }_1}}$$

(15)

After $S\left(t\right)$ becomes equal to zero, Equation (4) becomes

$$\dot{e}=-\Lambda e-\Gamma {\int }_0^{t}e\left(\tau \right)\hspace{0.17em}d\tau$$

(16)

The third Lyapunov function is defined as

$$V_3={\displaystyle \frac{1}{2}}{e}^{T}e+{\displaystyle \frac{1}{2}}{‖{\int }_0^{t}e\left(\tau \right)\hspace{0.17em}d\tau ‖}^2$$

(17)

Therefore,

$$\dot{V_3}=-e^T\Lambda e\le -{\lambda }_{min}\left(\Lambda \right){‖e‖}^2$$

(18)

Since $V_3$ is strictly decreasing, $e\left(t\right)\to 0$ and ${\int }_0^{t}e\to 0$ as $t\to \infty$. Therefore, the closed-loop system achieves robust finite-time convergence of $S$ and asymptotic convergence of the tracking error $e$. Although richer in operations, the added costs of our integral action, exponent shaped reaching law, and adaptive gain update are minor relative to the existing model-based computations. The result is a controller that remains fully real-time implementable on standard industrial hardware while delivering significant performance and robustness gains.

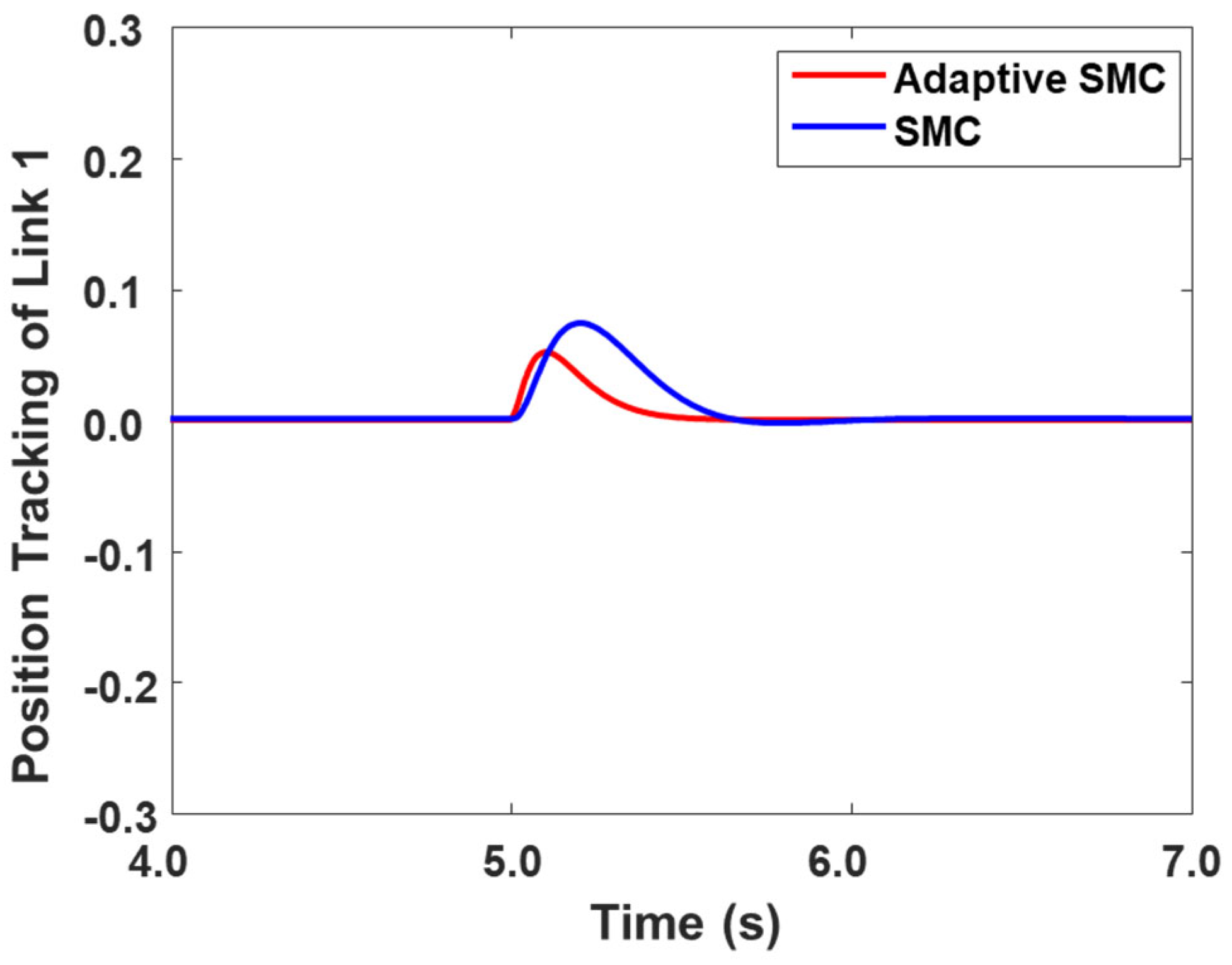
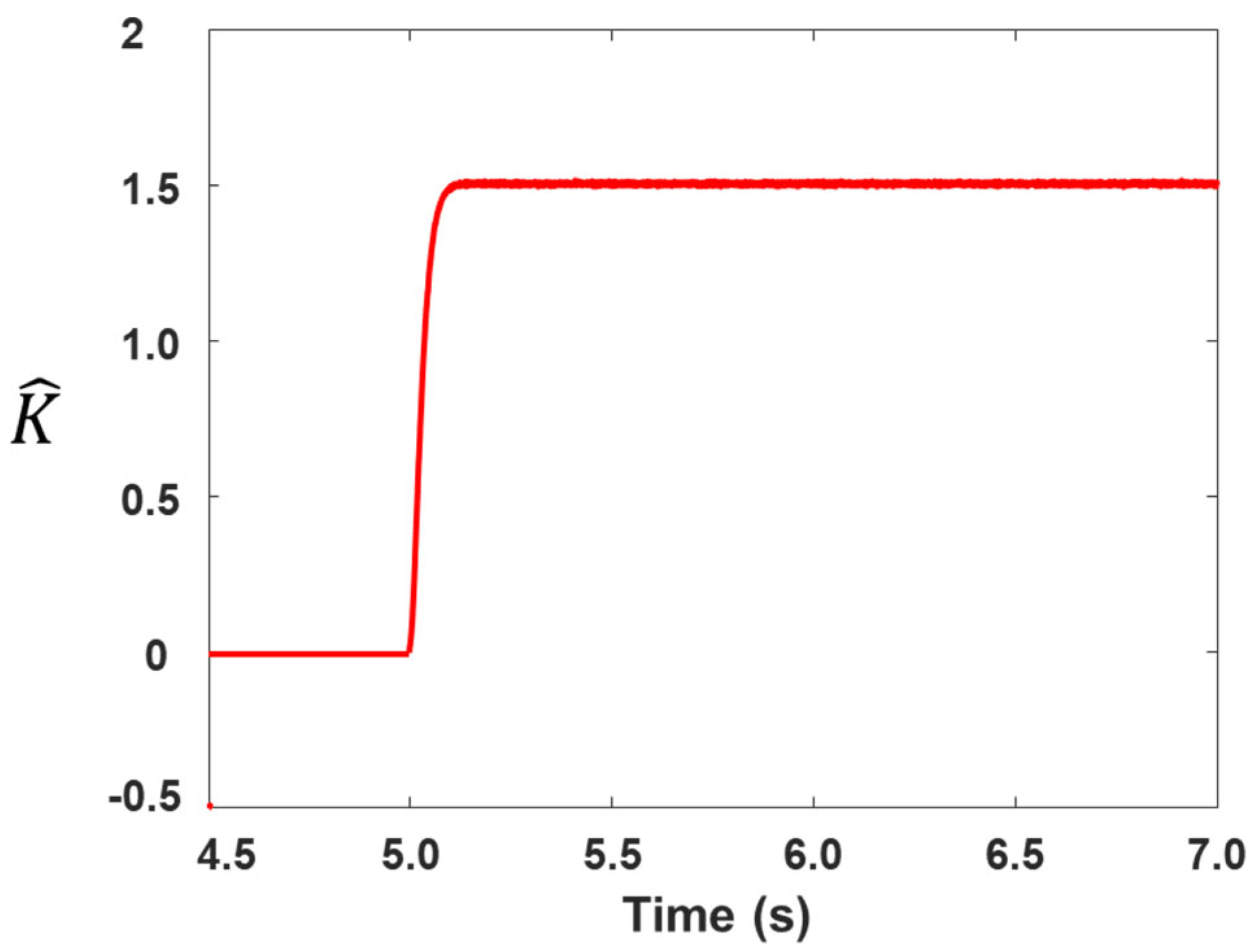
4. Results

In order to validate the performance of the proposed adaptive integral dynamic sliding–mode controller, a planar two-link robotic manipulator was simulated in MATLAB/Simulink 2022. The desired trajectories for both joints were chosen as smooth exponential functions over a 20 s horizon, as given below.

$$\begin{gathered} q_{d1}\left(t\right)=2e^{-t}+3e^{-4t} \\ {q}_{d2}\left(t\right)=3e^{-t}-0.25e^{-4t} \end{gathered}$$

The mass of link 1 and link 2 was 1 kg and 0.8 kg, respectively. The lengths of link 1 and link 2 were 1.0 m and 0.8 m, respectively. The proportional gain matrix was chosen as $\Lambda =\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\right[20,20\left]\right)$ in order to ensure sufficient stiffness in the surface dynamics without inducing high-frequency oscillations. The integral gain matrix was chosen as $\Gamma =\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\right[8,8\left]\right)$ so that the integral term corrected steady errors gradually. The value of $\alpha$ was selected as 0.7 to keep a balance between chattering and acceleration of reaching phase. The adaptation rate parameter $\gamma$ was selected as 0.1 to mitigate estimator noise while still tracking disturbance changes. The reaching law gains ${\rho }_1$ and ${\rho }_2$ were kept as 5 and 3, respectively, in order to enforce a faster approach to the manifold than dynamic smoothing. The sliding phase gain was selected as $\mathsf{\Xi }=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\right[18,18\left]\right)$ in order to shape the decay of $J$. The results were obtained by using a fixed-step solver with 1 ms step size.

Under nominal conditions (no disturbance), the controller achieved tracking errors below 0.01 rad within 0.7 s. Figure 1 and Figure 2 show joint-1 and joint-2 tracking responses overlapped almost perfectly with the references, and the sliding variable $S$ was brought to zero in finite time as predicted by Equation (15). The auxiliary variable $J$ decayed smoothly without overshoot, confirming the effectiveness of the dynamic extension and adaptation law. The corresponding profiles of the position error for link 1 and link 2 are given in Figure 1b and Figure 2b, respectively.

A matched disturbance consisting of a sudden 1.5 Nm payload torque at $t=5 \mathrm{s}$ was introduced. The controller reacted swiftly to the disturbance and the disturbance estimate $\widehat{K}$ rose from zero to the true bound within 0.1 s, and the sliding surface converged back to zero within 0.4 s. The maximum transient tracking error peaked at 0.05 rad, then returned to below 0.01 rad. In contrast, a classical SMC controller exhibited a larger overshoot of 0.08 rad and took over 0.75 s to recover, illustrating the effectiveness of our integral-augmented surface and tunable exponent adaptive controller. Figure 3 shows the comparison of the disturbance rejection performance of the classical SMC controller and our proposed adaptive SMC controller. The corresponding plot of the disturbance estimate $\widehat{K}$ is given in Figure 4.

In order to quantitatively demonstrate chattering reduction, we introduced two metrics evaluated over the steady-state window $t\in [7,10]$ s after all transients had died out.

(i) 

RMS Torque Variation

$${\mathit{CI}}_{\mathit{RMS}}=\sqrt{{\displaystyle \frac{1}{T}}{\int }_{t_0}^{t_0+T}{\left({\tau }_i\left(t\right)-{\overline{\tau }}_i\right)}^{2}dt}$$

where $\mathrm{CI}$ is the chattering index, ${\overline{\tau }}_i$ is the mean torque on joint $i$, and $T=3$ s.

(ii) 

Peak-to-Peak Amplitude

$$∆{\tau }_{pp}=max {\tau }_i\left(t\right)-\mathit{min}{\tau }_i\left(t\right), t\in [7,10]$$

The corresponding results for joint 1 are given in Table 1, which clearly indicates the effectiveness of the proposed adaptive controller.

Table 1. Chattering reduction comparison of the traditional SMC and our proposed ASMC.

Metric	Traditional SMC	Proposed Method	Reduction
${\mathit{CI}}_{\mathit{RMS}}$ (N-m)	0.046	0.027	41.3%
$∆{\tau }_{pp}$ (N-m)	0.21	0.13	38.1%

Table 1. Chattering reduction comparison of the traditional SMC and our proposed ASMC.

Metric	Traditional SMC	Proposed Method	Reduction
${\mathit{CI}}_{\mathit{RMS}}$ (N-m)	0.046	0.027	41.3%
$∆{\tau }_{pp}$ (N-m)	0.21	0.13	38.1%

5. Conclusions

A new adaptive sliding-mode controller is proposed featuring an integral-augmented sliding surface and a generalized dynamic extension. The three-stage Lyapunov design guarantees finite-time convergence of the sliding variable, zero steady-state error, and asymptotic tracking of joint positions in the presence of uncertainties. We conducted a simulation on a two-link manipulator under sudden load changes. The controller adaptively estimated unknown disturbances and ensured finite-time convergence of the sliding variable, while chattering and steady-state errors were suppressed by including the integral term in the dynamic extension. The results confirmed our model’s superior performance over the classical SMC controller in terms of faster recovery, smaller overshoot, and reduced chattering.