Selective Intersection Flow: A Lightweight Optical Flow Algorithm for Micro Drones ^†

Abstract

In this study, selective intersection flow (SIF), a lightweight optical flow algorithm, was used to enhance efficiency and accuracy by filtering out non-contributive pixels. SIF, derived from the differential category of algorithms, is used to compute optical flow by analyzing intersections of equations from selected pixels rather than solving for all pixels. It replaces warping with a minimal computational procedure for initial flow estimate and employs a sliding window for optimized single-core performance. SIF runs 1.7–1.8 times faster and achieves 1.2–1.4 higher accuracy than the single iteration of the Lucas–Kanade method, showing promise for real-time micro drone navigation.

1. Introduction

Optical flow estimation is essential to image processing, with modern techniques using deep learning and convolutional neural networks (CNNs) [1] that show high accuracy. However, these methods demand intensive graphics processing unit (GPU) resources and high power consumption to achieve real-time performance. Traditional approaches, in contrast, offer a trade-off: methods provide high speed but moderate accuracy, while block-matching methods [2] are more accurate yet slower.

This study aims to develop an optical flow algorithm for obstacle avoidance in micro drone navigation. Recent methods demand more computational power than the intended platform can provide. While traditional differential techniques are well-suited for real-time use, they often compromise accuracy. In the differential approach, it is assumed that the displacement of the image between two consecutive frames is small and approximately constant with neighboring points (x_n, y_n) under consideration. This assumption leads to the classic optical flow equation $IxVx+IyVy=-It$.

This is a linear equation of two variables, Vx and Vy, which represent the components of the optical flow vector in the x and y directions, while Ix, Iy, and It are the spatial and temporal gradient at (x, y, t). For each pixel, there is an infinite number of solutions for the flow (Vx and Vy). By assuming neighboring pixels share the same flow and solving the simultaneous equations within a small window, the Lucas–Kanade algorithm [3] yields an estimated flow that is refined through iterative processing. Enhanced versions of the algorithms employ pyramidal structures [4] and techniques, such as patch-and-stride [5] to lower computational costs.

We developed an optical flow algorithm that is more accurate and faster than the one-iteration Lucas–Kanade (simpleLK) variant. Optical flow techniques are either sparse or dense. Given that the motion in drone footage is primarily due to the camera rather than moving objects, the developed algorithm effectively produces dense optical flow.

2. Materials and Methods

2.1. Basic Concept

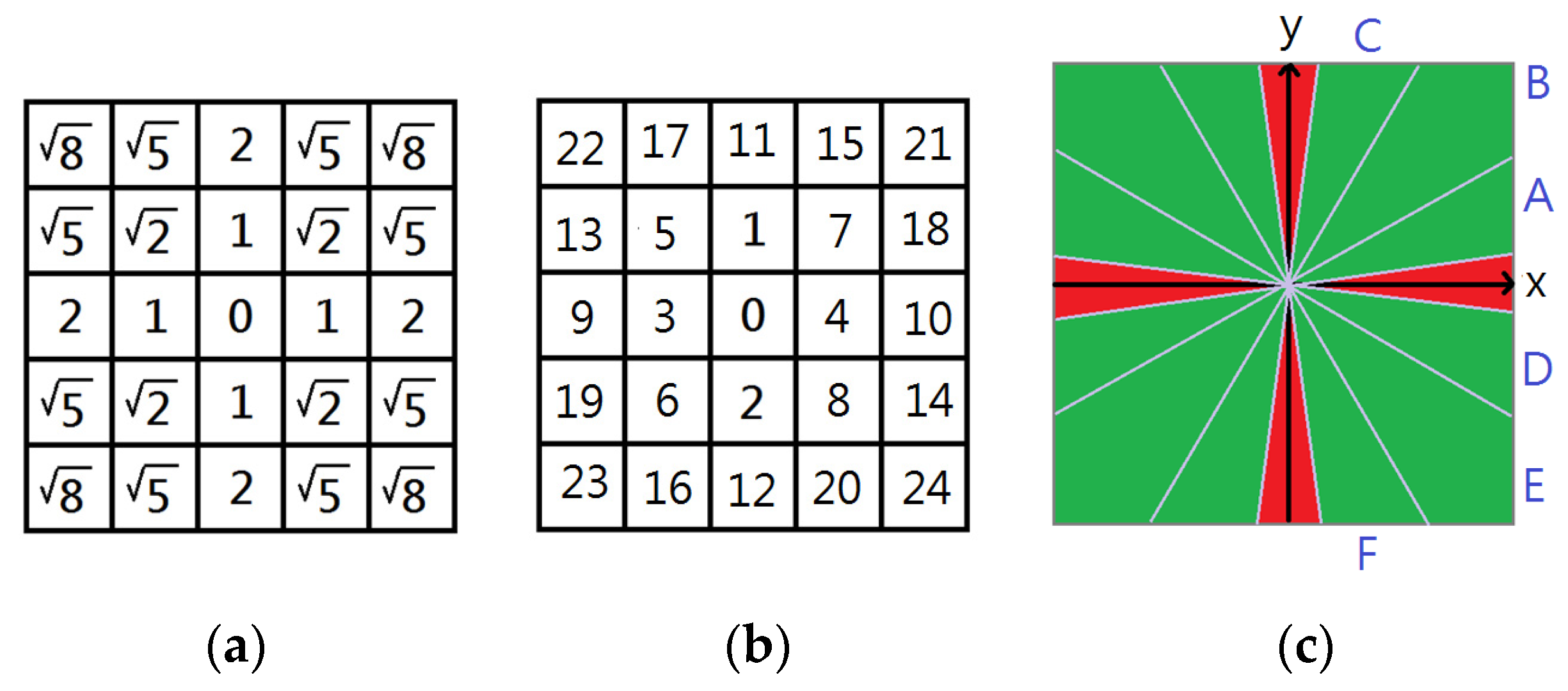
In the lines formed by $IxVx+IyVy=-It$ and a 5 × 5 window, 25 lines emerge on the Vx, Vy plane. While most lines converge near the true optical flow, several deviate significantly (Figure 1a). Removing these outliers reduces both computational load and errors (Figure 1b).

When enough qualified lines remain, we use a lightweight method to select the best ones and compute their intersections. The geometric center of these intersections approximates the true optical flow. When intersections stray from the estimated flow (Figure 1b), a filter is applied to remove them before the final calculations. The SIF algorithm performs this efficiently in eight non-iterative steps (Figure 1c).

2.2. SIF Step 1—Blurring

Blurring is a pre-processing step used in many optical flow algorithms. The optical flow algorithm better adapts to larger optical flows by incorporating pixels from a larger area. In SIF, unweighted square window blurring is applied with a window size of 5 × 5 pixels.

2.3. SIF Step 2—Gradient Computation

Considering the gradient Ix (or Iy) at position (x, y) is calculated using values at x + 1 (or y + 1) and x − 1 (or y − 1), we also compute the gradient at t using values at t + 1 and t − 1 (Equation (1)) rather than the traditional t + 1 and t as in most optical flow algorithms. This symmetric temporal and spatial gradient enhances the accuracy of optical flow estimates. The equation is improved through the computation of gradients Ix and Iy by including the second terms of the Taylor expansion as shown in Equations (2) and (3).

$$It=(I(x,y,t+1)-I(x,y,t-1))/2$$

(1)

$$Ix=(8\cdot I(x+1)-8\cdot I(x-1)-I(x+2)+I(x-2))/12$$

(2)

$$Iy=(8\cdot I(y+1)-8\cdot I(y-1)-I(y+2)+I(y-2))/12$$

(3)

2.4. SIF Step 3—Intercept Filtering

The filtering process removes lines that distort the optical flow computation by eliminating those far from the true solution in the Vx–Vy plane. In practice, since the true optical flow is unknown, we pre-estimate a potential flow—if unavailable, the coordinate origin serves as a reference.

Instead of calculating the computationally expensive point-to-line distance, we use the line’s intercepts with the coordinate axes as a surrogate. The absolute value of an intercept approximates the distance from the reference point, while its sign indicates the quadrants through which the line passes, which is useful in a later step.

A key parameter, InterceptFilter (CF), determines qualification: if both the absolute x- and y-intercepts are below CF, the line is kept (Figure 2a); otherwise, it is discarded. When a pre-estimated optical flow is available, shifting the coordinate origin to that flow markedly improves accuracy (Figure 2b).

2.5. SIF Step 4—Slope Filtering

This step involves another key parameter, SlopeFilter (abbreviated as SF), to eliminate lines with slopes that are nearly horizontal or vertical. For example, when SF = 10, lines with absolute slopes greater than 10 or less than 0.1 are deemed unqualified.

2.6. SIF Step 5—Sequential Line Selection

If a sufficient number of lines pass the intercept and slope filters, we then select a subset to reduce the intersection computation load cost-effectively. Two parameters guide this process: MinLine and MaxLine. If qualified lines number fewer than MinLine, the optical flow is deemed unreliable, and (0, 0) is returned; if there are more, only up to MaxLine lines are chosen. The selection prioritizes lines originating near the center pixel, based on a fixed prearranged order that eliminates extra distance calculations (Figure 3a,b). To further improve quality, diversity in slopes must be ensured by dividing the plane into three sections for positive slopes and three for negative slopes (Figure 3c). Qualified lines are assigned to their respective slope queues and then selected in a round-robin fashion.

2.7. SIF Step 6—Intersection Filter

Intersections between two lines with similar slopes can stray far from the main cluster (Figure 1b). Consequently, we accept only intersections formed by one positive-slope line and one negative-slope line. This rule, along with prior slope filtering, ensures sufficient slope difference and reduces the number of calculated intersections. Accordingly, during line selection, we count positive- and negative-slope lines separately relative to the MinLine and MaxLine thresholds.

2.8. SIF Step 7—Density Augmentation

After processing every pixel, a dense optical flow field is theoretically obtained. However, due to filtering and the MinLine requirement, several regions may lack computed flow, resulting in lower density than methods such as simpleLK. To remedy this, post-processing increases density: for any pixel without computed flow, the average of the flows from the pixels in the surrounding region (defined by the parameter window size) is used as the optical flow for that pixel.

2.9. SIF Step 0—Guessing Pre-Flow

In the Intercept Filter section, the term “pre-estimate optical flow” refers to a quick initial guess that can significantly boost accuracy if computed with minimal cost. We explored three methods for generating the pre-estimate.

• Temporal smoothing: If optical flow changes smoothly, use the flow from the previous frame.
• Low-resolution estimate: Compute the optical flow on a downscaled image (without a pre-estimate), then upscale it for full-resolution computation.
• Quadrant penalty: Analyze each line’s slope and intercept to determine which quadrant is least likely to contain the true flow. Assign penalties based on this analysis, then adjust the qualified range of CF according to the quadrant with the lowest total penalty.

For temporally smooth flows, the first method offers the best speed and accuracy. For rapid motions—such as from a fast-moving camera—the low-resolution approach (method 2) yields better results, while the third method is useful in other scenarios.

2.10. Evaluation

The performance of the developed optical flow algorithm is evaluated using three metrics: endpoint error (EPE), normalized endpoint error (NEPE), and density (den). Among these, NEPE is the primary metric, which is a scalar calculated by dividing EPE by the length of ground truth.

2.11. Dataset

The MidAir Dataset is used in the present study [6]. It contains 5 videos that simulate an observer (camera) flying in different environments under four weather conditions, with 325 frames in each video and the ground truth of optical flow between each frame.

3. Results

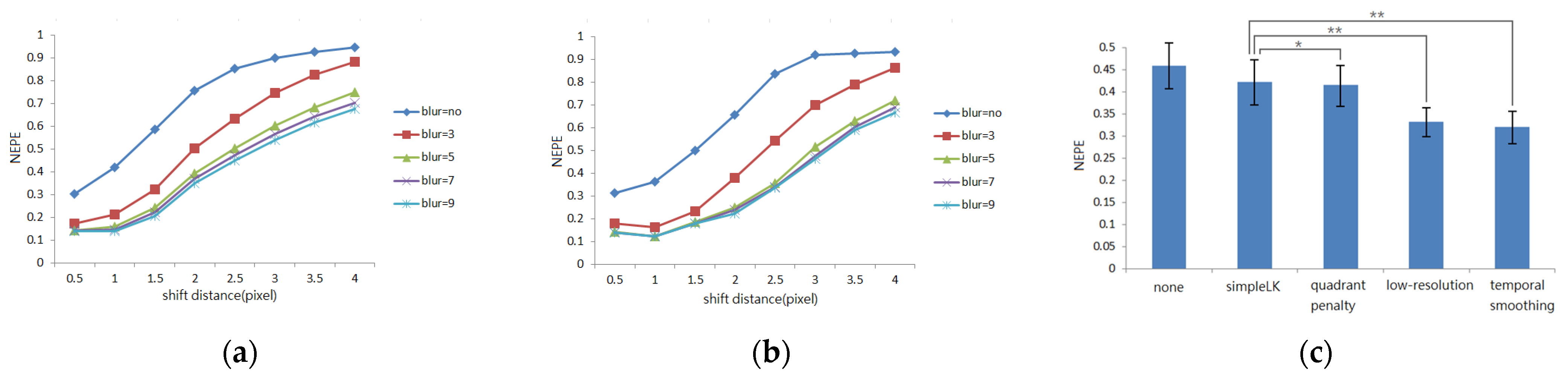
3.1. Windowsize of Blur and Improved Gradient

Blurring primarily improves the algorithm’s ability to handle larger optical flows. We tested window sizes from 3 to 9 and optical flow lengths from 0.5 to 4.0 pixels using both simpleLK and SIF (Figure 4a,b). To generate flows of specific lengths, we translated an image in three directions and used the average NEPE as the performance metric for each parameter combination. By combining blurring with enhanced gradient computation, both algorithms reliably process flows up to three pixels. Because accuracy improvements plateau with window sizes over five, we set windowsize = 5 in subsequent experiments.

3.2. Value of Other Parameters

Through similar experiments as above, we identified the optimal set of parameters as follows: Minline = 3, Maxline = 7, CF = 1.5 (with pre-estimate) or 8.5 (without pre-estimate), SF = 10.

3.3. Different Guesses of Pre-Flow

We evaluated various optical-flow pre-estimation methods using a video segment from the MidAir Dataset. Five methods were tested: a baseline with no pre-estimate (all zeros) and simpleLK for comparison. Each method was applied to five video segments with nine frames per segment (45 data points total). The results confirmed the effectiveness of our pre-estimation strategies (Figure 4c).

3.4. Performance on MidAir Dataset

We visualized the optical flow direction and magnitude using colors and compared the original images from the MidAir Dataset, the ground truth, and the results of the SIF algorithm both before and after density enhancement (Figure 5).

3.5. Comparison of Speed, Error, and Density

To compare the speed of the algorithms, we ran the C++ implementation repeatedly 10 times on an Intel i7 single-core computer processing unit (CPU) and took the average runtime (excluding image reading, error calculations, etc.) for each frame. The results confirmed that SIF is faster than simpleLK (

Table 1. Comparison of simpleLK and SIF.

Metric	simpleLK	SIF
NEPE (ratio)	0.432 (1)	0.333 (0.771)
Time(ms) (ratio)	157.6 (1)	84.4 (0.536)
Density (ratio)	0.970 (1)	0.786 (0.810)

). The SIF variation here uses low resolution as the pre-estimate.

4. Conclusions

In this study, we introduce SIF, a lightweight optical flow algorithm that balances efficiency with accuracy. Unlike traditional differential methods, SIF filters out non-contributory pixels and computes flow by analyzing intersections of filtered equations rather than solving equations for every pixel, thereby reducing computational overhead. We further enhance efficiency by replacing the costly warping step in pyramidal techniques with a lightweight initial flow estimate. SIF runs 1.7–1.8 times faster and achieves 1.2–1.4 higher accuracy than a single iteration of the Lucas–Kanade method. The primary application for the SIF algorithm is obstacle avoidance in micro drones. Given their low flight speeds and limited camera resolution, their inability to process flows larger than three pixels and their lower density are acceptable drawbacks. Nonetheless, there is still potential to improve accuracy, speed, and flow density. A further limitation is the algorithm’s inflexibility; its symmetric computation prevents the use of warping, which means iterative or pyramidal techniques cannot be applied to boost accuracy or handle larger flows. The developed SIF algorithm provides a lightweight method for optical flow estimation. Its integration into an optical flow-based obstacle avoidance system for micro drones highlights its potential for real-time navigation.