Abstract
An iterative method was developed in this study within a Petri net system (PNS) for flexible manufacturing systems (FMSs) to eliminate deadlocks. The algorithm employs variant tokens, ranging from a few to many, in idle places to identify subnet deadlocks through reachability states. Additionally, it utilizes the place invariant (PI) to resolve deadlocks. An algorithm with a simple example was developed and applied using a complex scenario. The developed algorithm is user-friendly and effectively eliminates deadlocks in the PNS of FMSs, producing optimal results.
1. Introduction
Deadlocks occur from simultaneous attempts to access and share a resource, creating an undesired situation in a Petri net of flexible manufacturing systems. The sole method to resolve deadlocks is to reassign the workflow of the shared resource. Three solutions are used to eliminate deadlocks: deadlock avoidance, deadlock detection and recovery, and deadlock prevention [1,2].
Deadlock avoidance involves implementing an online control method to identify the correct evolution of the Petri net system (PNS). The primary objective is to ensure that the PNS avoids deadlocks and operates smoothly. Consequently, this method does not eliminate all deadlocks in the PNS [3,4,5]. The second method is deadlock detection and recovery. When deadlocks happen, a deadlock-free state is detected, and the deadlock is omitted by relocating resources. Generally, this approach demands a large amount of data to guide the algorithm, making it complex, especially with shared resources [6,7,8,9,10]. The third method is the deadlock prevention policy. This method aims to prevent deadlocks statically for optimal reachability states. No dead markings are reached after implementing the deadlock prevention policy. We used the deadlock prevention policy to address deadlocks in the PNS to obtain optimal results [1,2,6,11]. We employed variant token numbers in specific locations to detect deadlocks and applied the PI to eliminate them through iterative computation. The algorithm yielded results consistent with those in Ref. [6].
2. Iterative Synthesis and PI
We introduced the deadlock prevention policy in this study [12]. We employed iterative syntheses as a proactive approach to eliminate deadlocks within the PNS. This strategy aligns with the findings and recommendations presented in the referenced report, contributing to the enhancement of deadlock resilience in our system.
For two idle places (p1, p4), two resource places (p7, p8), and operation places (active places), the saturated line is (p1, p4) = (2, 2) [13] and the maximal reachability states are 8. In this case, the PNS has one deadlock. The PI is obtained by using the control place (CP) equation ) where Dc is the PNS controller, L is an nc × n matrix, Dp is the PNS of the process, uc is the marking of the controller places which is an nc × 1 vector, b is an nc × 1 vector, and up is the marking vector of PNS modeling the process [12,14,15,16]. nc is the number of constraints by the ui + uj ≤ 1 where ui and uj are the marking places of pi and pj by the process PNS. One can refer to [12] for a more in-depth description.
The iterative number token of the idle places from the small to the saturated line [13] was used to search the deadlocks. Then, the PI was used to obtain CPs (Dc) and select dead marking minus 1. The algorithm is presented in Figure 1. The maximal reachability states (RSs) are 8, and the saturated line is (p1, p4) = (2, 2). When (p1, p4) is equal to (1, 1), a dead marking (M4 = p2 + p5) is obtained. The operation places are omitted. According to the dead marking, Dp is obtained using Equation (1). Dc () when Dc = t2 + t5 − t1 − t4. The dead marking coefficient sum (DMCS) is 2 in this case. By subtracting 1 from the DMCS, the marking of the controller places (uc = 1) is obtained.
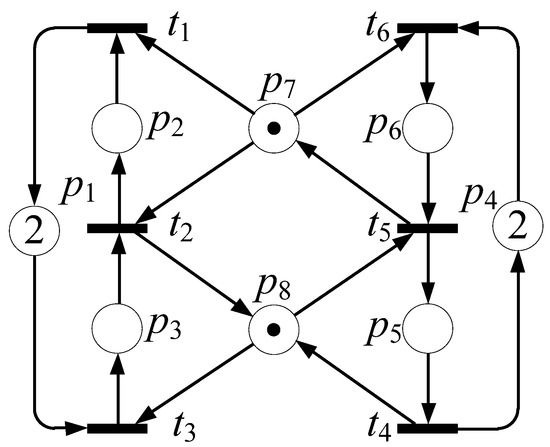
Figure 1.
Simple PNS [14].
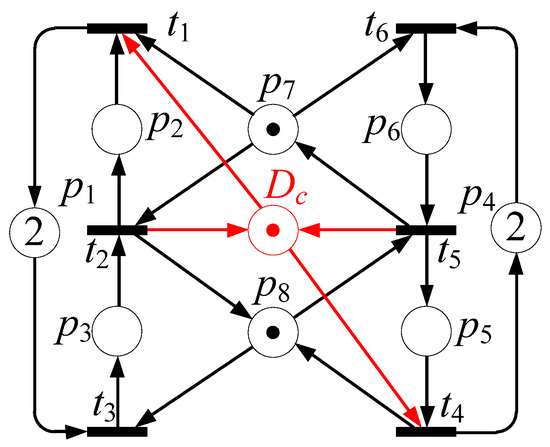
Figure 2.
Simple Petri net with CP.
In the above algorithm, the following parameters are defined.
- Input: PNM prone to deadlocks
- Output: PNM without deadlocks
- Saturated line for PNS
- Subtracting 1 from the saturated line as the token number in idle places
- Searching the dead markings
- to obtain CPs
- Zero deadlocks
- Obtaining the live PNS
- End
3. FMS
An FMS of the factory is shown in Figure 3a and its sequence production is illustrated in Figure 3b [6,11]. The PNS is illustrated in Figure 4. In the figure, p21 and p22 are I/O (input and output), p12, p13, and p15 are machines 1–3, p11, and p14 are robots 1–2. The initial reachability states are 380; this PNS has a live lock, so it is not live and not reversible.
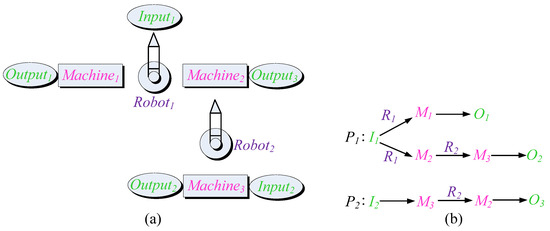
Figure 3.
(a) Layout of FMS and (b) sequences of production [6,11].
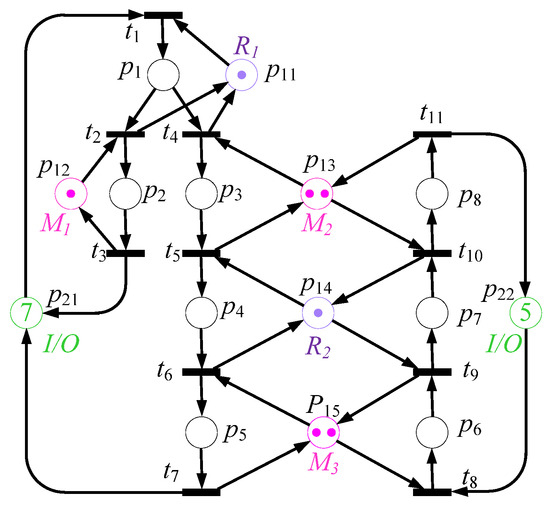
Figure 4.
PNS of FMS [3,4].
In the developed method, (p21, p22) = (1, 2) and the dead marking was (p11 + p12 + 2p13 + p4 + 2p6). From the deadlock, we only considered the operation places (p4 + 2p6) and omitted other places. The total token number in operation places was 3. To limit the step not to enter p4 + 2p6, d the dead marking must be avoided. This means that u4 + u6 ≤ 2 and the control token is 2 [12]. cis calculated as follows.
CP 1 is obtained as Dc1 = −t5 + t6 − t8 + t9 by using . When (p21, p22) = (2, 1), the dead marking is 2cp1 + p11 + p12 + 2p15 + 2p3 + p7. When u3 + u7 ≤ 2 and Dc2 = −t4 + t5 − t9 + t10, is calculated as follows.
When (p21, p22) = (2, 2), the dead marking is p11 + p12 + p14 + 2p3 + 2p6. When u3 + u6 ≤ 3 and Dc3 = −t4 + t5 − t8 + t9, is calculated as follows.
CPs are presented in Table 1 and Figure 5.

Table 1.
Three CPs.
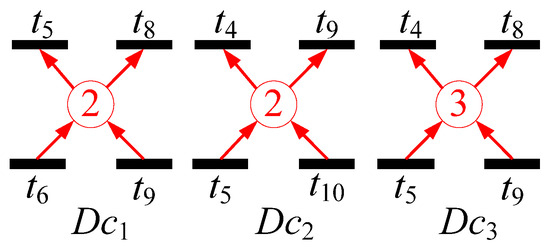
Figure 5.
CPs.
Table 2 presents a comparison of the CP number, the number of tokens in each CP, and the reachability states (RSs) with those in Ref. [6].

Table 2.
Comparison of results.
4. Conclusions
We identified deadlocks through the repeated analysis of small blocks and the application of the PI method. The developed algorithm in this study was experimentally proven to be feasible [18,19,20,21,22]. Optimal results were obtained by employing the theory of regions [23] and dividing the PNS structure into subnets to identify CPs. By utilizing simple variant tokens in idle places, we constructed the subnet PNS, thereby simplifying deadlocks in the reachability graph. This approach enables easy access to CPs and successfully mitigates the state exploration problem [18,19,20,21,22]. In future research, it is necessary to extend the applicability of the algorithm to larger PNSs and obtain optimal results.
Author Contributions
Conceptualization, S.-C.L. and T.-C.R.; methodology, S.-C.L. and T.-C.R.; software, T.-C.R.; validation, S.-C.L., J.-F.C. and T.-C.R.; formal analysis, S.-C.L. and T.-C.R.; investigation, S.-C.L. and T.-C.R.; resources, S.-C.L., J.-F.C. and T.-C.R.; data curation, S.-C.L. and T.-C.R.; writing—original draft preparation, S.-C.L. and T.-C.R.; writing—review and editing, S.-C.L. and T.-C.R.; visualization, J.-F.C.; supervision, S.-C.L. and T.-C.R.; project administration, S.-C.L. and J.-F.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study was exempt from ethical review and approval.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data provided in this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Uzam, M. An Optimal Deadlock Prevention Policy for Flexible Manufacturing Systems Using Petri Net Models with Resources and the Theory of Regions. IEEE Int. J. Adv. Manuf. Technol. 2002, 19, 192–208. [Google Scholar] [CrossRef]
- Uzam, M. The use of Petri net reduction approach for an optimal deadlock prevention policy for flexible manufacturing systems. IEEE Int. J. Adv. Manuf. Technol. 2003, 23, 204–219. [Google Scholar] [CrossRef]
- Hsieh, F.S.; Chang, S.C. Dispatching-driven deadlock avoidance controller synthesis for flexible manufacturing systems. IEEE Trans. Robot. Automat. 1994, 10, 196–209. [Google Scholar] [CrossRef]
- Fanti, M.P.; Maione, B.; Mascolo, S.; Turchiano, A. Event-based feedback control for deadlock avoidance in flexible production systems. IEEE Trans. Robot. Automat. 1997, 13, 347–363. [Google Scholar] [CrossRef]
- Yim, D.-S.; Kim, J.-I.; Woo, H.-S. Avoidance of deadlocks in flexible manufacturing systems using a capacity-designated directed graph. Int. J. Prod. Res. 1997, 35, 2459–2476. [Google Scholar] [CrossRef]
- Uzam, M.; Zhou, M.C. An Iterative Synthesis Approach to Petri Net-Based Deadlock Prevention Policy for Flexible Manufacturing Systems. IEEE Trans. Syst. Man Cybern. A Syst. Hum. 2007, 37, 362–371. [Google Scholar] [CrossRef]
- Row, T.C.; Pan, Y.L. An Optimal Deadlock Recovery Algorithm for Special and Complex Flexible Manufacturing Systems-S4PR. IEEE Access 2021, 9, 111083–111094. [Google Scholar] [CrossRef]
- Row, T.C.; Syu, W.M.; Pan, Y.L.; Wang, C.C. One Novel and Optimal Deadlock Recovery Policy for Flexible Manufacturing Systems Using Iterative Control Transitions Strategy. Math. Probl. Eng. 2019, 2019, 1–12. [Google Scholar] [CrossRef]
- Wysk, R.A.; Yang, N.S.; Joshi, S. Resolution of deadlocks in flexible manufacturing systems: Avoidance and recovery approaches. J. Manuf. Syst. 1994, 13, 128–138. [Google Scholar] [CrossRef]
- Cho, H.; Kumaran, T.K.; Wysk, R.A. Graph-theoretic deadlock detection and resolution for flexible manufacturing systems. IEEE Trans. Robot. Automat. 1995, 11, 413–421. [Google Scholar]
- Ezpeleta, J.; Colom, J.M.; Martinez, J. A Petri net based deadlock prevention policy for flexible manufacturing systems. IEEE Trans. Robot. Autom. 1995, 11, 173–184. [Google Scholar] [CrossRef]
- Yamalidou, K.; Moody, J.; Lemmon, M.; Antsaklis, P. Feedback control of Petri nets based on place invariants. Automatica 1996, 32, 15–28. [Google Scholar] [CrossRef]
- Row, T.C.; Lee, S.C.; Pan, Y.L. Identifying the Saturated Line Based on the Number of Idle Places: Achieving Precise Maximal Permissiveness without Deadlocks Using Control Transitions or CPs. Processes 2023, 11, 2325. [Google Scholar] [CrossRef]
- Li, Z.; Wu, N.; Zhou, M. Deadlock Control of Automated Manufacturing Systems Based on Petri Nets—A Literature Review. IEEE Trans. Syst. Man Cybern. Part C 2011, 42, 437–462. [Google Scholar]
- Row, T.C.; Pan, Y.L. Incomparable Single Controller for Solving Deadlock Problem of Flexible Manufacturing Systems. IEEE Access 2023, 11, 45270–45278. [Google Scholar] [CrossRef]
- Chen, Y.F.; Li, Z.W.; Zhou, M.C. Behaviorally optimal and structurally simple liveness-enforcing supervisors of flexible manufacturing systems. IEEE Trans. Syst. Man, Cybern. A Syst. Humans Syst. Hum. 2012, 42, 615–628. [Google Scholar] [CrossRef]
- TINA (Time Petri Net Analyzer) Is a Toolbox for the Editing and Analysis of Petri Nets, with Possibly Inhibitor and Read Arcs, Time Petri Nets, with Possibly Priorities and Stopwatches, and an Extension of Time Petri Nets with Data Handling Called Time Transition Systems. 2020. Available online: http://projects.laas.fr/tina/home.php (accessed on 9 June 2020).
- Notomi, M.; Murata, T. Hierarchical reachability graph of bounded Petri nets for concurrent-software analysis. IEEE Trans. Softw. Eng. 1994, 20, 325–336. [Google Scholar] [CrossRef]
- McMillan, K.L. A technique for state space search based on unfolding. Form. Methods Syst. Des. 1995, 6, 45–65. [Google Scholar] [CrossRef]
- Esparza, J.; Römer, S.; Volger, W. An Improvement of McMillan’s Unfolding Algorithm. Tools and Algorithms for the Construction and Analysis of Systems, Vol. 1055 of Lecture Notes in Computer Science; Springer: Passau, Germany, 1996; pp. 87–106. [Google Scholar]
- Heiner, M. Verification and optimization of control programs by Petri nets without state explosion. In Proceedings of the 2nd International Workshop on Manufacturing and Petri Nets, a Workshop Within the 28th International Conference on Applications and Theory of Petri Nets, Tolouse, France, 23 June 1997. [Google Scholar]
- Taubin, A.; Kondratvey, A.; Kishinevsky, M. Deadlock prevention using Petri nets and their unfoldings. Int. J. Adv. Manuf. Technol. 1998, 14, 750–759. [Google Scholar] [CrossRef]
- Badouel, E.; Darondeau, P. Theory of Regions; Reisig, W., Rozenberg, G., Eds.; Springer: Berlin, Germany, 1998; Volume 1491, pp. 529–586. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).