An Efficient Approach for Mining High Average-Utility Itemsets in Incremental Database ^†

Abstract

Traditional high-utility itemset (HUI) mining methods tend to overestimate utility for long itemsets, leading to biased results. High average-utility itemset (HAUI) mining addresses this problem by normalizing utility with itemset length. However, uniform utility thresholds fail to account for varying item importance. Recently, HAUI mining with multiple minimum utility thresholds (MMU) has been used for flexible utility evaluation. While the generalized HAUIM (GHAUIM) algorithm performs well, it requires two database scans and is limited to static datasets. Therefore, we developed a novel tree-based method that scans the database only once to improve efficiency by reducing storage and eliminating costly join operations. Additionally, pruning strategies and incremental updates were introduced to enhance scalability. The developed method outperformed GHAIM in efficiency.

1. Introduction

High utility pattern mining (HUPM) is widely used in stock market analysis, commodity market evaluation, and medical data processing. Unlike traditional frequent itemset mining (FIM), which considers only frequency, HUPM incorporates both quantity and profit. However, it does not account for pattern length, which misleads results. For example, in a store where most customers buy pencils, erasers, and rulers, a wealthy customer making a large purchase that includes apples and milk could distort the results. Since this transaction has high utility, HUPM may incorrectly classify the entire itemset as meaningful. However, the key pattern should consist only of pencils, erasers, and rulers, as they are commonly bought together. High average utility pattern mining (HAUPM) addresses this issue by refining meaningful pattern detection.

Despite its benefits, HAUPM has a major limitation, as it applies a single minimum high-utility threshold to all items, which is problematic due to the diversity in product attributes. In retail, items vary in price (e.g., diamonds vs. ceramics), purchase frequency (e.g., milk vs. refrigerators), and profit margin (e.g., gold vs. clothes). Using a single threshold biases evaluations. If set too high, important patterns may be missed; if too low, too many irrelevant patterns may be found. Integrating HAUPM with multiple minimum average utility threshold values (MATV) improves decision-making in pricing, promotions, and product placement.

Algorithms [1,2,3] have been developed for mining high average-utility patterns, but they rely on user-defined thresholds, which affect performance and accuracy. Multiple utility thresholds are introduced to handle item diversity [4,5,6,7]. However, existing algorithms often sort thresholds and average-utility upper bound (AUUB) values inconsistently, leading to inefficiencies. The GHAIM algorithm [7] addresses this problem by introducing the suffix minimum average utility (SMAU) and tighter upper bounds but is limited to static databases and requires multiple scans.

To overcome the previous problems, we developed a novel algorithm that scans the database once and constructs a TUR-Tree structure for efficient storage and retrieval of transactions. By leveraging bit strings, the algorithm identifies itemsets without extra item-joining operations. Additionally, we introduced a tighter upper bound than the eubr value in GHAIM [7], enhancing pruning efficiency. For incremental databases, re-scanning data is costly. The algorithm developed in this study maintains HAUI and non-HAUI candidate lists to track promising patterns dynamically. The developed TURHAIM algorithm is more efficient than GHAIM, making it superior for high average-utility pattern mining.

The remainder of this paper is structured as follows: Section 2 provides a review of high average-utility pattern mining algorithms and multiple minimum threshold approaches applied to HAUPM. Section 3 introduces the proposed algorithm in detail. Section 4 presents performance evaluations and comparisons with the GHAIM algorithm [7]. Finally, Section 5 concludes the article.

2. Algorithms for High Average Utility Itemsets (HAUIs) with Multiple Maximum Transmission (MMUT) Units

Various algorithms have been developed for mining HAUIs. However, most existing methods do not take multiple minimum thresholds into account. We designed algorithms for discovering high average utility itemsets and incorporating multiple minimum utility (MMU) thresholds for high-utility itemset mining.

2.1. TUB-HAUPM Algorithm

The tighter upper bound–high average utility pattern mining (TUB-HAUPM) algorithm [2], proposed by Wu et al., reduces the search space in high average-utility pattern mining by employing upper-bound constraints. Traditionally, three common upper bounds are used: the average utility upper bound, a looser upper bound, and a revised tighter upper bound. However, this algorithm introduces two even tighter upper bounds, the maximum following utility upper-bound (MFUUB) and the Top-k transaction-maximum utility upper-bound (KRTMUUB), to efficiently prune unpromising itemsets at an early stage. In the first database scan, the algorithm computes the AUUB for each item. Items with AUUB values below the threshold are eliminated. The second database scan then sorts transactions in ascending order based on AUUB values. During the exploration stage, the transaction-rival tight upper bound (TRTUB) is determined as the minimum of MFUUB and KRTMUUB. If TRTUB falls below the threshold, its supersets are not further explored. This process continues until all HAUIs are identified.

The multiple-threshold-based efficient mining of high average utility itemsets (MEMU) algorithm [6], proposed by Lin et al., addresses the limitations of the high utility itemset mining with multiple minimum average-utility thresholds (HUIM-MMAU) algorithm [5], which requires multiple database scans and generates an excessive number of candidate itemsets. To enhance efficiency in discovering HAUIs, MEMU utilizes the compact average-utility list (CAU-list) and the estimated average-utility matrix (EAUM) structure.

The algorithm consists of three stages. In the first stage, the database is scanned once to compute AUUB values. The multiple minimum high average-utility table (MAUTable) is then checked, and the smallest threshold is identified as the least minimum high average-utility count (LMAU). Items with AUUB values below LMAU are removed from the database. A second scan updates AUUB values and sorts the database in ascending order based on thresholds. The second stage begins the mining process, where EAUM is applied as a pruning strategy. If the EAUM value of an itemset exceeds LMAU, the algorithm proceeds to generate three itemsets and constructs the CAU-list. In the final stage, the CAU-list is further refined, and the length-average (LA) pruning strategy is applied to eliminate unpromising candidates early. This process continues until all HAUIs are efficiently identified.

2.2. Generalized High Average-Utility Itemset Mining (GHAIM) Algorithm

The GHAIM algorithm [7], proposed by Sethi et al., addresses the limitations of previous approaches in high average-utility pattern mining. The MEMU algorithm [6] improved upon HUIM-MMAU [5] by reducing database scans and candidate generation. Meanwhile, the MHUI algorithm [4] introduced generalized pruning techniques for the multiple minimum threshold method without sorting user-defined thresholds. However, MHUI focused on high utility patterns (HUPs) rather than HAUIs. GHAIM effectively overcomes the challenges faced by these earlier strategies [4,6]. In the first database scan, GHAIM computes AUUB values for each item and sorts them in ascending order. A second scan updates AUUB values, and items with AUUB values below the suffix minimum average-utility (SMAU) threshold are removed, applying the AUUB pruning strategy. After this step, two key data structures are created: the revised average utility list (RAUL) and the estimated average-utility co-occurrence matrix (EACM), both based on the sorted revised database.

3. Developed Algorithm

A tree-based algorithm was developed to minimize database scans while eliminating the additional time required for the join process and mine HAUIs in continuously growing databases with multiple minimum thresholds.

3.1. Basic Ideas

Table 1. Database used in this study.

TID	(Item, Quantity)
T1	(a, 5) (b, 2) (e, 2) (f, 1)
T2	(a, 2) (d, 1) (e, 1) (f, 2)
T3	(c, 1) (d, 2) (f, 1)
T4	(a, 1) (d, 3) (f, 1)
T5	(a, 2) (b, 2) (d, 1) (e, 1) (f, 2)

illustrates a database used in this study. The notation Q(I, T_n) represents the quantity of item I in transaction T_n. For instance, for item b in transaction T₅, Q(b, T₅) = 2. The profit of item I is denoted as Pr(I). As shown in

Table 2. Profit table.

Item	Profit
a	3
b	1
c	2
d	2
e	1
f	1

, the profit table indicates Pr(a) = 3. Using this, the utility of item I in a transaction T_n, represented as u_ti(I, T_n), is calculated. For an itemset, the total utility is the sum of the individual item utilities. Unlike traditional utility, in average utility calculation, the length of the itemset is considered. When evaluating a single item I, its average utility per transaction is simply its utility.

$${\mathrm{a}\mathrm{u}}_{\mathrm{t}\mathrm{i}}\left(\mathrm{I},{\mathrm{T}}_{\mathrm{n}}\right)={\displaystyle \frac{{\mathrm{u}}_{\mathrm{t}\mathrm{i}}(\mathrm{I},{\mathrm{T}}_{\mathrm{n}})}{1}}={\mathrm{u}}_{\mathrm{t}\mathrm{i}}(\mathrm{I},{\mathrm{T}}_{\mathrm{n}})$$

(1)

For an itemset X, the real length of X is considered, and the average utility is calculated as

$${\mathrm{a}\mathrm{u}}_{\mathrm{t}}\left(\mathrm{I},{\mathrm{T}}_{\mathrm{n}}\right)={\displaystyle \frac{{\mathrm{u}}_{\mathrm{t}\mathrm{i}}(\mathrm{X},{\mathrm{T}}_{\mathrm{n}})}{\left|\mathrm{X}\right|}}$$

(2)

To determine the total average utility across the entire database, we sum the average utility values from all transactions where the item or itemset appears. For example, for item a, we compute the following.

$${\mathrm{a}\mathrm{u}}_{\mathrm{D}}\left(\mathrm{a}\right)={\mathrm{a}\mathrm{u}}_{\mathrm{t}\mathrm{i}}\left(\mathrm{a},{\mathrm{T}}_1\right)+{\mathrm{a}\mathrm{u}}_{\mathrm{t}\mathrm{i}}\left(\mathrm{a},{\mathrm{T}}_2\right)+{\mathrm{a}\mathrm{u}}_{\mathrm{t}\mathrm{i}}\left(\mathrm{a},{\mathrm{T}}_4\right)+{\mathrm{a}\mathrm{u}}_{\mathrm{t}\mathrm{i}}\left(\mathrm{a},{\mathrm{T}}_5\right)$$

(3)

Similarly, for itemset ab:

$${\mathrm{a}\mathrm{u}}_{\mathrm{D}}\left(\mathrm{a}\mathrm{b}\right)={\mathrm{a}\mathrm{u}}_{\mathrm{t}\mathrm{i}}\left(\mathrm{a}\mathrm{b},{\mathrm{T}}_1\right)+{\mathrm{a}\mathrm{u}}_{\mathrm{t}\mathrm{i}}\left(\mathrm{a}\mathrm{b},{\mathrm{T}}_5\right)$$

To determine whether an item or itemset qualifies as HAUI, we compare its total average utility (AUD) with its corresponding threshold from the MATV table, as shown in

Table 3. MATV of each item.

Item	MATV
a	7
b	6
c	7
d	5
e	9
f	8

.

For example, given MATV(a) = 7 and AUD(a) = 30, itemset {a} (a 1-itemset) is classified as HAUI. For itemset {ab}, the threshold is calculated as the average of the individual MATV values.

$$\mathrm{M}\mathrm{A}\mathrm{T}\mathrm{V}\left(\mathrm{a}\mathrm{b}\right)={\displaystyle \frac{\mathrm{M}\mathrm{A}\mathrm{T}\mathrm{V}\left(\mathrm{a}\right)+\mathrm{M}\mathrm{A}\mathrm{T}\mathrm{V}\left(\mathrm{b}\right)}{2}}={\displaystyle \frac{7+6}{2}}=6.5$$

(4)

Since AUD(ab) = 12.5 is greater than MATV(ab) = 6.5, itemset {ab} is also considered an HAUI.

In the mining process of HAUIs, an upper bound is defined to reduce the search space. The most commonly used upper bound is the AUUB value. It is calculated by summing the TMU values of all transactions where the itemset X appears.

Table 4. AUUB value of each item.

Item	auub
a	33
b	21
c	4
d	22
e	27
f	37

displays all the AUUB values used in the database. TMU represents the highest utility value within a given transaction T_n. This upper bound helps eliminate unpromising itemsets early, improving mining efficiency.

After calculating AUUB for all items, we sort the item list in descending order based on their AUUB values. This sorting ensures that items with higher upper bounds are prioritized during the mining process. Next, the algorithm constructs a TUR-Tree following the order defined by the sorted item list. The TUR-Tree structure efficiently organizes transaction data, reducing the search space and improving mining performance.

In the TUR-Tree structure, the remaining maximum utility (RMU) excluding itemset X (rmue) represents the highest utility among all items in a transaction, excluding those in itemset X. For example, in transaction T₂, after sorting, we have T₂ = (d, e, a, f). The RMU of itemset {d, e} in T₂ is calculated as follows.

$$\mathrm{r}\mathrm{m}\mathrm{u}\mathrm{e}\left(\mathrm{d}\mathrm{e},{\mathrm{T}}_2\right)=\mathrm{m}\mathrm{a}\mathrm{x}\left(\mathrm{u}\mathrm{t}\mathrm{i}\left(\mathrm{a}\right),\mathrm{u}\mathrm{t}\mathrm{i}\left(\mathrm{f}\right)\right)=\max \left(\mathrm{6,2}\right)=6$$

(5)

Another important function is the suffix minimum average-utility (SMAU), which sets a minimum threshold by comparing MATV values of itemsets and their succeeding items in the sorted order. If we compute SMAU(ba), we consider the MATV values of b, a, and any items appearing after itemset {b, a}, which is only item f.

$$\mathrm{S}\mathrm{M}\mathrm{A}\mathrm{U}\left(\mathrm{b}\mathrm{a}\right)=\mathrm{m}\mathrm{i}\mathrm{n}\left(\mathrm{M}\mathrm{A}\mathrm{T}\mathrm{V}\left(\mathrm{b}\right),\mathrm{M}\mathrm{A}\mathrm{T}\mathrm{V}\left(\mathrm{a}\right),\mathrm{M}\mathrm{A}\mathrm{T}\mathrm{V}\left(\mathrm{f}\right)\right)=\min \left(\mathrm{6,7},8\right)=6$$

(6)

3.2. Data Structure

Based on three input datasets that include database DB, the profit table, and the MATV table (Table 1, Table 2 and Table 3), we developed six key data structures for the mining process, including (1) the item-based table, (2) the transaction set table, (3) the AUUB table, (4) the sorted item list, (5) the SMAU table, and (6) the EMURUM table.

3.2.1. Item-Based Table

The item-based table is implemented using a HashMap (in

Table 5. Item-based table.

TID\Item	a	b	c	d	e	f
T1	15	2	0	0	2	1
T2	6	0	0	2	1	2
T3	0	0	2	4	0	1
T4	3	0	0	6	0	1
T5	6	2	0	2	1	2

), a data structure in Java [8]. When constructing the TUR-Tree, items, transaction ID (TID), utility, and RMUE are inserted sequentially based on the sorted item list, eliminating the need for re-sorting. Unlike the GHAIM algorithm, which requires a sorting step, the developed TURHAIM algorithm streamlines the process. The item-based table stores the utility of each item (itemₖ) in each transaction (T_i). For instance, the utility of item a in transaction T₁ is 15. This table also helps construct the transaction set table and remains permanently in use. In an incremental mining process, if new data change the item order, the item-based table is essential for reconstructing the TUR-Tree. It efficiently stores utility values for each item within specific transactions (T_n).

3.2.2. Transaction Set Table

The transaction set table (

Table 6. Transaction set table.

Itemset\Transaction Set	The Transactions Where the Itemset Appears
a	T1, T2, T4, T5
b	T1, T5
c	T3
d	T2, T3, T4, T5
e	T1, T2, T5
f	T1, T2, T3, T4, T5

), is derived from the item-based table. It records the transactions in which each item appears based on its utility value. If an item’s utility is greater than 0, the item is present in that transaction, and its TID is included in the set. Conversely, if the utility value is 0, the item does not exist in that transaction and will not appear in the set. The primary function of the transaction set table is to locate transactions containing specific itemsets. It also plays a crucial role in the pruning strategy, as an empty transaction set indicates that the corresponding itemset is no longer relevant for further searching. The detailed process of utilizing the transaction set table in mining will be discussed later.

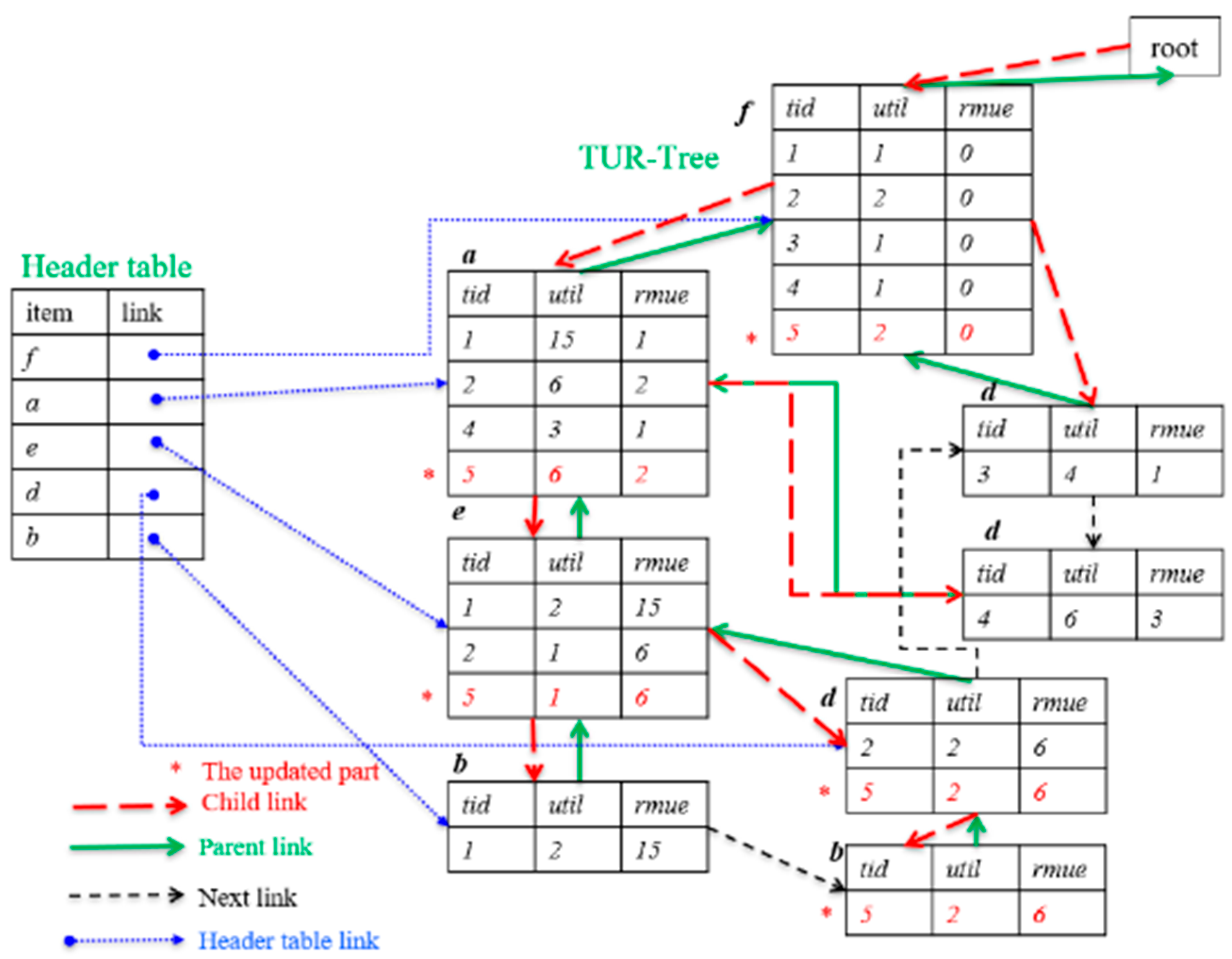
3.3. Construction of TUR-Tree

The TUR-Tree is built from the item-based table by inserting items in the order of the sorted item list. In insertion, items are added following the sorted order of AUUB values, maintaining the same transaction within the same path. The TUR-Tree consists of four types of links as shown in Figure 1.

• Child link: Connects a parent node to its child nodes;
• Parent link: Establishes the hierarchical structure;
• Next link: Helps locate the next occurrence of the same item for mining;
• Header table link: Serves as the starting point for the mining process.

Figure 1 shows the construction of the TUR-Tree after the insertion of sorted transactions.

3.4. Pruning Strategy

The developed TURHAIM algorithm incorporates multiple pruning strategies to enhance efficiency, including the following.

• AUUB pruning strategy [7]: Eliminates itemsets whose AUUB values fall below the SMAU value.
• Transaction set pruning strategy: Uses the transaction set table to quickly determine if an itemset is empty, avoiding unnecessary searches.
• TURUB pruning strategy [2,7]: Applies the Transaction-Rival Upper Bound (TURUB) to discard unpromising candidates early.
• Estimated maximum between utility and remaining utility matrix (EMURUM) pruning strategy [6,7]: Utilizes EMURUM to further reduce the search space.

By integrating these strategies, the algorithm efficiently identifies HAUIs while minimizing computation.

3.5. Mining Process for Static Database

Figure 2 presents the flowchart of the static database mining step. The developed TURHAIM algorithm begins with a depth-first search (DFS) following the ascending order of AUUB values. Using the database (Table 1), we analyzed itemset daf. The processing order is [b, d, e, a, f] since item c has been pruned using the AUUB pruning strategy. First, we examine the TID check set to determine whether it is empty. If it was empty, the transaction set pruning strategy skips searching the TUR-Tree. However, since TID check set = {T₂, T₄, T₅}, we mined. We locate item d in the header table and follow its link to find the first node where d appears. The matching TIDs are {T₂, T₅}, indicating a non-empty intersection. We then accumulate the utility of itemset daf for T₂ and T₅. Next, using the parent link, we locate nodes a and f, continuing the accumulation.

The last visited node is f, where we compute RMUE for T₂ and T₅, both of which are 0. Since f is the last item in daf, we backtrack to find the next d node. After processing T₂ and T₅, we remove them from the TID check set and verify if it is empty. Next, we continue searching for item d in the next link that intersects with our TID check set. We find TID = 4 in node d and follow the parent link to locate nodes a and f for TID = 4. After processing, we remove T₄ from the TID check set, which now becomes empty. Since there are no remaining TIDs to process, we stop searching for further d nodes.

Then, we compute the TURUB value for itemset daf. Since item f is the last item in daf and has the largest AUUB in the sorted list, its RMUE is 0. Therefore, rmue(daf, T₂) = 0, rmue(daf, T₄) = 0, rmue(daf, T₅) = 0, leading to TURUB(daf) = 0.

3.6. Mining Process for Incremental Database

In incremental mining, two possible scenarios exist: unchanged order and changed order. Before discussing these cases, we first define two special item types to reveal items and skippable items. A revealed item has been previously pruned due to the AUUB pruning strategy, but as new data increases its AUUB value, it is no longer pruned and is removed from the promising item list. A skippable item is present in the original dataset but does not appear in the updated data. In certain cases, the item is skipped during a depth-first search, optimizing the mining process. When the item order remains unchanged, only limited data structures need to be updated, including the item-based table, AUUB table, HAUI List, Non-HAUI Candidate List, TURUB List, and EMURUM. In this case, the TUR-Tree remains unaffected, which significantly improves efficiency. Compared with situations where the order changes, much of the previously created data can still be used, leading to faster performance.

When the item order changes, more data structures are affected, requiring significant updates. In this case, the TURUB List becomes unusable, and the TUR-Tree must be reconstructed to reflect the new order. Since the previous mining structure is no longer valid, the system must rebuild key data structures, leading to a higher computational cost compared to the unchanged order scenario. Despite this, updating the item-based table, AUUB table, HAUI List, Non-HAUI Candidate List, and EMURUM table remains essential for accurate incremental mining. When the order changes, the originally stored TURUB List becomes invalid because modifying its values directly would lead to incorrect results. As a result, the TURUB List cannot be used, and the TUR-Tree must be reconstructed to match the new order. After updating the necessary data structures—including the item-based table, AUUB table, HAUI List, Non-HAUI Candidate List, and EMURUM table—the mining process begins. The steps for mining remain similar to those in static database mining, with one key difference: determining HAUI must follow the process outlined in Figure 3. This is because the HAUI List and Non-HAUI Candidate List already contain values from previous mining iterations.

4. Performance Evaluation

We evaluated the performance of the developed TURHAIM algorithm by comparing it with the GHAIM algorithm [7] using both synthetic and real-world datasets.

4.1. Synthetic Datasets

In the synthetic dataset, the profit values and quantities of items were randomly assigned within the range of 1 to 15. The dataset was generated based on three key parameters: (1) the number of different items (ND), (2) total number of transactions (TN), and (3) the maximum number of items per transaction (MT). By adjusting these parameters, we controlled the dataset’s density.

To evaluate the efficiency of the proposed TURHAIM algorithm, we compared its running time with the GHAIM algorithm using synthetic datasets. Specifically, we experimented with the datasets: NIT200TN100000MT15. Figure 4a shows that TURHAIM outperformed GHAIM in running time on a static synthetic database, demonstrating higher efficiency. Then, we analyzed the performance of NIT200TN100000MT15 in an incremental database setting. We examined how running time changes with variations in the inserted TN. Figure 4b shows the processing time of our algorithm is consistently lower than that of the GHAIM algorithm.

4.2. Real Datasets

To evaluate the robustness of the TURHAIM algorithm, experiments were conducted on the Connect dataset [4,9]. Figure 5 demonstrates this trend in the connect real database, where the TURHAIM algorithm consistently outperformed the GHAIM algorithm in running time. The performance gap widens as the data size increases.

Next, we analyzed the performance of the Connect dataset under the incremental database. As shown in Figure 6, the TURHAIM algorithm consistently outperformed the GHAIM algorithm in terms of running time.

5. Conclusions

In this study, we developed a TURHAIM algorithm to discover high average utility itemsets with multiple minimum thresholds in an incremental database. The TURHAIM algorithm requires only a single database scan. When new data are inserted, provided the order remains unchanged, only the updated portion of the database is scanned, avoiding the entire dataset scan. We compared the performance of the TURHAIM algorithm with the GHAIM algorithm using static and incremental databases. The TURHAIM algorithm outperformed the GHAIM algorithm in terms of efficiency.