Stress and Temperature Monitoring of Bridge Structures Based on Data Fusion Analysis ^†

Abstract

Structural parameters, such as strain or deflection, were collected by sensors and analyzed to assess the bridge’s structural condition and obtain a reliable reference for bridge maintenance. In the data acquisition and transmission process, sensor data inevitably contains noise and interference, resulting in anomalies, especially data distortion during wireless transmission. These anomalies significantly impact data analysis and structural evaluation. To mitigate the effects of these abnormalities, we conducted the cause analysis. The Sanxia Viaduct was used to design a strain monitoring method as a bridge model. We analyzed vibrating string sensor data collected in the cold environment using the Nair method to eliminate outlier data. The analysis results of strain and temperature trends showed that the data fusion method developed in this study showed high precision and stability and effectively reduced the impact of noise and data anomalies. By monitoring actual bridges, the effectiveness and practicality of the method were validated. The model provides significant information on the development and application of bridge health monitoring technology.

1. Introduction

Structural stress is the most direct indicator of a structure’s load-bearing capacity. A sub-healthy state of the structure leads to excessive stress or abnormal redistribution of stress. Therefore, abnormal changes in stress must be monitored with sufficient attention. The changes, in conjunction with environmental factors and other monitoring results such as deformation, are critical for the assessment of the structure’s condition to judge a safe and controllable range [1]. The objective of structural stress monitoring is to determine whether the stress at the test location is at a safe level to verify and adjust the structural model and identify damages.

In China, with the acceleration of urbanization and continuous traffic growth, bridge safety has become increasingly important. Consequently, monitoring the stress and temperature of bridge structures becomes essential to ensure safety. Recently, Chinese scholars have conducted extensive research in this area [2]. To monitor bridge structural stress, a variety of sensor technologies, such as Fiber Bragg Grating sensors [3], resistive strain gauges [4], and acoustic emission sensors [5], are used. By monitoring changes in bridge stress, potential safety hazards are detected. To enhance the accuracy and reliability of monitoring, methods based on data fusion, such as the fuzzy C-means clustering algorithm [6] and Kalman filtering [7], have been used. Data collected from multiple sensors are integrated to produce more precise results [8]. To monitor bridge temperature, sensor technologies and data fusion methods are used. For instance, thermocouples [9], infrared thermography [10], and other equipment are used to monitor the temperature distribution on the surface and inside bridges [11]. Additionally, wavelet transform [12], neural networks [13], and other algorithms are applied to process and analyze temperature data, revealing inherent patterns and trends [14].

Monitoring bridge structural stress and temperature has received extensive attention for research, and significant advancements in related technologies have been made. These advancements include the development of advanced sensor technologies and data processing methods, which have been applied in practical engineering projects, accumulating a wealth of data [15]. Bridge structural stress, temperature monitoring, and the fusion analysis of the two types of data have been researched extensively, too. However, challenges and issues, such as the stability and reliability of sensors and the selection and optimization of data fusion algorithms, still exist. Therefore, we developed a strain monitoring method based on the bridge model of the Sanxia Viaduct. We analyzed the vibrating string sensor data in cold environments using the Nair method to eliminate outliers. The analysis results of the strain and temperature data using the developed data fusion method showed high accuracy and stability, effectively reducing the impact of noise and data anomalies. Moreover, effectiveness and practicality were validated through the monitoring of different bridges. The model provides a significant theoretical and practical basis for the development and application of bridge health monitoring technologies [16].

2. Data Processing and Fusion

2.1. Outlier Processing

Handling outliers and integration is important in data mining. Unknown abnormal data are detected by examining the database to increase the accuracy of statistical analysis. In bridge structure monitoring, sensor datasets include abnormally large or small data that significantly deviate from the majority of observed values or data without exhibiting anomalies that do not conform to the structure or reveal correlations between variables. Such data are termed as outliers. Outliers affect the analysis of bridge structure data; hence, understanding how to detect and handle these abnormal data are crucial. In many studies, the concept of statistical data quality and methods for evaluating statistical data quality have been researched.

In the residual analysis theory, a linear regression model is considered.

Y = Xβ + ε

(1)

where Y is an n-dimensional vector composed of response variables, X is an n × (p + 1) order design matrix, β is a p + 1 dimensional vector, and ε is an n-dimensional error vector.

The estimates of regression coefficients, fitted values, and residuals can be derived from this model. By analyzing the residuals and the confidence intervals of the residuals, outliers are identified in the original data. If the confidence interval of a residual does not include point zero, the set of observations is considered outliers.

In the regression analysis theory, the specific forms of relationships between variables are examined. The relationship between correlated variables is examined to establish a mathematical expression for the correlation and estimate unknown quantities based on known values, thus enabling accurate estimation and prediction.

Based on the determined correlation properties and historical data, a regression equation is formulated. Then, predictions are made on test data by comparing the predicted values with actual values. If the distance between the predicted value and the actual value exceeds a threshold, the data point is considered an outlier. The methods of regression analysis include simple, multiple, and nonlinear regressions.

When establishing a multiple regression model, the regression model must have enough explanatory power and predictive effectiveness. Independent variables are selected carefully with the following criteria.

• Independent variables must have a significant effect on the dependent variable and present a close linear correlation.
• The linear correlation between independent and dependent variables must be genuine rather than merely formal.
• Independent variables must have a certain degree of exclusivity, meaning the degree of correlation between independent variables must not be higher than that between the independent variables and the dependent variable.
• Independent variables must have complete statistical data, and their predicted values should be easily determined.

The parameter estimation of the multiple regression model, similar to that of the simple linear regression equation, is based on the minimized sum of squared errors. The parameters are used in the least squares method. The solution to the problem is a vector b, which is used to estimate the unknown parameters. This least squares estimation is given as follows.

$$b=\widehat{\beta }=(X^{\prime }X{)}^{-1}XY$$

(2)

$$Y=Xb=X(X^{\prime }X{)}^{-1}XY$$

(3)

Under the same measurement conditions, the standard deviation (SD) of repeated measurement data has been estimated as $s_m$. m is used to distinguish the abnormal value or corresponding gross error in the data column of n smaller than m. The Nair’s method for judging the gross error of normal data are used with SD $s_m$ to distinguish outliers among data samples. The test statistic is a single standardized extreme value of N data, and the SD is the estimated $s_m$ of the sample with large capacity.

$$u_{\left(1\right)}=(x_{\left(1\right)}-{\overline{x}}_n)/s_m$$

(4)

$$u_{\left(n\right)}=(x_{\left(n\right)}-{\overline{x}}_n)/s_m$$

(5)

The test limits $N_a$ (m, n) corresponding to different m and n values are also different. When $u_{\left(n\right)}$ > $N_a$ (m, n) or $u_{\left(1\right)}$ < −$N_a$ (m, n), the corresponding data can be considered as abnormal data and can be excluded. In the discrimination of non-normal small samples, according to the residual sequence {$e_k$, k = 1, 2… N}, inequality ${e_k}^2<{\sum }_{k-1}^n{e_k}^2$, that is, ${e_k}^2<(n-1)s^2$ must be satisfied, so a sufficient condition for judging gross errors is derived as follows.

$$e_p>\sqrt{n-1s}$$

(6)

$$u_p=e_p/s>\sqrt{n-1}$$

(7)

where $e_p$ and $u_p$ are the gross error and standardized value, respectively. Regardless of the probability distribution of the data population, the residuals satisfying this formula must be gross errors.

The Nair method is used to process abnormal values, and the abnormal data are eliminated according to the following process.

• Step 1: The characteristic quantification, data standardization, and smoothing of the extreme $u_{\left(n\right)}$ or $u_{\left(1\right)}$ of the standardized data are necessary to avoid calculation errors caused by large differences in values. According to Equation (2), if {$u_{\left(i\right)}$} is close to $\sqrt{n-1}$, there are abnormal data.
• Step 2: The gross error criteria is set according to the amount of data n, probability distribution, or skewness ${\widehat{r}}_3$ and peak ${\widehat{r}}_4$, and the number of abnormal data j.
• Step 3: Given the significance level $\alpha$, the two kinds of errors of discarding the true and taking the false in the gross error discrimination are identified. Generally, $\alpha$ = 0.05 or 0.01 is used for a small number of samples. In large samples, the required confidence probability is p = 1 − $\alpha$.
• Step 4: The statistics of the selected gross error are obtained to assess the influence of abnormal data.
• Step 5: The critical value of the test is determined to determine the critical value of the statistics under $\alpha$.
• Step 6: It is inferred whether there is a gross error according to the rejection field (Re) of the inspection. If there is a gross error, the corresponding abnormal data are eliminated. Otherwise, it is considered that there is no gross error, and the suspicious data are retained.

In case of abnormal data, the above process is conducted. In the case of multiple suspicious abnormal data, steps 4–6 are repeated until there is no abnormal data eliminated.

2.2. Improvement of Strain Outlier Processing Method

Sensor data were analyzed to obtain reliable reference data for bridge maintenance. However, sensor data inevitably include noise and interference, resulting in abnormal values. Data distortion is inevitable during the wireless transmission process, too. These abnormal data significantly impact data analysis and structural evaluation. To eliminate the impact of data anomalies, we used an improved Nair method to remove abnormal values.

The strain of test block 1 changed with the temperature trend between July 2013 and March 2014, with data spikes at the same time. These outliers caused significant interference in the subsequent data processing and analysis. We divided the test blocks into several groups based on a two-degree-per-group method. For example, the strain data of test block 1 at 25–−23 °C was included in array A, and the strain data of test block 1 at 23–−21 °C was assigned to array B. In each array, we used the Nair method to identify and remove abnormal values. Due to the large number of abnormal values, we repeated steps 4 and 6 until there was no more abnormal data found. The strain change curve after removing abnormal values and smoothing is shown in Figure 1.

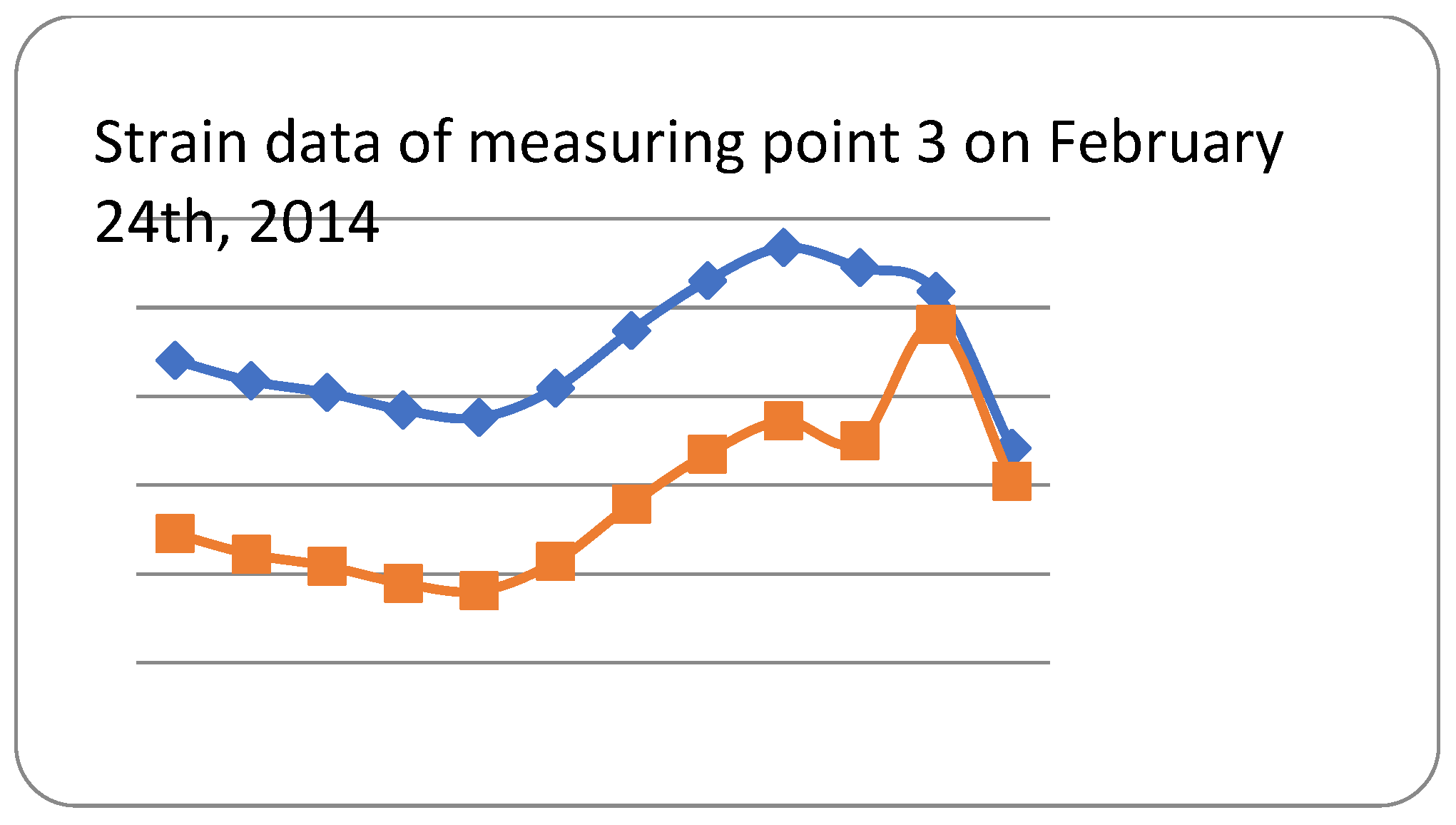
3. Monitoring Strain and Temperature

Due to the statically indeterminate structure of the three-stranded viaduct, the corresponding internal forces are generated as the temperature changes. The vibrating wire strain sensor collects data on the local stress anomalies caused by damage to the bridge structure and long-term temperature strain monitoring of the bridge structure. The schematic diagram of the bending moment generated by the overall temperature rise load of the bridge structure is shown in Figure 2, and the schematic diagram of the bending moment generated by the temperature gradient load is shown in Figure 3. The control sections of the box girder are concentrated on the 2nd and 3rd piers and the mid-span and side span of the main span. Therefore, 32 vibrating wire strain gauges are used for the three-stranded viaduct, mainly installed in the mid-span positions of each span, and two strain roses (one strain rose consists of three vibrating wire strain gauges) are installed at each of the two piers in the longest span of the key stress location. The stress section layout of the control section of the box girder is shown in Figure 4. The control section numbers are 1, 2, 3, 4, and 5, totaling five sections.

The design of strain warning values at each control section of box girders is created based on the “Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts” and finite element calculations. For prestressed concrete components that are not allowed to have tensile stress, the tensile strain warning value must be the absolute value of the compressive strain generated after the component is built and reinforced. For prestressed concrete components that are allowed to have tensile stress, the tensile strain warning value must be equal to the sum of the absolute value of the strain generated after the component is built and reinforced and the concrete cracking strain. In strain monitoring, if the strain exceeds the warning value, the monitoring system immediately alarms and reminds personnel to conduct a comprehensive inspection of the bridge, eliminate potential safety hazards, and develop corresponding maintenance measures.

3.1. Temperature Compensation for Strain Data

Vibrating wire strain sensors show high sensitivity, accuracy, and stability and are widely used in strain measurement for structures such as buildings, bridges, railways, hydropower, and dams, as well as in the long-term health monitoring of large-span bridges during construction and operation. The vibrating wire sensor consists of a stressed elastic deformation shell (or diaphragm), steel wire, fastening chuck, excitation, and receiving coils. The vibrating wire sensor is grouped into single-coil excitation mode and dual-coil excitation mode. The single-coil excitation mode refers to the excitation coil excitation string generating vibration and receiving the excitation signal generated by the string. The dual coil excitation mode is a coil excitation, with one coil excitation and the other coil receiving. In addition to the coil, the sensor has a thermistor to test the ambient temperature around the sensor for temperature correction.

The vibrating wire strain sensor measures the strain where the sensor is located by using the relationship between the frequency change of the wire and the change in tension. The factors affecting the sensitivity and accuracy of the vibrating wire sensor are the aging of the vibrating wire material, the structure of the vibrating wire sensor, the excitation method, and temperature. The linear expansion coefficient refers to the rate of change in the linear dimensions of an object with changes in external temperature and pressure (mainly temperature) due to changes in external temperature and pressure (mainly temperature). Currently, the linear expansion coefficient of concrete has been extensively researched, mainly in general ambient temperature or high-temperature environments.

The “Code for Design of Concrete Structures” in China stipulates that when designing concrete structures, the linear expansion coefficient is 0.00001/°C with a temperature range of 0–100 °C. Due to the high requirements for experimental conditions and the relative difficulty of testing in low-temperature environments, there are relatively few studies on the linear expansion coefficient of concrete. In Japan and Canada, the performance of concrete in low-temperature environments has been widely researched.

Miura et al. produced concrete specimens with different water-cement ratios and different water contents to investigate the influence of water content on the deformation properties, strength, elastic modulus, and other properties of concrete at low temperatures, which have been systematically studied. The deformation properties of concrete at low temperatures show the following properties. Concrete does not always shrink during the cooling process. Due to the presence of moisture in the specimen, the specimen slightly expands when it cools down to 0 °C. When the temperature is between 0 and −30 °C, the concrete specimen shrinks as the temperature decreases. When the temperature is between −30 and −60 °C, it expands as the temperature decreases. Below this temperature, the concrete specimen shrinks as the temperature decreases.

The research results of Monfor and Xiaogu showed that the concrete specimens did not shorten with the decrease in temperature at low temperatures, and the expansion ratio was different at each temperature range. The thermal expansion coefficient at 0–5 °C was about 4−5 × 10⁻⁶, 11−12 × 10⁻⁶/°C in the range of −5–30 °C, and 5–6 × 10⁻⁶ at −30–40 °C. The ambient temperature of the three-strand bridge is above −40 °C. In the research and comparison, we used the concrete expansion coefficient of Yamane Akira for calculation.

3.2. Influence of Temperature on Sensors

The linear expansion coefficient of the vibrating wire material in the sensor is the same as that of ordinary steel. The performance of steel materials under low-temperature conditions shows that the elastic modulus of steel increases by about 10% at low temperatures, while the linear expansion coefficient remains unchanged in the temperature range of −165–70 °C, which is ${10}^{-5}$. The thermal expansion coefficient of the vibrating wire material used in this study is 12.2 microstrain/°C.

The strain calculation formula is as follows.

$$\mathsf{\epsilon }=\mathrm{G}\times \mathrm{C}\times ({\mathrm{R}}_1-{\mathrm{R}}_0)$$

(8)

where G is the instrument standard coefficient, 3.7 $\mathsf{\mu }\mathsf{\epsilon }/\mathrm{d}\mathrm{i}\mathrm{g}\mathrm{i}\mathrm{t}$, C is the average correction factor (usually between 0.95 and 1.05; the average correction factor of the sensor selected for the project is 1.03); ${\mathrm{R}}_1$ is the current degree; and ${\mathrm{R}}_0$ is the initial degree.

Due to the difference in linear expansion coefficients between concrete and vibrating wire, the test values are corrected during calculation. The correction value K is calculated as follows.

$$\mathrm{K}=({\mathrm{Y}}_1-{\mathrm{Y}}_0)\times ({\mathrm{T}}_1-{\mathrm{T}}_0)$$

(9)

where ${\mathrm{Y}}_1$ is the expansion coefficient of a steel string, 12.2 $\mathsf{\mu }\mathsf{\epsilon }/$°C, ${\mathrm{Y}}_0$ is the temperature expansion coefficient of concrete, which is taken from

Table 1. Temperature compensation method for strain.

Temperature (°C)	−8	−10	−12	−14	−16	−18	−20
$\mathrm{Strain}(\mathsf{\mu }\mathsf{\epsilon }$)	−3.71325	−19.5113	−19.9027	−15.5107	−26.7253	−25.8405	−33.9823

, ${\mathrm{T}}_1$ is the current temperature, and ${\mathrm{T}}_0$ is the initial temperature.

During the installation process of the engineering system, two concrete test blocks were placed inside the box of the three-strand bridge of the supporting project, and string strain gauges were installed on the concrete test blocks. This thermometer test block provides data for studying strain data compensation in low-temperature environments. First, we collected data from test block 1 between August 2013 and March 2014. Since the project studied the temperature compensation of strain sensors in low-temperature environments, we selected data below −5 °C for research. We chose the data from test block 1 at 20:00 on 7 December 2013 as the initial time of the test block. At this time ${\mathrm{T}}_0$, ${\mathrm{R}}_0$ = 707.794 at −7 °C. A set of data from 2 °C to −8 °C was used. At −8 °C, the following data were used.

Table 2. Strain values.

Temperature	0–−5 °C	−5–30 °C	−30–40 °C
Coefficient of linear expansion	$4–5\times {10}^{-6}$/°C	$11–12\times {10}^{-6}$/°C	$5–6\times {10}^{-6}$/°C

shows that the strain of test block 1 at −8 °C was 3.71 microstrain. The strain value of this test block from −8 to 20 °C is also presented. The strain value caused by the load in Table 1 is the measured value of test point 3 minus the strain value of test block 1 at that temperature. The blue line in Figure 4 represents the measured strain of test point 3, which includes the concrete strain caused by temperature. The red line represents the pure load strain change curve after removing the corresponding temperature-induced strain. First, data from test block 1 between August 2013 and March 2014 was collected, and the temperature ranged from −21 to 25 °C. The corresponding strain values were taken every 2 °C from test block 1 and averaged as shown in Table 1.

4. Conclusions

In stress monitoring of bridge structures, there were significant differences in stress distribution among bridges under different periods and climatic conditions. Especially during peak traffic periods and extreme weather conditions, bridges experience high stress and require enhanced monitoring and maintenance. In terms of bridge temperature monitoring, the temperature of the bridge surface varies significantly in different seasons and at different times of the day. These temperature changes affect the material properties of the bridge, which in turn affect the safety and durability of the bridge. Through the fusion analysis of bridge structural stress and temperature monitoring data, the correlation between the two is observed. By establishing a corresponding data model, the stress of the bridge under various conditions can be predicted to take preventive measures in advance to ensure the safe operation of the bridge. Monitoring the stress and temperature of bridge structures is crucial for ensuring their safety. By integrating the analysis of these two types of data, predictive abilities are enhanced regarding the condition of bridges, thereby providing robust support for their management and maintenance.