Quantum Random Forest Regression for Indoor Localization ^†

Abstract

Accurate indoor localization is vital for smart environments and the Internet of Things (IoT) applications. Received signal strength indicator (RSSI)-based methods suffer from multipath fading, signal attenuation, and missing data. To address these issues, we developed quantum random forest indoor localization (QRF-IL), a quantum-inspired machine learning method that combines quantum random forests (QRFs) with weighted centroid regression. Each quantum decision tree in QRF uses a quantum support vector machine (QSVM) with Nyström quantum kernel estimation for efficient and accurate learning. On a public dataset, QRF-IL showed an average localization error of 2.3 m, which was reduced by 9% over a standalone QRF model and 21% over an adaptive path loss model (ADAM).

1. Introduction

Accurate indoor localization (IL) is essential for applications such as asset tracking, emergency response, and indoor navigation [1]. However, achieving high IL accuracy remains challenging due to signal multipath fading, signal fluctuation, and dynamic changes in the environment [2,3]. These factors affect signal measurements used in IL, introducing inconsistencies that degrade localization accuracy and limit the reliability of applications that depend heavily on precise IL.

In previous studies [2,4,5,6,7], received signal strength indicator (RSSI) values are used in IL systems. These systems rely on signal propagation models to estimate distances between devices [2,7]. However, challenges such as multipath effects, signal fluctuations, and environmental dynamics make it difficult to accurately map RSSI measurements to specific locations, even with advanced models including the adaptive path loss model (ADAM) [2]. These persistent challenges highlight the need for more robust and adaptable methods.

Quantum machine learning (QML) [8,9,10,11,12] offers promising solutions to longstanding challenges in IL, including multipath effects, signal fluctuations, and environmental dynamics. Unlike classical methods, QML operates within the Hilbert space, a complex vector space of infinite dimensions, to allow quantum systems to handle and analyze RSSI data [12]. This enables quantum algorithms to take advantage of key quantum properties, such as superposition, where data entangles in multiple states simultaneously with data points to reveal hidden patterns [10]. These quantum properties enhance QML’s ability to recognize complex patterns and relationships in RSSI data, which is particularly useful for handling uncertainty and noise in IL. Among QML models, the quantum random forest (QRF) has emerged as a promising technique for improving feature representation in IL by utilizing quantum properties.

Existing research on QRF has focused on classification [10,11,12]. Khadiev and Safina [10] introduced an early quantum version of the random forest for binary classification. Safina et al. [11] later developed a quantum circuit-based prediction method that is also limited to classification. Srikumar et al. [12] used quantum kernels to find complex patterns in data using the QRF model. However, the ability of the QRF to handle regression tasks, such as predicting continuous values, has received little attention although such a limitation is significant for IL applications, where precise numerical regression is essential for determining accurate locations.

We developed a quantum random forest for indoor localization (QRF-IL) method, an RSSI-based IL method using the QRF, which is a quantum-inspired extension of the classical random forest. QRF is designed to leverage quantum computing principles for improved classification and regression, especially in complex and noisy datasets. Similarly to its classical counterpart, QRF is an ensemble learning method that constructs multiple quantum decision trees (QDTs) during training and outputs the aggregated result, including the average prediction for regression or the majority vote for classification. QDT is a quantum-based version of traditional decision trees to improve learning efficiency. Srikumar et al. proposed incorporating the Nyström quantum kernel estimation (NQKE) into the QDT to further refine data processing [12]. QRF-IL also adopts the NQKE strategy to extract important features from noisy signals more effectively. Unlike earlier QRF models focused only on classification, QRF-IL applies regression techniques, making it well-suited for estimating precise indoor locations. Additionally, QRF-IL incorporates weighted centroid regression (WCR), which adjusts location predictions based on confidence levels to reduce localization errors. The mean localization error of QRF-IL is calculated based on a publicly available dataset [3] and compared with those of the IL method, using the standalone QRF proposed in ref. [12] and the ADAM IL method proposed in Ref. [2].

2. QRF-IL and Mechanisms

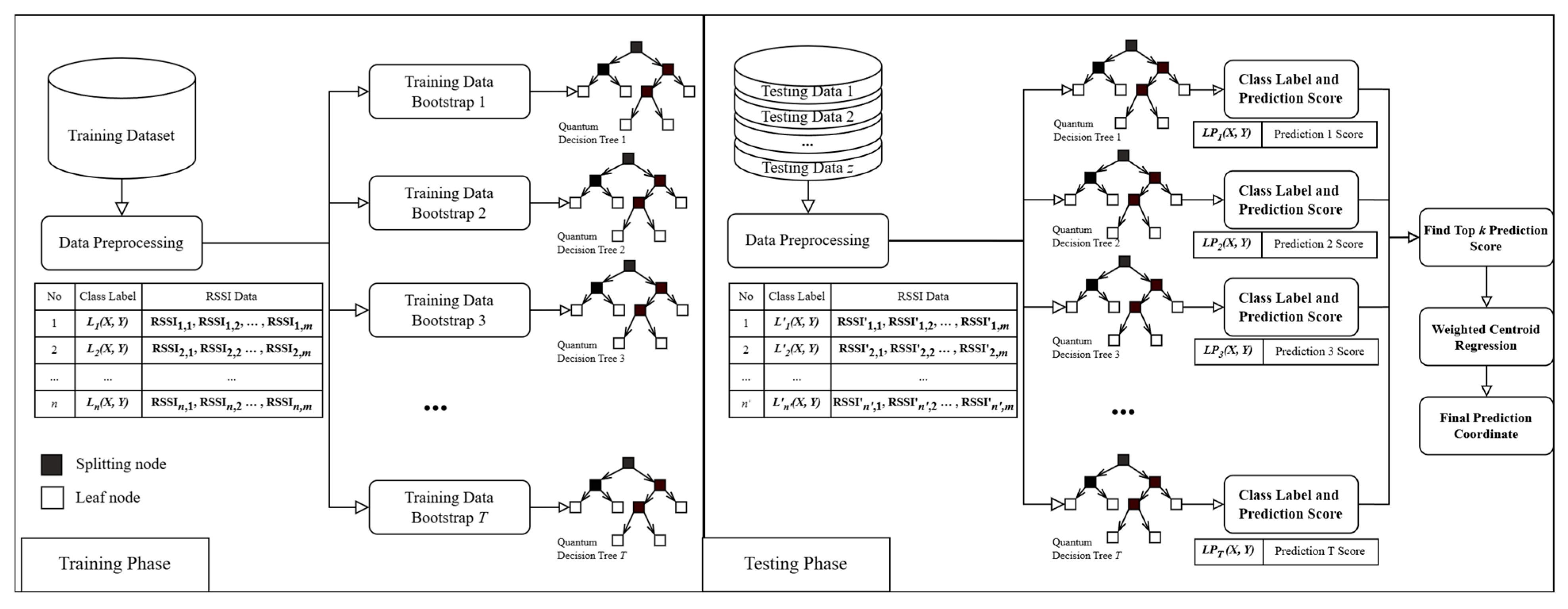
The workflow for the IL regression of QRF-IL is illustrated in Figure 1, which consists of the training phase and the testing phase which are adapted from the QRF framework for the classification task [10]. The QRF model is an ensemble of T-independent QDTs, denoted as ${\left\{Q_t\right\}}_{t=1}^T$. During the training phase, the developed QRF-IL method is used to construct a QRF model by training multiple QDTs on different subsets of the dataset. The training dataset contains n tuples of RSSI values, where the ith tuple contains m RSSI values and is associated with its corresponding location coordinate label L_i(X, Y), 1 ≤ i ≤ n. Before training, the data undergoes preprocessing, which includes data cleaning, normalization, and transformation. The transformation converts classical RSSI data into quantum states for QDT learning; its details will be provided later. Once preprocessed, bootstrap sampling [7] is conducted to generate T random subsets of the training data. Each subset is used to train an individual QDT, which serves as an essential decision-making unit in the QRF model consisting of T QDTs. Unlike classical decision trees, QDTs leverage quantum properties, such as superposition and entanglement, to enhance feature representation and pattern recognition. This enables QRF to capture complex relationships in RSSI data effectively, improving its ability to predict location coordinates across various indoor environments.

In the testing phase, the trained QRF-IL model predicts the associated locations for new test data samples. To ensure consistency with the training data, the test dataset undergoes the same data preprocessing, such as cleaning and normalization, before being fed into the model. After data preprocessing, each test data sample is passed through trained QDT to generate LP_t (X, Y), 1 ≤ t ≤ T, a location prediction of the coordinate label, along with a confidence score, indicating prediction reliability. Different QDTs generate different location predictions, which are collected and ranked according to their associated confidence scores. The WCR method is then used to calculate the final location prediction. WCR selects the top K predictions with the highest confidence scores and assigns greater weights to the more reliable ones for the final predicted location coordinate. This method reduces the influence of less confident predictions, leading to more accurate IL results.

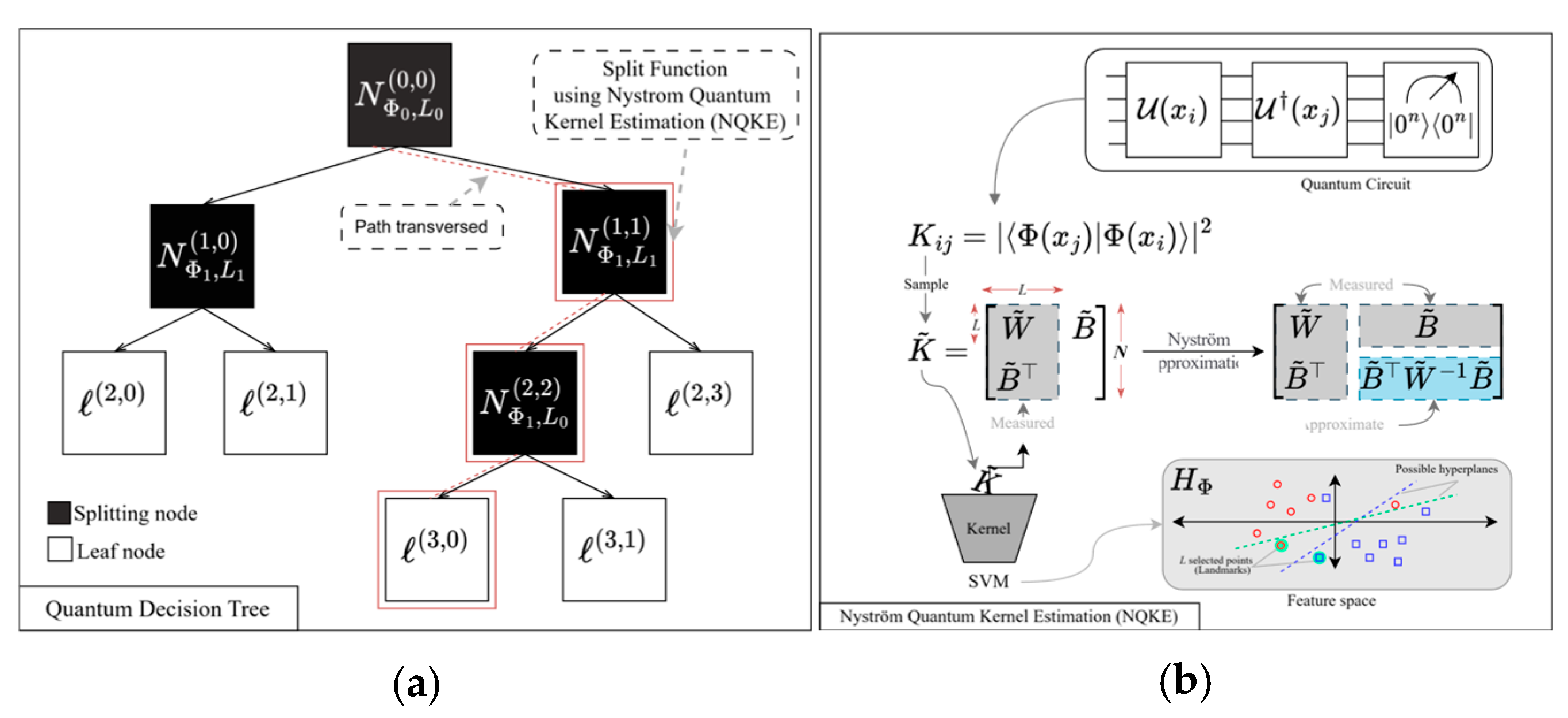
2.1. QDTs

QDT used in QRF [12] enhances classical decision trees by integrating quantum computation. To maintain the fundamental binary tree structure, QDTs recursively partition data at each node until reaching leaf nodes representing classification outcomes. In the hierarchical structure (Figure 2a), each black-colored node represents a splitting node, while white-colored nodes correspond to leaf nodes that indicate classification labels.

Unlike classical decision trees, which rely on simple threshold-based splitting, QDTs employ a quantum support vector machine (QSVM) at each splitting node to determine optimal splits. A QSVM operates in a higher-dimensional feature space defined by a quantum kernel, measuring the similarity between data points using quantum mechanical principles. This feature transformation enables QDTs to uncover complex, non-linear relationships in the data, which classical decision trees might miss.

However, computing the full quantum kernel matrix for the QSVM is computationally expensive, scaling quadratically with the number of data points. Srikumar et al. [12] proposed NQKE to reduce computational overheads. In Figure 2a, the dashed box labeled “Split Function using Nyström Quantum Kernel Estimation” signifies the role of Nyström approximation in estimating the kernel function efficiently at the QDT nodes. Instead of computing the full quantum kernel matrix, NQKE approximates it through a subset of landmark points. The NQKE split function notation (e.g., $N_{{\Phi }_1,L_0}^{\left(\mathrm{0,0}\right)}$) represents a splitting node in QDT where the tuple of indices (0, 0) refers to the depth or position, $\Phi$ denotes the quantum embedding used at that node, and $L$₀ indicates the number of landmark points used. NQKE is a hybrid technique that combines the quantum kernel estimation (QKE) [13] with the Nyström approximation [14]. It uses quantum embedding and landmark points to approximate the quantum kernel matrix, which measures the similarity between data points in a quantum feature space [12].

2.2. WCR

The QRF model classifies QDTs via majority voting over predictions of all QDTs. Taking class i for example, 1 ≤ i ≤ C (i.e., the number of classes), the voting process aggregates class probabilities by averaging the prediction probabilities (or scores) of class i across all QDTs, as defined in Equation (1).

$${\widehat{p}}_i={\displaystyle \frac{1}{T}}{\sum }_{j=1}^K{p}_{t,i}$$

(1)

where $\widehat{p}$_i represents the final prediction probability for class i, T is the number of QDTs, and $p_{t,i}$ is the class i prediction probability produced by the t-th tree.

To improve the accuracy of IL, the proposed QRF-IL method uses WCR instead of the above-mentioned majority voting process. Rather than simply averaging the probabilities of classification predictions, WCR enhances the final prediction by focusing on the top K most probable classes and mapping them to their corresponding spatial coordinates. The prediction process of WCR is modified as follows:

• Top K class selection

Instead of using only the most probable class, WCR selects the top K classes based on their prediction probabilities, as shown in Equation (2).

$$K^{*} =arg max\_K {\widehat{p}}_i, \mathrm{for} 1\le i\le C,$$

(2)

where K* represents the set of top K classes with the top K probabilities or confidence scores from the QDTs ensemble.

2.

Coordinate mapping

The selected top K classes are mapped to their corresponding spatial coordinates (X_j, Y_j) based on a precomputed dataset, where 1 ≤ j ≤ K.

3.

Weighted centroid computation

The final location prediction ($\widehat{X}$, $\widehat{Y}$) is obtained by computing a weighted average of the top K location coordinates by using their corresponding prediction probabilities or confidence scores as weights, as defined in Equation (3).

$$(\widehat{X}={\sum }_{j=1}^K{w}_j{X}_j, \widehat{Y}={\sum }_{j=1}^K{w}_j{Y}_j),$$

(3)

where the weights w_j are normalized based on the prediction scores, as defined in Equation (4):

$$w_j = \widehat{p}j/{\sum }_{i=1}^K{\widehat{p}}_i.$$

(4)

WCR is used to ensure that the location prediction is influenced by the most confident classifications while incorporating spatial information and improving localization accuracy.

3. Experimental Results

3.1. Experiment Setup and Dataset

We utilized a dataset [3] collected from a school environment consisting of multiple classrooms and hallways. The dataset was designed to evaluate ADAM [2], which is an adaptive path loss model for achieving IL. It was repurposed in this study to assess the effectiveness of the proposed QRF-IL. To construct the dataset, data were recorded at 150 unique test points. A mobile device was used at each test point to measure RSSI values from 15 fixed anchor nodes strategically placed throughout the area. The dataset consisted of 15,000 RSSI samples collected from 11 different Bluetooth Low Energy (BLE) devices. Each test point was sampled approximately 100 times over 1.5 min. The dataset was split into the training (75%) and testing datasets (25%). The maximum depth of QDT was set to 10. The experiments were conducted by using Python 3.8.10 and the IBM Qiskit library to implement the proposed model. The IBM Qiskit library was used as the provider of the quantum simulator.

3.2. Results for Different Values of K

We analyzed the performance of QRF-IL by evaluating the mean absolute error (MAE) of IL across different values of K adopted in WCR. MAE varied with different values of K across multiple QDT configurations (Figure 3). Generally, increasing the number of QDTs reduced the error, but the choice of the value of K was also important in performance. For smaller QDT counts (e.g., 8 or 16 trees), error fluctuated with increasing values of K. Initially, low values of K improved accuracy, but beyond a threshold, error increased, suggesting that WCR over too many centroids introduces noise rather than improving performance. Larger QDT counts (e.g., 32, 64, 96 trees) indicated a consistent decline in MAE, with optimal performance typically at K = 3 or 4, where errors were minimized before stabilizing. More QDTs made the model better generalize and benefit from moderate centroid weighting. However, very large values of K diminished returns. Balancing the value of K and the number of QDTs was crucial. A setup of K = 3 or 4 with at least 64 QDTs enabled the best trade-off between accuracy and efficiency. The lowest MAE (2.36 m) was obtained by QRF-IL with 96 QDTs and K = 3.

3.3. Comparison of QRF-IL with Standalone QRF

We evaluated the performance of QRF-IL to analyze the MAE by using the best value of K for each QDT count and the standalone QRF. For lower QDT counts (8 and 16), the mean Euclidean error of the QRF-IL model was slightly higher than that of the standalone QRF (Figure 3b). However, as the number of QDTs increased, the performance of QRF-IL improved, showing lower errors than the standalone QRF method. Notably, at 64 and 96 QDTs, QRF-IL outperformed the standalone QRF, with the lowest error (2.3648 m) recorded for 96 QDTs. Additionally, QRF-IL also outperformed the ADAM, whose mean error is 2.93 m.

4. Conclusions

In this study, we introduced QRF-IL, an enhanced QML approach that extends the QRF framework [12] for regression-based indoor localization. By integrating a WCR method and leveraging QRF with QDTs using QSVMs based on NQKE, QRF-IL efficiently reduces computational complexity while maintaining good IL accuracy. When the number of QDTs increases, IL performance improves. With 96 QDTs and the best value (i.e., 3) of K, QRF-IL showed a mean localization error of 2.3 m, outperforming the standalone QRF (2.53 m) and ADAM (2.93 m) by 9 and 21%. These results confirmed QRF-IL’s effectiveness in enhancing accuracy and scalability through quantum kernel approximation, QRF ensemble learning, and WCR.