Comparative Analysis of Symmetric Cryptographic Algorithms and Cryptanalysis Methods Through a Practical Software Tool for Educational Purposes ^†

Abstract

This paper presents the design and evaluation of an educational software tool aimed at facilitating the practical exploration of symmetric cryptographic algorithms. The application integrates widely used algorithms, including AES, DES, TripleDES, RC2, Blowfish, Twofish, and Camellia, allowing users to perform encryption, decryption, and cryptanalysis via dictionary and brute-force attacks. It provides performance benchmarking by measuring encryption and decryption speed, computational overhead, throughput, and resistance to attacks. Visual elements such as real-time charts and histograms aid in comparing algorithmic behavior. The tool is tailored for educational use, supporting cybersecurity and computer science students in understanding cryptographic principles, algorithm effectiveness, and cryptanalytic techniques. Its goal is to bridge theory and practice in a user-friendly and interactive manner, promoting deeper engagement with modern cryptographic methods.

1. Introduction

Symmetric-key cryptographic algorithms constitute a fundamental pillar of modern information-security infrastructures, facilitating confidentiality, integrity, and authenticity in applications ranging from secure communications to cloud storage and Internet-of-Things deployments [1]. Despite their widespread deployment, pedagogical methodologies for teaching symmetric cryptography often remain confined to theoretical expositions and static demonstrations [2], thereby impeding students’ capacity to appreciate the nuanced interplay between algorithmic design, performance characteristics, and resistance to cryptanalytic techniques.

Bridging this pedagogical divide necessitates an interactive environment in which learners can conduct empirical experiments that juxtapose encryption/decryption throughput, resource utilization, and the efficacy of fundamental attack strategies [3]. To this end, an educational tool has been developed. It integrates seven canonical block ciphers—AES, DES, TripleDES, RC2, Blowfish, Twofish, and Camellia—with two basic cryptanalysis modalities—brute-force and dictionary attacks. The cryptographic tool enables users to process files of varying sizes, launch controlled attack simulations, and observe real-time performance metrics alongside cryptanalytics.

2. Related Works

In today’s digital era, cryptography plays a pivotal role not only in securing information but also as a fundamental component of computer science education. As students increasingly engage with technology, understanding cryptographic principles becomes essential for fostering digital literacy and cybersecurity awareness.

Recent educational initiatives have introduced innovative tools to make cryptography accessible to younger audiences. For instance, CryptoScratch integrates cryptographic algorithms into a block-based programming environment, enabling K–12 students to grasp complex concepts through interactive learning. Similarly, CryptoEL employs experiential learning models to teach key cryptographic concepts, resulting in high comprehension rates among middle and high school students [4,5].

Studies have shown that incorporating cryptography into educational settings enhances students’ problem-solving abilities and fosters critical thinking. A study by Özer and Çetinkaya (2024) revealed that integrating cryptologic methods into the curriculum significantly improved students’ analytical skills and motivation [6].

Moreover, emerging technologies like the Metaverse are being explored to teach cryptographic concepts. A pilot study utilizing the CipherSphere platform demonstrated that immersive environments could enhance student engagement and understanding of cryptography [7].

As the field of cryptography evolves, especially with the advent of quantum computing, it is imperative to prepare students for future challenges. Educational resources are now focusing on post-quantum cryptography, ensuring that learners are equipped with knowledge relevant to upcoming technological advancements.

While platforms like CryptoScratch and CryptoEL excel at visualizing cipher structures and key-schedule operations for beginners, they do not provide integrated support for hands-on cryptanalysis or real-time performance benchmarking. Moreover, existing tools treat encryption/decryption and attack simulation as separate modules, preventing students from directly comparing algorithm resilience under identical conditions. Finally, none of the current educational environments offer an extensible framework that allows instructors to plug in new ciphers or custom attack routines without modifying the core codebase.

To address these gaps, a cryptographic tool is presented which unifies encryption, decryption, brute-force, and dictionary attacks in a single GUI, collects and visualizes real-time metrics—throughput, CPU overhead, attempts per second, and time-to-success—across seven symmetric algorithms, and exposes a modular architecture for the seamless integration of additional ciphers or cryptanalysis methods. This combination empowers students to explore speed-vs-security trade-offs in one cohesive educational environment.

3. Implemented Symmetric Encryption Algorithms and Cryptanalysis Methods

3.1. AES (Advanced Encryption Standard)

AES is a substitution–permutation–network block cipher standardized by the National Institute of Standards and Technology. It processes 128-bit blocks using keys of 128, 192, or 256 bits and performs an initial AddRoundKey operation followed by Nr–1 rounds of SubBytes, ShiftRows, MixColumns, and AddRoundKey, with a final round omitting MixColumns. This structure affords strong diffusion and confusion, and hardware acceleration (AES-NI) further enhances its performance. Empirical studies confirm AES’s superior throughput and resilience against known cryptanalytic attacks [8].

In Figure 1, the block diagram of the AES algorithm is shown. The process begins by reading the original file and converting its contents into bytes. These bytes are then padded to form 128-bit blocks, after which the symmetric key is generated (Generate AES Symmetric Key). Each 128-bit block undergoes the Initial Round Key Addition step, where it is first XORed with the initial round key derived from the master key.

The next phase consists of a loop of Nr–1 iterations (Nr = 10, 12, or 14 for 128-, 192-, and 256-bit keys, respectively). In each iteration, the following transformations are applied in sequence:

• SubBytes Transformation—a nonlinear substitution of each byte using the AES S-box;
• ShiftRows Transformation—a cyclic shift of the rows in the 4×4 state matrix to introduce diffusion;
• AddRoundKey Step—the result is XORed with the current round key.

Additionally, in each of these Nr–1 rounds, MixColumns Transformation is applied before AddRoundKey: it performs a linear mixing of each column in the block to further enhance byte-level diffusion.

In the final (Nth) round, MixColumns is omitted; only SubBytes and ShiftRows are performed, followed by AddRoundKey. The output of this final round is then written back to the file as ciphertext.

This AES structure, as illustrated in Figure 1, ensures both strong cryptographic diffusion and efficient implementation in hardware and software environments.

3.2. DES (Data Encryption Standard)

DES is a 16-round Feistel cipher operating on 64-bit blocks with a 56-bit key, as defined in FIPS-46-3. Each round expands a 32-bit half-block to 48 bits, XORs it with a subkey, substitutes via eight S-boxes, permutes the output, and swaps halves. Despite its historical importance, differential and linear cryptanalysis have demonstrated practical vulnerabilities, and its short key length renders it insecure for modern applications [9].

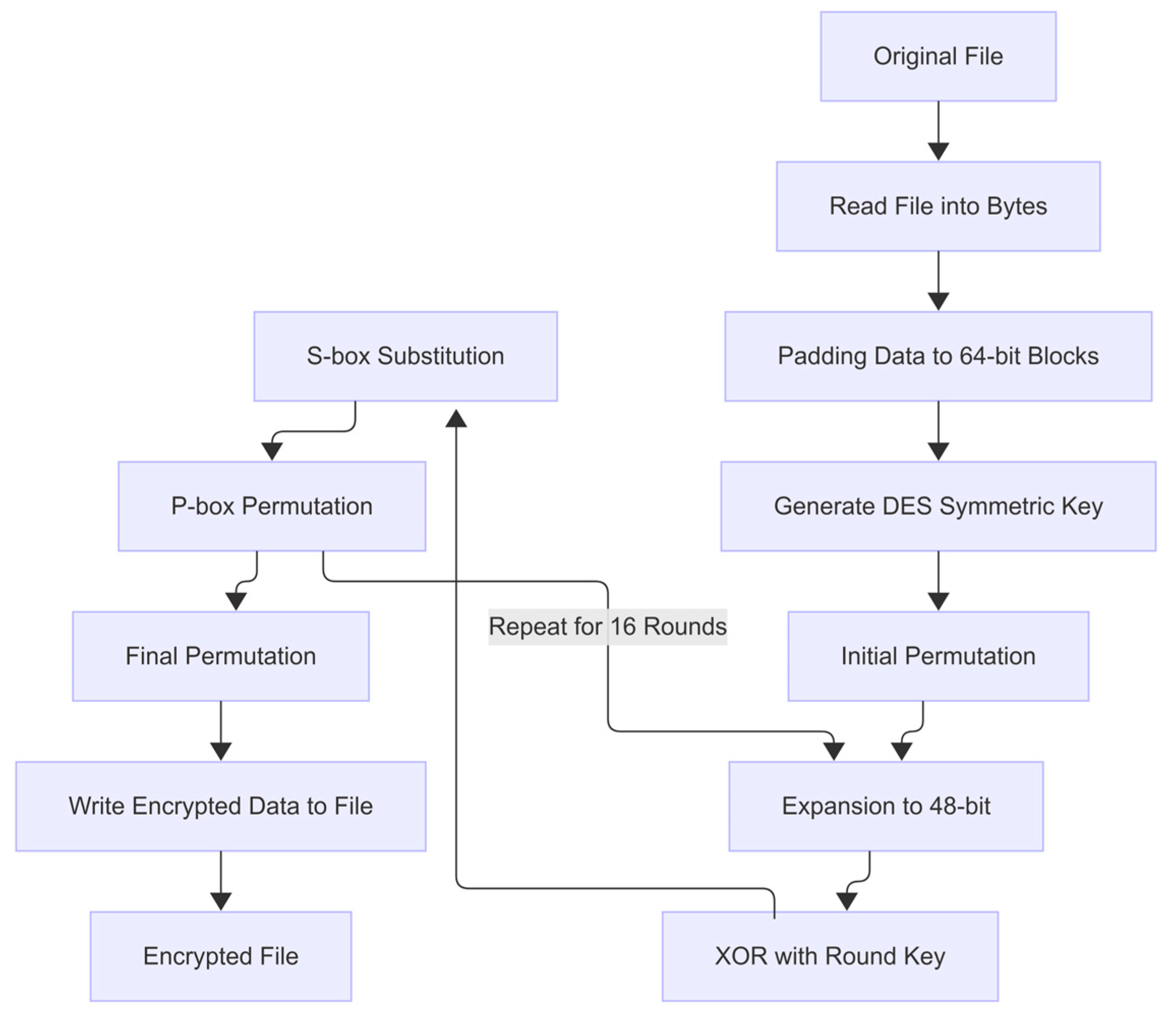
In Figure 2, the block diagram of the DES algorithm is presented. The encryption workflow proceeds as follows:

• Read and Pad: The original file is read into bytes and padded into 64-bit blocks (Padding Data to 64-bit Blocks).
• Key Generation: A 56-bit DES key is derived or provided.
• Initial Permutation (IP): Each 64-bit block undergoes the fixed initial permutation, reordering its bits to prepare for the Feistel network.
• Sixteen Feistel Rounds: For each of the 16 rounds, the 64-bit block is split into left (L) and right (R) 32-bit halves:
  • Expansion (E): The right half R is expanded from 32 to 48 bits via an expansion permutation, duplicating certain bits.
  • Key Mixing: The expanded half is XORed with the 48-bit round subkey (derived from the master key via the DES key schedule).
  • Substitution (S-boxes): The result is divided into eight 6-bit segments and passed through eight S-boxes, each mapping 6 bits to 4 bits, compressing back to 32 bits.
  • Permutation (P-box): A fixed P-permutation shuffles those 32 bits to further diffuse the outcome.
  • Feistel Swap: The output is then XORed with the left half L, and the halves are swapped, so that the previous right half becomes the new left half for the next round.
• Final Permutation (FP): After 16 rounds, the last swap is reversed and a final fixed permutation (the inverse of IP) is applied.
• Write Ciphertext: The resulting 64-bit block is written back to the output file as ciphertext (Write Encrypted Data to File).

This sequence—Initial Permutation → 16 × [Expansion → XOR with Round Key → S-box Substitution → P-box Permutation → Swap] → Final Permutation—exactly mirrors the DES specification in FIPS 46-3 and ensures a balanced trade-off between diffusion, confusion, and computational efficiency.

3.3. Triple DES (TDEA)

Triple DES applies the DES cipher three times in an encrypt–decrypt–encrypt sequence using two or three independent keys (K₁, K₂, K₃), achieving an effective key length of up to 168 bits. Specified in NIST SP 800-67 Rev 2, TDEA substantially increases brute-force resistance but at roughly three times the computational cost of single DES, motivating its deprecation in favor of AES [10].

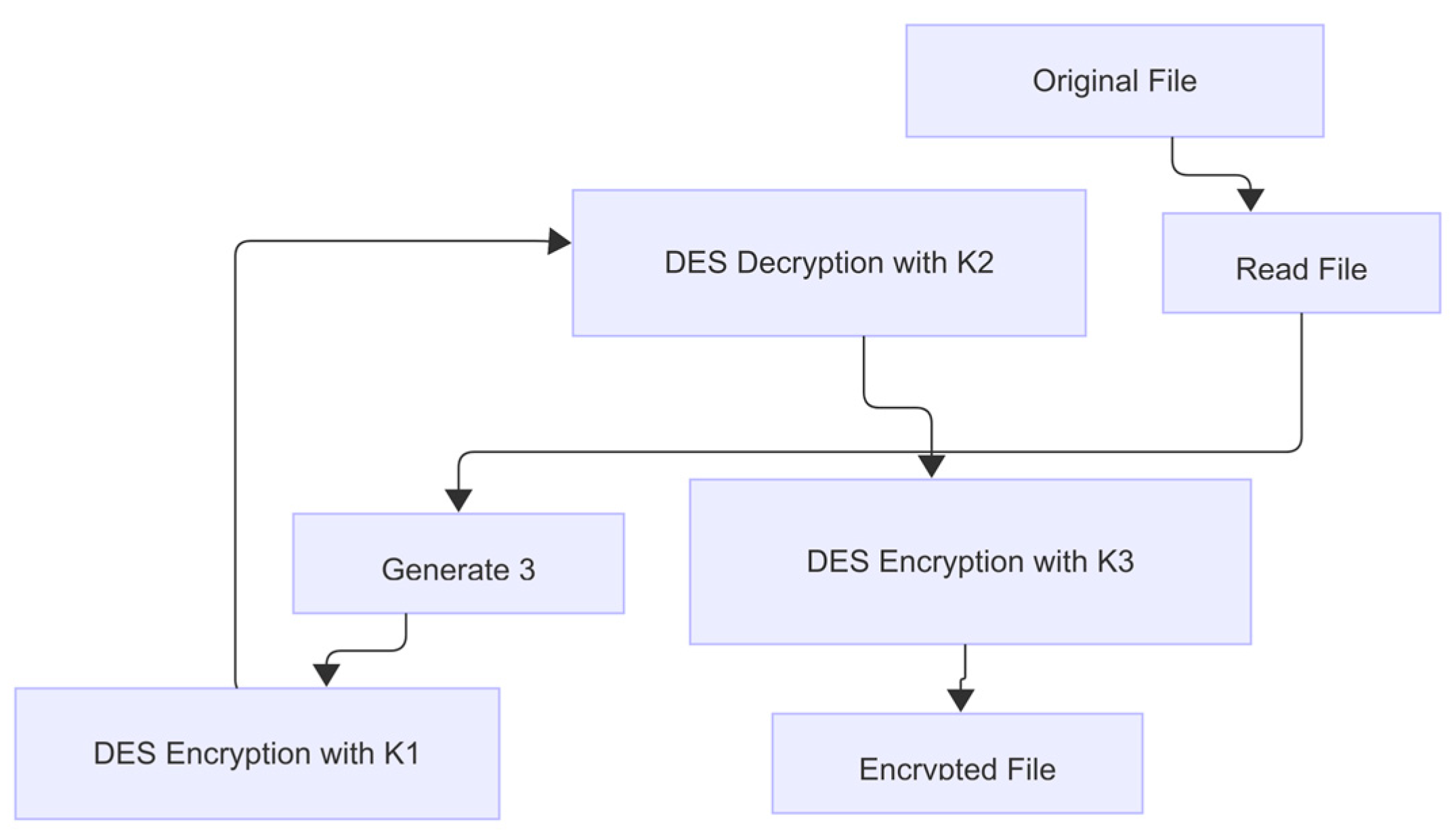
In Figure 3, the block diagram of the 3DES “EDE” construction is shown. The process proceeds as follows:

• Read and Pad—The original file is read into bytes and padded into 64-bit blocks.
• Key Generation—Three independent 56-bit keys (K₁, K₂, K₃) are derived or supplied (“Generate Three Keys: K₁, K₂, K₃”).
• DES Encryption with K₁—Each padded 64-bit block undergoes the full single-DES encryption sequence under key K₁ (Initial Permutation → 16 Feistel rounds → Final Permutation).
• DES Decryption with K₂—The intermediate ciphertext from step 3 is then fed back through the DES network in reverse subkey order under key K₂, effectively performing a single-DES decryption.
• DES Encryption with K₃—The output of step 4 is encrypted once more with key K₃ using the standard DES encryption rounds.
• Write Ciphertext—The final 64-bit block produced in step 5 is written back to the file as the 3DES ciphertext.

By chaining Encrypt_k1 → Decrypt_k2 → Encrypt_k3, 3DES amplifies DES’s brute-force resistance to an effective key length of up to 168 bits, while preserving its well-studied Feistel structure and ensuring backward compatibility when K₁ = K₂ = K₃.

3.4. RC2 and Camellia

RC2 is a 64-bit block Feistel cipher with variable key length (up to 128 bits), described in RFC 2268. It interleaves 16 mixing rounds—each involving modular addition, XOR, and bit rotations—with 2 mashing rounds that inject additional key-dependent nonlinearity. While flexible, RC2’s security and performance lag behind more modern ciphers and it is now primarily of historical interest [11].

Camellia is a Feistel-network cipher operating on 128-bit blocks with 18 rounds for 128-bit keys (24 for longer keys) and supports 128-, 192-, or 256-bit keys. It intersperses FL/FL⁻¹ functions for additional nonlinearity every six rounds and uses an MDS-based diffusion layer. Standardized by ISO/IEC, Camellia matches AES in both software and hardware performance and offers robust resistance to linear and differential cryptanalysis [12].

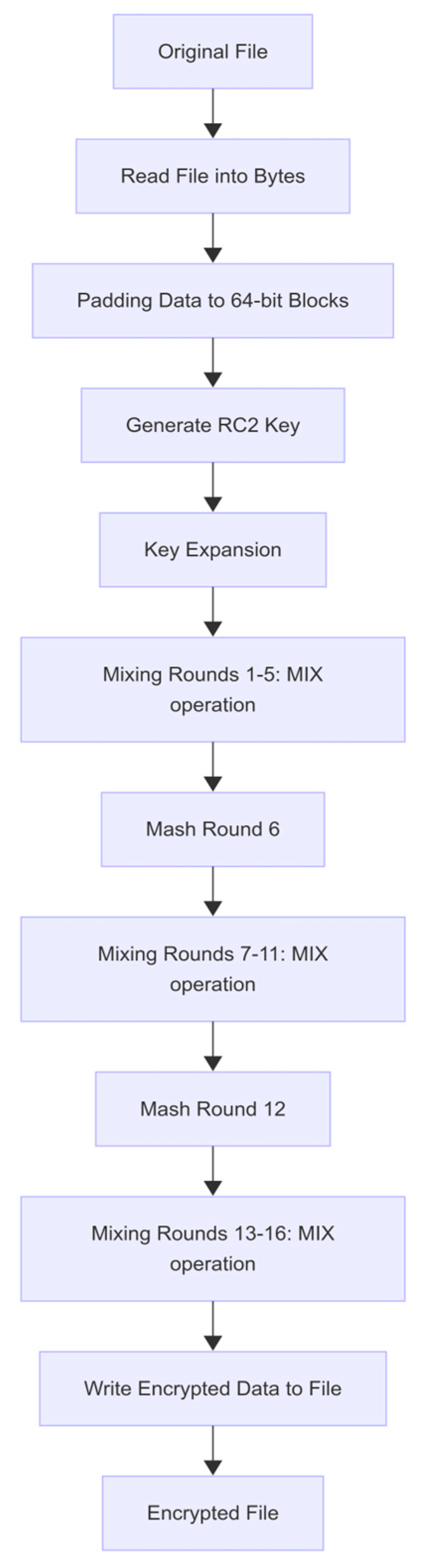
In Figure 4, the RC2 algorithm begins by reading the original file into bytes and padding these bytes into 64-bit blocks. A user-supplied key—up to 128 bits in length—is then generated and expanded into a schedule of 64 16-bit subkeys. The core encryption process interleaves 16 rounds of “MIX” operations—each combining two state words with a subkey through addition mod 2¹⁶ followed by a left rotation—into three phases (rounds 1–5, 7–11, and 13–16), with “MASH” rounds after rounds 5 and 11 that inject additional key-dependent nonlinearity by adding selected subkeys directly into the state. After completing all sixteen rounds, the transformed 64-bit block is written back to the output file as ciphertext.

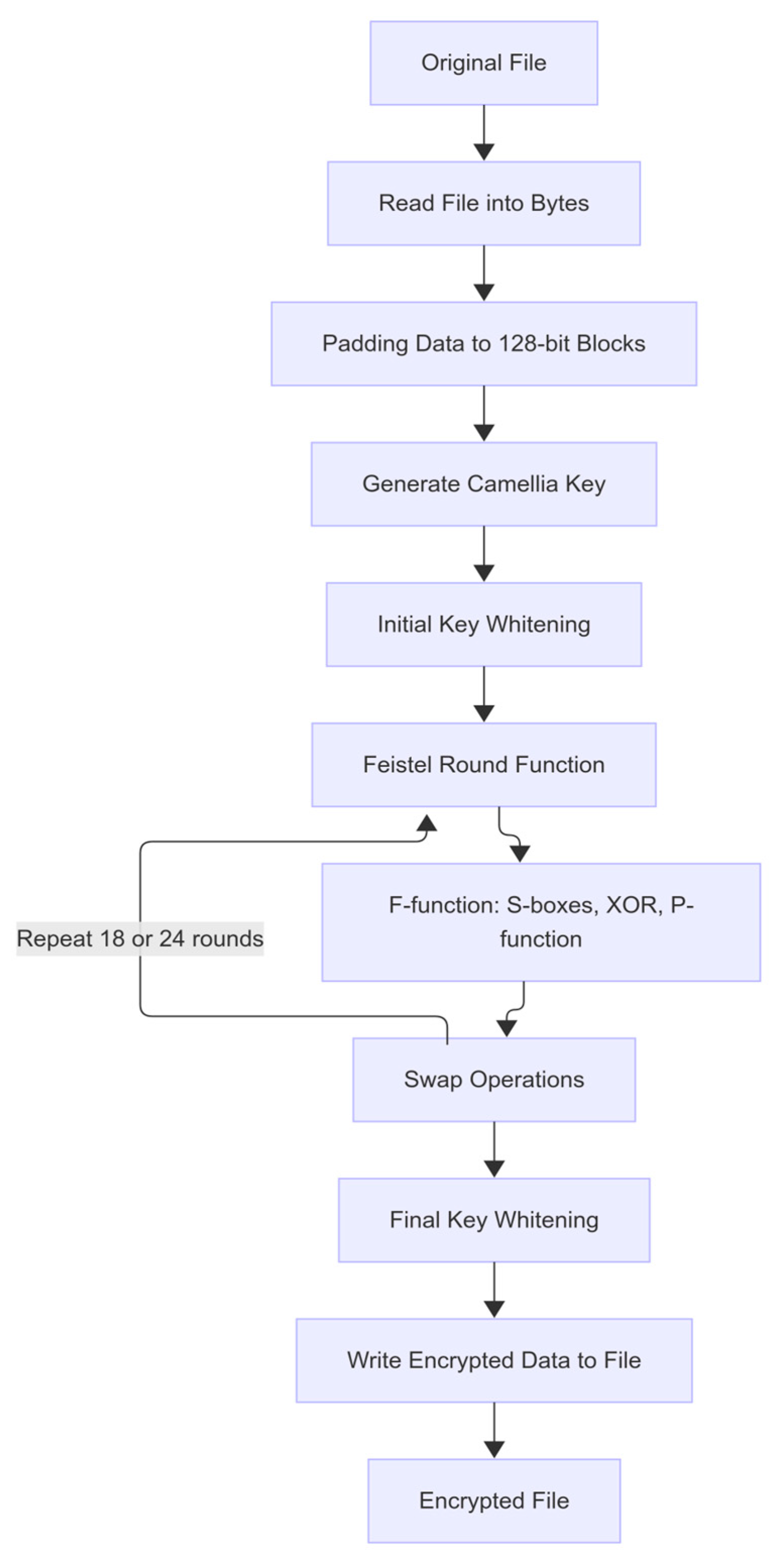
Figure 5 presents the Camellia encryption workflow. After the original file is read into a byte stream and padded to 128-bit blocks, a secret key (128, 192, or 256 bits) is expanded into a set of round keys and whitening keys. Each plaintext block undergoes initial key whitening by XORing both 64-bit halves with two of the derived subkeys. The core of the cipher consists of a Feistel network of either 18 or 24 rounds (depending on key length), where in each round one half is fed into the F-function; this function applies two parallel 8 × 8 S-box substitutions to the half-block’s bytes, combines the results via XOR, and then permutes the bits through a fixed P-function to ensure diffusion. The F-output is XORed into the other half, and the halves swap roles before the next round. After completing all Feistel rounds, a final swap restores the original half-block order, and final key whitening is applied by XORing each half with the remaining two subkeys. The fully encrypted blocks are then written to the output file.

3.5. Blowfish and Twofish

Blowfish is a 16-round Feistel cipher with a 64-bit block size and key lengths up to 448 bits, designed by Schneier in 1993. Its expensive key schedule initializes a large P-array and four S-boxes, after which each round applies S-box lookups, XOR, and modular addition. Recent FPGA-based implementations demonstrate that Blowfish can achieve high throughput with modest resource use, making it instructive for hardware-oriented studies [13].

Twofish is a 16-round Feistel cipher on 128-bit blocks supporting 128-, 192-, or 256-bit keys. A finalist in the AES competition, it employs key-dependent S-boxes, an MDS diffusion matrix, pseudo-Hadamard transforms, and input/output whitening. Twofish offers a compelling balance of security and performance and remains unencumbered by patents [14].

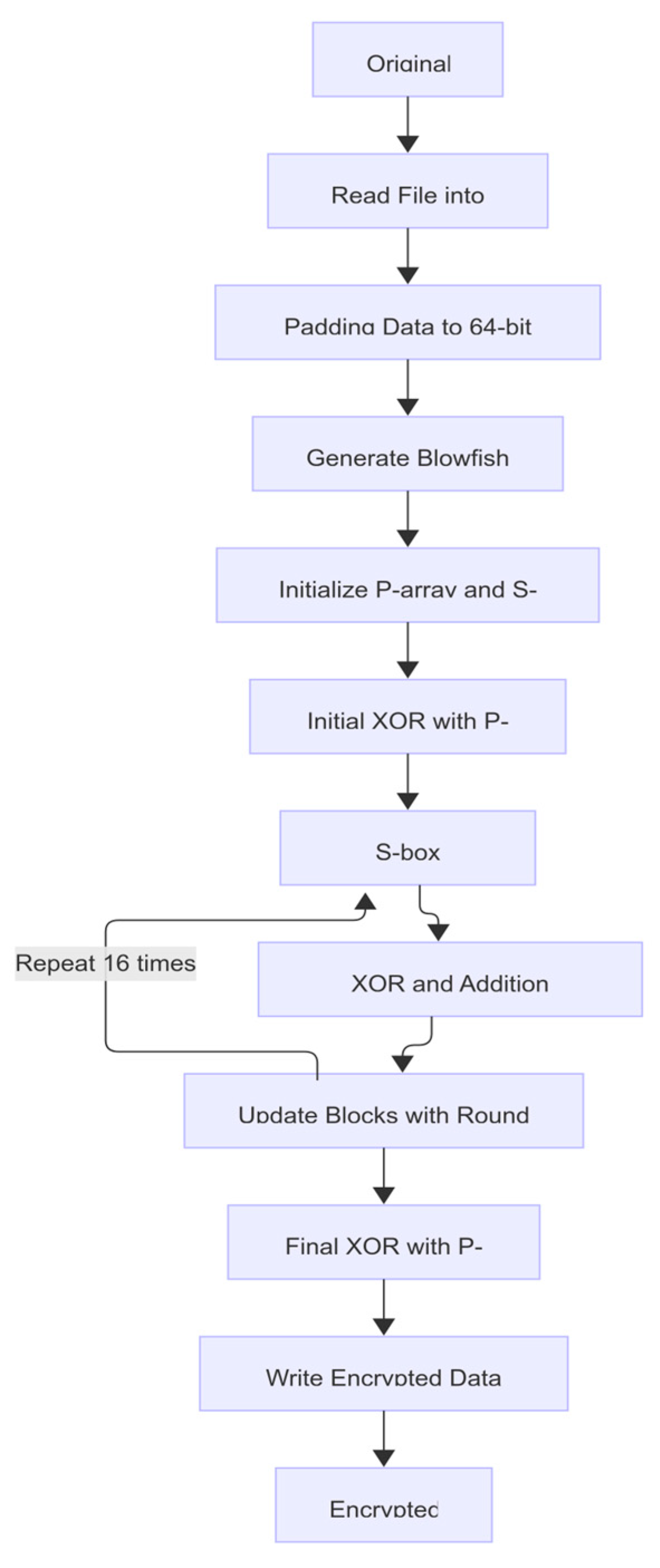
Figure 6 illustrates the Blowfish encryption workflow. After reading the original file into a byte stream and padding it to 64-bit blocks, a variable-length key (up to 448 bits) is expanded into an 18-entry P-array and four 256-entry S-boxes through an intensive key-schedule routine. Each 64-bit plaintext block is split into two 32-bit halves, the left half is XORed with P₀, and then the cipher executes 16 Feistel rounds: in each round, the right half enters the F-function—where it is subdivided into four bytes, each substituted via one of the four S-boxes, recombined, and subjected to two modular additions and an XOR—and the F-output is XORed into the left half, after which the halves swap roles and the next P-entry is used. Upon completion of the rounds, the halves are swapped one final time and each is XORed with the last two P-entries to produce the ciphertext block, which is then written to the output file.

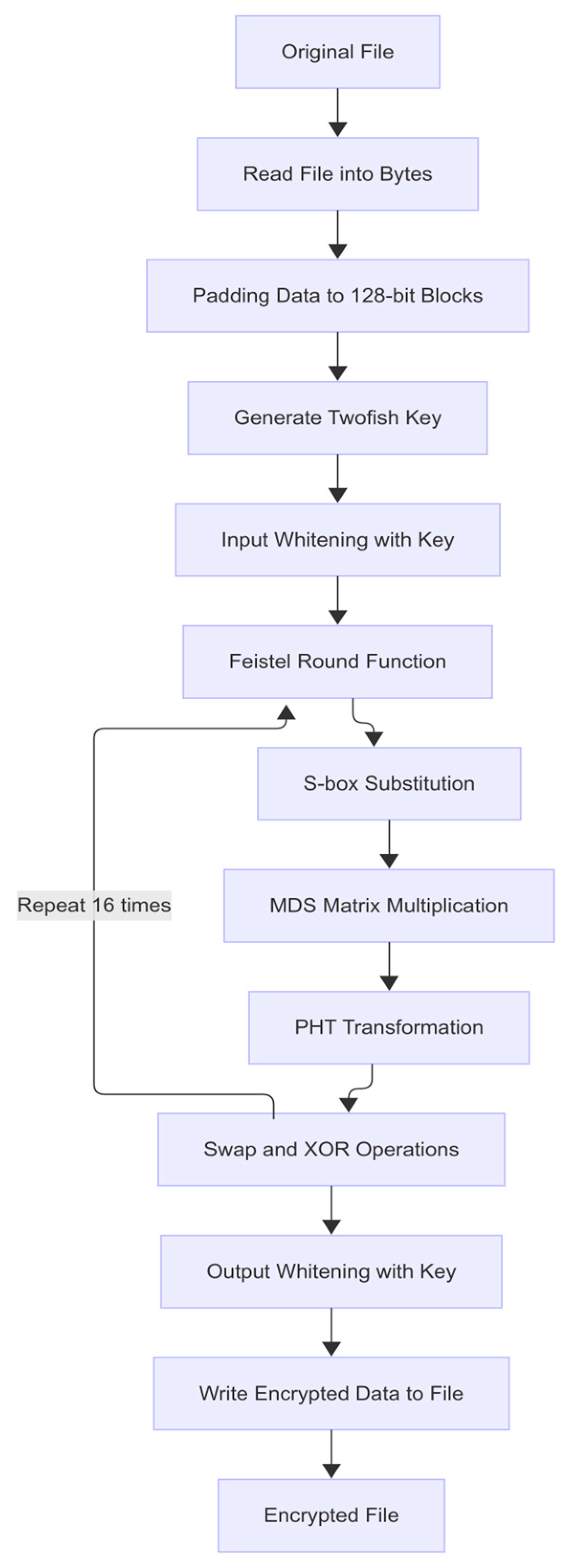
Figure 7 depicts the Twofish encryption process. Following file reading and padding to 128-bit blocks, the master key undergoes a complex key schedule that generates 40 round subkeys and 4 whitening keys. Each plaintext block is first “whitened” by XORing its two 64-bit halves with the first two subkeys (input whitening), then processed through 16 Feistel rounds. In each round, one half is fed into the g-function, which splits it into four bytes, substitutes them via two key-dependent 8 × 8 S-boxes, multiplies the resulting words by a fixed 4 × 4 Maximum Distance Separable (MDS) matrix for optimal diffusion, and mixes them with a Pseudo-Hadamard transform (PHT). The g-output is XORed into the other half, the halves swap, and the next two round subkeys are used. After all rounds, the halves undergo output whitening—XOR with the final two subkeys—and the fully encrypted block is written to the file.

3.6. Brute-Force Attack

A brute-force attack is the most straightforward cryptanalytic strategy: the adversary systematically tries every possible key or password until the correct one is found. In the context of password-based file encryption, this entails generating all strings over a chosen character set (the “alphabet”) of lengths within a specified range, applying each candidate to the decryption routine, and checking whether the result produces a valid plaintext (often via an integrity check such as a hash or padding validation). The strength of a brute-force attack lies in its guaranteed success given sufficient time and computational resources; its weakness is the exponential growth of the search space as password length or alphabet size increases, which makes it infeasible beyond modest key sizes or password lengths. Modern techniques to accelerate brute-force include GPU-based parallelization, FPGA and ASIC implementations, and distributed computing, but even these approaches are bounded by the inescapable combinatorial explosion of possibilities.

3.7. Dictionary Attacks

A dictionary attack narrows the search by leveraging precompiled lists of likely passwords—drawn from common user behavior, known data breaches, or language-model-generated candidates—instead of exploring the entire key space. By testing entries from a wordlist, an attacker can often recover weak or reused passwords orders of magnitude faster than with pure brute-force. However, dictionary attacks depend entirely on the quality and relevance of the wordlist: they fail against truly random or high-entropy passwords and may require supplemental strategies (e.g., rule-based mangling, phonetic substitutions) to increase coverage. In educational settings, comparing dictionary and brute-force attack performance vividly demonstrates how password complexity and user behavior impact cryptographic resilience, underscoring the importance of strong, unpredictable passwords.

4. Software Architecture and Implementation of the Tool

4.1. Architecture of the Simulation Tool

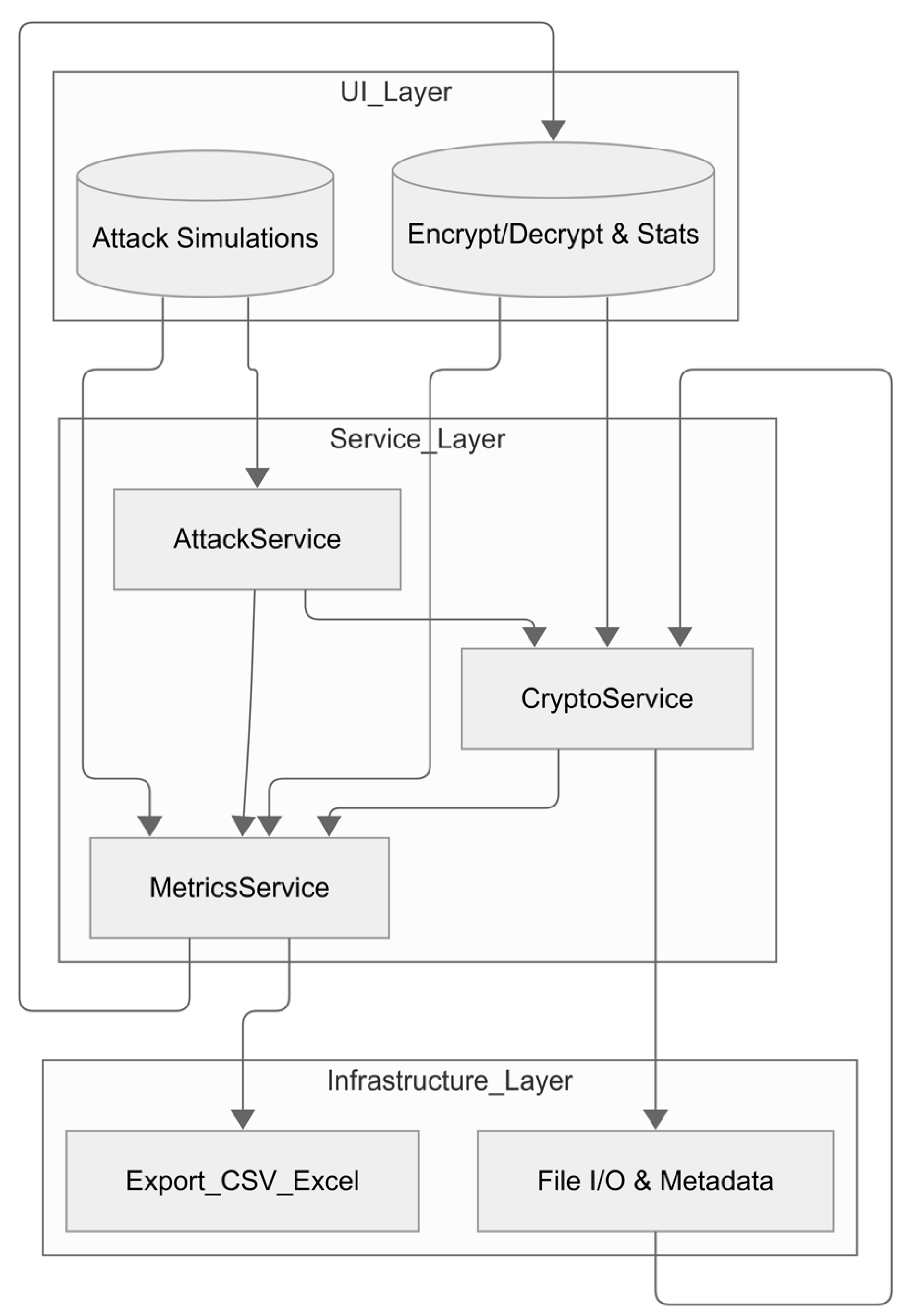
The prototype is implemented in C# 10 on the cross-platform .NET 8.0 runtime; its desktop interface is built with Windows Presentation Foundation (WPF). Figure 8 illustrates the three-layer architecture of the tool, which cleanly separates the application into a Presentation (UI) Layer, a Business Logic (Service) Layer, and an Infrastructure Layer. At the top, the UI Layer comprises two main modules: Encrypt/Decrypt and Stats, which orchestrates file selection, password entry, algorithm choice, and real-time display of performance metrics; and Attack Simulations, which provides interfaces for launching brute-force and dictionary attacks. Beneath that, the Service Layer encapsulates core business logic in three services:

• CryptoService, responsible for all symmetric-key operations (AES, DES, TripleDES, RC2, Blowfish, Twofish, Camellia) including key derivation, padding, and block-level transformations;
• AttackService, which drives both Brute-Force Attack (systematic keyspace enumeration) and Dictionary Attack (password list trials), feeding each attempt through the CryptoService and capturing success or failure;
• MetricsService, which collects timing, throughput, and success-rate data from both encryption/decryption runs and attack attempts and exposes these results to the UI.

Finally, the Infrastructure Layer handles persistence and I/O concerns via two components: File I/O and Metadata, which reads and writes files, manages salts and hashes, and preserves original file extensions; and Export_CSV_Excel, which formats and exports statistical and attack-result data to CSV or Excel workbooks.

4.2. User Interface

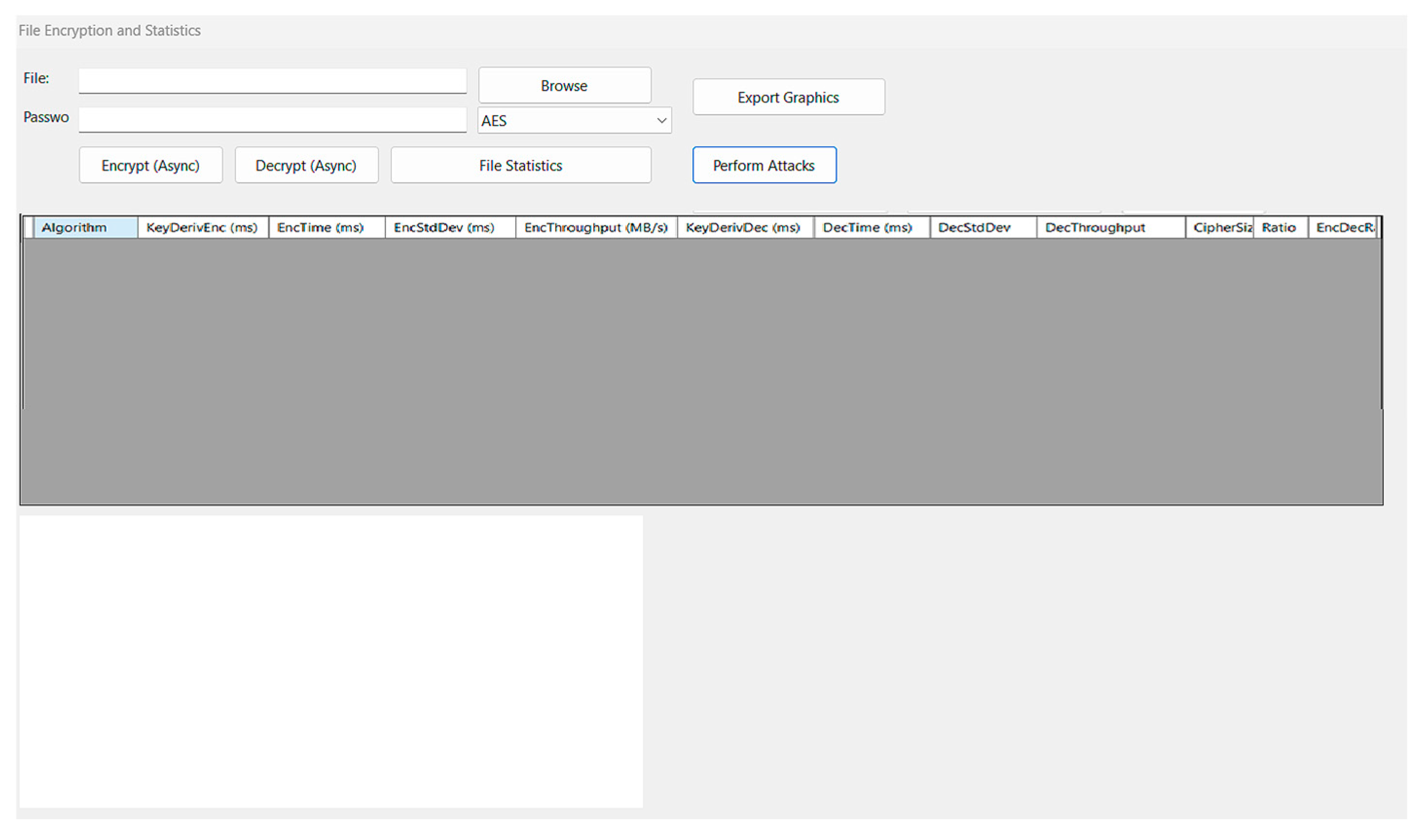
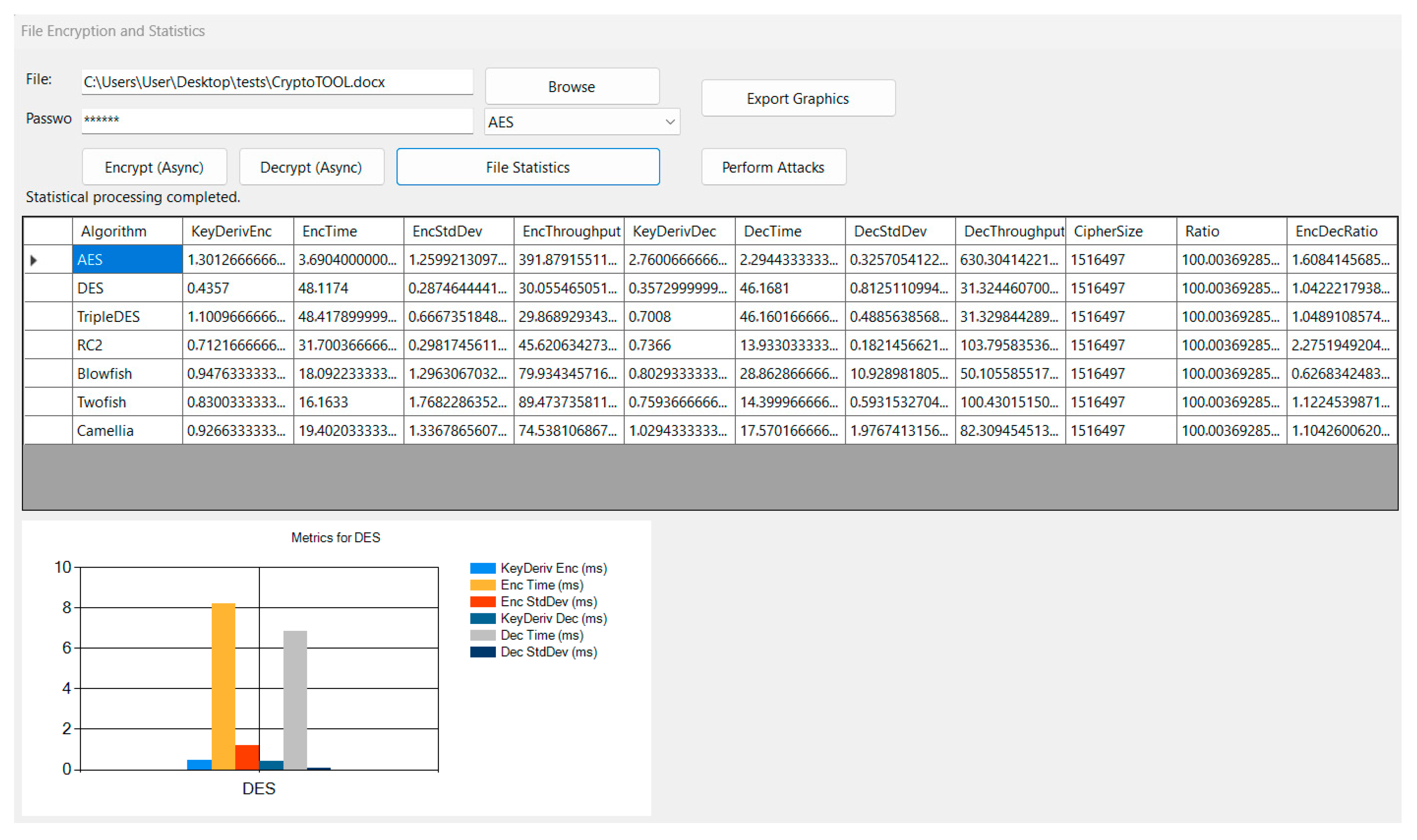
The application employs a cohesive, multi-panel interface to support encryption, benchmarking, and cryptanalysis within just two windows. In the File Encryption and Statistics form (Figure 9), users choose a source file and enter a passphrase, then select one of the seven built-in ciphers (AES, DES, TripleDES, RC2, Blowfish, Twofish, Camellia) from a dropdown. “Encrypt (Async)” and “Decrypt (Async)” buttons launch non-blocking operations—updating a progress bar and status label as the task proceeds. Clicking “File Statistics” automatically runs repeated encryption/decryption trials across all algorithms, gathering metrics (key-derivation time, execution time, throughput, output size, etc.) and populating them into a sortable DataGridView. The column descriptions are as follows:

• Algorithm—name of the cipher applied for encryption/decryption.
• Key Deriv (Enc) (ms)—time needed to derive the key + IV for the encryption run, measured in milliseconds.
• Enc Time (ms)—total time to encrypt the input file, in milliseconds.
• Enc StdDev (ms)—standard deviation of the individual encryption times, indicating their variability.
• Enc Throughput (MB/s)—average encryption data rate: file size (MB) ÷ Enc Time (s).
• Key Deriv (Dec) (ms)—time required to derive the key + IV for the decryption run, in milliseconds.
• Dec Time (ms)—total time to decrypt the encrypted file, in milliseconds.
• Dec StdDev (ms)—standard deviation of the individual decryption times.
• Dec Throughput (MB/s)—average decryption data rate: file size (MB) ÷ Dec Time (s).
• Encrypted Size (bytes)—size of the encrypted output file in bytes.
• Ratio (%)—encrypted-size-to-original-size percentage, showing storage overhead.
• Enc/Dec Ratio—Enc Time ÷ Dec Time; values > 1 mean encryption is slower than decryption.

An embedded chart beneath the grid visualizes any chosen metric, and users can export both the chart (PNG) and the detailed results table (Export Graphics).

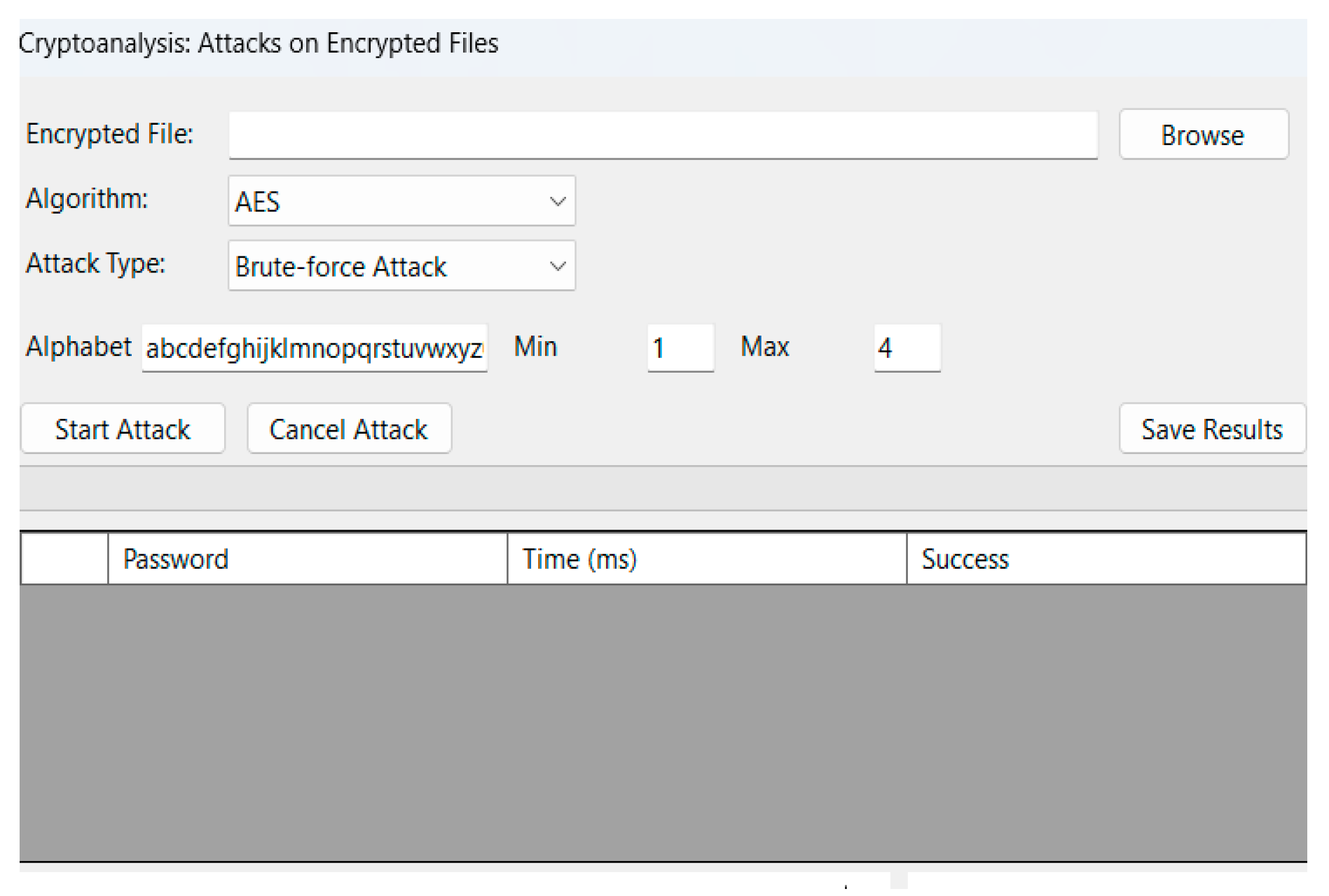
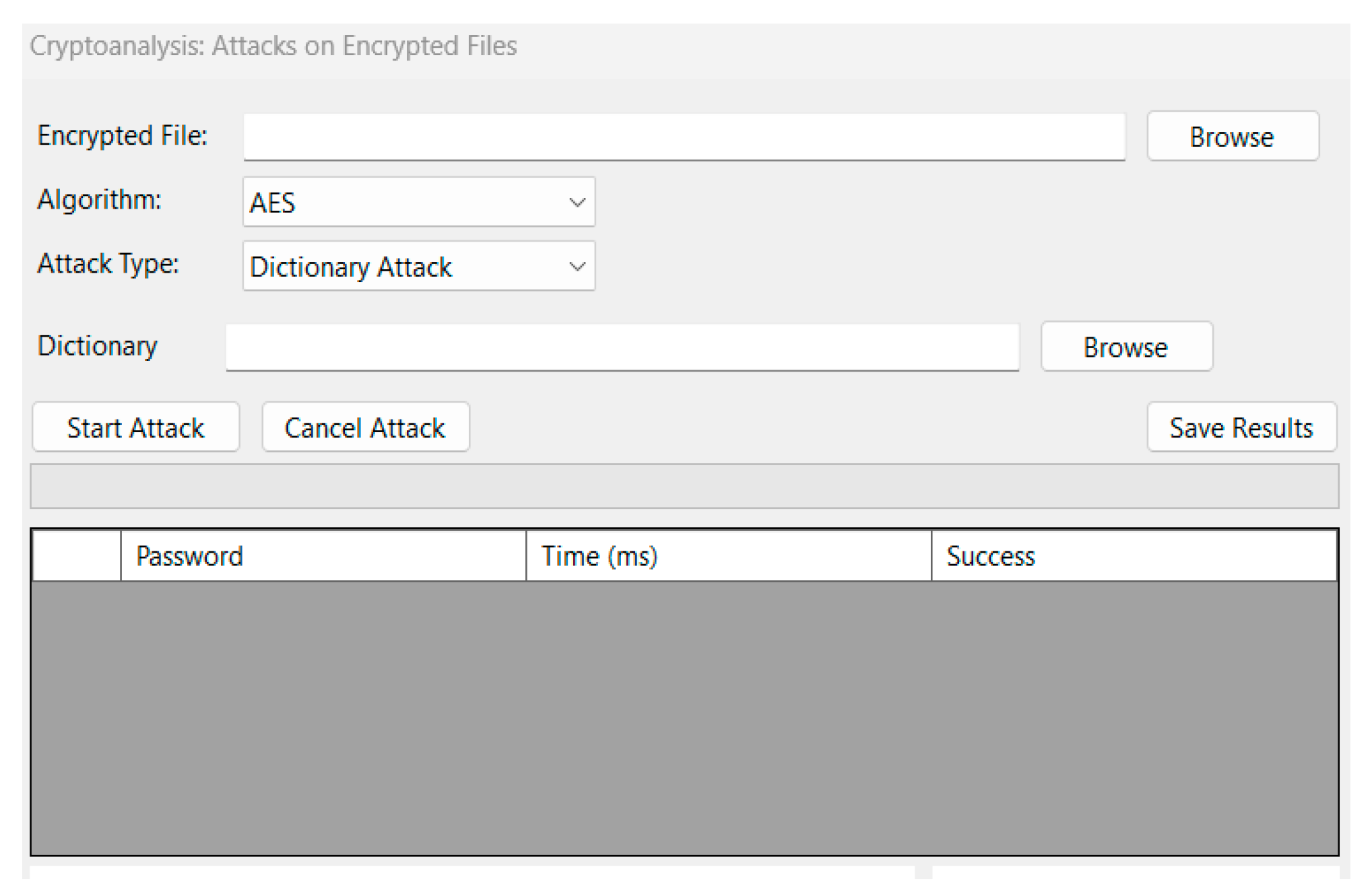
Cryptanalysis is integrated into a single Attacks on Encrypted Files form (Figure 10 and Figure 11). Here, the top section lets users pick the target encrypted file and algorithm. A second dropdown toggles between “Brute-force” and “Dictionary” attack modes: selecting “Brute-force Attack” (Figure 10) reveals controls for specifying the character set and password length bounds, while “Dictionary Attack” (Figure 11) exposes a file picker for a candidate list. Regardless of mode, a unified “Start Attack” button begins the chosen attack, and “Cancel Attack” stops it immediately. As each password is tried, the grid in the middle logs data (password, time ms, success). Below, a dual-axis line chart tracks per-attempt latency alongside an estimated time-to-recovery (ETR), and a histogram shows the distribution of attempt durations. Finally, “Save Results” exports the attack log to Excel.

By reusing one dynamic form for both attack types and providing consistent real-time feedback and export options, the UI offers a smooth learning curve: students can switch effortlessly between exploring encryption performance and hands-on cryptanalysis.

5. Testing and Results

To validate the functionality and performance of the cryptographic tool, end-to-end experiments are conducted on a Windows 10 workstation equipped with an Intel Core i7-9700K CPU (HP Elite 800 series, HP Inc., Palo Alto, CA, USA) (3.60 GHz) and 16 GB RAM. Two representative files—a 1 MB Microsoft Word document and a 5 MB PowerPoint presentation—are encrypted under AES with a six-character alphanumeric password. Each symmetric algorithm is benchmarked over three iterations to compute key-derivation time, encryption/decryption time, throughput, and standard deviation.

In Figure 12, the “File Statistics” interface presents aggregated metrics for all seven block ciphers applied to the 1 MB document. AES achieves the highest throughput (≈392 MB/s) and lowest mean encryption latency (≈3.7 ms), whereas DES exhibits the poorest performance and greatest variability. The tabular view supports sorting by any metric and exporting both the raw data and accompanying bar chart for external analysis.

Moreover, the UI supports interactive exploration: whenever the user clicks on a column header in the results grid (e.g., “EncTime” or “DecThroughput”), the bar chart is immediately redrawn to display that metric for all algorithms; similarly, clicking on a specific algorithm’s row filters the chart to show that cipher’s complete set of statistics. This dynamic behavior enables students to investigate individual performance dimensions or focus on a single algorithm’s behavior with a single click, fostering deeper insight into the trade-offs between key-derivation overhead, encryption/decryption latency, throughput, and variability.

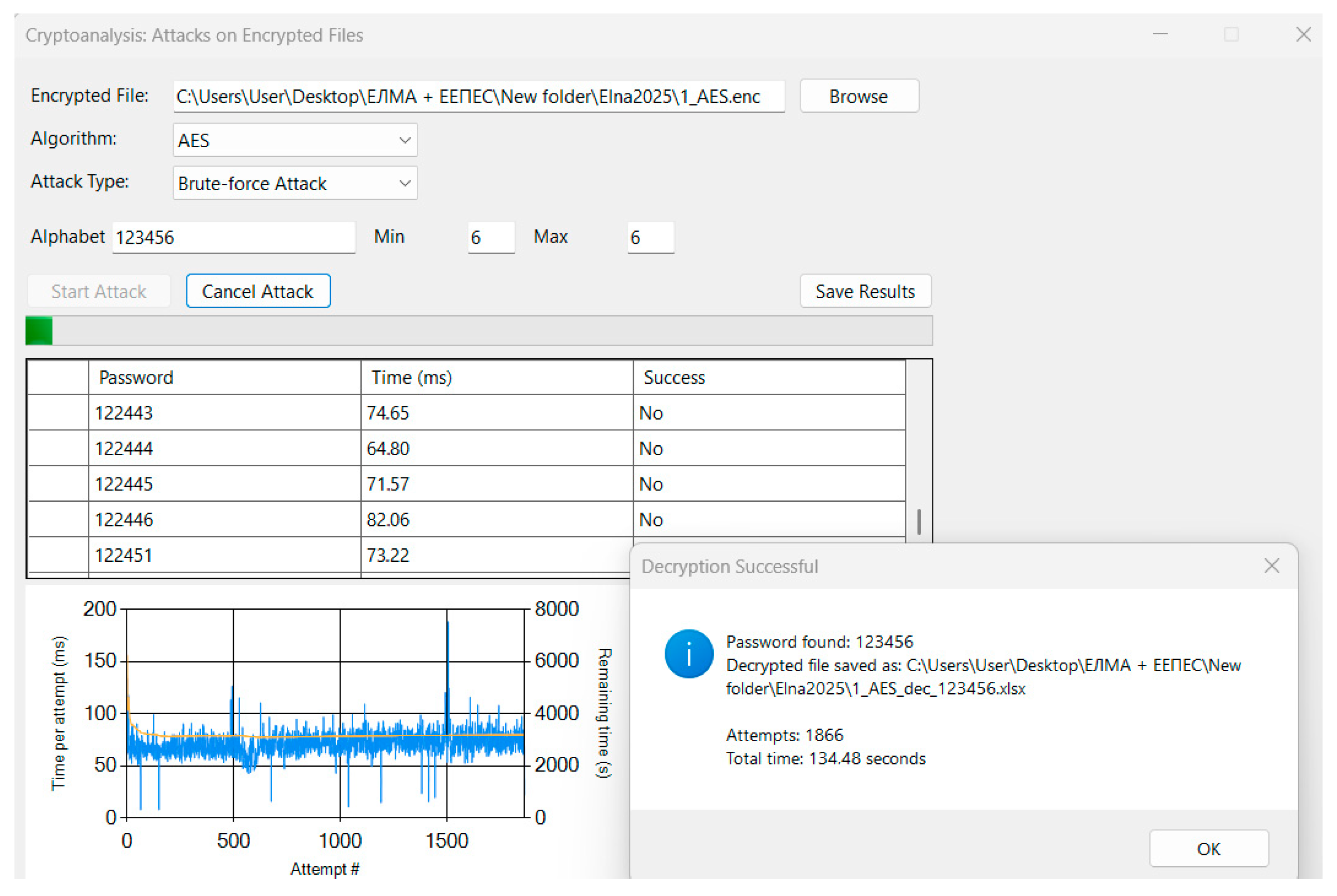
Figure 13, Figure 14, Figure 15 and Figure 16 illustrate the cryptanalysis module under real test conditions. In Figure 13, a dictionary attack is executed against an AES-encrypted PPTX: the progress bar advances as each candidate password is tried, the lower-left line chart plots attempts-per-second alongside estimated time remaining, and upon correctly guessing the password the tool automatically decrypts the file (restoring its original extension), saves it to disk, and displays a popup reporting the recovered password, number of attempts, and total elapsed time.

Figure 14 presents a brute-force attack on the same file using a restricted numeric alphabet (“123456”) and fixed length, showing how the histogram of attempt times (right panel) and the cumulative-attempts chart update in real time.

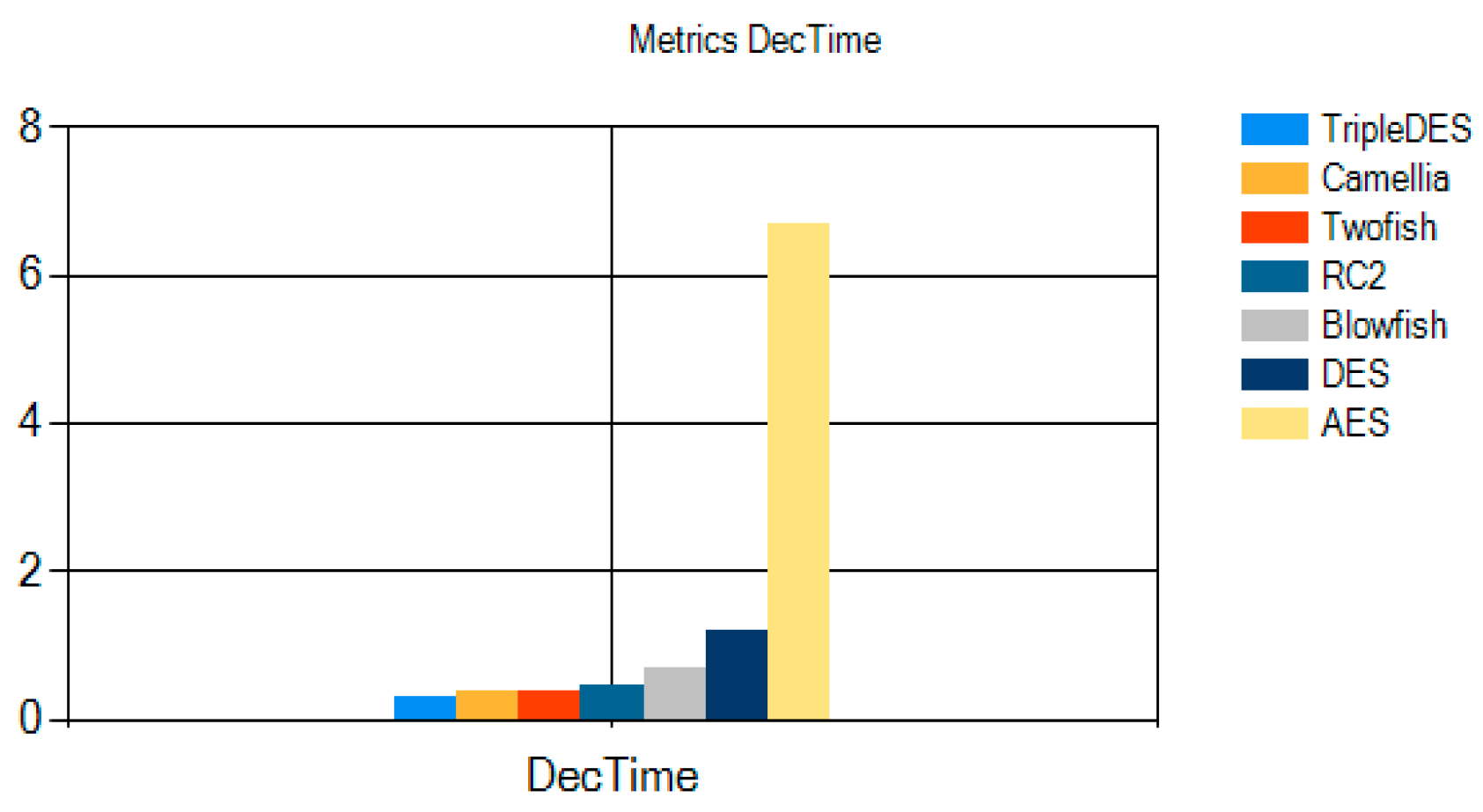
Figure 15 illustrates the average decryption times (DecTime) for all seven ciphers under test. AES exhibits a notably higher decryption latency—approximately 6.6 ms—reflecting its 10/12/14-round structure and heavier round functions. In contrast, Camellia, Twofish, TripleDES, RC2, Blowfish, and DES all complete decryption in under 1.3 ms, with DES and Twofish around 0.5 ms, Camellia and TripleDES near 0.3 ms, RC2 at about 0.4 ms, and Blowfish roughly 0.7 ms. These results emphasize AES’s comparatively greater computational cost at decryption time, while the other algorithms deliver more uniform and faster decryption performance.

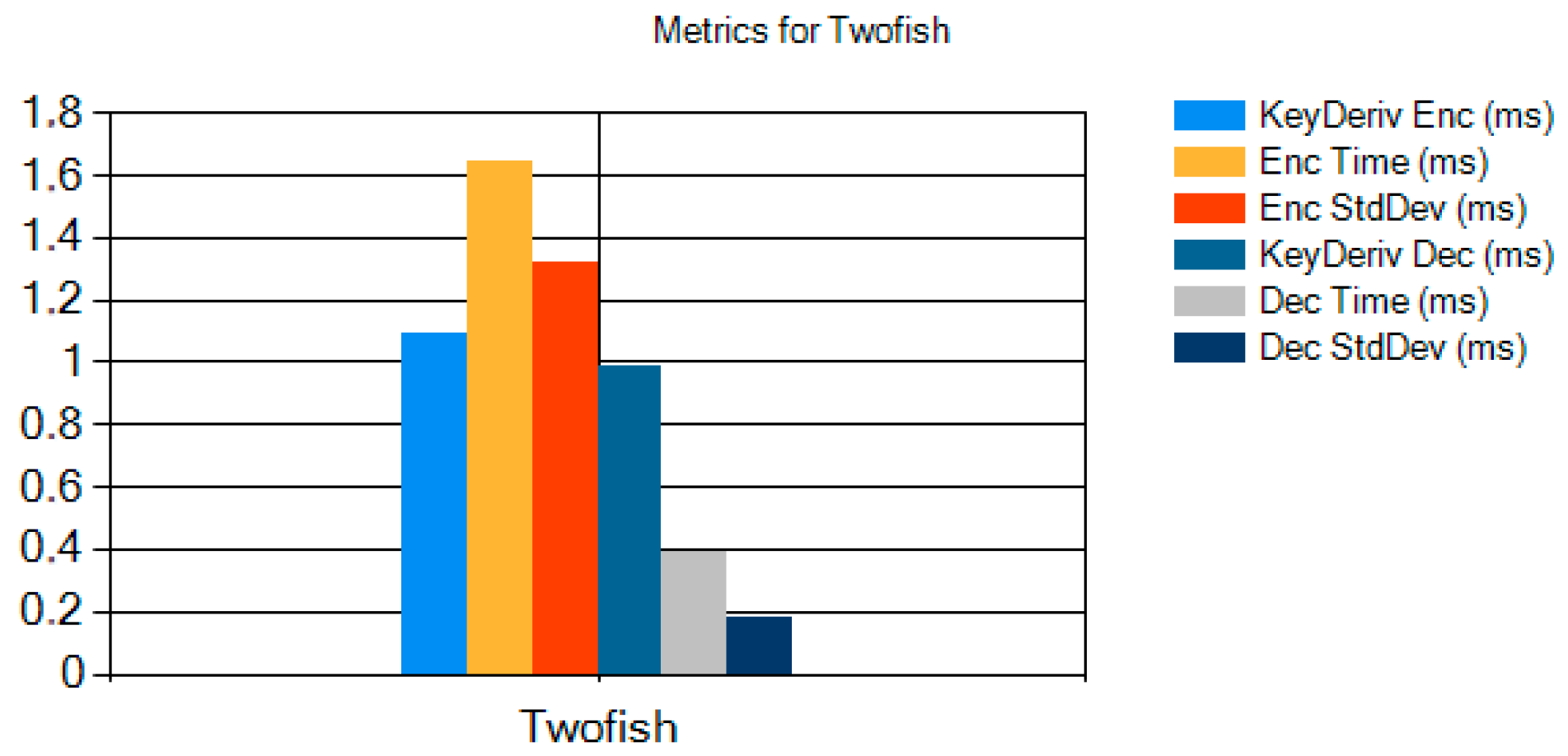
Figure 15 presents a detailed breakdown of Twofish’s performance metrics, as measured during our file-statistics experiments. The chart plots six values for Twofish: key-derivation time for encryption (KeyDeriv Enc), average encryption time (Enc Time), standard deviation of encryption time (Enc StdDev), key-derivation time for decryption (KeyDeriv Dec), average decryption time (Dec Time), and standard deviation of decryption time (Dec StdDev). As shown, Twofish’s key derivation requires approximately 1.05 ms, while its encryption routine completes in about 1.65 ms on average (with a variance of 1.34 ms). Decryption is faster, averaging 0.40 ms after roughly 0.93 ms spent in key derivation, with a small standard deviation (~0.18 ms). These results highlight Twofish’s efficient decryption path and relatively low timing variability, illustrating why it remains a strong candidate when balancing throughput and predictability under frequent key changes.

6. Conclusions

It can be concluded that the developed educational tool effectively demonstrates the practical operation and comparative performance of seven major symmetric-key ciphers—AES, DES, TripleDES, RC2, Blowfish, Twofish, and Camellia—while supporting both brute-force and dictionary cryptanalysis within a unified, interactive environment. The tool reliably performs file encryption and decryption, accurately records and visualizes key-derivation times, encryption/decryption latencies, throughput, and variability, and dynamically adapts its charts in response to user-selected algorithms or metrics. Empirical evaluations demonstrate accurate cryptographic functionality and highly responsive real-time visualization, validating the tool as a good educational resource for analyzing performance–security trade-offs and cryptanalytic methodologies.