Analysis of Loss Functions for Colorectal Polyp Segmentation Under Class Imbalance †
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khalifa, M.; Albadawy, M. AI in diagnostic imaging: Revolutionising accuracy and efficiency. Comput. Methods Programs Biomed. Update 2024, 5, 100146. [Google Scholar] [CrossRef]
- Birjais, R. Challenges and Future Directions for Segmentation of Medical Images Using Deep Learning Models. In Deep Learning Applications in Medical Image Segmentation: Overview, Approaches, and Challenges; Bhat, S.Y., Rehman, A., Abulaish, M., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2025; pp. 243–264. [Google Scholar] [CrossRef]
- Wang, R.; Lei, T.; Cui, R.; Zhang, B.; Meng, H.; Nandi, A.K. Medical image segmentation using deep learning: A survey. IET Image Process. 2022, 16, 1243–1267. [Google Scholar] [CrossRef]
- Li, Z.; Kamnitsas, K.; Glocker, B. Analyzing overfitting under class imbalance in neural networks for image segmentation. IEEE Trans. Med. Imaging 2020, 40, 1065–1077. [Google Scholar] [CrossRef]
- Gupta, M.; Mishra, A. A systematic review of deep learning based image segmentation to detect polyp. Artif. Intell. Rev. 2024, 57, 7. [Google Scholar] [CrossRef]
- Yu, H.; Li, J.; Zhang, L.; Cao, Y.; Yu, X.; Sun, J. Design of lung nodules segmentation and recognition algorithm based on deep learning. BMC Bioinform. 2021, 22, 314. [Google Scholar] [CrossRef] [PubMed]
- Yin, S.; Deng, H.; Xu, Z.; Zhu, Q.; Cheng, J. SD-UNet: A Novel Segmentation Framework for CT Images of Lung Infections. Electronics 2022, 11, 130. [Google Scholar] [CrossRef]
- Shelhamer, E.; Long, J.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 640–651. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015, Proceedings of the 18th International Conference, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Yao, W.; Bai, J.; Liao, W.; Chen, Y.; Liu, M.; Xie, Y. From CNN to transformer: A review of medical image segmentation models. J. Imaging Inform. Med. 2024, 37, 1529–1547. [Google Scholar] [CrossRef]
- Mukasheva, A.; Koishiyeva, D.; Sergazin, G.; Sydybayeva, M.; Mukhammejanova, D.; Seidazimov, S. Modification of U-Net with Pre-Trained ResNet-50 and Atrous Block for Polyp Segmentation: Model TASPP-UNet. Eng. Proc. 2024, 70, 16. [Google Scholar] [CrossRef]
- Ghosh, K.; Bellinger, C.; Corizzo, R.; Branco, P.; Krawczyk, B.; Japkowicz, N. The class imbalance problem in deep learning. Mach. Learn. 2024, 113, 4845–4901. [Google Scholar] [CrossRef]
- Xie, Z.; Shu, C.; Fu, Y.; Zhou, J.; Chen, D. Balanced Loss Function for Accurate Surface Defect Segmentation. Appl. Sci. 2023, 13, 826. [Google Scholar] [CrossRef]
- Nasalwai, N.; Punn, N.S.; Sonbhadra, S.K.; Agarwal, S. Addressing the class imbalance problem in medical image segmentation via accelerated tversky loss function. In Advances in Knowledge Discovery and Data Mining; Karlapalem, K., Cheng, H., Ramakrishnan, N., Agrawal, R.K., Reddy, P.K., Srivastava, J., Chakraborty, T., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2021; Volume 12714. [Google Scholar] [CrossRef]
- Jeong, S.-M.; Lee, S.-G.; Seok, C.-L.; Lee, E.-C.; Lee, J.-Y. Lightweight Deep Learning Model for Real-Time Colorectal Polyp Segmentation. Electronics 2023, 12, 1962. [Google Scholar] [CrossRef]
- Goceri, E. Polyp segmentation using a hybrid vision transformer and a hybrid loss function. J. Imaging Inform. Med. 2024, 37, 851–863. [Google Scholar] [CrossRef]
- Bourday, R.; Aattouchi, I.; Ait Kerroum, M. A Comparative Study of Deep Learning Loss Functions: A Polyp Segmentation Case Study. In Computing, Internet of Things and Data Analytics; García Márquez, F.P., Jamil, A., Ramirez, I.S., Eken, S., Hameed, A.A., Eds.; Springer: Cham, Switzerland, 2024; pp. 68–78. [Google Scholar] [CrossRef]
- Jha, D.; Smedsrud, P.H.; Riegler, M.A.; Halvorsen, P.; De Lange, T.; Johansen, D.; Johansen, H.D. Kvasir-seg: A segmented polyp dataset. In MultiMedia Modeling, Proceedings of the 26th International Conference, MMM 2020, Daejeon, Republic of Korea, 5–8 January 2020; Proceedings, part II 26; Springer International Publishing: Cham, Switzerland, 2020; pp. 451–462. [Google Scholar] [CrossRef]
- Gabdullin, M.T.; Mukasheva, A.; Koishiyeva, D.; Umarov, T.; Bissembayev, A.; Kim, K.S.; Kang, J.W. Automatic cancer nuclei segmentation on histological images: Comparison study of deep learning methods. Biotechnol. Bioprocess Eng. 2024, 29, 1034–1047. [Google Scholar] [CrossRef]
- Åkesson, J.; Töger, J.; Heiberg, E. Random effects during training: Implications for deep learning-based medical image segmentation. Comput. Biol. Med. 2024, 180, 108944. [Google Scholar] [CrossRef] [PubMed]
- Pravitasari, A.A.; Iriawan, N.; Nuraini, U.S.; Rasyid, D.A. On comparing optimizer of UNet-VGG16 architecture for brain tumor image segmentation. In Brain Tumor MRI Image Segmentation Using Deep Learning Techniques; Chaki, J., Ed.; Academic Press: Cambridge, MA, USA, 2022; pp. 197–215. [Google Scholar] [CrossRef]
- Tiwari, T.; Saraswat, M. A new modified-unet deep learning model for semantic segmentation. Multimed. Tools Appl. 2023, 82, 3605–3625. [Google Scholar] [CrossRef]
- Porter, E.; Solis, D.; Bruckmeier, P.; Siddiqui, Z.A.; Zamdborg, L.; Guerrero, T. Effect of Loss Functions in Deep Learning-Based Segmentation. In Auto-Segmentation for Radiation Oncology; CRC Press: Boca Raton, FL, USA, 2021; pp. 133–150. [Google Scholar]
- Hui, H.; Zhang, X.; Wu, Z.; Li, F. Dual-path attention compensation U-net for stroke lesion segmentation. Comput. Intell. Neurosci. 2021, 2021, 7552185. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, W.; Wu, L.; Chen, S.; Hu, X.; Li, J.; Yang, J. Generalized focal loss: Learning qualified and distributed bounding boxes for dense object detection. Adv. Neural Inf. Process. Syst. 2020, 33, 21002–21012. [Google Scholar]
- Altini, N.; Prencipe, B.; Brunetti, A.; Brunetti, G.; Triggiani, V.; Carnimeo, L.; Cascarano, G.D. A Tversky loss-based convolutional neural network for liver vessels segmentation. In Intelligent Computing Theories and Application, Proceedings of the 16th International Conference, ICIC 2020, Bari, Italy, 2–5 October 2020; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Celaya, A.; Riviere, B.; Fuentes, D. A generalized surface loss for reducing the hausdorff distance in medical imaging segmentation. arXiv 2023, arXiv:2302.03868. [Google Scholar] [CrossRef]
- Zhan, J.; Liu, J.; Wu, Y.; Guo, C. Multi-Task Visual Perception for Object Detection and Semantic Segmentation in Intelligent Driving. Remote Sens. 2024, 16, 1774. [Google Scholar] [CrossRef]
- Kato, S.; Hotta, K. Mse loss with outlying label for imbalanced classification. arXiv 2021, arXiv:2107.02393. [Google Scholar] [CrossRef]
- Qi, J.; Du, J.; Siniscalchi, S.M.; Ma, X.; Lee, C.H. On mean absolute error for deep neural network based vector-to-vector regression. IEEE Signal Process. Lett. 2020, 27, 1485–1489. [Google Scholar] [CrossRef]
- Yuan, Y.; Chao, M.; Lo, Y.C. Automatic skin lesion segmentation using deep fully convolutional networks with jaccard distance. IEEE Trans. Med. Imaging 2017, 36, 1876–1886. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, S.; Li, C.; Wang, J. Rethinking the dice loss for deep learning lesion segmentation in medical images. J. Shanghai Jiaotong Univ. (Sci.) 2021, 26, 93–102. [Google Scholar] [CrossRef]
- Müller, D.; Soto-Rey, I.; Kramer, F. Towards a guideline for evaluation metrics in medical image segmentation. BMC Res. Notes 2022, 15, 210. [Google Scholar] [CrossRef] [PubMed]
- Koishiyeva, D.; Bissembayev, A.; Iliev, T.; Kang, J.W.; Mukasheva, A. Classification of Skin Lesions using PyQt5 and Deep Learning Methods. In Proceedings of the 2024 5th International Conference on Communications, Information, Electronic and Energy Systems (CIEES), Veliko Tarnovo, Bulgaria, 20–22 November 2024. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Guillén, L.A. Accuracy assessment in convolutional neural network-based deep learning remote sensing studies—Part 1: Literature review. Remote Sens. 2021, 13, 2450. [Google Scholar] [CrossRef]
- Tolkynbekova, A.; Koishiyeva, D.; Bissembayev, A.; Mukhammejanova, D.; Mukasheva, A.; Kang, J.W. Comparative Analysis of the Predictive Risk Assessment Modeling Technique Using Artificial Intelligence. J. Electr. Eng. Technol. 2025, in press. [Google Scholar] [CrossRef]

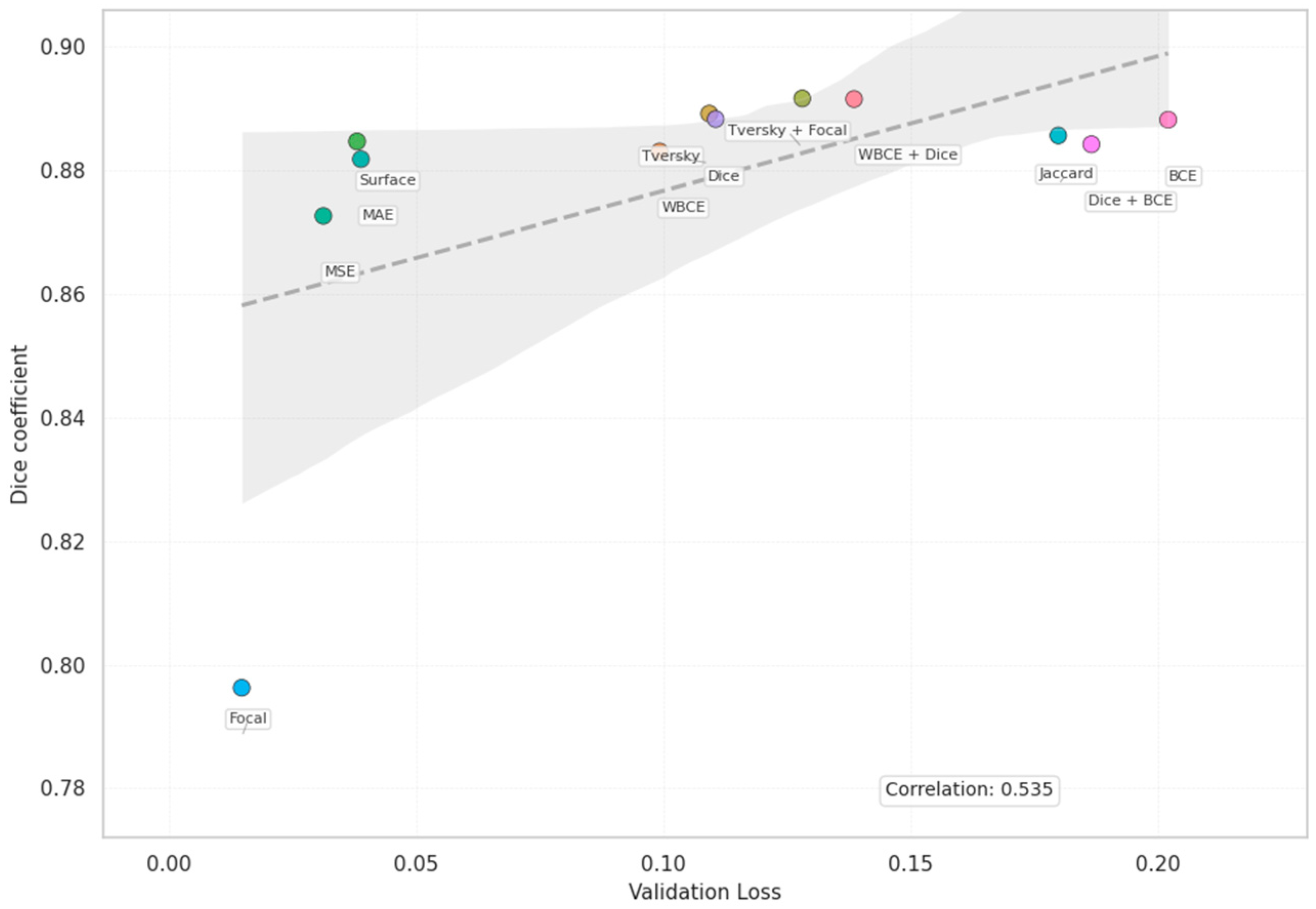
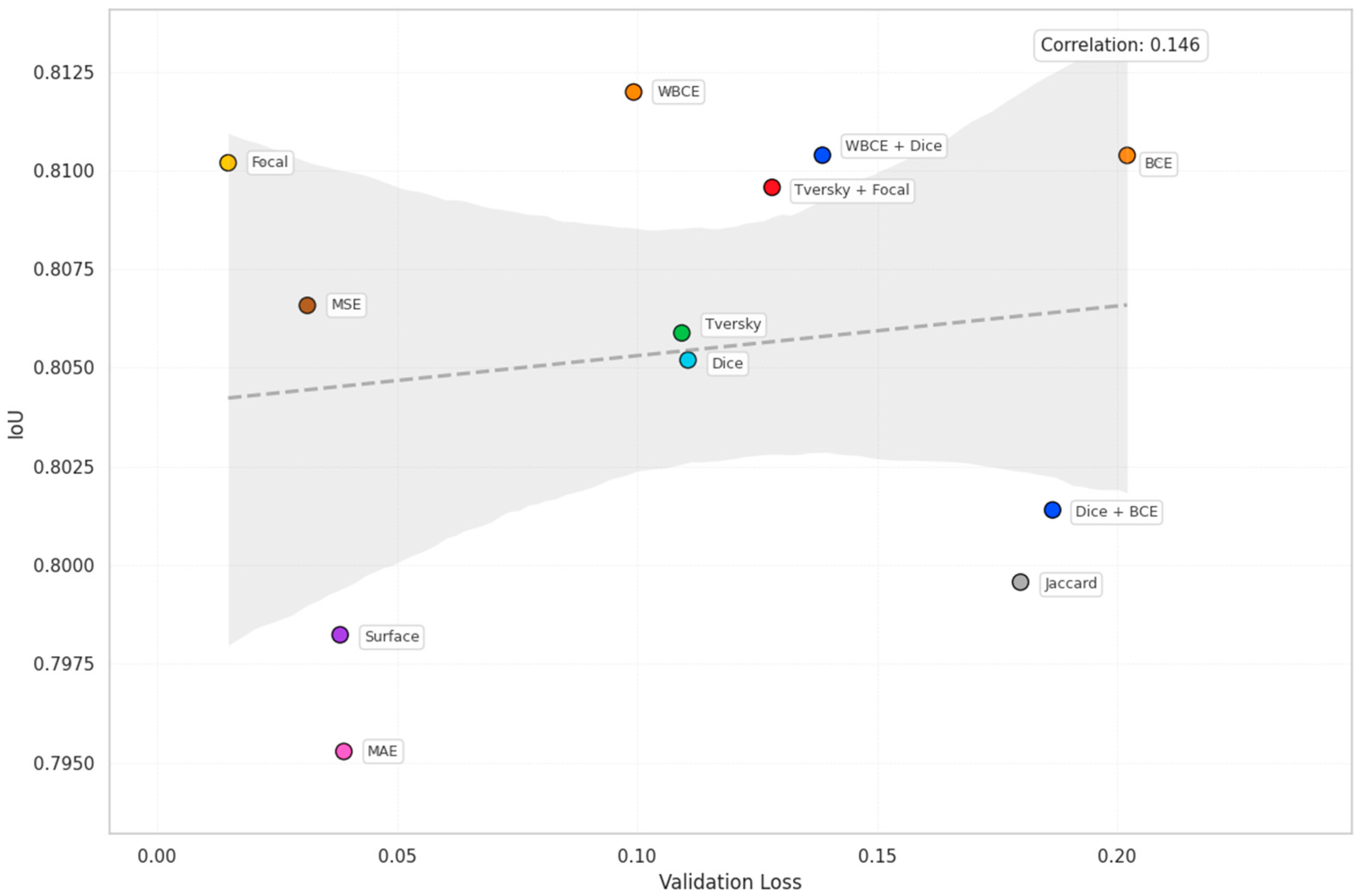

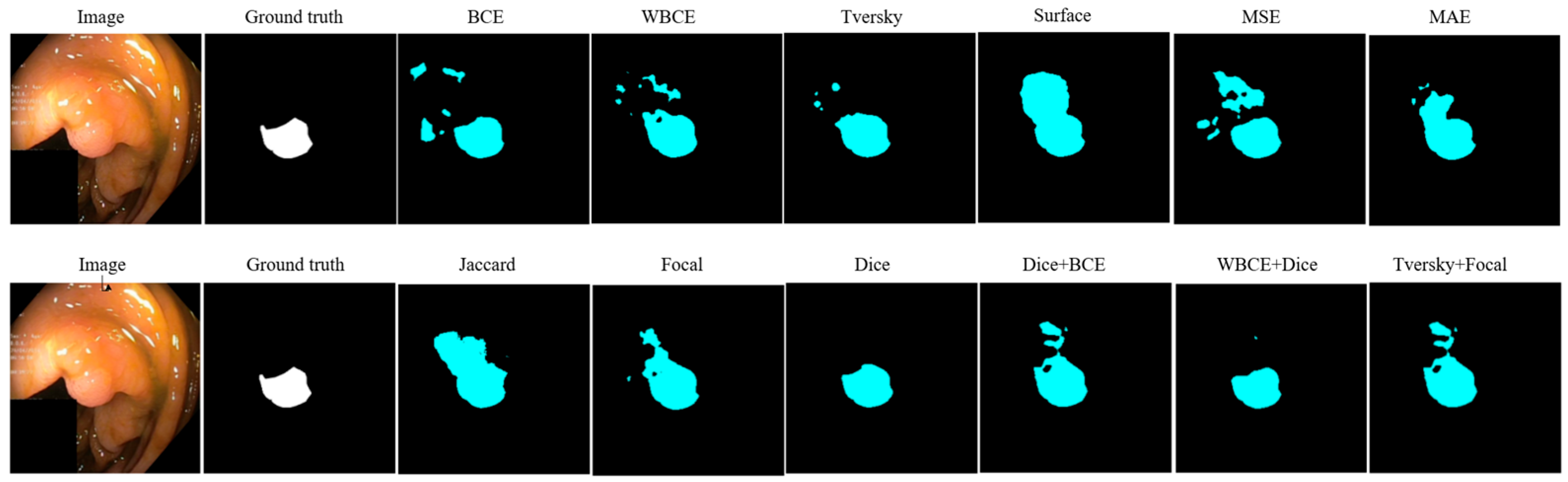
| Loss | Accuracy | Dice | Mean IOU | Sensitivity |
|---|---|---|---|---|
| BCE | 0.9553 | 0.8882 | 0.8104 | 0.8576 |
| WBCE | 0.9557 | 0.8831 | 0.8120 | 0.8593 |
| Tversky | 0.9546 | 0.8892 | 0.8059 | 0.8438 |
| Surface | 0.9525 | 0.8847 | 0.7982 | 0.8616 |
| MSE | 0.9543 | 0.8727 | 0.8066 | 0.8516 |
| MAE | 0.9518 | 0.8819 | 0.7953 | 0.8344 |
| Jaccard | 0.9529 | 0.8857 | 0.7996 | 0.8532 |
| Focal | 0.9552 | 0.7963 | 0.8102 | 0.8483 |
| Dice | 0.9539 | 0.8883 | 0.8052 | 0.8466 |
| Dice + BCE | 0.9538 | 0.8843 | 0.8014 | 0.8402 |
| WBCE + Dice | 0.9557 | 0.8916 | 0.8104 | 0.8498 |
| Tversky + Focal | 0.9540 | 0.8917 | 0.8096 | 0.8885 |
| Loss | Validation | Difference | Error Ratio |
|---|---|---|---|
| BCE | 0.2020 | 0.1935 | 23.6540 |
| WBCE | 0.0992 | 0.0932 | 16.5767 |
| Tversky | 0.1093 | 0.0874 | 4.9933 |
| Surface | 0.0381 | 0.0329 | 7.3658 |
| MSE | 0.0312 | 0.0290 | 13.6952 |
| MAE | 0.0388 | 0.0320 | 5.6681 |
| Jaccard | 0.1798 | 0.1243 | 3.2367 |
| Focal | 0.0147 | 0.0141 | 24.77 |
| Dice | 0.1105 | 0.0940 | 6.6742 |
| Dice + BCE | 0.1385 | 0.1266 | 11.6415 |
| WBCE + Dice | 0.2020 | 0.1935 | 23.6540 |
| Tversky + Focal | 0.1281 | 0.1200 | 15.9704 |
| Loss | Training | Epoch | FPS |
|---|---|---|---|
| BCE | 527.60 | 10.55 | 153.52 |
| WBCE | 524.68 | 10.49 | 154.38 |
| Tversky | 523.97 | 10.48 | 154.59 |
| Surface | 559.32 | 11.19 | 144.82 |
| MSE | 524.75 | 10.50 | 154.36 |
| MAE | 526.22 | 10.52 | 153.93 |
| Jaccard | 554.64 | 11.09 | 146.04 |
| Focal | 524.57 | 10.49 | 154.41 |
| Dice | 528.67 | 10.57 | 153.22 |
| Dice + BCE | 547.41 | 10.95 | 147.97 |
| WBCE + Dice | 535.44 | 10.71 | 151.28 |
| Tversky + Focal | 542.83 | 10.86 | 149.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koishiyeva, D.; Kang, J.W.; Iliev, T.; Bissembayev, A.; Mukasheva, A. Analysis of Loss Functions for Colorectal Polyp Segmentation Under Class Imbalance. Eng. Proc. 2025, 104, 17. https://doi.org/10.3390/engproc2025104017
Koishiyeva D, Kang JW, Iliev T, Bissembayev A, Mukasheva A. Analysis of Loss Functions for Colorectal Polyp Segmentation Under Class Imbalance. Engineering Proceedings. 2025; 104(1):17. https://doi.org/10.3390/engproc2025104017
Chicago/Turabian StyleKoishiyeva, Dina, Jeong Won Kang, Teodor Iliev, Alibek Bissembayev, and Assel Mukasheva. 2025. "Analysis of Loss Functions for Colorectal Polyp Segmentation Under Class Imbalance" Engineering Proceedings 104, no. 1: 17. https://doi.org/10.3390/engproc2025104017
APA StyleKoishiyeva, D., Kang, J. W., Iliev, T., Bissembayev, A., & Mukasheva, A. (2025). Analysis of Loss Functions for Colorectal Polyp Segmentation Under Class Imbalance. Engineering Proceedings, 104(1), 17. https://doi.org/10.3390/engproc2025104017







