1. Introduction
The task of navigation in a real environment involves safely moving among many obstacles and is applicable in a wide range of applications such as in manufacturing, logistics, transportation as well as are rescue missions or environments that are dangerous to humans, where robots can navigate through disaster-stricken areas. Nowadays, the task of navigation is accomplished using navigation systems (GPS) and precise mapping of the surrounding world. But, at the same time, conventional navigation systems for mobile robots lack the ability to learn autonomously. This can limit the adaptability of a robot’s behavior and reduce the quality of its operation in a specific working environment. In our study, we propose a navigation method without using maps or navigation methods, but only using Lidar sensor readings, which allows for faster decision-making by a robot in a rapidly changing world, close to that of a real scenario. This approach could help to reduce costs and improve robots’ autonomous adaptability.
Modern robots are trained using the Reinforcement Learning method [
1], and more specifically Deep Reinforcement Learning [
2], which allows for the training of an autonomous intelligent robot iteratively and intelligently without human intervention. The application of RL (Reinforcement Learning) in robotics has opened new avenues for autonomous navigation. This is a rapidly developing branch of Machine Learning that resembles the learning of any living organism through its iterative interaction with the real world and receiving feedback for each action taken. At the same time, the important aspect of this method is the precise definition of the reward function. In our research, we define this function by considering the goal of the task at hand, and thus manage to improve the speed and efficiency of learning.
The ROS (Robot Operating System) [
3] is the most famous SDK (Software Development Kit) used for robotics applications. Its popularity is due to many factors, including its widespread use in the robotics industry; it being an open source; and its application is similar in simulation and real-world environments, which ensures the easier integration of the developed code from a simulation into a physical robot.
For our research purpose we chose to conduct the training in the simulation environment Flatland [
4]—a lightweight alternative to the Gazebo [
5] simulator for ground robots on a flat surface with integration with ROS2. The Flatland simulator also utilizes a Data Distribution Service for communication purposes, which enables integration into distributed embedded systems in real time thanks to a variety of routing configurations and scalability.
In our study, we use Lidar sensor readings across 30 dimensions as the input environmental parameters. To reduce the input parameters, we divide these readings into nine sectors and take the closest distances to the obstacles from each resulting sector. The goal of the task is to reach the goal in the shortest time without encountering obstacles.
By implementing the improvements described above, we achieve a faster and higher-quality performance for the task at hand.
2. Related Work
The classical methods for mobile robot navigation include simultaneous localization and mapping methods [
6], and varieties of path-planning algorithms, such as A* and Dijkstra [
7], which offer a solution for the shortest length between two nodes in a graph search. On the other hand, the RL method has opened the horizons for new solutions in this area. This method has received increasing attention in recent years. The earliest studies of behavioral policy generation used tabular methods, which in turn, due to the high dimensionality of the state representation, made the table space incredibly large, especially when considering continuous action spaces. With the advent of neural networks in RL, this obstacle has been overcome. Using DRL allows for the approximation of value functions or policy functions, as well as a mixed approach using both (Actor–Critic). This allows robotic agents to deal with the high-dimensional spaces of states and actions.
Thus, the authors of [
8] used Deep Q-Networks (DQNs) with high-dimensional sensor inputs from graphic images. The authors of [
9] presented another approach, Deep Deterministic Policy Gradients (DDPGs), a Reinforcement Learning algorithm for robot control tasks, including navigation with continuous variables like speed and orientation. DDPGs combine Deep Q-Learning and Deterministic Policy Gradients (DPGs) [
10]. Since the policy is deterministic, it suffers from inefficient exploration during an agent’s exploration of an environment. Another approach to solving the navigation problem was proposed in [
11], which combined the use of Convolutional Neural Networks (CNNs) and an RL approach. This provided the robot with visual information about the environment and helped it to safely overcome obstacles. On the other hand, the input parameters involved large volumes of data to be processed and, accordingly, implied powerful computing resources. The authors of [
12] used an Actor–Critic model approach, where the policy was a function of the goal and the current state, which allowed for better policy generalization and faster learning, according to the study’s authors. In [
13], the authors studied a generalized computation graph, which included model-free value-based methods and model-based methods, with specific instances interpolating between the model-based and model-free ones. The methods utilize map observations to actions directly, without mapping or planning modules.
In our research, we use the Proximal Policy Optimization method (PPO) [
14] as the base algorithm. This approach has the benefit of a balance between the advantages of sampling efficiency and training stability. Also, it has been successfully applied to various robotic control tasks, including navigation in complex environments. This method is based on the Actor–Critic [
15] approach and utilizes a direct update to the combination of the policy and value functions. The most important advantages of the PPO approach over the Actor–Critic and DDPG methods are the following:
Sample efficiency—By allowing for multiple updates per sample and preventing too-large policy shifts, PPO makes better use of the available data, improving the sample efficiency.
Stability of updates—Actor–Critic methods use a direct update to the policy and value functions, which can sometimes lead to instability in training, especially when the policy updates are too large. PPO, on the other hand, addresses this issue by using a clipped objective function that restricts the size of the policy updates. Specifically, it uses a penalty for large deviations between the old and new policy distributions, thus preventing large, unstable updates. This clipping mechanism ensures that the policy changes are gradual and stable, making training more reliable.
Clipping objective and trust region—PPO simplifies the implementation of a trust region policy update, ensuring stable policy improvement with less computational overhead.
3. Proposed Method and Structure
3.1. Environment Setup and Objectives
For the task of finding the shortest and safest path to the goal, we developed a customized version of the environment using a Flatland simulation. Flatland is a performance-oriented 2D simulator for robotic environments developed by Avidbots Corp [
4]. This is a lightweight version of the Gazebo simulator, but at the same time it is equipped with the ROS2 robot programming environment. Our choice was dictated by its high performance, the availability of the necessary functions and sensors, and its ease of installation and subsequent use of it.
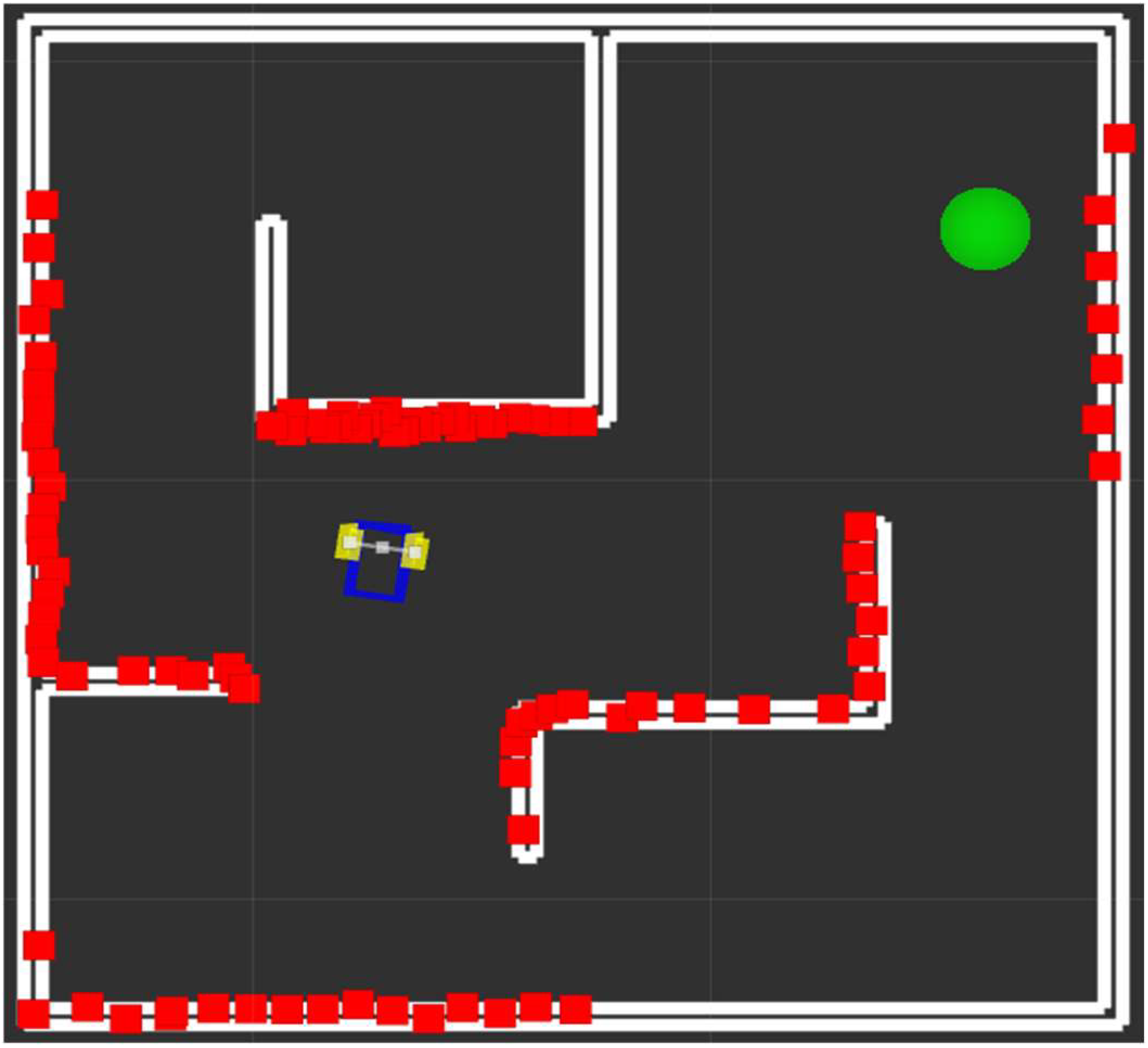
The experimental environment is shown in
Figure 1. The goal of the wheeled robot is to reach the target (green circle) as quickly as possible, avoiding obstacles. The Lidar sensor beams reflections are marked in red.
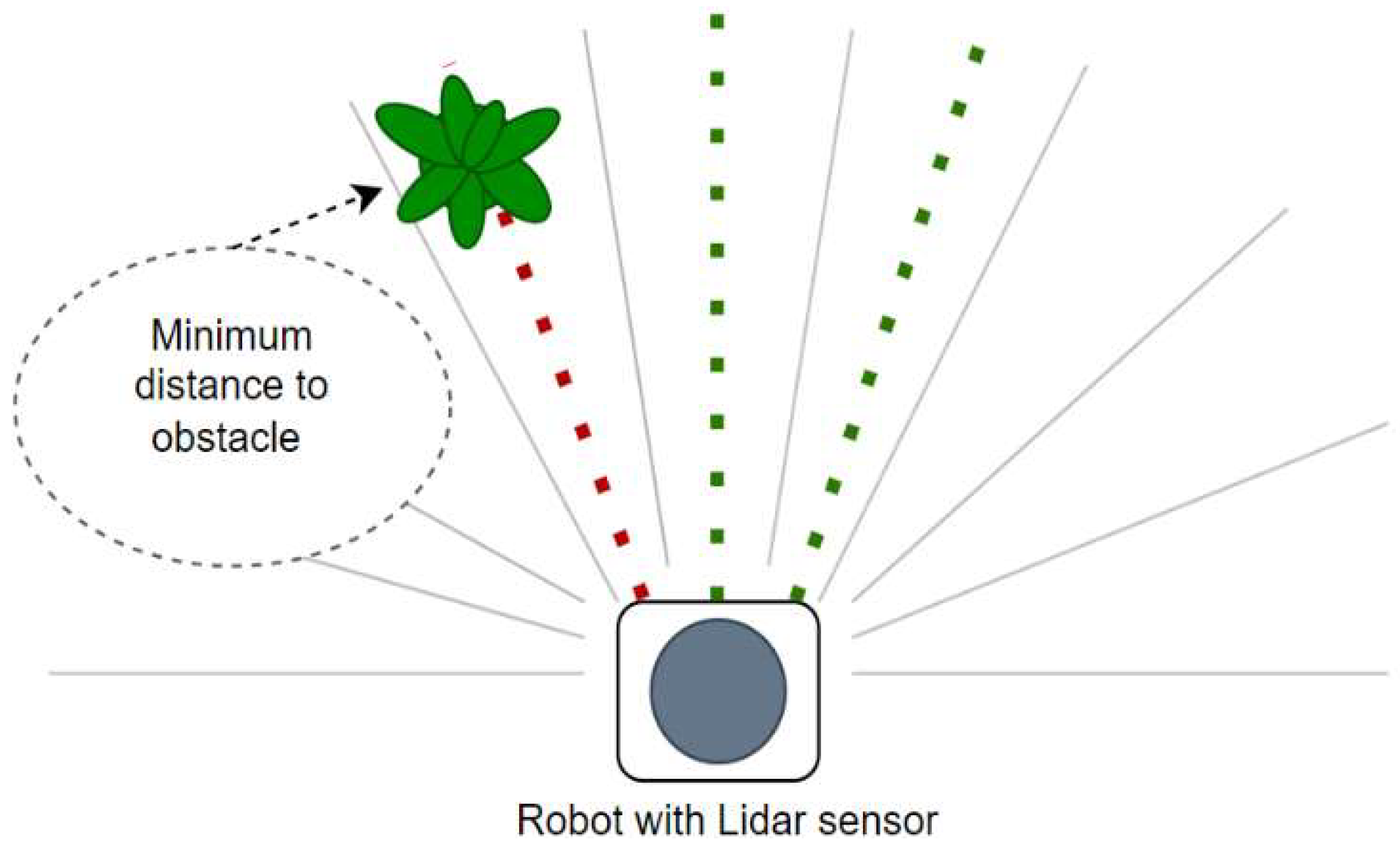
For the purposes of our study, we used a wheeled mobile robot equipped with a Lidar sensor, avoiding the use of all the rays from the Lidar to avoid overly large state spaces (which slow down the training process); instead, we used only a subset of the rays (9), equally sampled over the robot’s frontal 180º angular range (
Figure 2).
From each selected sector, we took the closest distance to the obstacles in that sector. By reducing the dimensionality of the input space in this way, we promoted the focusing on the nearest obstacles for safer navigation and speeded up the computation. The robotic agent was also equipped with a bumper to detect collisions with obstacles. The target had a Lidar sensor to measure the distance to the wheeled robot, and at a threshold value of = 0.2, the agent was considered to have reached its goal.
3.2. Reward Function
As for all RL algorithms, defining the reward function is one of the most important aspects. In our study, we consider the function as shown in (1).
We promote the quick approaching to the goal by giving at least a 500 points reward for the shortest trajectory taken (if the current distance is less than the critical defined distance . In case of a collision, the agent incurs a penalty of −200 discounted by the distance to target . Episode timeout incurs a penalty of −400; this encourages the agent to move as fast as possible to the target. Otherwise, for every move forward, the agent receives the reward . In this way, we encourage the agent to move towards a set goal as quickly and smoothly as possible, even in cases of collision and timeout. The constants in (1) are chosen arbitrarily by promoting the perceptible differences between the rewards for various events.
3.3. Proposed Algorithm
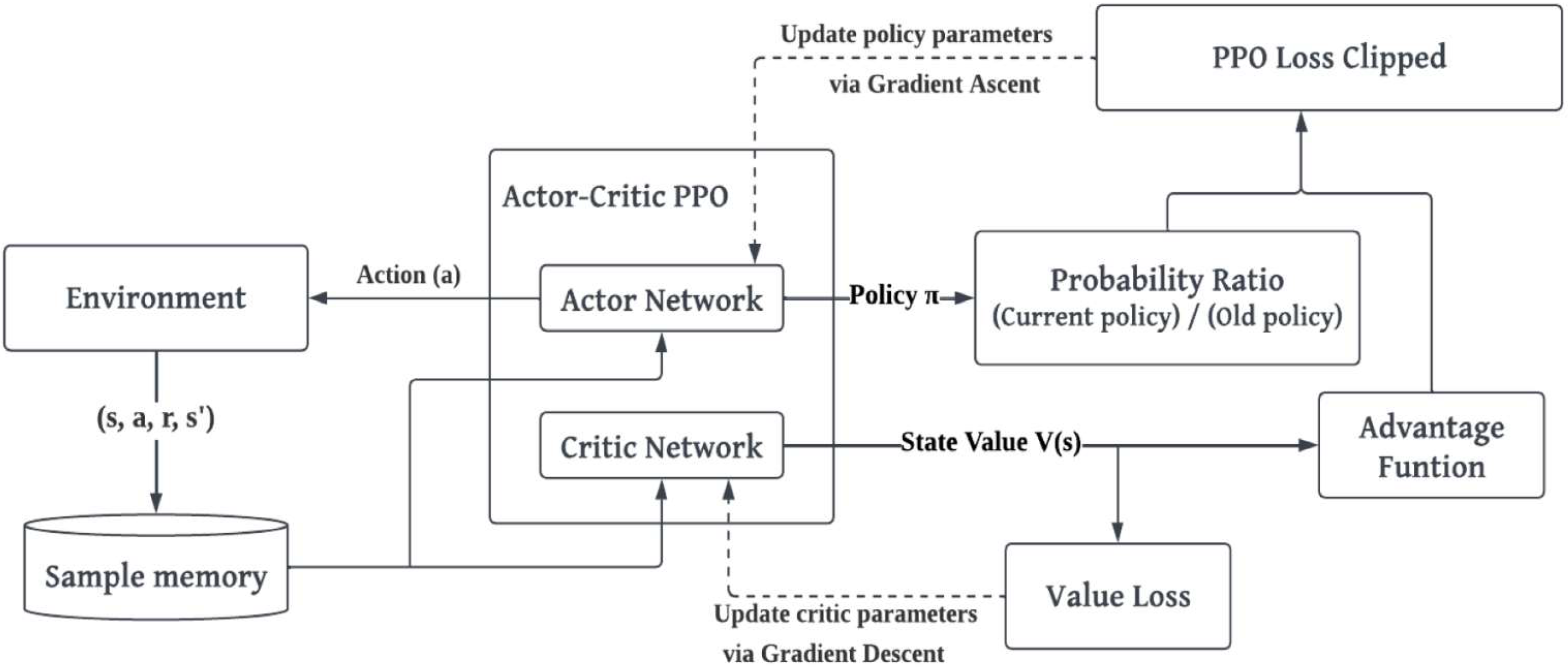
PPO is a type of policy gradient method, which directly optimizes the policy (a strategy or set of rules that dictates an agent’s actions) by maximizing the expected returns. It uses a surrogate objective function and modifies it with a clipping mechanism to enforce stable and gradual updates; the policy loss is described as follows (2):
where
denotes the policy parameters;
is the probability ratio between the new and old policies;
is a hyperparameter, controlling the clipping range ( = 0.2);
is an advantage function, measuring the difference between the discounted sum of the rewards () and the baseline estimate . IF , the actual return from the action is better than the expected return from experience, and vise versa.
On the other hand, the value loss, represented by the Critic, minimizes the difference between the predicted
and actual cumulative reward received for a given episode, as in (3).
The agent interacts with the environment and collects trajectories (state, action, and reward sequences). During this process, the agent follows the current policy (probabilistic model of actions’ given states) and gathers rewards for each action taken. The overall architecture of the PPO algorithm and update logic is shown in
Figure 3.
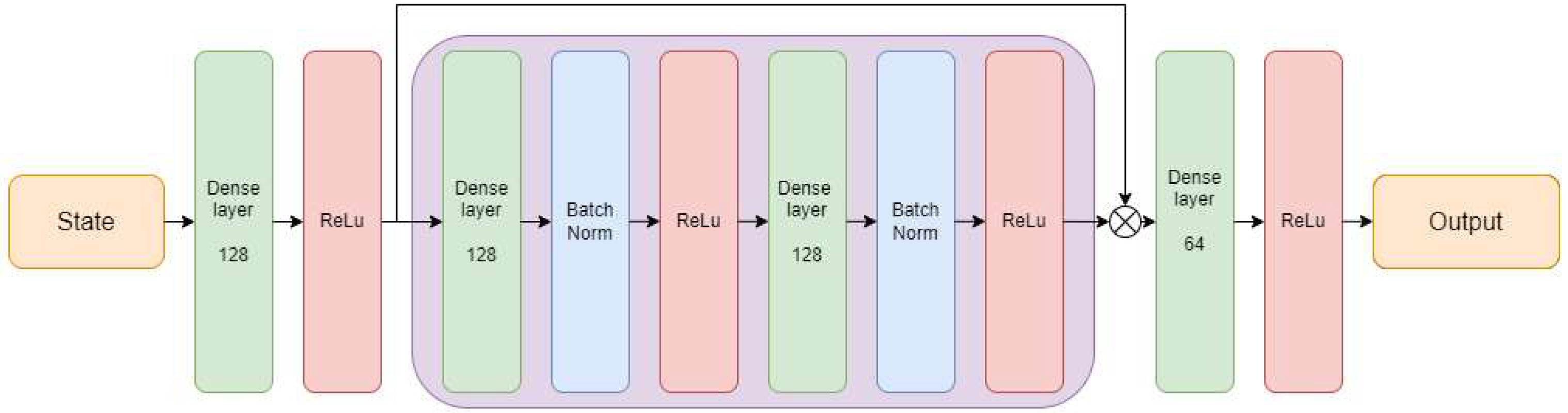
In our research we add residual blocks to the Actor and Critic Networks, which are a fundamental component of the ResNet architecture [
17], and were introduced to address the problem of vanishing gradients in deep neural networks. The skip connections of residual blocks allow for gradients to flow more easily during backpropagation. When training deep networks, the gradients from the output layer have a shorter path to travel through the layers that are closer to the input, making learning more efficient [
18]. We use identical architectures for the Actor and Critic Networks, as shown in
Figure 4. The input of the neural network (state) is presented by the robot’s Lidar readings per timestamp. The output from the Actor Network is the action
, and that from the Critic Network has an estimated value
. The control output from the PPO model is the velocity of each robot’s wheel.
4. Experiments and Results
In our experiments, we compared the speed and efficiency of training a wheeled robot with the innovations of the PPO algorithm described above with a simulation setup in a Flatland environment with a vanilla PPO. Both algorithms, the improved PPO and vanilla PPO, were implemented in Python 3.10.14 using the PyTorch 2.6.0 [
19] library. The vanilla PPO was defined with two fully connected layers with 64 neurons each, given the complexity of the simulation environment. Training was considered complete when the robot successfully reached its goal in at least 80% of the 20 test episodes. In
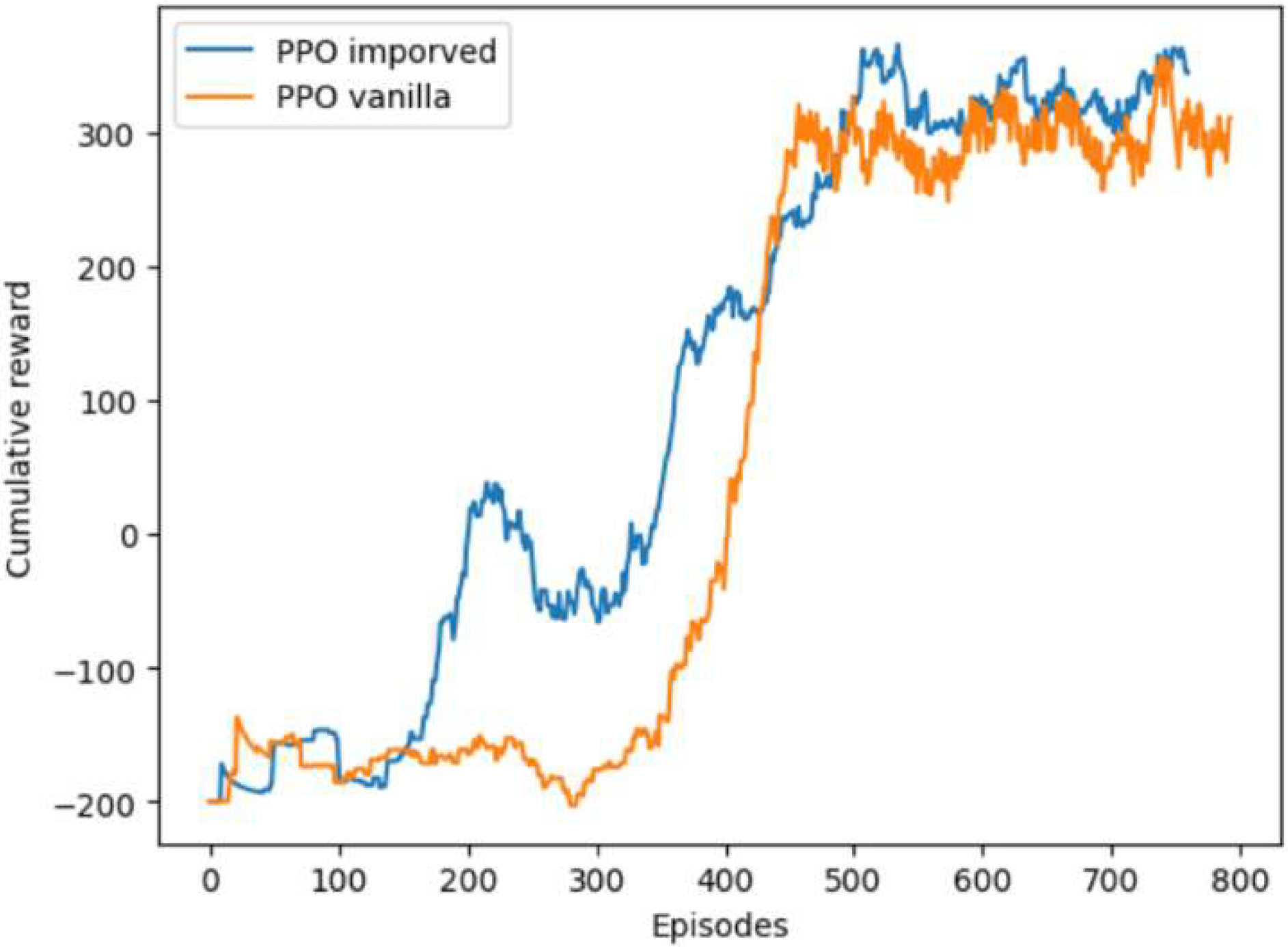
Figure 5 we show the cumulative reward for each of the models during training. The time frame is represented as the training episodes given a defined reward function as described above.
The improved architecture of the PPO algorithm contributes to a faster finding of the correct trajectories to the goal compared to the vanilla PPO by the quicker adaptation of behavior in a complex environment. At the same time, our algorithm presents a higher cumulative reward after finding an optimal solution, which suggests more optimal trajectories to the goal.
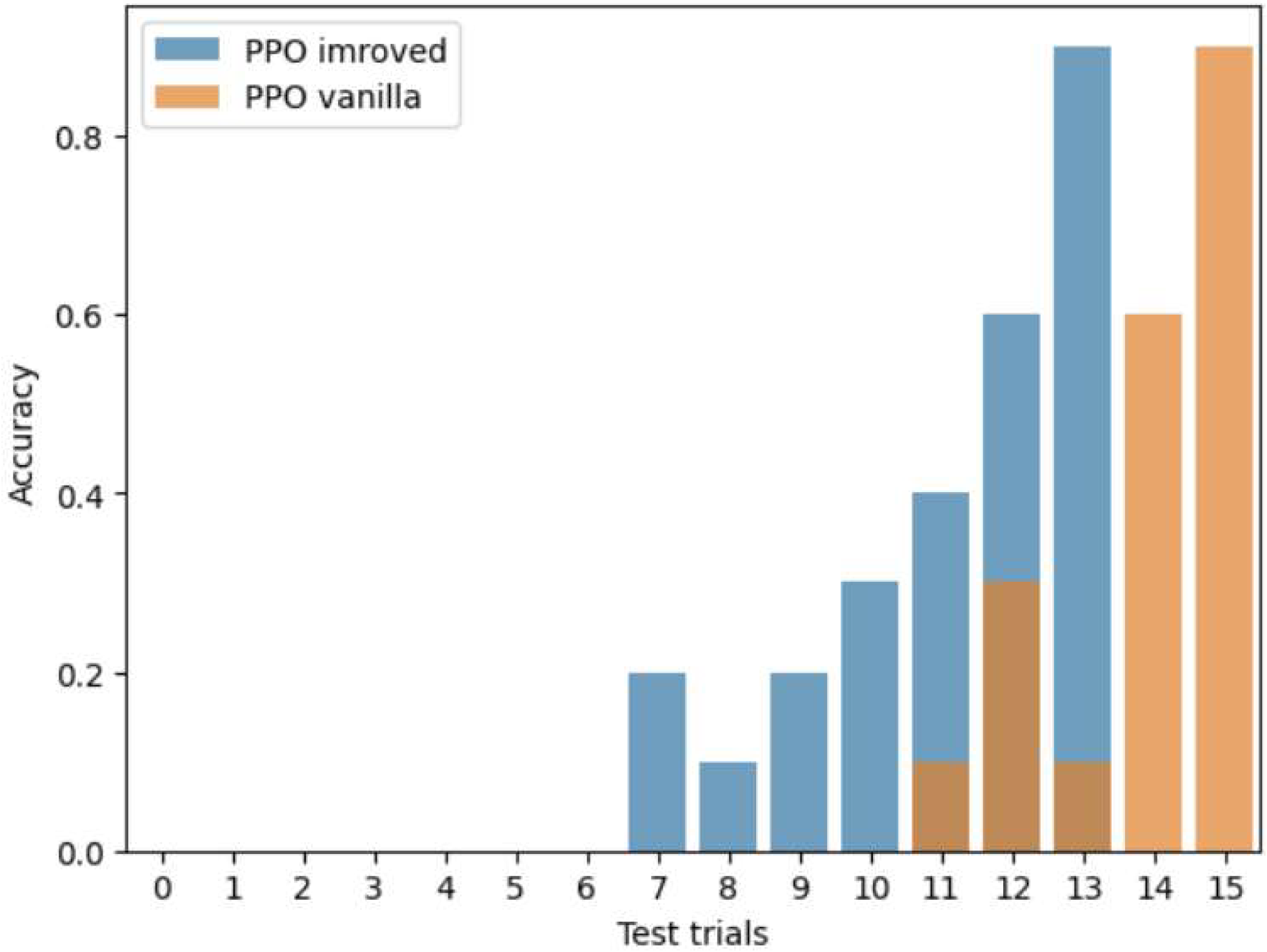
Figure 6 shows the distribution of accuracy per test trial. The test trials were conducted on every 2000 training iterations.
As in the previous chart, here we see a faster improvement in the accuracy of the modified algorithm compared to the vanilla PPO. On the 7th testing trial, after 14,000 iterations, the algorithm was able to produce the correct trajectories for the robot in the simulation in 20% of cases, and by the 13th attempt, in 90% of episodes the robot successfully reached its goal. In the vanilla PPO, this happened later, after another 4000 iterations. The training time for both algorithms took 2 clock hours each, but the proposed PPO reached 80% accuracy during testing 13 min earlier. In
Table 1, we summarize the average number of steps taken per episode, the average accuracy per number of test trials of the algorithms, and the average reward for each episode.
The table shows improved accuracy and rewards. The resulting reward values from the modified algorithm exceeded the reward of the regular PPO algorithm by 25%. The accuracy for both models did not exceed 20% because we also considered the test trials with 0% accuracy, thus including the rate of acquisition of non-zero accuracy values.
5. Conclusions
In our study, we demonstrated the use of the DRL method for training autonomous tasks in a complex environment. For this, we built a simulation environment representing an enclosed space with multiple obstacles in it and an agent—a wheeled autonomous robot equipped with Lidar and bump sensors. We improved the architecture of the PPO algorithm by using skip connections in the Agent and Critic Networks. The results obtained show that the improved PPO simultaneously improved the performance and provide faster convergence than the original vanilla PPO. In the future, we plan to apply this newly developed algorithm to a real environment.
Author Contributions
Conceptualization, A.S. and V.H.; methodology, A.S.; software, A.S.; validation, A.S.; formal analysis, A.S.; investigation, A.S.; resources, A.S.; data curation, A.S.; writing—original draft preparation, A.S.; writing—review and editing, A.S. and V.H.; visualization, A.S.; supervision, A.S.; project administration, A.S. and V.H.; funding acquisition, V.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Research and Development Sector at the Technical University—Sofia grant number 242ПД0019-08.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DRL | Deep Reinforcement Learning |
| RL | Reinforcement Learning |
| PPO | Proximal Policy Optimization |
| GPS | Global Positioning System |
| SDK | Software Development Kit |
| ROS | Robot Operating System |
| DQN | Deep Q-Network |
| DDPGs | Deep Deterministic Policy Gradients |
| DPGs | Deterministic Policy Gradients |
| CNNs | Convolutional Neural Networks |
References
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998; ISBN 10.0262039249. [Google Scholar]
- Hemming, N.; Menon, V. Deep Reinforcement Learning Based Efficient and Robust Navigation Method for Autonomous Applications. In Proceedings of the 2023 IEEE 35th International Conference on Tools with Artificial Intelligence (ICTAI), Atlanta, GA, USA, 6–8 November 2023; pp. 287–293. [Google Scholar]
- ROS—Robot Operating System. Available online: https://www.ros.org/ (accessed on 1 March 2025).
- Flatland Simulation. Available online: https://flatland-simulator.readthedocs.io (accessed on 1 March 2025).
- Gazebo Simulation. Available online: https://gazebosim.org/ (accessed on 1 March 2025).
- Riaz, Z.; Pervez, A.; Ahmer, M.; Iqbal, J. A fully autonomous indoor mobile robot using SLAM. In Proceedings of the 2010 International Conference on Information and Emerging Technologies, Karachi, Pakistan, 14–16 June 2010. [Google Scholar] [CrossRef]
- Alyasin, A.; Abbas, E.I.; Hasan, S.D. An Efficient Optimal Path Finding for Mobile Robot Based on Dijkstra Method. In Proceedings of the 2019 4th Scientific International Conference Najaf (SICN), Al-Najaf, Iraq, 29–30 April 2019. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Petersen, S. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Silver, D. Empowering mobile robots with DDPG for autonomous navigation. Robot. Auton. Syst. 2018, 123, 456–467. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic Policy Gradient Algorithms. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014. [Google Scholar]
- Zhu, H. End-to-end navigation for robots using convolutional neural networks and deep reinforcement learning. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1234–1245. [Google Scholar]
- Zhu, Y.; Mottaghi, R.; Kolve, E.; Lim, J.J.; Gupta, A. Target-driven visual navigation in indoor scenes using deep reinforcement learning. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3357–3364. [Google Scholar]
- Kahn, G.; Villaflor, A.; Ding, B.; Abbeel, P.; Levine, S. Self-Supervised Deep Reinforcement Learning with Generalized Computation Graphs for Robot Navigation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 5129–5136. [Google Scholar]
- Shulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017. [Google Scholar] [CrossRef]
- Konda, V.R.; Tsitsiklis, J.N. Actor-Critic Algorithms. Adv. Neural Inf. Process. Syst. 1999, 12, 1008–1014. [Google Scholar]
- Kalidas, A.P.; Joshua, C.J.; Quadir Md, A.; Basheer, S.; Mohan, S.; Sakri, S. Deep Reinforcement Learning for Vision-Based Navigation of UAVs in Avoiding Stationary and Mobile Obstacles. Drones 2023, 7, 245. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Popov, V.; Shakev, N.; Ahmed, S.; Toplaov, A. Recognition of Dynamic Targets using a Deep Convolutional Neural Network. In Proceedings of the ANNA ‘18—Advances in Neural Networks and Applications 2018, St. Konstantin and Elena Resort, Bulgaria, 15–17 September 2018; pp. 1–6. [Google Scholar]
- PyTorch. Available online: https://pytorch.org/ (accessed on 1 March 2025).
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).