Planning Resources by Model Predictive Control †
Abstract
1. Introduction
2. Forecasting Models
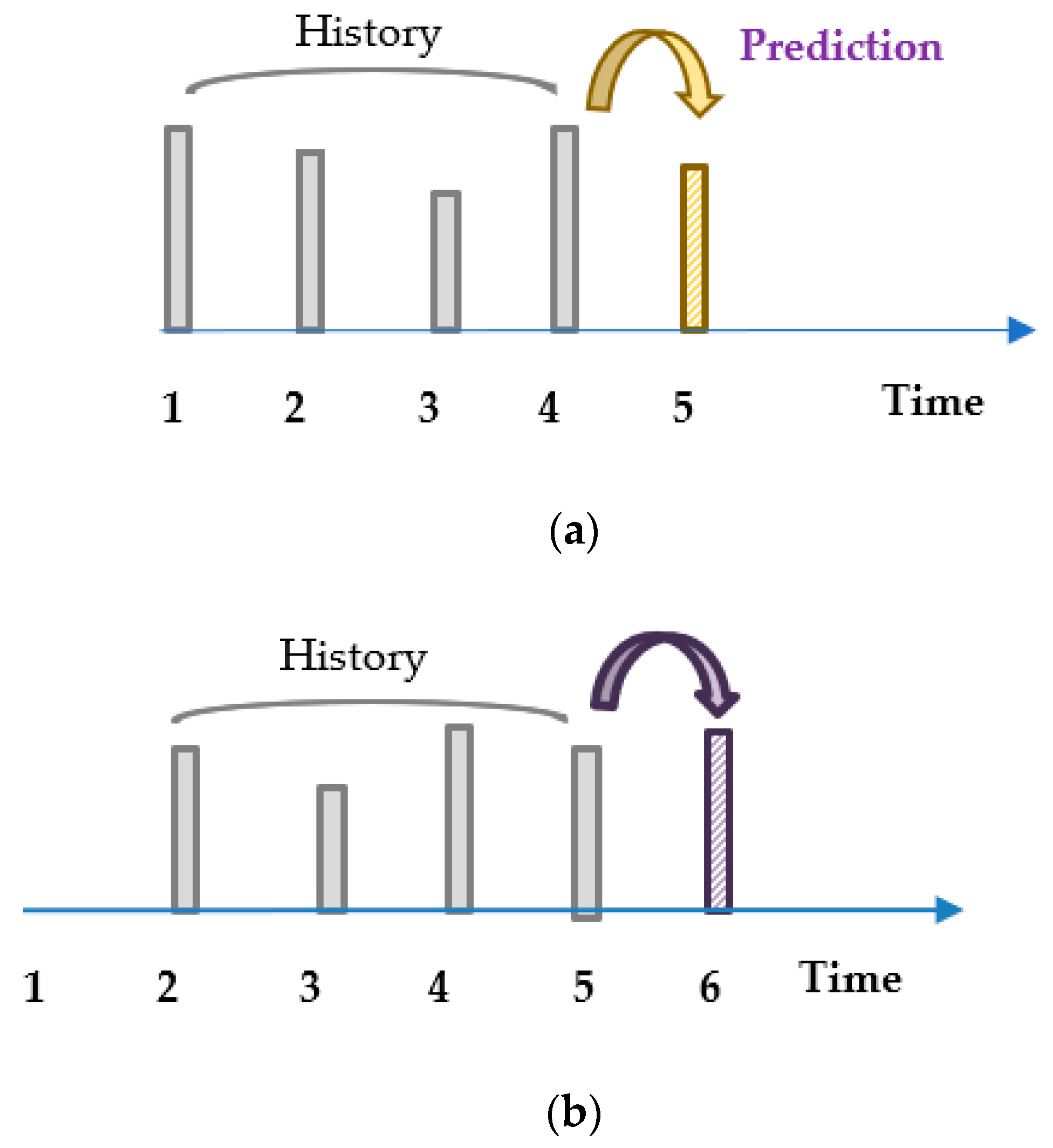
3. Model Predictive Control Using Linear Regression Models
4. Simulations and Results
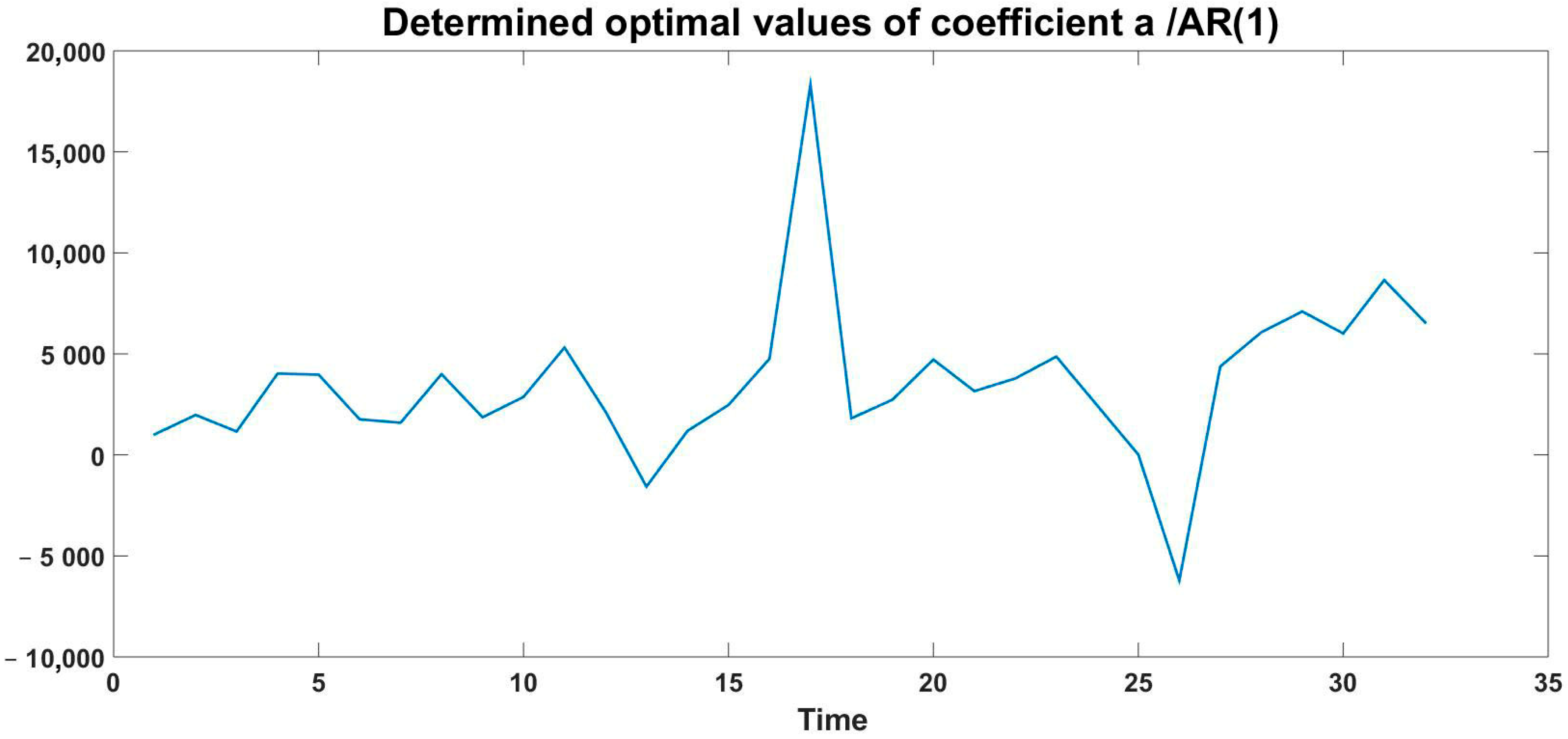
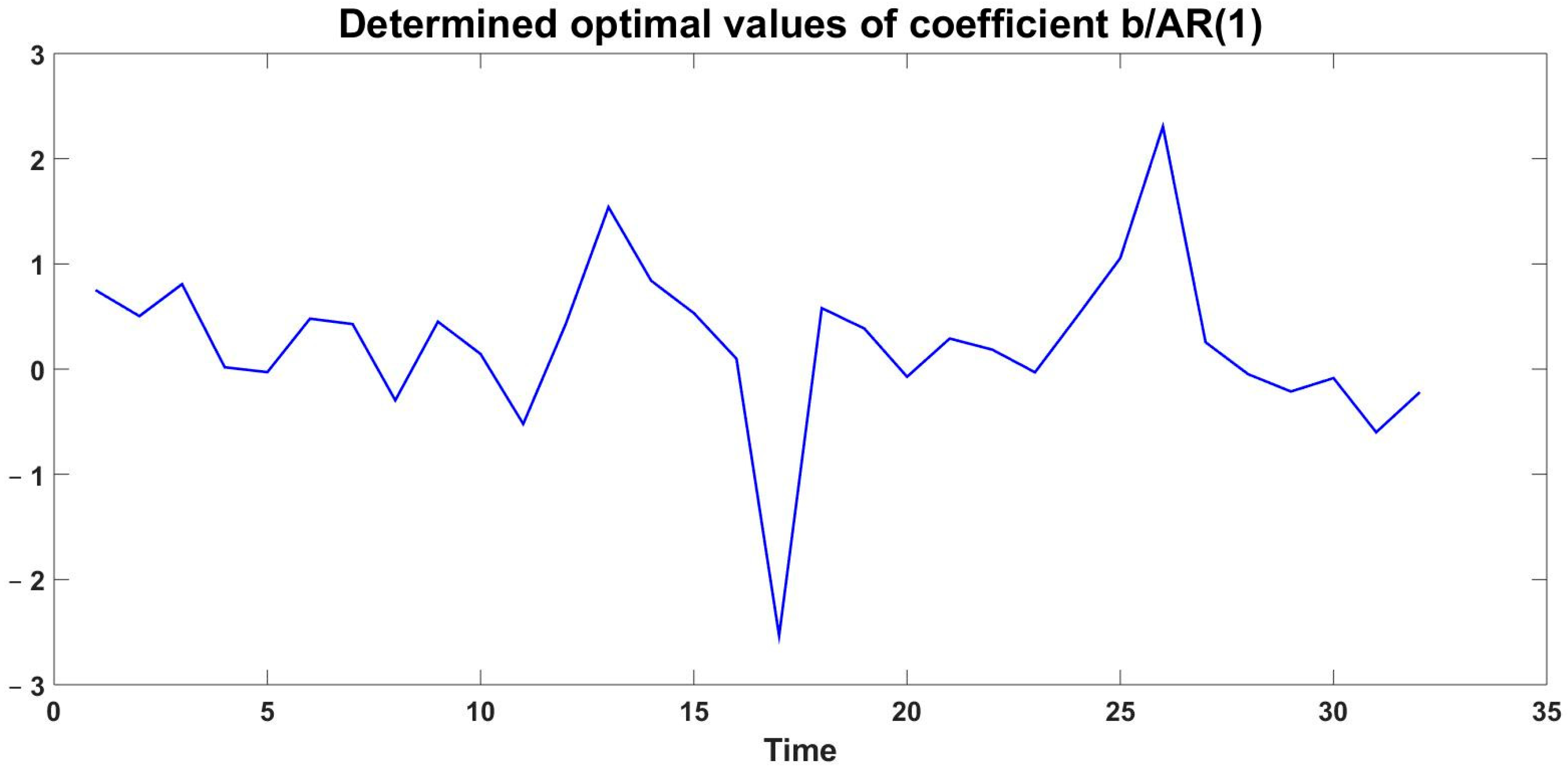
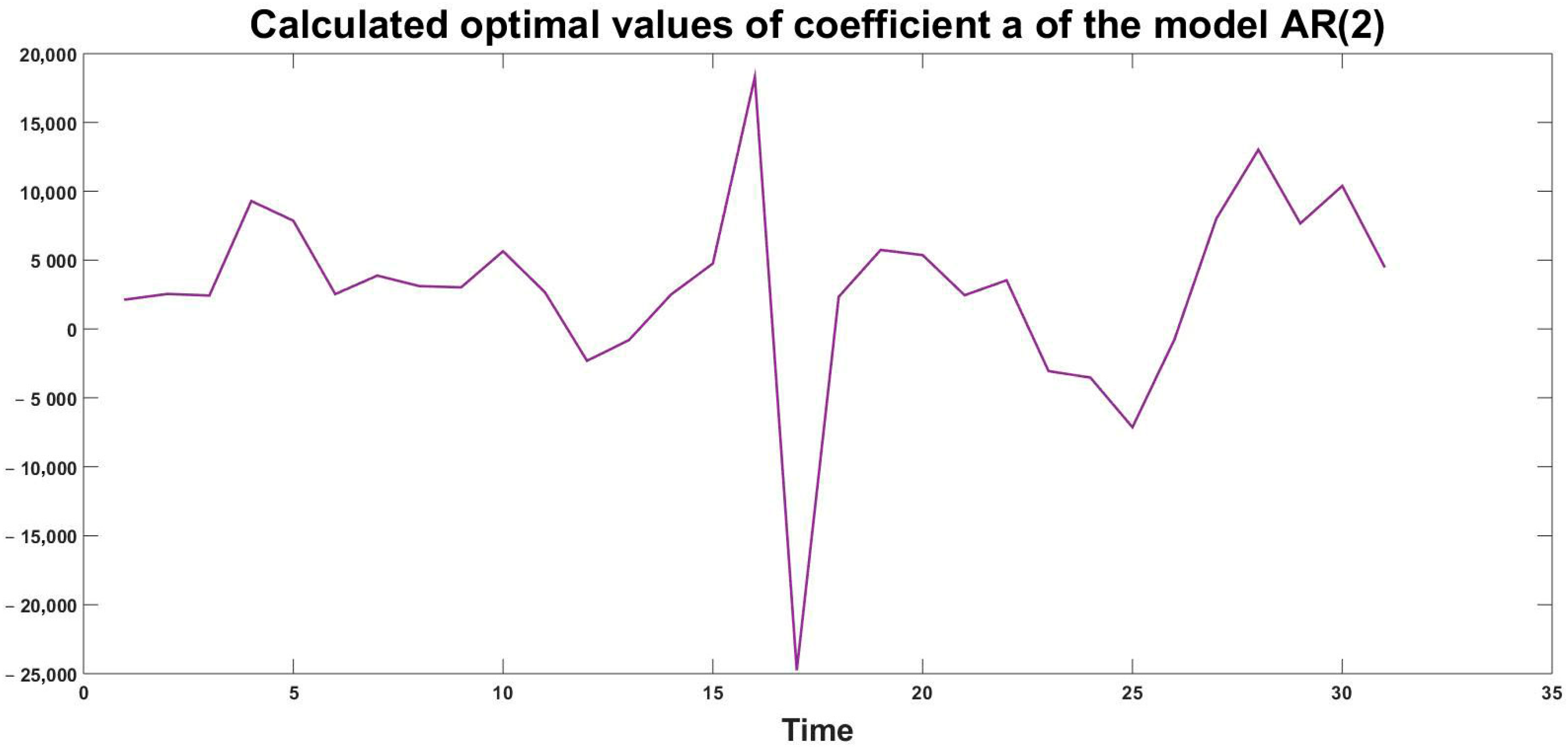
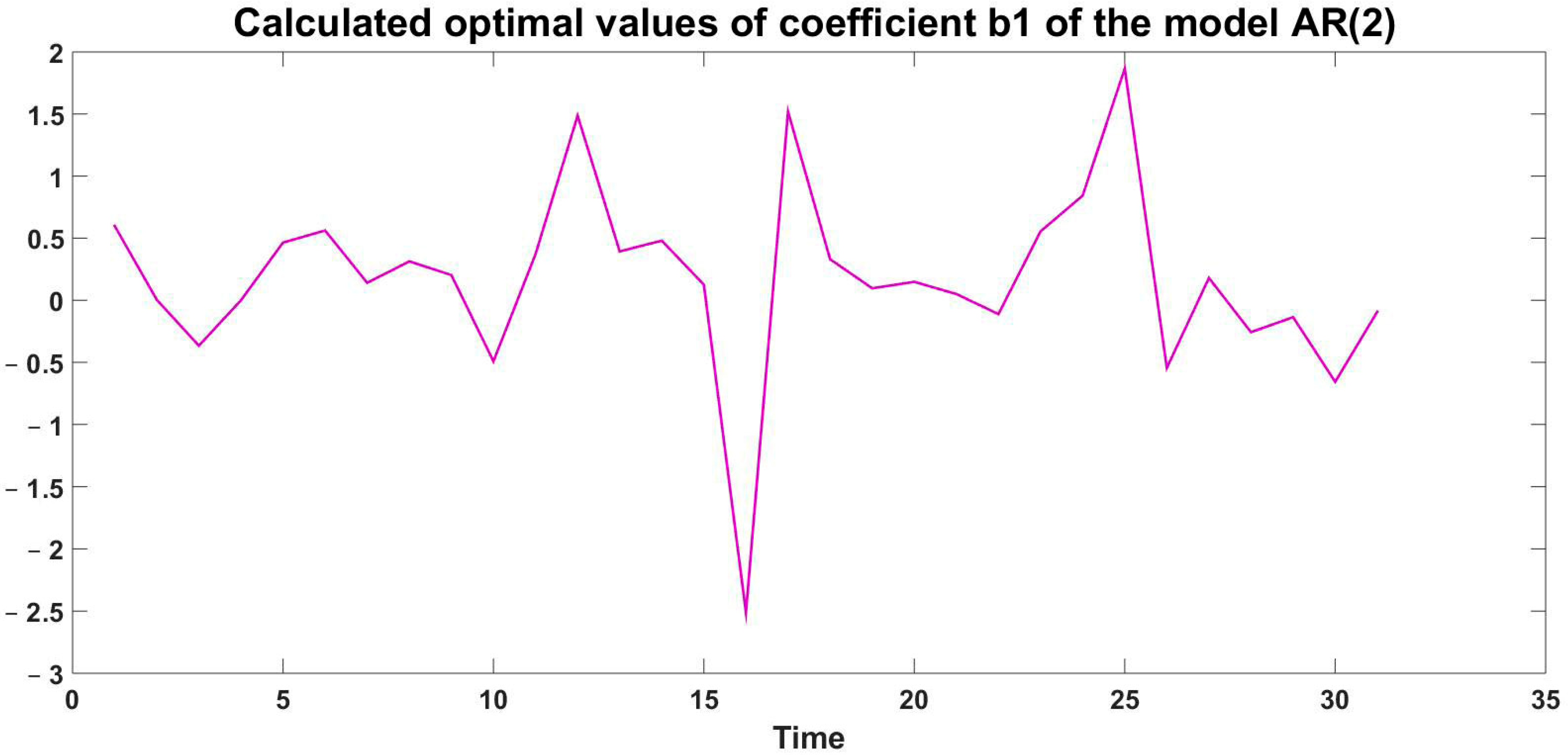
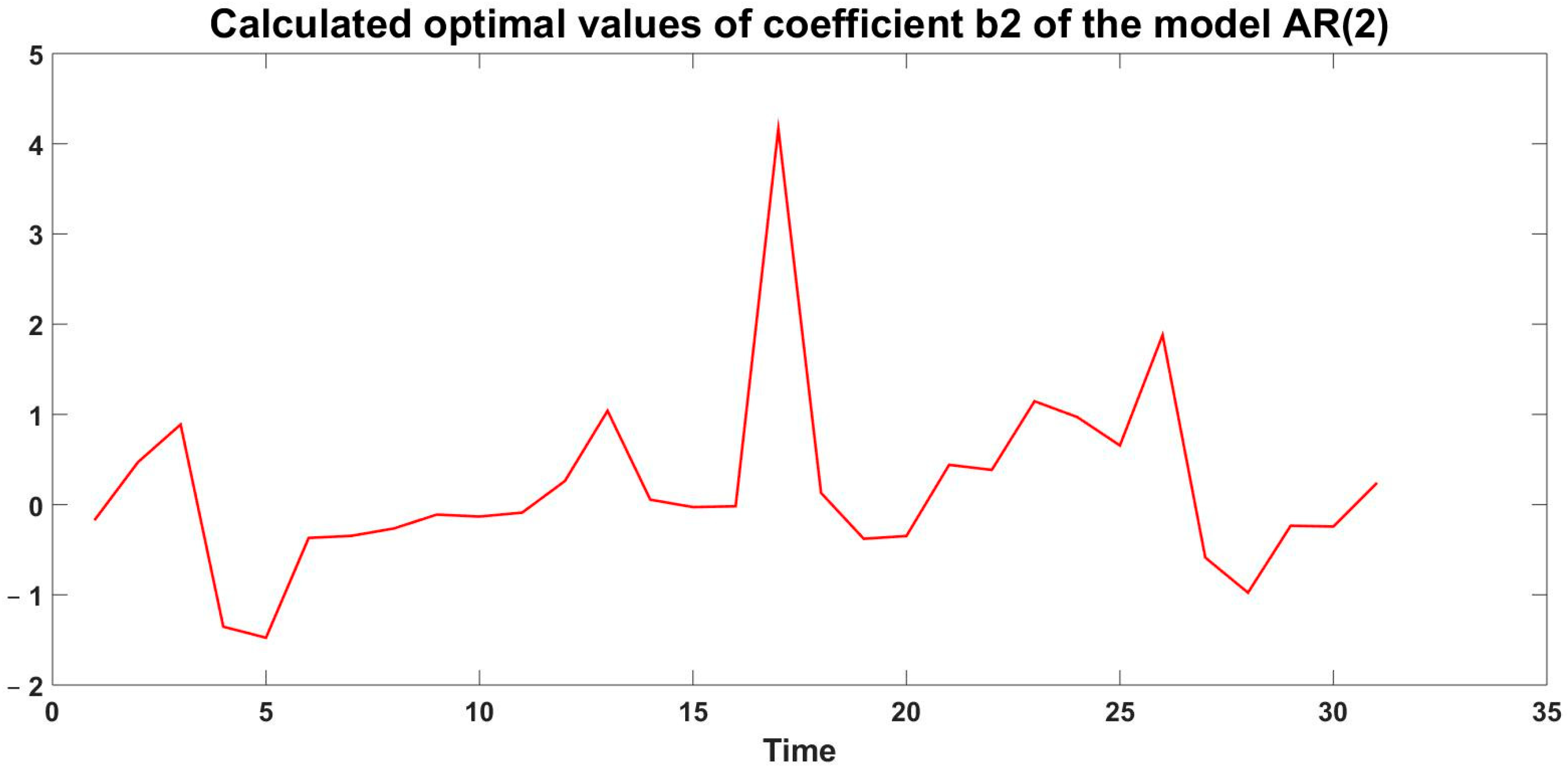
4.1. Use Case I: Evaluation of the Two Models Based on Existing Data
4.2. Use Case II: Model Predictive Control with Insufficient Data for Approximation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MPC | Model Predictive Control |
| AR(1) | Auto-regressive model with one previous value from the time series |
| AR(2) | Auto-regressive model with two previous values from the time series |
References
- Thery, R.; Zarate, P. Energy planning: A multi-level and multicriteria decision-making structure proposal. Cent. Eur. J. Oper. Res. 2009, 17, 265–274. [Google Scholar] [CrossRef]
- Prasad, R.D.; Bansal, R.; Raturi, A. Multi-faceted energy planning: A review. Renew. Sustain. Energy Rev. 2014, 38, 686–699. [Google Scholar] [CrossRef]
- Shahrom, S.F.; Aviso, K.B.; Tan, R.R.; Saleem, N.N.; Ng, D.K.S.; Andiappan, V. Regional Planning and Optimization of Renewable Energy Sources for Improved Rural Electrification. Process Integr. Optim. Sustain. 2023, 7, 785–804. [Google Scholar] [CrossRef]
- Jafar, H.T.; Tavakoli, O.; Bidhendi, G.N.; Alizadeh, M. Sustainable electricity supply planning: A nexus-based optimization approach. Renew. Sustain. Energy Rev. 2024, 195, 114316. [Google Scholar] [CrossRef]
- Narváez, F.A.S.; Castro, E.I.M. Energy planning with renewable energy sources. Int. J. Phys. Sci. Eng. 2021, 5, 44–51. [Google Scholar] [CrossRef]
- Joseph, C.; Gunton, T.I.; Day, J.C. Implementation of resource management plans: Identifying keys to success. J. Environ. Manag. 2008, 88, 594–606. [Google Scholar] [CrossRef] [PubMed]
- Schwenzer, M.; Ay, M.; Bergs, T.; Abel, D. Review on model predictive control: An engineering perspective. Int. J. Adv. Manuf. Technol. 2021, 117, 1327–1349. [Google Scholar] [CrossRef]
- Simmini, F.; Caldognetto, T.; Bruschetta, M.; Mion, E.; Carli, R. Model Predictive Control for Efficient Management of Energy Resources in Smart Buildings. Energies 2021, 14, 5592. [Google Scholar] [CrossRef]
- Karthigaiselvan, K.; Panda, R.C. Implementation of MPC Strategy in Reactive Separation Techniques and Its Benefits: A Demonstration with Natural Gas Sweetening Process. In Model Predictive Control—Theory and Applications; Volosencu, C., Ed.; SDG Publishers Compact: London, UK, 2023. [Google Scholar] [CrossRef]
- Castelletti, A.; Ficchì, A.; Cominola, A.; Segovia, P.; Giuliani, M.; Wu, W.; Lucia, S.; Ocampo-Martinez, C.; Schutter, B.D.; Maestre, J.M. Model Predictive Control of water resources systems: A review and research agenda. Annu. Rev. Control 2023, 55, 442–465. [Google Scholar] [CrossRef]
- Balaguer-Herrero, P.; Alfonso-Gil, J.C.; Martinez-Marquez, C.I.; Navarro, G.M.; Orts-Grau, S.; Segui-Chilet, S. Two-Scale Model Predictive Control for Resource Optimization Problems With Switched Decisions. IEEE Access 2022, 10, 57824–57834. [Google Scholar] [CrossRef]
- Hai, D.; Hao, Z.; Ping, L.Y. Model Predictive Control for inventory Management in Supply Chain Planning. Procedia Eng. 2011, 15, 1154–1159. [Google Scholar] [CrossRef][Green Version]
- Eslami, T.; Jungbauer, A. Control strategy for biopharmaceutical production by model predictive control. Biotechnol. Prog. 2024, 40, e3426. [Google Scholar] [CrossRef] [PubMed]
- Mechleri, E.; Dorneanu, B.; Arellano-Garcia, H. A Model Predictive Control-Based Decision-Making Strategy for Residential Microgrids. Engineering 2022, 3, 100–115. [Google Scholar] [CrossRef]
- Wei, H.; Shi, Y. MPC-based motion planning and control enables smarter and safer autonomous marine vehicles: Perspectives and a tutorial survey. IEEE/CAA J. Autom. Sin. 2023, 10, 8–24. [Google Scholar] [CrossRef]
- Bwambalea, E.; Wanyamaa, J.; Adongo, T.A.; Umukiza, E.; Ntole, R.; Chikavumbwa, S.R.; Sibale, D.; Jeremaih, Z. A review of model predictive control in precision agriculture. Smart Agric. Technol. 2025, 10, 100716. [Google Scholar] [CrossRef]
- Zohuri, B.; Mossavar-Rahmani, F.; Behgounita, F. Chapter 21—Statistical forecasting—Regression and time series analyses. In Knowledge Is Power in Four Dimensions: Models to Forecast Future Paradigm; Zohuri, B., Mossavar-Rahmani, F., Behgounia, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 709–722. [Google Scholar]
- Kamran, M. Chaper 8—Energy statistics and forecasting for smart grids. In Fundamentals of Smart Grid Systems; Elsevier: Amsterdam, The Netherlands, 2023; pp. 365–392. [Google Scholar] [CrossRef]
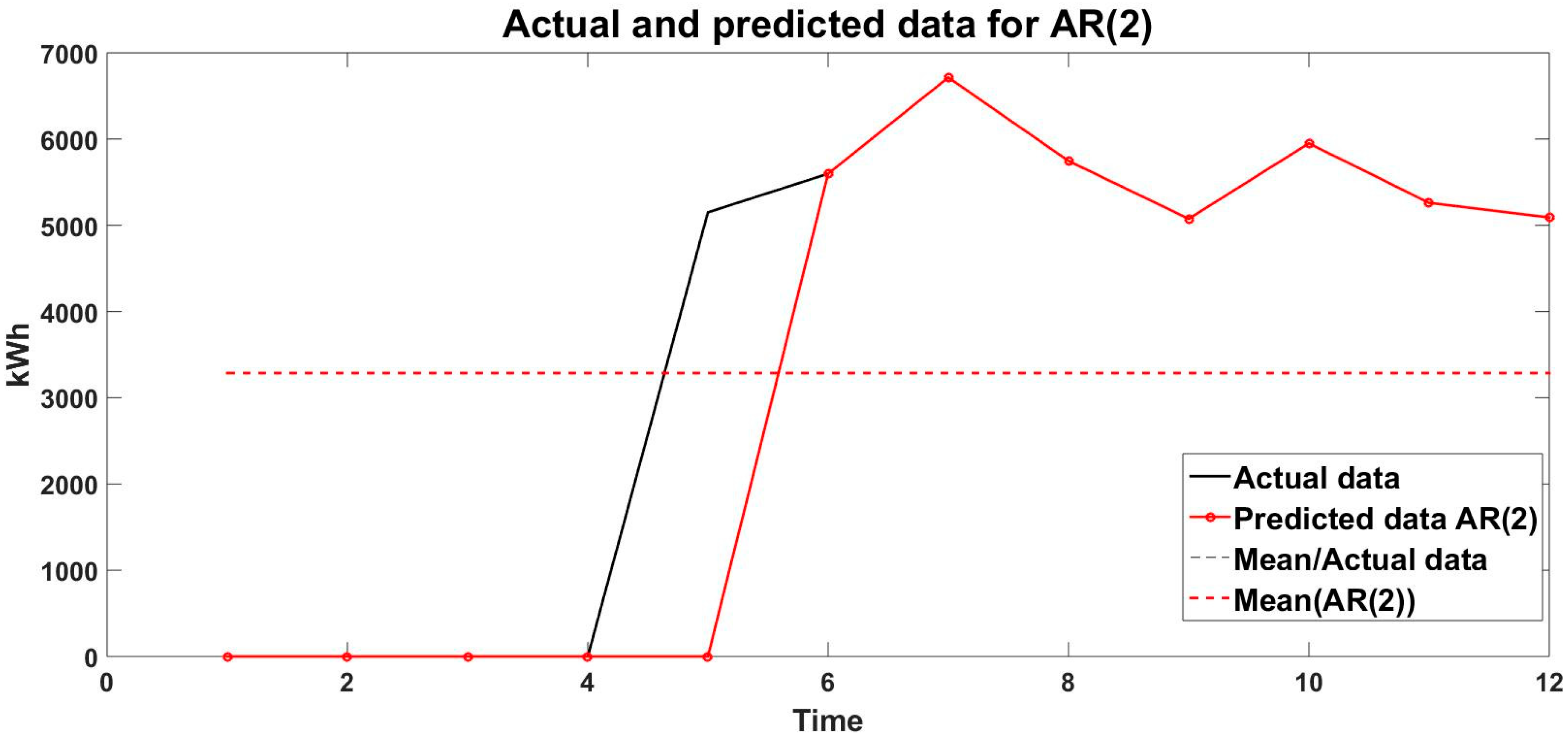
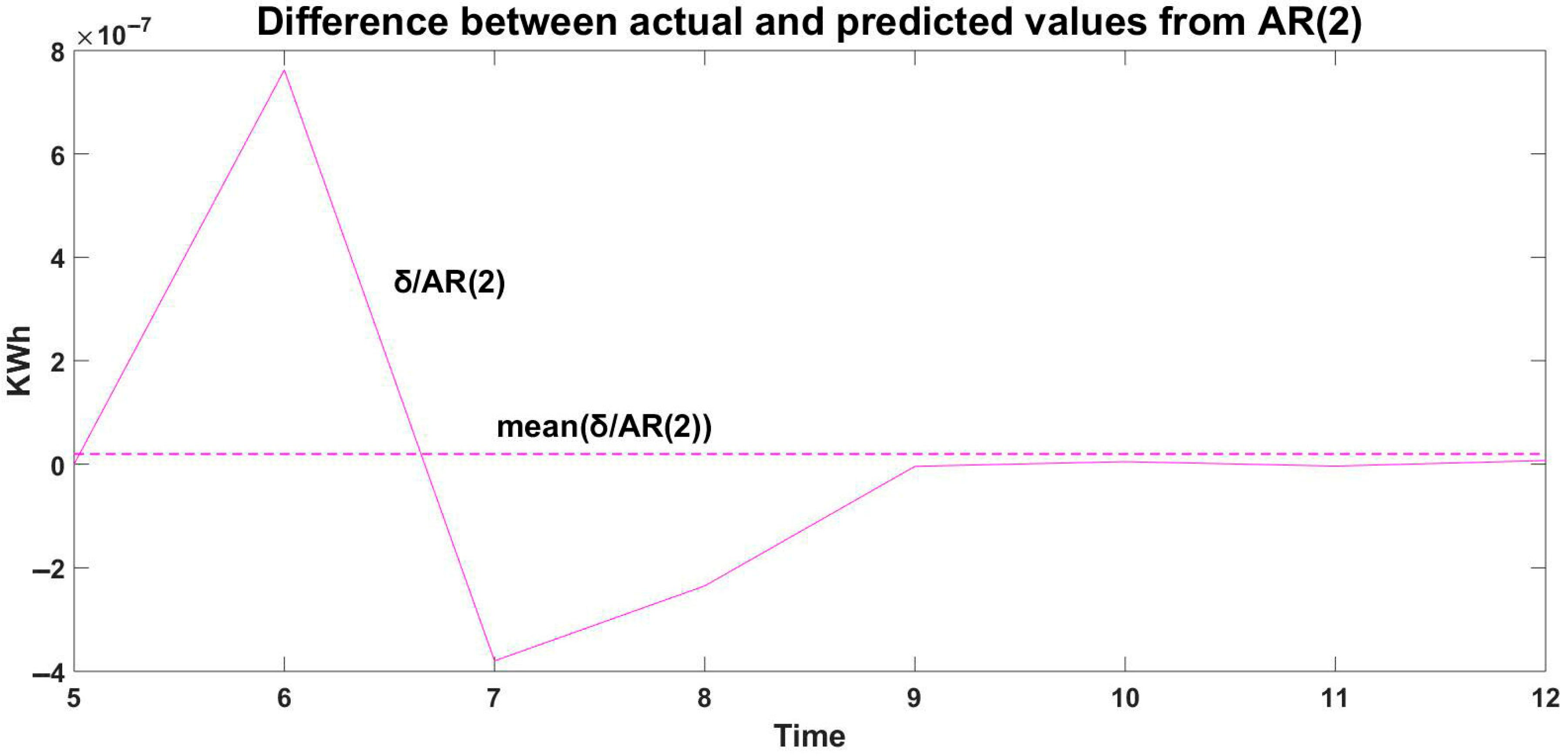
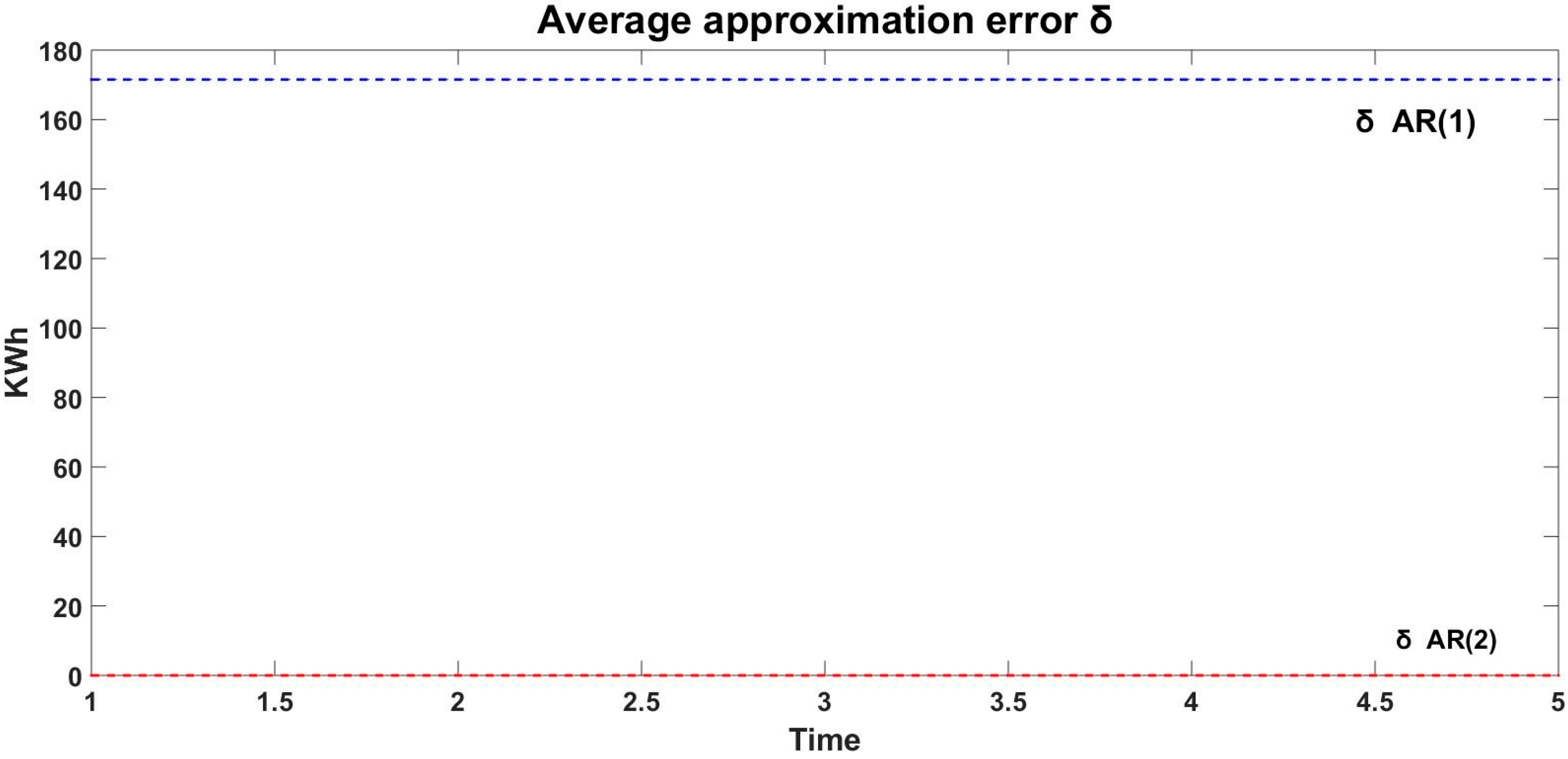
| 2023 | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [kWh] | 4387 | 4472 | 4851 | 4867 | 5150 | 5598 | 6714 | 5746 | 5075 | 5950 | 5260 | 5091 |
| Months 2023 | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual [kWh] | 4387 | 4472 | 4851 | 4867 | 5150 | 5598 | 6714 | 5746 | 5075 | 5950 | 5260 | 5091 |
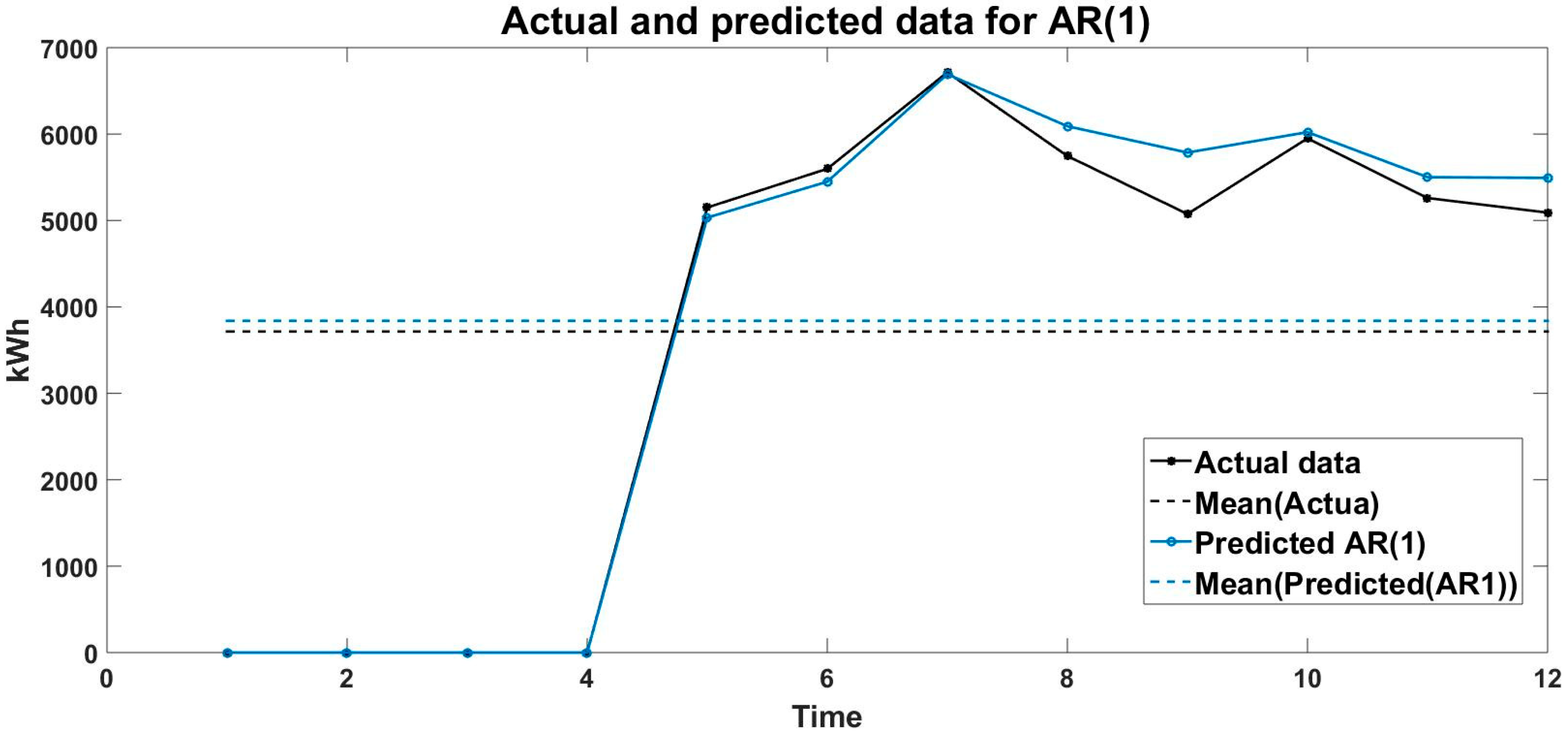
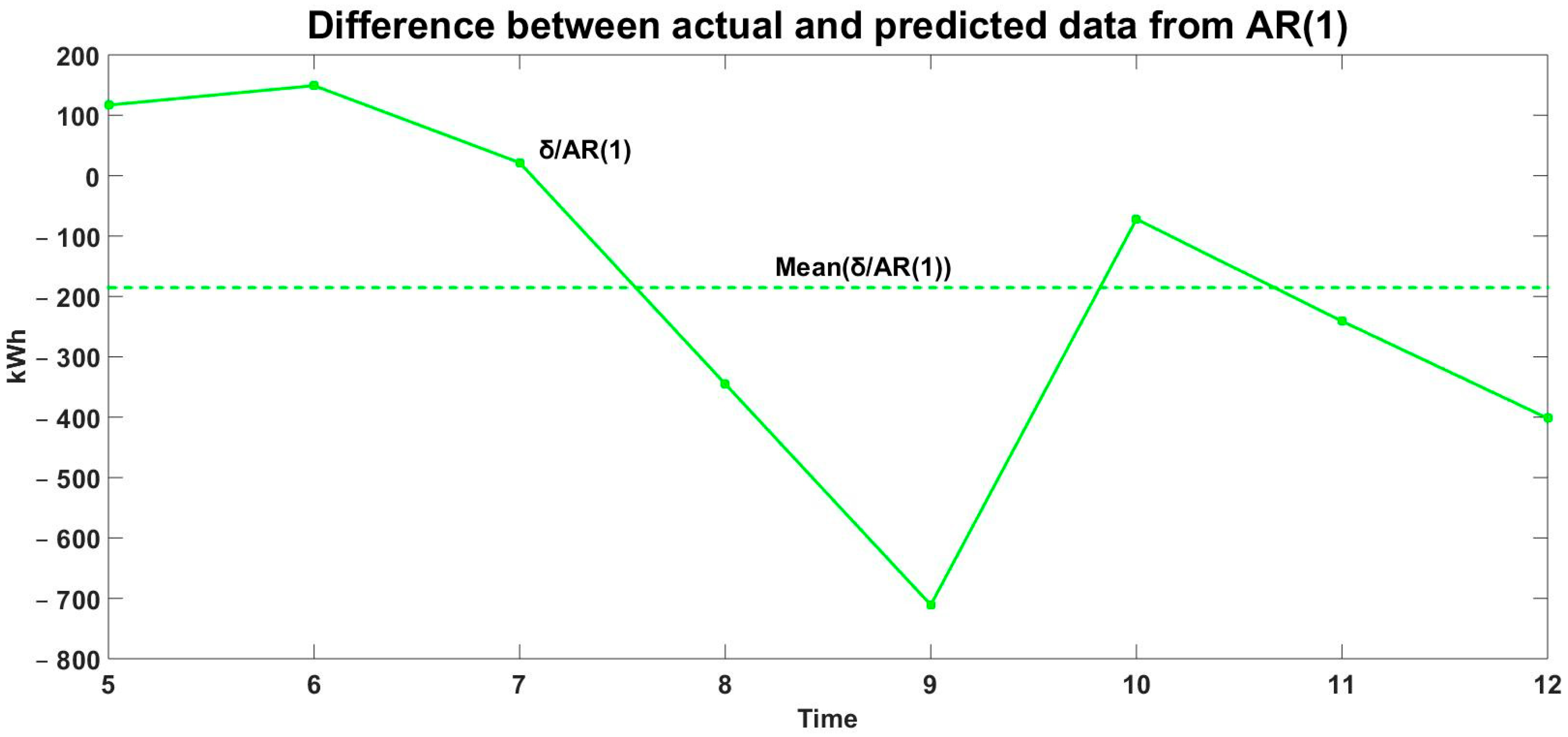
| AR(1) [kWh] | 0 | 0 | 0 | 0 | 5033 | 5449 | 6692 | 6091 | 5786 | 6022 | 5501 | 5493 |
| δ/AR(1) | 0 | 0 | 0 | 0 | 117 | 149 | 22 | −345 | −711 | −72 | −241 | −402 |
| AR(2) [KWh] | 0 | 0 | 0 | 0 | 0 | 5598 | 6714 | 5746 | 5075 | 5950 | 5260 | 5091 |
| δ/AR(2) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Months 2023 | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|
| [kWh] | 6714 | 5746 | 5075 | 5950 | 5260 | 5091 |
| Actual Data/History | Predicted | |||||||
|---|---|---|---|---|---|---|---|---|
| Time | Jul/2023 | Aug/2023 | Sep/2023 | Oct/2023 | Nov/2023 | Dec/2023 | Jan/2024 | |
| History | AR(1) [kWh] | 6714 | 574 | 5075 | 5950 | 5260 | 5091 | |
| AR(2) [kWh] | 6714 | 574 | 5075 | 5950 | 5260 | 5091 | ||
| Prediction | AR(1) [kWh] | 5594 | ||||||
| AR(2) [kWh] | 5697 | |||||||
| Actual + Predicted Data (Jan 2024)/History | Predicted Feb/2024 | ||||||
|---|---|---|---|---|---|---|---|
| Time | Aug/2023 | Sep/2023 | Oct/2023 | Nov/2023 | Dec/2023 | Jan/2024 | |
| AR(1) | 5746 | 5075 | 5950 | 5260 | 5091 | 5594 | |
| AR(2) | 5746 | 5075 | 5950 | 5260 | 5091 | 5697 | |
| AR(1) | 5348 | ||||||
| AR(2) | 5616 | ||||||
| Predicted Data as History (Feb + Mar + Apr + Jun + Jul 2024)/History | Predicted Aug/2024 | ||||||
|---|---|---|---|---|---|---|---|
| Time | Feb/2023 | Mar/2023 | Apr/2023 | May/2023 | Jun/2023 | Jul/2024 | |
| AR(1) | 5348 | 5347 | 5338 | 5410 | 5362 | 5368 | |
| AR(2) | 5616 | 5076 | 5368 | 5516 | 5222 | 5522 | |
| AR(1) | 5371 | ||||||
| AR(2) | 5553 | ||||||
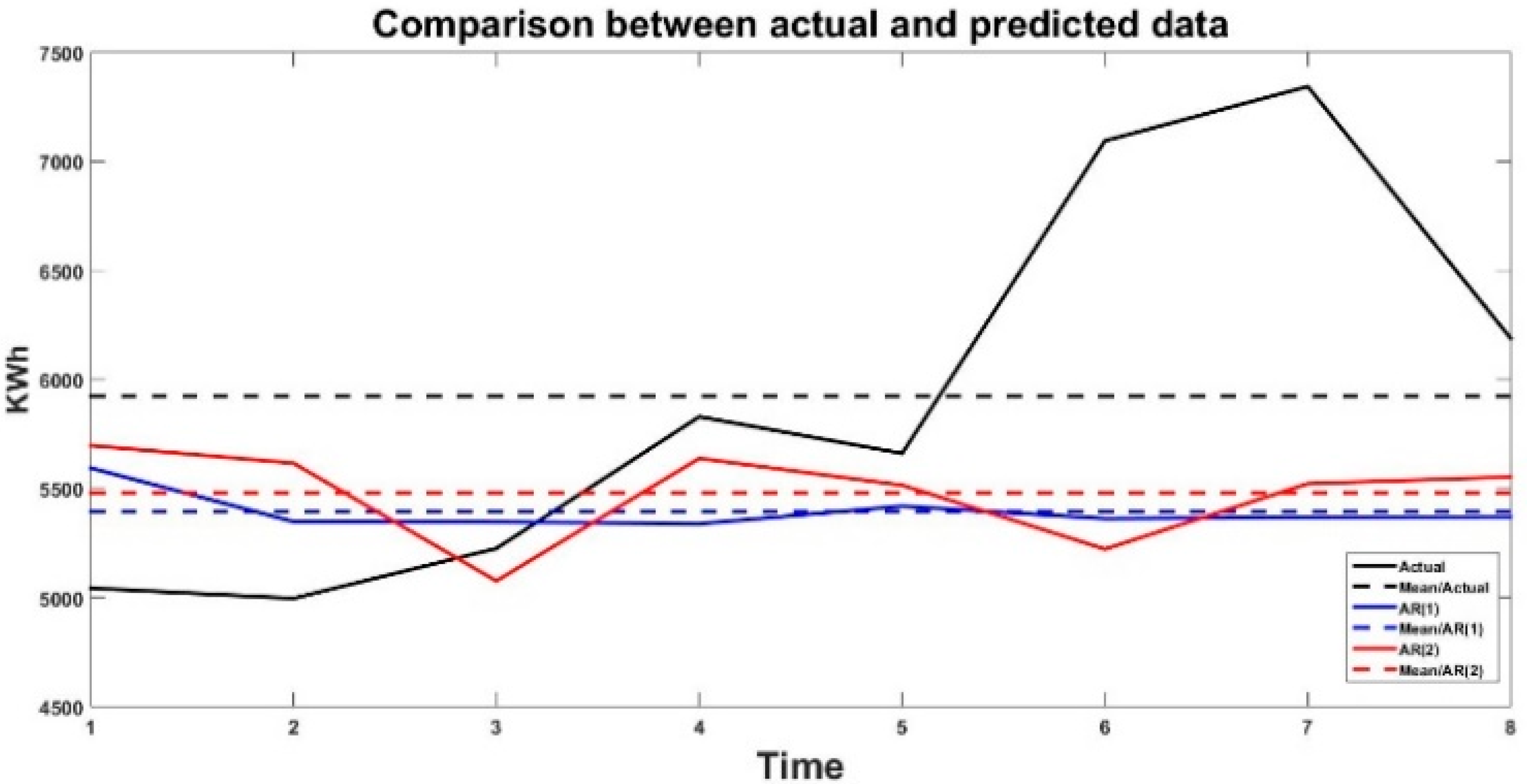
| Months/2024 | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug |
|---|---|---|---|---|---|---|---|---|
| Actual data [kWh] | 5043 | 4996 | 5225 | 5829 | 5661 | 7094 | 7343 | 6188 |
| Predicted data from AR(1) [kWh] | 5594 | 5348 | 5347 | 5338 | 5410 | 5362 | 5368 | 5371 |
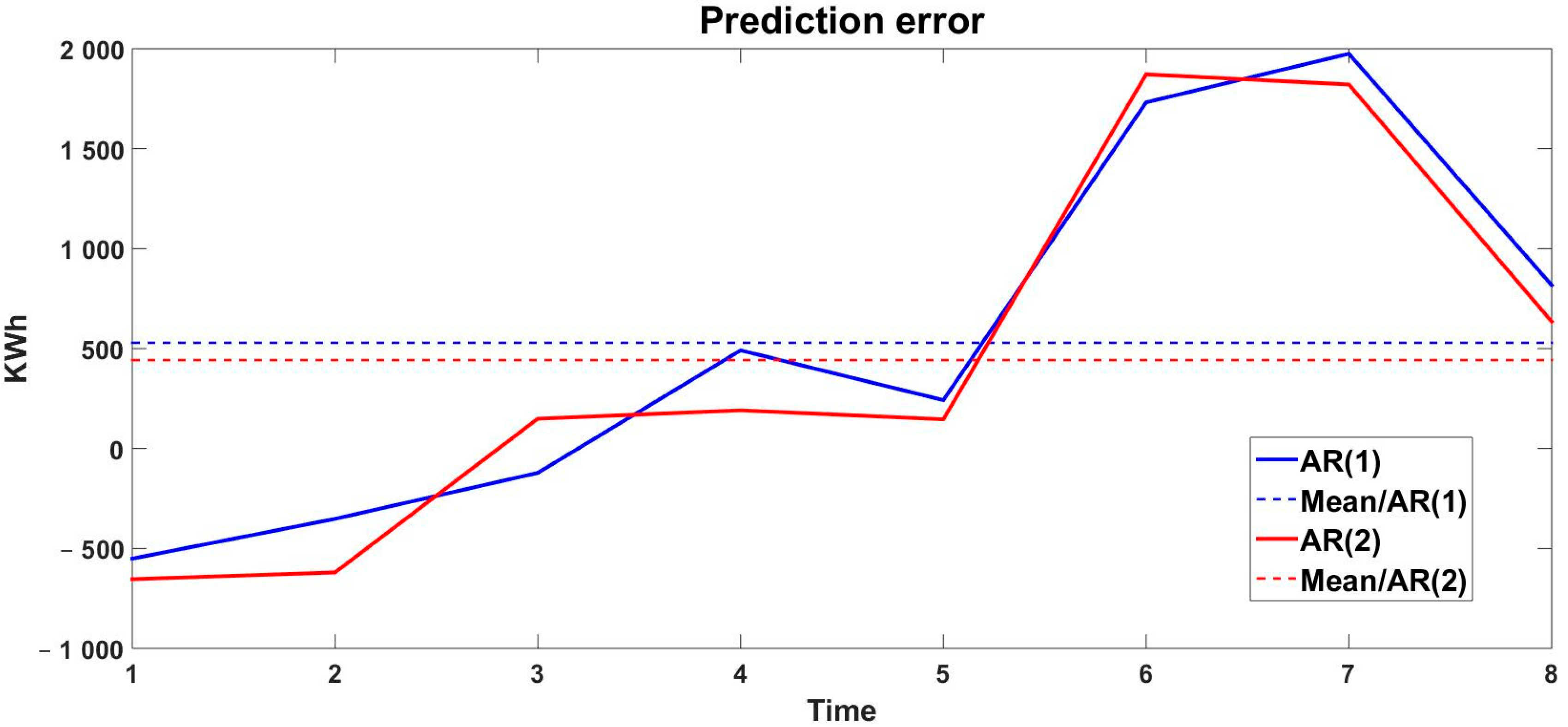
| Prediction error δ/AR(1) | −551 | −352 | −122 | 491 | 251 | 1732 | 1975 | 817 |
| Predicted data from AR(2) [kWh] | 5697 | 5616 | 5076 | 5368 | 5516 | 5222 | 5522 | 5553 |
| Prediction error δ/AR(2) | −654 | −620 | 149 | 191 | 146 | 1872 | 1821 | 635 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stoilova, K.; Stoilov, T.; Angelova, G. Planning Resources by Model Predictive Control. Eng. Proc. 2025, 100, 49. https://doi.org/10.3390/engproc2025100049
Stoilova K, Stoilov T, Angelova G. Planning Resources by Model Predictive Control. Engineering Proceedings. 2025; 100(1):49. https://doi.org/10.3390/engproc2025100049
Chicago/Turabian StyleStoilova, Krasimira, Todor Stoilov, and Galia Angelova. 2025. "Planning Resources by Model Predictive Control" Engineering Proceedings 100, no. 1: 49. https://doi.org/10.3390/engproc2025100049
APA StyleStoilova, K., Stoilov, T., & Angelova, G. (2025). Planning Resources by Model Predictive Control. Engineering Proceedings, 100(1), 49. https://doi.org/10.3390/engproc2025100049






