Helicopter Rotor Aerodynamic Characteristics in Ground Effect: Numerical Study †
Abstract
1. Introduction
2. Mathematical Modeling
2.1. Blade Element Theory for a Helicopter Rotor
2.2. Momentum Theory for a Helicopter Rotor
2.3. Blade Element–Momentum Theory for a Helicopter Rotor
2.4. Empirical Correction
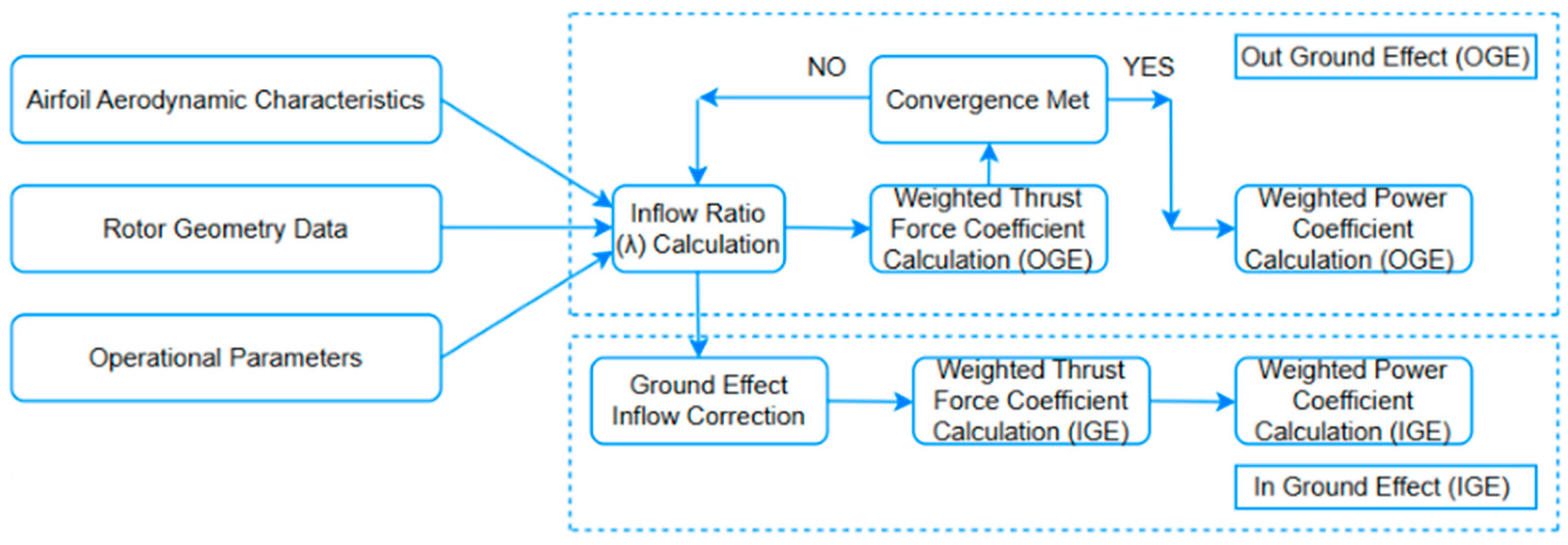
3. Calculation Procedure
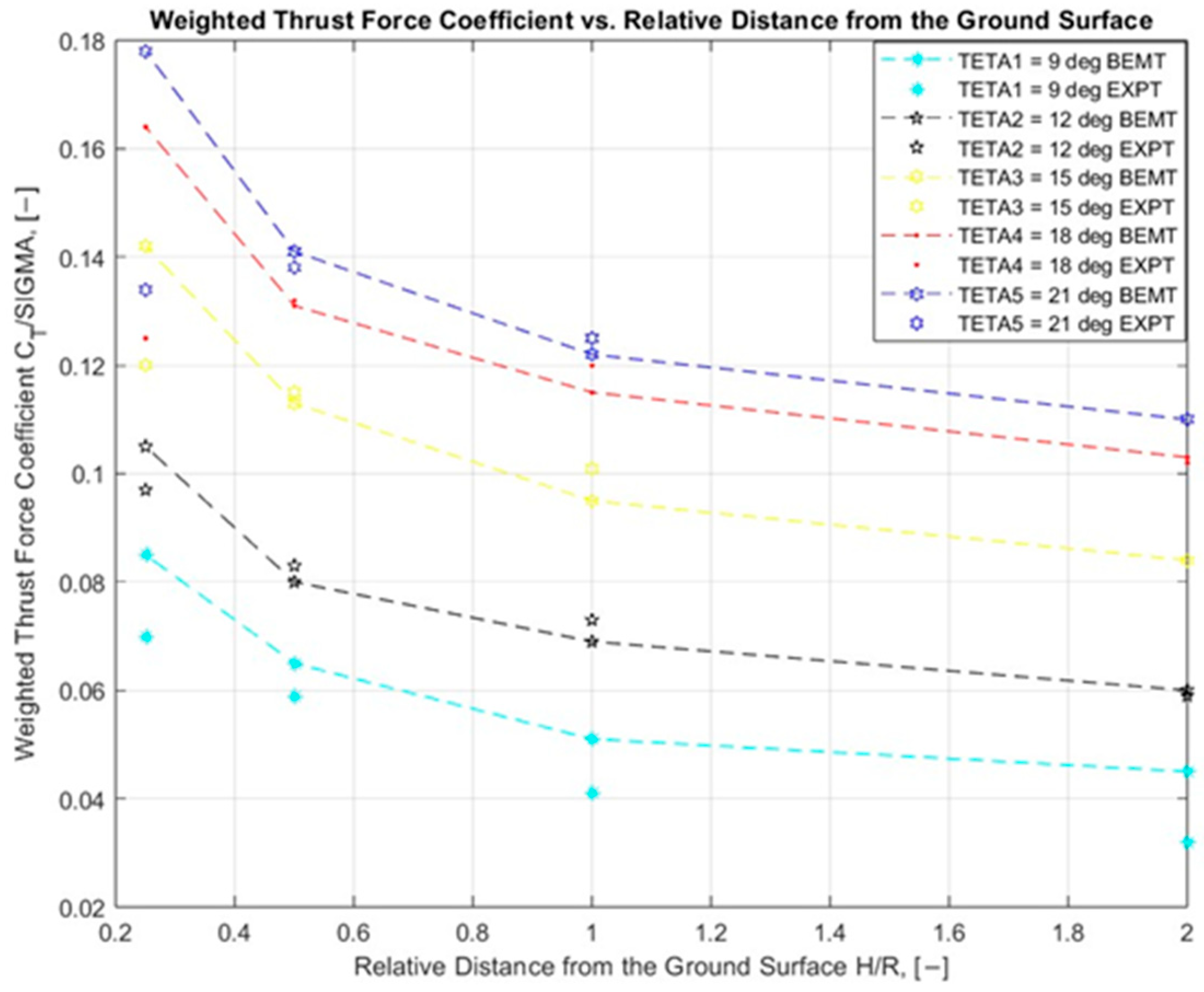
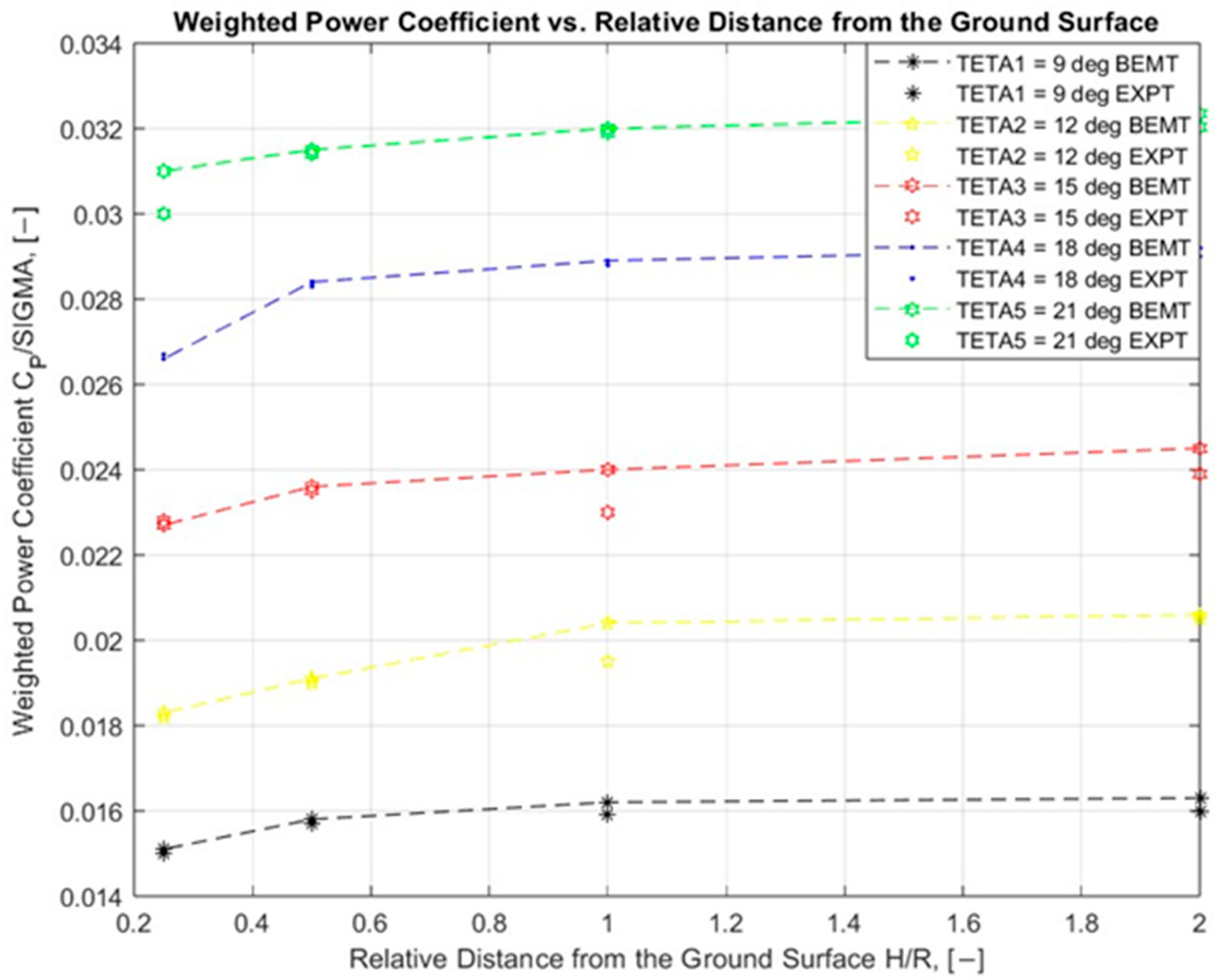
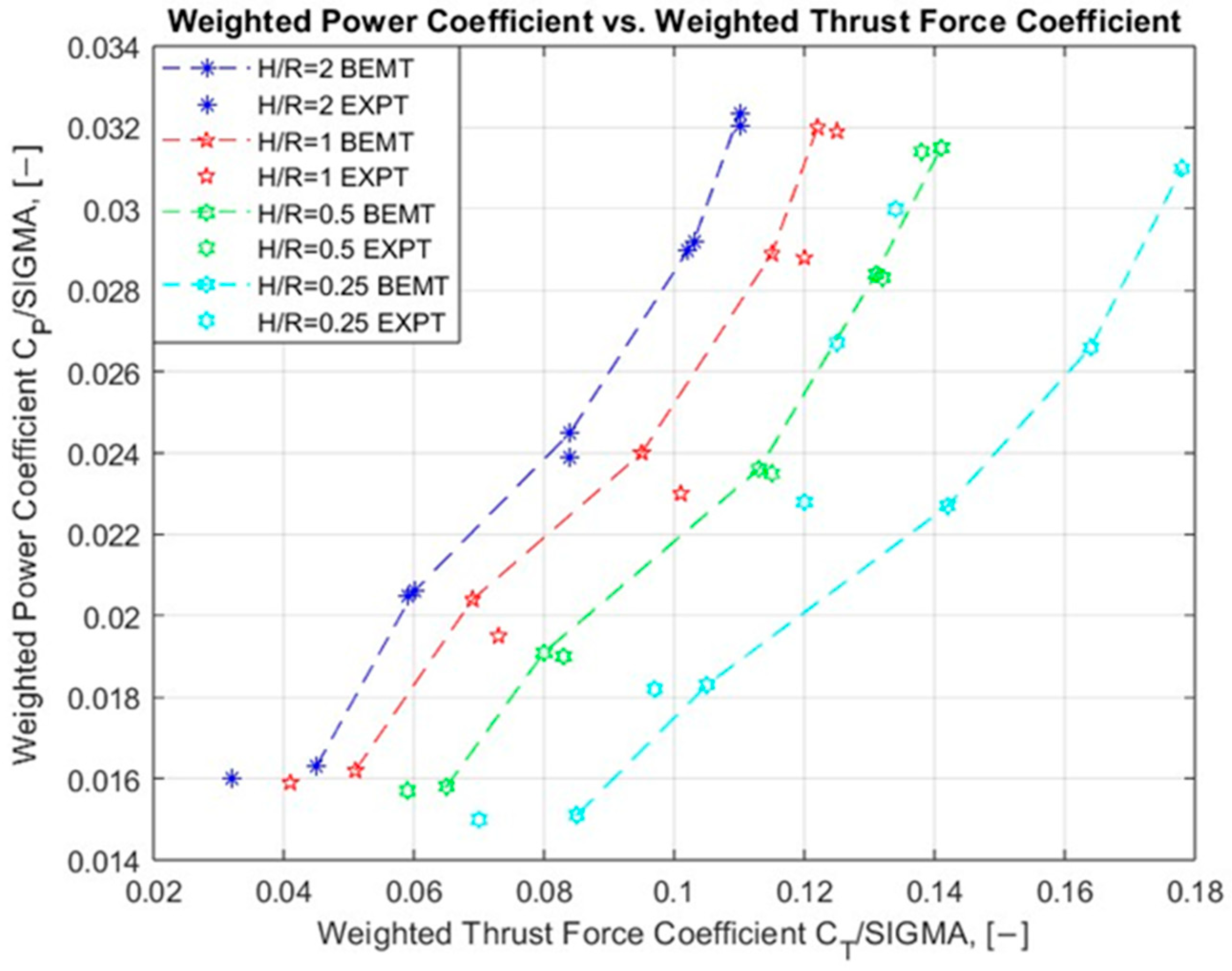
4. Results
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Knight, M.; Hefner, R. Analysis of Ground Effect on the Lifting Airscrew; NACA Technical Note 835; NASA: Washington, DC, USA, 1941.
- Fradenburgh, E. The Helicopter and the Ground Effect Machine. J. Am. Helicopter Soc. 1960, 5, 24–33. [Google Scholar] [CrossRef]
- Heyson, H. Ground Effect for Lifting Rotors in Forward Flight; National Aeronautics and Space Administration Technical Note D-234; NASA: Washington, DC, USA, 1960. [Google Scholar]
- Rotaru, C.; Todorov, M.B. Helicopter Flight Physics. In Flight Physics Models Techniques and Technologies; IntechOpen: Rijeka, Croatia, 2017. [Google Scholar] [CrossRef]
- Johnson, W. NASA Design and Analysis of Rotorcraft Theory, Release 1.14; NASA Ames Research Center: Washington, DC, USA, 2019. [Google Scholar]
- Xin, H.; Prasad, J.; Peters, D.; Itoga, N.; Iboshi, N.; Nagashima, T. Ground Effect Aerodynamics of Lifting Rotors Hovering Above Inclined Ground Plane. In Proceedings of the 17th Applied Aerodynamics Conference, Norfolk, VA, USA, 28 June–1 July 1999. [Google Scholar] [CrossRef]
- Gibertini, G.; Grassi, D.; Parolini, C.; Zagaglia, D.; Zanotti, A. Experimental Investigation on the Aerodynamic Interaction Between a Helicopter and Ground Obstacles. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 229, 1395–1406. [Google Scholar] [CrossRef]
- Georgiev, G.; Serbezov, V.; Todorov, M. Experimental Study of Multicopter Propeller Performance near the Ground at Different Inclination Angles. In Proceedings of the 13th International Scientific Conference on Aeronautics, Automotive and Railway Engineering and Technologies (BulTrans-2021), Sozopol, Bulgaria, 10–13 September 2021. [Google Scholar] [CrossRef]
- Georgiev, G.; Panayotov, F.; Serbezov, V.; Todorov, M. Experimental Study of Static Characteristics of a Helicopter Rotor in Ground Effect. In Proceedings of the 11th International Scientific Conference “TechSys 2022”—Engineering, Technologies and Systems, Plovdiv, Bulgaria, 26–28 May 2022. [Google Scholar] [CrossRef]
- Misiorowski, M.; Rothacker, B.; Cesnik, C. Extreme Ground Effect Characterization Testing for Human-Powered Helicopter Application. In Proceedings of the American Helicopter Society Forum 69, Phoenix, AZ, USA, 21–23 May 2013. [Google Scholar]
- Young, L. Simulated Tiltrotor Aircraft Operation in Close Proximity to a Building in Wind and Ground-Effect Conditions. In Proceedings of the 15th AIAA Aviation Technology, Integration, and Operations Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar] [CrossRef]
- Bauknecht, A.; Schwarz, C.; Raffel, M.; Mailänder, S. Flow Measurement Techniques for Rotor Wake Characterization on Free-Flying Helicopters in Ground Effect. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Kinzel, M.; Cornelius, J.; Schmitz, S.; Palacios, J.; Langelaan, J.; Adams, D.; Lorenz, R. An Investigation of the Behavior of a Coaxial Rotor in Descent and Ground Effect. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Light, J. Tip Vortex Geometry of a Hovering Helicopter Rotor in Ground Effect. In Proceedings of the American Helicopter Society Annual Forum, Boston, MA, USA, 22–24 May 1989. [Google Scholar]
- Hanker, E.; Smith, R. Parameters Affecting Helicopter Interactional Aerodynamics in Ground Effect. J. Am. Helicopter Soc. 1985, 30, 52–61. [Google Scholar] [CrossRef]
- Silva, P.; Tsoutsanis, P.; Antoniadis, A. Numerical Investigation of Full Helicopter with and without the Ground Effect. Elsevier Aerosp. Sci. Technol. 2022, 122, 107401. [Google Scholar] [CrossRef]
- Gao, H.; Agarwal, R. Numerical Study of a Hovering Helicopter Rotor Blade in Ground Effect. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Johnson, W. Rotorcraft Aeromechanics; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Hayden, J. The Effect of the Ground on Helicopter Hovering Power Required. In Proceedings of the AHS 32nd Annual Forum, Washington, DC, USA, 10–12 May 1976. [Google Scholar]
- Cheeseman, I.; Bennett, W. The Effect of the Ground on a Helicopter Rotor in Forward Flight; Aeronautical Research Council: London, UK, 1955. [Google Scholar]


| EXP | BEM | EXP | BEM | EXP | BEM | EXP | BEM | EXP | BEM | |
| H/R | ||||||||||
| 2 | 0.0160 | 0.0163 | 0.0205 | 0.0206 | 0.0239 | 0.0245 | 0.0290 | 0.0292 | 0.03203 | 0.03234 |
| 1 | 0.0159 | 0.0162 | 0.0195 | 0.0204 | 0.0230 | 0.0240 | 0.0288 | 0.0289 | 0.0319 | 0.0320 |
| 0.5 | 0.0157 | 0.0158 | 0.0190 | 0.0191 | 0.0235 | 0.0236 | 0.0283 | 0.0284 | 0.0314 | 0.0315 |
| 0.25 | 0.0150 | 0.0151 | 0.0182 | 0.0183 | 0.0228 | 0.0227 | 0.0267 | 0.0266 | 0.0300 | 0.0310 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Georgiev, G. Helicopter Rotor Aerodynamic Characteristics in Ground Effect: Numerical Study. Eng. Proc. 2025, 100, 13. https://doi.org/10.3390/engproc2025100013
Georgiev G. Helicopter Rotor Aerodynamic Characteristics in Ground Effect: Numerical Study. Engineering Proceedings. 2025; 100(1):13. https://doi.org/10.3390/engproc2025100013
Chicago/Turabian StyleGeorgiev, Gabriel. 2025. "Helicopter Rotor Aerodynamic Characteristics in Ground Effect: Numerical Study" Engineering Proceedings 100, no. 1: 13. https://doi.org/10.3390/engproc2025100013
APA StyleGeorgiev, G. (2025). Helicopter Rotor Aerodynamic Characteristics in Ground Effect: Numerical Study. Engineering Proceedings, 100(1), 13. https://doi.org/10.3390/engproc2025100013






