LIFE.PTML Model Development Targeting Calmodulin Pathway Proteins ^†

Abstract

Developing predictive models for drug efficacy is challenged by the complexity and heterogeneity of bioassay data. Here, we present LIFE.PTML, which is a methodology integrating drug Lifecycle (L), Information Fusion (IF), Encoding (E), Perturbation Theory (PT), and Machine Learning (ML) to predict compound activity across diverse experimental conditions. Using a dataset of 3748 molecule–assay combinations targeting calmodulin (CaM) and related proteins, LIFE.PTML combines chemical and protein descriptors, quantifies experimental variability via perturbation operators, and trains non-linear classifiers, including XGBoost and Gradient Boosting. XGBoost achieved the best performance, with 88.9% test accuracy and an ROC AUC of 0.959, while feature importance analysis highlighted contributions from both drug- and protein-level descriptors. The results demonstrate that LIFE.PTML provides a robust, flexible, and interpretable framework for predictive chemoinformatics, facilitating the integration of multi-source data for drug discovery applications.

1. Introduction

While developing new drug formulations holds promise for improved treatments, the process is long and expensive [1]. For this reason, improving efficiency and accuracy in predicting the efficacy of potential new drugs could save both time and resources, ultimately accelerating the development of effective therapies [2]. Computational tools, including chemoinformatics models, have transformed drug discovery, enabling more systematic exploration of chemical space and prediction of bioactivity [3,4]. However, many traditional chemoinformatic approaches struggle to handle the complexity, heterogeneity, and volume of modern biomedical data, limiting their predictive power.

To overcome these limitations, advanced machine learning (ML) techniques have been increasingly employed to extract patterns from large and diverse datasets. Our group has developed the LIFE.PTML methodology, which integrates Life cycle (L) of drugs, Information Fusion (IF), Encoding processes (E), Perturbation Theory (PT) and AI/ML techniques. LIFE.PTML allows for the combination of multiple data sources—including chemical descriptors, protein features, and assay conditions—while PT operators quantify experimental variability and perturbations, providing normalized inputs for ML models. Previous applications of LIFE.PTML have shown its effectiveness in predicting drug–target interactions and other medicinal chemistry problems [5,6,7].

These computational approaches are particularly valuable for studying protein targets with critical biological functions [8]. For example, calmodulin (CaM), a key mediator of calcium signaling, is of great interest due to its structural complexity, central role in cellular function [9], and involvement in various diseases [10,11,12]. By leveraging LIFE.PTML models, it is possible to predict compound activity across diverse assay conditions, including variations in target proteins, experimental concentrations, and assay types. In this context, LIFE.PTML provides a framework for predicting the likelihood that a compound will be active under specific conditions (i.e., f(v_ij) = 1), integrating information from both the chemical and protein sides of the system.

The main objective of this work is to develop and validate LIFE.PTML-based chemoinformatic models capable of predicting assay efficacy with high accuracy. These models are trained using both linear and non-linear ML algorithms, including Random Forest, SVM, Decision Tree, K-Nearest Neighbors, Gradient Boosting, and XGBoost. By combining multi-source data, perturbation quantification, and advanced non-linear modeling, the LIFE.PTML approach aims to improve predictive accuracy, generalizability, and interpretability of chemoinformatic models in complex biological systems.

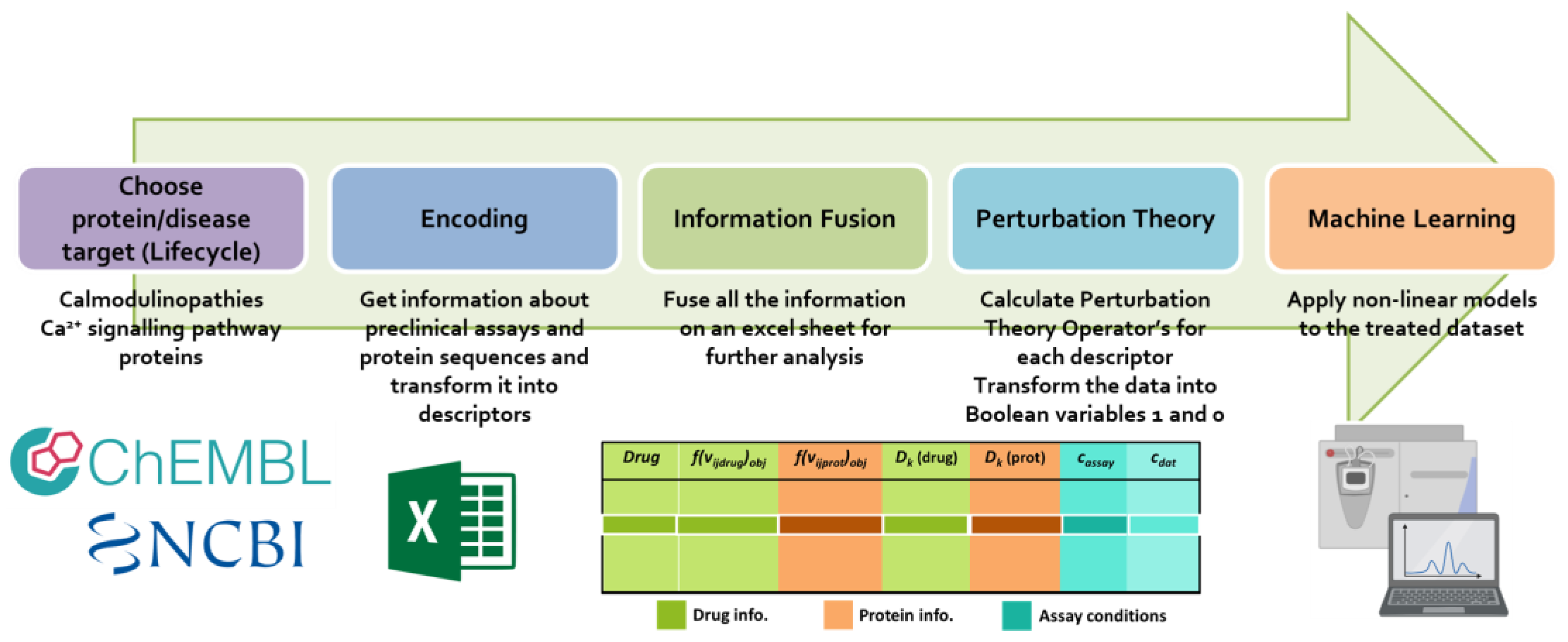
2. Materials and Methods

LIFE.PTML analysis involved four phases: the IF process, E part, PT variability quantification, and AI/ML algorithm training, validation, and use. In the initial IF phase, data gathering, data curation and data pre-processing tasks were carried out. In fact, system conceptualization is conceptual decomposition of the system into different sub-systems that are easy to study. In this case, the system was theoretically divided into two subsystems: drug information related to assays and protein data related to assays. Taking this into account, databases were examined and processed. Continuing the LIFE.PTML process, in the PT phase, the reference function and perturbation theory operators (PTO) or moving averages (MA) were calculated, which are used to quantify all the perturbations/variability on the input variables for all subsystems of the query system with respect to conditions or labels for the systems of reference. Lastly, the ML-Phase involved the training and validation of different ML models [6,7,8,13,14]. The general procedure followed in this part can be seen schematically in Figure 1.

Figure 1. Workflow of the LIFE.PTML model development.

2.1. Information Fusion

In the first stage, the Information Fusion (IF) phase, the dataset was constructed using the ChEMBL (ChEMBL_35)database by retrieving assays involving proteins associated with calmodulin (CaM) within the Ca²⁺ signaling pathway, as defined in KEGG [15,16,17]. This procedure provided approximately 4000 assays, including responses of CaM- and riluzole-related compounds, where the activity values varied according to the compound tested and the experimental conditions. To complement this information, protein data were collected from NCBI resources [18,19], using GenBank (268.0) and Protein BLAST to obtain the FASTA sequences and the three biologically active domains of each protein. Once gathered, descriptors were calculated and classified into drug-related and protein-related categories. Drug descriptors included molecular weight, Lipinski’s Rule of Five, LogP [20,21,22], interatomic electronegativity, van der Waals surface area, and assay-specific variables such as inhibitor and substrate concentrations [23]. Protein descriptors were obtained through the MARCH-INSIDE 2.0^® program, which encodes physicochemical properties such as electronegativity, polarity, and acidity along the amino acid sequence, propagating them through the residue network of each domain to generate quantitative values used as model inputs.

In the end, the dataset included ChEMBL compounds, biological activity data, and various assay types. Specifically, ChEMBL compounds included approximately 1000 chemical entities, many of which are FDA-approved drugs such as Gefitinib and Tamoxifen, along with investigational compounds. Biological activities were tested across 13 different measures, including parameters like IC₅₀ (nM), K_i (nM), inhibition percentages, and potency (nM). The assays covered various target proteins, with key examples including Calmodulin (CaM), Myosin light chain kinase, and Epidermal growth factor receptor (EGFR). Furthermore, different assay cell types were used, such as HEK293 (human embryonic kidney cells), CHO (Chinese hamster ovary cells), and RAW264.7 (mouse macrophage cell line). The assays also spanned diverse tissues and organisms, including human (Homo sapiens), mouse (Mus musculus), and the pathogen Plasmodium falciparum (causing malaria). The total number of data points and different assays included in the final dataset amounts to 3748.

2.2. Perturbation Theory Operator’s Calculation

In the second stage, the Perturbation Theory (PT) phase, Perturbation Theory Operators (PTOs) were calculated using Box–Jenkins moving average (MA) method [24]. The model considered two types of boundary conditions: those related to the assays themselves, such as target or assay type (c_assay = (c₁, c₂, c₃, c₄, c₅)), and those related to the dataset, including factors like organism or buffer (c_dat = (c₆, c₇, c₈, c₉, c₁₀)). For each condition, the mean descriptor values were calculated (MA), and deviations from these averages were expressed as delta values (ΔDk(c_j); Equation (1)). In this way, the perturbation operators quantified the extent to which experimental variability influenced descriptor behavior.

$$\Delta D_k\left(c_j\right)=D_k -<D_k\left(c_j\right)>$$

(1)

2.3. Objective and Reference Function Calculation

The third stage focused on the definition of the output variable and the reference function. Since assays reported different measures of activity, such as IC₅₀, K_i, or inhibition percentages, a desirability function was introduced to standardize the classification. Variables expected to increase, such as inhibition or residual activity, were assigned a desirability of +1, while those expected to decrease, including IC₅₀ or K_i, were assigned a value of –1. Cut-off criteria were then applied to distinguish active from inactive compounds, using 100 nM for concentration-based assays, 70% for inhibition percentages, and the dataset mean when no conventional threshold was available. These cut-offs allowed the transformation of activity data into Boolean variables (objective function), identifying compounds as active (f(v_ij)_obj = 1) or inactive (f(v_ij)_obj = 0). At the same time, a reference function (f(v_ij)_ref; Equation (2)) was calculated to estimate the probability of a compound being active under specific boundary conditions, providing a baseline measure for subsequent predictions.

$$f(v_{ij}{)}_{ref}=p({f(v_{ij}/c_j)}_{obj}=1){)}_{ref}={\displaystyle \frac{n({f(v_{ij}/c_j)}_{obs}=1)}{n\left({f(v_{ij}/c_j)}_{obs}\right)}}$$

(2)

2.4. Machine Learning Model Development

Finally, in the Machine Learning (ML) phase, several non-linear models were implemented to predict whether a compound will be successful or not under some boundary conditions (i.e., objective function). Non-linear algorithms included Random Forest, Support Vector Machine with RBF kernel, Decision Tree, K-Nearest Neighbors, Gradient Boosting, and XGBoost. All models were developed in Python (3.12) using scikit-learn (1.4) and pandas libraries (2.1) [25]. The dataset was divided into 80% for training and 20% for testing, with a performance threshold of 70% accuracy and sensitivity as the minimum requirement [26]. Hyperparameters were optimized through Grid Search and cross-validation, and model performance was evaluated using accuracy, sensitivity, specificity, AUC-ROC, and confusion matrices.

3. Results and Discussion

3.1. Dataset Construction

The information fusion stage resulted in a final dataset of 3748 molecule–assay combinations, corresponding to 1052 unique compounds. The distribution of the target variable was well-balanced, with 51.2% active cases and 48.8% inactive cases, providing favorable conditions for supervised learning without the need for additional resampling techniques. In terms of biological diversity, the dataset included 101 protein targets associated with Ca²⁺-dependent signaling pathways, such as calmodulin, myosin light chain kinase, and epidermal growth factor receptor (EGFR). This diversity confers both biological relevance and complexity to the dataset. Additionally, the presence of 19 species, 11 cell types, and multiple assay conditions captured a wide spectrum of experimental variability, enhancing the representativeness of the model. The definition of the objective function and reference function enabled the integration of heterogeneous bioactivity measures (IC₅₀, Kᵢ, inhibition %) into a binary classification scheme. A threshold of 100 nM for IC₅₀/K_i and 70% for inhibition assays was applied, resulting in a clear separation between active and inactive cases.

3.2. LIFE.PTML Non-Linear Models

Several non-linear machine learning models were trained to predict compound activity under specific assay conditions. These included ensemble methods (XGBoost, Gradient Boosting, Random Forest), support vector machines (SVM with RBF kernel), decision trees, and k-nearest neighbors (KNN). Each model was optimized via Grid Search or Randomized Search and evaluated using an 80/20 training/test split. ROC curves were calculated for both training and test sets to assess discriminative performance across models (Figure 2).

Figure 2. ROC Curves for non-linear models developed. ROC curves for training and test sets for XGBoost and Gradient Boosting classifiers, illustrating discriminative performance of LIFE.PTML models.

A detailed comparison of the optimized hyperparameters and performance statistics for all non-linear models is presented in Table 1. The comparison of non-linear classifiers highlighted substantial differences in predictive behavior. Ensemble methods, particularly XGBoost and Gradient Boosting, consistently outperformed other approaches across all evaluation metrics. XGBoost achieved the most balanced performance, with a test accuracy of 88.9% and ROC AUC of 0.959, indicating excellent discriminative power. Training metrics were markedly higher (accuracy 97.3%, AUC 0.999), suggesting a degree of overfitting; however, the test set performance confirmed good generalization capacity. Gradient Boosting displayed very similar performance (test accuracy 89.5%, ROC AUC 0.958), with slightly better calibration between sensitivity and specificity. In contrast, models such as Random Forest also reached strong AUC values (0.947), but with greater variability in sensitivity and precision. KNN severely overfit the training data (accuracy 99.6%) and underperformed in the test set (accuracy 83.3%), underscoring its limited applicability in high-dimensional descriptor spaces. SVM also lagged behind, with reduced ROC AUC (0.864), consistent with the challenges of capturing non-linear relationships without extensive kernel optimization (Table 1).

Table 1. Summary of hyperparameters and performance metrics for LIFE.PTML non-linear models.

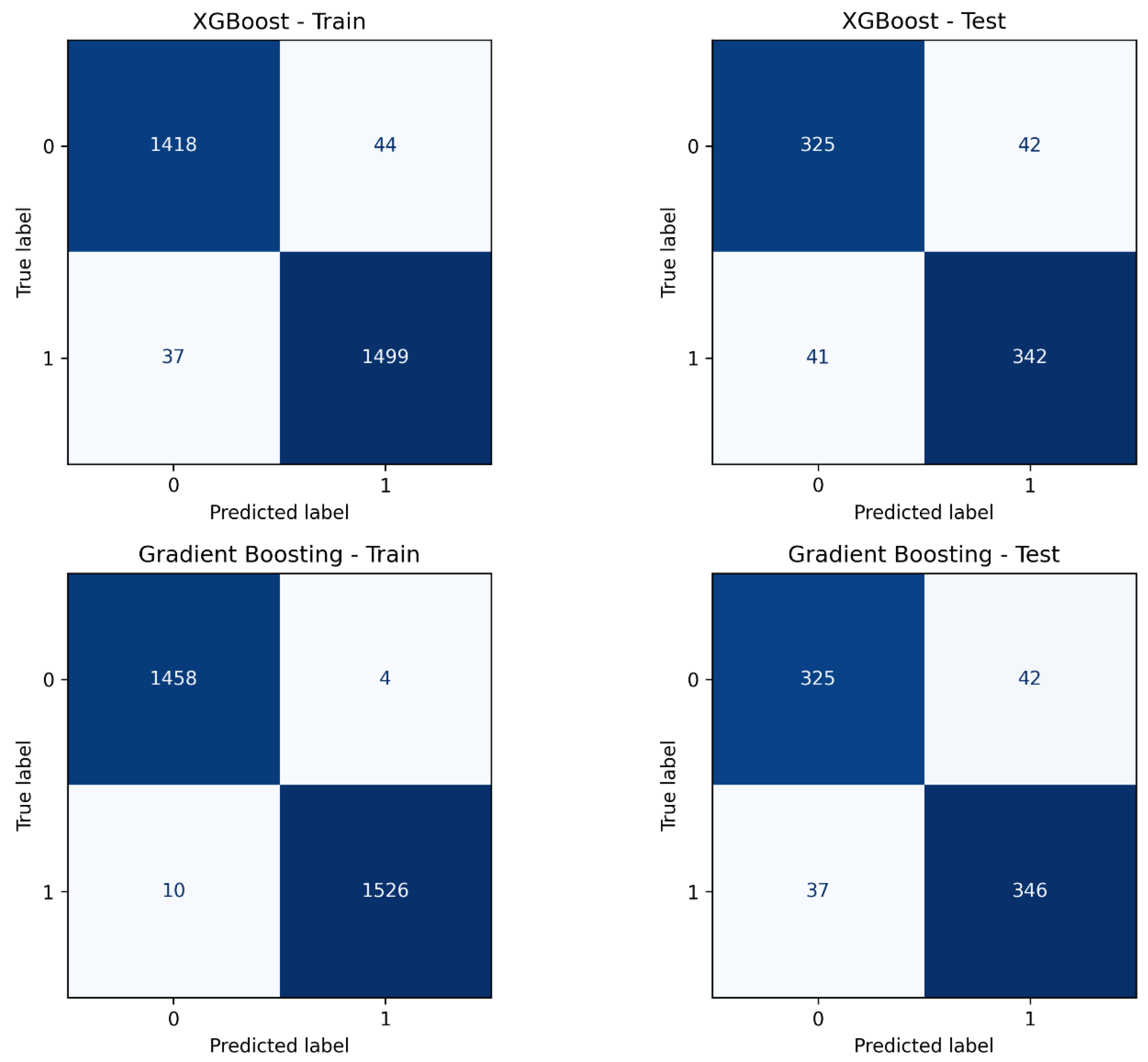
Model	Best Hyperparameters (Randomized/Grid Search)	Train Accuracy	Test Accuracy	Precision	Recall	F1-Score	ROC AUC
Random Forest	n_estimators = 610; max_depth = 26; criterion = entropy; max_features = sqrt; min_samples_split = 7; min_samples_leaf = 2	0.947	0.877	0.872	0.890	0.881	0.947
SVM (RBF)	C = 10; gamma = scale; kernel = rbf; degree = 3; probability = True	0.827	0.788	0.751	0.875	0.808	0.864
Decision Tree	criterion = entropy; max_depth = 32; min_samples_split = 7; min_samples_leaf = 5; max_features = sqrt	0.930	0.837	0.844	0.836	0.840	0.891
KNN	n_neighbors = 15; weights = distance; p = 2 (Euclidean)	0.996	0.833	0.827	0.851	0.839	0.912
Gradient Boosting	n_estimators = 310; learning_rate = 0.14; max_depth = 5; subsample = 0.75; max_features = sqrt	0.995	0.895	0.892	0.903	0.898	0.958
XGBoost	n_estimators = 160; learning_rate = 0.27; max_depth = 12; subsample = 1.0; colsample_bytree = 0.55; gamma = 1.7; reg_alpha = 0.3; reg_lambda = 1.5	0.973	0.889	0.891	0.893	0.892	0.959

Confusion matrices for XGBoost and Gradient Boosting (Figure 3) show high classification accuracy. XGBoost correctly classified 97.5% of training samples and 89.4% of test samples, while Gradient Boosting achieved 99.0% on training and 90.1% on test sets. Misclassifications remained low in both models, confirming robust generalization and reliable prediction of compound activity across assay conditions.

Figure 3. Confusion Matrices for Boosting-Based IFPTML Models.

The feature importance profile obtained from the XGBoost model (Figure 4) highlights the integration of both drug- and protein-derived descriptors within the LIFE.PTML framework. The most influential feature was the reference function f(v_ij)_ref, which represents the baseline activity probability under specific boundary conditions. This indicates that the perturbation-based normalization step provides a strong priority for classification. Among the experimental conditions, the inhibitor (ΔV(drug, assay)₂) and substrate concentrations (ΔV(drug, assay)₁) emerged as key contributors, underscoring the role of assay setup in determining compound performance. Several drug-level perturbation operators linked to global physicochemical properties, particularly electronegativity (ΔD(drug, dat)_1–2, ΔD(drug, dat)₀₁₃, ΔD(drug, dat)_053–054, ΔD(drug, dat)₁₀₁) and van der Waals terms (ΔV(drug, dat)₁), also ranked highly. This aligns with the chemical intuition that electronic distribution and steric interactions strongly influence ligand–protein binding within Ca²⁺-dependent pathways. Importantly, protein-derived features were also represented, notably the second-domain electronegativity (ΔD(prot, dom_II, dat)₁), reflecting the contribution of protein structural context to predictive power. Taken together, the feature ranking demonstrates that the LIFE.PTML methodology effectively captures multi-source information, balancing chemical, biological, and experimental descriptors to provide mechanistically plausible predictions.

Figure 4. Top 15 Feature Importances from XGBoost Model.

Taken together, these findings confirm that boosting-based classifiers, particularly XGBoost, represent the most reliable LIFE.PTML models in this study. While some overfitting is present, the balance between sensitivity, specificity, and ROC AUC supports their suitability for predictive applications in complex biological systems.

4. Conclusions

In this study, we developed and systematically applied the LIFE.PTML methodology, a combined framework of drug Lifecycle (L), Information Fusion (IF), Perturbation Theory (PT), and Machine Learning (ML), to handle complex, heterogeneous datasets arising from bioassays involving calmodulin (CaM) and related protein targets. The methodology provides a structured and reproducible pipeline for integrating chemical and protein descriptors, quantifying experimental variability, and predicting assay outcomes under diverse experimental conditions.

By combining these elements, the LIFE.PTML approach supports the development of non-linear predictive models capable of integrating multidimensional data while controlling for experimental variability. This framework has been designed to be flexible and generalizable, allowing the inclusion of diverse assay types, experimental conditions, and descriptor classes. Overall, the LIFE.PTML methodology represents a comprehensive and modular approach to predictive modeling in cheminformatics. It establishes a robust workflow that can be applied to future drug discovery efforts, offering a structured means to incorporate chemical, biological, and experimental variability into predictive ML frameworks.