Figure 1.
Experimental setup with 3D scanner—general view. (a) Without dark box; (b) with dark box.
Figure 1.
Experimental setup with 3D scanner—general view. (a) Without dark box; (b) with dark box.
Figure 2.
Steps of the algorithm for determining the HSVi index. (a) RGB image; (b) HSVi image; (c) Histogram of HSVi; (d) binary image.
Figure 2.
Steps of the algorithm for determining the HSVi index. (a) RGB image; (b) HSVi image; (c) Histogram of HSVi; (d) binary image.
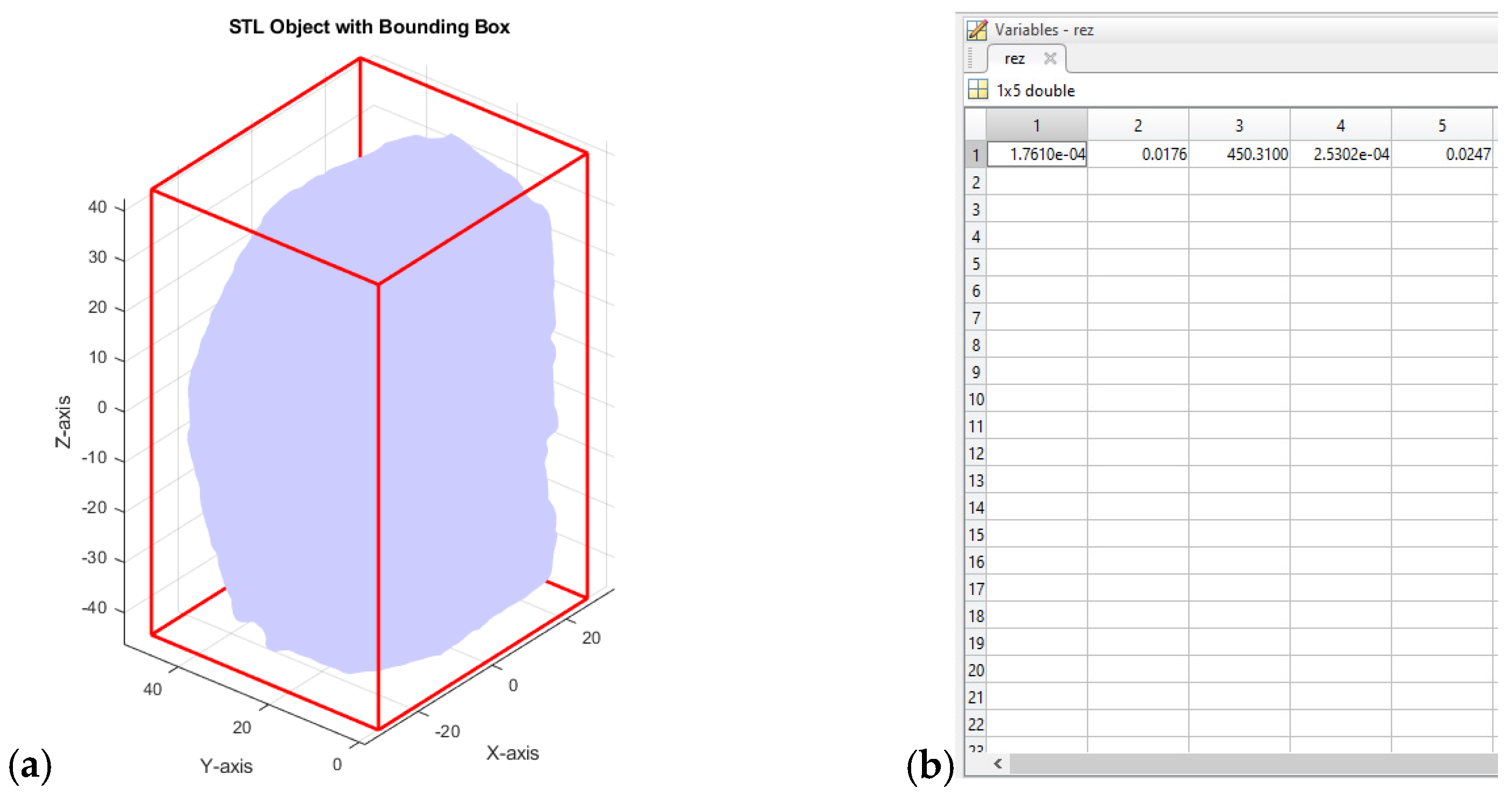
Figure 3.
Determining the main characteristics of bread from its three-dimensional image. (a) three-dimensional image of bread with a minimal parallelepiped; (b) calculated bread characteristics V, S, D, Vbb, Sbb.
Figure 3.
Determining the main characteristics of bread from its three-dimensional image. (a) three-dimensional image of bread with a minimal parallelepiped; (b) calculated bread characteristics V, S, D, Vbb, Sbb.
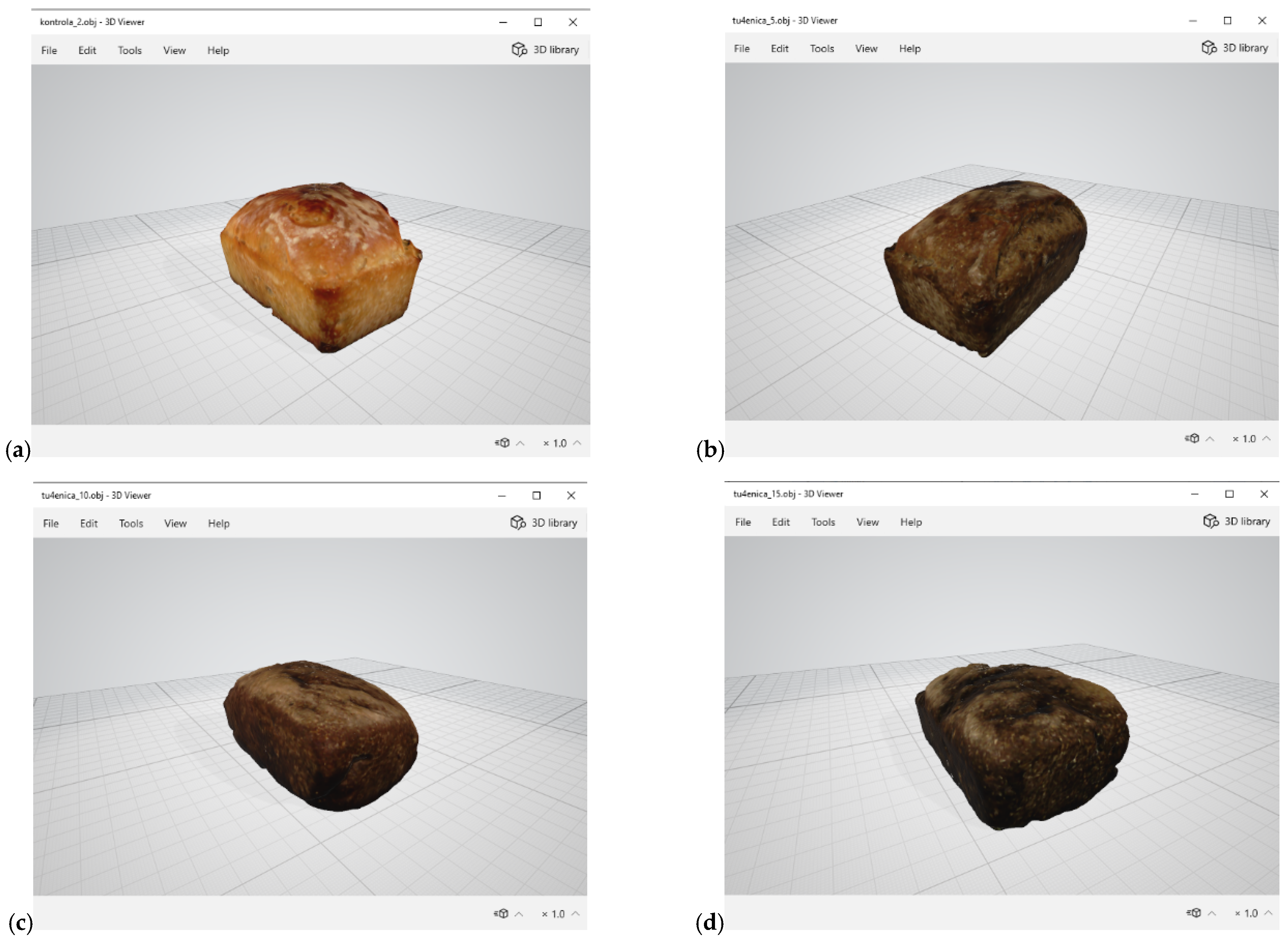
Figure 4.
3D-scanned images of pigweed bread (a) control sample; (b) 5%; (c) 10% (d) 15%.
Figure 4.
3D-scanned images of pigweed bread (a) control sample; (b) 5%; (c) 10% (d) 15%.
Figure 5.
3D-scanned images of purslane bread (a) control sample; (b) 5%; (c) 10% (d) 15%.
Figure 5.
3D-scanned images of purslane bread (a) control sample; (b) 5%; (c) 10% (d) 15%.
Figure 6.
Images of the top crust and crumb of wheat-pigweed bread (a) control sample; (b) 5% pigweed flour; (c) 10% pigweed flour; (d) 15% pigweed flour.
Figure 6.
Images of the top crust and crumb of wheat-pigweed bread (a) control sample; (b) 5% pigweed flour; (c) 10% pigweed flour; (d) 15% pigweed flour.
Figure 7.
Images of the top crust and crumb of wheat-purslane bread (a) control sample; (b) 5% purslane flour; (c) 10% purslane flour; (d) 15% purslane flour.
Figure 7.
Images of the top crust and crumb of wheat-purslane bread (a) control sample; (b) 5% purslane flour; (c) 10% purslane flour; (d) 15% purslane flour.
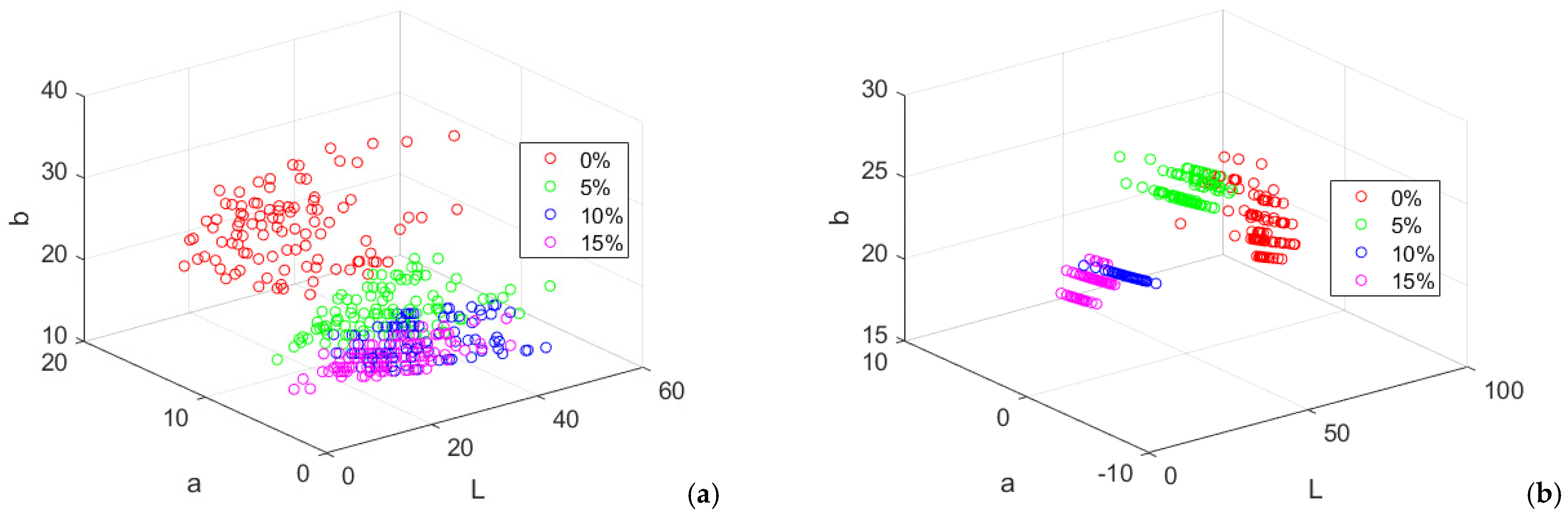
Figure 8.
Lab color components of wheat-pigweed bread. (a) crust; (b) crumb.
Figure 8.
Lab color components of wheat-pigweed bread. (a) crust; (b) crumb.
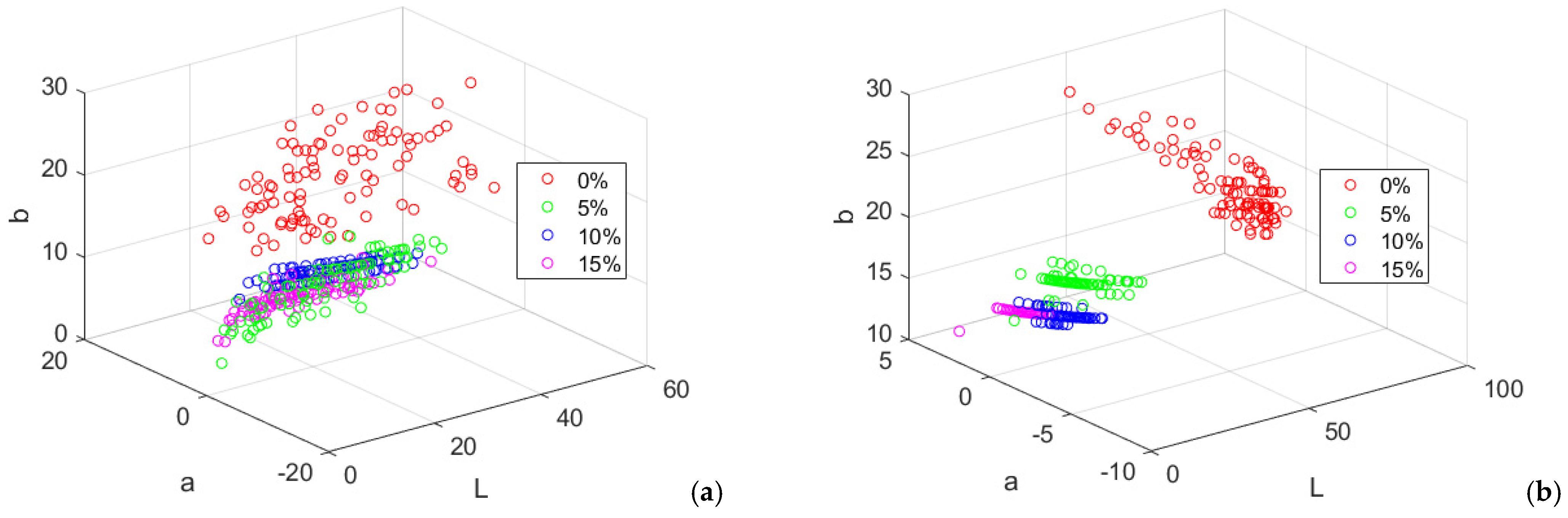
Figure 9.
Lab color components of wheat-purslane bread. (a) crust; (b) crumb.
Figure 9.
Lab color components of wheat-purslane bread. (a) crust; (b) crumb.
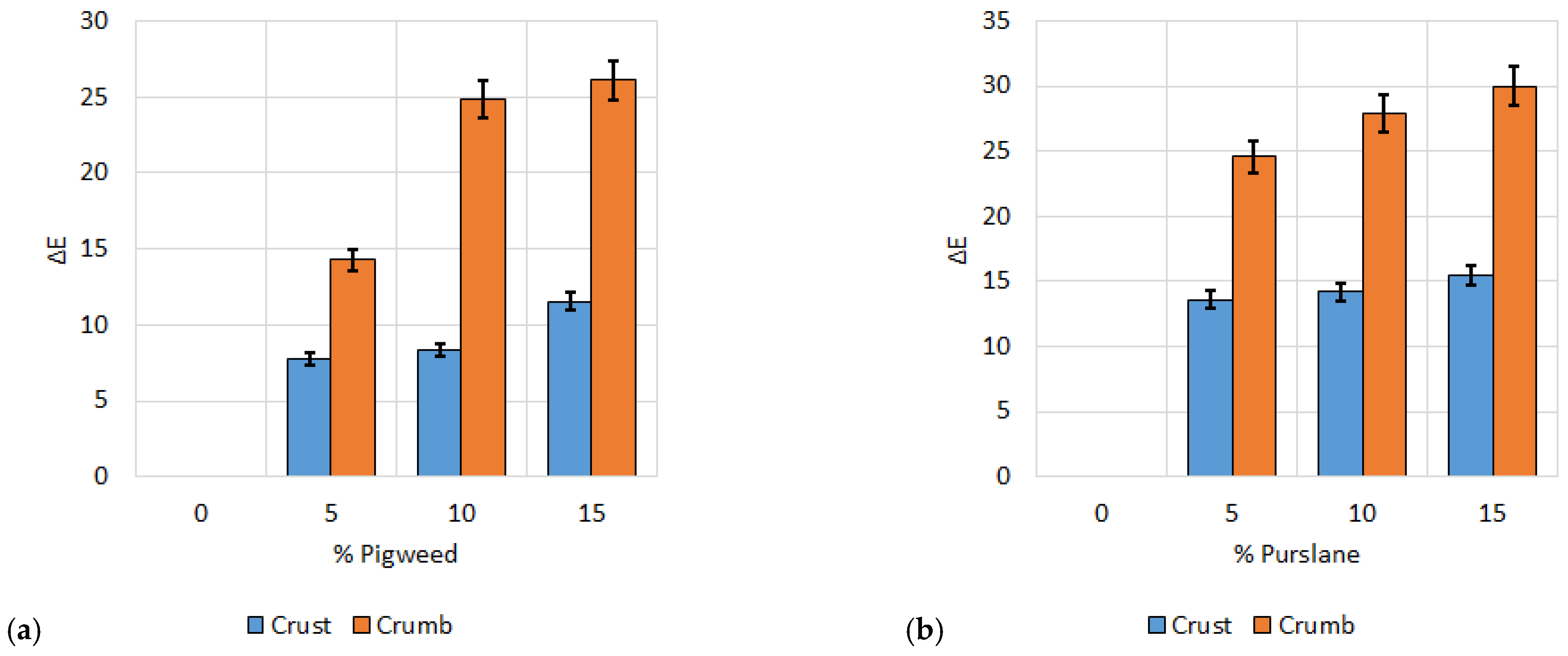
Figure 10.
Color difference for crust and middle of wheat bread with: (a) pigweed flour; (b) purslane flour. All data have statistically significant differences at p < 0.05.
Figure 10.
Color difference for crust and middle of wheat bread with: (a) pigweed flour; (b) purslane flour. All data have statistically significant differences at p < 0.05.
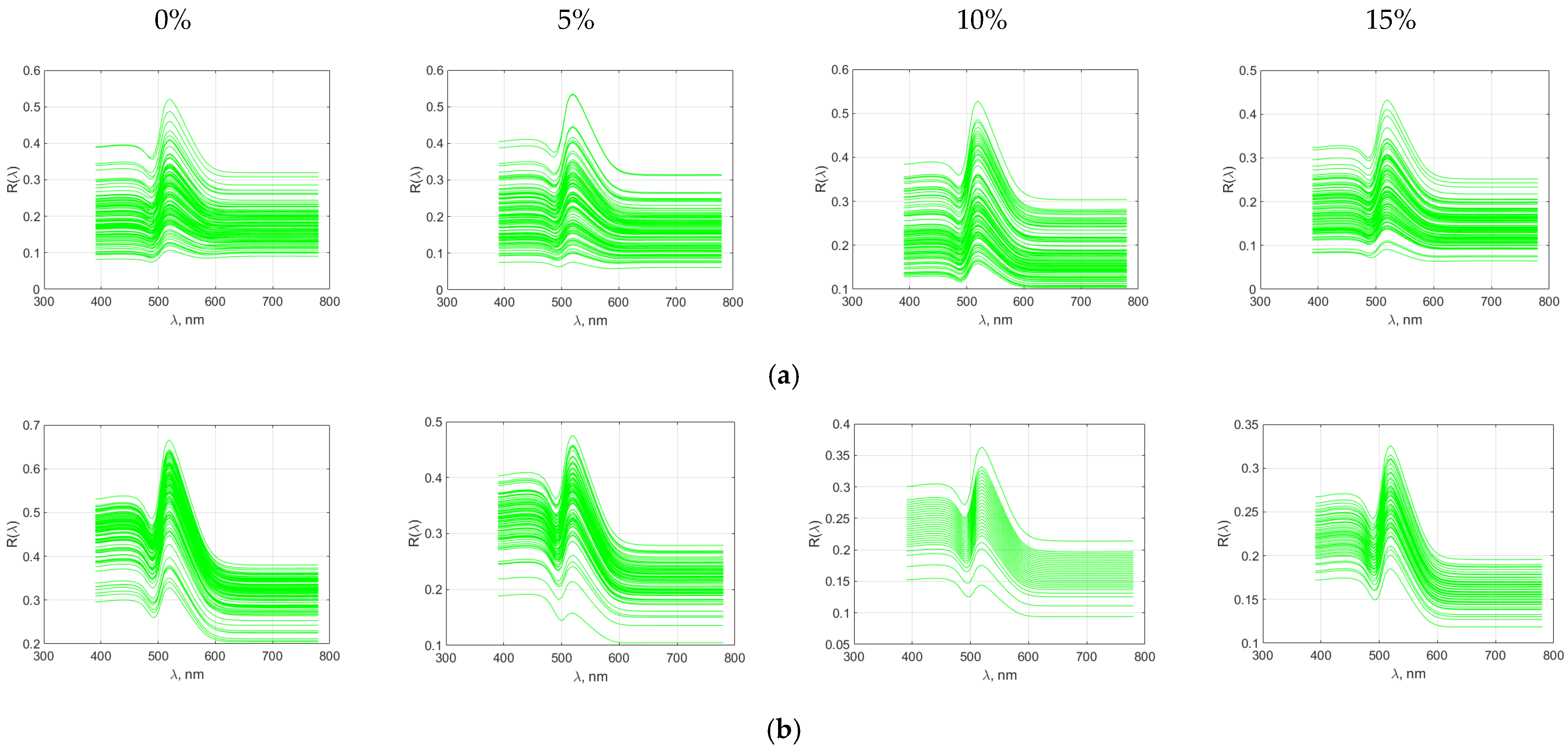
Figure 11.
Spectral characteristics of wheat bread with pigweed flour addition (a) crumb; (b) crust.
Figure 11.
Spectral characteristics of wheat bread with pigweed flour addition (a) crumb; (b) crust.
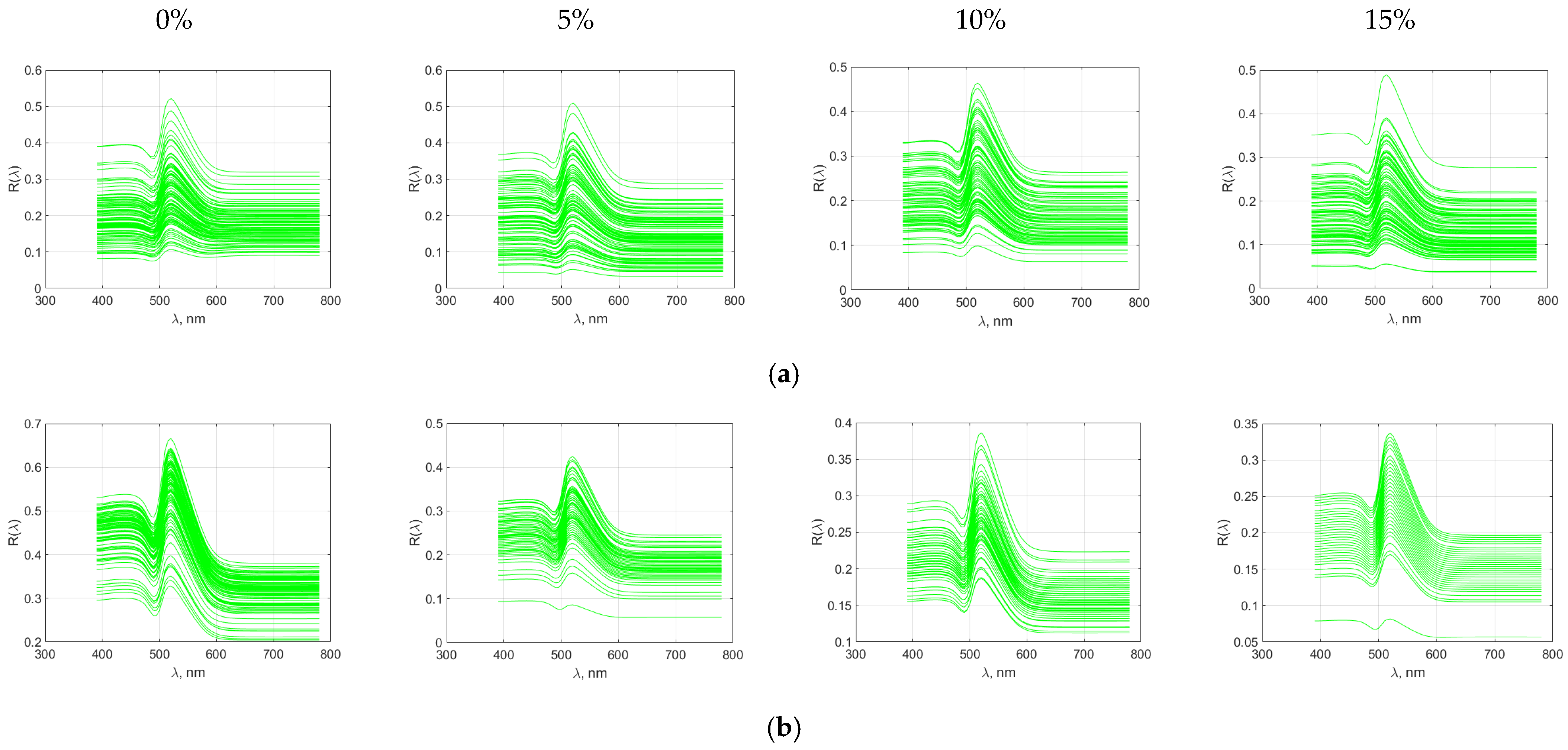
Figure 12.
Spectral characteristics of wheat bread with purslane flour addition (a) crumb; (b) crust.
Figure 12.
Spectral characteristics of wheat bread with purslane flour addition (a) crumb; (b) crust.
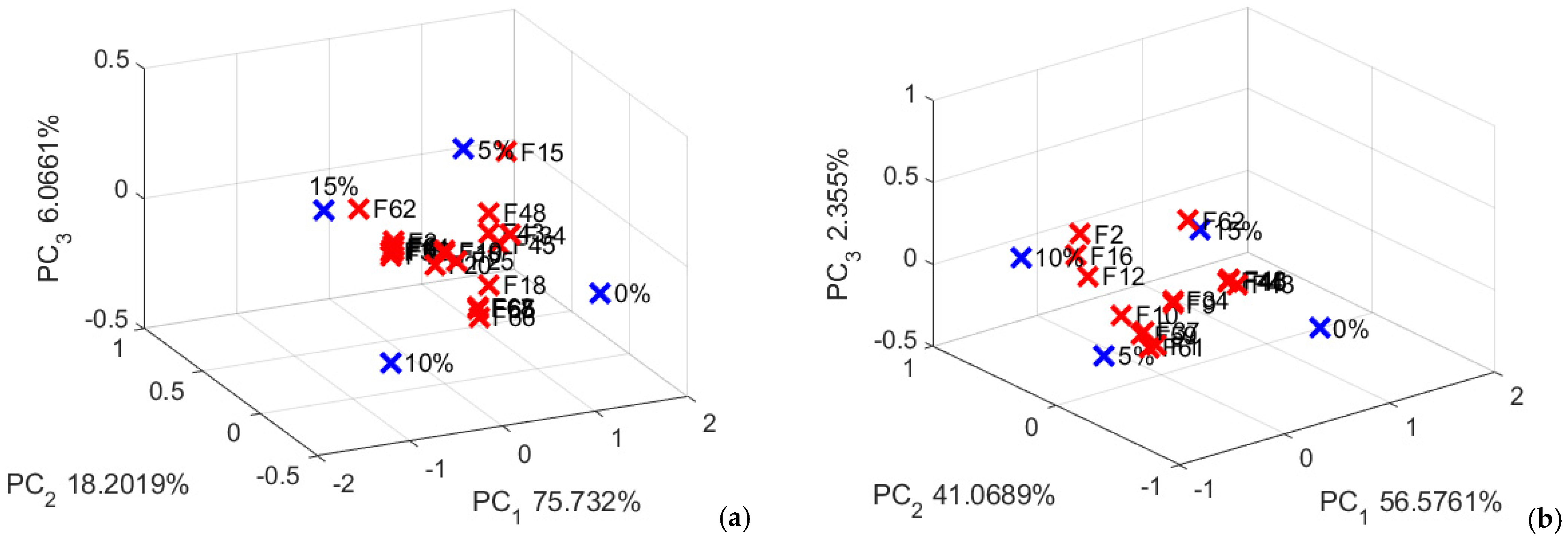
Figure 13.
Determining the effect of the alternative flour on the selected features. (a) pigweed bread; (b) purslane bread.
Figure 13.
Determining the effect of the alternative flour on the selected features. (a) pigweed bread; (b) purslane bread.
Figure 14.
Determining the required number of components to reduce the volume of data. (a) wheat-pigweed bread; (b) wheat-purslane bread.
Figure 14.
Determining the required number of components to reduce the volume of data. (a) wheat-pigweed bread; (b) wheat-purslane bread.
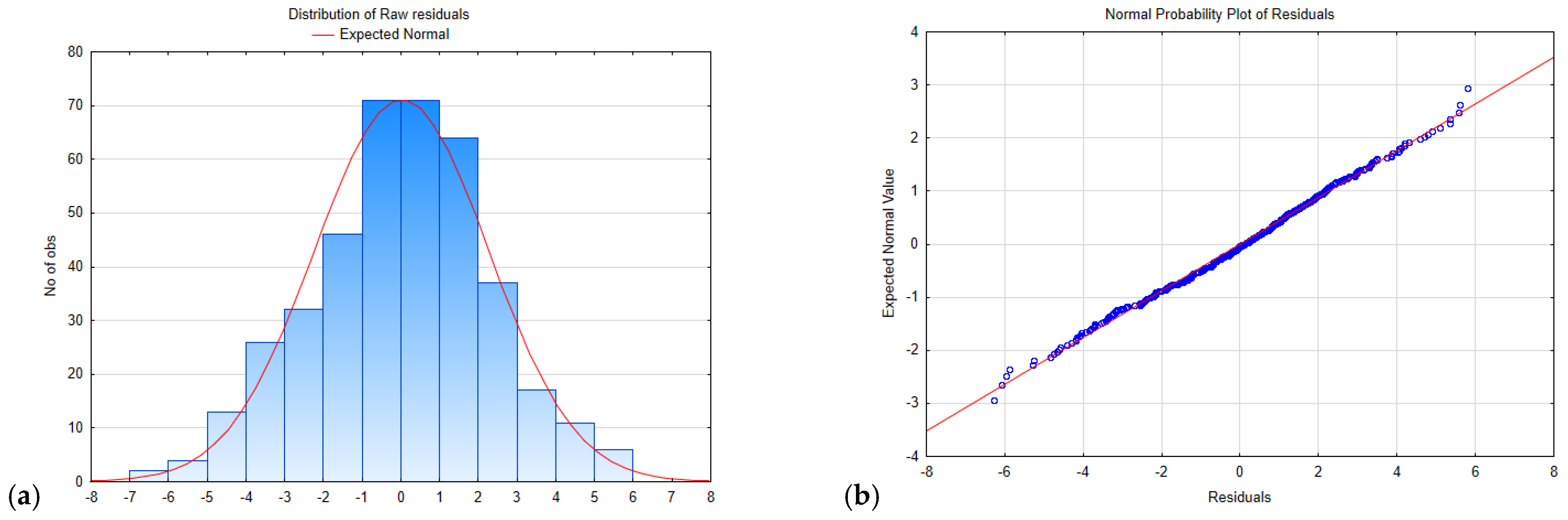
Figure 15.
Distribution and normal probability plot of the residuals for a model of the type S = f(LV1,LV2) for wheat-pigweed bread. (a) distribution of residuals; (b) normal probability plot of residuals.
Figure 15.
Distribution and normal probability plot of the residuals for a model of the type S = f(LV1,LV2) for wheat-pigweed bread. (a) distribution of residuals; (b) normal probability plot of residuals.
Figure 16.
Distribution and normal probability plot of the residuals for a model of the type T = f(LV1,LV2) for wheat bread with purslane flour. (a) distribution of residuals; (b) normal probability plot of residuals.
Figure 16.
Distribution and normal probability plot of the residuals for a model of the type T = f(LV1,LV2) for wheat bread with purslane flour. (a) distribution of residuals; (b) normal probability plot of residuals.
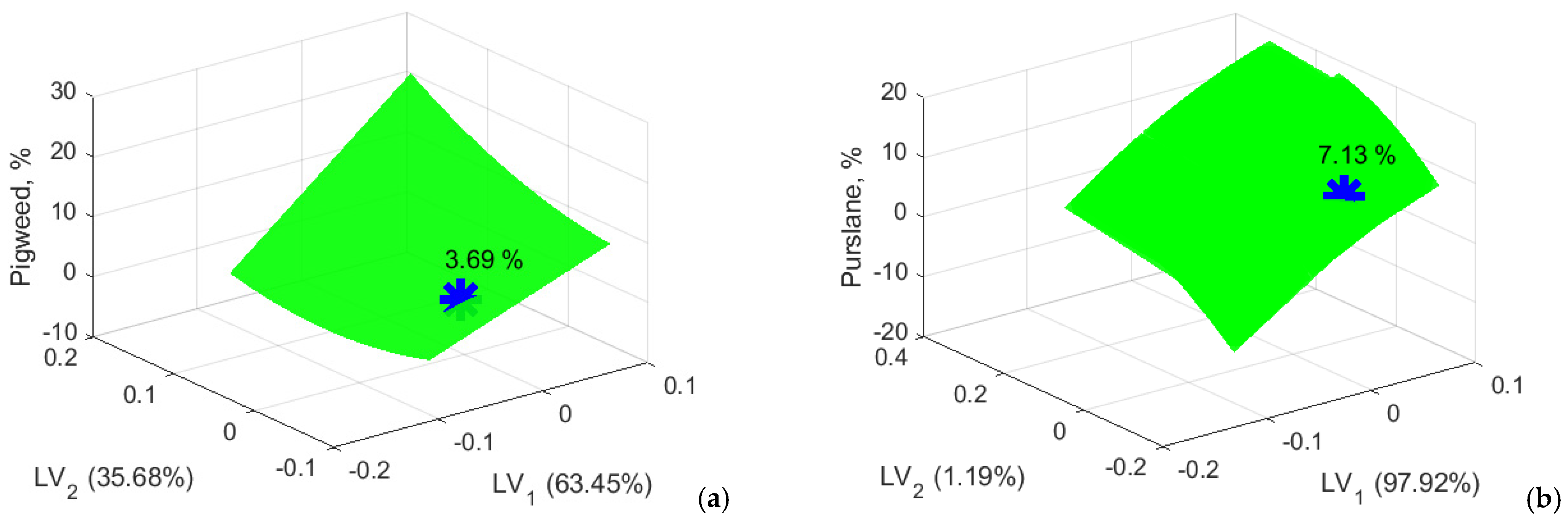
Figure 17.
Determining the appropriate amount of pigweed and purslane flour in wheat bread. (a) wheat-pigweed bread; (b) wheat-purslane bread.
Figure 17.
Determining the appropriate amount of pigweed and purslane flour in wheat bread. (a) wheat-pigweed bread; (b) wheat-purslane bread.
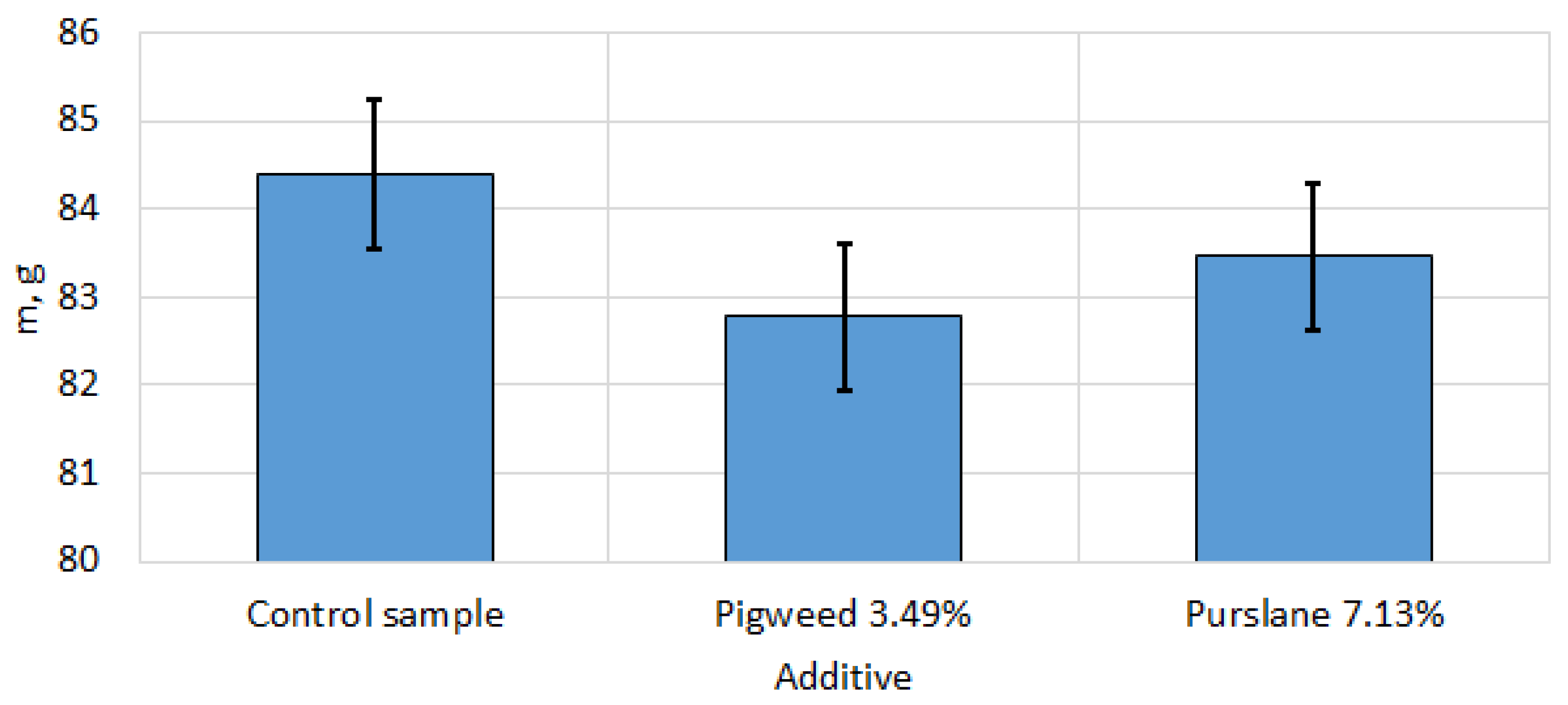
Figure 18.
Bread mass with appropriate amount of pigweed and purslane flour. All data have statistically significant differences at p < 0.05.
Figure 18.
Bread mass with appropriate amount of pigweed and purslane flour. All data have statistically significant differences at p < 0.05.
Figure 19.
Wheat bread with the appropriate amount of alternative flour. (a) Control sample; (b) 3.69% Pigweed flour; (c) 7.13% Purslane flour.
Figure 19.
Wheat bread with the appropriate amount of alternative flour. (a) Control sample; (b) 3.69% Pigweed flour; (c) 7.13% Purslane flour.
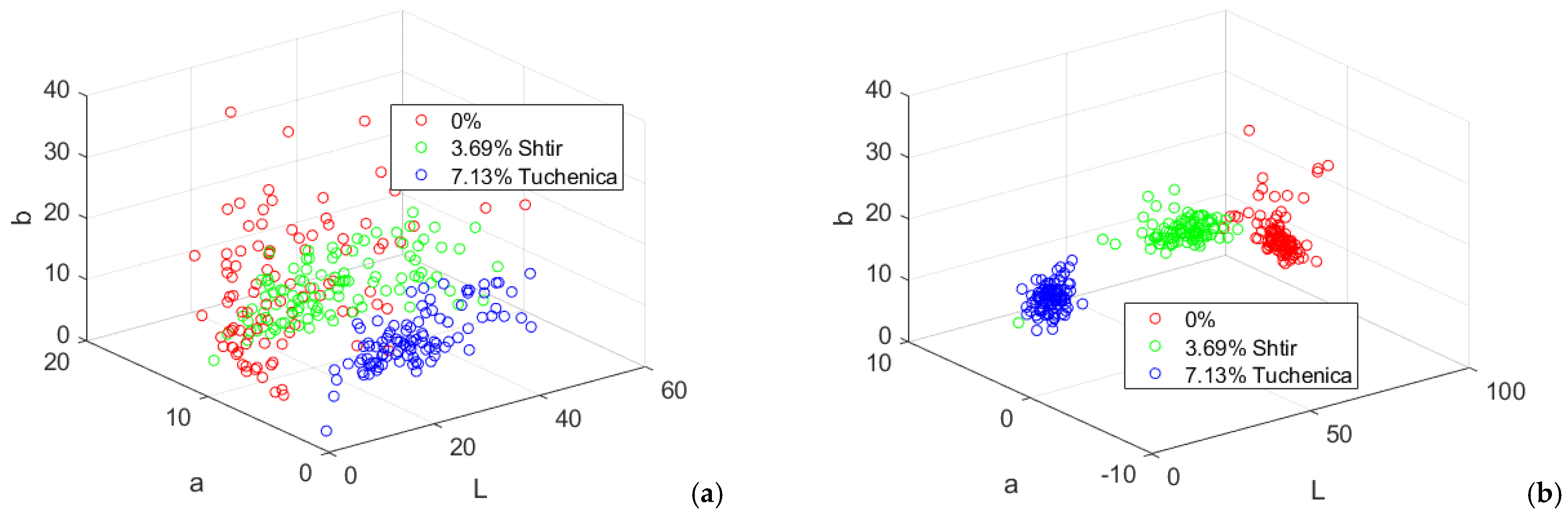
Figure 20.
Lab color characteristics of wheat bread samples with appropriate amounts of pigweed and purslane flour. (a) crust; (b) crumb.
Figure 20.
Lab color characteristics of wheat bread samples with appropriate amounts of pigweed and purslane flour. (a) crust; (b) crumb.
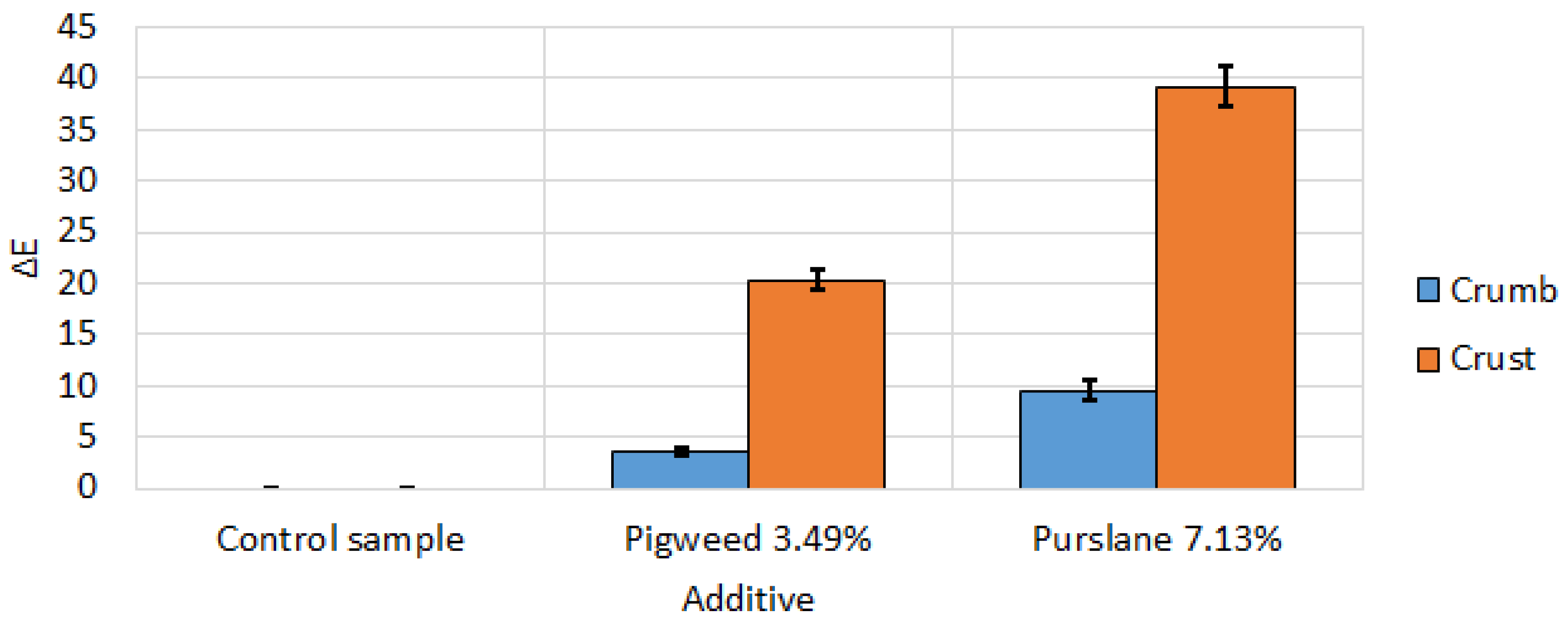
Figure 21.
Color difference between wheat bread samples with appropriate amounts of alternative flour. All data have statistically significant differences at p < 0.05.
Figure 21.
Color difference between wheat bread samples with appropriate amounts of alternative flour. All data have statistically significant differences at p < 0.05.
Figure 22.
Determination of wheat bread porosity with appropriate amounts of alternative flour. All data have statistically significant differences at p < 0.05.
Figure 22.
Determination of wheat bread porosity with appropriate amounts of alternative flour. All data have statistically significant differences at p < 0.05.
Figure 23.
Three-dimensional scanned images of wheat bread with appropriate amount of alternative flour. (a) Control sample; (b) 3.69% Pigweed flour; (c) 7.13% Purslane flour.
Figure 23.
Three-dimensional scanned images of wheat bread with appropriate amount of alternative flour. (a) Control sample; (b) 3.69% Pigweed flour; (c) 7.13% Purslane flour.
Figure 24.
Three-dimensional images of a loaf of wheat bread with a minimal parallelepiped circumscribed around it. (a) Control sample; (b) 3.69% Pigweed flour; (c) 7.13% Purslane flour.
Figure 24.
Three-dimensional images of a loaf of wheat bread with a minimal parallelepiped circumscribed around it. (a) Control sample; (b) 3.69% Pigweed flour; (c) 7.13% Purslane flour.
Table 1.
Nutritional value of type 500 flour (according to manufacturer’s data).
Table 1.
Nutritional value of type 500 flour (according to manufacturer’s data).
| Characteristic | Value | Characteristic | Value |
|---|
| Energy value, KJ/KCal | 1439/339 | Of which sugars, g | 2.1 |
| Fat, g | 0.9 | Fiber, g | 1.5 |
| Of which saturated fatty acids, g | 0.3 | Proteins, g | 11.8 |
| Carbohydrates, g | 70.2 | Salt, g | 0.02 |
Table 2.
Recipe composition of wheat bread samples with pigweed and purslane flour.
Table 2.
Recipe composition of wheat bread samples with pigweed and purslane flour.
| | Alternative Flour, % | 0 | 5 | 10 | 15 |
|---|
| Raw Material | |
|---|
| Wheat Flour, kg | 100 | 95 | 90 | 85 |
| Drinking water, L | 80 | 80 | 80 | 80 |
| Compressed (dry) Baker’s yeast, kg | 2 | 2 | 2 | 2 |
| Table salt, kg | 1.65 | 1.65 | 1.65 | 1.65 |
| Alternative flour, kg | 0 | 5 | 10 | 15 |
| Dough yield, kg | 184 | 184 | 184 | 184 |
Table 3.
Description of the technological process for wheat bread with the addition of pigweed or purslane flour.
Table 3.
Description of the technological process for wheat bread with the addition of pigweed or purslane flour.
| Stage | Time
t, min | Temperature
T, °C | Stage Name | Description |
|---|
| 1 | - | 20–22 | Preliminary preparation of raw materials | Sifting the flour, tempering the drinking water and pressed baker’s yeast |
| 2 | - | 20–22 | Manually dosing of raw materials | According to the working recipe |
| 3 | 10–15 | 18–20 | Preparation of bread dough using a single-phase dough kneading method | Mixing the wheat flour, the enrichment component, the solution of cooking salt and the suspension of water and dry baker’s yeast |
| 4 | 35–50 | 30–32 | Rising of the main dough | Fermentation of the prepared main dough at a certain technological regime—maturation temperature of the main dough (32 °C) for a certain time (35–50 min) |
| 5 | - | 20–25 | Dividing the main dough | The dough is manually divided into pieces of a certain mass |
| 6 | - | 20–25 | Shaping the dough piece | Dose 230 g for bread |
| 7 | - | 20–25 | Arranging in baking trays and molds | Dose 440 g for bread |
| 8 | 40–45 | 35 | Final fermentation | Final round shape for bread |
| 9 | 20–25 | 180 | Baking the dough pieces | Baguette shape for molded bread |
| 10 | 180 | 20–22 | Cooling | Pre-prepared baking trays for flat bread |
Table 4.
Table of Feature/Additive Combinations.
Table 4.
Table of Feature/Additive Combinations.
| | Feature (F) | F1 | F2 | … | Fm |
|---|
| Alternative Flour (A), % | |
|---|
| A0 | A0F1 | A0F2 | … | A0Fm |
| A1 | A1F1 | A1F2 | … | A1Fm |
| … | … | … | … | … |
| An | AnF1 | AnF2 | … | AnFm |
Table 5.
Physico-chemical characteristics of a basic raw material used as an additive in wheat bread.
Table 5.
Physico-chemical characteristics of a basic raw material used as an additive in wheat bread.
| | Raw Material |
|---|
| Characteristic | Pigweed Flour | Purslane Flour |
|---|
| pH | 5.4 ± 0.03 | 5.56 ± 0.08 |
| TDS, ppm | 2389.5 ± 15.5 | 2651.5 ± 43.5 |
| EC, µS/cm | 4788.5 ± 99.5 | 5354.5 ± 93.5 |
| ORP, mV | 191.5 ± 4.5 | 146.5 ± 12.5 |
Table 6.
Mass of bread with additions of pigweed and purslane.
Table 6.
Mass of bread with additions of pigweed and purslane.
| | Type of Wheat Bread | with Pigweed Flour
Mass, g | with Purslane Flour
Mass, g |
|---|
| Alternative Flour, % | |
|---|
| 0% | 79.03 ± 0.27 | 79.03 ± 0.27 |
| 5% | 85.47 ± 0.66 | 82.78 ± 0.4 |
| 10% | 83.34 ± 0.9 | 81.14 ± 0.37 |
| 15% | 87.83 ± 0.89 | 82.44 ± 0.14 |
Table 7.
Main physicochemical characteristics of wheat-pigweed bread.
Table 7.
Main physicochemical characteristics of wheat-pigweed bread.
| | Pigweed Flour, % | 0 | 5 | 10 | 15 |
|---|
| Characteristic | |
|---|
| pH | 6.15 ± 0.17 | 5.93 ± 0 | 5.84 ± 0.02 | 5.84 ± 0.01 |
| TDS, ppm | 1341.25 ± 67.75 | 1467 ± 11 | 1699 ± 16 | 1691.5 ± 3.5 |
| EC, µS/cm | 2712.5 ± 133 | 2953 ± 4 | 3430.5 ± 0.5 | 3439.5 ± 8.5 |
| ORP, mV | 261.75 ± 11.75 | 206.5 ± 7.5 | 183.5 ± 5.5 | 168.5 ± 4.5 |
Table 8.
Main physicochemical characteristics of wheat-purslane bread.
Table 8.
Main physicochemical characteristics of wheat-purslane bread.
| | Purslane Flour, % | 0 | 5 | 10 | 15 |
|---|
| Characteristic | |
|---|
| pH | 6.15 ± 0.17 | 6.12 ± 0 | 6.08 ± 0 | 6.01 ± 0.01 |
| TDS, ppm | 1341.25 ± 67.75 | 1627.5 ± 1.5 | 1621.5 ± 0.5 | 1800.5 ± 15.5 |
| EC, µS/cm | 2712.5 ± 133 | 3253.5 ± 0.5 | 3242.5 ± 0.5 | 3594 ± 23 |
| ORP, mV | 261.75 ± 11.75 | 227 ± 8 | 200.5 ± 7.5 | 174 ± 5 |
Table 9.
Results of organoleptic evaluation of wheat-pigweed bread.
Table 9.
Results of organoleptic evaluation of wheat-pigweed bread.
| | Sensory Attribute |
|---|
| Pigweed Flour, % | Appearance | Structure | Chewiness | Aroma | Taste | Overall
Assessment |
|---|
| 0% | 4.83 ± 0.24 | 4.97 ± 0.05 | 4.93 ± 0.09 | 4.93 ± 0.09 | 4.97 ± 0.05 | 4.93 ± 0.1 |
| 5% | 4.3 ± 0.22 | 4.33 ± 0.24 | 4.33 ± 0.24 | 4.5 ± 0.41 | 4.33 ± 0.47 | 4.36 ± 0.28 |
| 10% | 1.5 ± 0.41 | 1.73 ± 0.9 | 2.03 ± 1.39 | 2.33 ± 1.25 | 1.7 ± 0.92 | 1.86 ± 0.96 |
| 15% | 1 ± 0.45 | 1.33 ± 0.72 | 2 ± 1.52 | 2.33 ± 1.5 | 1 ± 0.45 | 1.53 ± 0.87 |
Table 10.
Results of organoleptic evaluation of purslane bread.
Table 10.
Results of organoleptic evaluation of purslane bread.
| | Sensory Attribute |
|---|
| Purslane Flour, % | Appearance | Structure | Chewiness | Aroma | Taste | Overall
Assessment |
|---|
| 0% | 4.83 ± 0.24 | 4.97 ± 0.05 | 4.93 ± 0.09 | 4.93 ± 0.09 | 4.97 ± 0.05 | 4.93 ± 0.1 |
| 5% | 4.23 ± 0.17 | 4.33 ± 0.24 | 4.37 ± 0.26 | 4.57 ± 0.42 | 4.3 ± 0.5 | 4.36 ± 0.28 |
| 10% | 2.5 ± 0.41 | 2.37 ± 0.45 | 2.5 ± 0.41 | 2.67 ± 0.47 | 2.33 ± 0.47 | 2.47 ± 0.41 |
| 15% | 1.37 ± 0.72 | 1.83 ± 1.1 | 1.53 ± 0.77 | 1.8 ± 1.1 | 1.1 ± 0.51 | 1.53 ± 0.81 |
Table 11.
Algorithm of a Matlab script for determining basic characteristics of bread from its three-dimensional (3D) image.
Table 11.
Algorithm of a Matlab script for determining basic characteristics of bread from its three-dimensional (3D) image.
| Stage | Name | Description |
|---|
| 1 | Input variables | STL file, mass of bread (m, kg) |
| 2 | Initializing the programming environment | Clear variables, command window, and figures using clc, clear all, and close all commands |
| 3 | Entering the mass value of the bread | Enter the mass of the loaf of bread (m), in kilograms (kg) |
| 4 | Loading the STL file | Load the STL file using the stlread function to obtain the faces and vertices of the 3D model |
| 5 | Calculating the volume | View each face of a triangle, calculate the signed volume of the tetrahedra formed by the origin, and sum the absolute values to calculate the total volume V |
| 6 | Calculating the surface area | Go through each face, calculate the area of each triangle using cross product and accumulation to calculate the total surface area of the 3D object S |
| 7 | Determining dimensions (dimensional profile) | Calculate the minimum and maximum coordinates along each axis, then calculate the length, width, and height of the bounding box in meters |
| 8 | Calculating the volume of the enclosing parallelepiped | Calculate the volume of the bounding box (Vbb) as Vbb = LWH |
| 9 | Calculating the surface area of the enclosing parallelepiped | Calculate the surface area of the bounding box (Sbb) as Sbb = 2(LW + LH + WH) |
| 10 | Calculating the density | Calculate the density (D) as m/V, where V is the calculated volume of the 3D object. |
| 11 | Visualizing the STL object | Draw the STL object with its minimal parallelepiped for visualization |
| 12 | Converting units of measurement | Convert the surface area S to square meters and the volume V to cubic meters |
| 13 | Storing results in an output variable | Combine the calculated values V, S, D, Vbb, Sbb into an output array |
| 14 | Measuring the execution time of the algorithm | Use the tic and toc commands to determine the script execution time |
| 15 | Output variables | V, S, D, Vbb, Sbb, time (t, s) for algorithm execution |
Table 12.
Main characteristics of wheat-pigweed bread, determined from its 3D images.
Table 12.
Main characteristics of wheat-pigweed bread, determined from its 3D images.
| | Characteristic | V, cm3 | S, cm2 | D, kg/m3 | Vbb, cm3 | Sbb, cm2 |
|---|
| Pigweed Flour, % | |
|---|
| 0% | 200 ± 2 | 180 ± 0.4 | 444.02 ± 6.29 | 300 ± 5 | 250 ± 2 |
| 5% | 200 ± 2 | 196 ± 0.4 | 430.08 ± 5.76 | 300 ± 7 | 260 ± 1 |
| 10% | 200 ± 0.2 | 190 ± 0.2 | 418.55 ± 4.87 | 300 ± 1 | 270 ± 1 |
| 15% | 200 ± 0 | 180 ± 0.6 | 482.37 ± 2.31 | 300 ± 6 | 250 ± 1 |
Table 13.
Main characteristics of wheat-purslane bread, determined from its 3D images.
Table 13.
Main characteristics of wheat-purslane bread, determined from its 3D images.
| | Characteristic | V, cm3 | S, cm2 | D, kg/m3 | Vbb, cm3 | Sbb, cm2 |
|---|
| Purslane, % | |
|---|
| 0% | 200 ± 2 | 180 ± 0.4 | 444.02 ± 6.29 | 300 ± 5 | 250 ± 2 |
| 5% | 200 ± 1 | 178 ± 0.4 | 461.67 ± 2.45 | 300 ± 7 | 260 ± 3 |
| 10% | 200 ± 1.4 | 160 ± 0.1 | 530.83 ± 5.7 | 200 ± 2 | 220 ± 2 |
| 15% | 100 ± 1 | 150 ± 0.4 | 625.82 ± 4.06 | 200 ± 4 | 210 ± 3 |
Table 14.
Color index values for wheat bread with the addition of pigweed flour.
Table 14.
Color index values for wheat bread with the addition of pigweed flour.
| BP | Crust | Crumb |
|---|
| | A, % | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% |
|---|
| CI | |
|---|
| L | 34.54 ± 10.42 | 26.93 ± 8.54 | 28.85 ± 7.79 | 23.41 ± 6.4 | 55.08 ± 5.33 | 40.98 ± 4.24 | 30.45 ± 2.97 | 28.97 ± 2.33 |
| a | 8.58 ± 2.95 | 6.98 ± 1.11 | 5.36 ± 1.09 | 5 ± 1.01 | 4.21 ± 1.76 | 2.59 ± 0.89 | 0.31 ± 0.14 | 2.3 ± 0.43 |
| b | 17.83 ± 3.74 | 17.97 ± 1.85 | 14.93 ± 1.55 | 14.18 ± 1.41 | 24.18 ± 1.73 | 26.41 ± 0.79 | 20.88 ± 0.29 | 19.68 ± 0.8 |
| C | 5.12 ± 0.49 | 4.99 ± 0.23 | 4.5 ± 0.24 | 4.38 ± 0.15 | 4.47 ± 0.38 | 4.88 ± 0.11 | 4.54 ± 0.05 | 4.69 ± 0.06 |
| h | 1.12 ± 0.16 | 1.2 ± 0.06 | 1.23 ± 0.06 | 1.23 ± 0.08 | 1.4 ± 0.08 | 1.47 ± 0.03 | 1.56 ± 0.01 | 1.45 ± 0.03 |
| ci1 | 78.57 ± 22.46 | 104.79 ± 32.71 | 78.81 ± 19.93 | 92.16 ± 23.12 | 63.66 ± 10.9 | 93.24 ± 12.34 | 99.09 ± 12.05 | 97.76 ± 9.67 |
| ci2 | 31.34 ± 9.64 | 24.36 ± 8.16 | 27.06 ± 7.59 | 21.92 ± 6.2 | 48.73 ± 5.09 | 35.26 ± 3.93 | 27.38 ± 2.93 | 26.25 ± 2.29 |
| ci3 | 29.53 ± 14.32 | 24.38 ± 8.89 | 29.28 ± 9.9 | 24.73 ± 8.52 | 769.91 ± 50.49 | 170.18 ± 81.85 | 59.53 ± 7.68 | 38.81 ± 4.38 |
| ci4 | 20.02 ± 3.63 | 19.31 ± 1.82 | 15.9 ± 1.61 | 15.09 ± 1.22 | 24.62 ± 1.57 | 26.55 ± 0.81 | 20.88 ± 0.28 | 19.82 ± 0.75 |
| ci5 | 4.85 ± 1.39 | 6.04 ± 1.74 | 5.64 ± 1.26 | 6.78 ± 1.61 | 3.07 ± 0.29 | 3.99 ± 0.41 | 5.22 ± 0.45 | 5.33 ± 0.37 |
| ci6 | 111.21 ± 6.12 | 118.94 ± 54.63 | 90.59 ± 34.26 | 110.34 ± 52.17 | 34.86 ± 15.21 | 25.99 ± 8.95 | 4.4 ± 1.81 | 34.37 ± 8.35 |
| ci7 | 0.5 ± 0.21 | 0.39 ± 0.07 | 0.36 ± 0.07 | 0.36 ± 0.09 | 0.18 ± 0.08 | 0.1 ± 0.03 | 0.01 ± 0.01 | 0.12 ± 0.03 |
| ci8 | 0.79 ± 0.35 | 0.69 ± 0.19 | 0.57 ± 0.15 | 0.6 ± 0.2 | 0.25 ± 0.11 | 0.16 ± 0.05 | 0.02 ± 0.01 | 0.2 ± 0.04 |
| ci9 | 16.76 ± 9.1 | 9.55 ± 7.45 | 13.92 ± 7.67 | 9.28 ± 5.79 | 30.9 ± 6.39 | 14.64 ± 4.2 | 9.61 ± 3.14 | 9.29 ± 2.58 |
| ci10 | 1.97 ± 0.58 | 1.5 ± 0.48 | 1.94 ± 0.55 | 1.65 ± 0.4 | 2.3 ± 0.32 | 1.55 ± 0.17 | 1.46 ± 0.16 | 1.48 ± 0.14 |
| ci11 | 275.96 ± 47.21 | 281.12 ± 121.44 | 195.6 ± 74.98 | 227.96 ± 104.88 | 77.15 ± 30.93 | 65.44 ± 21.62 | 10.41 ± 4.14 | 76.65 ± 18.37 |
Table 15.
Color index values for wheat bread with purslane flour addition.
Table 15.
Color index values for wheat bread with purslane flour addition.
| BP | Crust | Crumb |
|---|
| | A, % | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% |
|---|
| CI | |
|---|
| L | 34.54 ± 10.42 | 22.99 ± 9.61 | 24.97 ± 6.95 | 20.03 ± 7.47 | 55.08 ± 5.33 | 30.56 ± 4.66 | 27.23 ± 3.03 | 24.93 ± 3.66 |
| a | 8.58 ± 2.95 | 0.87 ± 0.75 | 2.18 ± 0.82 | 2.32 ± 1.03 | 4.21 ± 1.76 | 0.98 ± 0.34 | 0.49 ± 0.65 | 2.55 ± 0.19 |
| b | 17.83 ± 3.74 | 9.24 ± 2.05 | 9.98 ± 0.8 | 7.95 ± 1.24 | 24.18 ± 1.73 | 15.19 ± 0.65 | 12.78 ± 0.36 | 11.93 ± 0.29 |
| C | 5.12 ± 0.49 | 3.14 ± 0.33 | 3.48 ± 0.15 | 3.2 ± 0.18 | 4.47 ± 0.38 | 3.98 ± 0.11 | 3.64 ± 0.09 | 3.81 ± 0.05 |
| h | 1.12 ± 0.16 | 1.47 ± 0.1 | 1.35 ± 0.08 | 1.28 ± 0.15 | 1.4 ± 0.08 | 1.51 ± 0.02 | 1.53 ± 0.05 | 1.36 ± 0.01 |
| ci1 | 78.57 ± 22.46 | 66.64 ± 25.85 | 62.22 ± 19.99 | 64.77 ± 25.2 | 63.66 ± 10.9 | 73.19 ± 15.6 | 67.95 ± 8.87 | 70.47 ± 14.96 |
| ci2 | 31.34 ± 9.64 | 22.38 ± 9.4 | 24.27 ± 6.93 | 19.58 ± 7.41 | 48.73 ± 5.09 | 28.9 ± 4.58 | 26.12 ± 3.02 | 23.95 ± 3.66 |
| ci3 | 29.53 ± 14.32 | 38.36 ± 18.99 | 34.04 ± 11.4 | 27.16 ± 12.38 | 769.91 ± 550.49 | 51.84 ± 14.63 | 46.15 ± 7.42 | 32.04 ± 5.19 |
| ci4 | 20.02 ± 3.63 | 9.32 ± 2.02 | 10.25 ± 0.78 | 8.37 ± 1.07 | 24.62 ± 1.57 | 15.22 ± 0.66 | 12.8 ± 0.36 | 12.2 ± 0.3 |
| ci5 | 4.85 ± 1.39 | 8.24 ± 4.28 | 6.67 ± 1.71 | 8.63 ± 3.32 | 3.07 ± 0.29 | 5.3 ± 0.95 | 5.85 ± 0.57 | 6.34 ± 1.05 |
| ci6 | 111.21 ± 60.12 | 38.56 ± 52.88 | 56.78 ± 32.66 | 91.28 ± 67.22 | 34.86 ± 15.21 | 16.47 ± 6.6 | 10.15 ± 13.41 | 55.98 ± 18.5 |
| ci7 | 0.5 ± 0.21 | 0.1 ± 0.1 | 0.22 ± 0.08 | 0.31 ± 0.17 | 0.18 ± 0.08 | 0.06 ± 0.02 | 0.04 ± 0.05 | 0.21 ± 0.02 |
| ci8 | 0.79 ± 0.35 | 0.16 ± 0.17 | 0.32 ± 0.14 | 0.46 ± 0.26 | 0.25 ± 0.11 | 0.1 ± 0.03 | 0.06 ± 0.08 | 0.32 ± 0.05 |
| ci9 | 16.76 ± 9.1 | 13.75 ± 8.46 | 15 ± 7.22 | 12.08 ± 7.18 | 30.9 ± 6.39 | 15.42 ± 4.63 | 14.46 ± 3.2 | 13.03 ± 3.76 |
| ci10 | 1.97 ± 0.58 | 2.45 ± 0.87 | 2.54 ± 0.82 | 2.53 ± 0.91 | 2.3 ± 0.32 | 2.02 ± 0.33 | 2.14 ± 0.27 | 2.1 ± 0.34 |
| ci11 | 275.96 ± 147.21 | 53.04 ± 66.55 | 94.21 ± 55.24 | 134.3 ± 92.83 | 77.15 ± 30.93 | 31.65 ± 12.92 | 17.98 ± 24.16 | 100.79 ± 31.77 |
Table 16.
Results of determining porosity (%) of wheat bread with alternative flour.
Table 16.
Results of determining porosity (%) of wheat bread with alternative flour.
| | Type of the Wheat Bread | Pigweed Flour, % | Purslane Flour, % |
|---|
| Alternative Flour, % | |
|---|
| 0% | 79.06 ± 2.04 | 79.06 ± 2.04 |
| 5% | 81.92 ± 1.8 | 83.2 ± 1.37 |
| 10% | 77.27 ± 1.2 | 77.54 ± 1.25 |
| 15% | 73.16 ± 1.01 | 77.37 ± 3.76 |
Table 17.
Spectral index values for wheat bread with the addition of pigweed flour.
Table 17.
Spectral index values for wheat bread with the addition of pigweed flour.
| BP | Crumb | Crust |
|---|
| | A, % | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% |
|---|
| SI | |
|---|
| si1 | 0.93 ± 0 | 0.93 ± 0.01 | 0.93 ± 0 | 0.93 ± 0 | 0.92 ± 0 | 0.93 ± 0 | 0.93 ± 0 | 0.93 ± 0 |
| si2 | 0.03 ± 0 | 0.03 ± 0 | 0.03 ± 0 | 0.03 ± 0 | 0.03 ± 0 | 0.04 ± 0 | 0.04 ± 0 | 0.03 ± 0 |
| si3 | 0.12 ± 0.05 | 0.16 ± 0.06 | 0.13 ± 0.04 | 0.16 ± 0.05 | 0.06 ± 0.01 | 0.09 ± 0.01 | 0.12 ± 0.02 | 0.13 ± 0.01 |
| si4 | 7.98 ± 2.85 | 5.35 ± 2.52 | 6.59 ± 2.33 | 5.05 ± 1.73 | 11.54 ± 1.65 | 6.4 ± 1.41 | 4.88 ± 0.98 | 5.02 ± 0.77 |
| si5 | 0.79 ± 0.03 | 0.85 ± 0.05 | 0.81 ± 0.02 | 0.83 ± 0.03 | 0.87 ± 0.02 | 0.95 ± 0.05 | 0.93 ± 0.03 | 0.9 ± 0.02 |
| si6 | 0.05 ± 0.01 | 0.03 ± 0.01 | 0.04 ± 0.01 | 0.04 ± 0.01 | 0.02 ± 0.01 | 0.01 ± 0.01 | 0.01 ± 0.01 | 0.01 ± 0.01 |
| si7 | 0.07 ± 0.02 | 0.04 ± 0.02 | 0.06 ± 0.01 | 0.05 ± 0.01 | 0.03 ± 0.01 | 0.01 ± 0.02 | 0.01 ± 0.01 | 0.02 ± 0.01 |
| si8 | 0.07 ± 0.02 | 0.04 ± 0.02 | 0.06 ± 0.01 | 0.05 ± 0.01 | 0.03 ± 0.01 | 0.01 ± 0.02 | 0.01 ± 0.01 | 0.02 ± 0.01 |
| si9 | 0.07 ± 0.02 | 0.04 ± 0.02 | 0.06 ± 0.01 | 0.05 ± 0.01 | 0.03 ± 0.01 | 0.01 ± 0.02 | 0.01 ± 0.01 | 0.02 ± 0.01 |
| si10 | 0.13 ± 0.03 | 0.08 ± 0.04 | 0.12 ± 0.02 | 0.1 ± 0.03 | 0.06 ± 0.02 | 0.03 ± 0.04 | 0.02 ± 0.02 | 0.04 ± 0.02 |
| si11 | 0.04 ± 0.02 | 0.02 ± 0.02 | 0.03 ± 0.01 | 0.02 ± 0.01 | 0.03 ± 0.01 | 0.01 ± 0.01 | 0.01 ± 0 | 0.01 ± 0.01 |
Table 18.
Spectral indices values for bread with purslane flour addition.
Table 18.
Spectral indices values for bread with purslane flour addition.
| BP | Crumb | Crust |
|---|
| | A, % | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% |
|---|
| SI | |
|---|
| si1 | 0.93 ± 0 | 0.92 ± 0 | 0.92 ± 0 | 0.93 ± 0 | 0.92 ± 0 | 0.93 ± 0 | 0.93 ± 0 | 0.93 ± 0 |
| si2 | 0.03 ± 0 | 0.03 ± 0 | 0.03 ± 0 | 0.03 ± 0 | 0.03 ± 0 | 0.04 ± 0 | 0.04 ± 0 | 0.03 ± 0 |
| si3 | 0.12 ± 0.05 | 0.17 ± 0.1 | 0.14 ± 0.05 | 0.19 ± 0.08 | 0.06 ± 0.01 | 0.09 ± 0.01 | 0.12 ± 0.02 | 0.13 ± 0.01 |
| si4 | 7.98 ± 2.85 | 5.73 ± 2.63 | 6.3 ± 2.17 | 5.29 ± 2.17 | 11.54 ± 1.65 | 6.4 ± 1.41 | 4.88 ± 0.98 | 5.02 ± 0.77 |
| si5 | 0.79 ± 0.03 | 0.81 ± 0.03 | 0.8 ± 0.03 | 0.79 ± 0.04 | 0.87 ± 0.02 | 0.95 ± 0.05 | 0.93 ± 0.03 | 0.9 ± 0.02 |
| si6 | 0.05 ± 0.01 | 0.04 ± 0.01 | 0.05 ± 0.01 | 0.05 ± 0.01 | 0.02 ± 0.01 | 0.01 ± 0.01 | 0.01 ± 0.01 | 0.01 ± 0.01 |
| si7 | 0.07 ± 0.02 | 0.06 ± 0.02 | 0.07 ± 0.01 | 0.08 ± 0.02 | 0.03 ± 0.01 | 0.01 ± 0.02 | 0.01 ± 0.01 | 0.02 ± 0.01 |
| si8 | 0.07 ± 0.02 | 0.06 ± 0.02 | 0.07 ± 0.01 | 0.08 ± 0.02 | 0.03 ± 0.01 | 0.01 ± 0.02 | 0.01 ± 0.01 | 0.02 ± 0.01 |
| si9 | 0.07 ± 0.02 | 0.06 ± 0.02 | 0.07 ± 0.01 | 0.08 ± 0.02 | 0.03 ± 0.01 | 0.01 ± 0.02 | 0.01 ± 0.01 | 0.02 ± 0.01 |
| si10 | 0.13 ± 0.03 | 0.12 ± 0.04 | 0.13 ± 0.03 | 0.14 ± 0.03 | 0.06 ± 0.02 | 0.03 ± 0.04 | 0.02 ± 0.02 | 0.04 ± 0.02 |
| si11 | 0.04 ± 0.02 | 0.03 ± 0.02 | 0.03 ± 0.01 | 0.03 ± 0.01 | 0.03 ± 0.01 | 0.01 ± 0.01 | 0.01 ± 0 | 0.01 ± 0.01 |
Table 19.
Features of wheat bread with alternative flour and their meaning.
Table 19.
Features of wheat bread with alternative flour and their meaning.
| Feature | Meaning | Feature | Meaning | Feature | Meaning | Feature | Meaning | Feature | Meaning |
|---|
| F1 | m, kg | F15 | Taste | F29 | ci13 | F43 | ci11 | F57 | SI9 |
| F2 | V, m3 | F16 | Overall assessment | F30 | ci14 | F44 | ci12 | F58 | SI10 |
| F3 | S, m2 | F17 | ci1 | F31 | ci15 | F45 | ci13 | F59 | SI11 |
| F4 | D, kg/m3 | F18 | ci2 | F32 | ci16 | F46 | ci14 | F60 | SI1 |
| F5 | Vbb, m3 | F19 | ci3 | F33 | ci1 | F47 | ci15 | F61 | SI2 |
| F6 | Sbb, m2 | F20 | ci4 | F34 | ci2 | F48 | ci16 | F62 | SI3 |
| F7 | pH | F21 | ci5 | F35 | ci3 | F49 | SI1 | F63 | SI4 |
| F8 | TDS, ppm | F22 | ci6 | F36 | ci4 | F50 | SI2 | F64 | SI5 |
| F9 | EC, µS/cm | F23 | ci7 | F37 | ci5 | F51 | SI3 | F65 | SI6 |
| F10 | ORP, mV | F24 | ci8 | F38 | ci6 | F52 | SI4 | F66 | SI7 |
| F11 | Appearance | F25 | ci9 | F39 | ci7 | F53 | SI5 | F67 | SI8 |
| F12 | Structure | F26 | ci10 | F40 | ci8 | F54 | SI6 | F68 | SI9 |
| F13 | Chewiness | F27 | ci11 | F41 | ci9 | F55 | SI7 | F69 | SI10 |
| F14 | Aroma | F28 | ci12 | F42 | ci10 | F56 | SI8 | F70 | SI11 |
Table 20.
Results of selection of informative features.
Table 20.
Results of selection of informative features.
| Pigweed Bread | Purslane Bread |
|---|
| F1 | 0.61 | F29 | 0.03 | F57 | 0.03 | F1 | 0.63 | F29 | 0.07 | F57 | 0.05 |
| F2 | 0.02 | F30 | 0.00 | F58 | 0.03 | F2 | 1.00 | F30 | 0.06 | F58 | 0.05 |
| F3 | 1.00 | F31 | 0.03 | F59 | 0.00 | F3 | 0.00 | F31 | 0.08 | F59 | 0.61 |
| F4 | 0.07 | F32 | 0.01 | F60 | 0.06 | F4 | 0.63 | F32 | 0.06 | F60 | 0.01 |
| F5 | 0.06 | F33 | 0.12 | F61 | 0.61 | F5 | 0.02 | F33 | 0.02 | F61 | 0.60 |
| F6 | 0.61 | F34 | 0.61 | F62 | 0.61 | F6 | 0.06 | F34 | 0.62 | F62 | 0.60 |
| F7 | 0.05 | F35 | 0.13 | F63 | 0.10 | F7 | 0.06 | F35 | 0.03 | F63 | 0.00 |
| F8 | 0.05 | F36 | 0.62 | F64 | 0.61 | F8 | 0.07 | F36 | 0.04 | F64 | 0.01 |
| F9 | 0.05 | F37 | 0.61 | F65 | 0.62 | F9 | 0.63 | F37 | 0.63 | F65 | 0.01 |
| F10 | 0.63 | F38 | 0.11 | F66 | 0.62 | F10 | 0.63 | F38 | 0.03 | F66 | 0.01 |
| F11 | 0.10 | F39 | 0.11 | F67 | 0.62 | F11 | 0.21 | F39 | 0.02 | F67 | 0.01 |
| F12 | 0.09 | F40 | 0.01 | F68 | 0.62 | F12 | 0.62 | F40 | 0.06 | F68 | 0.01 |
| F13 | 0.01 | F41 | 0.12 | F69 | 0.17 | F13 | 0.17 | F41 | 0.02 | F69 | 0.01 |
| F14 | 0.08 | F42 | 0.14 | F70 | 0.16 | F14 | 0.17 | F42 | 0.03 | F70 | 0.03 |
| F15 | 0.61 | F43 | 0.64 | - | - | F15 | 0.14 | F43 | 0.61 | - | - |
| F16 | 0.10 | F44 | 0.13 | - | - | F16 | 0.64 | F44 | 0.63 | - | - |
| F17 | 0.09 | F45 | 0.62 | - | - | F17 | 0.03 | F45 | 0.62 | - | - |
| F18 | 0.62 | F46 | 0.11 | - | - | F18 | 0.06 | F46 | 0.00 | - | - |
| F19 | 0.62 | F47 | 0.07 | - | - | F19 | 0.01 | F47 | 0.03 | - | - |
| F20 | 0.62 | F48 | 0.63 | - | - | F20 | 0.01 | F48 | 0.61 | - | - |
| F21 | 0.05 | F49 | 0.00 | - | - | F21 | 0.08 | F49 | 0.05 | - | - |
| F22 | 0.03 | F50 | 0.03 | - | - | F22 | 0.08 | F50 | 0.04 | - | - |
| F23 | 0.03 | F51 | 0.01 | - | - | F23 | 0.03 | F51 | 0.02 | - | - |
| F24 | 0.01 | F52 | 0.03 | - | - | F24 | 0.06 | F52 | 0.05 | - | - |
| F25 | 0.63 | F53 | 0.02 | - | - | F25 | 0.01 | F53 | 0.04 | - | - |
| F26 | 0.03 | F54 | 0.03 | - | - | F26 | 0.01 | F54 | 0.05 | - | - |
| F27 | 0.01 | F55 | 0.03 | - | - | F27 | 0.05 | F55 | 0.05 | - | - |
| F28 | 0.03 | F56 | 0.03 | - | - | F28 | 0.07 | F56 | 0.05 | - | - |
Table 21.
Normalized values of the characteristics of wheat bread with the addition of pigweed and purslane flour.
Table 21.
Normalized values of the characteristics of wheat bread with the addition of pigweed and purslane flour.
| Type of Bread | Pigweed Bread | Purslane Bread |
|---|
| | Alternative Flour, % | 0% | 5% | 10% | 15% | | Alternative Flour, % | 0% | 5% | 10% | 15% |
|---|
| Feature | | Feature | |
|---|
| F1 | 0.00 | 0.07 | 0.04 | 0.10 | F1 | 0.00 | 0.04 | 0.02 | 0.04 |
| F3 | 0.00 | 0.10 | 0.07 | 0.01 | F2 | 0.50 | 0.50 | 0.50 | 0.00 |
| F6 | 0.00 | 0.08 | 0.07 | 0.00 | F9 | 0.00 | 0.16 | 0.15 | 0.25 |
| F10 | 0.36 | 0.16 | 0.06 | 0.00 | F10 | 0.34 | 0.21 | 0.10 | 0.00 |
| F15 | 0.80 | 0.67 | 0.14 | 0.00 | F12 | 0.63 | 0.50 | 0.10 | 0.00 |
| F18 | 0.68 | 0.13 | 0.02 | 0.00 | F16 | 0.70 | 0.58 | 0.20 | 0.00 |
| F19 | 0.35 | 0.17 | 0.03 | 0.00 | F34 | 0.88 | 0.11 | 0.00 | 0.49 |
| F20 | 0.28 | 0.10 | 0.02 | 0.00 | F37 | 0.02 | 0.10 | 0.11 | 0.00 |
| F25 | 0.44 | 0.16 | 0.03 | 0.00 | F43 | 0.44 | 0.11 | 0.00 | 0.82 |
| F34 | 0.93 | 0.51 | 0.00 | 0.44 | F44 | 0.65 | 0.12 | 0.00 | 0.82 |
| F36 | 0.00 | 0.09 | 0.02 | 0.05 | F45 | 0.61 | 0.12 | 0.00 | 0.82 |
| F37 | 0.00 | 0.06 | 0.11 | 0.04 | F48 | 0.59 | 0.14 | 0.00 | 0.82 |
| F43 | 0.88 | 0.58 | 0.00 | 0.81 | F59 | 0.34 | 0.00 | 0.13 | 0.04 |
| F45 | 0.91 | 0.51 | 0.00 | 0.65 | F61 | 0.06 | 0.04 | 0.02 | 0.00 |
| F48 | 0.88 | 0.66 | 0.00 | 0.79 | F62 | 0.00 | 0.39 | 0.46 | 0.56 |
| F61 | 0.00 | 0.07 | 0.06 | 0.04 | - | - | - | - | - |
| F62 | 0.00 | 0.22 | 0.47 | 0.52 | - | - | - | - | - |
| F64 | 0.00 | 0.08 | 0.07 | 0.03 | - | - | - | - | - |
| F65 | 0.64 | 0.07 | 0.00 | 0.16 | - | - | - | - | - |
| F66 | 0.66 | 0.05 | 0.00 | 0.20 | - | - | - | - | - |
| F67 | 0.64 | 0.07 | 0.00 | 0.16 | - | - | - | - | - |
| F68 | 0.64 | 0.07 | 0.00 | 0.16 | - | - | - | - | - |
Table 22.
PCR and PLSR results.
Table 22.
PCR and PLSR results.
| Type of Bread | Pigweed Bread | Purslane Bread |
|---|
| | Method | PCR | PLSR | PCR | PLSR |
|---|
| Assessment Criteria | |
|---|
| R2 | 0.83 | 0.83 | 0.72 | 0.82 |
| SSE | 1.79 | 1.77 | 2.54 | 1.85 |
| RMSE | 2.12 | 2.11 | 2.53 | 2.15 |
Table 23.
Main physicochemical characteristics of wheat bread with appropriate amounts of pigweed and purslane flour.
Table 23.
Main physicochemical characteristics of wheat bread with appropriate amounts of pigweed and purslane flour.
| | Alternative Flour | Control Sample | Pigweed Flour 3.49% | Purslane Flour 7.13% |
|---|
| Characteristic | |
|---|
| pH | 6.33 ± 0.02 | 6.21 ± 0.01 | 6.07 ± 0.02 |
| TDS, ppm | 1605.5 ± 1.5 | 1655.5 ± 40.5 | 1834.5 ± 25.5 |
| EC, µS/cm | 3207 ± 2 | 3349.5 ± 23.5 | 3673.5 ± 55.5 |
| ORP, mV | 232.5 ± 3.5 | 211 ± 3 | 204 ± 3 |
Table 24.
Organoleptic evaluation of wheat bread with appropriate amount of pigweed and purslane flour.
Table 24.
Organoleptic evaluation of wheat bread with appropriate amount of pigweed and purslane flour.
| | Alternative Flour, % | 0% | Pigweed Flour 3.49% | Purslane Flour 7.13% |
|---|
| Characteristic | |
|---|
| Appearance | 4.97 ± 0.05 | 4.57 ± 0.17 | 2.73 ± 0.52 |
| Structure | 4.97 ± 0.05 | 4.67 ± 0.12 | 2.77 ± 0.56 |
| Chewability | 4.97 ± 0.05 | 4.53 ± 0.05 | 4.17 ± 0.24 |
| Aroma | 4.97 ± 0.05 | 4.83 ± 0.12 | 4.57 ± 0.17 |
| Taste | 4.97 ± 0.05 | 3.77 ± 0.88 | 4.63 ± 0.12 |
| Overall assessment | 4.97 ± 0.05 | 4.47 ± 0.15 | 3.77 ± 0.15 |
Table 25.
Main characteristics of wheat bread with appropriate amounts of alternative flour, determined from its 3D images.
Table 25.
Main characteristics of wheat bread with appropriate amounts of alternative flour, determined from its 3D images.
| | Alternative Flour, % | 0% | Pigweed Flour 3.49% | Purslane Flour 7.13% |
|---|
| Characteristic | |
|---|
| V, cm3 | 300 ± 1 | 300 ± 1 | 200 ± 4 |
| S, cm2 | 242 ± 0.12 | 234 ± 0.46 | 182 ± 0.08 |
| D, kg/m3 | 301.27 ± 4.5 | 314.13 ± 11.12 | 464.5 ± 3.68 |
| Vbb, cm3 | 500 ± 4 | 400 ± 3 | 300 ± 2 |
| Sbb, cm2 | 374 ± 4.1 | 351 ± 4.8 | 258 ± 3.0 |
Table 26.
Comparative analysis of wheat bread with pigweed and purslane flour.
Table 26.
Comparative analysis of wheat bread with pigweed and purslane flour.
| Compared Characteristic | Wheat-Pigweed Bread | Wheat-Purslane Bread |
|---|
| Physicochemical characteristics | Increasing the amount of the additive leads to a decrease in pH and ORP. EC and TDS increase their values | Increasing the amount of the additive leads to a decrease in pH and ORP. EC and TDS increase their values |
| Organoleptic evaluation | Increasing the amount of the additive leads to a deterioration in organoleptic indicators | Increasing the amount of the additive leads to a deterioration in the organoleptic indicators |
| Geometric characteristics | Reduction in volume and surface area, increase in density compared to the control sample | Reduction in volume and surface area, density is higher compared to the control sample and bread with pigweed |
| Color characteristics | Darker color compared to the control sample | Color much darker compared to the control sample and samples with pigweed |
| Spectral characteristics | Increasing the amount of the additive reduces the reflectance values for both the crust and the core | Increasing the amount of the additive reduces the reflectance values for both the crust and the core |
| Selection of informative features | 22 informative features | 15 informative signs |
| Data volume reduction | Possible with two latent variables | Possible with two latent variables |
| Model for determining the appropriate amount of additive | R2 = 0.85 | R2 = 0.84 |
| Appropriate amount of additive | 3.69% of the total amount of wheat flour | 7.13% of the total amount of wheat flour |