Study on the Influence of Ambient Temperature and RPV Temperature on Operation Performance of HTR-PM Reactor Cavity Cooling System †
Abstract
1. Introduction
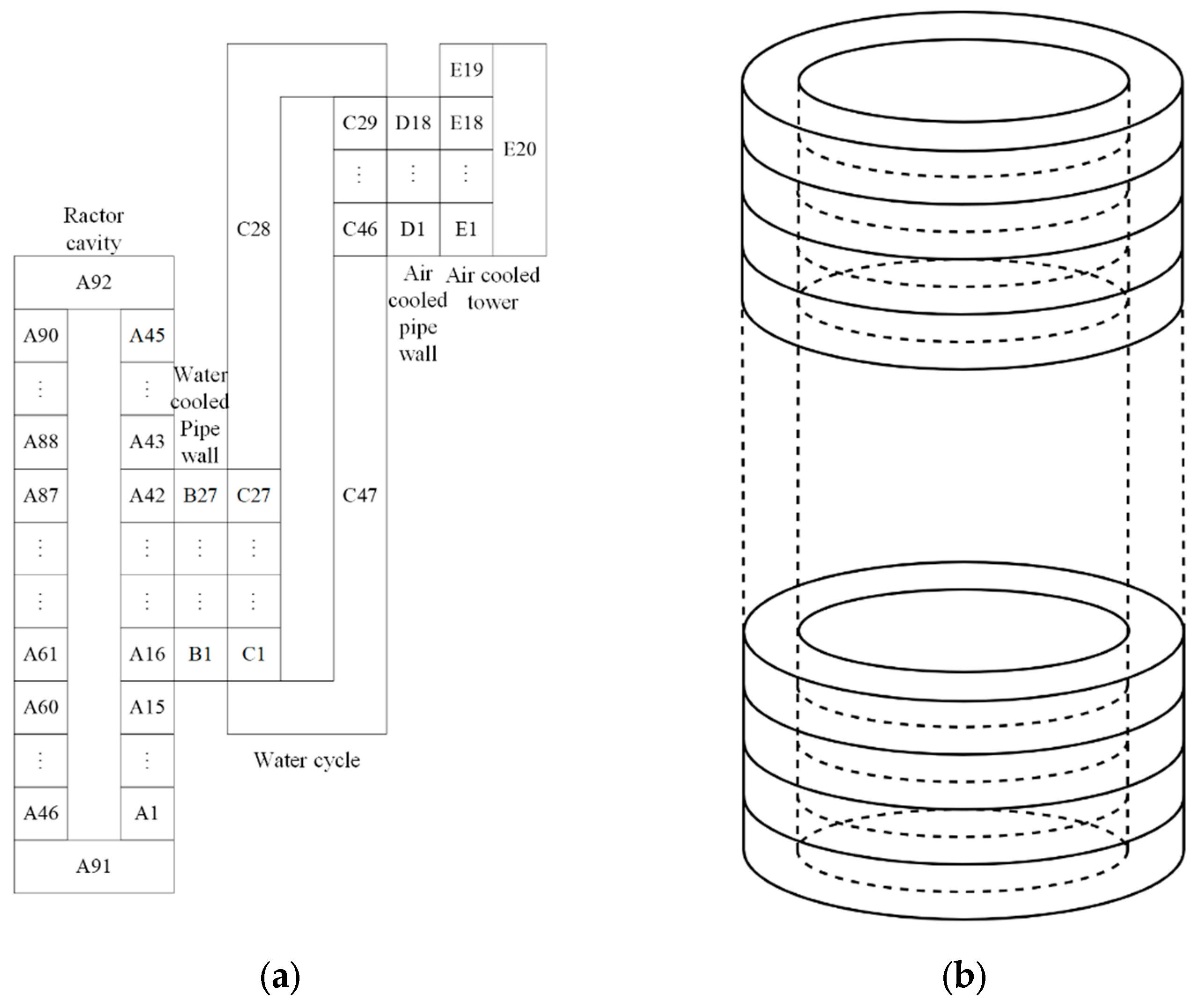
2. Code and Model
3. Results and Discussion
3.1. Calculation Condition
3.2. Calculation Results
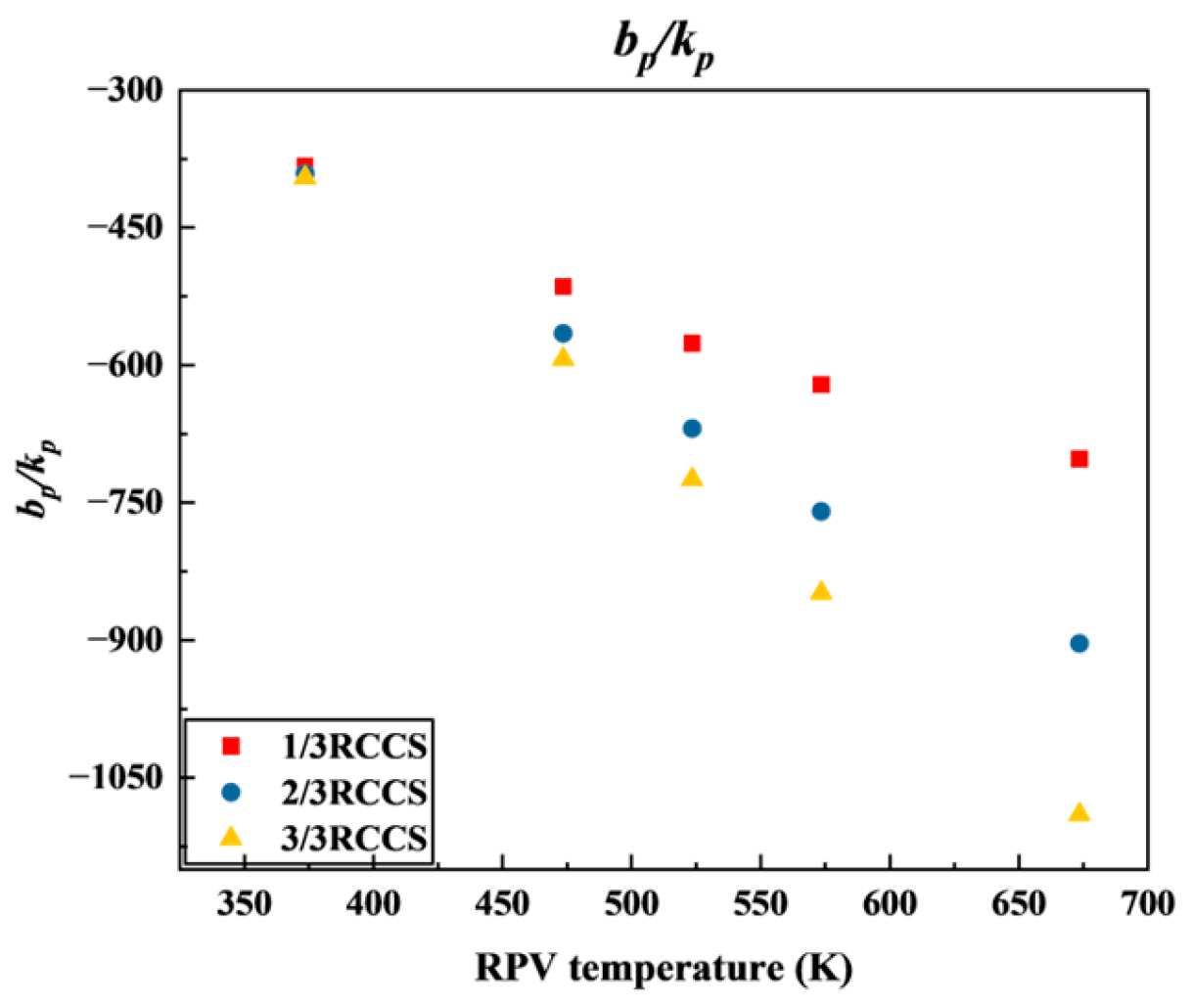
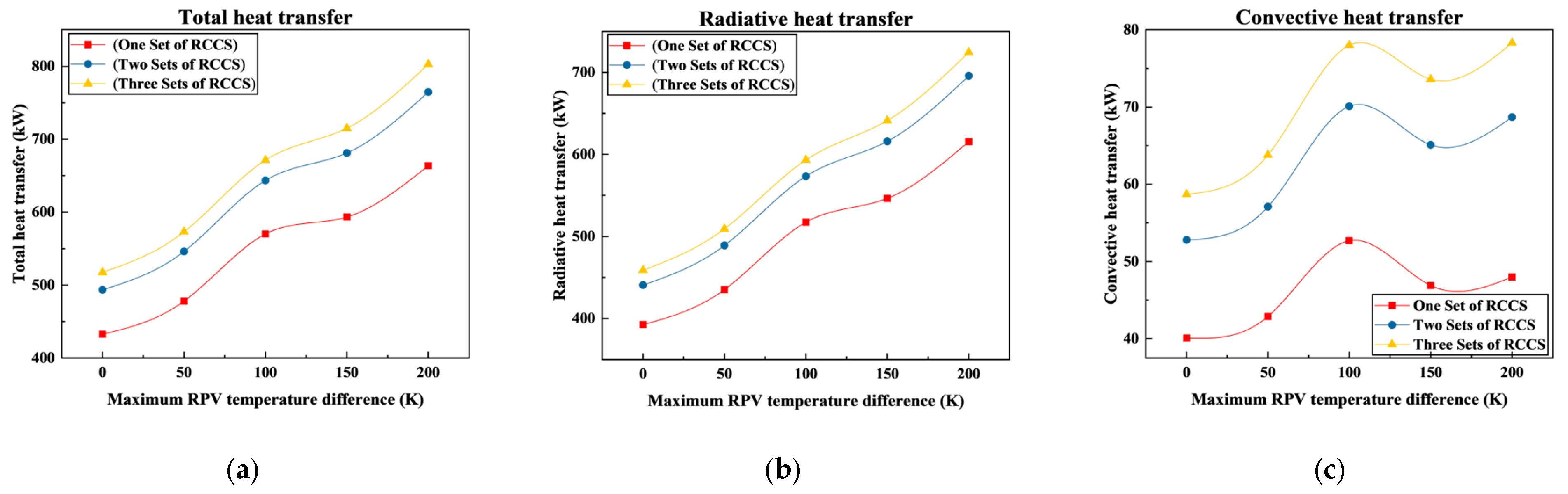
3.2.1. Heat-Carrying Capacity
= 1 + ∆Ta/(bp/kp + ∆Ta)
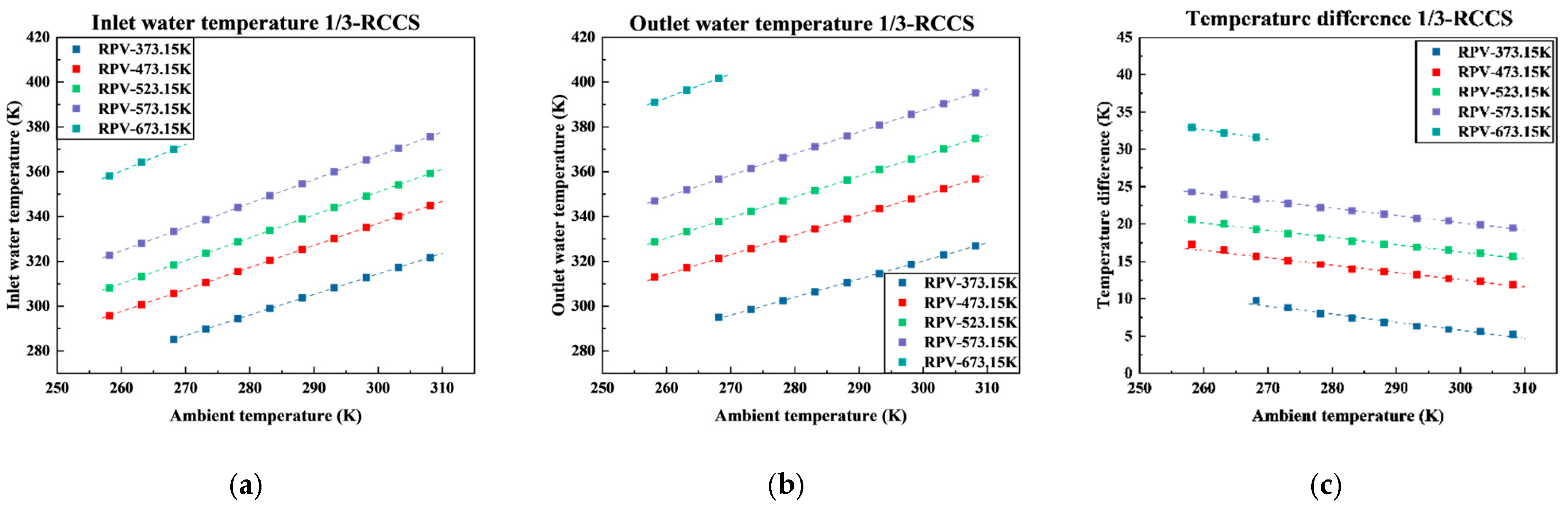
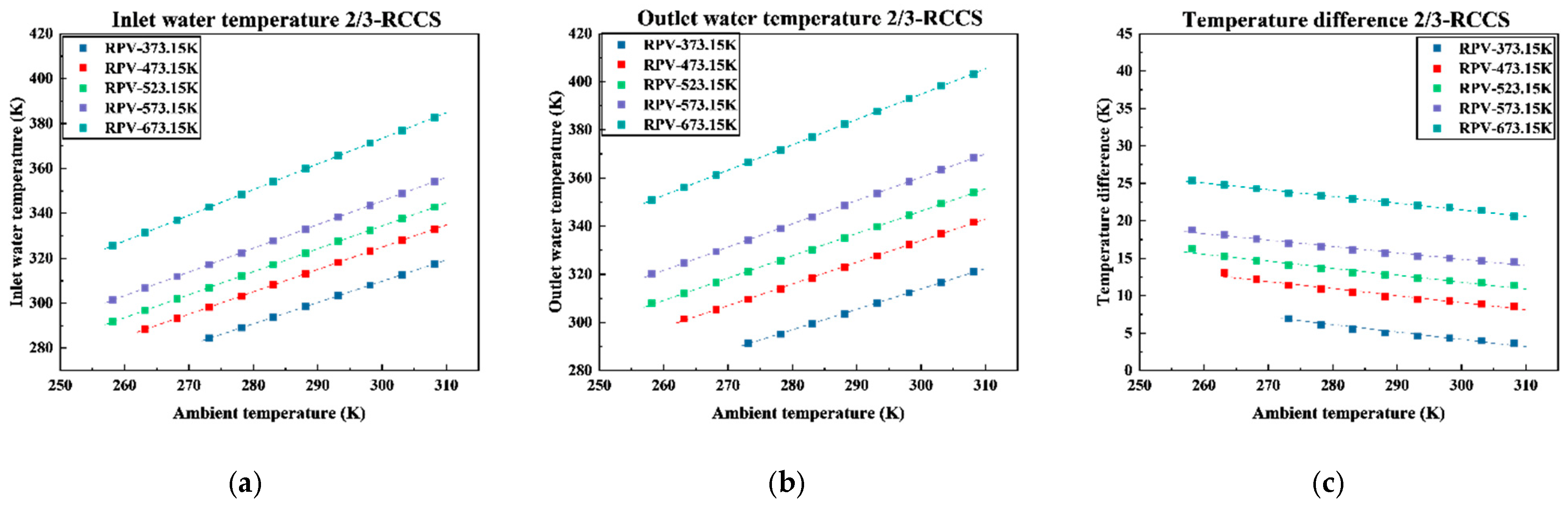
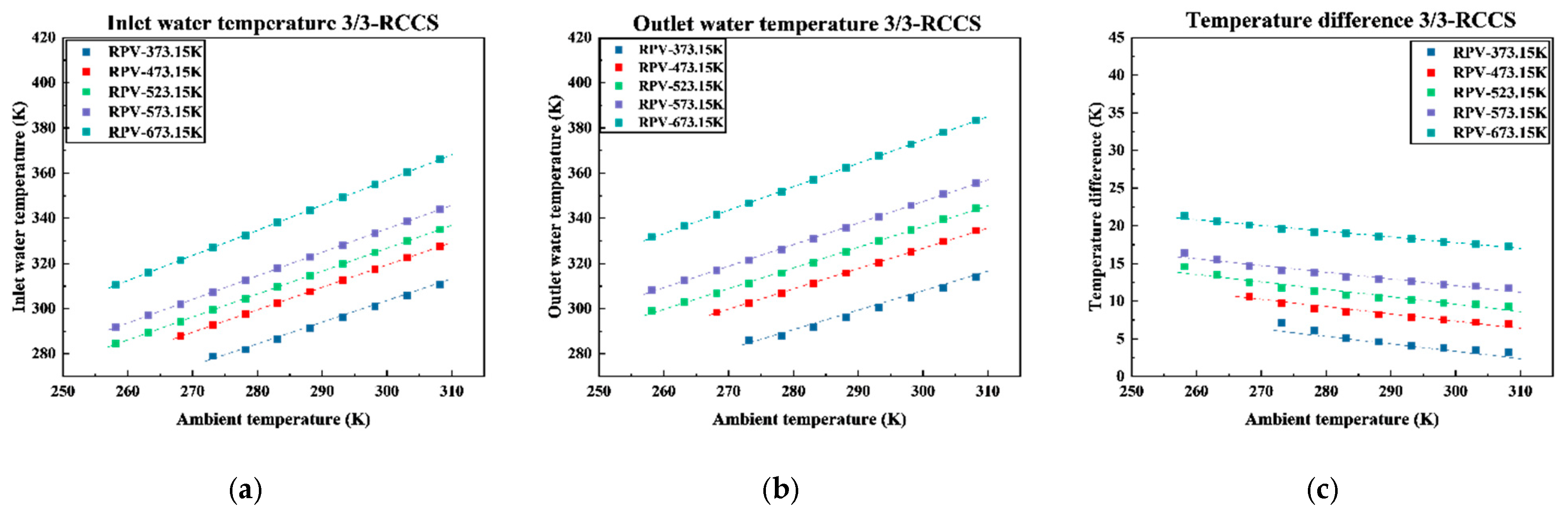
3.2.2. Cooling Water Temperature
3.2.3. RPV Temperature Distribution
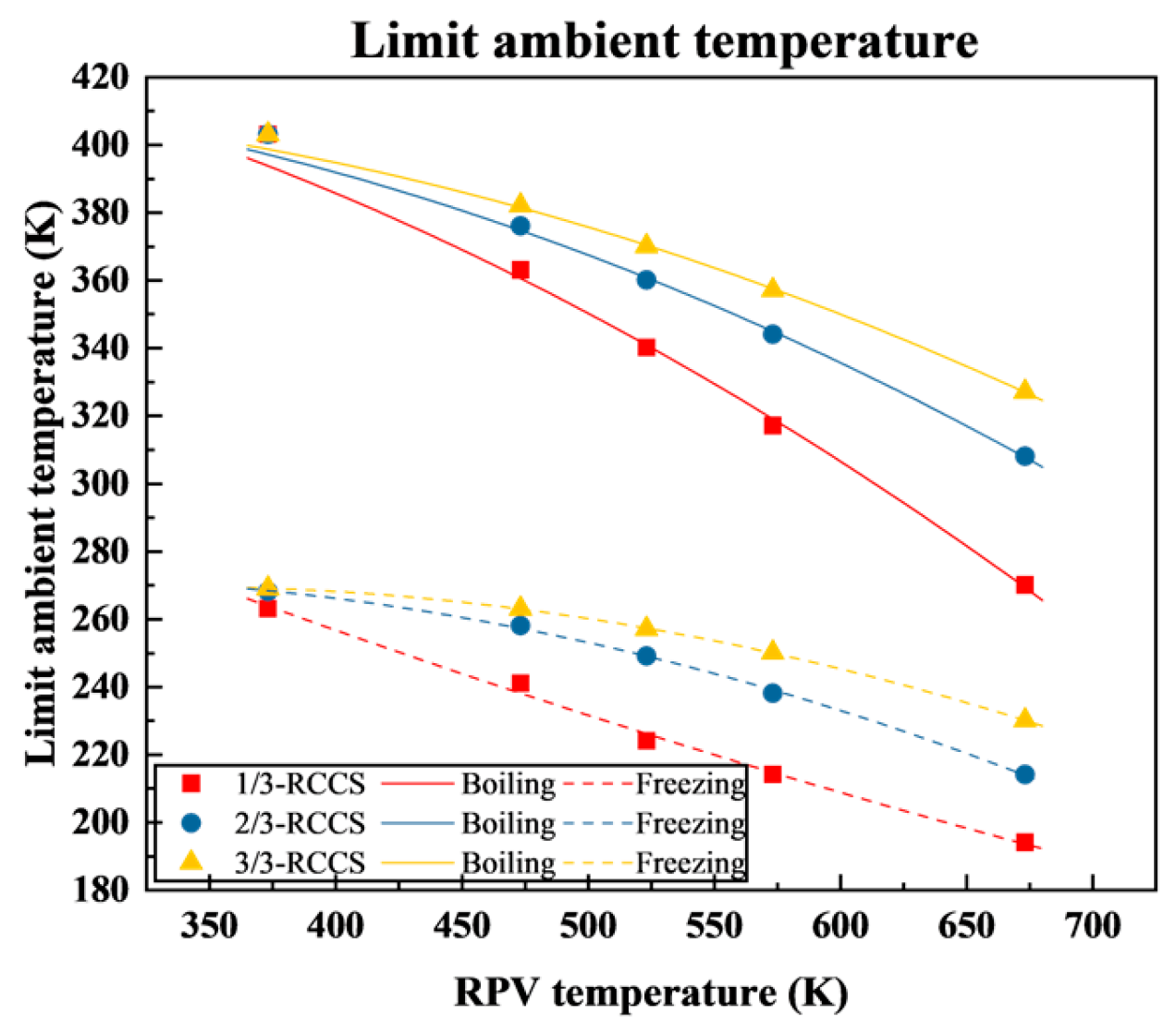
3.2.4. Temperature Limit
4. Discussion
4.1. High Temperature Failure Analysis
4.2. Low Temperature Failure Analysis
4.3. System Heat-Carrying Capacity
5. Conclusions
- (1)
- During normal operation of the HTR-PM, when the RPV temperature is maintained at a relatively low level, a single RCCS set is sufficient to ensure the safety of the reactor cavity. However, in certain accident scenarios involving emergency reactor shutdowns, the core and RPV temperatures may rise due to the decay heat and lack of forced cooling. In such cases, two RCCS sets can effectively remove the residual decay heat and keep the RPV and reactor cavity safe.
- (2)
- The RCCS may experience boiling or freezing of the cooling water during operation, potentially leading to heat transfer deterioration or even system failure. According to the calculation results, cooling-water boiling does not occur during normal operation of the reactor. However, under accident conditions with elevated RPV temperatures, it is essential to maintain an adequate number of operating RCCS sets to prevent boiling. Compared to boiling, the freezing of the cooling water and the resulting pipe rupture need more attention. Especially during the winter and at lower RPV temperatures, partial or full shutdown of the RCCS sets may be necessary to avoid freezing. Alternatively, closing the air inlet door of the air cooler to increase the cooling water temperature is also a feasible measure.
- (3)
- Heat transfer within the cavity primarily occurs through thermal radiation, with natural convection contributing less than 20% of the total heat transfer. The system’s heat-carrying capacity is predominantly determined by the RPV temperature and is positively correlated with the temperature difference between the inlet and outlet of cooling water. Additionally, the spatial distribution of the RPV temperature influences the heat transfer performance; a more uneven temperature distribution enhances the radiative heat emission from the RPV, thereby increasing the overall heat load of the system. Based on the analysis results and operation experience, it was found that the heat-carrying capacity of the RCCS of the HTR-PM exceeds the design requirement of 1.2 MW when two of three sets are operating normally.
- (4)
- Nevertheless, since the RPV temperature is also influenced by the operational characteristics of the RCCS, future studies should incorporate coupled simulations of the reactor, RPV, and RCCS behaviors. Such integrated analyses will enhance the understanding of RCCS performance and support further design optimization of the system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, X.; Ye, Y.; Zheng, Y. Study on the influence of ambient temperature and RPV temperature on operation performance of HTR-PM reactor cavity cooling system. In Proceedings of the PSAM17&ASRAM2024, Sendai, Japan, 7–11 October 2024. [Google Scholar]
- Zhang, Z.; Yu, S. Future HTGR developments in China after the criticality of the HTR-10. Nucl. Eng. Des. 2002, 218, 249–257. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Z.; Wang, D.; Xu, Y.; Sun, Y.; Li, F.; Dong, Y. Current status and technical description of Chinese 2 × 250 MWth HTR-PM demonstration plant. Nucl. Eng. Des. 2009, 239, 1212–1219. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Z.; Wang, D.; Tong, J. Development strategy of high temperature gas cooled reactor in China. Strateg. Study Chin. Acad. Eng. 2019, 21, 12–19. [Google Scholar] [CrossRef]
- Conklin, J. Modeling and Performance of the MHTGR (Modular High-Temperature Gas-Cooled Reactor) Reactor Cavity Cooling System; Nuclear Regulatory Commission, Division of Regulatory Applications: Washington, DC, USA, 1990. [Google Scholar]
- Fujiwara, Y.; Goto, M.; Iigaki, K.; Iyoku, T.; Ho, H.Q.; Kawamoto, T.; Kondo, M.; Kunitomi, K.; Morita, K.; Nagasumi, S. Design of high temperature engineering test reactor (HTTR). In High Temperature Gas-Cooled Reactors; Elsevier: Amsterdam, The Netherlands, 2021; pp. 17–177. [Google Scholar]
- Takada, S.; Suzuki, K.; Inagaki, Y.; Sudo, Y. Experimental and numerical studies on performance of passive decay heat removal by a water cooling panel from a high-temperature gas-cooled reactor. J. Nucl. Sci. Technol. 1999, 36, 413–423. [Google Scholar] [CrossRef]
- Takamatsu, K. Thermal-hydraulic analyses of the High-Temperature engineering Test Reactor for loss of forced cooling at 30% reactor power. Ann. Nucl. Energy 2017, 106, 71–83. [Google Scholar] [CrossRef]
- Freile, R.; Tano, M.; Balestra, P.; Schunert, S.; Kimber, M. Improved natural convection heat transfer correlations for reactor cavity cooling systems of high-temperature gas-cooled reactors: From computational fluid dynamics to Pronghorn. Ann. Nucl. Energy 2021, 163, 108547. [Google Scholar] [CrossRef]
- Koster, A.; Matzner, H.; Nicholsi, D. PBMR design for the future. Nucl. Eng. Des. 2003, 222, 231–245. [Google Scholar] [CrossRef]
- Qin, H.; Li, X.; Zhang, L.; Liu, X.; Zheng, Y.; Wu, X. Heat Removal Performance Analysis of HTR-PM Reactor Cavity Cooling System under Accident Condition. At. Energy Sci. Technol. 2025, 59, 838–845. [Google Scholar]
- Li, X.-w.; Wu, X.-x.; Zhang, L.; He, S.-y. Analysis of passive residual heat removal system of modular high temperature gas-cooled reactor. At. Energy Sci. Technol. 2011, 45, 790–795. [Google Scholar]
- Zhang, W.; Jia, D.; Qiu, S. Calculation of radiation in the primary cavity of HTR-10. Nucl. Power Eng. 2002, 23, 10–16. [Google Scholar]
- Wang, D.; Hao, C.; Li, F. Operating characteristic analysis of passive residual heat removal system of HTR-PM. Sci. Technol. Rev. 2012, 30, 33–38. [Google Scholar]
- Qin, H.; Li, X.; Zhang, L.; Wu, X. Flow distribution in the air cooler of HTGR passive cavity cooling system. Ann. Nucl. Energy 2023, 180, 109478. [Google Scholar] [CrossRef]
- Zhao, H.; Zheng, Y.; Chen, X.; Ma, T.; Dong, Y. A one-dimensional code of the passive residual heat removal system for the modular high temperature gas-cooled reactor. Prog. Nucl. Energy 2019, 110, 374–383. [Google Scholar] [CrossRef]
- Zhao, H.; Zheng, Y.; Ma, T.; Dong, Y. A multi-scale CFD-system coupled code for transient analysis of the passive residual heat removal system of MHTGR. Ann. Nucl. Energy 2020, 141, 107304. [Google Scholar] [CrossRef]
- He, D. Simulation of Residual Heat Removal System in HTR-PM. Master’s Thesis, Tsinghua University, Beijing China, 2010. [Google Scholar]
- Wang, D. Simulation of High Temperature Gas Cooled Reactor’s Multi-Loop System. Ph.D. Thesis, Tsinghua University, Beijing China, 2011. [Google Scholar]
- Ye, Y. Development of Coupling Program for High-Temperature Gas-Cooled Reactor Cavity Cooling System Based on TINTE and Analysis of RCCS Characteristics. Ph.D. Thesis, Tsinghua University, Beijing China, 2023. [Google Scholar]
- Xu, X.; Zhang, H.; Zheng, Y.; She, D. Three-dimensional Radiation View Factor Calculation in DAYU3D Program. In Proceedings of the HTR, Beijing, China, 14–18 October 2024. [Google Scholar]
- Modest, M.F.; Mazumder, S. Radiative Heat Transfer; Academic Press: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Zhang, H.; Zheng, Y.; She, D.; Shi, L. Preliminary Study on Three-Dimensional Characteristics of Modular High Temperature Gas-Cooled Reactor. In Proceedings of the International Conference on Nuclear Engineering, Weihai, China, 22–27 June 2022; p. V015T016A057. [Google Scholar]
- Zhang, H.; Tan, B.; She, D.; Shi, L. An efficient method for solving flow field in high temperature gas-cooled reactor. Prog. Nucl. Energy 2025, 180, 105599. [Google Scholar] [CrossRef]
- Zhang, H.; Wen, Y.; She, D.; Zheng, Y.; Shi, L. DAYU3D: A modern code for HTGR thermal-hydraulic design and accident analysis. Nucl. Sci. Technol. 2025, accepted. [Google Scholar] [CrossRef]
- Gerwin, H.; Scherer, W.; Lauer, A.; Strydom, G. Tinte-a Two-Dimensional Code for Reactor Dynamics; Forschungszentrum Jülich GmbH·Zentralbibliothek: Jülich, Germany, 2009; pp. 1–40. [Google Scholar]
- Zheng, Y.; Stempniewicz, M.M.; Chen, Z.; Shi, L. Study on the DLOFC and PLOFC accidents of the 200 MWe pebble-bed modular high temperature gas-cooled reactor with TINTE and SPECTRA codes. Ann. Nucl. Energy 2018, 120, 763–777. [Google Scholar] [CrossRef]
- Xu, X.; Ye, Y.; Zheng, Y.; Marek, M.S. Study on Reactor Cavity Cooling System of HTR-PM in DLOFC Accident with TIN-CAVCO Code and SPECTRA Code. In Proceedings of the International Conference on Nuclear Engineering, Prague, Czech Republic, 4–8 August 2024; p. V006T007A028. [Google Scholar]
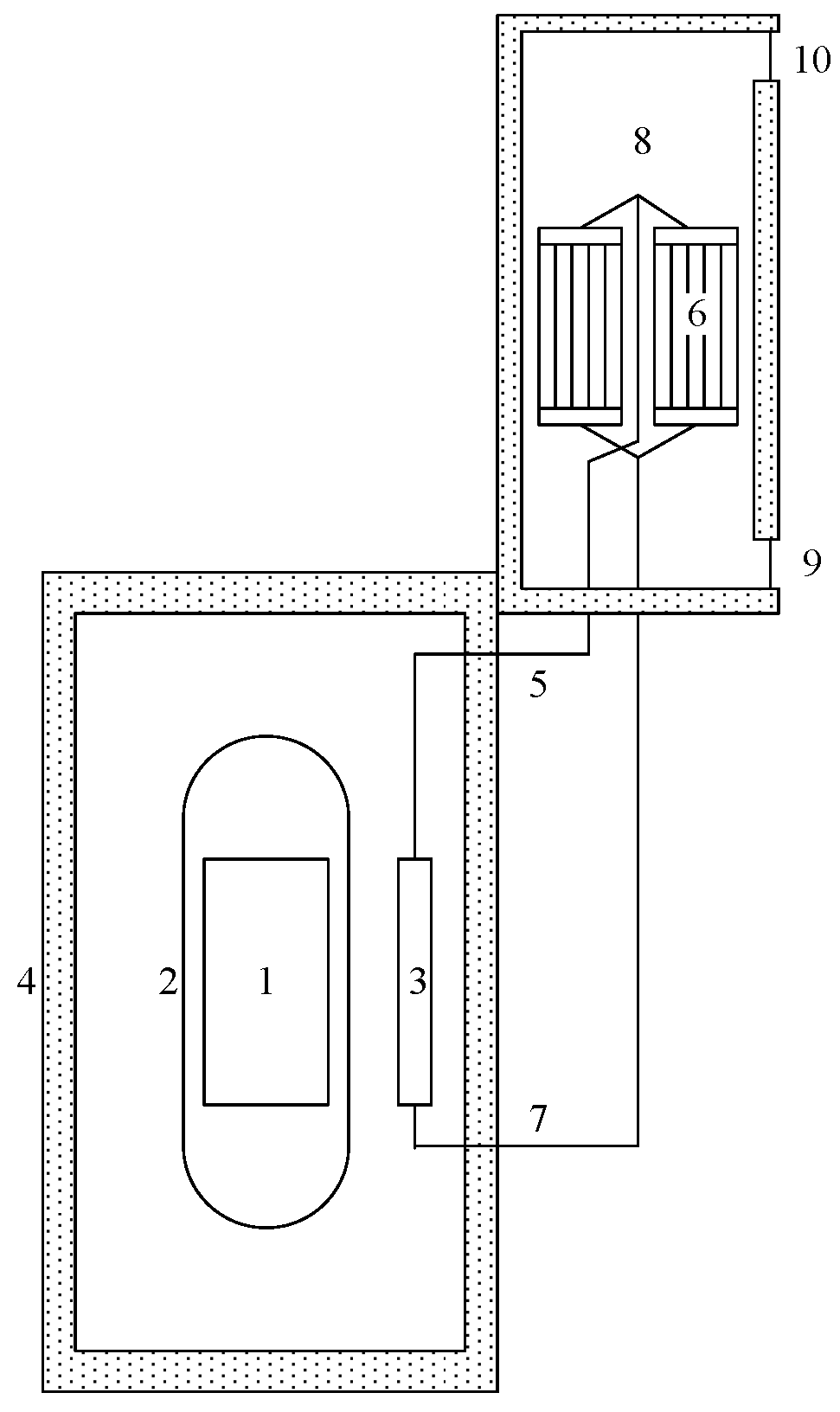
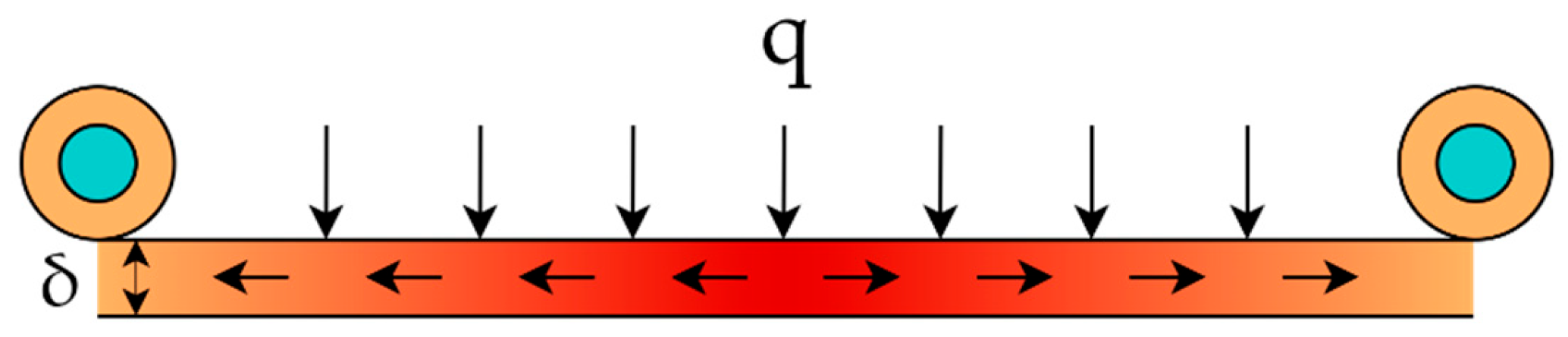



| Set of RCCS | Sketch | h (W/(m2·K)) |
|---|---|---|
| 1 | 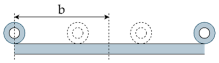 | 3λpδ/b2 |
| 2 |  | 3λpδ/(b12 − b1b2 + b22) |
| 3 | 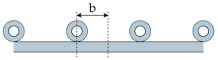 | 3λpδ/b2 |
| Case | RPV Temperature (K) | Ambient Temperature (K) | Set of RCCS | |
|---|---|---|---|---|
| 1 | 373.15 | 258.15/263.15/268.15/ 273.15/278.15/283.15/ 288.15/293.15/298.15/ 303.15/308.15 | 1/2/3 | |
| 2 | 473.15 | |||
| 3 | 523.15 | |||
| 4 | 573.15 | |||
| 5 | 673.15 | |||
| 6 | 6-1 | −100cos(2π × h/23.446) + 473.15 | 293.15 | |
| 6-2 | −75cos(2π × h/23.446) + 473.15 | |||
| 6-3 | −50cos(2π × h/23.446) + 473.15 | |||
| 6-4 | −25cos(2π × h/23.446) + 473.15 | |||
| 6-5 | 473.15 | |||
| Variable | Unit | Physical Significance |
|---|---|---|
| Ac | m2 | Cross-sectional area of the pipe |
| ARPV | m2 | Area of RPV |
| Ak | m2 | Area of surface k |
| bp | kW | Intercept of the line |
| J/(kg∙K) | Specific heat capacity | |
| d | m | Diameter of the pipe |
| g | m/s2 | Gravitational acceleration |
| Hc | WCP height to annular cavity height ratio | |
| heff | W/(m2∙K) | Equivalent heat transfer coefficient |
| Jk | W/m2 | Net radiative heat transfer of surface k |
| kp | kW/K | Slope of the line |
| l | m | Length of the pipe |
| n | Operational sets of the RCCS | |
| P | kW | Heat-carrying capacity |
| Qc | W | Natural convection heat power on the outer wall of the annular cavity |
| Qr,k | W | Net radiative heat transfer of surface k |
| qx | W/m | Linear heat rate |
| Rc | Ratio of inner and outer wall radius in the annular cavity | |
| Ta | K | Ambient temperature |
| TRPV | K | RPV temperature |
| TWCP | K | WCP temperature |
| Tfreezing | K | Ambient temperature corresponding to the water zero point |
| Tboiling | K | Ambient temperature corresponding to the water boiling point |
| Tpipe | K | Temperature of the pipe wall |
| K | Average temperature of the steel panel | |
| ∆Tc | K | The difference between the highest and lowest temperatures on the RPV wall |
| ∆tc | K | The average temperature difference between the inner and outer walls of the annular cavity |
| u | m/s | Velocity of the fluid |
| Xk-i | View factor from surface k to surface i | |
| εk | Emissivity of surface k | |
| σ | W/(m2·K4) | Stefan–Boltzmann constant |
| kg/m3 | Density | |
| Friction factor | ||
| Local loss coefficient | ||
| δ | m | Thickness of the panel |
| λp | W/(m·K) | Thermal conductivity of the panel |
| Set of RCCS | Equation | |
|---|---|---|
| 1 | Tfreezing = 0.000114TRPV2 − 0.354TRPV + 379.903 | Tboiling = 0.000416TRPV2 − 0.0199RPV + 444.231 |
| 2 | Tfreezing = −0.000352TRPV2 − 0.187TRPV + 247.845 | Tboiling = 0.000370TRPV2 − 0.0889TRPV + 415.496 |
| 3 | Tfreezing = −0.000343TRPV2 + 0.228TRPV + 231.553 | Tboiling = 0.000335TRPV2 − 0.112TRPV + 403.750 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Ye, Y.; Wu, Y.; Zheng, Y. Study on the Influence of Ambient Temperature and RPV Temperature on Operation Performance of HTR-PM Reactor Cavity Cooling System. J. Nucl. Eng. 2025, 6, 48. https://doi.org/10.3390/jne6040048
Xu X, Ye Y, Wu Y, Zheng Y. Study on the Influence of Ambient Temperature and RPV Temperature on Operation Performance of HTR-PM Reactor Cavity Cooling System. Journal of Nuclear Engineering. 2025; 6(4):48. https://doi.org/10.3390/jne6040048
Chicago/Turabian StyleXu, Xinsheng, Yiyang Ye, Yingjie Wu, and Yanhua Zheng. 2025. "Study on the Influence of Ambient Temperature and RPV Temperature on Operation Performance of HTR-PM Reactor Cavity Cooling System" Journal of Nuclear Engineering 6, no. 4: 48. https://doi.org/10.3390/jne6040048
APA StyleXu, X., Ye, Y., Wu, Y., & Zheng, Y. (2025). Study on the Influence of Ambient Temperature and RPV Temperature on Operation Performance of HTR-PM Reactor Cavity Cooling System. Journal of Nuclear Engineering, 6(4), 48. https://doi.org/10.3390/jne6040048







