Two-Phase Flow Studies in Steam Separators Using Interface Capturing Simulations †
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Simulations of a Simplified Model Geometry
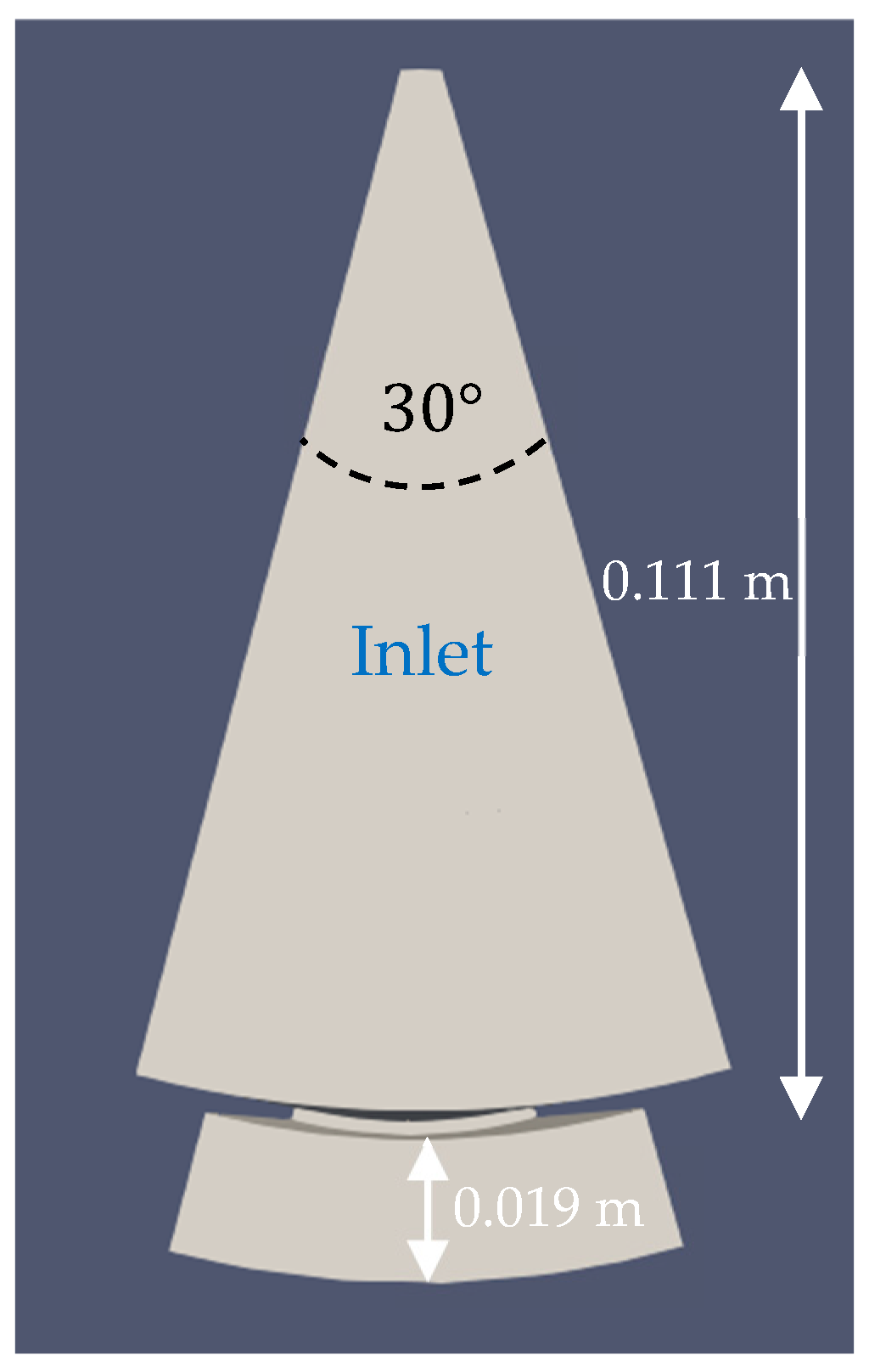
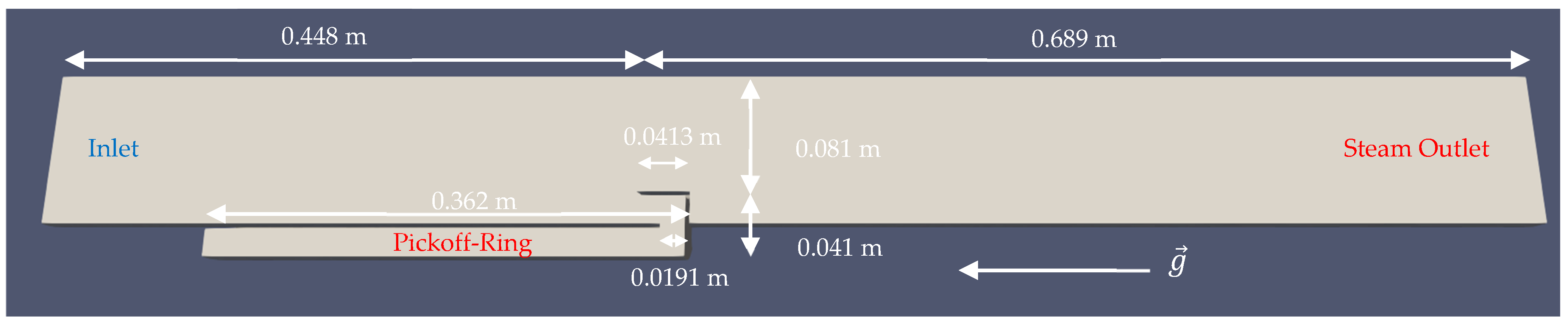
3.1.1. Boundary Conditions and Mesh Design
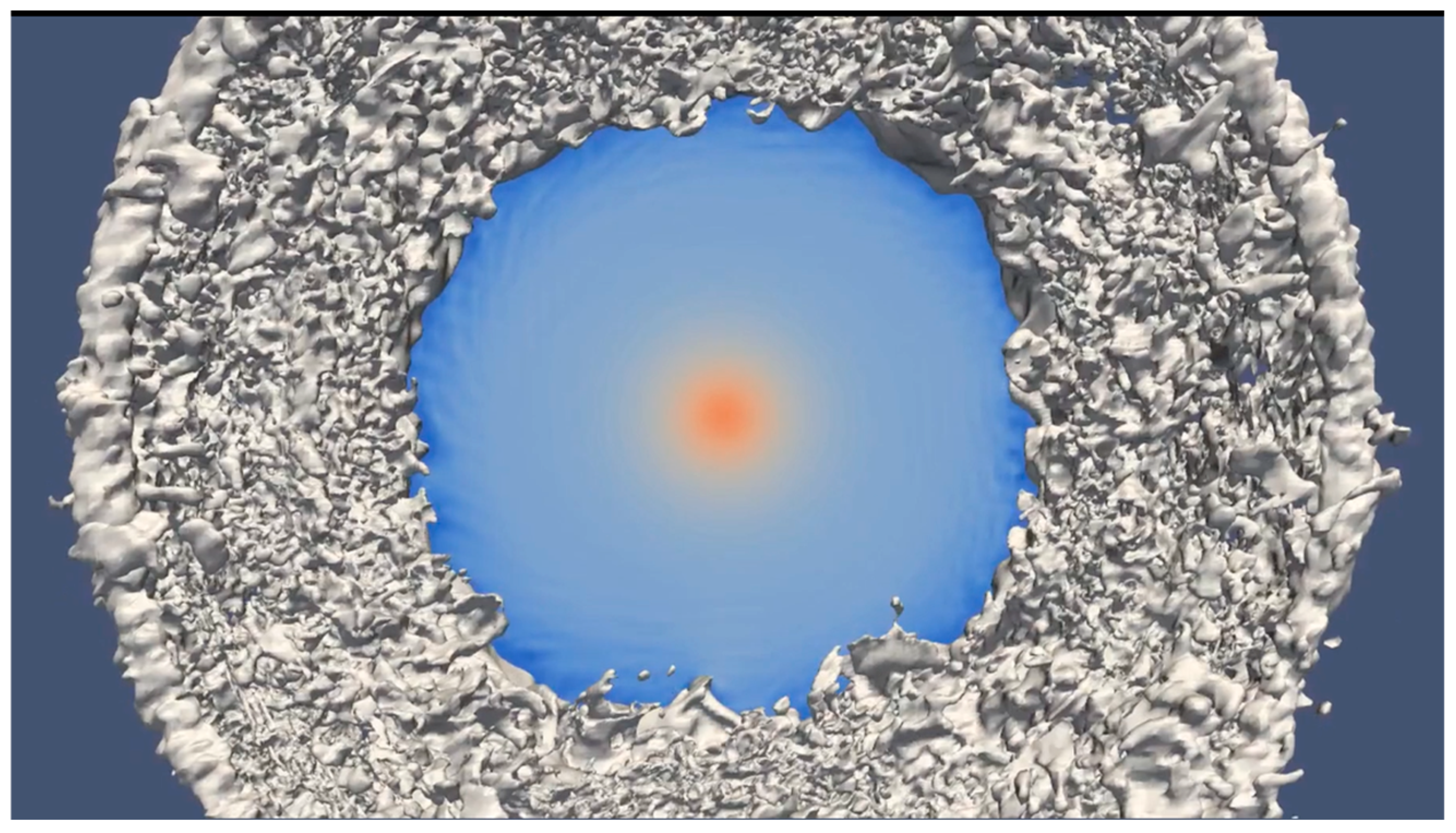
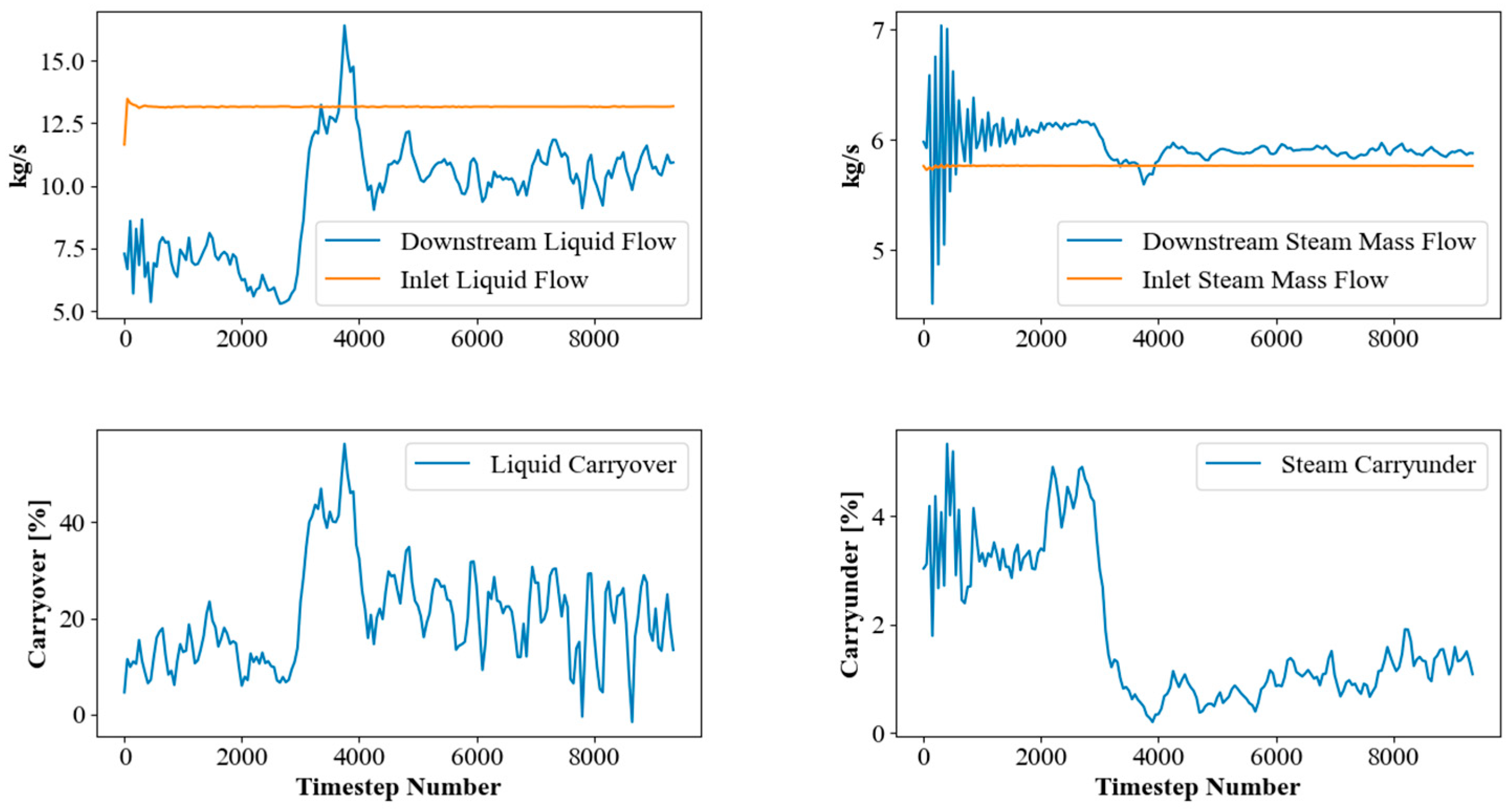
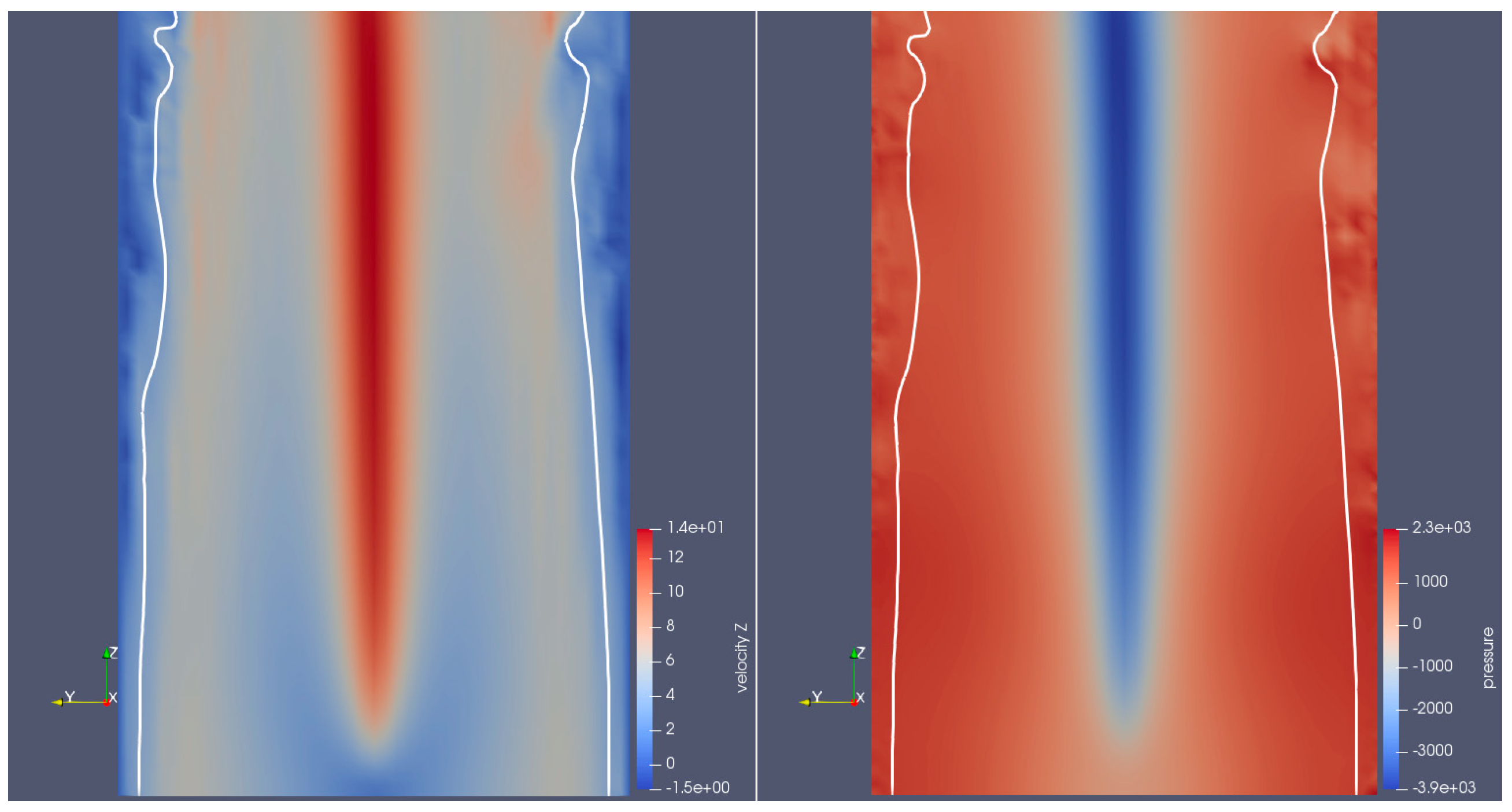
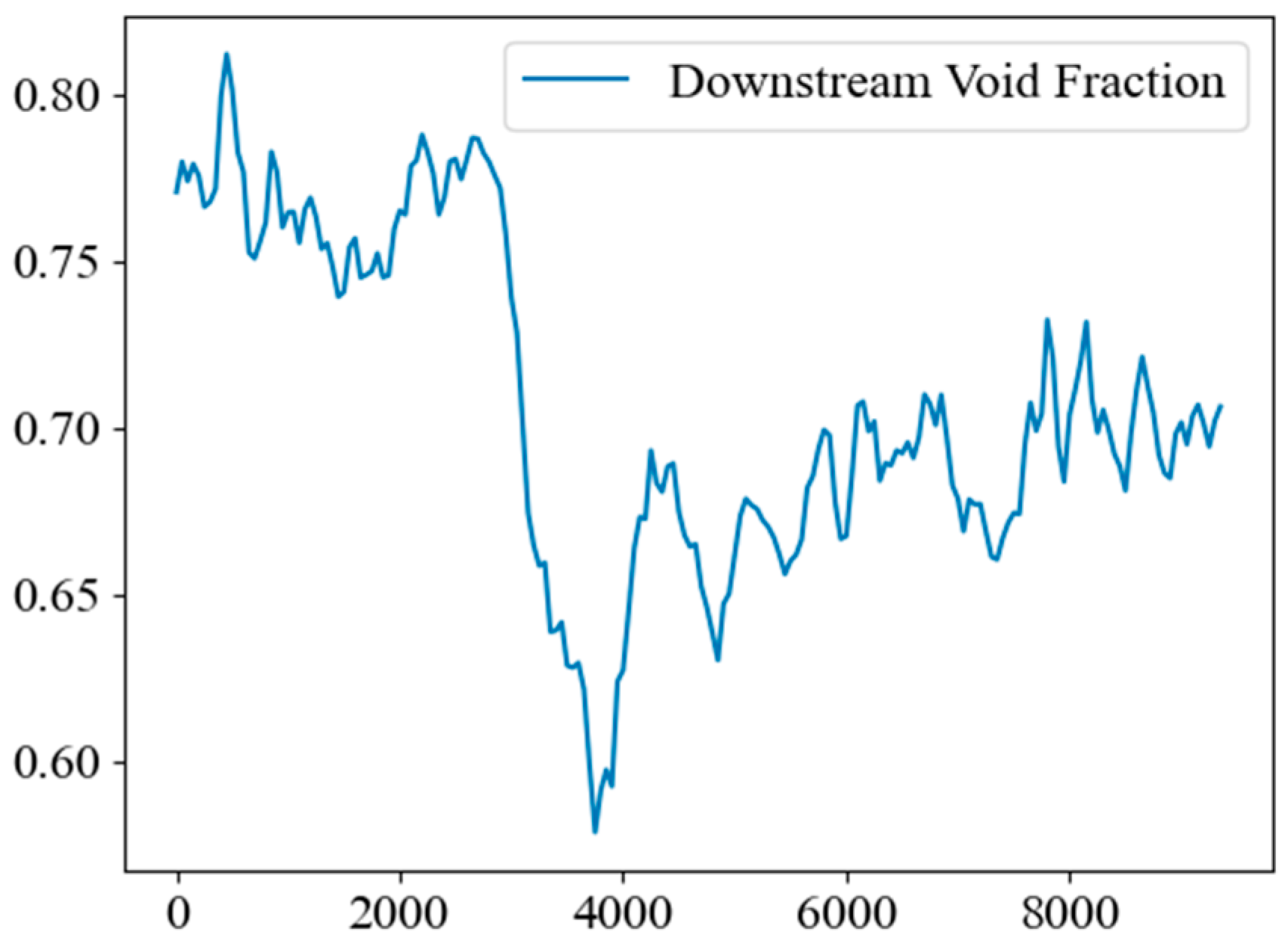
3.1.2. Results
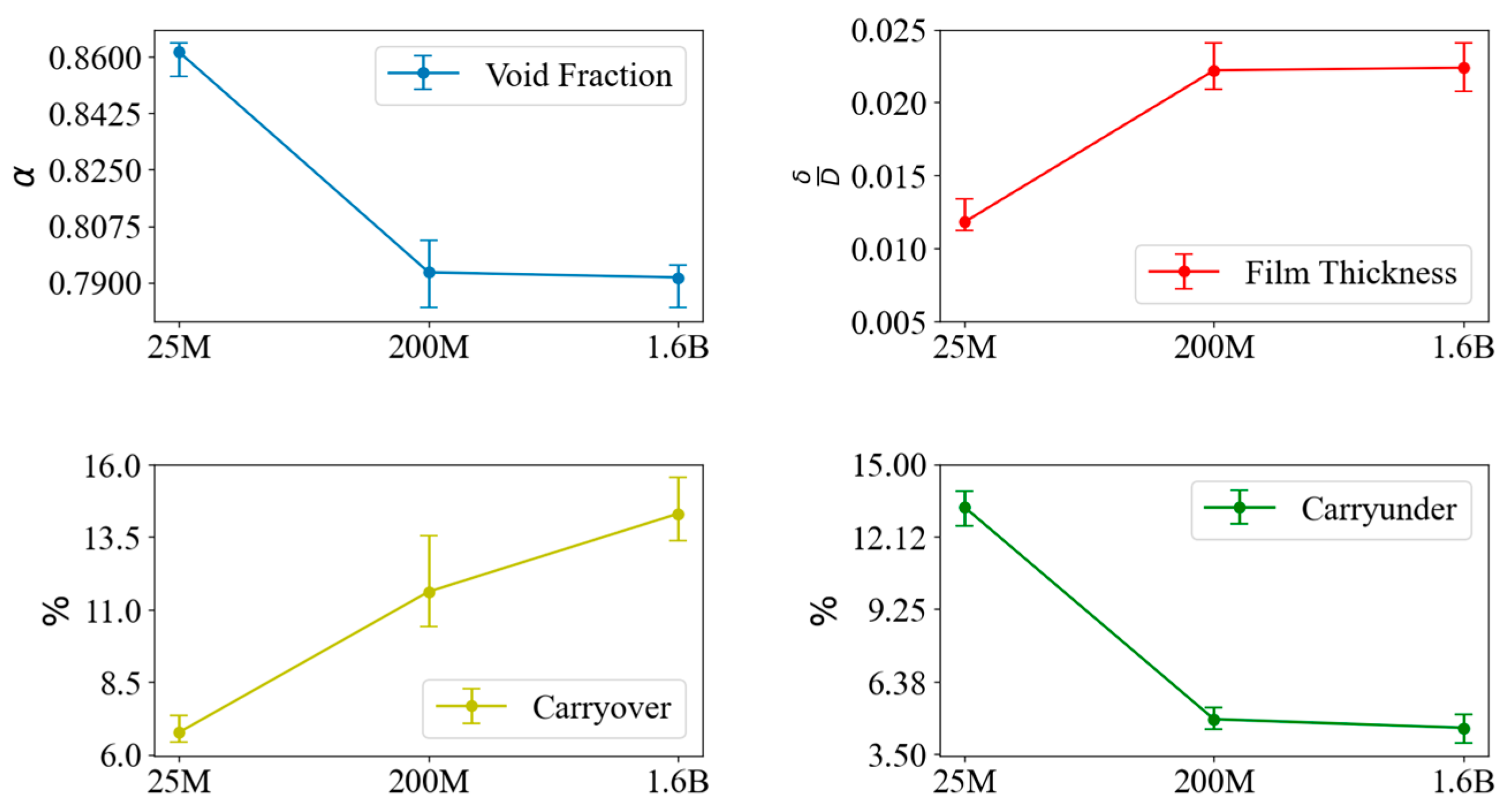
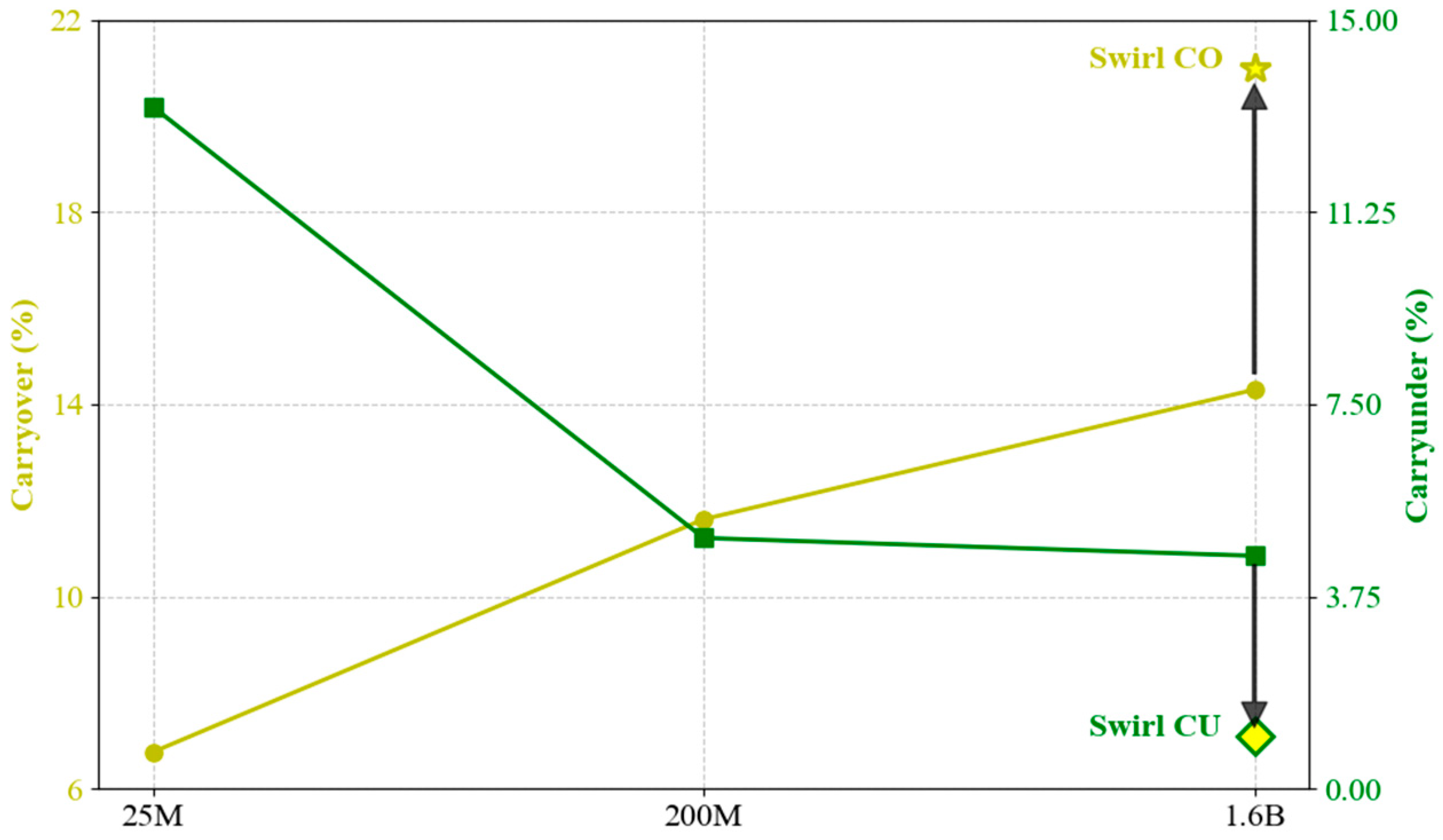
3.1.3. Discussion
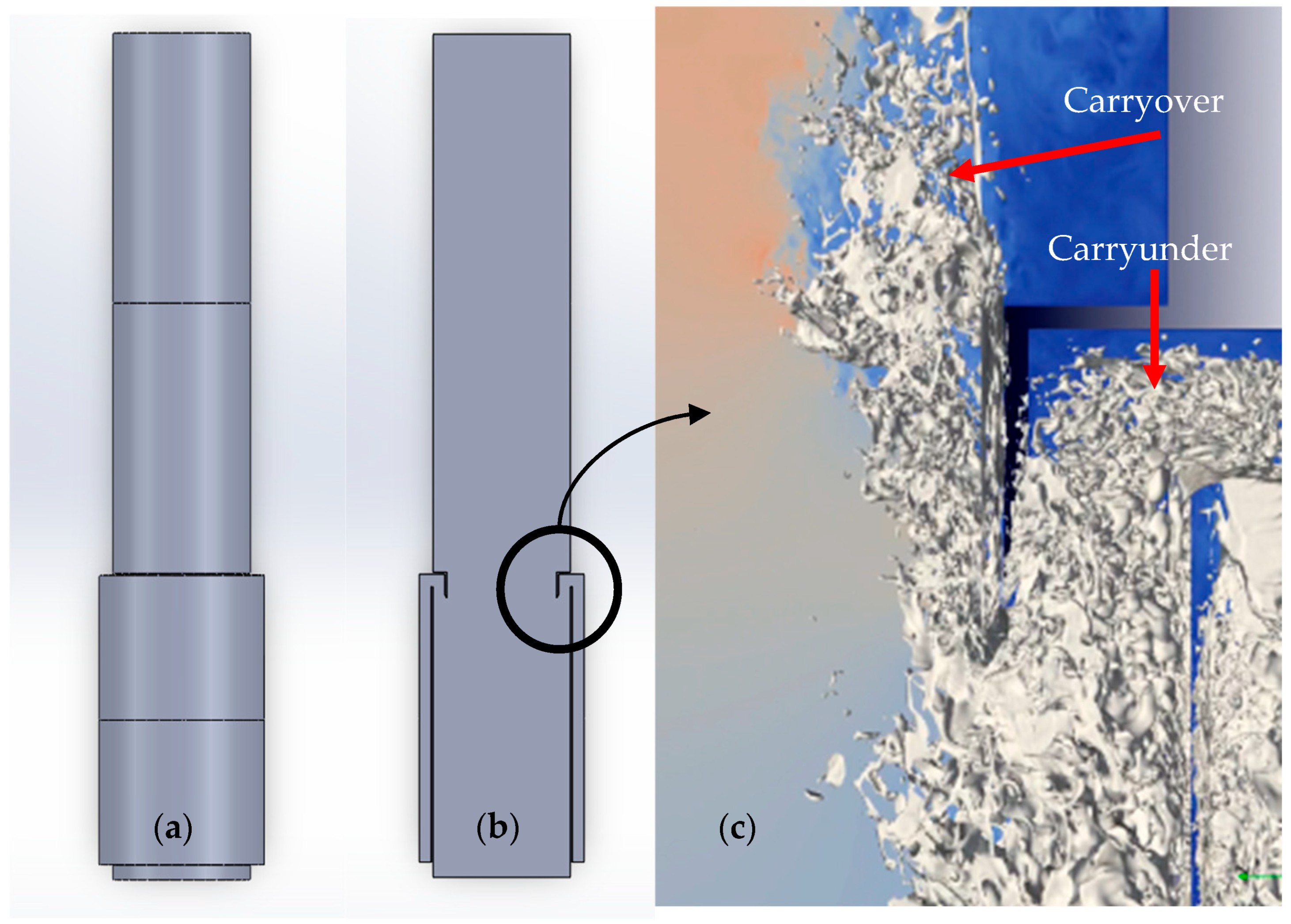
3.2. Simulations of a Swirler Geometry
3.2.1. Boundary Conditions and Mesh Design
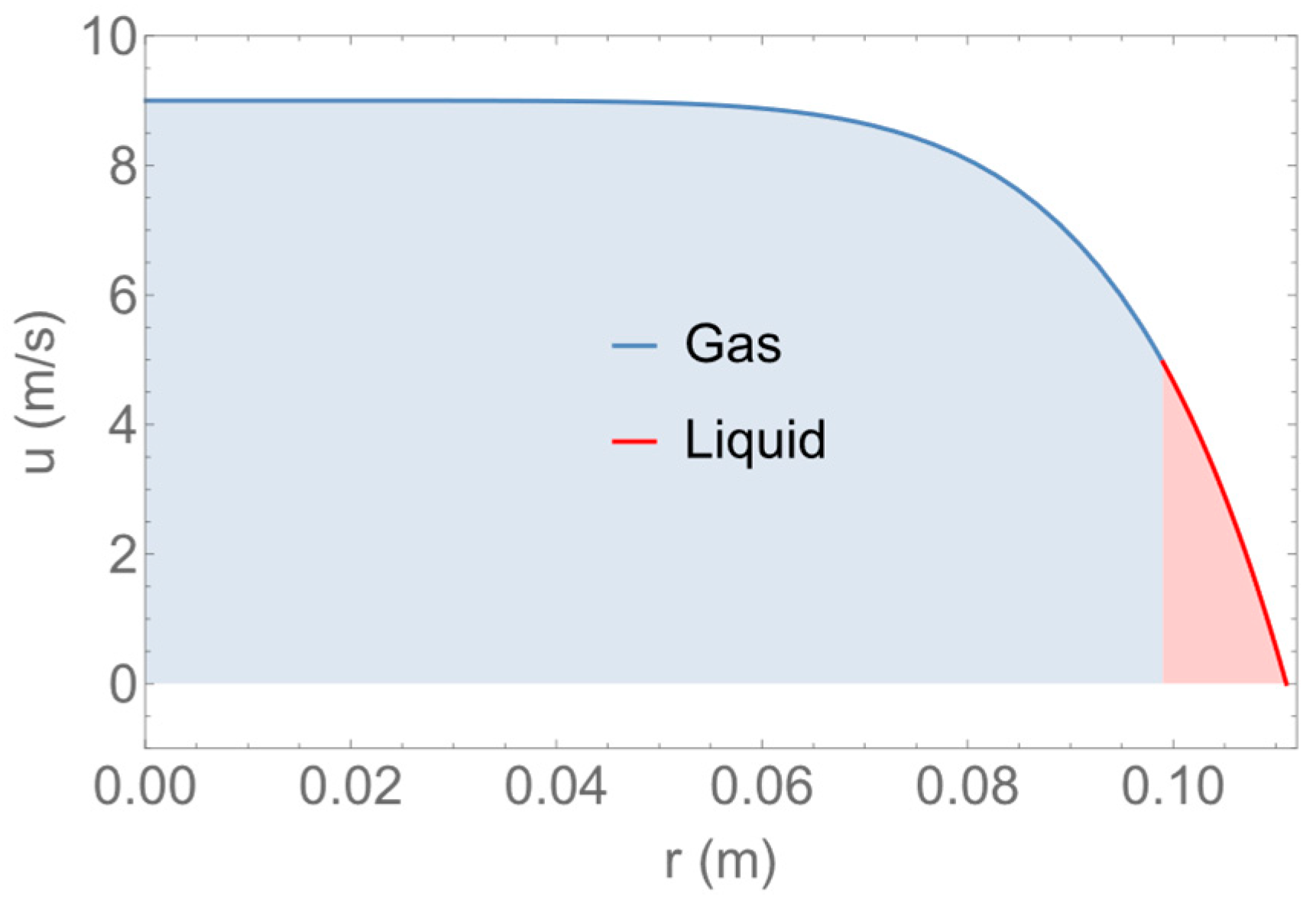
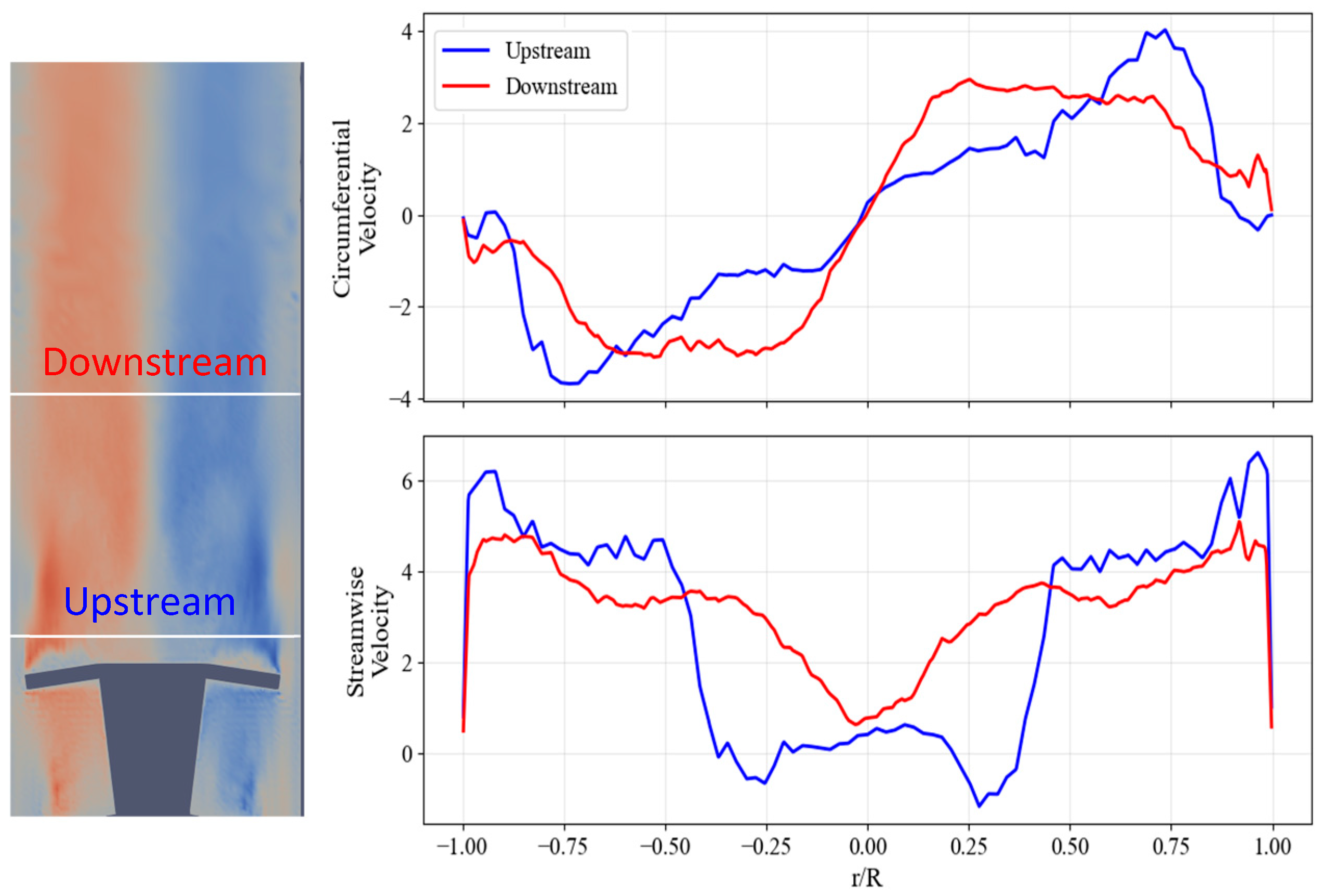
3.2.2. Results
3.3. Simulations of a 360 Model
3.3.1. Boundary Conditions and Mesh Design
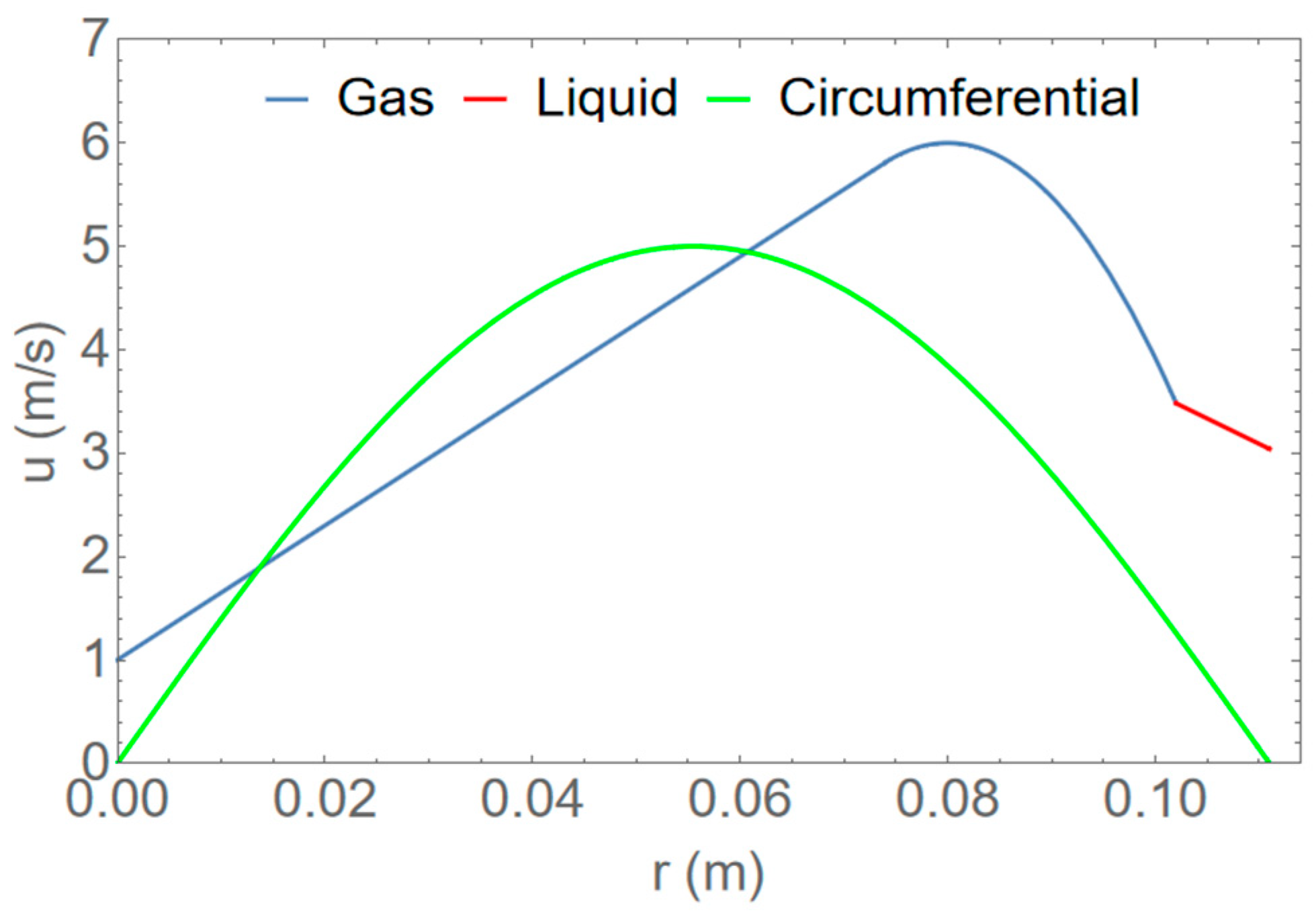
3.3.2. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lahey, R.T.; Moody, F.J. The Thermal-Hydraulics of a Boiling Water Nuclear Reactor; American Nuclear Society: Washington, DC, USA, 1993. [Google Scholar]
- Kataoka, H.; Shinkai, Y.; Hosokawa, S.; Tomiyama, A. Swirling Annular Flow in a Steam Separator. J. Eng. Gas Turbines Power 2009, 131, 032904. [Google Scholar] [CrossRef]
- Katono, K.; Ishida, N.; Sumikawa, T.; Yasuda, K. Air–water downscaled experiments and three-dimensional two-phase flow simulations of improved steam separator for boiling water reactor. Nucl. Eng. Des. 2014, 278, 465–471. [Google Scholar] [CrossRef]
- Funahashi, H.; Hayashi, K.; Hosokawa, S.; Tomiyama, A. Study on two-phase swirling flows in a gas–liquid separator with three pick-off rings. Nucl. Eng. Des. 2016, 308, 205–213. [Google Scholar] [CrossRef]
- Funahashi, H.; Vierow Kirkland, K.; Hayashi, K.; Hosokawa, S.; Tomiyama, A. Interfacial and wall friction factors of swirling annular flow in a vertical pipe. Nucl. Eng. Des. 2018, 330, 97–105. [Google Scholar] [CrossRef]
- Matsubayashi, T.; Katono, K.; Hayashi, K.; Tomiyama, A. Effects of swirler shape on swirling annular flow in a gas–liquid separator. Nucl. Eng. Des. 2012, 249, 63–70. [Google Scholar] [CrossRef]
- Carson, W.R.; Williams, H.K. Method of Reducing Carry-Over and Reducing Pressure Drop Through Steam Separators; Combustion Engineering, Inc.: Chattanooga, TN, USA, 1980; EPRI-NP-1607, 6711746. [Google Scholar] [CrossRef]
- Kataoka, H.; Shinkai, Y.; Tomiyama, A. Pressure Drop in Two-Phase Swirling Flow in a Steam Separator. J. Power Energy Syst. 2009, 3, 382–392. [Google Scholar] [CrossRef]
- Mochizuki, H.; Hirao, Y. Development of Steam Separator Performance Analysis Code and Its Validation, (III): Validation of Code for Carryover. J. Nucl. Sci. Technol. 1994, 31, 782–795. [Google Scholar] [CrossRef]
- Fang, J.; Bolotnov, I.A. Bubble tracking analysis of PWR two-phase flow simulations based on the level set method. Nucl. Eng. Des. 2017, 323, 68–77. [Google Scholar] [CrossRef]
- Fang, J.; Cambareri, J.J.; Rasquin, M.; Gouws, A.; Balakrishnan, R.; Jansen, K.E.; Bolotnov, I.A. Interface Tracking Investigation of Geometric Effects on the Bubbly Flow in PWR Subchannels. Nucl. Sci. Eng. 2019, 193, 46–62. [Google Scholar] [CrossRef]
- Popov, E.L.; Mecham, N.J.; Bolotnov, I.A. Direct Numerical Simulation of Involute Channel Turbulence. J. Fluids Eng. 2024, 146, 081301. [Google Scholar] [CrossRef]
- Iskhakova, A.; Kondo, Y.; Tanimoto, K.; Dinh, N.T.; Bolotnov, I.A. Interface Capturing Flow Boiling Simulations in a Compact Heat Exchanger. ASME J. Heat Mass Transf. 2023, 145, 041605. [Google Scholar] [CrossRef]
- Fang, J.; Purser, M.K.; Smith, C.; Balakrishnan, R.; Bolotnov, I.A.; Jansen, K.E. Annular Flow Simulation Supported by Iterative In-Memory Mesh Adaptation. Nucl. Sci. Eng. 2020, 194, 676–689. [Google Scholar] [CrossRef]
- Rodriguez, J.M. Numerical Simulation of Two-Phase Annular Flow; Rensselaer Polytechnic Institute: Troy, NY, USA, 2009. [Google Scholar]
- Sussman, M.; Smereka, P.; Osher, S. A Level Set Approach for Computing Solutions to Incompressible Two-Phase Flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Nagrath, S. Adaptive Stabilized Finite Element Analysis of Multi-Phase Flows Using Level Set Approach; Rensselaer Polytechnic Institute: Troy, NY, USA, 2004. [Google Scholar]
- Whiting, C.H. Stabilized Finite Element Methods for Fluid Dynamics Using a Hierarchical Basis; Rensselaer Polytechnic Institute: Troy, NY, USA, 1999. [Google Scholar]
- Whiting, C.H.; Jansen, K.E. A stabilized finite element method for the incompressible Navier-Stokes equations using a hierarchical basis. Int. J. Numer. Methods Fluids 2001, 35, 93–116. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Jansen, K.E.; Whiting, C.H.; Hulbert, G.M. A generalized-α method for integrating the filtered Navier–Stokes equations with a stabilized finite element method. Comput. Methods Appl. Mech. Eng. 2000, 190, 305–319. [Google Scholar] [CrossRef]
- Funahashi, H.; Hayashi, K.; Hosokawa, S.; Tomiyama, A. Improvement of separator performance with modified pick-off ring and swirler. Nucl. Eng. Des. 2017, 322, 360–367. [Google Scholar] [CrossRef]
- Povolny, A.; Katono, K.; Heck, C.; Zhang, Z. BWRX-300 SMR Chimney Evaluations (2): Strategy for Qualifying TRACG Evaluations of Chimney Void Fractions. In Proceedings of the 20th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH-20), Washington, DC, USA, 20–25 August 2023; American Nuclear Society: Washington, DC, USA, 2023; pp. 5824–5837. [Google Scholar] [CrossRef]
- Grubbs, T.; Faizee, I.; Bolotnov, I.A. Interface Resolved Simulation of Two-Phase Flow within a Steam Separator Geometry. In Proceedings of the NUTHOS-14, Vancouver, BC, Canada, 25–28 August 2024. [Google Scholar]
- Moser, R.D.; Kim, J.; Mansour, N.N. Direct numerical simulation of turbulent channel flow up to Reτ=5200. Phys. Fluids 1999, 11, 943–945. [Google Scholar] [CrossRef]
- Wallis, G.B. Annular Two-Phase Flow—Part 2: Additional Effects. J. Basic Eng. 1970, 92, 73–81. [Google Scholar] [CrossRef]
- Tornberg, A.-K.; Engquist, B. A finite element based level-set method for multiphase flow applications. Comput. Vis. Sci. 2000, 3, 93–101. [Google Scholar] [CrossRef]
- Russo, G.; Smereka, P. A Remark on Computing Distance Functions. J. Comput. Phys. 2000, 163, 51–67. [Google Scholar] [CrossRef]
- Ibanez, D.A.; Seol, E.S.; Smith, C.W.; Shephard, M.S. PUMI: Parallel Unstructured Mesh Infrastructure. ACM Trans. Math. Softw. 2016, 42, 17. [Google Scholar] [CrossRef]
- Ahrens, J.; Geveci, B.; Law, C. ParaView: An End-User Tool for Large-Data Visualization. In Visualization Handbook; Elsevier: Amsterdam, The Netherlands, 2005; pp. 717–731. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef]
- Grubbs, T.; Bolotnov, I.A. Steam Flow Simulation through the Swirler Section of a Steam Separator. In Proceedings of the ANS Advances in Thermal Hydraulics, Orlando, FL, USA, 17–21 November 2024. [Google Scholar]
- Grubbs, T.; Bolotnov, I.A. Interface Resolved Simulation of Two-Phase Flow within a 360 Steam Separator Geometry. In Proceedings of the the American Physical Society—Gallery of Fluid Motion, Salt Lake City, UT, USA, 24–26 November 2024. [Google Scholar] [CrossRef]
- Olsson, E.; Kreiss, G. A conservative level set method for two phase flow. J. Comput. Phys. 2005, 210, 225–246. [Google Scholar] [CrossRef]
- Talley, M.; Zimmer, M.; Bolotnov, I. Coalescence Prevention Algorithm for Level Set Method. J. Fluids Eng. 2017, 139, 081301. [Google Scholar] [CrossRef]









| Water Density (kg/m3) | 736.65 |
| Steam Density (kg/m3) | 37.5 |
| Water Viscosity (Pa s) | 2.27 × 10−3 |
| Steam Viscosity (Pa s) | 4.85 × 10−4 |
| Surface Tension Coefficient (N/m) | 0.02 |
| Inlet Superficial Gas Velocity (m/s) | 6.45 |
| Inlet Superficial Liquid Velocity (m/s) | 0.55 |
| Inlet Flow Quality (%) | 37.2 |
| Inlet Void Fraction | 0.795 |
| Name | Smallest Element Size | Element Count | Simulated Time | Elements per Core | Core Hours Used |
|---|---|---|---|---|---|
| Coarse | 0.6 mm | 25 million | 0.94 s | 3052 | 0.126 million |
| Intermediate | 0.3 mm | 200 million | 0.91 s | 6103 | 2.45 million |
| Fine | 0.15 mm | 1.6 billion | 0.24 s | 24,414 | 6.44 million |
| Quantity | Order of Convergence | GCI |
|---|---|---|
| Void Fraction | 5.40 | 0.01% |
| Film Thickness | 5.78 | 0.02% |
| Carryover | 0.85 | 29.42% |
| Carryunder | 4.61 | 0.4% |
| Steam Density (kg/m3) | 37.5 |
| Steam Viscosity (Pa s) | 1.94 × 10−5 |
| Inlet Velocity (m/s) | 3.75 |
| Inlet Volumetric flow rate (m3/s) | 0.145 |
| Mesh size (millions of elements) | 5.43 |
| 90 |
| Water Density (kg/m3) | 736.65 |
| Steam Density (kg/m3) | 37.5 |
| Water Viscosity (Pa s) | 9.06 × 10−5 |
| Steam Viscosity (Pa s) | 1.94 × 10−5 |
| Surface Tension Coefficient (N/m) | 0.02 |
| Inlet Superficial Gas Velocity (m/s) | 3.975 |
| Inlet Superficial Liquid Velocity (m/s) | 0.46 |
| Inlet Flow Quality (%) | 30.5 |
| Inlet Void Fraction/Film Thickness | 0.84/9 mm |
| Case | Carryunder (%) | Carryover (%) |
|---|---|---|
| No swirl | 4.54 | 14.3 |
| With swirl | 1.02 | 21.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grubbs, T.E.; Bolotnov, I.A. Two-Phase Flow Studies in Steam Separators Using Interface Capturing Simulations. J. Nucl. Eng. 2025, 6, 42. https://doi.org/10.3390/jne6040042
Grubbs TE, Bolotnov IA. Two-Phase Flow Studies in Steam Separators Using Interface Capturing Simulations. Journal of Nuclear Engineering. 2025; 6(4):42. https://doi.org/10.3390/jne6040042
Chicago/Turabian StyleGrubbs, Taylor E., and Igor A. Bolotnov. 2025. "Two-Phase Flow Studies in Steam Separators Using Interface Capturing Simulations" Journal of Nuclear Engineering 6, no. 4: 42. https://doi.org/10.3390/jne6040042
APA StyleGrubbs, T. E., & Bolotnov, I. A. (2025). Two-Phase Flow Studies in Steam Separators Using Interface Capturing Simulations. Journal of Nuclear Engineering, 6(4), 42. https://doi.org/10.3390/jne6040042






