Development of Importance Measures Reflecting the Risk Triplet in Dynamic Probabilistic Risk Assessment: A Case Study Using MELCOR and RAPID ^†

Abstract

While traditional risk importance measures in probabilistic risk assessment are effective for ranking safety-significant components, they often overlook critical aspects such as the timing of accident progression and consequences. Dynamic probabilistic risk assessment offers a framework to quantify such risk information, but standardized approaches for estimating risk importance measures remain underdeveloped. This study addresses this gap by: (1) reviewing traditional risk importance measures and their regulatory applications, highlighting their limitations, and introducing newly proposed risk-triplet-based risk importance measures, consisting of timing-based worth, frequency-based worth, and consequence-based worth; (2) conducting a case study of Level 2 dynamic probabilistic risk assessment using the Japan Atomic Energy Agency’s RAPID tool coupled with the severe accident code of MELCOR 2.2 to simulate a station blackout scenario in a boiling water reactor, generating probabilistically sampled sequences with quantified timing, frequency, and consequence of source term release; (3) demonstrating that the new risk importance measures provide differentiated insights into risk significance, enabling multidimensional prioritization of systems and mitigation strategies; for example, the timing-based worth quantifies the delay effect of mitigation systems, and the consequence-based worth evaluates consequence-mitigating potential. This study underscores the potential of dynamic probabilistic risk assessment and risk-triplet-based risk importance measures to support risk-informed and performance-based regulatory decision-making, particularly in contexts where the timing and severity of accident consequences are critical.

1. Introduction

This article is a revised and expanded version of a paper entitled Tanaka et al. [1].

Risk-informed decision making (RIDM) integrates probabilistic risk assessment (PRA), deterministic safety analysis, and operational experience to support rational and safety-focused regulatory and operational decisions. Institutions such as the U.S. Nuclear Regulatory Commission (USNRC) and the Nuclear Regulation Authority of Japan (JNRA) advocate for RIDM as a means to enhance regulatory efficiency, optimize safety margins, and allocate resources based on actual risk significance [2,3]. Within this framework, PRA is essential. Unlike traditional deterministic approaches, PRA provides a structured methodology to analyze accident scenarios, frequencies, consequences, and associated uncertainties. It enables the identification of risk-significant systems and accident sequences, supporting prioritization of safety measures based on their contributions to overall plant risk [4]. Under the risk-informed performance-based (RIPB) regulatory framework, the PRA approach has been widely embedded in the USNRC regulatory practices [5], including the maintenance rule (10 CFR 50.65) [6], reactor oversight process (ROP) [7], risk-informed decisions on plant-specific changes to the licensing basis (e.g., Regulatory Guide 1.174) [8], risk-informed in-service inspection (RI-ISI) [9], risk-informed categorization and treatment of structures, systems, and components (SSCs) in 10 CFR 50.69 [10], and risk-informed performance-based fire protection programs in 10 CFR 50.48 [11].

Particularly, in the USNRC regulation 10 CFR 50.69, SSCs are categorized into four risk-informed safety classes (RISC). This categorization uses a risk-informed process, often involving insights from PRA, to determine the safety significance of an SSC’s function. The categorization considers both the deterministic regulatory judgment of an SSC (safety-related or nonsafety-related) and its determined safety significance (high or low risk significance). A “safety significant function” is defined as a function where degradation or loss could significantly negatively impact defense-in-depth, safety margin, or risk. Four categories are RISC-1 (safety-related SSCs that perform safety-significant functions), RISC-2 (nonsafety-related SSCs that perform safety-significant functions), RISC-3 (safety-related SSCs that perform low safety-significant functions) and RISC-4 (nonsafety-related SSCs that perform low safety-significant functions). To facilitate an overall assessment of the safety significance of SSCs, an integrated computation is performed using risk importance measures (RIMs). The risk significance assessment process uses two standard PRA importance measures, risk achievement worth (RAW) and Fussell–Vesely (FV), as screening tools to identify candidate safety-significant SSCs [12]. In general safety assessments of complex engineering systems, some components and their arrangements may be more critical than others in terms of system reliability. There are traditional indices for measuring the importance of components: Birnbaum, criticality, FV, risk reduction worth (RRW), RAW [13].

Despite their utility, traditional RIMs are typically derived from static PRA models based on event trees (ETs) and fault trees (FTs). These models treat component failures as binary and do not fully capture the timing of events or the progression of complex accident scenarios. As a result, traditional RIMs may overlook key factors in severe accidents, such as the time margin available for accident mitigation measures or the evolving magnitude of radiological releases. To address these limitations, dynamic PRA has emerged as an advanced methodology. It integrates time-dependent deterministic simulations with probabilistic modeling of system behaviors, enabling consideration of system interactions, operator responses, and physical phenomena as they evolve over time. In other words, dynamic PRA uses a time-dependent phenomenological model of plant evolution along with its stochastic behavior [14], and stochastic and deterministic behaviors of plant elements are modeled as building blocks of the risk model [15]. This allows for a richer estimation of the risk triplets, which are defined as $R=〈S_i,P_i,C_i〉,i=\mathrm{1,2},\cdots ,N$, where $S$ is the scenario, $P$ is the frequency, and $C$ is the consequence [16].

New risk importance measures that can reflect timing thereby need to be developed for identifying the risk significance of pivotal events such as the actuation of accident mitigation and the loss of containment function, in which the actuation and dysfunction timing are crucial for system reliability. To complete the dynamic PRA methodology, the authors have proposed a new concept of risk-triplet-based RIMs that can provide more information for risk-informed decision making, such as the timing and amount of source term release into the environment during severe accidents [17]. The new RIMs are written as $\mathrm{R}\mathrm{I}\mathrm{M}\mathrm{s}=\langle \mathrm{T}\mathrm{B}\mathrm{W},\mathrm{F}\mathrm{B}\mathrm{W},\mathrm{C}\mathrm{B}\mathrm{W}\rangle$. It includes timing-based worth (TBW), frequency-based worth (FBW), and consequence-based worth (CBW). While the FBW is in accordance with the traditional PRA importance measures, the TBW and CBW indicate the adequacy of time-margin increase and consequence mitigation for assessing the effects of accident countermeasures. To prove the applicability of the new RIMs, the authors try to perform a Level 2 dynamic PRA application.

The remainder of this paper is organized as follows. Section 2 reviews traditional RIMs and their applications in risk-informed regulation, then introduces the definitions of the proposed RIMs. Section 3 introduces the dynamic PRA approach and the computational tool of RAPID (risk assessment with plant interactive dynamics) [18]. Section 4 presents a case study using the severe accident code of MELCOR [19] and RAPID to evaluate the new RIMs. Section 5 concludes with key insights and future research directions.

2. Investigation of Importance Measures and Their Regulatory Applications

2.1. Traditional Risk Importance Measures

RIMs are essential tools in PRA for quantifying how individual components or systems influence overall plant risk. These indices provide structured ways to assess safety significance by estimating the extent to which a component’s performance, whether successful or failed, affects the likelihood of adverse outcomes such as core damage or radiological release. Within the risk-informed framework, these RIMs serve as analytical tools for prioritizing regulatory actions, maintenance, inspection, and design enhancements. Table 1 summarizes the definitions of the widely used traditional RIMs [20,21], each of which offers a distinct perspective on component significance depending on the system structure and the reliability or unreliability of individual components [13]. The RIMs are compared as follows.

• Birnbaum importance reflects how frequently a component is involved in minimal cut sets (MCSs) leading to system failure, providing an absolute sensitivity metric purely based on system structure.
• Criticality importance quantifies the change in system failure probability due to perturbations in the failure probability of a component, again as an absolute measure.
• FV is a relative measure indicating the proportion of total system risk attributable to failure paths involving the component. FV is often used to identify components whose failure paths are dominant contributors to risk, useful in prioritizing inspection or system upgrades.
• RRW represents the decrease in system risk when a component is assumed to operate with perfect reliability. RRW helps to identify components where enhanced reliability would yield the most risk reduction, guiding system redesign or upgrade decisions.
• RAW quantifies the increase in system risk when a component is assumed to fail with certainty, relative to the baseline condition. RAW is essential for highlighting components whose failure would significantly degrade safety, supporting preventive maintenance strategies.

These RIMs are extensively used because of their simplicity and compatibility with classical PRA methods. FV, RAW, and RRW are particularly useful in regulatory applications due to their normalized, dimensionless nature, allowing for comparisons across systems and scenarios [22]. As such, their use is best suited for steady-state risk profiles or aggregated metrics such as core damage frequency (CDF) or large early release frequency (LERF).

Table 1. Traditional RIMs and definitions [23].

RIM	Definition	Interpretation and Comments
Birnbaum	${Bi}_i={R_i^{+}-R}_i^{-}$	Absolute measure; $\mathrm{Shows} \mathrm{how} \mathrm{often} \mathrm{component} i$ is needed to prevent system failure.
Criticality	${Cr}_i=\left(R_i^{+}-R_i^{-}\right){\displaystyle \frac{p_i}{R_0}}$	Absolute measure; $\mathrm{Shows} \mathrm{the} \mathrm{sensitivity} \mathrm{of} \mathrm{system} \mathrm{failure} \mathrm{probability} \mathrm{with} \mathrm{respect} \mathrm{of} \mathrm{failure} \mathrm{probability} \mathrm{of} \mathrm{component} i$.
FV	${FV}_i={\displaystyle \frac{R_0-R_i^{-}}{R_0}}$	Dimensionless and relative measure; $\mathrm{Shows} \mathrm{the} \mathrm{fraction} \mathrm{of} \mathrm{system} \mathrm{risk} \mathrm{involving} \mathrm{failure} \mathrm{of} \mathrm{component} i$.
RRW	${RRW}_i={\displaystyle \frac{R_0}{R_i^{-}}}$	Dimensionless and relative measure; $\mathrm{Shows} \mathrm{relative} \mathrm{overall} \mathrm{system} \mathrm{improvement} \mathrm{by} \mathrm{improving} \mathrm{component} i$.
RAW	${RAW}_i={\displaystyle \frac{R_i^{+}}{R_0}}$	Dimensionless and relative measure; $\mathrm{Shows} \mathrm{relative} \mathrm{overall} \mathrm{deterioration} \mathrm{due} \mathrm{to} \mathrm{the} \mathrm{failure} \mathrm{of} \mathrm{component} i$.

$R_0$: the present “nominal” risk level; $R_i^{+}$: the increased risk level with component $i$ assumed failed; $R_i^{-}$: the decreased risk level with component $i$ assumed to be perfectly reliable; $p_i$: failure probability of component $i$.

Table 1. Traditional RIMs and definitions [23].

RIM	Definition	Interpretation and Comments
Birnbaum	${Bi}_i={R_i^{+}-R}_i^{-}$	Absolute measure; $\mathrm{Shows} \mathrm{how} \mathrm{often} \mathrm{component} i$ is needed to prevent system failure.
Criticality	${Cr}_i=\left(R_i^{+}-R_i^{-}\right){\displaystyle \frac{p_i}{R_0}}$	Absolute measure; $\mathrm{Shows} \mathrm{the} \mathrm{sensitivity} \mathrm{of} \mathrm{system} \mathrm{failure} \mathrm{probability} \mathrm{with} \mathrm{respect} \mathrm{of} \mathrm{failure} \mathrm{probability} \mathrm{of} \mathrm{component} i$.
FV	${FV}_i={\displaystyle \frac{R_0-R_i^{-}}{R_0}}$	Dimensionless and relative measure; $\mathrm{Shows} \mathrm{the} \mathrm{fraction} \mathrm{of} \mathrm{system} \mathrm{risk} \mathrm{involving} \mathrm{failure} \mathrm{of} \mathrm{component} i$.
RRW	${RRW}_i={\displaystyle \frac{R_0}{R_i^{-}}}$	Dimensionless and relative measure; $\mathrm{Shows} \mathrm{relative} \mathrm{overall} \mathrm{system} \mathrm{improvement} \mathrm{by} \mathrm{improving} \mathrm{component} i$.
RAW	${RAW}_i={\displaystyle \frac{R_i^{+}}{R_0}}$	Dimensionless and relative measure; $\mathrm{Shows} \mathrm{relative} \mathrm{overall} \mathrm{deterioration} \mathrm{due} \mathrm{to} \mathrm{the} \mathrm{failure} \mathrm{of} \mathrm{component} i$.

$R_0$: the present “nominal” risk level; $R_i^{+}$: the increased risk level with component $i$ assumed failed; $R_i^{-}$: the decreased risk level with component $i$ assumed to be perfectly reliable; $p_i$: failure probability of component $i$.

Nonetheless, the limitations of these indices become apparent when applied to more complex or time-dependent situations. Traditional RIMs are typically derived from static models, using ETs and FTs to represent system configurations and accident sequences. These models assume binary component states and predefined logic, which simplifies quantification but may omit time-dependent phenomena. Traditional RIMs do not reflect the sequence or timing of events, but such factors are crucial in severe accident scenarios. For example, a component may have limited impact on accident frequency but may be critical for delaying containment failure or reducing offsite consequences.

2.2. Regulatory Applications of Risk Importance Measures

RIMs are widely adopted in risk-informed regulatory frameworks, particularly within the United States and increasingly in Japan. The USNRC has embedded RIMs into numerous licensing and oversight activities. Except for the traditional RIMs, incremental risk (e.g., ∆CDF and ∆LERF) can be found in regulatory activities for importance determination. As shown in Equation (1), the risk increment caused by the failure of component $i$ can also be written in a unified form, the same as the RIMs in Table 1.

$$∆R=R_i^{+}-R_0$$

(1)

Table 2. The use of RIMs in regulatory activities.

	Risk-Informed Regulatory Activities	Representative RIMs	References
1	Risk-informed SSC categorization and treatment of SSCs for nuclear power reactors	FV, RAW	10 CFR 50.69 [10] NEI 00-04 [12]
2	Risk-informed changes to technical specifications, evaluation of completion time and surveillance frequency	ICDF, ILERF, incremental core damage probability (ICDP), incremental large early release probability (ILERP)	USNRC RG 1.177 [24] NEI 06-09 [25] NEI 04-10 [26]
3	Maintenance rule	RRW, RAW, CDF contribution (ranking of cut sets inclusion)	10 CFR 50.65 [6] USNRC RG 1.160 [27] NUMARC 93-01 [28]
4	Reactor oversight process: significance determination process, inspection planning	∆CDF, ∆LERF	NUREG-1649 [7] USNRC Inspection Manual Manual chapter 0609 [29] Inspection procedure 71111 [30]
5	Licensing application activities of small modular reactors	Birnbaum, FV, RRW, RAW	Design certification applications [31]: NuScale VOYGR, Westinghouse AP300, HOLTEC SMR-160

outlines the representative USNRC regulatory applications where importance measures serve as foundational tools.

• In the categorization of SSCs under 10 CFR 50.69, FV and RAW are used to assign components into safety significance categories, thereby influencing requirements for inspection, maintenance, and quality assurance.
• For technical specification changes (10 CFR 50.59, RG 1.177), incremental CDF (ICDF) and incremental LERF (ILERF) are evaluated to support changes in surveillance frequency (SF) and allowed outage time (AOT).
• Under the maintenance rule (10 CFR 50.65), FV, RAW, and RRW are used to identify critical components for reliability-centered maintenance strategies.
• The reactor oversight process (ROP) utilizes these RIMs to support the significance determination process (SDP), which classifies inspection findings by their risk significance. The ROP approach has also been introduced by the JNRA as part of Japan’s regulatory modernization.
• In the licensing of small modular reactors (SMRs), risk insights derived from RIMs are employed to assess the adequacy of safety design features and proposed regulatory exemptions.

In all these applications, RIMs provide the quantitative foundation for RIDM. Their ability to rank and screen SSCs based on their impact on risk allows regulators and licensees to focus resources where they matter most. However, as system behaviors become more time-sensitive and interdependent, new importance measures are required to accurately reflect their influence on risk outcomes, especially when the increasing complexity of reactor systems and the growing use of dynamic simulations in PRA highlight the limitations of conventional RIMs.

2.3. Risk-Triplet-Based Importance Measures for Dynamic PRA

The use of traditional RIMs for dynamic PRA has been presented previously, and it has been confirmed that traditional RIMs (e.g., FV and RAW) can also be determined from simulation-based data from dynamic PRA instead of MCSs [32]. Traditional RIMs are effective for ranking component significance within static models but do not readily capture dynamic phenomena such as timing of failure, mitigation onset, or consequence evolution. Recognizing the limitations of traditional frequency-based RIMs, a new class of RIMs based on the risk triplet concept has been proposed by Narukawa et al. [17] and is adopted in this study. These measures facilitate nuanced evaluation of accident mitigation strategies and support advanced RIDM by providing insights into the feasibility (timing), likelihood (frequency), and severity (consequence) of events under dynamic conditions. Written in the form of triplets, $RIMs=\langle TBW, FBW, CBW\rangle$ as well, these new measures are defined as follows.

• TBW (Timing-Based Worth): Reflects the relative delay or advancement in the expected time to an adverse end state (e.g., core damage or source term release) due to a basic event. Note that the expectations and conditional expectations in the numerators and denominators of Equations (2)–(4) are intentionally structured and differ in order. Specifically, Equation (2) is formulated such that a TBW value greater than 1 indicates that the failure of the component tends to accelerate the progression toward adverse end states. This design emphasizes the component’s temporal significance in the context of accident evolution and underscores its importance from a timing-based perspective.

$${TBW}_i={\displaystyle \frac{E\left[t\right]}{E\left[t\left|i\right.\right]}}$$

(2)

• FBW (Frequency-Based Worth): Represents the change in frequency or probability of the adverse end state due to the event, analogous to FV or RAW.

$${FBW}_i={\displaystyle \frac{E\left[f\left|i\right.\right]}{E\left[f\right]}}$$

(3)

• CBW (Consequence-Based Worth): Measures the variation in radiological consequence (e.g., source term release magnitude) due to the event.

$${CBW}_i={\displaystyle \frac{\mathrm{E}\left[c\left|i\right.\right]}{E\left[c\right]}}$$

(4)

where:

• $E\left[t\right]$: Expected timing of end state (e.g., source term release),
• $E\left[f\right]$: Expected frequency of the end state,
• $E\left[c\right]$: Expected consequence (e.g., source term magnitude),
• $\mathrm{E}\left[t\left|i\right.\right]$, $\mathrm{E}\left[f\left|i\right.\right]$, $\mathrm{E}\left[c\left|i\right.\right]$: The conditional expectations are computed assuming the occurrence of basic event $i$.

By incorporating the timing and consequence considerations, these RIMs allow for more granular evaluation of event significance by capturing whether an event accelerates accident progression, increases its likelihood, or worsens its consequences. As such, risk-triplet-based RIMs better support modern risk-informed regulation, especially in contexts involving severe accidents, passive systems, or operator-driven mitigation strategies. The following sections explore the practical application of these new RIMs using a dynamic Level 2 PRA of a boiling water reactor (BWR) station blackout (SBO) scenario simulated via the RAPID tool and MELCOR code.

3. JAEA’s Dynamic PRA Approach and Computational Tool

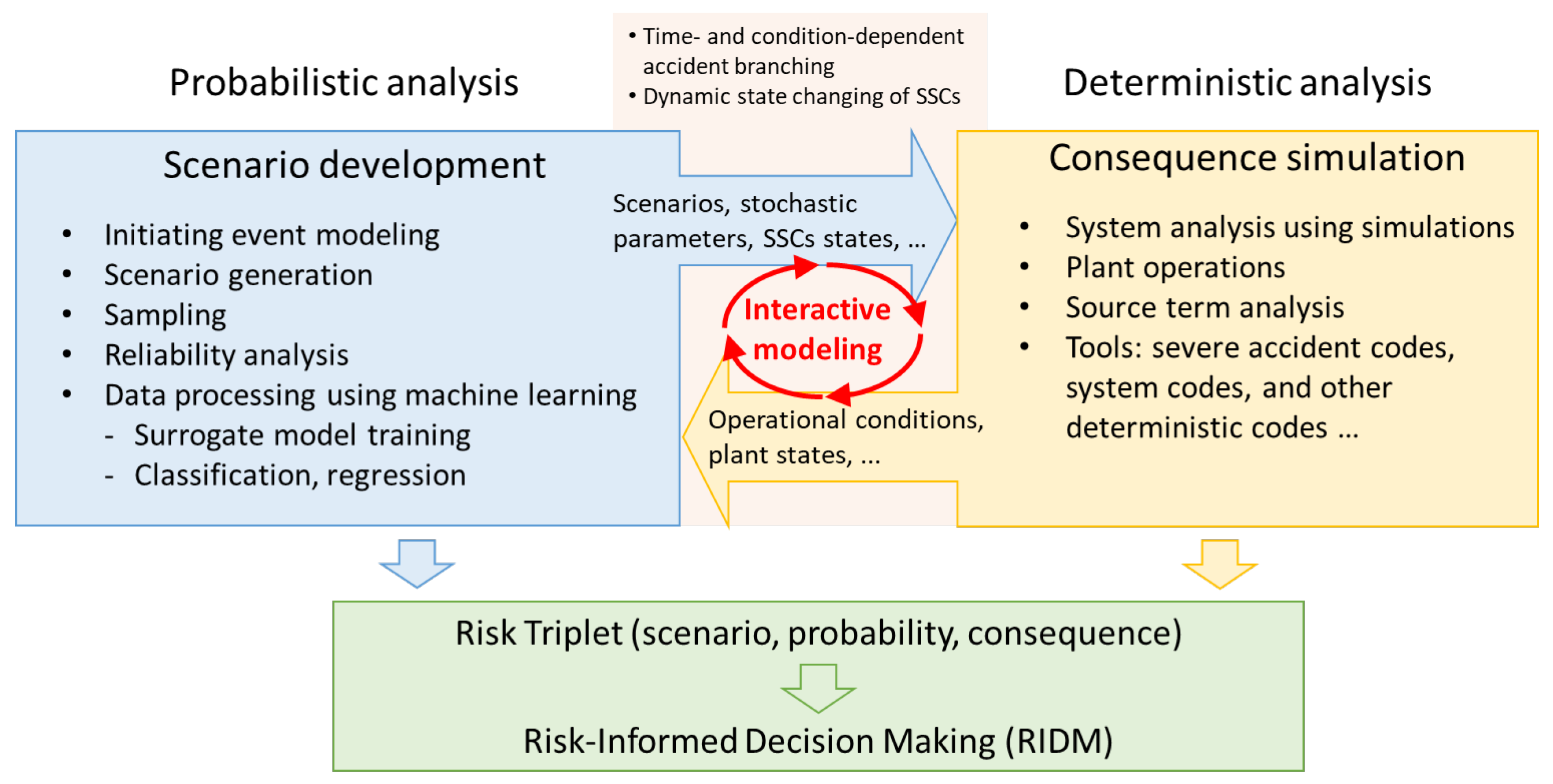
3.1. Overview of the Dynamic PRA Approach

Dynamic PRA extends the traditional PRA framework by explicitly modeling the time-dependent evolution of accident sequences and system behaviors. It integrates probabilistic sampling of initiating events and uncertain parameters with high-fidelity deterministic simulations, thus enabling comprehensive exploration of system responses over time. This capability is critical for modeling complex phenomena such as operator intervention timing, gradual equipment degradation, delayed system failures, and physical processes like hydrogen accumulation, containment pressurization, core relocation, or radiological source term release. Traditional PRA techniques based on ETs and FTs rely on a binary, static representation of system states and discrete sequence branching. These methods often overlook the dynamic interplay of component interactions and time-critical events, especially in the context of severe accidents. In contrast, dynamic PRA supports the probabilistic exploration of accident scenarios in a continuous time framework. It allows analysts to quantify not only whether safety functions are successful or failed but also when and under what conditions such successes or failures occur.

Over the past decades, dynamic PRA approaches have been developed and advanced, and numerous computational tools have emerged worldwide, with various applications to nuclear reactor risk assessment. As depicted in Figure 1, at JAEA, the development of dynamic PRA follows concepts from both the Integrated Deterministic and Probabilistic Safety Assessment (IDPSA) approach [33] and the Risk-Informed Safety Margin Characterization (RISMC) methodology [34], both aiming to incorporate temporal and stochastic variations systematically into the PRA process. The dynamic PRA framework under development comprises two key elements: a probabilistic scenario generator, which stochastically samples uncertain inputs and branching events, and a deterministic simulator, which evaluates the physical progression of each accident scenario. The outputs of these simulations are then synthesized to produce quantitative risk information, typically expressed as a spectrum of risk triplets—scenario, frequency, and consequence—known as Kaplan and Garrick’s foundational definition of risk [16]. By doing so, dynamic PRA addresses both aleatory uncertainty (inherent variability of accident outcomes) and epistemic uncertainty (parameter, model, and incompleteness uncertainties) in a consistent and traceable manner [14]. This framework enables the analysis of risk in a more holistic and time-sensitive manner, supporting applications that extend beyond static CDF or LERF estimation. For example, it allows for assessment of the duration time of mitigation measures, the timing and efficiency of recovery actions, and the comparative benefit of design alternatives under uncertainty. These features align with contemporary needs for RIDM and performance-based safety assessment.

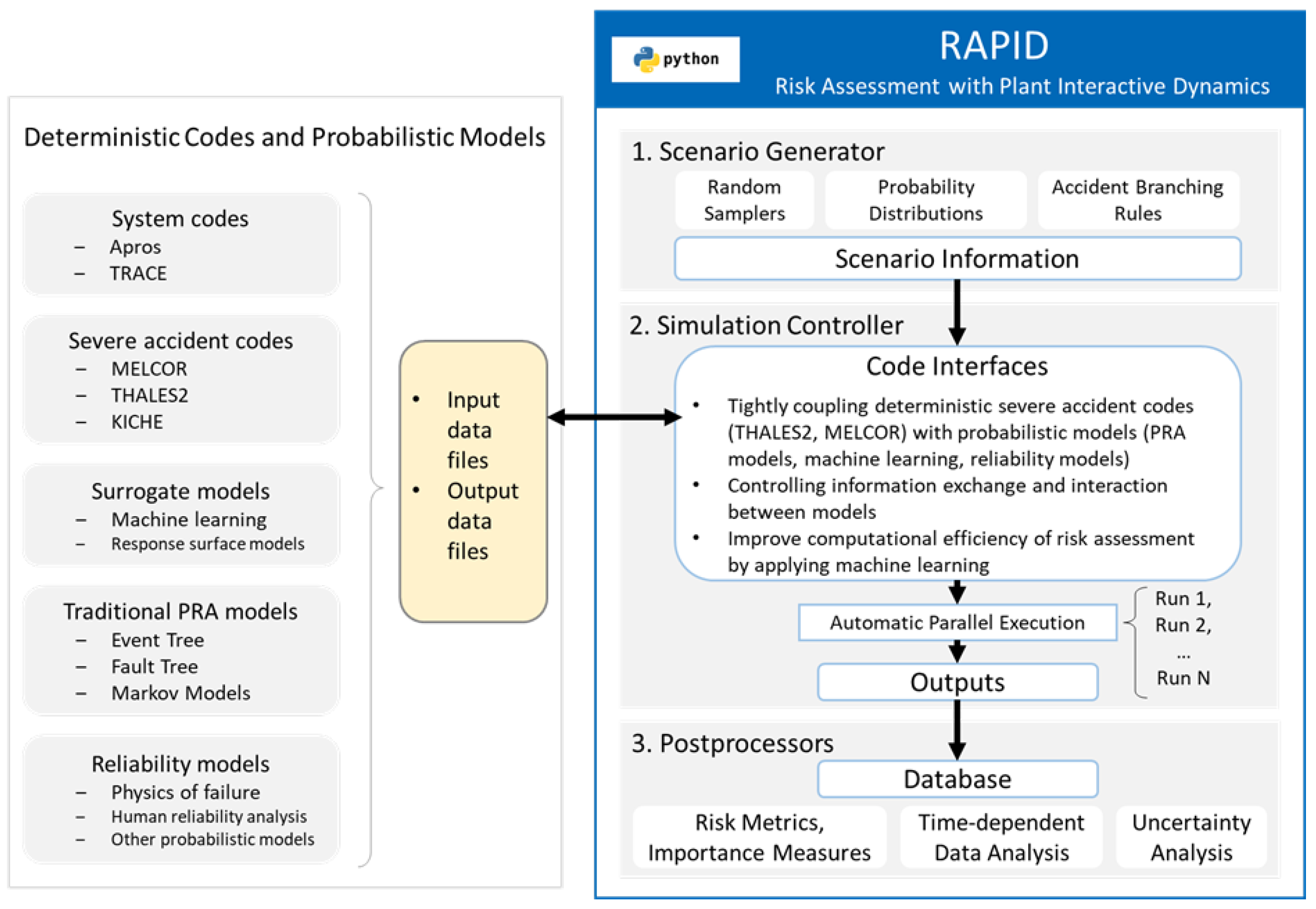
3.2. The RAPID Tool for Dynamic PRA Implementation

To implement the dynamic PRA methodology, JAEA is developing a computational platform named RAPID, a modular simulation framework designed to support dynamic PRA. RAPID integrates probabilistic modeling, deterministic safety code execution, and risk metric evaluation into a unified computational platform. Its architecture is designed for flexibility, scalability, and compatibility with multiple analysis tools and reactor types.

As illustrated in Figure 2, the RAPID tool consists of three primary modules: The first is the scenario generator, which creates accident scenarios by sampling probabilistic distributions assigned to initiating events, system or component failures, and timing uncertainties. These scenarios are encoded with the logic of event tree branches but allow for stochastic variation in both system states and occurrence timings.

The second module is the simulation controller, which orchestrates the execution of deterministic simulations using external simulation codes. In this study, RAPID interfaces with MELCOR 2.2, a severe accident analysis code developed by Sandia National Laboratories. MELCOR models the detailed thermal–hydraulic and structural behavior of reactor systems as well as the transportation behaviors of radiological source terms under the condition of severe accidents. Through RAPID, hundreds or thousands of MELCOR simulations can be run with varied inputs to capture the probabilistic space of accident evolutions.

The third module is the post-processor, which compiles the simulation outputs to compute key risk metrics. These include traditional risk metrics (CDF, LERF, etc.), event timing (e.g., time to core damage or containment breach), and radiological consequence (e.g., source term release time and magnitude). This output can be used to quantify risk triplets and compute advanced risk importance measures, such as TBW, FBW, and CBW.

RAPID supports large-scale simulations on high-performance computing (HPC) platforms and can be extended with surrogate modeling techniques to alleviate computational burden. For sequences with low probability but high consequence, machine learning-based surrogate models may be trained to approximate MELCOR outputs, enabling broader coverage of the risk space with limited sacrifices of accuracy. By enabling direct integration between probabilistic models and detailed simulations, RAPID provides a platform for generating time-dependent, triplet-based risk assessments. This capability enhances the realism and regulatory relevance of PRA and facilitates its application to modern challenges such as advanced reactor designs, passive system evaluations, and integrated risk-informed planning.

The modular and extensible architecture of RAPID facilitates integration with various simulation tools and allows for tailored configurations for different PRA levels (e.g., Level 1 PRA of core damage, Level 2 PRA of source terms, Level 3 PRA of offsite consequences). In the next section, the application of RAPID and the risk-triplet-based RIMs to a Level 2 dynamic PRA case study for a BWR under an SBO scenario is presented in detail.

4. Trial Measurement of the Proposed Risk Metrics Using Level 2 Dynamic PRA

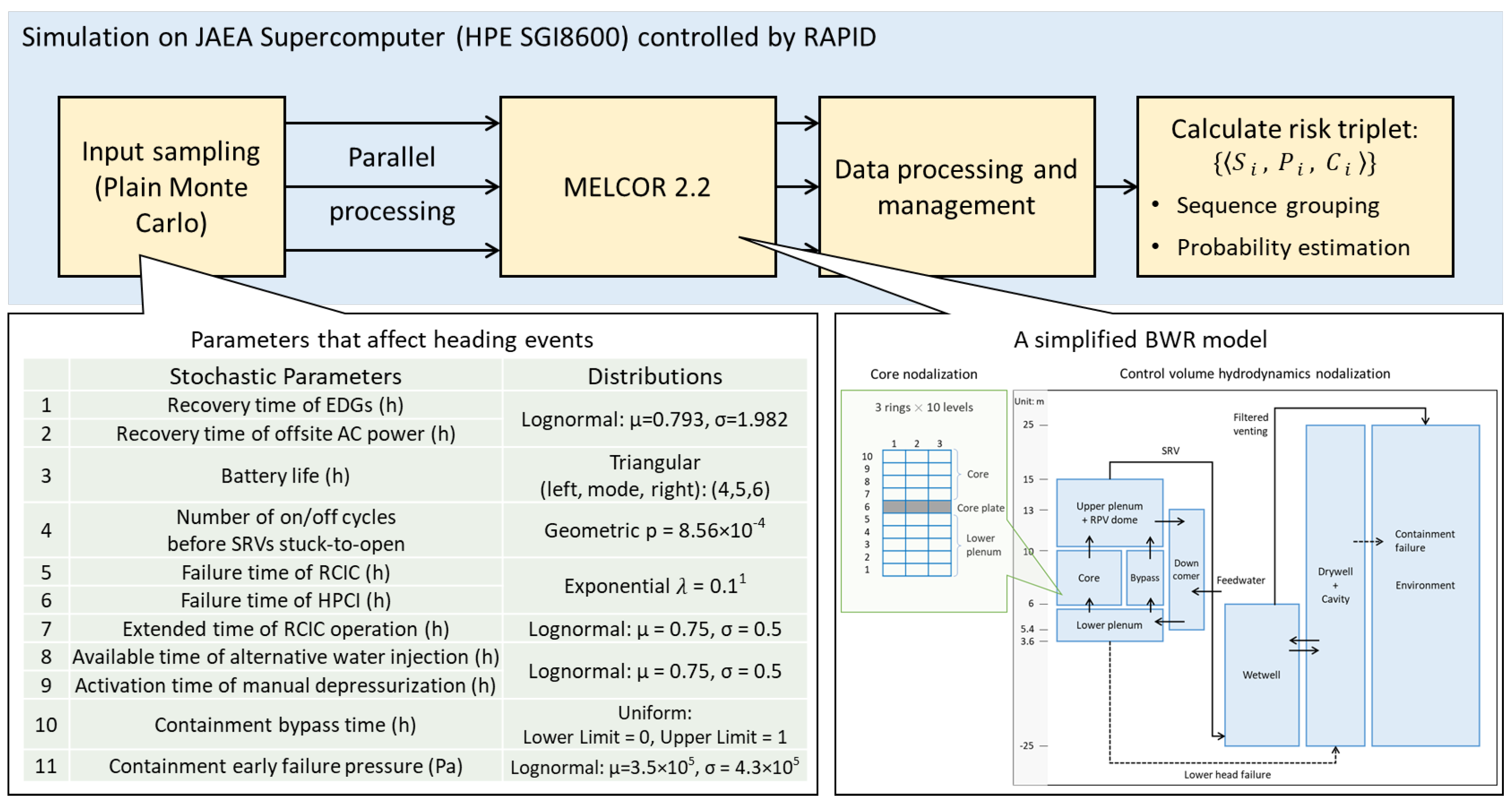
4.1. Scenario Setup and Model Description

To assess the utility of the proposed RIMs, a Level 2 dynamic PRA was conducted for a BWR experiencing an SBO that is historically recognized (e.g., the Fukushima Daiichi nuclear power plant accident) for its severe accident potential. This study employs the RAPID tool in conjunction with the MELCOR 2.2 code to simulate probabilistic accident sequences and their deterministic progression.

Practical PRA models are typically complex, involving numerous ET headings and interdependent system interactions. To focus the analysis on the proposed RIMs and enable clearer comparison with prior dynamic PRA studies [35], a simplified ET model was applied. This model emphasizes the most critical safety functions, specifically, core cooling and containment integrity.

The plant model is based on a representative BWR plant with a Mark I containment design. Key engineered safety features are retained to preserve realism while reducing model complexity. These include the reactor pressure vessel (RPV), with detailed representations of the core region, bypass paths, and upper/lower plenums; hydraulic connectivity between the RPV and containment volumes (drywell and wetwell); and essential safety systems such as the safety relief valve (SRV), high-pressure coolant injection (HPCI), reactor core isolation cooling (RCIC), and the containment venting system.

Moreover, to manage computational complexity while maintaining representativeness, the containment event tree (CET) was reduced to focus on two dominant containment failure modes for the Mark I containment, including bypass failure, representing direct release pathways through failed isolation, and overpressure failure, representing structural failure due to uncontrolled pressure rise [36].

Figure 3 illustrates the integrated calculation process, showing the interaction between stochastic event tree sampling, MELCOR-based scenario simulation, and risk metric extraction. The input deck used for MELCOR simulations is adapted from a BWR benchmark model originally developed by Sandia National Laboratories [19]. Eleven stochastic parameters, with probability distributions shown in Figure 3, are introduced to reflect uncertainties in system availability and response timing. These include branch points related to the success or failure of mitigation actions, timing of offsite power recovery, and containment integrity under varying conditions.

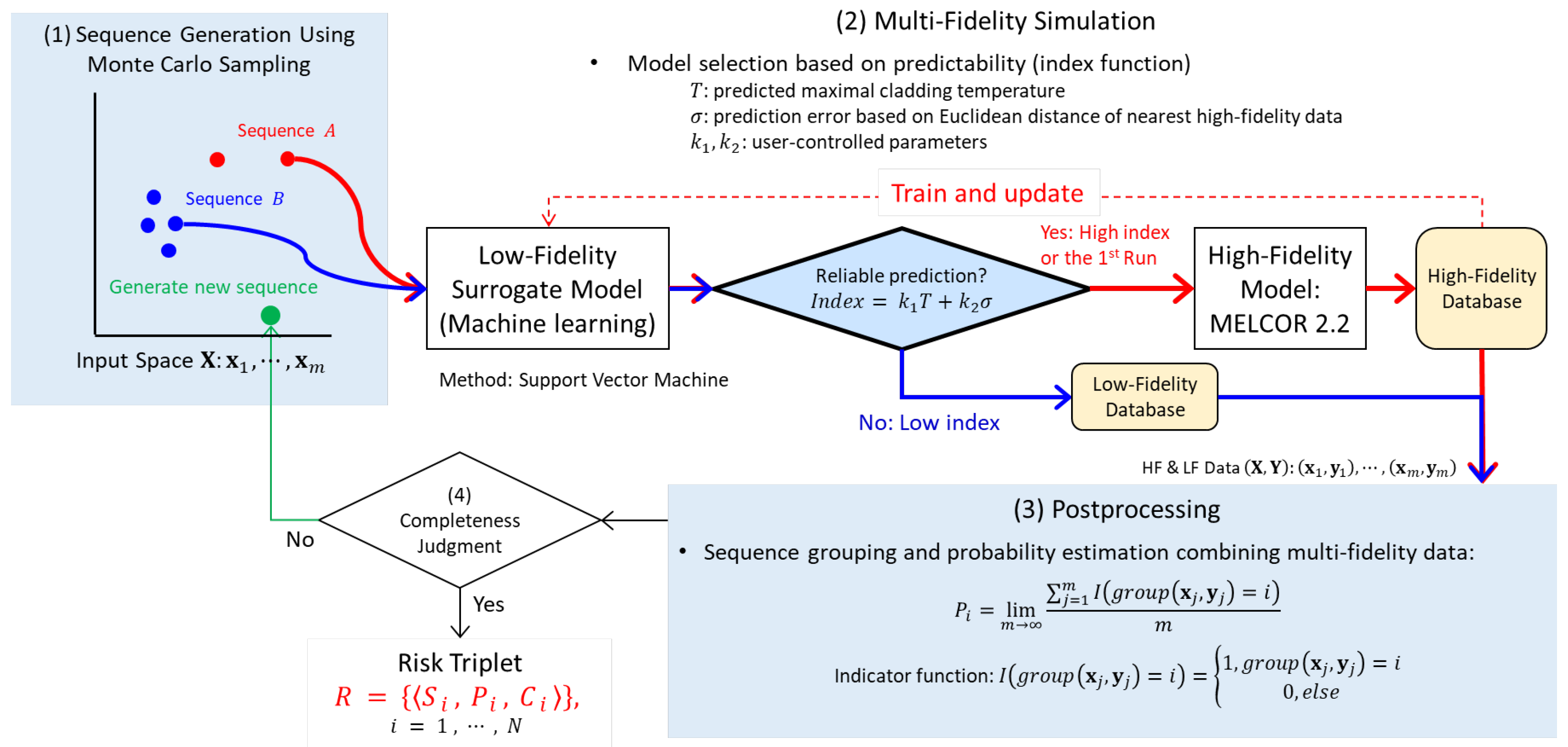
4.2. Simulation Process and Computational Enhancements

A large number of accident sequences were generated using RAPID’s scenario sampling module. Each sequence represents a unique realization of the SBO scenario, characterized by different outcomes for key event-tree branches. These sequences are simulated using MELCOR to capture the time-dependent physical phenomena relevant to core heat-up and degradation, onset and timing of core damage and vessel breach, hydrogen generation and transport, containment pressurization and failure, and source term release quantities and timing.

To address the computational burden associated with sampling low-frequency but high-consequence accident sequences, this study adopts a multi-fidelity Monte Carlo (MFMC) approach enhanced by a machine learning-based surrogate model [37,38]. As illustrated in Figure 4, the MFMC approach consists of four primary steps:

(1)

Sequence generation using Monte Carlo sampling

At each simulation iteration, a new accident sequence is generated using conventional Monte Carlo sampling. This sampled accident sequence setting becomes the input for the second multi-fidelity simulation step.

(2)

Multi-fidelity simulation using MELCOR and a machine learning surrogate

The simulation begins with high-fidelity MELCOR runs to generate an initial dataset. This dataset is then used to train a support vector machine (SVM) surrogate model that predicts accident progression metrics; for example, peak cladding temperature (PCT). In subsequent iterations, the framework dynamically selects between the high-fidelity MELCOR code and the surrogate model based on an index function, shown in Equation (5).

As an example, this function combines the surrogate-predicted PCT (T) and an estimated prediction uncertainty (σ), derived from the Euclidean distance to the nearest training data points. The parameters $k_1$ and $k_2$ are user-defined weights balancing consequence magnitude and prediction confidence.

If the surrogate prediction is deemed reliable (i.e., the index is below a threshold), the surrogate is used; otherwise, MELCOR is executed. As high-fidelity simulations accumulate, the surrogate is incrementally retrained to improve accuracy and coverage.

$$Index=k_{1}T+k_2\sigma$$

(5)

(3)

Post-processing for risk characterization

For each scenario, the conditional probability is calculated based on the frequency of occurrence within each accident category. Consequences such as core damage metrics and sequence timing are also extracted.

(4)

Completeness check via probability distribution convergence

The simulation concludes when the estimated probability distributions converge. Final risk triplets, comprising extracted sequences, probabilities, consequences, and timing, are then synthesized from the MFMC dataset. This hybrid MFMC framework enabled efficient exploration of the accident sequence space for obtaining stable probability estimations. A total of 1.34 × 10⁶ sequences were simulated, balancing surrogate predictions with high-fidelity MELCOR runs to optimize both computational efficiency and modeling realism.

A specific parameter setting was examined for detailed results: the probability of the SRV stuck-open condition was fixed at a representative value. To make the simulation data more understandable, Figure 5 summarizes the results using the ET model, presenting the estimated frequency of each accident sequence, the timing of the source term release, and the release fraction to the environment. These parameters provide insight into both the temporal and severity dimensions of risk. Based on the assumptions, 20 dominant accident sequences were identified with non-negligible contributions to the risk profile. Among them, sequences 4, 5, 9, 10, 14, 15, 19, and 20 led to core damage followed by containment failure, resulting in direct environmental release of the source term. These sequences form the basis for evaluating the proposed RIMs.

4.3. Risk Importance Measure Evaluation and Results

The proposed risk-triplet-based RIMs were quantitatively evaluated for selected ET headings using results from dynamic Level 2 PRA simulations. These simulations were performed and analyzed using the postprocessing module of the RAPID tool. Following the generation of randomized accident sequences, the resulting data were categorized by ET sequence type, and representative statistical features were extracted. Specifically, the key parameters used for RIM calculation include sequence occurrence probability, average source term release time, and source term release fraction, as illustrated in Figure 5.

These statistical descriptors form the basis for calculating RIMs for each ET heading.

Table 3. Preliminary results of importance analysis using the new RIMs.

Event-Tree Headings	TBW	FBW	CBW
SRV Close	1.044	4.888	1.156
HPCI or RCIC	1.656	19.28	0.990
Depressurization and Alternative Water Injection	0.999	1.297	1.000
Offsite or EDGs Recovery	0.999	71.53	1.000
Containment Isolated or Not Bypass	1.128	298.1	3.707
No Containment Overpressure Failure	0.971	59.61	0.289

presents the calculated TBW, FBW, and CBW for six pivotal event-tree headings. Each metric reflects a distinct dimension of risk importance. TBW quantifies the influence on the timing of adverse outcomes, FBW captures the frequency-related sensitivity, and CBW measures the severity or consequence variation due to basic events. Table 3 summarizes the computed RIM values for six pivotal ET headings. The following key insights were derived from the analysis:

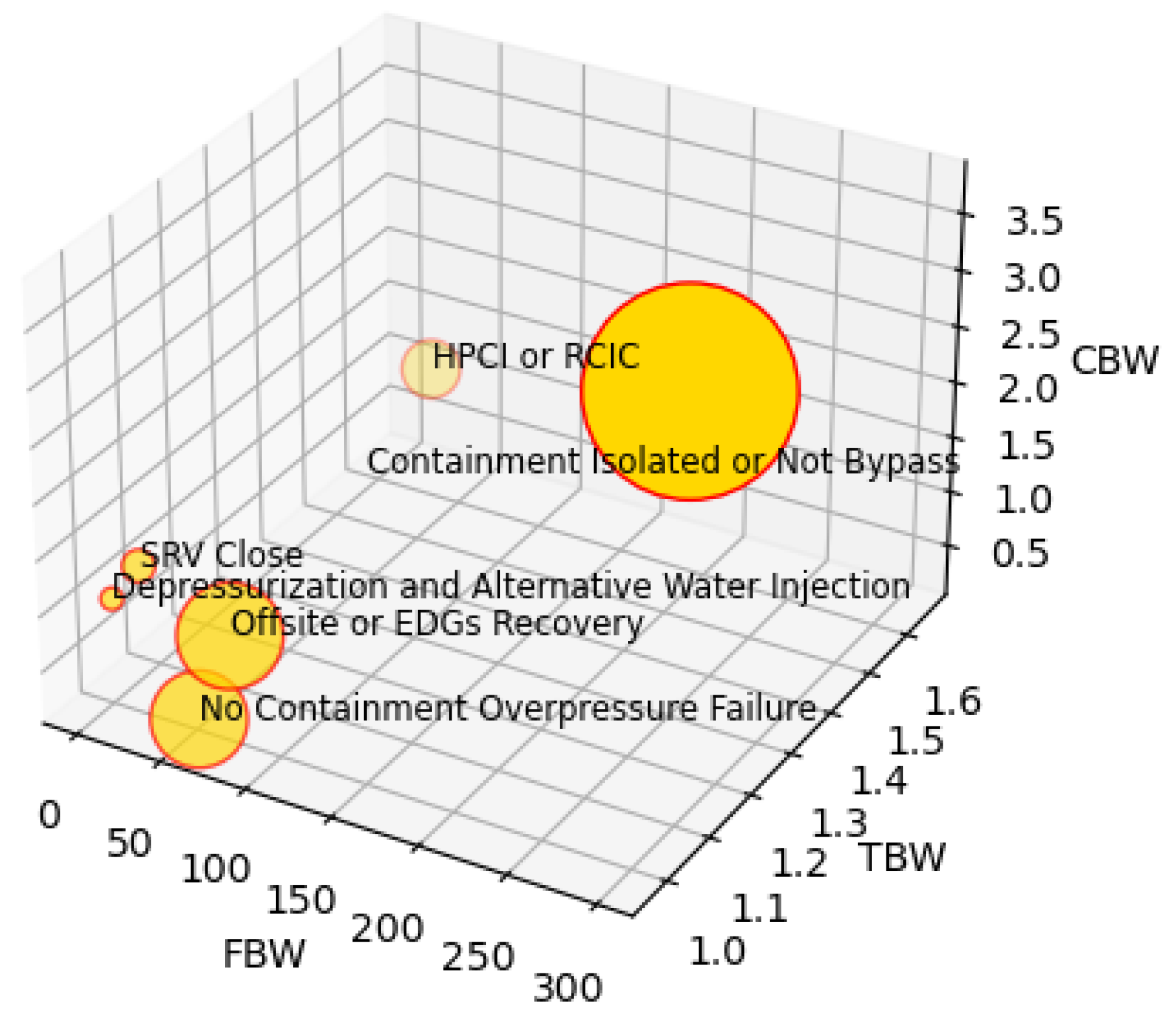
• The heading of “Containment Isolation or Not Bypass” exhibits the highest FBW (298.1) and CBW (3.707), emphasizing its critical function as the last barrier preventing uncontrolled release of radionuclides. Failure to isolate the containment significantly increases both the probability and magnitude of radiological consequences due to direct bypass paths.
• For the heading of “No Containment Overpressure Failure”, FBW is also high (59.61) and CBW is notably low (0.289), suggesting that overpressure failures tend to result in more gradual or filtered releases compared to bypass failures. TBW < 1 (0.971) indicates that the overpressure failure tends to occur later than the containment bypass.
• This mitigation systems of “HPCI or RCIC” have a prominent TBW of 1.656, confirming its effectiveness in delaying core damage and source term release. Although FBW (19.28) is substantial, CBW (0.990) remains near unity, indicating neutral impact on consequence magnitude, consistent with its delay-oriented function.
• The heading of “Offsite or EDGs Recovery” shows substantial FBW (71.5), with TBW and CBW values close to 1.0, implying their primary contribution lies in reducing the frequency of severe accidents, rather than influencing timing or consequence severity.
• The heading of “SRV Close” shows modest TBW (1.044) and FBW (4.888), with a relatively low CBW (1.156), suggesting only a limited role in altering release conditions compared to containment-related events.

These results demonstrate the practical capability of the proposed metrics to capture nuanced roles of key systems. TBW uncovers time-critical systems for accident mitigation, FBW efficiently identifies risk-reducing systems, and CBW reveals systems pivotal to radiological consequence mitigation. This multidimensional insight is particularly valuable for risk-informed system prioritization, mitigation strategy design, and emergency planning. It also enables regulators and operators to evaluate systems not only by how often they matter but also when and how much they influence safety outcomes.

From a regulatory and plant safety perspective, these results may provide meaningful insights; for example, (1) insights for risk-informed SSC prioritization: headings with high FBW and CBW should be prioritized for design, maintenance, and operational robustness (e.g., containment isolation or not bypass); (2) insights for timing-critical countermeasures: headings with high TBW highlight systems that can delay critical events, buying time for recovery or operator intervention (e.g., HPCI or RCIC); (3) insights for consequence-sensitive decision support: high CBW events (e.g., containment isolation or not bypass) affect public health risk and emergency response planning, guiding strategies for filtered venting, sheltering, or evacuation. Furthermore, by quantifying these effects through simulation-based metrics, the approach overcomes the limitations of MCS-based importance analysis in traditional PRA and aligns with risk-informed, performance-based regulation, as advocated by the USNRC and increasingly recognized internationally.

The bubble chart in Figure 6 illustrates the importance rankings of key event-tree headings based on the RIMs. The horizontal axes represent the TBW and FBW, while the vertical axis shows the CBW. The area of each circle corresponds to the sum of three metrics, as shown in Equation (6), thus collectively visualizing the multidimensional impact of each heading on overall risk. The chart highlights the differentiated roles of components, enabling effective prioritization of risk-significant systems from the perspectives of timing, frequency, and consequence. This figure visually reinforces the numerical findings in Table 3 and enables intuitive interpretation for stakeholders involved in safety assessments, plant design reviews, or regulatory evaluations.

$$Area of circle=sum(TBW, FBW, CBW)$$

(6)

5. Conclusions and Future Work

This study proposed and applied a new set of risk importance measures based on the risk triplet (timing, frequency, and consequence) using a dynamic Level 2 PRA case study. The RIMs, namely TBW, FBW, and CBW, were evaluated using RAPID-MELCOR simulations of an SBO in a BWR with Mark I containment. The simulation-based approach enabled the direct quantification of each risk dimension as influenced by the selected ET headings. The key technical conclusions are summarized below.

• Traditional RIMs have shown applicability in nuclear regulation; for instance, the risk-informed categorization of SSCs, risk-informed changes to technical specifications, application of maintenance rule, the reactor oversight process, which has also been introduced to the regulatory system by the JNRA, and licensing application activities of small modular reactors, to name a few. While traditional RIMs offer valuable insights, they primarily reflect frequency-based influence. They often fall short in addressing time-critical mitigation actions or consequence-limiting system behavior, which are increasingly important in RIDM, especially for severe accident management.
• The newly proposed RIMs enable a more nuanced characterization of component and system importance. TBW introduced a time-resolved dimension that proved valuable for identifying components and systems that delay the progression of severe accidents, which is particularly relevant for emergency response planning and mitigation timing. FBW aligned closely with traditional frequency-based importance measures, reaffirming its role in quantifying the probability of adverse outcomes. CBW added consequence sensitivity to the analysis, revealing which events and systems most influence the magnitude of radionuclide release.
• The proposed risk-triplet-based RIMs offer a more comprehensive foundation for RIDM by incorporating not only the probability of events but also the timing and severity of their consequences. This multidimensional perspective enables more informed system prioritization, particularly in applications such as severe accident management, design optimization for advanced reactors, and emergency response planning. By leveraging a simulation-driven framework, the approach is especially well-suited for evaluating emerging technologies, such as accident-tolerant fuels (ATFs), that exhibit enhanced performance in delaying core damage progression and reducing hydrogen generation. These new metrics enhance the realism and relevance of PRA results in guiding safety-focused innovation.
• This study also demonstrated the technical feasibility and practical utility of RAPID as a dynamic PRA platform capable of handling extensive simulations and integrating with deterministic analysis tools such as MELCOR. The use of surrogate modeling further expanded the scope of scenario coverage while maintaining computational efficiency, highlighting a scalable pathway for broader applications.

This approach aligns with the emphasis on integrating both deterministic and probabilistic information for regulatory decision-making, particularly for complex or evolving new reactor technologies (e.g., small modular reactors). By extending the concept of risk importance to include timing and consequence dimensions within a dynamic PRA context, this study offers a concrete step forward toward more comprehensive RIDM. As nuclear systems become increasingly complex and societal expectations for safety transparency grow, such multidimensional risk insights will be essential for sustaining public confidence and regulatory credibility.

In advancing the state of PRA, the proposed metrics and tools offer a pathway toward more holistic, data-informed, and context-sensitive approaches to nuclear safety regulation. However, the dynamic PRA approach and the proposed RIMs inherently depend on computationally intensive simulations, which can present practical challenges in applying risk insights to real-time decision-making or regulatory evaluations. Moreover, these methods introduce various sources of uncertainty, including those related to modeling assumptions, input data variability, and scenario sampling, which currently lack comprehensive validation and verification frameworks. To ensure that dynamic PRA can support credible, risk-informed decisions, future research must address these limitations by developing systematic uncertainty quantification (UQ) methodologies and integrating them into the risk assessment process. This includes exploring probabilistic treatment of modeling parameters, temporal variability, and human reliability, as well as leveraging surrogate modeling via machine learning methods to improve computational efficiency. These efforts will be essential to enhance the realism, transparency, and robustness of dynamic PRA applications, especially as they are extended to the regulation of advanced reactors and innovative fuel technologies such as ATFs.