Dynamic Probabilistic Risk Assessment of Passive Safety Systems for LOCA Analysis Using EMRALD

Abstract

This research explores Dynamic Probabilistic Risk Assessment (DPRA) using EMRALD to evaluate the reliability and safety of passive safety systems in nuclear reactors, with a focus on mitigating Loss of Coolant Accidents (LOCAs). The BWRX-300 Small Modular Reactor (SMR) is used as an example to illustrate the proposed DPRA methodology, which is broadly applicable for enhancing traditional Probabilistic Safety Assessment (PSA). Unlike static PSA, DPRA incorporates time-dependent interactions and system dynamics, allowing for a more realistic assessment of accident progression. EMRALD enables the modelling of system failures and interactions in real time using dynamic event trees and Monte Carlo simulations. This study identifies critical vulnerabilities in passive safety systems and quantifies the Core Damage Frequency (CDF) under LOCA scenarios. The findings demonstrate the advantages of DPRA over traditional PSA in capturing complex failure mechanisms and providing a more comprehensive and accurate risk assessment. The insights gained from this research contribute to improving passive safety system designs and enhancing nuclear reactor safety strategies for next-generation reactors.

1. Introduction

Nuclear energy continues to be a crucial component of the global energy landscape, valued for its ability to deliver stable and low-carbon power. Over the years, technological advancements have significantly enhanced the safety, efficiency, and reliability of Nuclear Power Plants (NPPs) [1]. One notable innovation in nuclear technology is the development of Small Modular Reactors (SMRs). These reactors, designed to produce up to 300 megawatts of electricity per unit, are factory-fabricated, which reduces construction time and provides flexibility in deployment [2,3,4,5].

One of the leading SMR designs is the BWRX-300, an evolution of the Economic Simplified Boiling Water Reactor (ESBWR), developed by GE Hitachi Nuclear Energy. Built upon decades of experience with Boiling Water Reactor (BWR) technology, the BWRX-300 is distinguished by its simplified operation, lower capital costs, and enhanced safety features. A key aspect of its safety framework is the incorporation of Passive Safety Systems (PSSs) [6], which function autonomously relying on natural forces such as gravity and natural circulation instead of external power or human intervention [7,8,9,10]. These passive systems represent a major advancement in reactor safety, particularly for mitigating risks associated with Loss of Coolant Accidents (LOCAs), where the system is designed to respond automatically to manage the emergency and reduce reliance on active components [11,12]. However, due to the interdependent and complex nature of these systems, thorough safety assessments are essential to ensure their reliability under extreme conditions [13,14]. This study focuses on the safety assessment of the BWRX-300’s PSSs, employing the Dynamic Probabilistic Risk Assessment (DPRA) model to evaluate their effectiveness during a LOCA scenario.

Probabilistic Safety Assessment (PSA) provides a systematic and comprehensive methodology for evaluating NPP safety by identifying potential failure modes and their consequences [15,16,17]. It quantifies the risks associated with various operational scenarios, including equipment malfunctions and human errors [18]. PSA plays a vital role in nuclear safety by assessing the probability and potential impact of accident scenarios such as core damage or radiological release [19,20]. Fault Tree Analysis (FTA) and Event Tree Analysis (ETA) are key techniques within PSA, used to model system reliability and accident progression pathways [21,22]. These techniques help in identifying vulnerabilities in system design and maintenance protocols, contributing to the enhancement of overall safety measures [17]. Recent advancements, such as the integration of DPRA, have significantly enhanced traditional PSA techniques, enabling more precise risk evaluations in complex systems, including multi-unit NPPs [23,24].

Dynamic Probabilistic Risk Assessment (DPRA) is an advanced methodology that enhances traditional PRA by incorporating time-dependent interactions, system dynamics, and stochastic behaviors [25,26]. Unlike traditional PRA, which evaluates risks using static event sequences and fixed probabilities, DPRA models include evolving system states and interactions over time. This approach allows DPRA to reflect the real-time progression of accidents, human interventions, and changing environmental conditions, improving the accuracy of risk assessments under complex scenarios, such as Loss of Coolant Accidents (LOCAs) [27]. Key to DPRA is the use of Dynamic Event Trees (DETs), which map potential sequences of system events and transitions as they evolve [28,29]. DETs were first introduced to improve the treatment of operator actions and system dynamics in accident progression, as demonstrated in early applications such as SGTR analysis [28] and dynamic fault-tree models for fault-tolerant systems [29]. Subsequently, Dynamic Probabilistic Safety Assessment (DPSA) methodologies have evolved with the integration of Discrete-Time Bayesian Networks (DTBNs) and Dynamic Bayesian Networks (DBNs), enabling more accurate representation of state dependencies, common-cause failures, and time-based transitions in complex systems [30,31,32]. These event trees, often combined with Monte Carlo simulations, allow for a probabilistic evaluation of different failure outcomes, considering various uncertainties and temporal dependencies [33]. By capturing the stochastic nature of system failures, DPRA offers a more comprehensive understanding of how risk unfolds during critical incidents [34]. It also addresses both aleatory and epistemic uncertainties, providing a more robust risk evaluation [35,36,37]. One of DPRA’s strengths is its integration with physics-based models, such as thermal–hydraulic codes, which enables detailed modelling of physical phenomena during accidents [38]. This combination helps to assess how system components perform under specific conditions, especially in nuclear reactors where passive safety systems play a significant role [39]. In the context of next-generation nuclear reactors, such as SMRs, DPRA provides enhanced risk assessments by modelling the complex interdependencies and passive safety mechanisms essential for accident mitigation. Its ability to offer real-time risk evaluation and improve operational decision-making makes DPRA a critical tool for advancing nuclear safety [27,33].

In this work, the Event Modelling Risk Assessment using Linked Diagrams (EMRALD) tool is used to implement DPRA for assessing the reliability of passive safety systems in the BWRX-300 during a LOCA scenario. EMRALD provides a flexible framework for modeling complex system interactions, integrating state diagrams, fault trees, and event sequences in a time-dependent manner [40]. By capturing real-time accident progression and system responses, EMRALD facilitates a more detailed risk assessment compared with traditional PSA approaches. This study aims to demonstrate the advantages of DPRA in identifying critical failure points, quantifying Core Damage Frequency (CDF), and enhancing the overall understanding of passive safety system performance in next-generation nuclear reactors. The findings contribute to the ongoing development of more resilient and reliable safety assessment methodologies for SMRs, ensuring their long-term viability as a safe energy source.

This paper is organized as following: Section 2 provides an overview of the passive safety systems in the BWRX-300 and their functions during a LOCA. Section 3 presents the DPRA modeling using EMRALD tool for LOCA analysis; dynamic modeling for Reactor Isolation (RI), Reactor Scram (RS), and Isolation Condenser System (ICS); and the simulation results. Section 4 compares the outcomes from static PRA and DPRA. Lastly, Section 5 concludes the paper with key findings and recommendations for future work.

2. Safety Systems of BWRX-300 During LOCA

The BWRX-300 is equipped with multiple safety mechanisms designed to respond effectively to emergencies such as a Loss of Coolant Accident (LOCA). These systems play a crucial role in regulating reactivity, maintaining core cooling, ensuring long-term heat removal and preserving reactor isolation. While Level 1 PSA primarily focuses on core damage, some analyses may not explicitly account for the containment of radioactive materials. However, the confinement of radioactive materials remains a fundamental safety function during accident scenarios.

Reactor Isolation (RI) systems consist of Reactor Pressure Vessel Isolation Valves (RPVIVs), which act as a safeguard by sealing off the affected sections during a system breach, ensuring that coolant levels within the Reactor Pressure Vessel (RPV) are maintained to prevent core exposure. These integrated safety systems collectively enhance the BWRX-300’s ability to prevent core damage, manage emergencies, and maintain operational stability during LOCA scenarios [6,41].

In emergency situations such as LOCA, the Reactor Scram (RS) mechanism is activated to promptly terminate the nuclear reaction. It comprises the Control Rod Drive System (CRDS) and the Boron Injection System (BIS), which function to rapidly shut down the reactor by introducing negative reactivity. The CRD system rapidly inserts control rods to absorb neutrons, thereby halting fission. Alternatively, the BIS introduces borated water into the reactor core, effectively providing negative reactivity to shut down the reaction [6].

For heat dissipation, the Isolation Condenser System (ICS) transfers excess heat from the reactor core to the ultimate heat sink, preventing overheating and overpressure conditions. Although the BWRX-300 does not include a conventional active Emergency Core Cooling System (ECCS), this safety function is inherently provided by the isolation condensers. The ICS acts as a passive ECCS by removing decay heat through natural circulation and condensation, without relying on active pumps or external power sources [6].

In the event of a LOCA, the plant’s protocol is significantly streamlined to ensure rapid response and mitigation. If a breach occurs and is not immediately isolated, it is assumed that the reactor core will be exposed, thereby risking severe damage. To mitigate this risk, the successful activation of isolation valves is crucial, as it confines the loss of coolant and necessitates a reactor trip to prevent further complications. The final safeguard is the ICS, which must function effectively to maintain continuous cooling of the core.

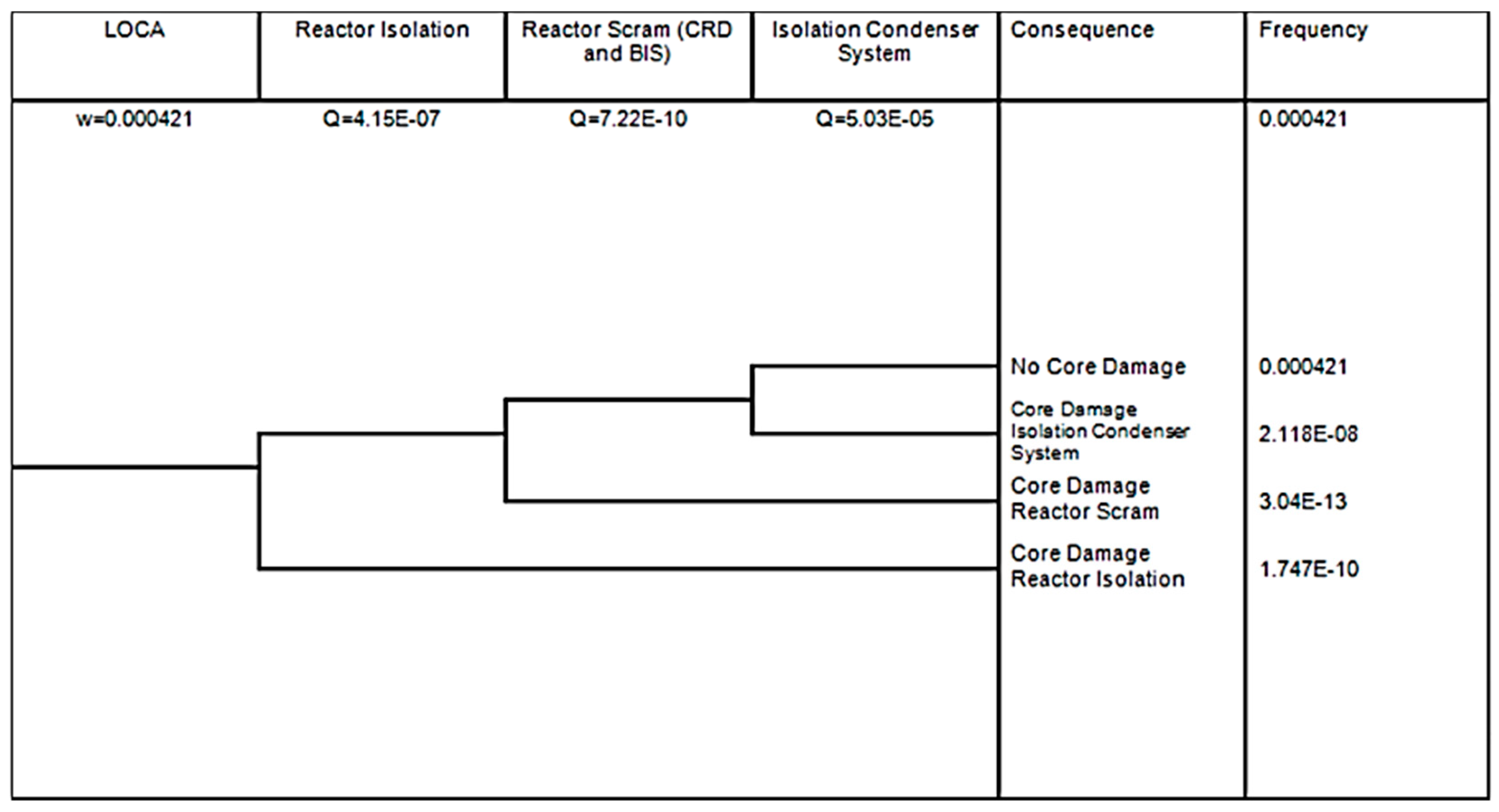
The event tree was developed for the initiating event of a LOCA, detailing the accident progression and the relevant safety function barriers to core damage. The initiating event frequencies for LOCA in BWR are reported in NUREG/CR-6928 using data through 2020. The scope of this study focuses on small- to medium-break LOCAs, based on the initiating event frequencies outlined in NUREG/CR-6928, and the LOCA frequency is $4.21\times {10}^{-3}$ [42]. Figure 1 illustrates the event tree for a LOCA, including the CDF of sequences.

Fault Tree Analysis (FTA) estimates the failure probabilities of the RI, RS, and ICS systems as $4.15\times {10}^{-7}$, $7.22\times {10}^{-10}$, and $5.03\times {10}^{-5}$, respectively. Event Tree Analysis (ETA) calculates the resulting CDF due to RI, RS, and ICS failures as $1.75\times {10}^{-10}$, $3.04\times {10}^{-13}$, and $2.12\times {10}^{-8}$, respectively.

3. DPRA Modelling Using EMRALD

This section details the implementation of the EMRALD-based DPRA model for assessing passive safety systems during a LOCA scenario. It presents the modelling approach, system analyses, and simulation results, highlighting key failure contributors and their impact on core damage frequency.

3.1. EMRALD Overview

EMRALD is a DPRA tool developed at Idaho National Laboratory that enhances traditional PRA by incorporating time-dependent interactions and system behaviors. Unlike static PRA, which relies on predefined event sequences, EMRALD enables real-time event evolution analysis using dynamic event trees and Monte Carlo simulations. Developed under the Light Water Reactor Sustainability (LWRS) project, EMRALD has been tested for various time-dependent scenarios and coupled with physics-based simulations, including seismic-induced internal flooding analysis [40,43]. It integrates DPRA capabilities while maintaining key aspects of traditional PRA, featuring an intuitive web-based graphical interface that allows for seamless modelling of elements, such as basic events, fault trees, and event trees within a dynamic state diagram. Additionally, its open framework supports straightforward coupling with physics codes, enabling a more comprehensive risk assessment by analyzing both probabilistic results and the timing and sequence of events [40].

Several studies have demonstrated EMRALD’s effectiveness in nuclear safety applications. Prescott et al. (2018) highlighted its adaptability to multi-hazard scenarios through seismic-induced internal flooding modeling [40]. Earthperson et al. (2023) applied EMRALD to fission battery risk assessments, showcasing its integration with physics-based simulations for complex failure analysis [44]. Researchers explored its application in human reliability analysis, demonstrating its ability to dynamically model operator actions [45,46,47]. Ulrich et al. (2020) further reinforced its benefits by applying EMRALD to human reliability analysis in nuclear operations, enabling the modeling of evolving human interactions with system states [48]. Beyond nuclear safety, Christian et al. (2021) incorporated EMRALD into security risk assessments, using force-on-force models to evaluate sabotage attack mitigation strategies [49]. These studies confirm EMRALD’s potential as a comprehensive DPRA tool, improving risk assessment across nuclear and other critical infrastructure systems. However, no physics-based models were integrated into this study. The EMRALD analysis was performed using internally defined event logic, state diagrams, and fault trees. While EMRALD supports coupling with thermal–hydraulic codes such as RELAP5 or MELCOR, this capability was not utilized in this analysis.

3.2. DPRA Modelling

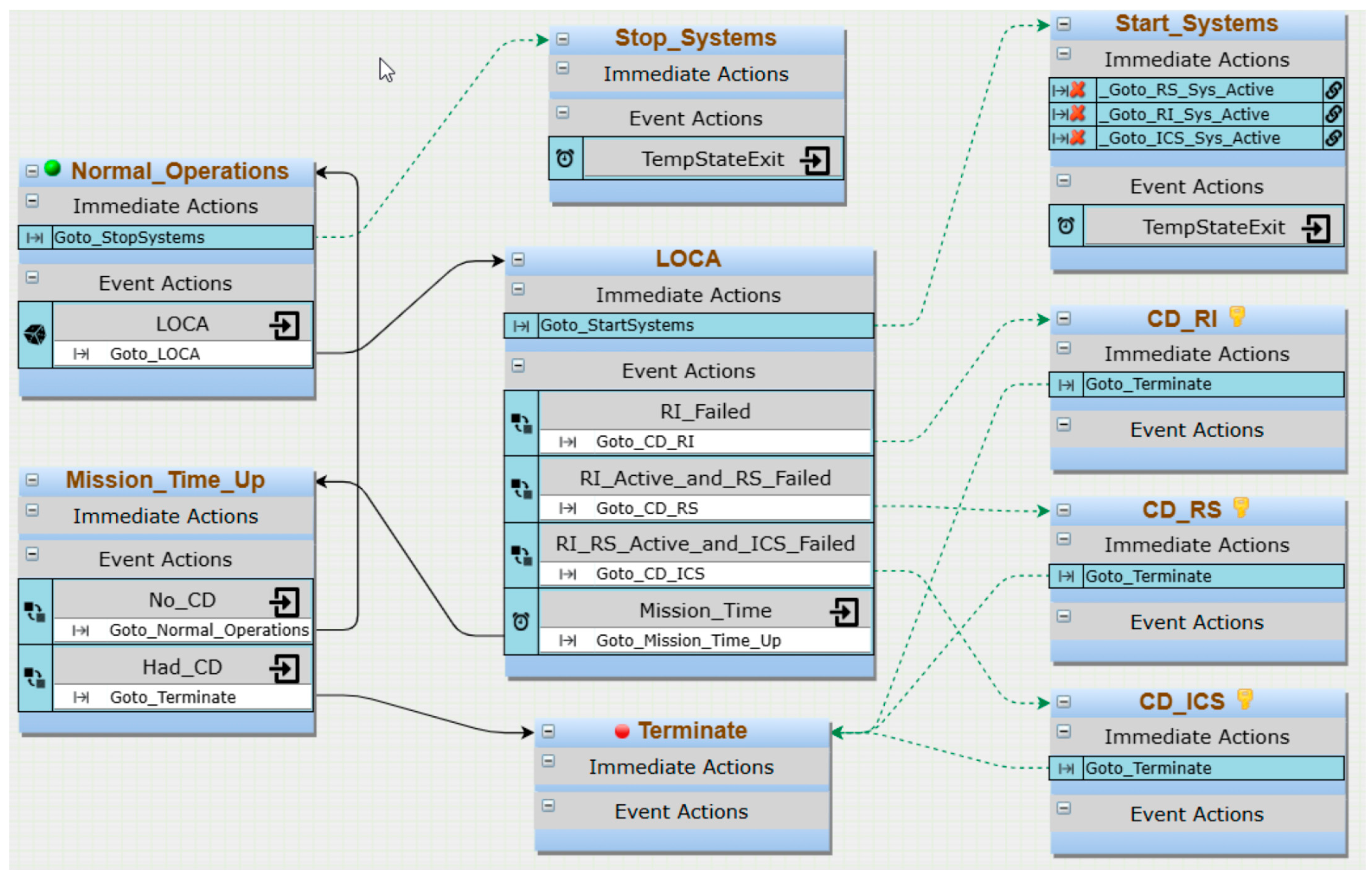
The EMRALD model illustrated in Figure 2 provides a comprehensive analysis of a LOCA and its potential consequences, particularly focusing on CDF. The model is structured around interconnected states and actions, capturing the progression of events and system responses. Initially, the system begins in the “Normal Operations” state, continuously monitoring for any incidents. If a LOCA occurs, the model transitions to the “LOCA” state, triggering immediate actions to start systems, moving next to the “Start_Systems” state. Following this, the “Start_Systems” state initiates emergency responses, such as RS, RI, and ICS.

The model includes state for starting systems, ensuring that the appropriate responses are activated to manage the LOCA. Each of the RS, RI, and ICS systems has its own state, indicating its activation and effectiveness. In the event of system failures, the model transitions to various core damage states. If the RI system fails, the model moves to the “CD_RI” state, indicating core damage due to RI failure. If RI remains active but RS fails, the model moves to “CD_RS,” and if both RI and RS are active but ICS fails, the model transitions to “CD_ICS.”

Additionally, the model tracks the overall mission time through the “Mission_Time_Up” state. If no core damage occurs by the mission’s end, the system returns to “Normal Operations,” but if core damage occurs, it concludes the sequence in the “Terminate” state. By analyzing the timing and sequence of these events, the EMRALD model provides a detailed probabilistic risk assessment, identifying critical points where core damage may occur and quantifying CDF. This dynamic model captures interactions between systems during a LOCA event, offering a thorough framework for understanding and mitigating the risks associated with core damage in nuclear power plants.

The EMRALD model was constructed using a combination of fault trees and state diagrams that represent the logic of the RI, RS, and ICS. Each system was assigned Boolean variables representing operational states (e.g., active or failed), with associated failure probabilities defined for basic events such as component malfunction and signal unavailability. Conditional logic within the EMRALD framework governed transitions between states, allowing the simulation to dynamically explore different event sequences. The Monte Carlo simulation engine sampled these variables across numerous iterations to generate a diverse set of system response pathways under LOCA conditions.

The success criteria for each safety system were defined as follows: RI was considered successful upon full closure of the isolation valves; RS was successful if either control rod insertion or boron injection achieved reactor shutdown; and ICS was successful if two ICS loops operated to remove decay heat.

3.2.1. Reactor Isolation (RI)

The RI system plays a vital role in nuclear reactor safety systems, ensuring the isolation of the reactor from various process lines during emergency conditions [6]. Assessing the safety of RIs is critical to understanding their performance and maintaining the overall safety of the reactor system. Typically, the RI system consists of two series-configured valves, each capable of independently isolating the line [6]. This redundancy guarantees that if one valve fails, the other can still complete the isolation function, enhancing the system’s safety and reliability. The standard RI configuration is designed to fail in the closed position upon loss of power, ensuring that the reactor remains isolated if electrical power is lost. However, there are specific RIs in the steam supply and condensate return lines of the ICS that do not follow this fail-safe design. These RIs are designed to fail-as-is due to their crucial role in maintaining safety during various transient events and LOCA scenarios [6].

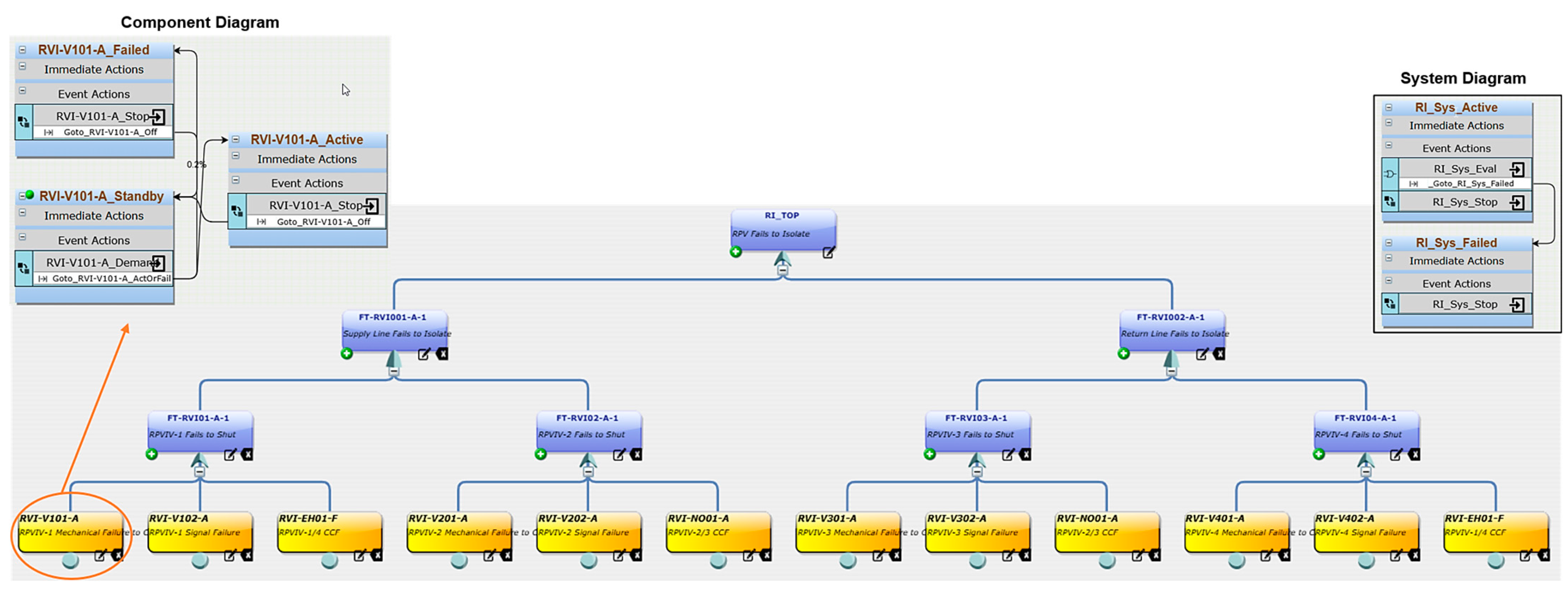
Each Fault Tree (FT) represents a Top Event (TE), which is the final undesired outcome (e.g., system failure), and contains multiple Basic Events (BEs), which represent individual failure modes of components or subsystems contributing to the TE. Figure 3 illustrates the FT for the RI system failure, with the system diagram shown in the top-right corner and a component diagram of the RI system in the left corner. The lowest level of the FT represents the components or BEs associated with RI system failure, while the top level, labeled “RI_Top,” represents the TE of RI system failure. The system diagram, typically a simple depiction consisting of two states, RI active and RI failed, references the components within a logic tree built from gates and leaf nodes. This tree is evaluated whenever a child component diagram changes, determining any transition from “active” to “failed,” as depicted in Figure 3.

Each component has its own individual diagram. For example, the top-left corner of Figure 3 shows the component diagram for the Reactor Pressure Vessel Isolation Valve (RPVIV-1), labeled “RVI-V101-A,” detailing its mechanical failure to close. A component diagram illustrates the transitions between different states, such as standby, running, and failed. Each state in the diagram is assigned a Boolean value, which is utilized when the component is evaluated in logic trees. Due to space limitations, only the component diagram for the RI system is provided in this paper, and the FTs, system diagrams, and component diagrams for the RS and ICS systems are not included. The failure probabilities for the components or BEs of the RI, RS, and ICS systems were obtained from data provided in the ESBWR certification PSA report [50]

3.2.2. Reactor Scram (RS)

Assessing the safety of the reactor scram mechanism is crucial to ensure that it performs effectively during emergency situations like LOCA. The safety assessment involves evaluating the performance and dependability of both the CRDS and BIS. This includes analyzing the system performance using probabilistic safety assessment techniques to quantify the likelihood of system failures and their impacts. By thoroughly assessing these systems, the reliability of the reactor scram mechanism can be ensured, enhancing the overall safety and operational readiness of the BWRX-300 [6].

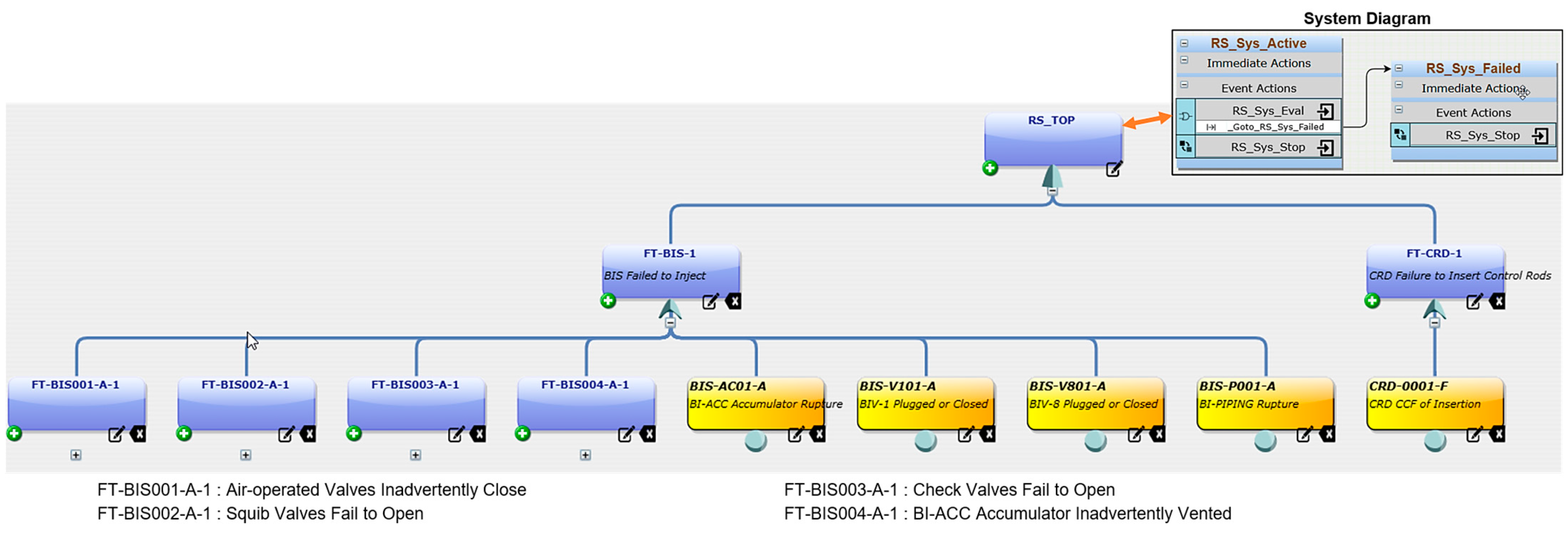
In Figure 4, the fault tree for the RS system failure is displayed, with the system diagram positioned in the top right corner. The fault tree outlines IEs such as the Boron Injection System (BIS) failing to inject and the Control Rod Drive (CRD) failing to insert control rods. The top-level event, labeled “RS_Top,” represents the TE for the RS system failure. The system diagram, which consists of two states, RS active and RS failed, maps the components using a logic tree made up of gates and BEs for RS failure.

The event “BIS Failed to Inject” outlines various failure events that could lead to the malfunction of the BIS. Key contributing failures include air-operated valves inadvertently closing, which would block boron flow and squib valves failing to open, preventing the injection process. Additional failures involve check valves that do not open, the boron injection accumulator being inadvertently vented, resulting in a loss of pressure, or a physical rupture of the accumulator. Other events include the plugging or closure of BIV-1 and BIV-8 valves, as well as the rupture of boron injection piping, all of which would hinder the system’s ability to inject boron into the reactor.

3.2.3. Isolation Condenser System (ICS)

The safety assessment of the ICS is crucial for determining its ability to perform vital safety functions during emergency scenarios, such as cooling the reactor in the event of a system failure. This assessment involves a detailed analysis of the ICS components and quantification of the failure probabilities to ensure that the system can effectively manage reactor cooling across various operational conditions. Due to resource constraints, the evaluation focused on two ICS loops, Loop A and Loop B, rather than the system’s three-loop configuration. Failure probabilities for components within these two ICS loops, identified as BEs contributing to ICS failure, were derived from data in the ESBWR certification PSA report [50].

Figure 5a presents the fault tree for ICS failure, with the system diagram located in the top-right corner. This fault tree delineates the IEs associated with the failures of ICS Loop A and ICS Loop B. The top event, denoted as “ICS_Top,” corresponds to the ICS system failure. The system diagram, which reflects two possible states, ICS active and ICS failed, illustrates how the components are represented in a logic tree composed of gates and BEs contributing to the ICS failure. The diagram reveals that the failure of each loop is driven by several contributing factors, including actuation valves not opening, unintended closure of isolation valves, heat exchanger malfunctions, and failure caused by maintenance activities.

Figure 5b–d offers a thorough FTA of the specific failure modes contributing to ICS Loop A malfunctions. The FT for ICS Loop B follows a similar structure. In Figure 5b, the analysis focuses on actuation valve failures, driven by mechanical issues, CCF, and signal failures. Figure 5c highlights the failure of the ICHX-1A/2A heat exchanger, where tube plugging and CCF are identified as key causes. Figure 5d investigates the inadvertent closure of isolation valves, caused by spurious closures as well as mechanical or signal failures. This detailed analysis serves to pinpoint and quantify the critical failure paths impacting the reliability of the ICS system.

Passive system reliability, particularly for the ICS, was modeled using basic events representing component-level failures, such as valve malfunction or signal loss. The ICS loops were modeled independently, and system failure was defined as the unavailability of both loops due to either maintenance or fault conditions.

3.3. EMRALD Simulation

The Monte Carlo engine within EMRALD stochastically explores the timing and sequence of events over repeated runs, capturing rare combinations of failures, including component behavior and signal failures. This stochastic sampling enhances the realism of the CDF estimation under LOCA scenarios.

In total, one billion simulations refer to Monte Carlo runs performed by EMRALD, with a maximum simulation time of 365 days. Each simulation represents a distinct accident progression scenario in which the operational states and timing of RI, RS, and ICS are sampled based on their respective failure probabilities and event logic. The simulations dynamically evaluate whether these systems succeed or fail during a LOCA and whether the scenario ultimately results in core damage. The entire simulation process took 1 d 4 h 54 min to complete. The simulations were run on an Intel Core i5 8th Generation processor (2.3 GHz, 8 CPUs) with 16 GB of RAM, using a 64-bit Windows 10 operating system.

In

Table 1. Simulation result for core damage count for LOCA.

Failed Components		Failure Count	Failure Rate in %
Component IDs	Component Descriptions
ICS-A-LUV0_Failed, ICS-B-LUV0_Failed	ICS-A Loop Test or Maintenance, ICS-B Loop Test or Maintenance	3	16.67
ICS-A-V402_Failed, ICS-B-V302_Failed	ICV-4A Signal Failure, ICV-3B Signal Failure	2	11.11
ICS-A-V102_Failed, ICS-B-V402_Failed	ICV-1A Signal Failure, ICV-4B Signal Failure	1	5.56
ICS-A-V202_Failed, ICS-B-V402_Failed	ICV-2A Signal Failure, ICV-4B Signal Failure	1	5.56
ICS-A-V202_Failed, ICS-B-V102_Failed	ICV-2A Signal Failure, ICV-1B Signal Failure	1	5.56
ICS-A-V302_Failed, ICS-B-V102_Failed	ICV-3A Signal Failure, ICV-1B Signal Failure	1	5.56
ICS-A-V402_Failed, ICS-B-V102_Failed	ICV-4A Signal Failure, ICV-1B Signal Failure	1	5.56
ICS-A-V402_Failed, ICS-B-V202_Failed	ICV-4A Signal Failure, ICV-2B Signal Failure	1	5.56
ICS-A-V302_Failed, ICS-B-LUV0_Failed	ICV-3A Signal Failure, ICS-B Loop Test or Maintenance	3	16.67
ICS-A-LUV0_Failed, ICS-B-V402_Failed	ICS-A Loop Test or Maintenance, ICV-4B Signal Failure	1	5.56
ICS-A-LUV0_Failed, ICS-B-V302_Failed	ICS-A Loop Test or Maintenance, ICV-3B Signal Failure	1	5.56
ICS-A-V202_Failed, ICS-B-LUV0_Failed	ICV-2A Signal Failure, ICS-B Loop Test or Maintenance	1	5.56
ICS-A-V402_Failed, ICS-B-LUV0_Failed	ICV-4A Signal Failure, ICS-B Loop Test or Maintenance	1	5.56
Total CDF		18	~100

, the simulation output revealed that core damage occurred 18 times due to the failure of the ICS, with a failure rate of $1.8\times {10}^{-8}$. The mean time to failure was calculated to be 212 d 7 h 24 min, with a standard deviation of 149 d 13 h 51 min. Specifically, CDF due to ICS failure was recorded eight times (44.22%) as a result of signal failure of one of the four ICS isolation valves of both ICS loop-A and loop-B and three times (16.67%) as a result of both ICS-A and ICS-B loops being in test or maintenance. Therefore, by effectively reducing failures associated with ICS isolation valve signal failure and ICS loop tests or maintenance, we can significantly minimize the CDF resulting from ICS failure.

No core damage was recorded due to RI or RS failures, indicating that the CDF due to RI or RS failure is lower than $1\times {10}^{-9}$. It is possible that increasing the number of simulation runs beyond 1 billion could result in CDF occurrences related to RI or RS failures. However, due to resource limitations, we were not able to extend the simulation beyond 1 billion runs.

The vulnerabilities in the ICS isolation valves’ signal failure and ICS during test or maintenance activities indicate a need for design modifications to ensure the system’s reliability during these critical periods. Introducing additional redundancy or enhancing the robustness of ICS loops could mitigate the risk of simultaneous failures, particularly during maintenance. Redundant loops or independent configurations would allow continued operation even when one loop is under maintenance, significantly reducing CDF.

4. Comparison of CDF Using Static PRA and DPRA

Table 2. Comparison of CDF estimates for ICS, RS, and RI systems using static PRA and DPRA.

CDF due to System Failure	CDF from Static PRA	CDF from DPRA
Isolation Condenser System (ICS)	2.12 × 10−8	1.80 × 10−8
Reactor Scram (RS)	3.04 × 10−13	<1 × 10−9
Reactor Isolation (RI)	1.75 × 10−10	<1 × 10−9

compares the CDF due to system failures as calculated by Static PRA and DPRA for the Isolation Condenser System (ICS), Reactor Scram (RS), and Reactor Isolation (RI) systems.

It should be noted that, while the DPRA approach provides a more realistic estimation of system response by incorporating time-dependent interactions and dynamic system behavior, the CDF results obtained from traditional static PRA remain conservative. This conservatism stems from the use of simplified logic structures that do not reflect temporal variations or conditional system states.

For the ICS, the CDF calculated using DPRA is slightly lower, at $1.8\times {10}^{-8}$ compared with $2.12\times {10}^{-8}$ in Static PRA. This demonstrates DPRA’s ability to model time-dependent interactions and system dynamics more effectively, refining the risk estimates for the ICS system.

For the RS system, static PRA estimates a very low CDF of $3.04\times {10}^{-13}$, while DPRA provides an upper limit of $1\times {10}^{-9}$. Due to resource limitations, only $1\times {10}^9$ simulation runs could be performed. DPRA could not achieve a resolution below $1\times {10}^{-9}.$ However, with an extended simulation count approaching $1\times {10}^{15}$, more insights into rare failure scenarios could emerge, providing a clearer picture of low-probability CDF events for the Reactor Scram system.

For the RI system, similarly, its static PRA result of $1.75\times {10}^{-10}$ is contrasted with a DPRA upper limit of $1\times {10}^{-9}$. This outcome highlights the robustness of DPRA in capturing complex interdependencies and temporal accident progressions. Again, increasing the simulation runs would yield further insights into critical failure mechanisms.

Overall, while DPRA provides a more realistic and comprehensive safety assessment compared with static PRA, the resource-constrained limitation of $1\times {10}^9$ simulations restricted its ability to uncover lower-probability events. Future studies with higher simulation counts (e.g., $1\times {10}^{15}$) are necessary to refine the CDF results, particularly for events with extremely low probabilities during LOCA scenarios.

5. Conclusions

This study applied DPRA using EMRALD to assess the reliability of passive safety systems in mitigating LOCAs. By modelling time-dependent interactions and system behaviors, DPRA provided a more dynamic and comprehensive risk evaluation compared with traditional PSA. The results revealed that the ICS was the most vulnerable safety function due to isolation valve signal failures and maintenance-related unavailability. Reducing these failure modes could significantly lower the overall CDF.

The findings also highlight the limitations of static PSA in capturing evolving accident scenarios and emphasize the importance of DPRA in identifying critical system vulnerabilities. While DPRA provided more accurate risk insights, the simulation was constrained to 1 billion runs due to resource limitations, preventing the evaluation of extremely rare failure events. Expanding simulations to $1\times {10}^{15}$ runs could yield additional insights into low-probability core damage scenarios.

Overall, this research underscores the importance of integrating DPRA into nuclear safety assessments. The EMRALD tool has been proven effective in modelling passive safety system behavior under LOCA conditions, demonstrating its capability to enhance risk analysis for next-generation nuclear reactors. Future work should focus on refining DPRA models, expanding simulation capabilities, and integrating physics-based thermal–hydraulic modelling to further improve accuracy in safety assessments.