Abstract
The need to model the effect of the assembly environment on the neutronic data has been felt since Smith’s topical article on assembly homogenization techniques. Indeed, simply homogenizing the cross sections using the spatial distribution and energy spectrum of the neutron flux calculated in a single assembly with reflective boundary conditions, neglecting the effect of the proximity of other types of assemblies, can induce inaccuracies affecting the results of core calculations. Many approaches have been proposed to take into account the real environment of the assembly. The purpose of this article is to review these methods to allow the reader to compare them.
1. Introduction
Fuel assemblies in PWR cores consist of fairly regular pin fuel lattices with some heterogeneities such as water pins designed to host control rods, instrumentation or discrete burnable poisons, and water gaps separating fuel assemblies. The analysis of these reactors requires modeling the various elements and devices. Pin-by-pin calculations in two-dimensional geometry and two-energy-groups was the traditional method employed in PWR core analysis until the end of the 1980s [1,2]. A synthesis approach, combining 2D power distributions, representative of horizontal planes, with 1D axial distributions allowed to obtain a pseudo-three-dimensional pin power distribution. The aim of homogenization in these early PWR simulations was to replace a heterogeneous square pin cell, composed of the fuel rod, the cladding, with a gap between them, and the moderator/coolant region, with a uniform material having neutronic properties equivalent to those of the original pattern. This approach cannot be applied to BWR cores, because the continuous varying void fraction in the axial directions makes it difficult to determine typical 2D horizontal configurations. For this type of reactor 3D coarse nodal codes were used, with a one energy group diffusion model corrected by appropriate coefficients to take into account resonance captures [3].
At the end of the 1980s the synthesis approach was abandoned and PWRs were analyzed with 3D coarse nodal codes. A two-step approach was adopted. Fine transport calculations with reflective boundary conditions on single fuel assemblies were devoted to solve the detailed physics equations providing an angular neutron flux distribution with fine spatial and energy resolution. To make these calculations as realistic as possible, a critical condition was imposed via the fundamental buckling search [4,5]. By post-processing the results of these calculations, homogeneous cross sections and 2D pin cell flux and power distributions were generated. These constants are computed for many conditions representative of the possible operating and accidental reactor conditions and are provided in the form of multi-parameterized tables. A 3D nodal code is used to obtain a coarse mesh solution of the two-group diffusion equation [6], interpolating in the multi-parameterized tables to obtain the input cross sections. An iterative procedure is executed to take into account thermal feedbacks. However, comparison of the results with reference fine transport calculations revealed large discrepancies, attributed to the weakness of the homogenization approach: classical flux-weighting cross sections could not reproduce reference results [7]. A simple solution to this issue was provided by directly correcting the power distribution via a supplemental power ratio. This ratio was determined by solving three independent 1D diffusion equations in each of the space directions [8]. A substantial progress in mitigating this issue was made by the introduction of equivalence techniques. The superhomogenization (SPH) method, proposed by Kevenoky [9], considered a fuel assembly made of a few different heterogeneous pin-cells. A two-dimensional transport theory solution was obtained and taken as reference. The heterogeneous cross sections distributions were then homogenized in each pin-cell and a new transport calculation was performed. In the first Kavenoky’s implementation, a procedure was applied to reduce this cell-homogenized transport problem into several homogeneous problems—one for each cell. SPH correction factors for each cell were then computed as the ratio of the reaction rates in the heterogeneous and homogeneous problem and applied to the cell-wise homogenized cross sections. A second-generation SPH equivalence technique, designed to preserve the pin-cell reaction rates and the assembly integrated fluxes, was introduced by Hébert [10]. An improvement was further made by Hébert and Mathonnière with a third-generation SPH method [11], by using a surface radial leakage model in the flux calculation to represent the macroscopic flux curvature in the assembly. Another equivalence approach, the Equivalence Theory (ET), was proposed by Koebke [12] who introduced the concept of heterogeneity factor. Within this theory, a choice had to be made between neutron current and neutron flux continuity. The choice fell on neutron current continuity and the flux continuity was addressed via the use of the heterogeneity factor. However, heterogeneity factors allow for neutron current continuity only if the net leakage distribution in the homogenized problem is the same as the net leakage distribution in the heterogeneous problem. This constraint can be met if a consistent diffusion coefficient is computed via an iterative equivalence procedure. The need to comply with this constraint was removed by the Generalized Equivalence Theory (GET) introduced by Smith [7,13], which replaced the heterogeneity factor with a surface dependent equivalence factor: the discontinuity factor. An extension of the method with neutron current discontinuity factors was proposed by Sanchez [14].
The preservation of the reaction rates and continuity of the neutron current is guaranteed if the flux distribution inside the assembly in the core is close to the infinite medium flux shape (computed with single assembly lattice calculations). This is the case when the assembly is far away from the reflector and surrounded by assemblies of similar type. When assemblies of very different design are located in close proximity to each other, this condition is no longer met. To obtain equivalence between the fine and coarse model in this case other types of information are required. This type of information must take into account the change in reaction rate when the neutron flux is distorted within the assembly, especially if the assembly is very heterogeneous. In order to address this issue several methods have been designed to take into account the real assembly environment in the core. These methods can be organized into two main classes: rehomogenization and leakage correction via boundary conditions. They are mainly meant for coarse nodal methods, but the rehomogenization of pin-by-pin data was also proposed. This type of correction is performed inside the iterative loop that evaluates the cross sections in the non-linear feedback calculation; therefore, the correction is provided progressively.
A review of the methods designed to take into account the environmental effects is made in the following sections. The symbolism used differs slightly from the one used in the original literature. This choice is made in order to use the same symbolism within the description of the various methods, allowing to better highlight the differences and common points between them.
2. Cross Section Corrections for Coarse Nodal Methods
The methods devised to take into account the effect of the environment on the homogenized cross sections are reviewed separating them in methods that focus on the neutron spatial distribution and others that focus on the energy neutron spectrum. These corrections are applied iteratively as part of the feedback process, as illustrated in Figure 1.
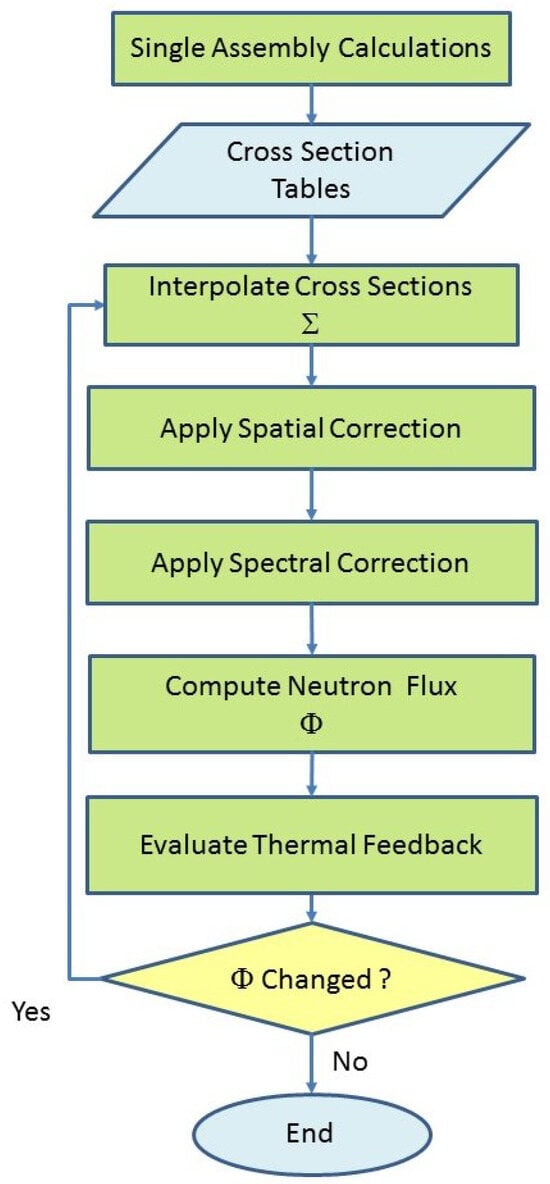
Figure 1.
Flow chart of the iterative cross section correction process.
2.1. Correction Methods in Space
2.1.1. Spatial Rehomogenization
The conventional homogenization procedure is performed on the single assembly with reflective boundary conditions. When the assembly is in the reactor core, this homogenization is no longer consistent with the new environment and a complementary procedure is necessary to restore consistency. The objective of this type of procedure is to further homogenize, or rehomogenize, the cross sections.
The rehomogenization method was proposed by K.S. Smith [15]. The basis of the theory is the pin-by-pin dehomogenization, which is used to reconstruct the pin-wise flux distribution as a combination of an intranodal smooth flux shape, obtained through an expansion on basis functions , and the single assembly pin-wise flux distribution. Homogenizing the single assembly pin-wise cross section distribution over the reconstructed pin-wise flux distribution, reaction x group g cross section in the environment can be written as:
where and are the cross sections and assembly flux from the fine-flux single assembly calculation, respectively. The terms are the expansion coefficients related to the intranodal flux shape computed prior to the spatial rehomogenization. Using the definition of infinite medium cross section:
and inserting it into Equation (1) one obtains the correction − to the cross section:
Equation (3) is the expression used to compute the adjusted cross sections for the nodal calculation. Since the integral ratio terms in the RHS of Equation (3) do not depend on the perturbed configuration, they can be computed during the single assembly homogenization process and used like the other homogenized constants. The above calculation, which is performed iteratively, is embedded inside the feedback process.
A variant of this method, based on the difference existing between the intranodal heterogeneous flux distributions in the environmental situation (estimated from nodal homogeneous results using the discontinuity factors) and in the infinite medium configuration, was developed [16]. The idea of this type of spatial rehomogenization comes from the following observation: if we compare two flux shapes inside a heterogeneous assembly, one in the infinite medium and the other in the environment, both the shapes have high local flux variations. However, the difference between the two shapes is slightly dependent on the heterogeneities location and the behavior is smooth as shown in Figure 2. It is therefore assumed that during the transverse integrated nodal calculation in the x (or y) direction it is possible to get an approximation of the difference between the transverse integrated flux shapes in the environment and infinite medium configuration. According to the nodal expansion method, the Cartesian coordinate x (or y) inside the 1D region (the node) is replaced by the dimensionless coordinate , with x the size of the node in the x direction, and the flux shape variation is expressed as an expansion on basis functions (i = 1, …, 4):
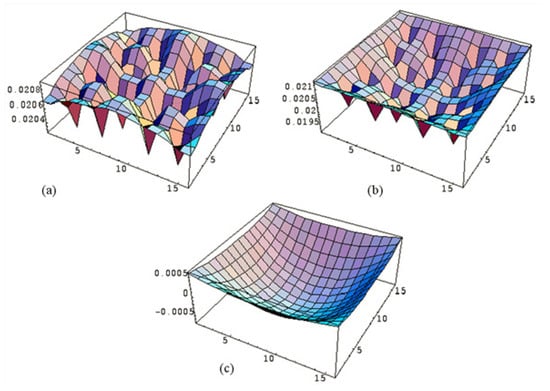
Figure 2.
Epithermal neutron flux shape in a assembly with control bank inserted: in infinite medium condition (a), environment condition (b) and their difference (c).
The variation from group g reaction x cross section (x = absorption, scattering or fission) due to the flux shape change along one of the horizontal directions identified by u can be expressed as:
where is the transverse integrated pin-by-pin cross section distribution from the single assembly calculation. Substituting Equation (4) into Equation (5) one obtains:
where is the number of basis functions and the terms :
are referred to as rehomogenization coefficients. Two corrections are computed, one for each orthogonal direction, and are superposed. The coefficients of the expansion in Equation (4) are determined by solving a linear system of four equations for each group and each direction. Two equations are obtained by enforcing the average value of function on the node surfaces to be equal to the difference between the values of the heterogeneous surface flux in the environment (coming from the actual nodal calculation) and in the infinite medium. The other two equations are obtained by enforcing the average values of the net surface current , computed by applying Fick’s law to the expansion, to be equal to the actual current (coming from the actual nodal calculation). In a two-group model, the basis functions are assumed to be polynomials for the fast range and a combination of polynomials and hyperbolic functions for the thermal range. This choice is based on the analytical solution of the 1D diffusion equation. The method was improved by evaluating a correction to the discontinuity factors [17]. The two additional equations needed to determine the two corrections (in each one of the faces) are obtained by inserting the expansion into the neutron balance equation and projecting it onto two weighting functions (i = 1,2). Functions are assumed to be equal to the basis functions . Spatial heterogeneity caused by non-uniform intranodal depletion was modeled by Wagner et al. [18] with a separable (along each coordinate axis) quadratic expansion of the nodal cross sections, associated with an intranodal Legendre polynomial expansion of the neutron flux. The method was improved by Forslund et al. [19].
The weak point of this approach is to separate the problem into orthogonal directions and neglecting 2D effects which can be treated only with a simultaneous expansion in the two directions. This point was addressed by Gamarino et al. [20] by approximating the flux change with a 2D modal expansion where four cross terms between the x and y directions are introduced. Both the cross sections and discontinuity factors (DF) are corrected with this approach. The spatial rehomogenization provides a good correction to the cross sections when the assemblies in the environment have a similar neutron spectrum. In the case where the design of the assemblies is very different, a big part of the difference between the infinite medium and environment is due to the energy collapse. In this case a spectral correction is also necessary [21] (Section 2.2).
2.1.2. Leakage Correction via Boundary Conditions
Single assembly calculations are performed with reflective boundary conditions, which means that no neutron leakage is assumed from the assembly. Inserting the assembly into the reactor core results in a deviation from this condition, which must be compensated for by a leakage correction.
A leakage correction approach was proposed by Clarno and Adams [22], to capture neighbor effects during the single assembly calculation via spatial superposition of typical four-assembly configurations. New branch cases on parameters that describe the difference between the given assembly and its neighbors were added to build the parameterized cross section tables, the new independent parameter being the surface albedo (ratio of incident-to-exiting partial current). Rahnema and Nichita [23] employed a more consistent boundary approach to take into account environment effects. Additional single assembly calculations were performed with reflective boundary conditions except for one side k and one energy group g’, where an albedo condition (current-to-flux ratio) was applied, with (), being the number of current-to-flux ratio values used to build the cross section tables. These calculations enabled the computation of the cross section (and DF) change related to the albedo on side k () and group g. The correction was then computed during the core simulation by linear interpolation using the actual value of the current-to-flux ratio on the sides of the node:
where < < . The nodal cross section is determined using linear superposition:
Similar expressions were used for the DFs.
A method having the purpose to achieve homogenized parameter accuracy of arbitrary order was introduced by McKinley and Rahnema [24]. High order perturbation theory was applied to an arbitrary ratio of linear functionals of the solution of the diffusion equation. This functional was formulated to estimate the homogenized group cross sections and the group heterogeneous discontinuity factors as an expansion in powers of the current-to-flux ratios :
The expansion coefficients are precomputed as the standard GET parameters, using high order perturbation theory; therefore, they do not require additional lattice calculations. The perturbation method was applied in the framework of coarse nodal methods [25] to correct the homogenized parameters to an arbitrary order of accuracy for the effect of fuel assembly neutron leakage. The method was extended to transport theory in order to explicitly account for the angular dependence of the coarse-group total cross section [26]. This extension does not address the core-environment effect and further work was done to remove this limitation in the framework of transport theory [27] and in the framework of a hybrid diffusion-transport approach [28]. Both in the transport and diffusion theory approaches, on-the-fly rehomogenization at the assembly level was performed in order to correct the cross sections for core environment effects.
Another type of procedure taking into account leakage effects adopts the albedo-corrected parameterized equivalence constants (APEC) method [29]. In the APEC method, the fuel assembly cross sections are corrected with an additive term. The fast group correction is expressed as a linear relationship of the assembly-averaged current-to-flux ratio (CFR) in the fast and thermal group:
The correction in the thermal group is a quadratic polynomial function of the thermal-group CFR only:
To determine the expansion coefficients for an assembly type, several checkerboard-colorset calculations with a different assembly type as a neighbor are performed. Changing the neighbor assembly, one obtains a sufficient number of equations relating the cross section change to the CFR. The solution of this linear system gives the coefficients. The APEC method has been improved by adding the spectral index change ΔSI as a linear term in the relationships for the cross sections’ change [30,31]:
Furthermore, the method has been extended to also correct for discontinuity factors. The DF change in the fast group is neglected, because analyses have shown that for this group the DFs differ slightly from the ones computed in a single assembly [31]. The DF change in the thermal group is a linear relationship of the CFR ratio in the thermal group only. The least-squares method was used to fit the functions to various colorset models. The APEC corrections were determined on a full assembly basis. An improvement was obtained determining the APEC corrections on a quarter assembly basis [32].
In the framework of the variational nodal expansion method (VNM), environment effects are captured in a natural way [33]. The flux distribution within a node is decomposed into two components:
The first component represents the contribution of the group source within a node to the flux. The second component represents the contribution of the boundary flux at the node interface j to the flux within the node. The expansion functions and are obtained by numerical solution of two diffusion equations. For it is a diffusion equation with a fixed neutron fission source expanded on 2D Legendre polynomials and reflective boundary conditions. For , it is a diffusion equation without source and a boundary condition on face j expressed with 1D Legendre functions. These operations are done within single assembly calculations. The expansion coefficients are determined by the variational principle. A functional of the neutron flux is obtained by integration over the core. By differentiating the functional, with respect to the expansion coefficients, a linear system of equations is obtained. The solution provides the expansion coefficients and .
2.1.3. Environment Effect Treatment via Adapted Mesh
Environmental effects can be handled by refining the mesh near the boundaries between assemblies. Calloo et al. [34] developed a multi-domain homogenization that allows to refine the mesh at the assembly periphery. This multi-domain discretization is composed of 4 × 4 regions with 3 different homogenized materials. A total of 4 corner regions result from the homogenization of 4 corner pins, 2 × 4 peripheral regions result from the homogenization of 2 pin rows (26 pins for a 17 × 17 fuel assembly). The remaining central part of the assembly constitutes the main homogenized 4 regions (Figure 3). For the same purpose Mala and Pautz [35] applied a progressive mesh approach which enables to capture the flux gradients on the and fuel/reflector interfaces. The pin-by-pin mesh is refined at the edges of the assembly dividing by 2 the pin cells belonging to the peripheral pin rows (Figure 4). Another way to adapt the mesh is the submesh method [36], where each radial node is subdivided into N × N homogeneous rectangular subnodes (typically with N = 5). The 2D diffusion equation is solved, one axial plane at a time, relying on the submesh geometry. The axial leakage, known from the 3D solution, is converted into an equivalent absorption and added to the infinite-medium homogenized cross sections used in the calculation. The resulting flux distribution is used to homogenize the submesh-wise cross sections over the radial node and to estimate the environmental discontinuity factors at the assembly outer edges.
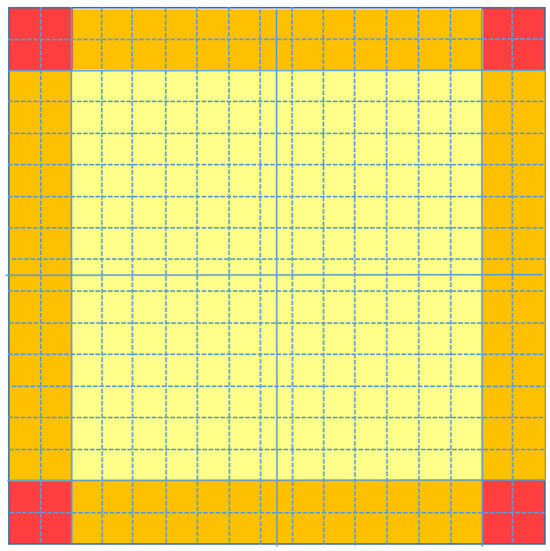
Figure 3.
A 17 × 17 fuel assembly with a 4 × 4 non uniform nodal mesh (solid lines). Dashed lines delimit the pin cell lattice.

Figure 4.
A 17 × 17 fuel assembly with pin-by-pin mesh refined in the edges.
2.1.4. Control Rod Treatment
Rehomogenization is also applied to the treatment of the control rod cusping effect. This numerical behavior appears when a node contains the tip of a control rod. The high heterogeneity inserted causes a high discontinuity in the partial derivative of the flux in the axial direction (Figure 5). As a result, the control rod worth is not continuous. First attempts aimed to mitigate this effect perform an approximate flux-weighting in the node using the flux shape resulting from the solution of the nodal expansion problem [37,38]. This approach was improved computing the two-group flux shape near the control rod tip as analytical solution of a one-dimensional two-region problem using the neutron current resulting from the global nodal solution as boundary conditions [39]. The axial discontinuity factors for the top and bottom of the node were also computed. In a variant of this approach, the inter-nodal flux shape was computed with an equivalence procedure [40].
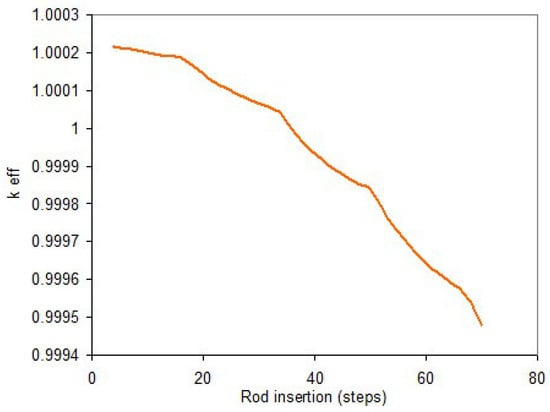
Figure 5.
An example of the control rod cusping effect.
The above improvements reduce but do not eliminate the cusping effect: small oscillations on the control rod worth curve still remain. The control rod cusping effect was directly handled by using the heterogeneous variational nodal method [41]. Within this approach the flux, net current and fission source are expanded on orthogonal spatial basis functions with unknown coefficients. The insertion of this expansion into the diffusion equation followed by integration in the nodal volumes leads to vectorial functionals of the expansion coefficients. Requiring that the functional be stationary, with respect to variations in the expansion coefficients, leads to a matrix response problem which constitutes the basis of the heterogeneous variational nodal method (VNM). The control rod cusping effect was also directly handled by another heterogeneous VNM [42]. A drastic reduction in the cusping effect was obtained within the heterogeneous VNM with the use of heterogeneous discontinuity factors and expanding cross sections and surface DFs into the sum of orthogonal piece-wise polynomials to construct the nodal response matrices [43].
2.2. Correction Methods in Energy Spectrum
2.2.1. Heuristic Spectral Corrections
One of the first approaches to handle spectral effects was proposed by Palmtag and Smith [44]. A spectral one-dimensional correlation composed of two parts, a leakage correction and a spectrum correction, was introduced in the transverse integrated nodal diffusion equation. The leakage correction accounts for spectrum changes in the fast group due to neutron leakage. It is assumed to be proportional to the change of the leakage-to-removal ratio, with respect to the single assembly configuration. The spectrum correction accounts for changes in the spectrum due to external sources and is correlated to the spectral index (defined as the thermal to fast flux ratio) change.
In a spectral correction proposed by Lee and Cho [45], the fine multigroup flux in a point r is approximated by the product of a magnitude function f and an energy spectrum , where g indicates the fine group energy discretization. Using the classical expression for the homogenization, the average coarse group cross section is obtained:
where the sum is performed on the fine groups g belonging to coarse group G and the integration is done on the volume of the node. A spectral correction is applied to to take into account the real environment of the assembly, by solving the local multigroup neutron diffusion equation for the homogenized assembly in infinite medium condition. A simple solution to this problem is given in ref. [46]. The corrected flux is defined as:
where is the average energy spectrum given by the single assembly calculation, and and are solutions of the local fine group diffusion equation with critical and zero buckling, respectively. The corrected flux is used to homogenize the fine group cross section, according to Equation (16).
2.2.2. Spectral Rehomogenization
As observed in case of environmental effects in the spatial range, the change of the flux shape in energy from the infinite medium state (Figure 6) to the core environment is a smooth function (Figure 7 and Figure 8). Therefore, a modal approach similar to the one adopted for the spatial rehomogenization [16] was applied to the energy dimension: the spectral rehomogenization [47]. The spectrum change is expanded on basis functions of a reduced variable u:
Variable u, called pseudo-lethargy, is defined as:
where is the upper bound of the g-th energy group. The associated cross section change is:
where is the spatially homogenized cross section. Substituting Equation (18) into Equation (20) one obtains:
where:
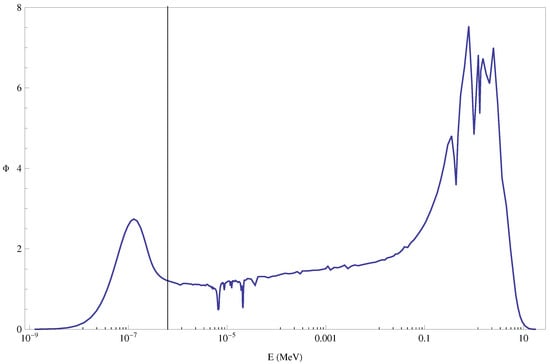
Figure 6.
Neutron spectrum (neutron flux per unit lethargy versus energy) in a PWR fuel assembly. The vertical line separates the thermal neutrons range.
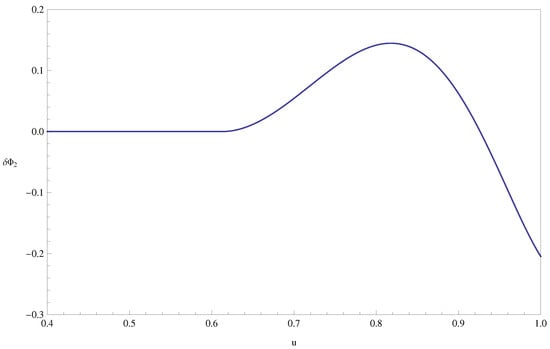
Figure 7.
Thermal neutron spectrum deformation in a PWR fuel assembly from the infinite medium to the environment configuration. Variable u is the pseudo-lethargy.
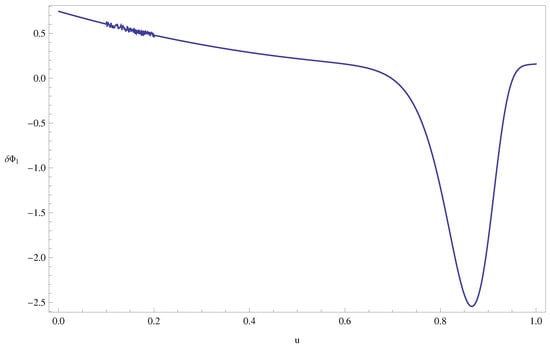
Figure 8.
Epithermal and fast neutron spectrum deformation in a PWR fuel assembly from the infinite medium to the environment configuration. Variable u is the pseudo-lethargy.
Two sets of basis functions are employed for the fast and thermal range, respectively. In the fast range, one exponential and three Chebyshev polynomials of the first kind are used. In the thermal range, a set of truncated exponentials is selected. The choice of the exponential in the fast range follows the Maxwellian distribution of the emitted fission neutrons. In the thermal range the exponentials are consistent with the Maxwellian distribution of the neutrons slowing down in the water moderator. This approach needs the pre-calculation of rehomogenization coefficients during the single assembly calculation. Two sets of rehomogenization coefficients are produced. A set is used to prepare the linear system giving the expansion coefficients. The other one is used to compute the spectral correction of the two-group cross sections using Equation (21). Rehomogenization coefficients (Equation (22)) can also be defined for the two-group microscopic cross sections. Equation (21) can then be used to correct the isotopic cross sections as well [48]. In this way the spectral effects of the environment can be accounted for in the nodal isotopic depletion and the spectral history can be better modeled. This is especially important for BWRs.
The accuracy of the spectral corrections depends on the choice of the basis and weighting functions used for the expansion. A search for better basis functions was done by Gamarino et al. [49], exploring: a combination of analytical functions (with a physically justified model) and a mathematical approach based on the Proper Orthogonal Decomposition.
In the theoretical formulation, the spectrum of the neutron leakage, which appears in the equations of the rehomogenization problem, is assumed to be equal to the spectrum of the fundamental buckling leakage obtained in single assembly calculations. When this assumption is valid to represent the neutron exchange between assemblies the spectral rehomogenization gives good results. When the core loading pattern is highly heterogeneous, non-negligible errors appear. Indeed, in this kind of situation, the leakage spectrum is very far from the fundamental buckling leakage spectrum. The analyses in [49] have shown that using the leakage spectrum from a reference fine-group heterogeneous transport calculation in the real environment, the results of the nodal calculation are consistent with the reference results. This observation showed that a more realistic leakage spectrum model was needed. This was obtained via the diffusive leakage approach [50], where an expression derived from Fick’s diffusion law was used to compute the spectrum of the neutron current at the node interface. As shown in [48], spectral rehomogenization can incorporate not only the spectral effects due to neighboring assemblies with different characteristics, but also those of local changes in the water density and in the concentrations of soluble boron and xenon. These three state parameters are commonly used for the interpolation of two-group nodal cross sections. Leveraging this property of spectral rehomogenization, the cross section model can be simplified to a significant extent. Heterogeneity due to non-uniform intranodal depletion can be handled with the use of spectral rehomogenization coefficients associated with the isotopic densities [48].
2.2.3. Recondensation via the Discrete Generalized Multigroup Method
Rehomogenization can be naturally embedded in calculation methods. Another spectral rehomogenization (or recondensation) approach was proposed [51] in the context of the discrete generalized multigroup (DGM) method. This rehomogenization approach differs from the one reviewed in Section 2.2.2 in that the angular flux spectrum in the environment (and not the difference in the scalar flux spectrum between the environmental and infinite-medium conditions) is approximated with a modal expansion. In the DGM method, the angular flux is expanded in energy using the discrete Legendre orthogonal polynomials (DLOP):
where is the index of the fine energy group point within the coarse group g, is the total number of fine group points within the coarse group g, is the discrete Legendre polynomial and is the i-th angular flux moment within the coarse group g. The angular flux in Equation (23) is that in the real environment. Comparison with reference fine group calculations showed that the unfolded flux spectrum provided by the DGM calculation is a very accurate estimate of the solution. This indicates that the DGM solution can be used as a weighting function to regenerate improved cross section moments used in the DGM iterative calculation. However, moving to other spatial methods, such as the method of characteristics, spatial inconsistencies in the DGM equations were revealed. In order to address this issue, local spatial dependence of the angular and scalar fluxes has been introduced into the cross section moments and the correction terms [52].
2.2.4. Generalized Energy Condensation
A modal expansion in energy of the angular flux was also adopted via generalized energy condensation theory [26,53]. According to this theory, the energy dependence of the angular flux is expanded on a set of general orthogonal functions (Legendre polynomials). The expansion leads to a set of equations for the angular flux moments in the few-group framework. The orthogonal expansion moments expressing the energy dependence of the few-group cross sections are obtained using the fine-group transport solution within each fuel assembly as a weighting function. They are computed during the classical single assembly calculations. The orthogonality property of the expansion functions enables decoupling the few-group equations allowing for a very efficient solution. The method was extended to explicitly account for the angular dependence of the few-group total cross section [54]. This is accomplished by modifying the treatment of the total cross section to include orthogonal expansions in both energy and angle. The expansion functions used for this purpose are spherical harmonics.
2.2.5. Dynamic Homogenization
A method to address simultaneously spatial and spectral homogenization is the dynamic homogenization [55]. The method solves the full core problem with a one-step approach via an iterative process, between fine transport assembly calculations and two-group diffusion core calculations, preserving assembly macro-exchanges, as in the domain decomposition method. The role of the transport operator is not to give a solution at full core level, but to generate homogenized parameters for the coarse nodal operator. A big part of the computation time is spent in the 3D transport solution. In order to optimize the method, a modification of the approach consisted in replacing the 3D transport solution with a 2D transport solution [56], which improved the runtime performance.
2.3. Numerical Verification of the Correction Methods
The different methods aimed to correct the homogenized cross sections in order to take into account the effect of the environment have been verified by their authors on various configurations: reactor cores or colorsets (i.e., sets of several assemblies with mirror or albedo boundary conditions), with and without control rod, in 3D, 2D or 1D. They have been mainly applied in the framework of 3D diffusion theory with the nodal expansion method (NEM), the variational NEM (VNM), and the analytic function NEM (AFEN). Calculation in 2D (SP3) and 1D transport (S8, MOC) or hybrid diffusion–transport (HDT) have also been performed. The calculations precision attained with and without environmental correction is summarized in Table 1. It can be seen that the greater the heterogeneity of the configuration, the greater the error reduction due to the environmental correction, as seen in configurations with control rod or Gd pins.

Table 1.
Summary of precision attained in coarse mesh calculations with and without environmental correction in several configurations taken from the reference articles. The configurations with symbol r contain control rods. The compared quantities are the k-eff (error in %) and the power (maximum and root mean square error in %). Label “env” refers to the corrected values. Label “std” refers to the standard single assembly values.
The effectiveness of the environmental correction was also verified by comparing the rehomogenized cross sections with the reference values obtained by spatial homogenization on flux distributions resulting from pin-by-pin colorset calculations [16,29]. As far as the spectral rehomogenization is concerned, the verification was carried out by comparison, with respect to cross sections homogenized on fine neutron spectra obtained with 281 energy groups calculations [49]. The method was also verified by applying it to depletion calculations [19,31,32,48].
3. Corrections on Direct Pin-by-Pin Calculations
The concept of rehomogenization used in assembly homogenization can also be applied to the correction of cell-homogenized cross sections in the framework of direct pin-by-pin calculations, as suggested by Yamamoto et al. [57]. Some implementations are summarized below. The precision attained in pin-by-pin calculations with and without environmental correction is summarized in Table 2.
3.1. Correction Based on the Leakage Index
A method devoted explicitly to pin-by-pin calculations utilizes a correction technique based on the leakage index [58], defined as the volume-averaged neutron leakage in a pin-cell:
where is the group g surface neutron current. The variations in coarse-group cross sections are represented as a linear expansion on the difference between the values of leakage index LI in the environment and in the reflective single assembly configuration:
where and is the group g leakage index from the single assembly calculation. To compute the expansion coefficients , several colorset assembly calculations are performed in order to obtain the relationship between the variations in coarse-group cross sections and the variations in LI, followed by a least-squares best-fit. However, this method is able to correct only spatial effects. In order to extend the method to handle spectral variations, the SPH factors (or DFs) were introduced as cell-wise data and an attempt was made to correct them on the basis of LI variations [59]. The attempt failed because SPH factors and DFs were not sensitive to spectral changes. Therefore, they were assumed as spectrum-independent and the single assembly value was used. But the introduction of the SPH factors as input data causes spectral variations that interfere with the -driven cross section changes, acting eventually as a SPH spectral correction. Alternative parameters to LI, the heterogeneous surface current divided by the homogeneous surface flux and the heterogeneous transverse leakage divided by the homogeneous surface flux, have been proposed by Herrero et al., to fit pin-by-pin DFs with the least-squares technique [60].
3.2. Correction Based on the SPH Factor
An improvement to the SPH method with the purpose to handle the configurations where different assembly types are adjacent, was proposed by Yamamoto et al. [61]. In this improvement the SPH factor is divided by an average cell-level discontinuity factor obtained in each fuel assembly. The cell-level flux discontinuity factor is defined as:
where: is the average heterogeneous surface flux of the assembly obtained by cell-heterogeneous calculations; is the homogeneous surface flux of the assembly obtained by cell-homogeneous calculations including the SPH factor. The discontinuity factor is computed in each cell of the assembly peripheral (outermost) region and the assumption that it is constant throughout the assembly surface is made. By using this assumption, just one discontinuity factor is obtained for each assembly. This discontinuity factor is then incorporated by dividing all pin-wise cross sections in the assembly. An improved leakage corrected SPH (LC-SPH) method was proposed by Wang et al. [62]. The idea of the LC-SPH method is to represent the neutron leakage difference between homogeneous and heterogeneous models in the environment as an absorption reaction rate, which preserves the total neutron removal rate after homogenization.

Table 2.
Summary of precision attained in pin-by-pin calculations with and without environmental correction in several configurations taken from the reference articles. The configurations with symbol r contain control rods. The compared quantities are the k-eff (error in %) and the power (maximum and root mean square error in %). Label “env” refers to the corrected values. Label “std” refers to the standard single assembly values.
Table 2.
Summary of precision attained in pin-by-pin calculations with and without environmental correction in several configurations taken from the reference articles. The configurations with symbol r contain control rods. The compared quantities are the k-eff (error in %) and the power (maximum and root mean square error in %). Label “env” refers to the corrected values. Label “std” refers to the standard single assembly values.
| Ref. | Configuration | Method | keff (%) | P max (%) | P RMS (%) | |||
|---|---|---|---|---|---|---|---|---|
| env | std | env | std | env | std | |||
| [58] | BWR asb r | FDM | 0.020 | 0.070 | 0.28 | 0.86 | 0.16 | 0.55 |
| [61] | PWR cset | FDM | 0.003 | 0.001 | 0.59 | 1.07 | 0.18 | 0.53 |
| [63] | PWR core | HCMFD | 0.033 | 0.173 | −1.78 | 3.94 | 0.34 | 1.15 |
| [64] | PWR core | NEM | 0.018 | 0.069 | 1.64 | −2.95 | 0.21 | 0.82 |
| [65] | PWR core | HCMFD | 0.024 | 0.085 | 1.46 | −2.95 | 0.24 | 0.82 |
| [66] | PWR core | HCMFD | 0.006 | 0.069 | −0.13 | 0.90 | - | - |
3.3. The GPS Method
Another type of pin-wise leakage correction, called GET plus SPH (GPS) method was introduced by Yu and Kim [63] and Yu et al. [64]. In the GPS method, modified SPH factors are applied to the pin-wise cross sections of the standard GET-based two-step pin-by-pin core analysis. The aim of the modification is to remove a shortcoming of the SPH method, which, in its standard form, cannot preserve the neutron balance in each node, because it only preserves the reaction rates (Section 1). This is done by using the pin-wise DFs from the single FA lattice calculation as further input data, in order to preserve surface net currents as well. However, the pin-wise group constants are sensitive to the pin environment. Therefore, the change in the pin-wise SPH factors from their initial values (single assembly) are expressed as a function of the change of the pin-wise current-to-flux ratio (CFR) for reaction x and group g. The parameters of the correlations expressing the SPH factor change were obtained by fitting the results of several colorset calculations. An application of the GPS method to cross section correction in MOX-loaded PWRs was done by Yu and Kim [65]. When using the GPS in a burnup depletion, it was observed that the CFR parameter was not sufficient to capture spectrum changes and a further degree of freedom was needed. The spectral index was adopted as further parameter [66].
4. Conclusions
The survey conducted in this article shows the importance of modeling the effect of the assembly environment on the neutronic data. The numerous methods devised to handle this problem spread from analytical to heuristic based algorithms and suggest that the potential synergies between them should be explored. Some limitations affect these methods. Spatial and spectral effects associated with the real assembly environment are mostly taken into account separately and then superposed. However, in some configurations, such as assemblies loaded near MOX assemblies, these effects are tightly coupled and mixed energy-space terms cannot be neglected. A sequential application of the spectral and spatial rehomogenization may therefore not always fully correct the homogenization defects [67]. A possible improvement is to apply simultaneous form functions of the space and energy spectrum. In order to avoid increasing the complexity of the methods, an analysis of the efficiency in the contributions of the different form functions is needed, and eventually select the most effective ones. As far as discontinuity factors are concerned, it is assumed that the errors to be corrected are originated from spatial homogenization and that the spectral component can be neglected [59,67]. An investigation of potential corrections to handle the spectral component of the discontinuity factor correction should be made. Although the methods summarized in this paper have been applied primarily to diffusion calculations, most of them can also be applied to simplified transport calculations. This aspect is interesting if in the future diffusion is abandoned in favor of simplified transport calculations (such as SP3). From the runtime perspective, the environmental correction procedure only slightly increases the computational cost. Actually, this type of procedure is embedded inside the feedback process, which requires about six or seven iterations under normal operating conditions. Most of the time is spent interpolating the cross sections and calculating the neutron flux. The environmental correction takes less than 10% of this time [67]. Its implementation in reactor core simulation codes is easy because it is performed in sequence after the cross section interpolation, as shown in Figure 1. We have shown that environmental corrections are being applied to pin-by-pin calculations, and could be implemented in the next years thanks to the progress in computing power. In this context, the extension of the rehomogenization technique to pin-by-pin calculation suggested by Yamamoto et al. [57] should be resumed.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The author is grateful to Matteo Gamarino (NRG, Arnhem, The Netherlands) for his advice that helped improve this article and to Mathis Caprais (CEA, Gif-sur-Yvette, France) for his suggestions.
Conflicts of Interest
The author was employed by the company Framatome. The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
| AFEN | Analytic Function NEM |
| APEC | Albedo-corrected Parameterized Equivalence Constants |
| asb | Fuel assembly |
| BWR | Boiling Water Reactor |
| CFR | Current-to-Flux Ratio |
| CISE | Centro Informazioni Studi Esperienze (Italy) |
| cset | Color set (cluster of few fuel assemblies) |
| DF | Discontinuity Factor |
| DGM | Discrete Generalized Multigroup |
| ET | Equivalence Theory |
| FDM | Finite Difference Method |
| GET | Generalized Equivalence Theory |
| GPS | GET plus SPH |
| HCMFD | Hybrid coarse-mesh finite difference |
| HDT | Hybrid Diffusion-Transport |
| LWR | Light Water Reactor |
| MOC | Method of Characteristics |
| MOX | Mixed Oxide |
| NEM | Nodal Expansion Method |
| Spherical harmonics approximation (order N) of the transport | |
| PWR | Pressurized Water Reactor |
| RHS | Right Hand Side |
| SMR | Small Modular Reactor |
| Discrete ordinates approximation (order N) of the transport | |
| SP3 | Simplified with |
| SPH | Superhomogenization |
| VNM | Variational NEM |
References
- Altomare, S.; Barry, R.F. The TURTLE 24.0 Diffusion Depletion Code; Technical Report WCAP-7758; Westinghouse Electric Corporation: Pittsburgh, PA, USA, 1971. [Google Scholar]
- Liu, Y.S.; Meliksetian, A.; Rathkopf, J.A.; Little, D.C.; Nakano, F.; Poploski, M.J. ANC: A Westinghouse Advanced Nodal Computer Code; Technical Report WCAP-10966-A; Westinghouse Electric Corporation: Pittsburgh, PA, USA, 1986. [Google Scholar]
- General Electric. Steady-State Nuclear Methods; Technical Report NED0-30130; General Electric Company: San Jose, CA, USA, 1983. [Google Scholar]
- Tomatis, D.; Cufe, J. The Homogeneous B1 Model as Polynomial Eigenvalue Problem. J. Comput. Theor. Transp. 2021, 50, 220–235. [Google Scholar] [CrossRef]
- Hébert, A. Applied Reactor Physics; Presses Internationales Polytechnique: Montreal, ON, Canada, 2009. [Google Scholar]
- Lawrence, R.D. Progress in nodal methods for the solution of the neutron diffusion and transport equations. Prog. Nucl. Energy 1986, 17, 271–301. [Google Scholar] [CrossRef]
- Smith, K.S. Spatial Homogenization Methods for Light Water Reactor Analysis. Ph.D. Thesis, MIT, Cambridge, MA, USA, 1980. [Google Scholar]
- Becker, M. Incorporation of Spectral Effects into One-Group Nodal Simulators. Nucl. Sci. Eng. 1976, 59, 276–278. [Google Scholar] [CrossRef]
- Kavenoky, A. The SPH Homogenization Method. In Proceedings of the a Specialists’ Meeting on Homogenization Methods in Reactor Physics, Lugano, Switzerland, 13–15 November 1978; IAEA-TECDOC-231. International Atomic Energy Agency: Vienna, Austria, 1980; pp. 181–187. [Google Scholar]
- Hébert, A. A consistent technique for the pin-by-pin homogenization of a pressurized water reactor assembly. Nucl. Sci. Eng. 1993, 113, 227–238. [Google Scholar] [CrossRef]
- Hébert, A.; Mathonnière, G. Development of a Third-Generation Superhomogeneisation Method for the Homogenization of a Pressurized Water Reactor Assembly. Nucl. Sci. Eng. 1993, 115, 129–141. [Google Scholar] [CrossRef]
- Koebke, K. Advances in homogenization and dehomogenization. In Proceedings of the International Topical Meeting on Advances in Mathematical Methods for the Solution of Nuclear Engineering Problems, Munich, Germany, 27–29 April 1981; Volume 2, p. 59. [Google Scholar]
- Smith, K.S. Assembly Homogenization Techniques for Light Water Reactor Analysis. Prog. Nucl. Energy 1986, 17, 303–333. [Google Scholar] [CrossRef]
- Sanchez, R. Assembly homogenization techniques for core calculations. Prog. Nucl. Energy 2009, 51, 14–31. [Google Scholar] [CrossRef]
- Smith, K.S. Practical and efficient iterative method for LWR fuel assembly homogenization. Trans. Am. Nucl. Soc. 1994, 71, 238–241. [Google Scholar]
- Dall’Osso, A. A spatial rehomogenization method in nodal calculations. Ann. Nucl. Energy 2006, 33, 869–877. [Google Scholar] [CrossRef]
- Dall’Osso, A. Spatial rehomogenization of cross sections and discontinuity factors for nodal calculations. In Proceedings of the International Conference PHYSOR 2014, Kyoto, Japan, 28 September–3 October 2014. [Google Scholar]
- Wagner, M.R.; Koebke, K.; Winter, H.J. A nonlinear extension of the nodal expansion method. In Proceedings of the International Conference in Advances in Mathematical Methods for the Solution of Engineering Problems, Munich, Germany, 27–29 April 1981; Volume 2. [Google Scholar]
- Forslund, P.; Müller, E.; Lindahl, S. Investigation of intranodal depletion effects. Ann. Nucl. Energy 2001, 28, 225–250. [Google Scholar] [CrossRef]
- Gamarino, M.; Dall’Osso, A.; Lathouwers, D.; Kloosterman, J.L. A two-dimensional modal method for spatial rehomogenization of nodal cross sections and discontinuity-factor correction. Ann. Nucl. Energy 2019, 125, 157–185. [Google Scholar] [CrossRef]
- Gamarino, M.; Tomatis, D.; Dall’Osso, A.; Lathouwers, D.; Kloosterman, J.L.; van der Hagen, T.H.J.J. Investigation of rehomogenization in the framework of nodal cross section corrections. In Proceedings of the Conference PHYSOR 2016, Sun Valley, ID, USA, 1–5 May 2016; pp. 3698–3707. [Google Scholar]
- Clarno, K.T.; Adams, M.L. Capturing the Effects of Unlike Neighbors in Single-Assembly Calculations. Nucl. Sci. Eng. 2005, 149, 182–196. [Google Scholar] [CrossRef]
- Rahnema, F.; Nichita, E.M. Leakage corrected spatial (assembly) homogenization technique. Ann. Nucl. Energy 1997, 24, 477–488. [Google Scholar] [CrossRef]
- McKinley, M.S.; Rahnema, F. Higher-order boundary condition perturbation theory for the diffusion approximation. Nucl. Sci. Eng. 2000, 136, 15–33. [Google Scholar] [CrossRef]
- Rahnema, F.; McKinley, M.S. High-order cross-section homogenization method. Ann. Nucl. Energy 2002, 29, 875–899. [Google Scholar] [CrossRef]
- Douglass, S.; Rahnema, F. Cross section recondensation method via generalized energy condensation theory. Ann. Nucl. Energy 2011, 38, 2105–2110. [Google Scholar] [CrossRef]
- Yasseri, S.; Rahnema, F. On the Consistent Spatial Homogenization Method in Neutron Transport Theory. J. Comput. Theor. Transp. 2014, 43, 240–261. [Google Scholar] [CrossRef]
- Kooreman, G.; Rahnema, F. Hybrid diffusion-transport spatial homogenization method. Ann. Nucl. Energy 2014, 72, 95–103. [Google Scholar] [CrossRef]
- Kim, W.; Heo, W.; Kim, Y. Improvement of Nodal Accuracy by Using Albedo-Corrected Parameterized Equivalence Constants. Nucl. Sci. Eng. 2017, 188, 207–245. [Google Scholar] [CrossRef]
- Kim, W.; Lee, K.; Kim, Y. Functionalization of the Discontinuity Factor in the Albedo-Corrected Parameterized Equivalence Constants (APEC) Method. Nucl. Sci. Eng. 2018, 192, 1–20. [Google Scholar] [CrossRef]
- Lee, K.; Kim, W.; Kim, Y. Improved nodal equivalence with leakage-corrected cross sections and discontinuity factors for PWR depletion analysis. Nucl. Eng. Technol. 2019, 51, 1195–1208. [Google Scholar] [CrossRef]
- Jang, S.; Kim, Y. Improved macroscopic depletion in 2-D nodal analysis by 2x2 albedo-corrected parameterized equivalence constants method. Ann. Nucl. Energy 2022, 175, 109209. [Google Scholar] [CrossRef]
- Tsuiki, M.; Hval, S. A Variational Nodal Expansion Method for the Solution of Multigroup Neutron Diffusion Equations with Heterogeneous Nodes. Nucl. Sci. Eng. 2002, 141, 218–235. [Google Scholar] [CrossRef]
- Calloo, A.; Couyras, D.; Févotte, F.; Guillo, M.; Brosselard, C.; Bouriquet, B.; Dubois, A.; Girardi, E.; Hoareau, F.; Fliscounakis, M.; et al. COCAGNE: EDF new neutronic core code for ANDROMÈDE calculation chain. In Proceedings of the International Conference on Mathematics & Computational Methods Applied to Nuclear Science & Engineering (M&C 2017), Jeju, Republic of Korea, 16–20 April 2017. [Google Scholar]
- Mala, P.; Pautz, A. Development and verification of pin-by-pin homogenized simplified transport solver Tortin for PWR core analysis. Nucl. Eng. Technol. 2020, 52, 2431–2441. [Google Scholar] [CrossRef]
- Bahadir, T.; Lindahl, S.; Palmtag, S.P. SIMULATE-4 multigroup nodal code with microscopic depletion model. In Proceedings of the Conference on Mathematics and Computation (M&C 2005), Avignon, France, 12–15 September 2005. [Google Scholar]
- Joo, H.S. Resolution of the Control Rod Cusping Problem for Nodal Methods. Ph.D. Thesis, Department of Nuclear Engineering, MIT, Cambridge, MA, USA, 1984. [Google Scholar]
- Gehin, J.C. A Quasi Static Polynomial Nodal Method for Nuclear Reactor Analysis. Ph.D. Thesis, Department of Nuclear Engineering, MIT, Cambridge, MA, USA, 1992; pp. 59–60. [Google Scholar]
- Smith, K.S.; Rempe, K.R.; Rhodes, J.D.; Stevens, J.G. Enhancements of the Studvick core management system. In Proceedings of the Topical Meeting on Advances in Reactor Physics, Charleston, SC, USA, 8–11 March 1992; Volume 1, pp. 117–128. [Google Scholar]
- Dall’Osso, A. Reducing Rod Cusping Effect in Nodal Expansion Method Calculations. In Proceedings of the International Conference PHYSOR 2002, Seoul, Republic of Korea, 7–10 October 2002. [Google Scholar]
- Li, Y.; Wang, Y.; Wu, H.; Cao, L. Heterogeneous Variational Nodal Method with Continuous Cross Section Distribution in Space. Trans. Am. Nucl. Soc. 2014, 111, 727–729. [Google Scholar]
- Wang, Y.; Wu, H.; Li, Y. Comparison of two three-dimensional heterogeneous variational nodal methods for PWR control rod cusping effect and pin-by-pin calculation. Prog. Nucl. Energy 2017, 101, 370–380. [Google Scholar] [CrossRef]
- Li, Y.; Liang, B.; Wu, H.; Li, Z.; Yang, J. Heterogeneous discontinuity factor treatment in Variational Nodal Method. Ann. Nucl. Energy 2019, 127, 341–350. [Google Scholar] [CrossRef]
- Palmtag, S.; Smith, K.S. Two-group spectral corrections for MOX calculations. In Proceedings of the International Conference on the Physics of Nuclear Science and Technology, Long Island, NY, USA, 5–8 October 1998; Volume 1, pp. 3–7. [Google Scholar]
- Lee, K.T.; Cho, N.Z. A Spectrum Correction Method for Fuel Assembly Rehomogenization. In Proceedings of the Korean Nuclear Society Spring Meeting, Gyeongju, Republic of Korea, 27–28 May 2004. [Google Scholar]
- Dall’Osso, A.; Brault, L. On the neutron spectrum and multiplication factor in the infinite homogeneous reactor. Ann. Nucl. Energy 2009, 36, 1287–1293. [Google Scholar] [CrossRef]
- Dall’Osso, A.; Tomatis, D.; Du, Y. Improving Cross Sections via Spectral Rehomogenization. In Proceedings of the International Conference PHYSOR 2010, Pittsburgh, PA, USA, 9–14 May 2010. [Google Scholar]
- Gamarino, M.; Dall’Osso, A.; Lathouwers, D.; Kloosterman, J.L. A rehomogenization-based approach to model spectral effects of local nuclide density changes in nodal calculations. Ann. Nucl. Energy 2019, 126, 142–168. [Google Scholar] [CrossRef]
- Gamarino, M.; Dall’Osso, A.; Lathouwers, D.; Kloosterman, J.L. Rehomogenization of Nodal Cross Sections via Modal Synthesis of Neutron Spectrum Changes. Nucl. Sci. Eng. 2018, 190, 1–30. [Google Scholar] [CrossRef]
- Gamarino, M.; Dall’Osso, A.; Lathouwers, D.; Kloosterman, J.L. A neutron-leakage spectrum model for on-the-fly rehomogenization of nodal cross sections. Ann. Nucl. Energy 2018, 116, 257–279. [Google Scholar] [CrossRef]
- Zhu, L.; Forget, B. An Energy Recondensation Method Using the Discrete Generalized Multigroup Energy Expansion Theory. Ann. Nucl. Energy 2011, 38, 1718–1727. [Google Scholar] [CrossRef]
- Everson, M.S.; Forget, B. Spatial recondensation using the Discrete Generalized Multigroup method. Ann. Nucl. Energy 2013, 62, 487–498. [Google Scholar] [CrossRef]
- Rahnema, F.; Douglass, S.; Forget, B. Generalized energy condensation theory. Nucl. Sci. Eng. 2008, 160, 41–58. [Google Scholar] [CrossRef]
- Douglass, S.; Rahnema, F. Consistent generalized energy condensation theory. Ann. Nucl. Energy 2012, 40, 200–214. [Google Scholar] [CrossRef]
- Galia, A.; Sanchez, R.; Zmijarevic, I. A method of dynamic homogenization: Application to 2D core calculation. Ann. Nucl. Energy 2021, 151, 107774. [Google Scholar] [CrossRef]
- Galia, A.; Sanchez, R.; Zmijarevic, I. A dynamic homogenization method for 3D core calculations. Ann. Nucl. Energy 2021, 160, 108360. [Google Scholar] [CrossRef]
- Yamamoto, A.; Kitamura, Y.; Yamane, Y. Cell homogenization methods for pin-by-pin core calculations tested in slab geometry. Ann. Nucl. Energy 2004, 31, 825–847. [Google Scholar] [CrossRef]
- Fujita, T.; Endo, T.; Yamamoto, A. A new technique for spectral interference correction on pin-by-pin BWR core analysis. J. Nucl. Sci. Technol. 2014, 51, 783–797. [Google Scholar] [CrossRef]
- Fujita, T.; Endo, T.; Yamamoto, A. Application of correction technique using leakage index combined with SPH or discontinuity factors for energy collapsing on pin-by-pin BWR core analysis. J. Nucl. Sci. Technol. 2014, 52, 355–370. [Google Scholar] [CrossRef]
- Herrero, J.J.; García-Herranz, N.; Cuervo, D.; Ahnert, C. Neighborhood-corrected interface discontinuity factors for multi-group pin-by-pin diffusion calculations for LWR. Ann. Nucl. Energy 2012, 46, 106–115. [Google Scholar] [CrossRef]
- Yamamoto, A.; Tatsumi, M.; Kitamura, Y.; Yamane, Y. Improvement of the SPH Method for Pin-by-Pin Core Calculations. J. Nucl. Sci. Technol. 2004, 41, 1155–1165. [Google Scholar] [CrossRef]
- Wang, X.; Zhuang, K.; Qiu, Z.; Wang, L.; Lu, D.; Zhang, B.; Wang, S. Research on reactor core pin-by-pin calculation based on new leakage corrected SPH method. Ann. Nucl. Energy 2025, 213, 111150. [Google Scholar] [CrossRef]
- Yu, H.; Kim, Y. A Leakage Correction with SPH Factors for Two-group Cross-section in MOX-loaded PWR Core. In Proceedings of the Transactions of the Korean Nuclear Society Autumn Meeting, Yeosu, Republic of Korea, 25–26 October 2018. [Google Scholar]
- Yu, H.; Kim, W.; Kim, Y. A leakage correction with SPH factors for two-group constants in GET-based pin-by-pin reactor analyses. Ann. Nucl. Energy 2019, 129, 30–55. [Google Scholar] [CrossRef]
- Yu, H.; Kim, Y. A Study on in situ Two-group SPH Factor Correction in GET-based Pin-by-Pin Core Analysis. In Proceedings of the Transactions of the Korean Nuclear Society Autumn Meeting, Jeju, Republic of Korea, 17–18 May 2018. [Google Scholar]
- Jeong, H.S.; Oh, T.; Kim, Y. A leakage correction with burnup-dependent GPS method in two-step core depletion analysis. Ann. Nucl. Energy 2023, 183, 109624. [Google Scholar] [CrossRef]
- Gamarino, M. Modal Methods for Rehomogenization of Nodal Cross Sections in Nuclear Reactor Core Analysis. Ph.D. Thesis, Nuclear Science and Engineering Department, Delft University of Technology, Delft, The Netherlands, 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).