An Overview of Probabilistic Safety Assessment for Nuclear Safety: What Has Been Done, and Where Do We Go from Here?

Abstract

The paper provides an introduction to the concept of Probabilistic Safety Assessment, an evaluation of its recent developments, and perspectives on the future research directions in this area. To do so, a conceptual understanding to safety assessment is first provided, followed by an introduction to what Probabilistic Safety Assessment is about. From this, the historical background and development of Probabilistic Safety Assessment in the context of nuclear safety are discussed, including a brief description and evaluation of some methods implemented to perform such analysis. After this, the paper reviews some of the recent research developments in Probabilistic Safety Assessment in the aspects of multi-unit safety assessment, dynamic Probabilistic Safety Assessment, reliability analysis, cyber-security, and policy-making. Each aspect is elaborated in detail, with perspectives provided on its potential limitations. Finally, the paper discusses research topics in six areas and challenges within the Probabilistic Safety Assessment discipline, for which further investigation might be conducted in the future. Hence, the objectives of the review paper are (1) to serve as a tutorial for readers who are new to the concept of Probabilistic Safety Assessment; (2) to provide a historical perspective on the development of the Probabilistic Safety Assessment field over the past seven decades; (3) to review the state-of-the-art developments in the use of Probabilistic Safety Assessment in the context of nuclear safety; (4) to provide an evaluative perspective on the methods implemented for Probabilistic Safety Assessment within the current literature; and (5) to provide perspectives on the future research directions that can potentially be explored, thereby also targeting the wider research community within the nuclear safety discipline towards pushing the frontiers of Probabilistic Safety Assessment research.

1. Introduction

1.1. Background

In recent years, the option of nuclear energy is increasingly being considered or implemented to provide an alternative energy source to meet the increasing global energy demand. Coupled with the pressing issue of global warming and climate change, the use of nuclear energy has become an increasingly promising option, given that it is carbon-free and has the potential to allow countries to reduce emissions while meeting their domestic energy demand. In fact, as of April 2024, there have been 417 operational nuclear reactors across the world with another 58 of such reactors under construction. Of the operational nuclear reactors, 27.10% are situated within Northern America, 30.46% are situated within Asia, and 40.29% are situated within Europe [1].

However, this option comes with risks, as nuclear reactors require the highest reliability, down to their smallest components and in the human/organisational factors that manage them. History has shown the potential impacts of nuclear accidents as seen from the Windscale fire accident in 1957 [2,3], Three Mile Island accident in 1979 [4], Chernobyl accident in 1986 [5], and the recent Fukushima-Daiichi accident in 2011 [6]. Details on each accident are found in the respective references. Hence, this brings forth the need for nuclear safety, security, and safeguards (i.e., the nuclear 3S concept) which is promoted by the International Atomic Energy Agency (IAEA) and its statute, while the responsibility of managing the nuclear 3S falls on its member states [7,8,9]. The focus of the paper is on the nuclear safety aspect, which is of critical importance within the nuclear industry [10]. As the saying goes, “Safety is freedom, freedom from unaffordable harm, and, thus, a human right” (Zio, 2018) [11].

A key approach towards evaluating the safety level of the nuclear reactor technology is Probabilistic Safety Assessment, also referred to as Quantitative Risk Analysis [12,13,14]. Such analysis seeks to address three key questions [15]:

• What could possibly happen? This involves identifying the accident scenario(s) leading to core damage and source term release (e.g., loss of coolant, steam-generator pipe rupture, and station black-out).
• How likely is the accident event? This involves quantifying the associated probability of the accident scenario(s).
• What is/are the consequence(s) of the accident? This involves identifying the outcome(s) of the accident scenario for the environment and life forms.

In doing so, it facilitates the risk-informed decision-making process in the reactor design, as well as in the human factors and emergency mitigation so as to minimise the associated risks of a severe accident. This makes Probabilistic Safety Assessment an informative and useful technique for risk analysis [16,17].

It is to be highlighted that there are key differences in the safety approaches between the nuclear fission and the nuclear fusion technology installations, details of which are found in [18,19,20]. In the interest of the work presented, the context of the paper is on the nuclear fission reactor technologies.

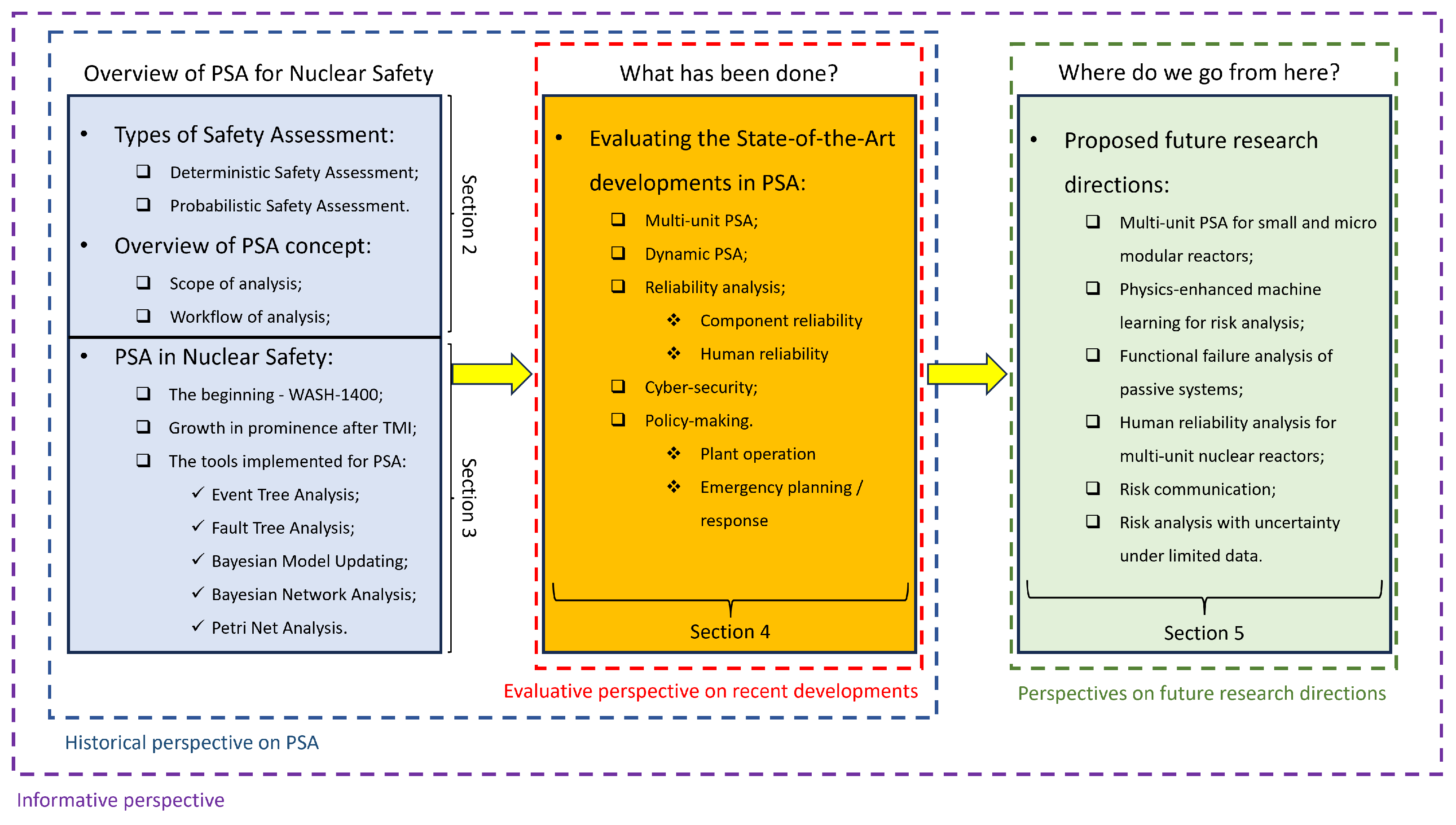
1.2. Objectives and Scope

In the interest of the paper, the technique of Probabilistic Safety Assessment is studied and reviewed with the following objectives: (1) to serve as a tutorial for readers who are new to the concept of Probabilistic Safety Assessment; (2) to provide a historical perspective on the development of the Probabilistic Safety Assessment field over the past seven decades; (3) to provide an evaluative perspective on the methods implemented for Probabilistic Safety Assessment in the literature; (4) to review the state-of-the-art developments in the field of Probabilistic Safety Assessment for nuclear safety; and (5) to provide perspectives over the future research directions that can be potentially explored, thereby serving as a reference for the wider nuclear safety research community towards developing the state-of-the-art in the field of Probabilistic Safety Assessment.

To achieve the objectives, the scope of the paper is as follows: (1) the objectives of safety assessment; (2) the need for Probabilistic Safety Assessment in nuclear safety and a brief history of its developments; (3) the tools for Probabilistic Safety Assessment and an evaluation of the methods; (4) the recent developments in Probabilistic Safety Assessment and perspectives; and (5) the research gaps that present an opportunity for future research works. As such, the paper is structured as follows: Section 2 outlines the concept of safety assessment and its objectives, followed by an overview of the concept of Probabilistic Safety Assessment. After, Section 3 provides a historical perspective of Probabilistic Safety Assessment in the nuclear industry, and its rise to prominence in the field of nuclear safety, as well as evaluating the tools implemented to perform such assessment. From there, Section 4 proceeds to discuss and review the state-of-the-art developments in the following aspects of Probabilistic Safety Assessment in nuclear safety: (1) multi-unit Probabilistic Safety Assessment; (2) dynamic Probabilistic Safety Assessment; (3) reliability analysis; (4) cyber-security; and (5) policy-making. Penultimately, Section 5 presents a series of research gaps identified which can serve as open research problems for future research works. Finally, Section 6 summarises the contents presented in the paper before drawing the paper to a close.

To illustrate the organisational structure of the paper and the categorisation of the sections based on their respective coverage, a flow-chart is presented in Figure 1.

2. What Is Safety Assessment

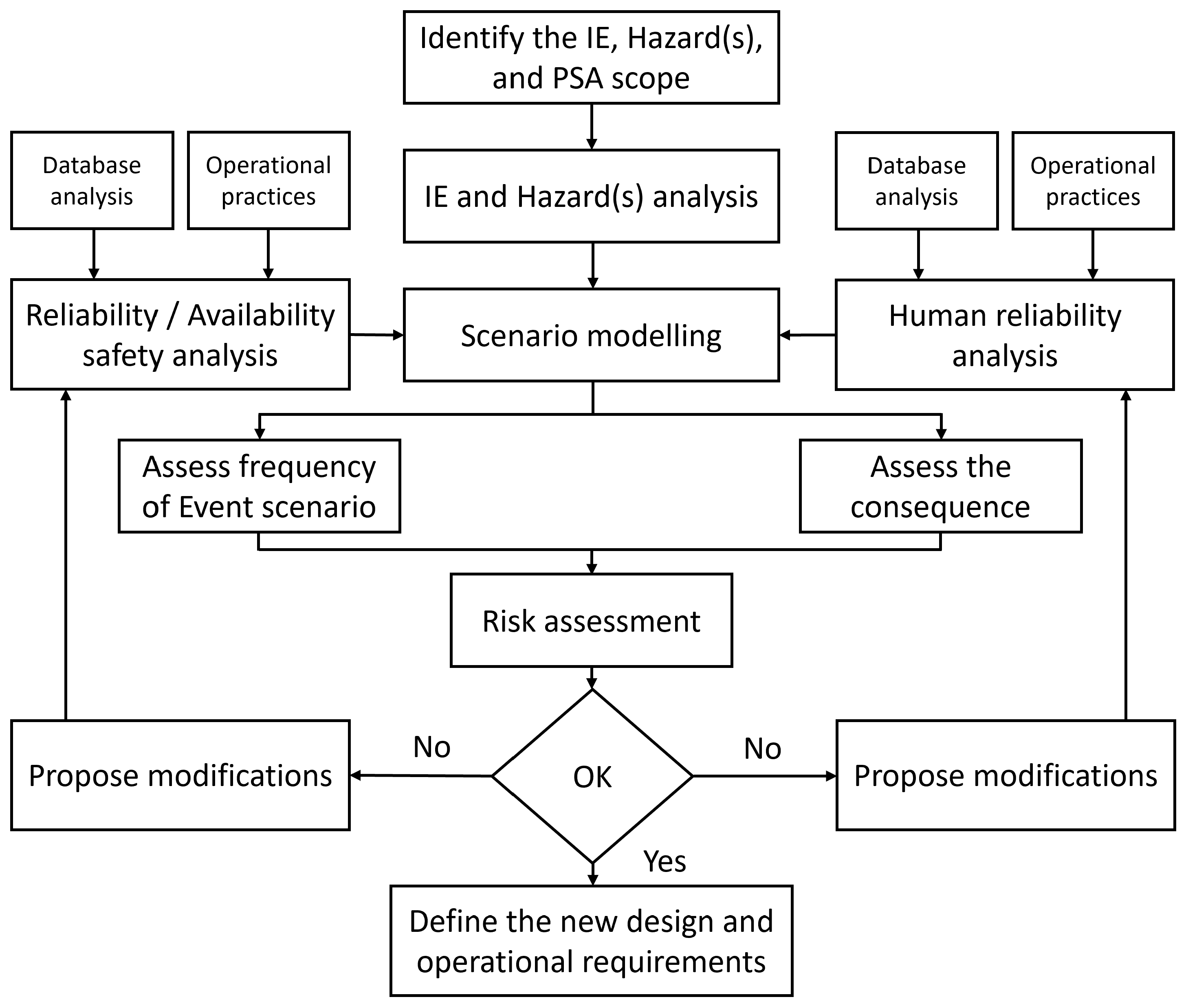
2.1. Concept and Philosophy

The general concept of safety assessment can be understood as a procedure to assess and evaluate the potential hazards associated with the design, operation, decommissioning, or maintenance of a facility [21]. In practice, such a procedure is mostly carried out before and during the operational lifetime of complex industrial facilities such as the nuclear reactors, where the relevance of safety assessment is seen in the evaluation of the facility design, construction and/or operational licensing, and life extension [22,23,24]. The safety assessment procedure usually involves modelling the physical phenomena (e.g., the loss of coolant) and analysing the response by the safety systems in place. This is to ensure that the safety requirements are met by the plant facility in dealing with the postulated accident scenarios. As such, the objective of performing such assessments is to verify whether the risks—defined as the probability that an initiating event (IE) eventually leads to an undesirable outcome (e.g., the atmospheric release of the source terms)—are of acceptable levels [22]. This makes such an assessment equivalent to a form of risk assessment [25].

There are multiple considerations through which the safety assessments can be performed, including the following:

• As Low As Reasonably Achievable: The understanding that risks are not completely reducible, as there are either no viable options available (i.e., impossible to reduce), or they are not cost-effective to reduce (i.e., the cost to reduce risk outweighs any potential benefits of reducing, either because cost is too high, or the risk is already negligible) [26];
• Defence-in-Depth: A safety philosophy achieved by multiple layers of protection (i.e., lines of defence) rather than relying solely on one layer for the plant to operate safely. Those layers may be provided by either redundant means or diverse means, thereby reducing the failure probability [27,28];
• Design Basis Accidents: A set of postulated accidents which the design of the facility must account for such that it is resilient towards these postulated accidents without any loss to the Structures, Systems, or Components (SSC) [29];
• Hazards: Anything that has the potential to cause an undesired event (e.g., such as a Loss of Coolant Accident (LOCA)) or condition that leads to equipment damage [30];
• Single Failure: A sole failure occurrence which leads to the loss in the capability of the nuclear reactor to operate safely [21]. This can be prevented through the introduction of multiple barriers (i.e., Defence-in-Depth) [22].

Based on the safety standards set by the IAEA, the scope of the safety assessment should encompass the following [31]: (1) the consideration of all sources of radioactive material, which includes the reactor core, irradiated fuel in transit, irradiated fuel in storage, and stored radioactive waste (e.g., spent fuel); (2) the assessment and evaluation of the plant performance under different plant states (i.e., operational and accidental conditions) against the deterministic and probabilistic criteria for safety and the risk of source term release; (3) the assessment of the design and safety features of the plant in fulfilling the required safety functions in response to the identified hazards; (4) the demonstration of the plant meeting the safety requirements and the hazard risks associated with the plant being acceptably low; and (5) the evaluation of the proposed plant design improvements by identifying potential design weakness and then highlighting the plant conditions along with the IEs which were not considered adequately a priori in the proposed design. In fact, these five points listed above are especially essential when assessing the safety of the Generation II to IV reactor designs. Many countries seek to improve existing safety system designs through the adoption of passive safety systems so as to improve the safety performance of such reactors and to mitigate a potential severe nuclear accident (e.g., NuScale’s reactor design). As such, the existence of the nuclear industry is heavily dependent on nuclear safety standards—nuclear safety is the lifeline of the nuclear industry.

Broadly speaking, the safety assessment can be performed through two approaches: (1) Deterministic Safety Assessment (DSA) and (2) Probabilistic Safety Assessment (PSA). In line with the scope of the paper, an overview and explanation of the concept of PSA is provided in Section 2.2. Readers may refer to references [32,33,34] for details on DSA.

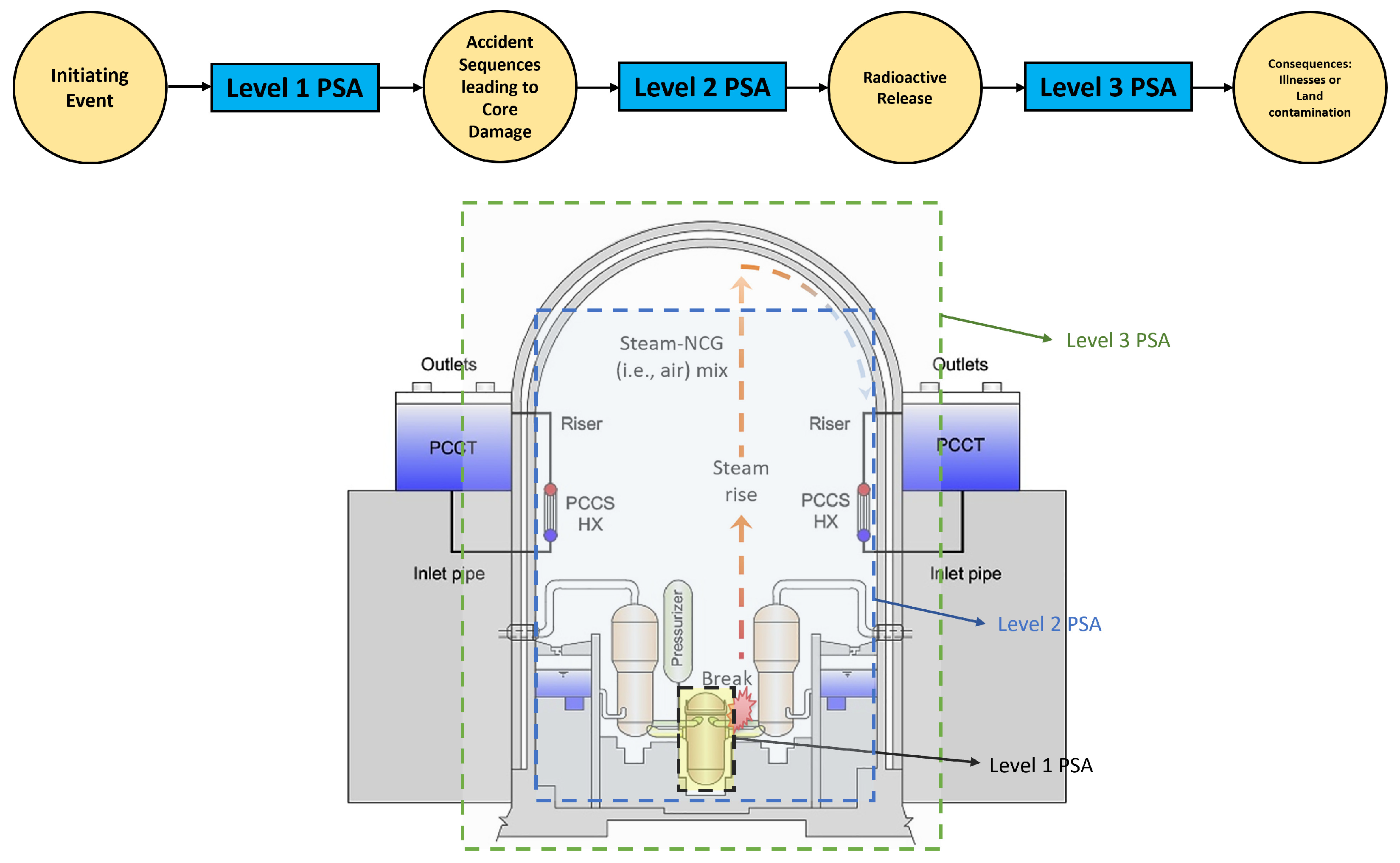
2.2. Overview of Probabilistic Safety Assessment

The PSA approach is a form of data-centric stochastic risk modelling and, hence, is also commonly referred to as a probabilistic risk assessment [35]. Its main purposes are to provide an understanding of the undesired consequences (e.g., core damage or the atmospheric release of source terms) by modelling such events with their associated probabilities and consequences using available information, usually based on the operating history of reactors of interest. In doing so, the analysis serves to provide a systematic and sophisticated analysis of the different risk management approaches, which are supported by the computed probabilities [31,36]. Hence, the objectives of PSA are [15] (1) identifying and delineating the different scenarios that could possibly result in a severe accident; (2) assessing the expected probability of occurrence for each of the corresponding combination of events; and (3) evaluating the consequences associated with each combination of events.

To achieve the aims and objectives, the scope of the analysis by the PSA approach is usually categorised into three distinct levels described as follows [37,38]:

• Level 1 PSA: The scope of the assessment is on the nuclear reactor design and its operating states, with the main focus being the accident sequences from a given IE that could result in core damage. This level of analysis serves to evaluate the strengths and weaknesses in the plant design, thereby facilitating the development of the necessary modifications in the safety systems and/or human factors towards the prevention of core damage and subsequent large release of source terms [36].
• Level 2 PSA: The scope of the assessment includes that of the Level 1 PSA and the phenomenon of the core damage accident, with the main focus being the response of the containment structure(s) to the expected load and the eventual release of the radioactive materials into the environment. This level of analysis serves to reflect the information pertaining to the associated probabilities of the source term releases, thereby highlighting the relative importance of the events pertaining to the primary safety concerns due to the potential atmospheric releases, and allowing for the identification of actions towards mitigating the consequences of such accidents [39].
• Level 3 PSA: The scope of the assessment includes that of the Level 2 PSA and the eventual atmospheric release of the source terms. A full Level 3 PSA serves to investigate the dispersion of the radioactive nuclides into the surrounding environment and analyse the potential environmental and health consequences of such a release [40].

To illustrate the relationship between the three levels of PSA, a flow-chart is provided in Figure 2.

Broadly speaking, there are two types of analyses that can be achieved through PSA [43]. The first type of analysis is called the a posteriori analysis. Such an analysis is performed on the existing nuclear reactors with operating histories based on the plant-specific data (e.g., the component failure data) obtained from operating experience. Should such data be lacking, generic non-plant-specific data can also be used in their place. Based on information from past operating experience, key accident events are identified and analysed to determine their associated conditional probabilities of progression towards the identified accident of interest (i.e., the Top event). From the derived conditional probabilities, an estimate of the Core Damage Frequency (CDF) can be obtained. Hence, the a posteriori analyses is performed on the basis of the total operating experience of the plant of interest to identify the aspects of operational vulnerability and propose improvements from there [43]. The second type of analysis is called the a priori analysis. Such an analysis is performed on a nuclear reactor with no operating history (i.e., one that is in the stage of conceptual design or under regulatory review) from which a prediction is made on the probability of a severe accident such as a core damage or the atmospheric release of source terms. Due to the absence of any plant-specific data, generic non-plant-specific data are used for the study [43].

A simplified and general procedure towards performing PSA is as follows [44]: The analysis is initiated by identifying the IE of interest, the hazard(s), and defining the scope of analysis (i.e., Level 1, Level 2, or Level 3 PSA). This serves as the basis for the safety assessment. Next, the IE and the hazard(s) are analysed, for which the subsequent possible sequences of events leading up to the consequence(s) (e.g., core damage or large atmospheric release of source terms) are identified. This is the scenario modelling stage, from which the plant response is analysed by evaluating the design reliability of the safety system and/or the human reliability in response to each event within the accident sequence. Such an analysis is performed using the information provided by the existing operational practices and the availability of plant-specific data in the case of the a posteriori analysis, or the availability of generic non-plant-specific data in the case of the a priori analysis. Based on such analysis, the information pertaining to the event sequence frequency and its consequence are obtained, from which an evaluation on the resulting risk of the severe accident scenario is performed against a defined safety goal. Should this safety goal not be met, the analyst may propose modifications to the equipment design and/or improvements for the operating procedures or technical competencies of the plant operators. Given the proposed modifications and the same initial conditions (i.e., the IE and scope of the analysis), the plant response is then re-evaluated against the same safety goal. Otherwise, the PSA procedure terminates, and the current/updated design and operational requirement of the plant are defined to be sufficiently robust in complying with the safety standards given the IE and the scope of the analysis. As a summary, a flow-chart outlining the work-flow for PSA is illustrated in Figure 3.

There are three notable strengths of the PSA approach [12]: (1) It can quantify the severity and the frequency of the severe accident, thereby providing a more comprehensive and systematic safety analysis. (2) It accounts for the uncertainties associated with the data, the approach used in modelling the event scenarios, and the completeness of the analysis. In doing so, it proves to be robust towards uncertainty propagation. (3) Finally, it considers thousands of different accident scenarios, including those not considered by DSA, involving multiple failures, which facilitates the understanding of the different system failure modes. Owing to such strengths, the PSA method thus serves as a cost-effective tool for (1) risk-based decision-making towards plant design improvements and operational support (e.g., risk-based maintenance and repair strategies; this motivates the NRC to encourage its implementation in complementing the DSA approach in the safety analysis requirements in 1995 [45]); (2) facilitating emergency planning and preparedness; and (3) serving as a tool to aid risk communication and outreach to various stakeholders (e.g., government, regulatory board, and the general public).

However, there remain two significant drawbacks to the PSA approach: First, its robustness and capabilities are limited by the availability and quality of the necessary data required for such an analysis to be possible [46]. This drawback becomes especially pronounced when performing an a priori analysis with available generic non-plant-specific data that may not be applicable to the plant design of interest. And second, it remains relatively challenging to model human errors and organisational factors (e.g., safety culture) and to account for them in the overall analysis, although there is significant ongoing research being conducted to try to overcome this challenge [47,48].

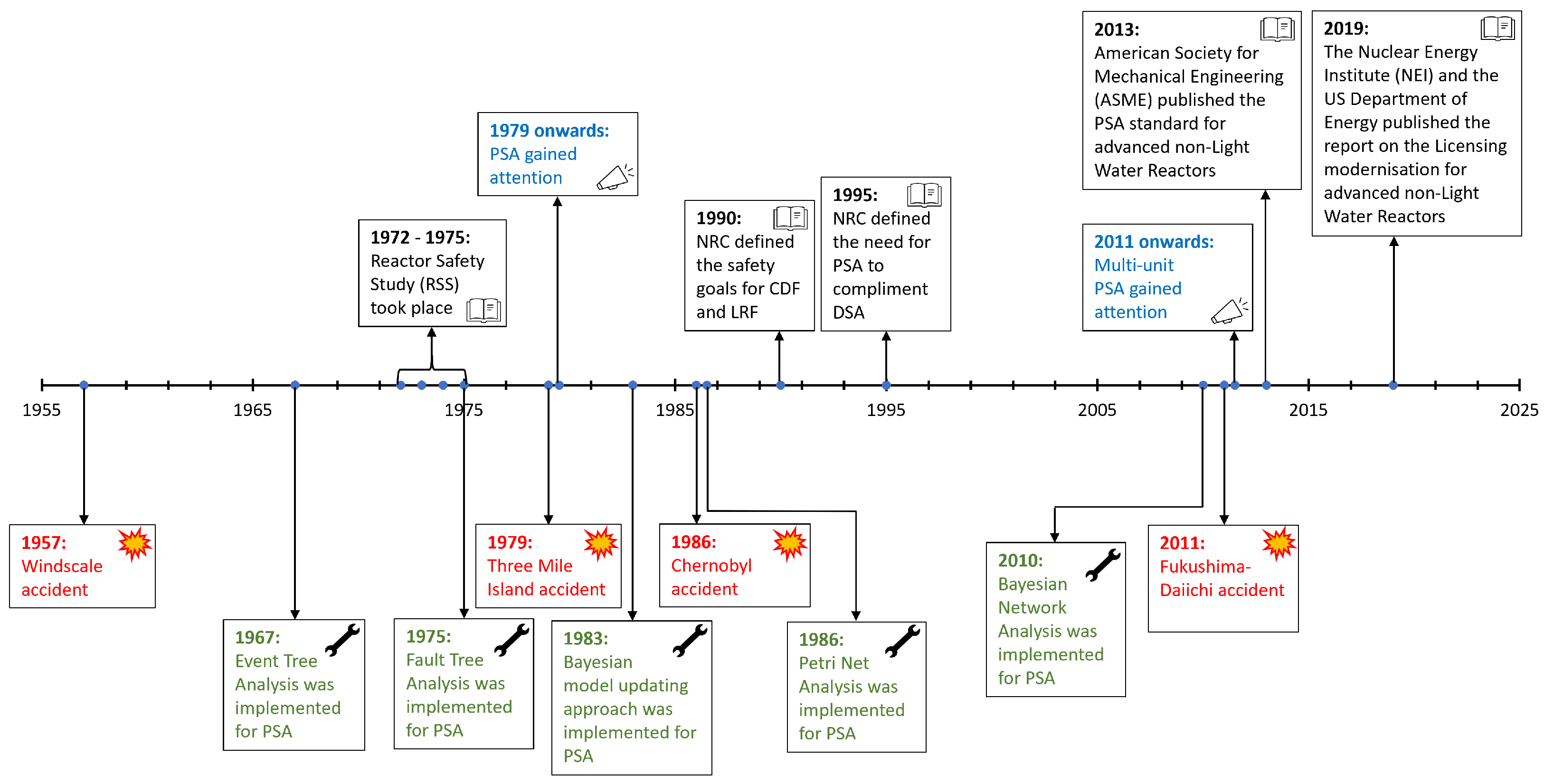
3. Historical Perspective of Probabilistic Safety Assessment in the Nuclear Industry

The concept of reactor safety gained significant attention and importance between the late 1960s and early 1970s when an increasing number of nuclear reactors were either completed or under construction [49]. This attention was accompanied by increased public and political opposition towards nuclear reactors, due to the perception that the US Atomic Energy Commission (AEC) safety criteria for the licensing of such plants were insufficiently robust relative to the apparent safety significance of the various SSCs within the plants [50]. Furthermore, there was a debate through the years as to whether the emergency core cooling system would work, as well as an increased demand for the risk estimate in the failure of the safety systems. These factors motivated the AEC to initiate a much more comprehensive study on the safety evaluation of the light water reactors designs and hence the Reactor Safety Study (RSS) [51].

The analysis considered the following two key areas: (1) the failure in the major systems such as the engineered safety systems; and (2) the resilience of the plant containment system towards preventing the atmospheric release of the source terms in the event of an accident. To perform the analysis, the RSS looked at six specific LOCA events as the IE [49]:

• Small pipe breaks (i.e., less than 2 inches in diameter);
• Intermediate pipe breaks (i.e., between 2 and 6 inches in diameter);
• Large pipe breaks (i.e., larger than 6 inches in diameter);
• Large disruptive reactor vessel ruptures;
• Gross steam generator ruptures;
• Ruptures in systems that interface with the reactor coolant system.

In addition to this, the RSS also considered the different possible reactor transients and IEs. In the context of the study, a transient refers to the situation whereby the key reactor operating parameter shows a significant deviation from the normal operating value. This includes all non-LOCA events, such as equipment failure or human error, which can lead to a reactor shut-down to minimise any potential damage to the fuel. The three main areas for transients considered in the RSS are instances where there is an increase in the reactor power, a decrease in the flow of the coolant, or an increase in the pressure of the coolant. Broadly speaking, the transients can be categorised into two distinct categories: (1) anticipated transients (e.g., loss of off-site power and loss of feedwater); and (2) unanticipated transients (e.g., vessel rupture, turbine missiles, and sabotage). However, through some preliminary analysis of the frequency and the consequences, it was found that the unanticipated transients’ contribution towards the overall risk was small compared to that of the anticipated transients, which produced the same consequences. This led to the removal of the unanticipated transients and some of the relatively low-frequency anticipated transients from consideration, allowing for a significant reduction in the number of possible IEs, leading to a core damage and radioactive release to be considered.

To perform the PSA, the industrial data were utilised on the component failure rates along with expert elicitation on aspects for which data were unavailable. In order to account for the epistemic uncertainties (i.e., uncertainty due to a lack of knowledge associated with the availability of limited data) [52,53], the probabilities of the key events in a given the accident sequence were modelled to follow a Log-normal distribution instead of point estimates. Based on the available techniques and information provided, the study was able to quantify that the CDF for a Generation II PWR is of the order ${10}^{-5}$ per reactor year [49]. This result was significantly higher than that obtained from previous studies of such reactors, which yielded failure probabilities of the order ${10}^{-6}$ per reactor year. The reason for this is that the RSS managed to determine that small-break LOCAs had the highest contribution towards the overall failure probabilities through the modelling techniques implemented, while previous analyses would usually neglect the contribution of small-break LOCA towards the eventual core damage [49]. This allowed for the RSS to produce relatively accurate and realistic results compared to prior studies, effectively making the RSS the first in implementing the PSA framework within the nuclear industry.

Despite such robust results presented by the RSS, the initial series of hearings held in June 1976 by the Committee on Interior and Insular Affairs of the US House of Representatives found the study to be misleading in its conclusions. Subsequently, a series of meetings held between August 1977 and September 1978 was conducted by the Risk Assessment Review Group (i.e., the Lewis Committee) aimed at performing a detailed review over the RSS [54]. While the committee found the RSS to be generally commendable in the completeness and depth of its analysis, the review raised numerous concerns, including [54] (1) the lack of “scrutability" in the calculation procedure; (2) the lack of accurate data to perform the risk analysis; (3) the lack of consideration of some external events (e.g., earthquakes, fires, and human accident initiation) towards the overall risk quantification; (4) the scepticism over the peer review process of the RSS by the US NRC; (5) the difficulty in finding the content discussing the health impact of radiation release; and (6) the poor communication of information within the Executive summary. Following the criticism by the Lewis Committee, the NRC withdrew its support towards the RSS and focused on the continued implementation of the DSA approach towards performing safety assessments of nuclear reactors, effectively casting the PSA approach and the RSS aside.

In March 1979, there was revived interest towards the RSS and the PSA approach by the NRC in the wake of the Three Mile Island accident in Unit 2 [49]. This was due to the fact that the RSS had considered an event sequence similar to that of the Three Mile Island accident in the PSA analysis for another another plant, while the accident also validated the conclusion of the RSS that a small-break LOCA is more risk significant than a large-break one. Subsequently, the NRC began investing heavily towards expanding the PSA implementation within the nuclear industry [55]. This resulted in two follow-up PSA studies which were conducted between 1979 and 1982 known as (1) the Reactor Safety Study Methodology Application Program, which aimed at applying the methodology presented in the RSS to other plant designs [56,57], and (2) the Interim Reliability Evaluation Program which aimed at developing and standardising the reliability methods implemented towards reliability and safety assessments [58,59,60]. Since then, significant efforts have been invested by the NRC and the nuclear industry into improving and developing the state-of-the-art PSA approaches and implementing extensive PSA methods for the licensing of nuclear reactors [49]. A result of such efforts was the definition of the Safety Goals by the NRC in 1990 pertaining to the CDF and the Large Release Frequency (LRF), where the following values were set as the “benchmark”: ${10}^{-4}$ for the CDF and ${10}^{-5}$ for the LRF.

To date, numerous risk modelling approaches have been implemented to perform PSA on the nuclear reactor designs, for which some examples, along with their corresponding references to their implementation, are presented in

Table 1. Examples of some of the approaches implemented for PSA.

Approach	Acronym
Fault Tree Analysis	FTA
Event Tree Analysis	ETA
Bayesian Model Updating	BMU
Bayesian Network Analysis	BNA
Petri Net Analysis	PNA

. An overview of each of the PSA approaches listed in the table are presented in Section 3.1, Section 3.2 and Section 3.3.

3.1. Fault Tree Analysis

The FTA is a commonly implemented approach to perform PSA and was first utilised for such a purpose in 1975. It provides a systematic analysis of the cause of an identified Top event through the use of a graphical and logical model (i.e., the Fault Tree) to express the parallel and serial combinations of faults leading to the eventual Top event. As such, the Fault Tree itself illustrates the logical inter-relationships (e.g., the “AND” or “OR” logic) of the basic/root events that result in the Top event. Based on the constructed Fault Tree, the minimal cut sets are identified, which highlight the smallest combination of basic event and represent the most important event sets which will lead to the Top event [61,62]. From this, a quantitative analysis on the Fault Tree is performed by computing the probability of occurrence of the Top event from the probability of occurrence of the basic events. The computation process, along with the subsequent uncertainty, sensitivity, and importance analyses, can be supported using computer code [63,64,65]. This is especially so when performing the analysis on complex Fault Trees, which may be the case when analysing the risk of CDF or LRF for a nuclear reactor. Hence, the FTA is a useful technique in carrying out the reliability and the availability analysis on a nuclear reactor design [66].

The main advantages of the FTA approach are threefold:

• It can model many hazards from different event combinations;
• It can be used to identify common cause failures;
• It provides a clear and logical presentation of the cause of a Top event.

However, its main disadvantages are twofold:

• Such an analysis can only be performed for one Top event at a time;
• The construction of the Fault Tree and the subsequent analysis can be time-consuming and complicated for complex/complicated sub-systems of the nuclear reactor.

3.2. Event Tree Analysis

The ETA is another commonly implemented approach to perform PSA, and the first recorded implementation of such a methodology was in an IAEA study on the containment and siting of nuclear reactors by Farmer in 1967 [67]. The approach was based on the decision analysis field and its subsequent implementation in the RSS stemmed from the realisation that the FTA approach for the entire nuclear reactor was deemed too complex at the time of the study [49]. Such a decision proved to be worthwhile, as the ETA approach was able to address the time and resource constraints associated with the FTA approach [51].

Like the FTA approach, the ETA approach provides an alternative way to perform a systematic analysis of the sequence of events starting from a given IE all the way to the eventual Top event. However, the difference between the FTA and the ETA is that the latter is performed through the use of a branched graph model which illustrates all possible sequence of the plant states, operating performance, emergency response, and their corresponding probability of occurrence. The individual branch denotes a particular Defence-in-Depth level, and its associated failure probability is obtained from either the historical data or previous studies such as reliability analysis. Hence, an Event Tree allows for a logical presentation of the different end states of the given nuclear reactor that is studied along with the associated probability of occurrence for each end state. This makes the approach useful towards estimating the risk and consequence of each accident scenario given an identified IE [49].

The main advantages of the ETA approach are threefold:

• It simplifies the accident sequence through clear and logical presentation;
• It is applicable towards a wide range of hazards in qualitative risk analysis;
• It can diagnose both equipment-related events and those related to human reliability.

However, its main disadvantages are fourfold:

• It is inefficient in modelling accident sequences where many events have to occur in combination, as it yields many redundant branches;
• The independence assumptions between distinct events can lead to missing systematic and common-mode failures;
• The analysis is limited to only one initiating event at a time;
• The binary logic (i.e., Yes or No) becomes inapplicable when involving elements of uncertainty such as human error or adverse weather conditions.

3.3. Bayesian Model Updating

The BMU approach provides a quantitative method to update one’s subjective knowledge over the failure parameter(s) (e.g., component failure probability) as new information/data become available and has seen numerous applications in the field of engineering [68], especially nuclear [17,69,70,71]. The earliest recorded implementation of such an approach for PSA in NRC was in the NUREG/CR-2300 technical report published in 1983 [72] and is based on Bayes’ theorem, which is mathematically defined as [73,74]:

$$P\left(\mathit{\theta }\right|\mathit{D},M)={\displaystyle \frac{P\left(\mathit{\theta }\right|M)·P(\mathit{D}|\mathit{\theta },M)}{P\left(\mathit{D}\right|M)}}$$

(1)

where $\mathit{\theta }$ is the vector of failure parameter(s) to be estimated, $\mathit{D}$ is the vector of data used to infer the failure rates, and M is the model relating $\mathit{\theta }$ to $\mathit{D}$. The terms in Equation (1) are as follows [75,76]:

• $P\left(\mathit{\theta }\right|M)$ is the prior distribution denoting the a priori knowledge of $\mathit{\theta }$ before observing $\mathit{D}$ through the given model M;
• $P\left(\mathit{D}\right|\mathit{\theta },M)$ is the likelihood function quantifying how likely it is that $\mathit{\theta }$ represents the observed $\mathit{D}$ through the given model M;
• $P\left(\mathit{D}\right|M)={\int }_{-\infty }^{\infty }P\left(\mathit{\theta }\right|M)·P\left(\mathit{D}\right|\mathit{\theta },M)·d\mathit{\theta }$ is the numerical normalisation constant;
• $P\left(\mathit{\theta }\right|\mathit{D},M)$ is the posterior distribution denoting the a posteriori knowledge on $\mathit{\theta }$ after observing $\mathit{D}$.

Generally speaking, the integral of $P\left(\mathit{\theta }\right|\mathit{D},M)$, and therefore the mean and variance estimates on $\mathit{\theta }$ may not be obtained analytically. As such, the estimates on $\mathit{\theta }$ are performed numerically by sampling from $P\left(\mathit{\theta }\right|\mathit{D},M)$ using sampling tools such as the Markov Chain Monte Carlo or the Sequential Monte Carlo samplers [77,78,79]. However, there exists a specific case where the posterior distribution is of the same distribution class as the prior distribution given a likelihood function. In this case, the posterior and prior distributions are conjugate distributions, and a closed-form solution of the posterior distribution can be obtained analytically.

The main advantages of the BMU approach are threefold:

• It yields a distribution estimate of the inferred parameter(s) characterising its uncertainty;
• It is applicable and efficient in performing estimates on the inferred parameter(s) when dealing with a limited or small dataset;
• It can also perform online learning on the inferred parameter(s) when the data are obtained sequentially.

However, its main disadvantages are twofold:

• High computational cost is incurred in cases where the model M is computationally expensive;
• The choice of the prior is subjective to the analyst, which affects the probabilistic estimates of the inferred parameter(s), especially when the data are scarce, which makes the estimates on the inferred parameter(s) highly dependent on such a choice.

3.4. Bayesian Network Analysis

The BNA methodology was developed by Pearl in 1986 and was first implemented in the domain of artificial intelligence before subsequently being implemented in the areas of information technology, industrial, reliability, and safety fields [80]. The approach was first implemented for PSA in 2010 [81] and involves the construction of a graphical model consisting of nodes and edges to illustrate the polymorphism and the failure dependencies between the root, intermediate and the Top events along with their associated uncertainties. There are two features to a given Bayesian network with N nodes [81]. The first feature is the mode structure. Such a structure is illustrated a N-node directed acrylic graph with a given nodes set $V=\{V_1,\dots ,V_N\}$, which represents the variables such as the equipment state and personnel operations. The causal relationship between the variables is represented by the directed edges between the node pairs. For a given pair of nodes $\{V_i,V_j\}$ (for $i\ne j$) related by a directed edge from $V_i$ to $V_j$, node $V_j$ is known as the parent node of $V_i$, and conversely, node $V_i$ is known as the child node of $V_j$. A node without an associated parent node is a root node, while a node without an associated child node is the leaf node. A parent node set of $V_i$ is denoted as Pa$\left(V_i\right)$. The second feature is the associated probability of the root node and the conditional probabilities between the nodes. Under the conditional independence assumption, the conditional probability distribution which quantifies the association between the node and its parent nodes is denoted as $P\left(V_i\right|\mathrm{Pa}\left(V_i\right))$. By the same assumption, the joint distribution of the nodes $P(V_1,\dots ,V_N)$ is defined as

$$P(V_1,\dots ,V_N)=\prod _{i=1}^{N}P\left(V_i\right|\mathrm{Pa}\left(V_i\right))$$

(2)

The main advantages of the BNA approach are threefold:

• It is able to update the joint and conditional probabilities as more data and observations are made;
• It can illustrate graphically the causal relationships between the root and intermediate events leading to the Top event, making such approach useful in risk communication;
• It can quantify and propagate the uncertainties in the conditional probability estimates though the network.

While its main disadvantages are twofold:

• Complex Bayesian networks with large number of nodes can incur high computational costs;
• It is unable to handle continuous data well, implying the need for the analyst to discretise the initial continuous data before the analysis.

3.5. Petri Net Analysis

The PNA approach involves the use of a graph-based structure referred to as a Petri Net which was proposed by Petri during his PhD [82] and was first implemented for PSA in 1986 [83]. Like the Bayesian Network, the structure itself is made up of nodes and edges, which are referred to in this context as places and transitions. As such, the Petri Net is able to simulate the dynamic behaviour of a given nuclear reactor system through the continuous “firing” of enabled transitions, which allow for tokens to be removed or inserted into the various places. In doing so, it is able to capture the information pertaining to the impact of the response, maintenance, and recovery processes for the different modes of failure associated with the plant. In fact, the approach is applicable to systems which are either concurrent, asynchronous, distributed, or parallel, which provides flexibility to the PNA framework. This allows the PNA to serve two purposes in PSA: (1) to provide a mathematical representation of the system via state equations, algebraic equations, and numerous mathematical models describing the dynamics of the system being studied; and (2) serving as a tool to aid in the visual communication when communicating the risk of a severe accident to the various target audiences, such as the general public, policy-makers, and the government personnel.

The main advantages of the PNA approach are twofold:

• It is useful in modelling the transition dynamics between the different operating states of the nuclear reactor being studied;
• It illustrates graphically the causal relationships between the root and intermediate events leading to the Top event, making such an approach useful in risk communication.

However, its main disadvantage is as follows:

• The configuration of the Petri-net can be inherently complex, especially when studying the relatively complex sub-systems of a nuclear reactor.

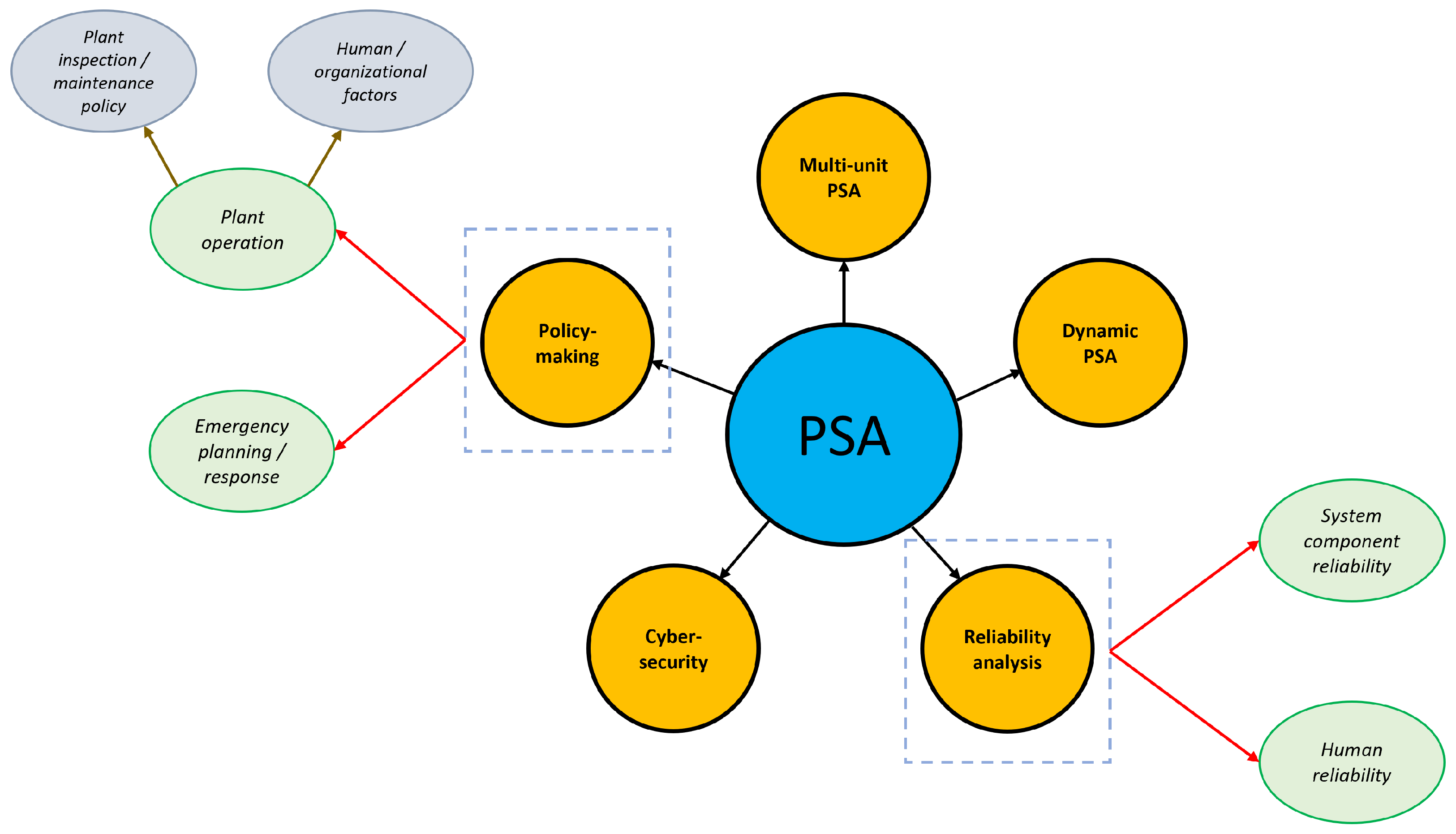
4. Review of the State-of-the-Art Developments

In recent years, the implementation of the PSA techniques described in Section 3.1, Section 3.2, Section 3.3, Section 3.4 and Section 3.5 has increased significantly owing to the development of robust computational techniques which facilitate the study of complex nuclear reactor designs and compute the small failure probabilities (i.e., the order of ${10}^{-6}$ and below). To provide an understanding and an evaluation of such recent developments, the relevant works in the literature published between 2022 and 2024 are reviewed and are categorised according to the aspect of PSA being studied. The scope of the review covers the following five main aspects:

• Multi-unit PSA;
• Dynamic PSA;
• Reliability analysis, which can be further sub-classified into component, and human reliability;
• Cyber-security;
• Policy-making, which can be further sub-classified into plant inspection/maintenance policy, human/organisational factors, and emergency planning/response.

A chart is presented in Figure 4 to illustrate the structuring of the main aspects and the sub-aspects (if any), while

Table 2. Examples of recent works published between 2022 and 2024 categorised according to the respective aspects of the PSA reviewed, approaches implemented, and scope of the analysis.

Aspect	Sub-Aspect	Approach	PSA Level	Reference
		FTA	3	[84]
		FTA/ETA/BNA	1	[85]
Multi-unit PSA	-	ETA	2	[86]
		ETA	3	[87]
		ETA	1	[88]
		FTA/BNA	1	[89]
Dynamic PSA	-	ETA	1	[90,91]
		PNA	1	[92,93]
Reliability analysis		BMU	1	[94,95,96]
	Component reliability	BMU/BNA	1	[97]
		BNA	1	[98]
	Human reliability	BMU	1	[99,100]
		BNA	1	[101]
		ETA	1	[102]
		ETA/BNA	2	[103]
		PNA	1	[104,105]
Cyber-security	-	ETA	1	[106,107]
		BNA	1	[108]
Policy-making	Plant inspection/maintenance policy	BMU	1	[109,110,111]
		ETA/FTA	1	[112]
		PNA	1	[113]
	Human/Organisational factors	BNA	1	[114]
		BMU/BNA	1	[115]
		ETA	1	[116]
		FTA	1	[117]
		ETA/FTA	1	[118]
	Emergency planning/response	FTA/ETA	2	[119]
		BNA	2, 3	[120]
		BMU	3	[121,122]
		FTA/ETA	3	[123]

presents the categorisation of the literature in their respective aspects and sub-aspects along with the list of the implemented approach(es) and the scope of analysis (i.e., PSA level).

4.1. Multi-Unit Probabilistic Safety Assessment

Traditionally, PSA studies have been restricted to single reactor units and are referred to as single-unit PSAs [124]. Such studies consider only the accident scenarios which are exclusive to one specific reactor unit and this is performed under the assumption that the accident impact by the other reactor units is less critical. For this reason, the single-unit PSAs account only for the dependencies between the SSCs within the single reactor unit of interest whose failure(s) may lead to a station black-out or a common cause failure, for example [125]. This is known as intra-unit dependency.

Multi-unit PSAs, on the other hand, account for the dependencies across the multiple different reactor units co-located at the same site, and such dependencies are referred to as inter-unit dependencies. Examples of such inter-unit dependencies may include [126] (1) IEs which occur across multiple reactor units simultaneously; (2) the occurrence of a transient event in one reactor unit which also affects some or all of the other reactor units of the multi-unit nuclear power plant; (3) the proximity of the individual reactor units to one another; and (4) the shared SSCs such as batteries, diesel generators, and common operation practices. Hence, this brings to light the importance of characterising such dependencies properly, as well as the site-level dependencies that are essential towards obtaining an accurate and robust risk profile of the nuclear power plant site.

The history of multi-unit PSA dates back to the early 1980s when the first of such studies was conducted on the Indian Point Station which investigated the dual-unit atmospheric source term releases as a result of seismic and high wind hazards (i.e., Level 3 PSA) [127]. Despite the risk, the question of nuclear safety among multi-unit plants was initially deemed to be relatively insignificant by the nuclear community and was not raised again until the Fukushima-Daiichi accident, which demonstrated the following [128]:

• There were no accident management plans for multi-unit accidents then;
• The recovery of Unit 2 was delayed by the hydrogen explosion occurring at the adjacent Unit 1;
• The hydrogen gas production in Unit 3 led to a hydrogen explosion of the unit and the subsequent delayed recovery of Unit 4.

This made the PSA community re-evaluate the current safety regulations to consider inter-unit dependencies, which are critical in severe accident risks, such as multiple core damages, spent fuel pool damages, and damages to the other radioactive waste storage facilities.

Since then, the relevance of multi-unit PSA has continued to gain significant importance in light of the increasing number of multi-unit nuclear power plants on a global scale [129]. In fact, the IAEA reported in 2020 that $73\%$ of the world’s existing nuclear power plants are multi-unit plants [130] and that $61.40\%$ of these existing multi-unit plants are based within the United States [131]. This motivated the investment of research efforts towards developing methods for multi-unit PSA as seen in the recent works: (1) the implementation of FTA to perform a Level 3 PSA study on the adverse effects of inter-unit radioactive release on operator actions at a multi-unit site [84]; (2) the implementation of ETA, FTA, and BNA to perform a Level 1 PSA study on the effects of the varying correlation in spatial ground motion on the extent of core damage within a hypothetical dual-unit reactor site [85]; (3) the implementation of ETA to perform a Level 2 PSA study on a high-temperature gas-cooled reactor via a multi-unit event sequence modelling method accounting for the dependencies between events of single-unit event trees, aiming at computing the LRF of each release category [86]; (4) the implementation of ETA to perform a Level 3 PSA study via a plume segmentation optimisation method to analyse the subsequent off-site consequences of a multi-unit accident [87]; and (5) the implementation of ETA to perform a Level 1 PSA study on a dual-unit reactor under the loss of offsite power initiating event using multi-unit event trees derived via a combinatorial computation [88].

Based on the review of the above literature, the following insights were obtained: First, ETA is the most implemented approach towards performing multi-unit PSA, owing to its simplicity in modelling accident sequences, diagnosing both equipment-related events and those related to human reliability, and the dependencies between individual reactor units through numerous approaches, such as linking [84] or combinatorial [88] approaches. However, the ETA method mostly assumes independence between the individual events of the accident sequence, which can result in an underestimation of the accident probability. Second, while the multi-unit PSA analyses have generally managed to characterise and model the inter-unit dependencies of the reactor facilities, they fail to accurately model and account for the physical site configurations, such as the physical distance/layout between the individual reactor and the wind directions when performing a Level 3 PSA. Such shortcomings may compromise the interpretation of the PSA results, as it is not representative of the physical site conditions. Finally, the analysis is performed mostly in a deterministic manner, in that point values are used in the ETA computation without accounting for the variability due to uncertainties or characterising the uncertainty in the resulting risk estimates. This presents a limitation in such analysis towards a risk-based and risk-informed decision-making pertaining to emergency planning or response.

4.2. Dynamic Probabilistic Safety Assessment

The dynamic nature of the operating behaviour/state is an important characteristic of many engineering systems, especially that of a nuclear reactor. This emphasises the need to also model the time-dependent interactions between the system components and the reactor units, and subsequently quantifying the associated risk. This gives importance to the aspect of dynamic multi-unit PSA [132,133,134].

Unlike the traditional approach towards PSA, the dynamic PSA approach couples the implementation of the safety analysis codes such as the ASTEC and MELCOR along with the stochastic simulation methods such as the Risk Analysis and Virtual ENvironment (RAVEN) [135] or Monte Carlo methods to complement the logic structures such as the Event Trees and the Fault Trees (i.e., see Section 2.2) [136,137]. In doing so, it allows for an increased robustness and realism in the safety assessment by accounting for the time-varying effects on the plant system and the dynamics of the physics-based models, thereby providing a real-time update on the analysis [138]. Hence, the dynamic PSA approach becomes favourable in modelling the numerous component behaviour of the reactor which include [139] (1) the thermal–hydraulic behaviour and (2) the operators’ responses towards the accident. From these, the probabilistic aspect of the analysis is implemented by defining a set of stochastic parameters characterising the time-dependent accident progression [133,134,140,141].

Recent developments within the aspect of dynamic PSA include (1) the implementation of FTA and BNA to perform a Level 1 PSA study in the form of a dynamical reliability analysis of the emergency diesel generator within a boiling water reactor [89]; (2) the implementation of ETA to perform a Level 1 PSA study in the form of a risk analysis of a LOCA for hypothetical three-loop pressurised water reactor via a proposed dynamic integrated consequence evaluation approach [90]; (3) the implementation of ETA to perform a Level 1 PSA study in the form of a risk analysis of a small-break LOCA by incorporating the operator action timing within the human reliability evaluation method and considering such effects on the conditional core damage probability [91]; (4) the implementation of PNA to perform a Level 1 PSA study involving the dynamical reliability analysis of the reactor’s liquid poison injection system [92]; and (5) the implementation of PNA to perform a Level 1 PSA study involving the dynamical resilience analysis of nuclear reactors under the threat of natural hazards [93].

Based on the review of the above literature, the following insights are obtained: First, the analysis is mostly focused on Level 1 PSA involving the reliability computation of SSCs and the human factors under dynamic scenarios. Such an analysis can be extended towards Level 3 PSA, where the dynamical feature, in the form of the radioactive nuclide dispersion evolution, becomes more pronounced. Second, the PNA method is shown in [93] to be capable in not only computing the CDF under different accident scenarios (e.g., LOCA or station black-outs) but also predicting how soon the reactor system recovers from the different scenarios considered, an aspect which should also be of interest in PSA. Such predictive capability is yet to be explored with the ETA, FTA, and the BNA approaches. Finally, the BNA method is gaining interest among researchers and experts, as it serves as an effective tool to capture causal relationships between the events, although such a method still falls short when defining the acyclic relationship between the events.

4.3. Reliability Analysis

Reliability analysis is a fundamental aspect of PSA and the objective is to assess the likelihood of the key components of a nuclear reactor, or the reactor as a whole, functioning as intended (or otherwise) during the operation time. Such an analysis is crucial for the following reasons: First, it allows for the reliability quantification of the critical equipment and systems, from which the operators and the key decision-makers (e.g., reactor engineers and policy-makers) can estimate the probability of accidents or failures occurring. Second, it identifies the most critical SSCs within the reactor via a sensitivity analysis, allowing for its prioritisation for maintenance, upgrades, or replacement. Third, such an analysis evaluates the effectiveness of safety systems and barriers within the reactor facility to mitigate the consequences of accidents or failures. And fourth, such an analysis is often required by regulators as part of the overall reactor safety assessments to instil confidence and trust to the public, and the relevant stake-holders that the reactor complies with the safety standards.

4.3.1. System Component Reliability

Recent developments within the aspect of the reactor system component reliability include (1) the implementation of BMU to update the Thermo-Hydro-Mechanical and Leakage model based on the strains, global leakage, and local leak measurements toward inferring the model parameters associated with the representative structural volume of a nuclear containment building and assessing the structural component’s reliability [94]; (2) the implementation of BMU to infer the uncertain parameters of the Thermo-Hydro-Mechanical model, based on the uncertain strain predictions, towards providing a reliable prognosis of the nuclear containment building structural mechanical state [95]; (3) the implementation of BMU to calibrate the finite element pre-stressed concrete containment vessel, based on the displacement measurements, towards assessing the structural reliability of the vessel under different internal pressure conditions [96]; (4) the implementation of BNA and BMU to estimate and update the reliability parameters for a helium circulator of a high-temperature gas-cooled reactor [97]; and (5) the implementation of BNA to develop a reactor reliability model and a reliable life analysis method for the Stirling integrated space reactor which is robust to manipulation and can obtain system reliability indicators with small confidence intervals for engineering decisions [98].

Based on the review of the above literature pertaining on the use of PSA to perform a reactor system component reliability, the following insights were obtained: First, most of the reliability analysis involves the use of a physics-guided machine learning approach, where a physics-based model is used to perform a model updating and reliability analysis on the system component. This provides the element of interpretability and explainability for the reliability results. Second, the reliability analysis thus far via the BMU approach is performed in an offline manner, where the updating of the inferred parameters is performed with all the available data at once. Such an analysis can be extended towards cases where the data are obtained across different time-steps, thereby paving way for an online BMU approach to be implemented towards a real-time dynamical reliability analysis on the system components. Finally, the Bayesian approaches (i.e., BMU and BNA methods) fall short under extreme data scarcity with large epistemic uncertainty, although this can be addressed via Monte Carlo simulation or expert judgement.

4.3.2. Human Reliability

Besides ensuring the reliability of the reactor’s system mechanical components, the human reliability analysis is also a critical component of PSA. It focuses on evaluating and quantifying the likelihood and consequences of human errors in nuclear facilities, recognising that human factors play a significant role in overall safety performance.

Recent developments within the aspect of human reliability include (1) the implementation of BMU to quantitatively compare human reliability analysis methods of interest using both prior knowledge and human performance data [99]; (2) the implementation of BMU to update prior human reliability estimates with the simulator evidence to obtain the posterior human error probability to study the risk of postulated accidents on an advanced reactor via a plant simulator [100]; (3) the implementation of BNA to assess the team situational awareness aspect of the plant operators during a steam generator tube rupture accident scenario within a Chinese digital magnetically controlled reactor [101]; (4) the implementation of ETA to facilitate the process of removing operator actions that do not contribute to the risk and identify all key operator actions that are critical to the safety of the Xe-100 high-temperature gas-cooled pebble-bed reactor design [102]; and (5) the implementation of ETA and BNA to facilitate the dependency analysis of human failure events and accurately evaluating the probability of human failure events leading to a large release as part of a Level 2 PSA study on a reactor [103].

Based on the review of the above literature pertaining on the use of PSA to perform a human reliability analysis, the following insights were obtained: First, the analysis is mostly performed with quantitative data such as the human error probability data provided by the experts. A way to improve the level of information on the human reliability analysis would be to incorporate the qualitative data (e.g., good operating procedural practices) into the analysis. Second, like in the case of the system component reliability analysis, the human reliability analysis is limited by the scarce availability of relevant data, on which the Bayesian approach can be used to update the prior information. Although there are databases available such as the Scenario Authoring, Characterisation and Debriefing Application (SACADA) [142] and the Human Reliability data Extraction (HuREX) [143], the human error data may not necessarily be sufficiently informative or relevant across all types of reactors. Finally, the human reliability analysis is thus far performed before (i.e., early design stages of advanced reactors) and during the reactor operation. An area of potential interest would also be the human reliability analysis for the Level 3 PSA during the decommissioning phase of the reactor.

4.4. Cyber-Security

With the increasing demand and importance of the engineering system performance of the nuclear power plants, it brings the need to optimise the development life cycle of nuclear reactors if it is to remain cost competitive in the energy market [144]. An approach towards enhancing such competitiveness is to develop advanced and robust digital technologies and integrate such technologies with the plant’s physical system such as the reactor protection systems, the engineering safety features actuation systems, the safety instrumentation systems, the safety monitoring systems, and the information processing and monitoring systems [144,145]. Such integration allows for improved performance by the numerous critical infrastructures such as the smart grids and the plant itself, as well as improving the efficiency, reliability, cost competitiveness, and the capability of remote supervision on the physical systems of the plant [144]. This leads to an increasing popularity towards the digitalisation of the plant operating systems and the implementation of digital instrumentation and control systems especially in the era of Industry 4.0 [144].

However, the increased need and reliance on such digital technologies comes with the increased risk of the critical infrastructures and the plant system being subjected to the numerous cyber-threats or attacks that would severely compromise the safety in the operation of the nuclear power plant. Generally speaking, such attacks can be classified into four categories [145]:

• Type I: Direct attack;
• Type II: Indirect attack;
• Type III: Operator failure; and
• Type IV: Initiating event

A Type I cyber-attack involves the hacking of the digital systems such as the reactor protection systems and the engineering safety features actuation systems. This results in the unavailability or the abnormal operations of such systems, leading to the failure of the system to respond to an accident [146]. An example to such would be the Stuxnet worm attack on June 2010, which occurred at the Iranian nuclear facility at Natanz [147]. A Type II cyber-attack involves the hacking of the digital controllers which control the analog components such as the pumps and valves, which may lead to the operational failure or the physical damage of such components [148]. Examples include the Slammer worm attack on January 2003 which occurred at the Davis-Besse nuclear power plant in Ohio [149] and the cyber-attack on August 2006 leading to the subsequent shut-down of Unit 3 of Browns Ferry nuclear power plant in Alabama [150]. A Type III cyber-attack is one that compromises the human–machine interface, which in turn leads to operator failures due to poor or incorrect information (i.e., error of commission). An illustrative example would be to consider a Type II cyber-attack on the digital control system, which results in the operators receiving incorrect information on the operating state of a component, and subsequently taking the incorrect response actions, leading to an accident such as a LOCA. As a result, the safety injection system is switched off when in fact it should remain switched on [145]. A Type IV cyber-attack is one that causes initiating events such as LOCA or a station black-out. This can also occur as a result of Type I and II cyber-attacks. An illustrative example would be to consider a Type II cyber-attack on the letdown valves or the safety depressurisation valves such that they remain open, which could eventually lead to a LOCA [145].

The significance of the consequence(s) of such cyber-attacks on the operating state and safety levels of the nuclear power plant motivates the need to develop PSA approaches towards assessing and improving the resilience, reliability, and the response measures against such attacks (i.e., cyber-security). Recent developments within the aspect of cyber-security include (1) the implementation of PNA to perform a resilience assessment of the digital feed water control system of a pressurised water reactor and mitigate the risk of Type I, II, and III cyber-attacks [104]; (2) the implementation of PNA to analyse the effect of integrating the preventive and reactive measures on a digital feedwater control system against Type I and II cyber-attacks, and study the subsequent impact such attacks on the sub-system’s control node disturbance and manual recovery probability [105]; (3) the implementation of ETA to develop a risk analysis framework to evaluate the vulnerabilities of the instrumentation and control systems within the TRIGA research reactor and improve its resilience against a Type IV cyber-attack [106]; (4) the implementation of ETA to improve the reliability of a fission battery system in transmitting operational data securely to a monitoring facility and minimising the risk of a Type III cyber-attack [107]; and (5) the implementation of BNA in developing a flow intrusion model used to evaluate the resilience of the reactor’s security system against a Type I cyber-attack [108].

Based on the review of the above literature, the following insights were obtained: First, the analysis thus far is limited to Level 1 PSA involving the reliability and resilience analysis of SSCs against cyber-attacks. Such an analysis can be extended towards Level 2 and 3 PSA to further understand the impact(s) of such attacks on the environment due to the risk of source term release. Second, the dynamic modelling approaches such as PNA and BNA are favoured for such an analysis, owing to their capability in modelling the time evolution of the accident sequence initiated by a cyber-attack, and facilitating the subsequent analysis of the recovery time of the SSCs. Finally, the modelling approaches implemented assume independence between the different components. Such an assumption may not always hold true in general and such an analysis could incorporate the information on the varying dependencies between the components.

4.5. Policy-Making

A key aspect of PSA is its capability to quantify the risks and consequences associated with the identified severe accident scenario as highlighted in Section 2.2. By doing so, it provides a tool and basis for risk-informed decision-making (i.e., risk management), an important step beyond the risk assessment phase towards managing risk. In fact, the NRC supports such a stance, and this is reflected in its policy statement that the use of PSA technology in its regulatory activities should be increased and supported by the state-of-the-art PSA methods and data in a manner that complements the NRC deterministic safety analysis [151]. This stance is further reinforced with its endorsement of the updated technical requirements published by the Nuclear energy Institute in 2019, which looks at the risk-informed performance-based technology extending towards non-light water reactors [152]. Parallel efforts were invested by the American Society of Mechanical Engineers which published its updated standard on the PSA methods on non-light water reactors in 2013 [153].

Risk-informed decision-making involves the process of evaluating and accounting for the risk associated with the identified accident scenario, based on its probability of occurrence, and using such information to make informed choices and come up with policies towards accident response, mitigation, and prevention [154]. In the context of nuclear safety, the implementation of such policies towards risk management can be broadly targeted towards numerous area which include the following:

• Plant inspection/maintenance policy;
• Human/organisational factors;
• Emergency planning/response.

4.5.1. Plant Inspection/Maintenance Policy

Recent work pertaining to the implementation of PSA to devise plant inspection/maintenance policy include (1) the implementation of BMU to develop an improved Bayesian filtering framework, predict the remaining useful life, and devise a maintenance schedule of the reactor’s electric gate valves [155]; (2) the implementation of BMU to develop a reliability analysis framework to monitor the deterioration state of the reactor’s pipe, and devise the maintenance planning of the component [110]; (3) the implementation of BMU to develop an adaptive maintenance policy optimisation for a reactor pump component under imperfect knowledge of the degradation model and partial observation of system states [111]; (4) the implementation of ETA and FTA to develop a safety inspection methodology on an APR1400 based on the Defence-in-Depth principle [112]; and (5) the implementation of PNA to develop a dynamic risk-aware maintenance framework, combining both condition-based and risk-based maintenance principle, for the pump and valve components of the reactor high-pressure injection system [113].

Based on the review of the above literature pertaining on the use of PSA to devise plant inspection/maintenance policy, the following insights were obtained. First, the online Bayesian model updating framework is mostly implemented owing to its capability in allowing the analyst to sequentially update the degradation model of SSCs with data coming in across different time-steps. This allows for a real-time update of the degradation model as well as the operating state of the SSCs which, in turn, allows for a data-driven update on the predictive maintenance policy and improving the reliability of such SSCs. Second, the works of [110,155] present a physics-guided Bayesian updating framework while that of [111] presents a more data-driven Bayesian updating framework towards updating the degradation model. The latter approach is limited to the quality and availability of the data and hence, the extrapolation of the degradation model needs to be treated with due caution due to the lack of information on the physics of the system (e.g., the material’s physical property). Third, the implementation of the ETA along with the FTA approach in [112] provides an added advantage in this context in that it allows for the analyst to better visualise the accident sequence and its root causes, as well as identifying the vulnerable components and the areas where redundancy is required. This facilitates a risk-informed maintenance policy planning, although it needs to be noted that such an approach still assumes independence between the accident events when computing the Top event probability. Finally, the PNA approach, while useful in performing a dynamic risk modelling of the operating state as part of the risk-aware maintenance framework, is only as good as the knowledge of the SSCs’ degradation profile.

4.5.2. Human/Organisational Factors

Recent works pertaining to the implementation of PSA to evaluate the human/organisational factors include (1) the implementation of BNA to assess technical capabilities of the operator during the start-up and shut-down of the reactor, and identify the tasks needing attention and to be addressed via training or improved operating procedures [114]; (2) the implementation of BMU and BNA to perform a technical assessment with scarce data and expert judgement towards quantifying the level of decision-related “Errors of Commission”, and thus, the procedural expertise of the operators [115]. (3) the implementation of ETA to perform a dynamical core damage risk assessment, and evaluate the technical capabilities of the operator in responding to a steam line break accident [116]; (4) the implementation of FTA towards quantifying the effectiveness of the risk mitigation measures by decision-makers and plant operators on the safety level of the VVER-1000 systems [117]; and (5) the implementation of ETA and FTA to identify human failure events and crew failure modes and evaluate the preparation and response level towards external flooding events in a reactor [118].

Based on the review of the above literature pertaining on the use of PSA to evaluate the human/organisational factors, the following insights were obtained: First, the BNA approach implemented in [114] evaluates the human factors on individual operator actions during the start-up and shut-down of reactors but is yet to account for the case where multiple operators are involved in such procedures (i.e., the case in most reactors) which provides a more realistic assessment of the human factors. Second, the ETA approach implemented in [116] identified a significant correlation between the human error probability and the reactor’s available time during a main steam line break accident for a pressurised water reactor. However, such a conclusion is yet to be verified against other types of accident such as a pressuriser failure. Finally, the analyses in the work presented thus far were performed with the available dataset. None of them has yet considered an online approach towards evaluating the human factors in real-time while data collection is ongoing.

4.5.3. Emergency Planning/Response

Recent works pertaining to the implementation of PSA to facilitate emergency planning/response include: (1) the implementation of ETA and FTA to estimate the containment failure frequency of a reactor and develop a framework to model severe accident management guidelines based on a Level 2 PSA [119]; (2) the implementation of BNA to develop an integrated assessment method for the real-time source term release for a high temperature gas-cooled reactor and facilitate emergency planning [120]; (3) the implementation of BMU to update the turbulent dispersion model and subsequently infer/track the radioactive leakage location to facilitate an early emergency response [121]; (4) the implementation of BMU to infer the height of the Iodine-131 release source and the wind direction via an Artificial Neural Network surrogate model to facilitate the emergency response after a nuclear accident [122]; and (5) the implementation of ETA and FTA to develop a risk-informed comprehensive path-planning method for the road transportation of radioactive materials based on the accident radiological consequence assessment [123].

Based on the review of the above literature pertaining on the use of PSA to facilitate emergency planning and response, the following insights were obtained: First, while the work in [119] has provided a detailed Level 2 PSA analysis and severe accident management guidelines, the analysis can be extended towards a Level 3 PSA to provide a more comprehensive approach for accident mitigation and emergency planning. Second, the BMU-based method in [121] provides a data-driven deep-learning framework towards inferring radioactive leakage location. Such an approach, however, is subjected to the availability and the quality of the data available. As an extension to such work, a physics-informed neural network can be implemented to improve the inference and prediction performance by the prediction model. Finally, the analyses in the works presented thus far have only been performed for a single-unit reactor. Such studies can be extended towards the case of a multi-unit reactor under different physical configurations and uncertainties in the dependencies between the individual reactor unit.

5. Future Research Directions

Following from the literature review presented in Section 4, the subsequent sub-sections identify and provide perspectives on the latest research challenges in six areas within the PSA discipline on which further investigations can be embarked.

5.1. Multi-Unit PSA of Small and Micro Modular Reactors

Since the Fukushima-Daiichi accident, there have been more stringent requirements in place for the improved passive safety systems for licensing, which has increased the operational costs of commercial reactors [156]. This has motivated the nuclear industry to look into small modular reactors which refer to advanced reactors with a power capacity of up to 300 MW per unit [157,158]. Some key traits of a small modular reactor include [156] (1) factory built; (2) modular in design; (3) can be easily transported to the plant site; and (4) the capability to provide additional on-demand capacity additions [157]. Examples, along with their design status and corresponding references, are presented in

Table 3. Examples of some of the small modular reactors and their operational statuses (at the time of writing). Details on the respective reactor are found in [157].

Full Name	Acronym	Status
Boiling Water Reactor X-300	BWRX-300	Conceptual Design
High Temperature Gas-cooled Reactor - Pebble-bed Module	HTR-PM	In Operation
NUWARD	NUWARD	Conceptual Design
Advanced Lead Fast Reactor European Demonstrator	ALFRED	Under Design
KLT-40S	KLT-40S	Under Construction
NuScale SMR	NuScale	Under Regulatory Review
Xe-100	Xe-100	Conceptual Design
SMR-300	SMR-300	Seeking UK Licensing
ACP-100 Linglong One	ACP-100	Under Construction
CANada Deuterium Uranium SMR	CANDU SMR	Conceptual Design
System-integrated Modular Advanced ReacTor	SMART	Conceptual Design
Kairos Power Fluoride Salt-Cooled High-Temperature Reactor	KP-FHR	Seeking US Licensing

.

As most of the recent research works have focused on performing a single-unit PSA, there have been relatively few works that have looked into the multi-unit PSA on the small modular reactors under different physical configurations or site settings. Such work would be of relevance given that a plant site would typically implement multiple such reactors in numerous configurations (e.g., 12-module configuration in the case of NuScale’s reactor design, and the 6-module configuration in the case of HTR-PM600 design [159]).

In addition, the PSA procedure can be made more robust by deviating from the independence assumption and accounting for the inter-modular dependencies or characterising the uncertainty in the dependencies between the individual modules while computing the overall probability of a core damage or source term release. The robustness of such an analysis can be further reinforced by accounting for the updated PSA standards set by the Nuclear Energy Institute and the American Society of Mechanical Engineers (i.e., see Section 4.5), given that some small modular reactors are non-light water reactors by design such as the HTR-PM and the Xe-100. This remains an open research topic.

Finally, the multi-unit PSA on small modular reactors can be extended to incorporate the time-varying aspect of the risk analysis as the accident progresses, thereby providing an opportunity to develop real-time dynamic PSA approaches as information pertaining to the accident is provided to the analyst sequentially across different time sequences.

It is to be highlighted that the proposed investigation can be extended towards micro modular reactors (e.g., the Ultra Safe Nuclear Corporation micro modular reactor), which are a sub-category of small modular reactors with a power capacity of up to 20 MW per unit [160].

5.2. Functional Failure Analysis of Passive Systems

The functional failure analysis of passive safety systems is an ongoing research topic within the area of reliability analysis for PSA being heavily studied [161,162,163,164] and reviewed [165,166,167]. While not a new research area, its importance is becoming of greater significance with the increased interest and safety analysis of small modular reactor designs in recent years. Through the literature review process, however, it has been identified that most such analyses were performed without considering the dynamic nature of the reliability of the passive system (i.e., accounting for the system degradation across the operational lifetime). As such, future research efforts can be dedicated towards treating such a system as a multi-state system and performing a dynamic PSA via a time-varying reliability analysis.

In addition, the literature survey presented in Table 2 found that most component reliability analyses are performed through time-independent Bayesian model updating. Such an analysis can be extended to time-varying reliability analysis through the implementation of sequential Bayesian filtering technique involving Sequential Monte Carlo methods to infer the time-varying physical parameters of the passive safety system such as the water pressure and temperature parameters. This generalises the reliability analysis.

Penultimately, a recent work by [161] highlighted the logical “AND” relationship between the functional failure and the system fault/configuration when calculating the failure probability of the passive safety system via FTA. However, such an analysis was performed under the independence assumption between these two events. In reality, such an analysis may not hold true, and future research efforts may be invested in considering the uncertain dependencies between these two events in the eventual imprecise failure probability computation of the passive safety system.

Finally, further investigations can be conducted to study the dependencies between the reliability of the safety-related passive safety systems and that of the active safety systems, especially during nuclear transients (e.g., LOCA and station black-out). This would improve the robustness of the functional failure analysis of the passive safety systems, making the result of the analysis more realistic due to the relaxation of the independence assumption between the passive and active safety systems. The independence assumption can lead to an underestimation of the failure probabilities, which is undesired.

5.3. Physics-Enhanced Machine Learning for Risk Analysis

Based on the literature survey, a data-driven approach is implemented in most of the research to perform the necessary PSA, thereby being a data-driven risk analysis. However, such an approach is only as effective as the availability and the quality of the data (e.g., the component reliability data) and may fail to fully characterise the physics-based performance of the system. The latter is noteworthy given that the physical phenomena such as the heat flux and the fluid dynamics within the system can affect the system performance/functional reliability. This becomes of greater importance when studying the passive safety systems of small modular reactors or other advanced reactors which rely heavily on convection current and gravity to ensure the circulation of the coolant without the need of mechanical pumps.

To address this, a physics-enhanced machine learning approach can be implemented to perform a physics-informed risk analysis on the passive safety systems or the reactor steam generator sub-system. This can be achieved through the use of physics-informed neural networks developed by Raissi (2019) [168], which have recently been implemented to develop a reduced-order model for the digital-twinning of a reactor [169] as well as to perform a physics-enhanced risk assessment on a Westinghouse three-loop 900 MW pressurised water reactor. Such works can be extended towards small modular reactors and other advanced reactor designs to perform a real-time health monitoring of the reactor during its operational lifetime—i.e., an online Level 1 PSA of the reactor.

In addition, such an approach can also be applied towards performing a Level 3 PSA in predicting the time-evolving dispersion profile of the radioactive nuclide release. This provides an improved model interpretation and prediction explanation, which facilitates the risk-based emergency planning and response to such accident scenarios. The physics-enhanced machine learning approach for this purpose is more favourable should the analyst deviate from the use of the simplified Gaussian plume model and instead opt for a more complex physics-based differential equation, which can only be solved numerically, to describe the fluid dynamics of the radioactive nuclide release.

5.4. Human Reliability Analysis for Multi-Unit Nuclear Reactors

In operating a nuclear reactor facility, the psychological confidence level of the plant operators is of importance. A high psychological confidence level leads to less technical error or decision error associated with the operator which leads to an increased human reliability and the overall reactor reliability. However, such a confidence level would differ between operating a single-unit plant and a multi-unit plant, given the significant difference in the operating conditions and the operational configuration of the plant. This is especially so given that the configuration of a multi-unit plant is relatively more complex and its operating states require greater attention by the plant operators on site.

In this aspect, further works can be invested towards performing a dynamic PSA to assess the psychological confidence levels on the operators of the multi-unit plant. In doing so, it not only serves to identify the factors which contribute to the psychological confidence of the operators but also assists decision-makers in devising the necessary training or operating procedures aimed towards improving the technical expertise on a multi-unit plant as well as the mental well-being of the operators who may experience a higher degree of stress associated with having to operate a more complex system. The analysis can also be extended towards improving the control room design with user-friendly digital instrumentation and control configuration.

5.5. Risk Communication

An essential and challenging aspect of nuclear-related communication would be the risk communication to the general public. Such an aspect is of great importance if it is targeted towards an audience seeking to understand the impact of radiation on their daily lives and to broaden their perspectives on nuclear energy and its risks [170].

To the best of the authors’ knowledge based on the literature survey, there not been any investigation on employing the PSA methods studied here (e.g., FTA, BNA, and PNA) as educational tools towards such outreach efforts. As such, future studies can delve deeper into studying the effectiveness of such PSA methods as visual aid for nuclear risk communication. In essence, the interest is to investigate how effective such tools are in educating the layman on the benefits and risk of nuclear energy, and what impact such an approach has on the eventual public perception of the nuclear technology.

5.6. Risk Analysis with Uncertainty under Limited Data

At the conclusion of Section 2.2, it is identified that one key challenge in performing PSA is the lack of data. The issue can arise in two ways: (1) when the data are incomplete (i.e., filled with missing data and gaps); or (2) when the volume of data is limited due to the limited experiment campaigns conducted. Such a problem still persists at present, and remains an active research challenge [171].

To address such a research challenge, uncertainty quantification approaches can be implemented, such as interval arithmetic and approximate Bayesian computation [79]. This allows for one to quantify the epistemic uncertainties associated with the estimate on the probability of the Top event or the small failure probability of the nuclear reactor system (i.e., best estimate plus uncertainty). This presents opportunities to further develop numerical/computational techniques, and allows for the propagation of intervals and Bayesian updating procedures on the reliability models of the nuclear reactor system. Such research would be beneficial especially when there is a high number of correlated uncertain model parameters to infer from the limited data and the need for the computational costs to be minimised.

6. Conclusions

The review paper has attempted to address the following three questions pertaining to research efforts in Probabilistic Safety Assessment for nuclear safety:

• What is Probabilistic Safety Assessment in the context of nuclear safety and how did it come to be?
• What has been done thus far in this area?
• Where do we go from here in terms of future research efforts?

To address the first question, a conceptual introduction on Probabilistic Safety Assessment, its historical development in nuclear safety, and a description and evaluation on the standard tools implemented for such an analysis are provided in Section 2 and Section 3. This aims to provide the readers with an overview and a historical perspective of Probabilistic Safety Assessment within the nuclear industry.

To address the second question, a literature survey of the recent research developments between 2022 and 2024 is provided in Section 4 across the five different aspects of Probabilistic Safety Assessment: (1) multi-unit Probabilistic Safety Assessment; (2) dynamic Probabilistic Safety Assessment; (3) reliability analysis; (4) cyber-security; and (5) policy-making. For each aspect, a review of the recent literature is provided, highlighting what has been performed and the limitations/gaps still yet to be addressed in the research. This provides an evaluative perspective on the recent developments.

To address the third question, the paper proceeds to provide suggestions on future research developments in Section 5 based on the research gaps identified from the literature survey. Such future research works are proposed for the following six areas: (1) multi-unit Probabilistic Safety Assessment of small and micro modular reactors; (2) functional failure analysis of passive systems; (3) physics-enhanced machine learning for risk analysis; (4) human reliability analysis for multi-unit nuclear reactors; (5) risk communication; and (6) risk analysis with uncertainty under limited data. For each area, the perspective(s) on the proposed research direction is provided for potential consideration to address the current research limitations/gaps.

Hence, the review paper has sought to provide historical and evaluative perspectives, as well as a prospective on the area on Probabilistic Safety Assessment. Through such coverage, the paper targets readers who are new to the topic and would require a comprehensive introduction; those who are at the literature review phase and striving to understand the current state-of-the-art developments; and the wider research community within the nuclear safety discipline towards pushing the frontiers of Probabilistic Safety Assessment research.

To conclude the paper, a timeline is illustrated in Figure 5, summarising the historical development of Probabilistic Safety Assessment in nuclear safety and the key milestones over the past seven decades.