Abstract
Neutron thermalization leads to the complexity of the scattering cross-section calculation, which influences the accuracy of the neutron transport calculation in the thermal energy range. The higher precision of thermal scattering data is demanded in the small modular reactors (SMRs) design, especially for small-sized PWRs and SCWRs. Additionally, the thermal neutron scattering problems in supercritical water have not yet been solved. In this study, the thermal neutron scattering problems in subcritical water are tested. Based on thermal neutron scattering theory, the GA model and IKE model were analyzed. This work selected the corresponding input parameters, such as the frequency spectrum, the discrete oscillator energy, weight parameters and so on, as well as preliminary studies on how to calculate the thermal scattering data for HinH2O to accomplish the calculation at various temperatures by developing LIPER code. The deviation between the calculated and reference results, which were both obtained by the Monte Carlo code, COSRMC, was below 0.2 pcm. The deviation of the scattering cross-section between the calculation results and reference was below 0.1%, indicating the reasonability of this study’s thermal scattering data calculation.
1. Introduction
With the development of the nuclear power industry, small modular reactors (SMRs) have attracted attention. They possess the characteristics of less radioactive source terms, a simple structure, and a unique advantage compared to large-scale PWRs. Small-sized PWRs and SCWRs are the two potential SMRs because of their convenience and more prevalent research [1].
In past research, the light water scattering cross-section data was the basic parameter of the reactor core transport calculation. Among them, the scattering cross-section and function of light water in the thermal energy region increased its complexity and computational difficulty due to the influence of nuclear thermal motion, intramolecular chemical bond binding and the scattered-wave interference effect. In order to calculate the light water thermal scattering cross-section and meet the accuracy requirements in nuclear engineering design, research on the HinH2O thermal neutron scattering treatment method is significant.
The problem of light water thermal scattering has been extensively studied internationally. At present, the HinH2O thermal scattering data comes from the evaluated nuclear data libraries, mainly from the calculation of two scattering nuclear models. One of them was proposed by the General Atomics Group in the 1960s (referred to as the GA model [2]), which was established by the GASKET program [3] and published in the ENDF/B-III. In 1994, MacFarlane published the GA model as a light water scattering nuclear model for the LEAPR module in the nuclear data processing program NJOY [4], and its thermal scattering data was published in the ENDF/B-VI library [5]. Another model was proposed in the 1980s by Mates and Keinert from the Institute of Nuclear Technology and Energy Systems of the University of Stuttgart (the IKE model for short), which was originally encoded with GASKET, where the JEF-1 [6] stored its thermal scattering data. In 2003, the IKE model was updated as a solution model for the LEAPR module of the NJOY program, and its thermal scattering data was published in the ENDF/B-VII library.
In this study, the above two scattering models were preliminarily analyzed, and the GA model assumed that the scattering law of the main scatterer (H) could be represented by three excitation spectra: the solid-state spectrum, translation spectrum, and discrete vibration spectrum. Based on the above model, the IKE model further improved the three excitation spectra to make the thermal scattering data calculation flow more in line with physical laws. By combining the relevant input parameters of the two models, the calculation of thermal scattering data at different temperatures (including 293.6 K, 350 K, 400 K, 450 K, 500 K, 550 K, 600 K, 650 K and 800 K) was performed by programming the LIPER code. According to the parameters of the above temperature points, the relevant parameters of 323.6 K were obtained by interpolations. The results prove the feasibility of calculating thermal scattering data at any temperature by LIPER.
2. Scattering Model
2.1. HinH2O Thermal Neutron Scattering Equation
The double differential cross-section is:
where:
indicates the neutron momentum transfer,
indicates the neutron energy transfer,
is the scattering law in a symmetrical form, which can be expressed as:
where
In Equation (3), is the spectrum of the scattering system, which satisfies the normalized condition and can be resolved into summation forms of different excitation spectra:
The different excitation spectra in Equation (4) include discrete vibration, solid-state spectroscopy, and translational spectra.
2.2. GA Model
The GA model considers the scattering motion of hydrogen atoms in water, and the free gas model provides the scattering of oxygen atoms. It assumes that the scattering law of hydrogen atoms of the principal scatterer is calculated by convolution from three excitation spectra: the solid-state spectrum, translation spectrum, and discrete vibration spectrum. Among them, the solid-state spectrum represents the hindered rotation of hydrogen atoms, and spectrum data are given by Haywood and Thorson [7]. The translation motion of water molecules is represented by the free gas model, which has an approximate mass of 18.0. The discrete vibration spectrum represents the vibration pattern of hydrogen atoms in water. It includes two energies: 0.205 eV represents the bending vibration of water molecules, and 0.480 eV represents the symmetrical telescopic vibration and asymmetric telescopic vibration of water molecules. The parameters of the GA model are shown in Table 1.
2.3. IKE Model
The IKE model [8] differs from the GA model in calculated data for the three excitation spectra. Its solid-state spectrum data is derived by interpolating measurements at 294 K and 624 K [9]. The translation motion of water molecules is represented by the free gas model; however, the approximate mass of free gas is temperature dependent and needs to be determined by combining the proportion of water molecular clusters at different temperatures. The approximate mass of free gas is different at various temperatures. The discrete vibration energy is changed from 0.480 eV to 0.436 eV, which better considers the liquid nature of water molecules. Compared to the GA model, the IKE model has improved the processing of the translation spectrum and discrete vibration spectrum, which is more in line with physical laws. The parameters of the IKE model are also shown in Table 1.

Table 1.
Parameters for GA Model and IKE Model [10].
Table 1.
Parameters for GA Model and IKE Model [10].
| Parameter | GA Model | IKE Model |
|---|---|---|
| Translation weights | 1/18 | 1/46 |
| Continuous spectral weights | 0.444 | 0.478 |
| Bending vibration energy (eV) | 0.205 | 0.205 |
| Bending vibration energy weight | 0.166 | 0.166 |
| Telescopic vibration energy (eV) | 0.480 | 0.436 |
| Telescopic vibration energy weight | 0.333 | 0.333 |
3. HinH2O Thermal Scattering Calculation
3.1. Relevant Parameters
The spectrum is one of the basic parameters for calculating the scattering law, and for the selection of the spectrum, data from the literature [10] are used, as shown in Figure 1. The spectrum data in Figure 1 must be normalized to satisfy it:
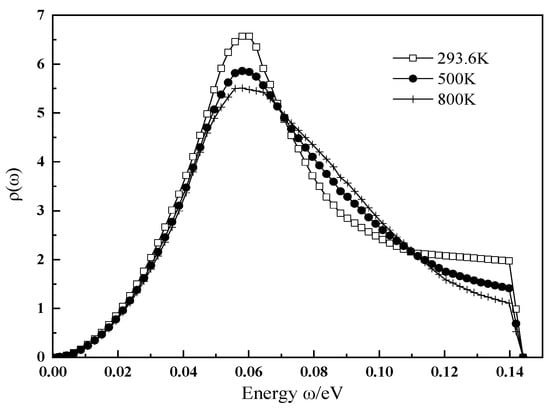
Figure 1.
The frequency spectrum used for HinH2O. The square represents the spectrum at 293.6 K. The dot represents the spectrum at 500 K. The cross represents the spectrum at 800 K.
Discrete vibration spectroscopy describes the vibration state of hydrogen atoms in water, which is another basic parameter for calculating the scattering law, and the relevant data in the IKE model are selected, where 0.205 eV represents the bending vibration energy, and 0.436 eV represents the symmetric and asymmetric telescopic vibration energy.
The three motions of hydrogen atoms in water include hindered rotation, translation, and vibration, and each state of motion has its own proportion or weight. Weighted data include continuous spectrum weights, translation weights, and discrete vibration weights and specify that the sum of the weights of each part is equal to 1. Among them, the hindered rotation and vibration each have three degrees of freedom, assuming that these six degrees of freedom are equally weighted, and thus, the weights of each part are satisfied:
where represents the translation weight; represents the continuous spectrum weight; represents the bending vibration weight; represents the symmetric and asymmetric telescopic vibration weights. The selection of the translation weights refers to the IKE model, which only provides the translation weights of some temperature points, and for the ungiven temperature, the translation weights can be obtained by interpolation.
3.2. Calculation Process
For the calculation of the HinH2O scattering law, based on Equations (3) and (4), it is defined that each excitation spectrum corresponds to a local scattering law, Si. When using the convolution theory, the scattering law can be written as an equation in the recursive form:
Among them, the local scattering law Si includes the solid-state spectrum scattering law Ss; the translation spectrum scattering law St; and the discrete vibration spectrum scattering laws S1 and S2. Therefore, the local scattering law is found and then convolved by Equation (7) to calculate the desired scattering law. The calculation flow is shown in Figure 2.
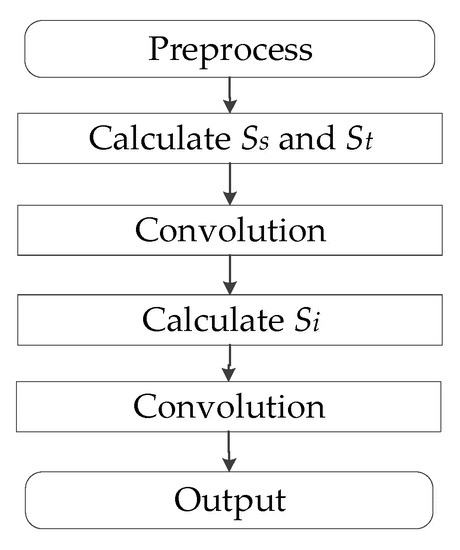
Figure 2.
The process of scattering law calculation for HinH2O.
3.3. Results and Testing
The experimental measurements of the thermal neutron scattering cross-sections should be performed to validate the simulations in reactor design as being similar to studies on spent isotopic PWR composition assay data [11]. Unfortunately, the measured thermal scattering cross-sections have not been reported in relevant works of literature. In this study, the calculated results were compared to the Evaluated Nuclear Data File, ENDF/B-VII.0 (as a reference) with the selected benchmarks.
The scattering law file, produced by LIPER, was then processed by the NJOY, and Figure 3 shows the HinH2O thermal neutron scattering cross-section at 293.6 K. Based on the evaluation of the HinH2O scattering law file provided in ENDF/B-VII.0, the calculated scattering cross-sections were used as a reference value, and the two were compared. In the incidence neutron energy range of 1 × 10−5 to 4 eV, the scattering cross-section is ideal, and the relative deviation is within 0.1%, which is in good agreement with the reference value.
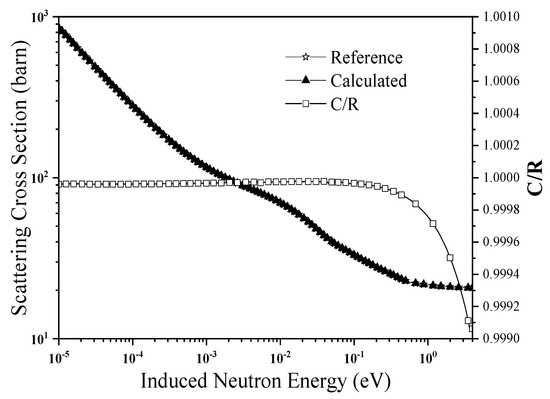
Figure 3.
Neutron scattering cross-sections for HinH2O at 293.6 K. The five-pointed star represents the reference (R) cross-section from ENDF/B-VII.0. The triangle represents the calculated (C) cross-section from LIPER. The square represents the value of C/R.
For the HinH2O thermal scattering data, 69 groups of WIMS-D [12] format libraries were generated by NJOY, and the selected IAEA WLUP critical lattice benchmarks [13] were tested by the reactor physics program, DRAGON [14], and the calculated keff are shown in Table 2.

Table 2.
The results of benchmarks for keff at 293.6 K.
It can be seen from Table 2 that the calculated keff of the two are very similar because the neutron flux density at low energy is very small, and the scattering cross-section at low energy is grouped. The scattering cross-section deviation after grouping becomes smaller, which has a lesser impact on the calculated keff.
In addition, the scattering law at other temperature points was also calculated, including 350 K, 400 K, 450 K, 500 K, 550 K, 600 K, 650 K and 800 K. Figure 4 shows the scattering cross-section results for some of them. The figure shows that the calculated value of the scattering cross-section and the reference at different temperature points are in good agreement.
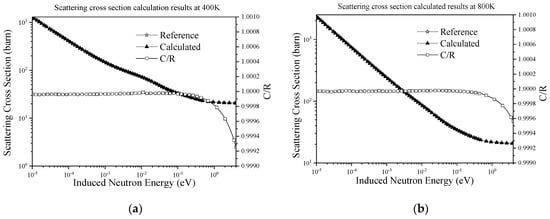
Figure 4.
Neutron scattering cross-sections for HinH2O at different temperatures: (a) Scattering cross-section calculated results at 400 K; (b) scattering cross-section calculated results at 800 K. The five-pointed star represents the reference (R) cross-section from ENDF/B-VII.0. The triangle represents the calculated (C) cross-section from LIPER. The square represents the value of C/R.
According to the molecular water spectra at 293.6 K and 350 K, the spectrum under 323.6 K is calculated by interpolation, and the corresponding discrete vibration energy, weight, and other parameters are selected to calculate the thermal scattering law and then compared with the IKE model. Figure 5 shows a comparison of the calculation results of the scattering cross-section. It can be seen that the calculation results are in good condition. Therefore, it can be inferred that as long as the relevant parameters of various temperature points are known, the parameters of other temperatures can theoretically be calculated by interpolation so as to achieve the purpose of calculating the scattering law at any temperature.
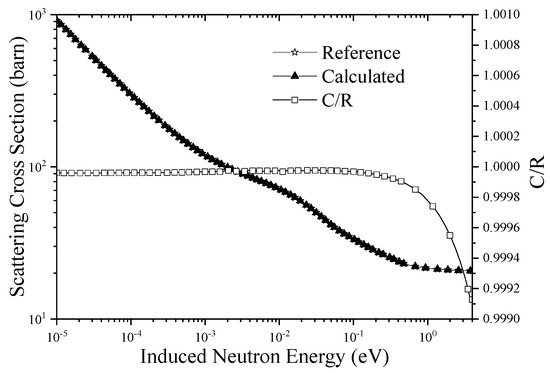
Figure 5.
Neutron scattering cross-sections for HinH2O at 323.6 K. The five-pointed star represents the reference (R) cross-section from ENDF/B-VII.0. The triangle represents the calculated (C) cross-section from LIPER. The square represents the value of C/R.
The scattering law data at various temperatures, calculated by LIPER, were processed into an ACE format thermal scattering library by NJOY, which was suitable for calculating the Monte Carlo code COSRMC [15]. The HMF004 benchmark was selected from the International Criticality Safety Benchmark Evaluation Project (ICSBEP) [16] for testing. It was to provide a very accurate estimate of the critical mass of a sphere of highly enriched uranium (HEU) with an effectively infinite water reflector. The keff of the HMF004 benchmark was calculated by using the COSRMC with the ACE format thermal scattering library at each temperature. At the same time, the scattering law file in the evaluated nuclear data library was processed into an ACE thermal scattering library. The calculated keff was used as a reference value to verify the accuracy of the LIPER process.
The critical benchmark HMF004 comprises a uranium metal sphere and a spherical light water reflective layer, with a fuel zone radius of 6.5537 cm, a moderation zone radius of 33.471 cm, and a regional temperature of 293.6 K. In order to test the scattering law data calculated by LIPER at various temperatures, only the thermal scattering library was changed during the use of the COSRMC. The data at 293.6 K were used for other nuclides. The calculation condition is to initially input 20,000 particles, cycle 550 generations, and discard the first 50 generations. The result is shown in Figure 6. It can be seen that the maximum deviation between the calculated result and reference is 60 pcm. It indicates that the calculated results compared to the reference are in good agreement, proving the LIPER process’s accuracy.
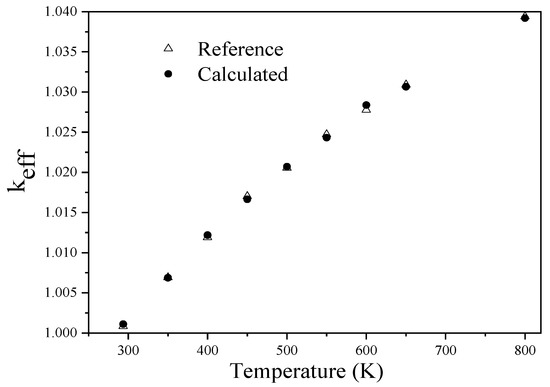
Figure 6.
The results of keff at different temperatures.
4. Conclusions
Based on the theory of thermal neutron scattering, the calculation of the HinH2O scattering law at various temperatures was performed. In the calculation process, the GA model and IKE model were analyzed and compared, and the spectrum, discrete vibration energy, correlation weights, and other data were selected. The correlation testing shows that the calculated results of the scattering cross-sections are reasonable.
In the HinH2O thermal scattering cross-section calculation, the temperature points and accuracy of the scattering law need to be improved, and the solution method can be improved in the next step to meet higher calculation accuracy. Based on the production of some temperature point scattering law files, the LIPER code function can be improved to calculate the scattering law at any temperature point. In addition, based on the realization of subcritical hydrothermal scattering research, this study may pave the way for the research of supercritical hydrothermal scattering for small-sized SCWRs.
Author Contributions
Conceptualization, J.W.; methodology, J.W.; software, J.W.; validation, J.W.; formal analysis, J.W.; investigation, J.W.; resources, Y.C.; data curation, J.W.; writing—original draft preparation, J.W.; writing—review and editing, Y.C.; visualization, J.W.; supervision, Y.C.; project administration, J.W.; funding acquisition, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, X. Compare and Analysis in Safety Features of Some Small Sized PWRs in the World. Nucl. Saf. 2015, 14, 56–59. (In Chinese) [Google Scholar]
- Koppel, J.; Houston, D. Reference Manual for ENDF Thermal Neutron Scattering Data; GA-8774; Gulf General Atomic, Inc.: San Diego, CA, USA, 1978. [Google Scholar]
- Koppel, J.; Triplett, J.; Naliboff, Y. GASKET: A Unified Code for Thermal Neutron Scattering; GA-7417 (Rev.). Gulf General Atomics Technical Report; General Dynamics Corp.: San Diego, CA, USA, 1967. [Google Scholar]
- Macfarlane, R.E. NJOY 99/2001: New Capabilities in Data Processing; Los Alamos National Lab.: Los Alamos, NM, USA, 2002. [Google Scholar]
- MacFarlane, R.E. New Thermal Neutron Scattering Files for ENDF/B-VI Release 2; Los Alamos National Lab.: Los Alamos, NM, USA; Funding Organization: Washington, DC, USA, 1994. [Google Scholar]
- Keinert, J.; Mattes, M.; Sartori, E. JEF-1 Scattering Law Data; JEF Report; OECD-NEA: Paris, France, 1984; p. 2. [Google Scholar]
- Haywood, B.C.; Thorson, I.M. The scattering law for light and heavy water at 20 °C and 150 °C. In Proceedings of the Brookhaven Conference on Neutron Thermalization, Upton, NY, USA, 30 April–2 May 1962; Volume 1. [Google Scholar]
- Mattes, M.; Keinert, J. Thermal Neutron Scattering Data for the Moderator Materials H2O, D2O and ZrHx in ENDF-6 Format and as ACE Library for MCNP(X) Codes; International Atomic Energy Agency, International Nuclear Data Committee: Vienna, Austria, 2005. [Google Scholar]
- Page, D.I.; Haywood, B.C. The HARWELL Scattering Law Programme: Frequency Distributions of Moderators; Atomic Energy Research Establishment: Harwell, UK, 1968. [Google Scholar]
- Damian, J.I.M.; Granada, J.R.; Malaspina, D.C. CAB models for water: A new evaluation of the thermal neutron scattering laws for light and heavy water in ENDF-6 format. Ann. Nucl. Energy 2014, 65, 280–289. [Google Scholar] [CrossRef]
- Oettingen, M.; Cetnar, J. Comparative analysis between measured and calculated concentrations of major actinides using destructive assay data from Ohi-2 PWR. Nukleonika 2015, 60, 571–580. [Google Scholar] [CrossRef]
- Deen, J.R.; Woodruff, W.L.; Costescu, C.I. WIMS-D4M User Manual (Rev. 0); ANL/RERTR/TM-23; Argonne National Laboratory: Lemont, IL, USA, 1995. [Google Scholar]
- Leszczynski, F.; Aldama, D.L.; Trkov, A. WIMS-D Library Update; International Atomic Energy Agency: Vienna, Austria, 2007. [Google Scholar]
- Hébert, A. DRAGON5: Designing Computational Schemes Dedicated to Fission Nuclear Reactors for Space. In Proceedings of the International Conference on Nuclear and Emerging Technologies for Space, Albuquerque, NM, USA, 25–28 February 2013. [Google Scholar]
- Ma, X.; Yao, Y.; Hu, J.; Wu, J.; Chen, Y.; Yu, H.; Qu, G. Preliminary study on COSRMC verification strategy of reactor Monte Carlo procedure. Nucl. Power Eng. 2014, S2, 108–111. (In Chinese) [Google Scholar]
- Rugama, Y.; Thompson, M.A.; Briggs, J.B. International Criticality Safety Benchmark Evaluation Project; Organization for Economic Cooperation and Development—Nuclear Energy Agency (OECD-NEA): Paris, France, 2006. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).