Coupled Thermal-Hydraulic Analysis and Species Mass Transport in a Versatile Experimental Salt Irradiation Loop (VESIL) Using CTF
Abstract
:1. Introduction
Importance of IFP Transport and Resulting Effects
2. Materials and Methods
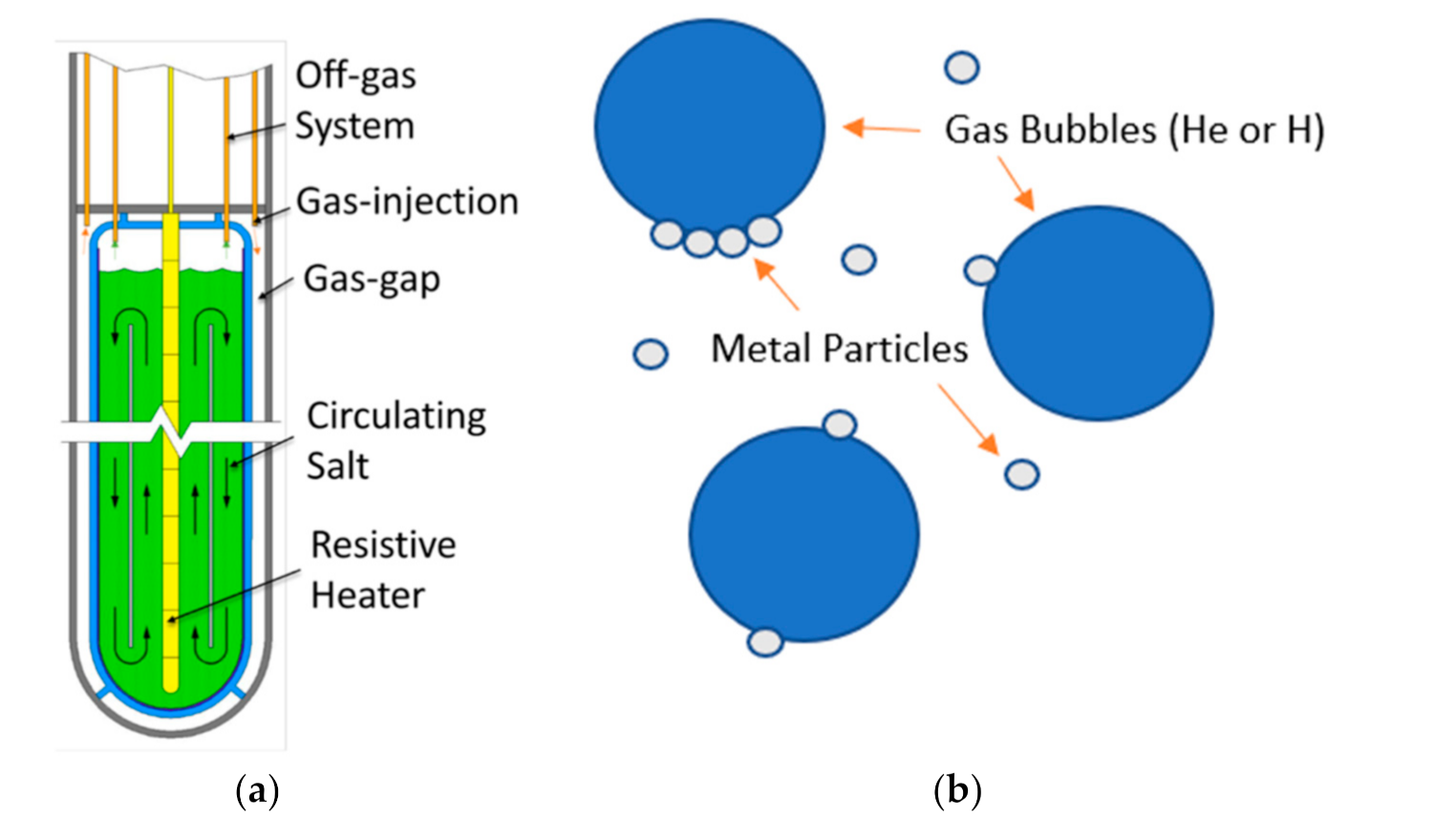
2.1. VESIL Design & Parameters
2.2. Noble Metal Deposition Model Review & Assumptions
2.3. Helium Bubbling Model Review & Assumptions
2.4. Noble Metal Helium Bubble Coupling & Off-Gas Mass Accounting Methodology
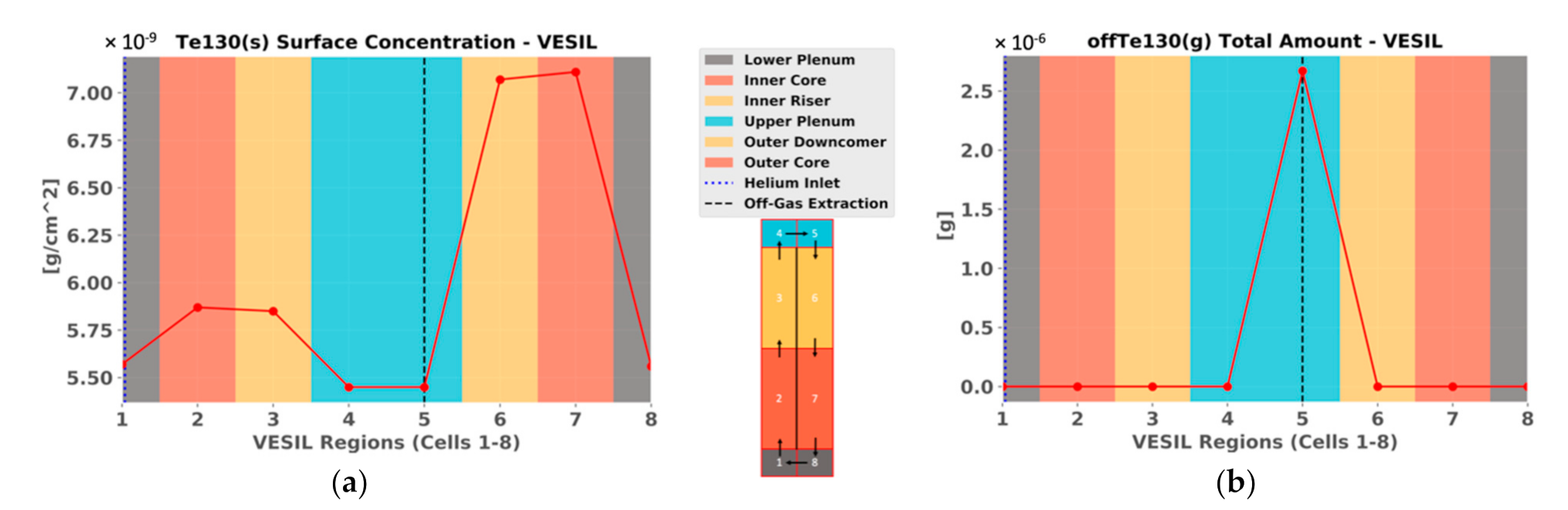
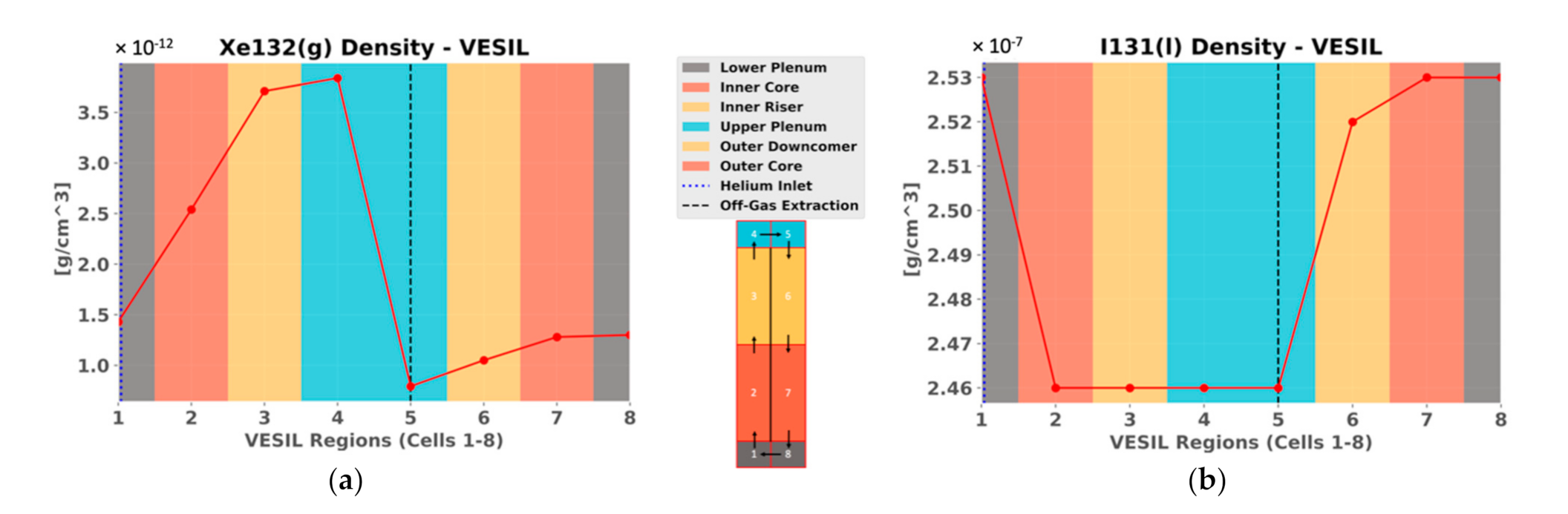
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abou-Jaoude, A.; Palmer, J.; Sterbentz, J.; Calderoni, P. Evaluation of a Versatile Experimental Salt Irradiation Loop (VESIL) inside the Advanced Test Reactor. In INL/EXT-19-52917; Idaho National Laboratory: Idaho Falls, ID, USA, 2019. [Google Scholar]
- Taylor, Z.; Salko, R.; Collins, B. Implementation of General Species Transport Capability into VERA-CS for Molten Salt Reactor Analysis. In Proceedings of the 2018 ANS Annual Meeting, Philadelphia, PA, USA, 17–21 June 2018; Volume 118, pp. 1061–1064. [Google Scholar]
- Walker, S.A.; Taylor, Z.; Salko, R.; Collins, B.; Ji, W. Noble Metal Mass Transport Model for Molten Salt Reactor Analysis in VERA-CS. In Proceedings of the M&C 2019, Portland, OR, USA, 25–29 August 2019; pp. 2268–2277. [Google Scholar]
- Taylor, Z. Implementation of Multi-Phase Species Transport into VERA-CS for Molten Salt Reactor Analysis. Master’s Thesis, University of Tennessee Knoxville, Knoxville, TN, USA, 2019. [Google Scholar]
- Compere, E.L.; Bohlmann, E.G.; Kirslis, S.S.; Blankenship, F.F.; Grimes, W.R. Fission Product Behavior in the Molten Salt Reactor Experiment. In ORNL-4865; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1975. [Google Scholar]
- Carter, W.L. Decay Heat Generation by Fission Products and 233Pa in a Single-Region Molten Salt Reactor. In ORNL-CF-68-3-38; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1968. [Google Scholar]
- Bhaskar, S.; Abou-Jaoude, A. Preliminary Design Evaluation of a Natural Circulation Molten Salt Irradiation Loop. In Proceedings of the 2019 ANS Winter Meeting, Washington, DC, USA, 17–21 November 2019; Volume 121, pp. 1895–1896. [Google Scholar]
- Mourogov, A.; Bokov, P. Potentialities of the fast spectrum molten salt reactor concept: REBUS-3700. Energy Convers. Manag. 2006, 47, 2761–2771. [Google Scholar] [CrossRef]
- Kedl, R.J. The Migration of a Class of Fission Products (Noble Metals) in the Molten-Salt Reactor Experiment. In ORNL-TM-3884; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1972. [Google Scholar]
- Yang, Q.; Ge, J.; Zhang, J. Electrochemical Study on the Kinetic Properties of Fe2+/Fe, Ni2+/Ni, Cr2+/Cr and Cr3+/Cr in Molten MgCl2-KCl-NaCl Salts. Electrochem. Soc. 2021, 168, 012504. [Google Scholar] [CrossRef]
- Zhang, J.; Forsberg, C.W.; Simpson, M.F.; Guo, S.; Lamb, S.T.; Scarlat, R.O.; Carotti, F.; Chan, K.J.; Singh, P.M.; Doniger, W.; et al. Redox potential control in molten salt systems for corrosion mitigation. Corros. Sci. 2018, 144, 44–53. [Google Scholar] [CrossRef]


| Parameter | Value (Units) |
|---|---|
| Maximum Temperature | 1011.87 (K) |
| Minimum Temperature | 910.35 (K) |
| ∆T | 101.52 (K) |
| Fission Power Density in Core | 100.00 (W/cm3) |
| Salt Velocity | 0.226 (m/s) |
| Total Height | 78.00 (cm) |
| Height of Core | 39.00 (cm) |
| Outer Salt Radius | 2.778 (cm) |
| Inner Salt Radius | 1.964 (cm) |
| Salt Mass | 6.513 (kg) |
| Parameter | Value (Units) |
|---|---|
| He injection rate | 2.0 × 10−6 (moles/s) |
| Initial Bubble Diameter: Dref | 0.3175 (mm) |
| Removal Efficiency | 80.0 (%) |
| Property | Value (Units) |
|---|---|
| Density (ρ) | 3860.4 − 0.837 × T (K) (kg/m3) |
| Dynamic Viscosity (µ) | 0.00217 (kg/m-s) |
| Thermal Conductivity (kT) | 0.7 (W/m-K) |
| Specific Heat Capacity (Cp) | 950 (J/kg-K) |
| Prandtl Number (Pr) | 2.9450 |
| Total Stable Xenon | Stable Xenon in Off-Gas | Percentage (%) | |
|---|---|---|---|
| 132Xe | 5.56 mg | 5.54 mg | 99.68% |
| 131Xe | 1.63 mg | 1.62 mg | 99.43% |
| 130Xe | 8.90 × 10−2 mg | 8.87 × 10−2 mg | 99.67% |
| 129Xe | 1.80 × 10−13 mg | 1.79 × 10−13 mg | 99.88% |
| 128Xe | 6.15 × 10−4 mg | 6.13 × 10−4 mg | 99.68% |
| Total Xe | 7.28 mg | 7.25 mg | 99.63% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walker, S.A.; Abou-Jaoude, A.; Taylor, Z.; Salko, R.K.; Ji, W. Coupled Thermal-Hydraulic Analysis and Species Mass Transport in a Versatile Experimental Salt Irradiation Loop (VESIL) Using CTF. J. Nucl. Eng. 2021, 2, 309-317. https://doi.org/10.3390/jne2030025
Walker SA, Abou-Jaoude A, Taylor Z, Salko RK, Ji W. Coupled Thermal-Hydraulic Analysis and Species Mass Transport in a Versatile Experimental Salt Irradiation Loop (VESIL) Using CTF. Journal of Nuclear Engineering. 2021; 2(3):309-317. https://doi.org/10.3390/jne2030025
Chicago/Turabian StyleWalker, Samuel A., Abdalla Abou-Jaoude, Zack Taylor, Robert K. Salko, and Wei Ji. 2021. "Coupled Thermal-Hydraulic Analysis and Species Mass Transport in a Versatile Experimental Salt Irradiation Loop (VESIL) Using CTF" Journal of Nuclear Engineering 2, no. 3: 309-317. https://doi.org/10.3390/jne2030025
APA StyleWalker, S. A., Abou-Jaoude, A., Taylor, Z., Salko, R. K., & Ji, W. (2021). Coupled Thermal-Hydraulic Analysis and Species Mass Transport in a Versatile Experimental Salt Irradiation Loop (VESIL) Using CTF. Journal of Nuclear Engineering, 2(3), 309-317. https://doi.org/10.3390/jne2030025






