Abstract
The MORET 5 code, which has been developed over more than 50 years at IRSN, has recently evolved, in its continuous energy version, from a criticality oriented code to a code also focused on reactor physics applications. Some developments such as the implementation of kinetics parameters contribute to that evolution. The aim of the paper is to present the validation of the code for the keff multiplication factor used in criticality studies as well as for other parameters commonly used in reactor physics applications. Special attention will be paid on commission tests performed in the CABRI French Reactor (CABRI is a pool-type research reactor operated by CEA and located in the Cadarache site in southern France used to simulate a sudden and instantaneous increase in power, known as a power transient, typical of a reactivity-initiated accident (RIA).) and the IPEN/MB-01 LCT-077 benchmark.
1. Introduction
The “Institut de Radioprotection et de Sûreté Nucléaire” (IRSN) has developed, for many years, its own neutron transport Monte Carlo code called MORET [1]. The MORET code is coupled with the APOLLO2 deterministic code [2] in the frame of the CRISTAL package [3]. Since the mid-2000s, IRSN made it evolve into a continuous energy version offering more flexibility with regards to the choice of nuclear data and limiting the biases due to physical approximations associated with the multi-group treatment of cross sections (self-shielding, energy mesh collapsing…). Several versions of the MORET code have been delivered, the last one being MORET 5.D.1 [1], which was recently made available at the OECD NEA databank. The continuous energy version of the MORET code has been validated on a suite of more than 2000 criticality benchmarks issued from the International Criticality Safety Benchmark Evaluation Project (ICSBEP) Handbook [4] and French proprietary experiments, allowing thus covering the main applications encountered in criticality safety. Since the release of version 5, the MORET code, which was mainly focused on criticality, has been adapted to reactor physics. In particular, additionally to flux and reaction rates calculations, MORET 5 is able to perform sensitivity calculations and to determine kinetics parameters for various sets of nuclear data evaluations. In this framework, an experimental validation database targeting reactor physics applications has been created. It is mainly based on benchmarks taken from the International Handbook of Evaluated Reactor Physics Benchmark Experiments (IRPhEP [5]), and also on the neutron commissioning measurements performed in the CABRI1 Water Loop reactor prior to the CIP-Q program [6]. Around 175 experimental cases corresponding to 20 IRPhEP evaluations are available so far in the MORET validation database. For these benchmarks, reference values of keff, reaction rates ratios, spectral indices, reactivity coefficients of control rods, reflector and kinetics parameters are provided, allowing comparison with calculated values from the MORET 5 code. This paper presents calculations performed with the MORET 5.D.1 code using the JEFF-3.1.1, JEFF-3.2 and ENDF/B-VII.1 libraries. For most of the cases, a good agreement is obtained with the benchmark values, taking into account experimental uncertainties, which validates the developments performed in the MORET 5 code and allows confidence in the reported results using various nuclear data libraries. Moreover, sensitivity calculations with the Iteration Fission Probability method (IFP [7]) recently implemented in the MORET 5 code were also performed in order to discriminate elements for which a feedback on nuclear data could be done.
2. Selection of Criticality and Reactor Physics Benchmarks
2.1. Selection of Benchmarks
To have a good feedback on nuclear data using integral benchmark experiments, one needs to select experiments that are sensitive to the main reactions and isotopes of interest, and show well assessed and not too high experimental uncertainties. Indeed, the effect of nuclear data should be larger than the propagated uncertainty of experimental uncertainties in order to have a feedback.
IRSN decided to select experiments that could serve to the validation of the MORET 5.D.1 code for criticality and light water reactor physics applications. The list of available experiments is therefore mainly limited to the thermal energy range. These experiments come from the ICSBEP and IRPhEP Handbooks, which are the main sources of evaluated criticality experiments in the world and cover a wide variety of configurations and labs, testing a wide range of neutron spectra, having reliable statistics and highlighting potential experimental biases. A brief description of the reactor physics benchmarks is provided in Table 1. Other benchmarks coming from the ICSBEP Handbook were selected since they were considered to provide validation for reactor physics applications or constituted cross reference links with the IRPhEP Handbook. A total of 91 benchmarks from the ICSBEP and 107 from the IRPhEP Handbooks were finally selected for the analysis.

Table 1.
Description of reactor physics benchmarks.
The French Institut de Radioprotection et de Sûreté Nucléaire (IRSN) CABRI reactor was first built to study reactivity accidents, but also the behavior of fast reactor fuel during accidents (Na loop) and thermal reactors during accidents (water loop). The reactor is made of a driver lattice core with an average power of 25 MW cooled by water, polyethylene reflector blocks and a water loop hosting a cavity containing the tested fuel rod in the middle of the driver lattice core.
2.2. Methodology for Validation
The calculated parameter (keff, kinetics parameters, reactivity worth…) of the benchmark was systematically compared to the benchmark experimental parameter. When the difference between the calculated value (C) and the benchmark experiment parameter (E) exceeded three times the square root of the sum in quadrature of the experimental uncertainties and the Monte Carlo standard deviation, a bias was identified. Otherwise, a good agreement was considered between the calculation and the benchmark.
In order to have feedback on nuclear data, the Monte Carlo standard deviation was chosen sufficiently low (<0.00020) in comparison with experimental uncertainties.
The calculations were performed using the MORET 5.D.1 continuous energy code, which consists of a 3D transport calculation and determines keff as well as quantities used in reactor physics such as kinetics parameters, reaction rates and fluxes, but also all kinds of tallies that can be defined by the user.
The MORET 5 calculations were run using the JEFF-3.1.1, JEFF-3.2 and ENDF/B-VII.1 evaluations of nuclear data. The libraries were processed using the GAIA 1 tool [8] based on NJOY 99.259 (for JEFF‑3.1.1 and ENDF/B-VII.1) and NJOY 2012.50 (for JEFF-3.2) [9].
C-E results reported in colored points on the plots are given in pcm (10−5) and 3σ experimental uncertainties are reported in black dashed lines. The nomenclature used to name the experiments is taken from the ICSBEP Handbook.
3. Analysis of KEFF Results
Keff results are compared with benchmark keff in Figure 1 for criticality experiments and in Figure 2 for reactor physics experiments. When looking at Figure 1, one can conclude that, for most cases, there is a good agreement between the calculated keff and the benchmark keff. However, for four series (HMI-001, HMF-067, HMF-070, PMI-004), discrepancies stand outside the 3σ uncertainty margins for JEFF-3.1.1 and JEFF-3.2 evaluation of nuclear data. The HMF-067 and HMF-070 are ZPR experiments involving highly enriched uranium cylinders with large quantities of tungsten in the fissile and aluminum reflectors. The overestimation is mainly due to the JEFF-3.1.1 and JEFF-3.2 evaluations of tungsten cross sections. The ENDF/B-VII.1 evaluation leads to satisfactory results for all experiments, except for HMF-07-001 and HMF-070-003.
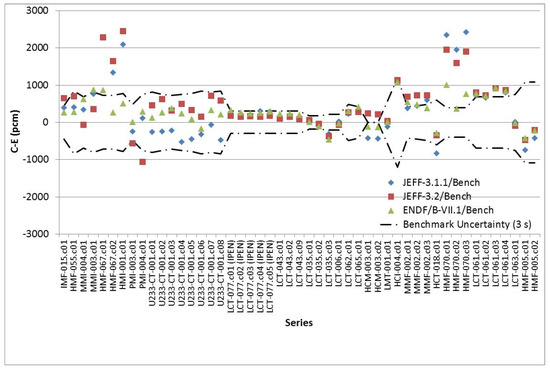
Figure 1.
Calculated keff vs. benchmark keff for criticality experiments.
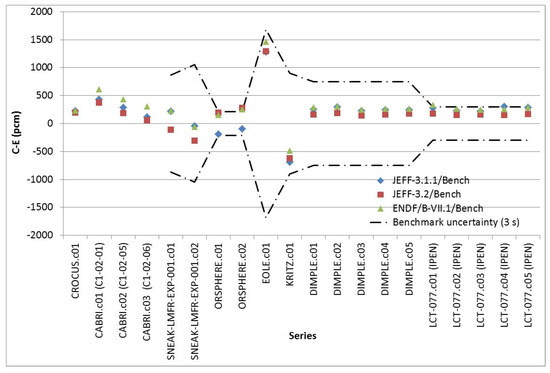
Figure 2.
Calculated keff vs. benchmark keff for reactor physics experiments. No uncertainty is available for CABRI and CROCUS experiments.
The underestimation observed for the PMI-004-001 experiment is mainly due to the JEFF-3.2 evaluation of 239Pu in the epithermal energy spectrum.
The overestimation and the discrepancies between libraries observed for HMI-001 experiments are partly due to the evaluation of 56Fe in the iron reflector and to the evaluation of 235U in epithermal energy range.
For HCT-018 involving oxide rods of highly enriched uranium and thorium, the varying tendency of keff with respect to the library can be explained by the evaluation of 232Th.
Finally, in the evaluation of 233U, being different between the JEFF-3.1.1 and JEFF-3.2 or ENDF/B-VII.1 evaluation, it is not surprising that we detect significant keff discrepancies between libraries for U233-CT-001 and all libraries leading to C-E values in the uncertainty margins.
Concerning reactor physics experiments, quite good agreement is obtained between the calculated keff and the benchmark keff. Marginal discrepancies between libraries can be pointed out, except for SNEAK and ORSPHERE experimental programs, for which up to 400 pcm discrepancies can be highlighted. For ORSPHERE, the increase of keff is mainly due to the new evaluation of 235U in JEFF-3.2 and ENDF/B‑VII.1, which differs from the one in JEFF-3.1.1 evaluation. As for SNEAK, the 300 pcm discrepancy between JEFF-3.2 and JEFF-3.1.1/ENDF/B-VII.1 is due to the evaluations of 239Pu and 238U which strongly differ between JEFF-3.2 and less recent evaluations.
4. Sensitivity/Uncertainty Analysis
Nuclear data are one of the main sources of uncertainties in the calculation of reactor configurations. In this section, uncertainties of nuclear data have been propagated in terms of Δkeff using the TSUNAMI sequence [10] of the SCALE 6.2 package [11]. To compute the so called “prior uncertainty”, the TSUNAMI sequence uses sensitivity coefficients produced by the MORET 5.D.1 continuous energy code based on the IFP methodology (which is also implemented in the MCNP6.2 code [12]) but also covariance matrices. The covariance matrices express the uncertainty of nuclear data (diagonal terms) and the cross correlated uncertainties between isotopes and reactions (anti-diagonal terms). Two covariance matrices available in the SCALE 6.2 package were used in this study: the 44groupcov based on ENDF/B‑VII.0 and the 56groupcov7.1 based on ENDF/B-VII.1. The prior uncertainty for our selection of reactor physics experiments is reported in Table 2. The uncertainty can vary depending of the fissile media and reflectors. For KRITZ and EOLE experimental programs, which involve plutonium, higher prior uncertainty values are obtained with the 44groupcov covariance matrix. It is quite understandable since the 239Pu nubar has been strongly unrealistically reduced between the ENDF/B-VII.0 and ENDF/B‑VII.1 evaluations of nuclear data. For other series, the overall uncertainty is quite comparable. However, when looking at the main contributors to the uncertainty, the hierarchy depends of the covariance library. We chose to make the comparison for the 4–6 major contributors determined with the 44groupcov covariance library. Generally, 239Pu nubar, 238U (n,n′), 239Pu fission, 235U fission and 238U (n,gamma) are in the top list. However, this analysis allows for showing the impact of other nuclides (56Fe for IPEN and CABRI, 232Th for HCT-018, 167Er for CROCUS) as can be seen in Figure 3.

Table 2.
Prior uncertainty of benchmark experiments with two covariance libraries.
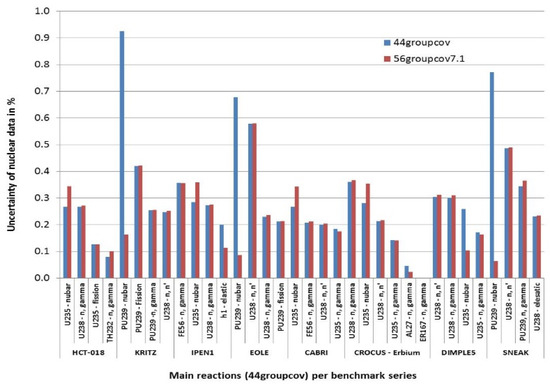
Figure 3.
Contribution of main reactions to the prior uncertainty for two covariance matrices.
5. Other Parameters
Other parameters than keff are necessary to validate the use of a code for reactor physics applications. For that purpose, benchmarks from the IRPheP database were used for the calculation of dedicated parameters by the MORET 5.D.1 transport code. Moreover, results from the CABRI reactor commissioning tests are reported in this paper.
5.1. Kinetics Parameters
The and kinetics parameters in the MORET 5.D.1 code are calculated using formulas (1) and (2).
where F is the operator for the total fission source, is the angular flux, V is the velocity, + is the adjoint flux, Peff and Peffd are, respectively, calculated using formulas (3) and (4).
In Figure 4, one can see the comparison of both kinetics parameters. Quite good agreement is obtained between the benchmark value and the value calculated with the MORET 5.D.1 code using the ENDF/B‑VII.1 evaluation of nuclear data.
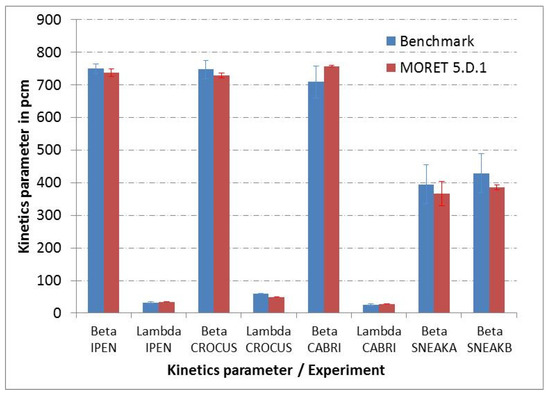
Figure 4.
Comparison of MORET 5.D.1 calculated kinetics parameters with benchmark values.
5.2. Reactivity Parameters
Various reactivity effects were calculated with the MORET 5.D.1 code for the IPEN and CABRI reactor (boron concentration, heavy water reactivity coefficients, spectral indices, temperature isothermal coefficients, control rods reactivity worth…). We chose to focus only on the light/heavy water reactivity excess for the IPEN reactor, on the efficiency of control rods (BCS) and transient rods and on the isothermal temperature coefficient for the CABRI reactor. The excess reactivity in IPEN consists of replacing the initial reflector by light/heavy water.
The results are reported in Figure 5 for CABRI and in Figure 6 for IPEN. Quite good agreement is obtained for the parameters regarding the CABRI reactor. The significant uncertainty pertaining to the BCS efficiency is due to the uncertainty of the Monte Carlo calculation (45 pcm at 3σ level).
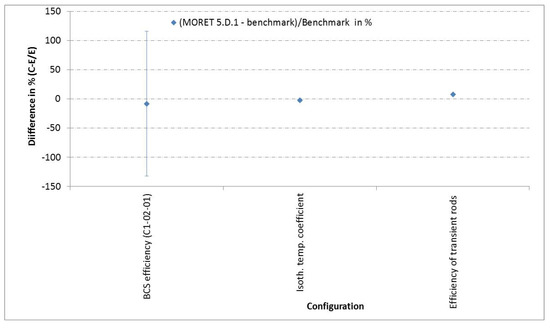
Figure 5.
Validation of reactivity parameters for the CABRI reactor—uncertainty at 3σ.
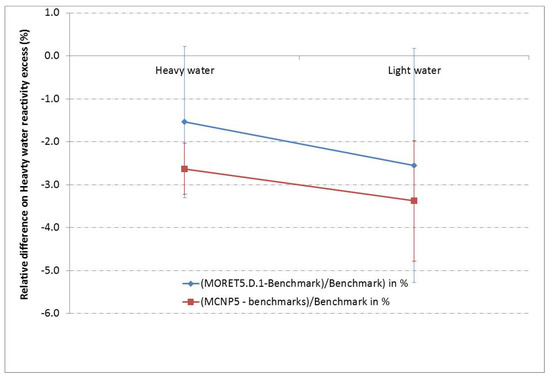
Figure 6.
Validation of the light/heavy water excess reactivity for IPEN reactor—uncertainty at 3σ.
Similar conclusions can be drawn for the IPEN reactor where excess reactivity in light and heavy water are in good agreement with the benchmark within 3σ uncertainty margins using either the MORET 5 code or the MCNP5 code. Moreover, the MORET 5 and MCNP5 results overlap.
6. Conclusions
Usually dedicated to criticality safety applications, the MORET 5 code, now available at the NEA databank, in its continuous energy version, is not limited to criticality safety anymore but can deal with reactor physics applications. A validation database of more than 1300 experiments can support the justification of keff calculations. More than 200 experiments contribute to the validation of reactor physics applications through the calculation of reactivity coefficients, control rods reactivity worth, etc. Recent developments allowed for introducing the calculation of kinetics parameters for IRSN use but also for the production of sensitivity coefficients. This is an important step in the development of the code for it gives us an opportunity to prioritize between reactivity effects, and also to have feedback on nuclear data. Comparisons made between calculated values and benchmark values, and especially on the French CABRI commissioning experiments, showed that the MORET 5.D.1 code is generally in very good agreement with the benchmark within the uncertainty margins. Future works will consist of extending the validation database for reactor physics, selecting other parameters and trying to have feedback on nuclear data using other covariance matrices through the use of in-house sensitivity/uncertainty tool MACSENS [13].
Author Contributions
Methodology, N.L.; validation, N.L., I.D.; formal analysis, N.L.; writing—original draft preparation, N.L.—review and editing, N.L., I.D.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Acknowledgments
The authors would like to thank Valentin Jouault, subcontractor from the URANUS Company, who modeled many reactor physics experiments and performed most of the calculations. His support was really appreciated.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cochet, B.; Jinaphanh, A.; Heulers, L.; Jacquet, O. Capabilities overview of the MORET 5 Monte Carlo code. Ann. Nucl. Energy 2015, 82, 74–84. [Google Scholar] [CrossRef]
- Sanchez, R.; Zmijarevic, I.; Coste-Delclaux, M.; Masiello, E.; Santandrea, S.; Martinolli, E.; Villate, L.; Schwartz, N.; Guler, N. APOLLO2 year 2010. Nucl. Eng. Technol. 2010, 42, 474–499. [Google Scholar] [CrossRef]
- Gomit, J.M.; Duhamel, I.; Richet, Y.; Entringer, A.; Magnaud, C.; Malouch, F.; Carmouze, C. CRISTAL V2: New package for criticality calculations. In Proceedings of the Nuclear Criticality Safety Division Topical Meeting (NCSD 2017), Carlsbad, CA, USA, 11–14 September 2017. [Google Scholar]
- International Criticality Safety Benchmark Evaluation Project. International Handbook of Evaluated Criticality Safety Benchmark Experiments, Organization of Economic Cooperation and Development-Nuclear Energy; NEA/NSC/DOC(95)03; United States Department of Energy: Washington, DC, USA, 2016. [Google Scholar]
- International Reactor Physics Experiment Evaluation Project. International Handbook of Evaluated Reactor Physics Benchmark Experiments, Organization of Economic Cooperation and Development-Nuclear Energy; NEA/NSC/DOC(2006)01; United States Department of Energy: Washington, DC, USA, 2018. [Google Scholar]
- Ritter, G.; Rodiac, F.; Beretz, D.; Jammes, C.; Guéton, O. Neutron Commissioning in the new CABRI Water Loop Facility. In Proceedings of the International Group on Research Reactors 13th Conference, Knoxville, TN, USA, 19–23 September 2010. [Google Scholar]
- Jinaphanh, A.; LeClaire, N.; Cochet, B. Continuous-Energy Sensitivity Coefficients in the MORET Code. Nucl. Sci. Eng. 2016, 184, 53–68. [Google Scholar] [CrossRef]
- Ichou, R.; Jeannesson, C.; Haeck, W. Feedback on JEFF-3.3 Processing with GAIA 1.1; JEFDOC 1930; OECD: Paris, France, 2018. [Google Scholar]
- MacFarlane, R.; Kahler, A. Methods for Processing ENDF/B-VII with NJOY. Nucl. Data Sheets 2010, 111, 2739–2890. [Google Scholar] [CrossRef]
- Rearden, B.T.; Reed, D.A.; Lefebvre, R.A.; Mueller, D.; Marshall, W. SCALE/TSUNAMI Sensitivity Data for ICSBEP Evaluations. In Proceedings of the International Conference on Nuclear Criticality 2011, Edinburgh, UK, 19–22 September 2011. [Google Scholar]
- Petrie, L.M.; Jordon, W.C.; Edwards, A.L.; Williams, P.T.; Ryman, J.C.; Hermann, O.W.; Landers, N.F.; Bucholz, J.A.; Knight, J.R.; Parks, C.V.; et al. SCALE: A Modular Code System for Performing Standardized Computer Analyses for Licensing Evaluations; NUREG/CR-0200, Rev. 7 (ORNL/NUREG/CSD-2/R7); Radiation Safety Information Computational Center: Oak Ridge, TN, USA, 2004; Volume 1–3. [Google Scholar]
- Brown, F.; Kiedrowski, B.; Bull, J. MCNP5-1.60 Release Notes; LA UR 10 06235; US Department of Energy: Washington, DC, USA, 2010. [Google Scholar]
- Jinaphanh, A.; Fernex, F.; Leclaire, N. Uncertainty and Bias Quantification with the MACSENS Software; EGUACSA-2017; OECD NEA: Paris, France, 2017. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).