Power Density and Thermochemical Properties of Hydrogen Magnetohydrodynamic (H2MHD) Generators at Different Pressures, Seed Types, Seed Levels, and Oxidizers
Abstract
1. Introduction
1.1. Background
1.2. Goal of the Study
2. Research Method
2.1. Assumptions
2.2. Mathematical Equations
2.3. Varied Conditions
2.4. Power Density Criterion
3. Results
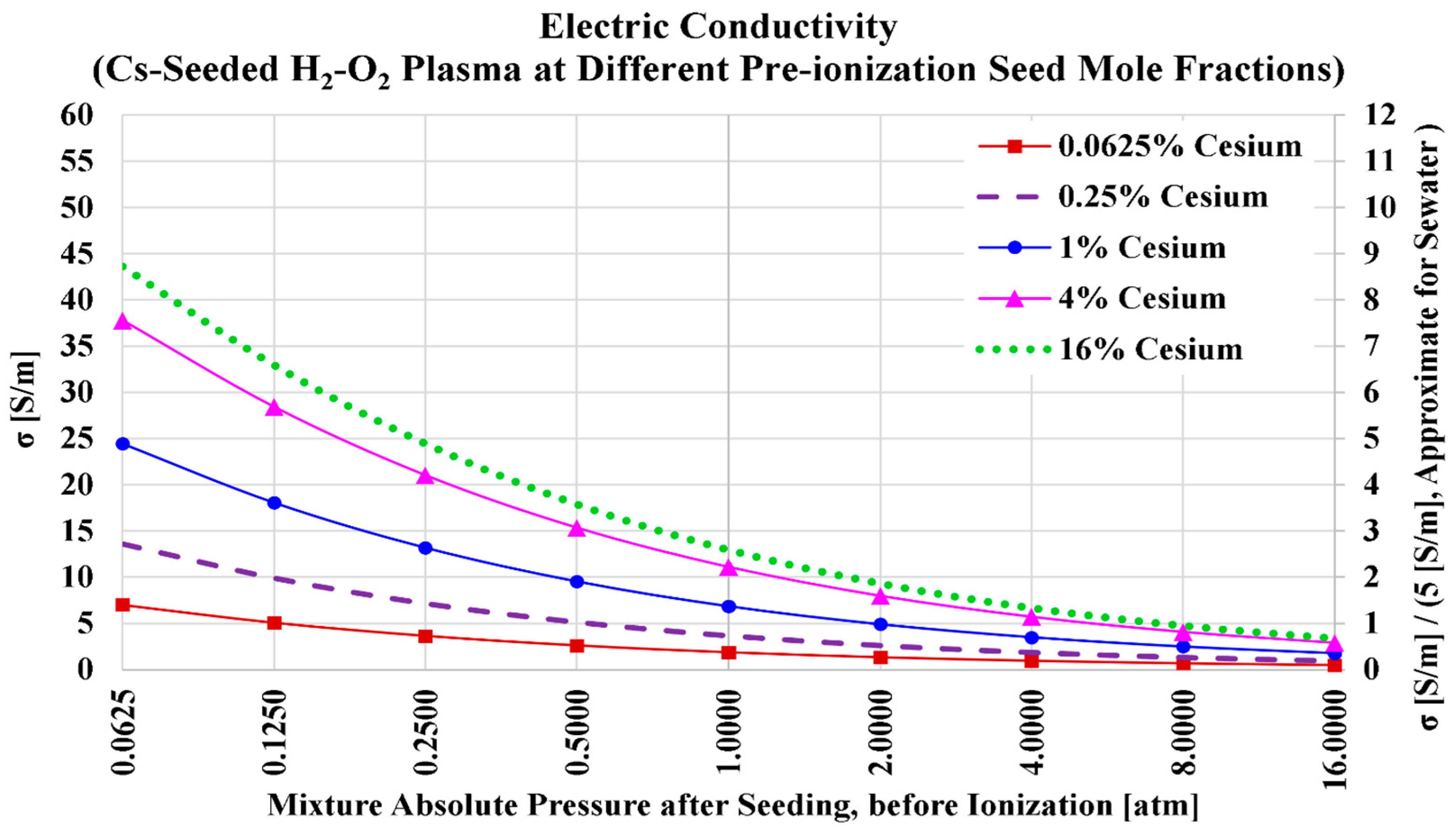
3.1. Cesium Seed and Air Oxidizer
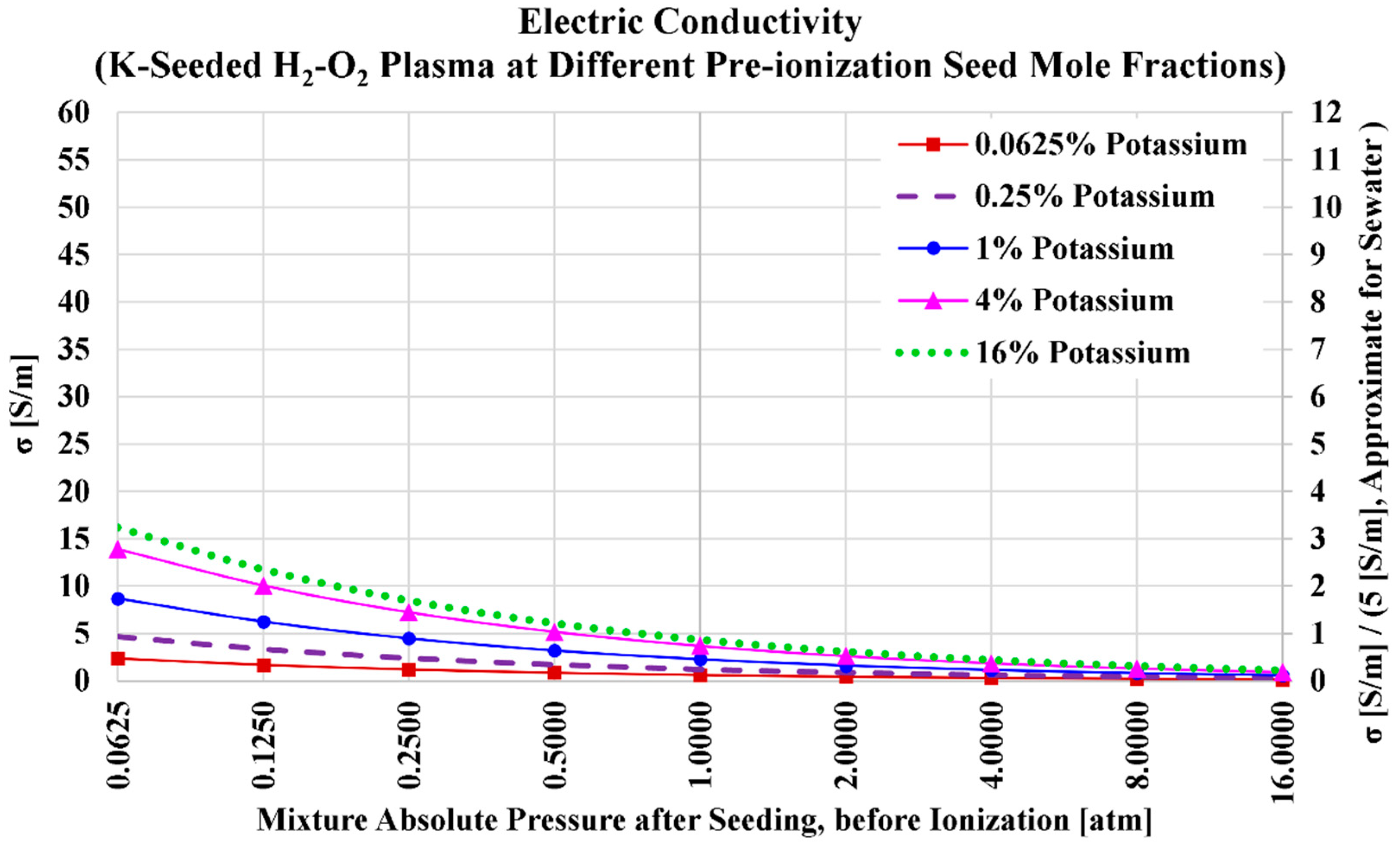
3.2. Potassium Seed and Air Oxidizer
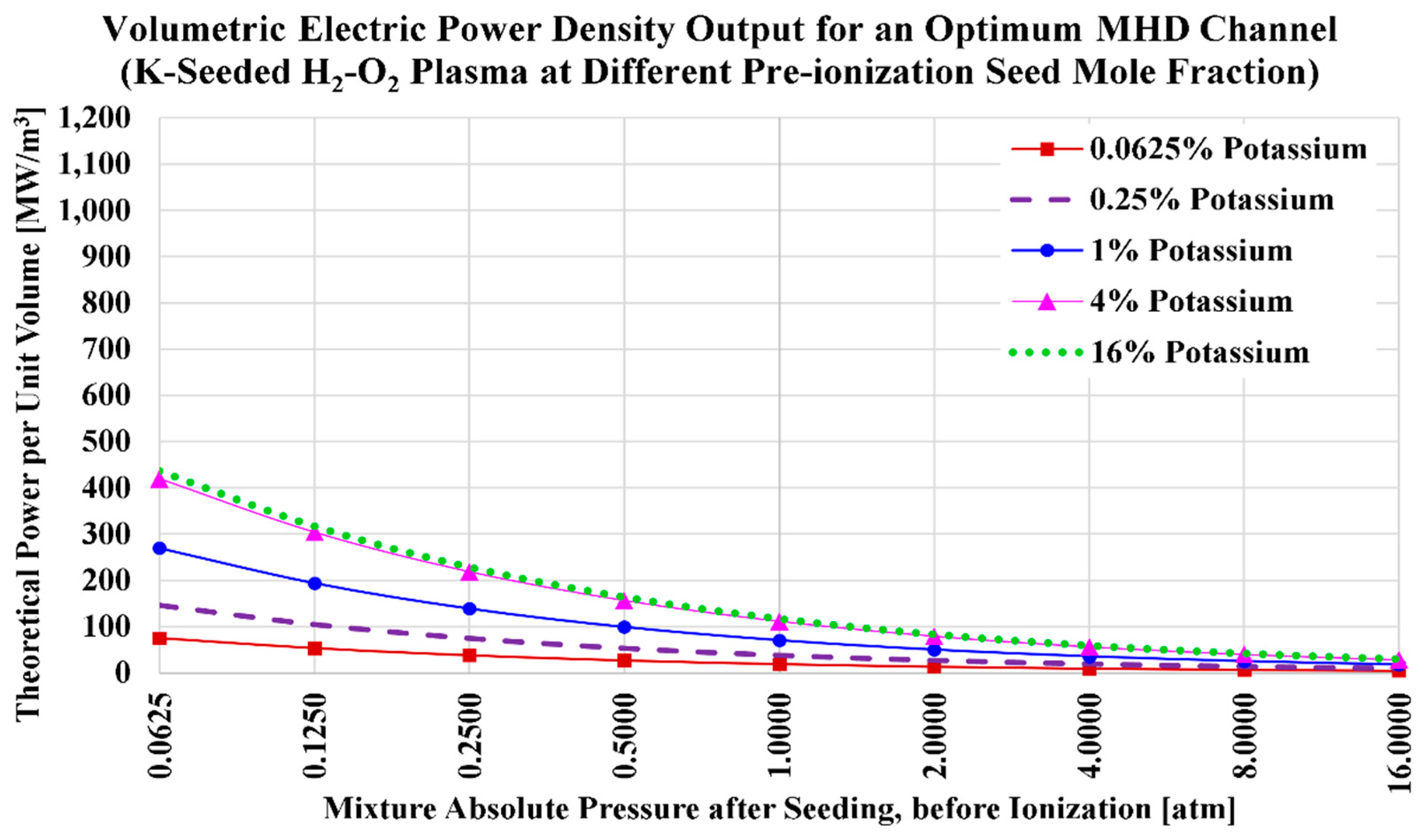
3.3. Potassium Seed and Oxygen Oxidizer
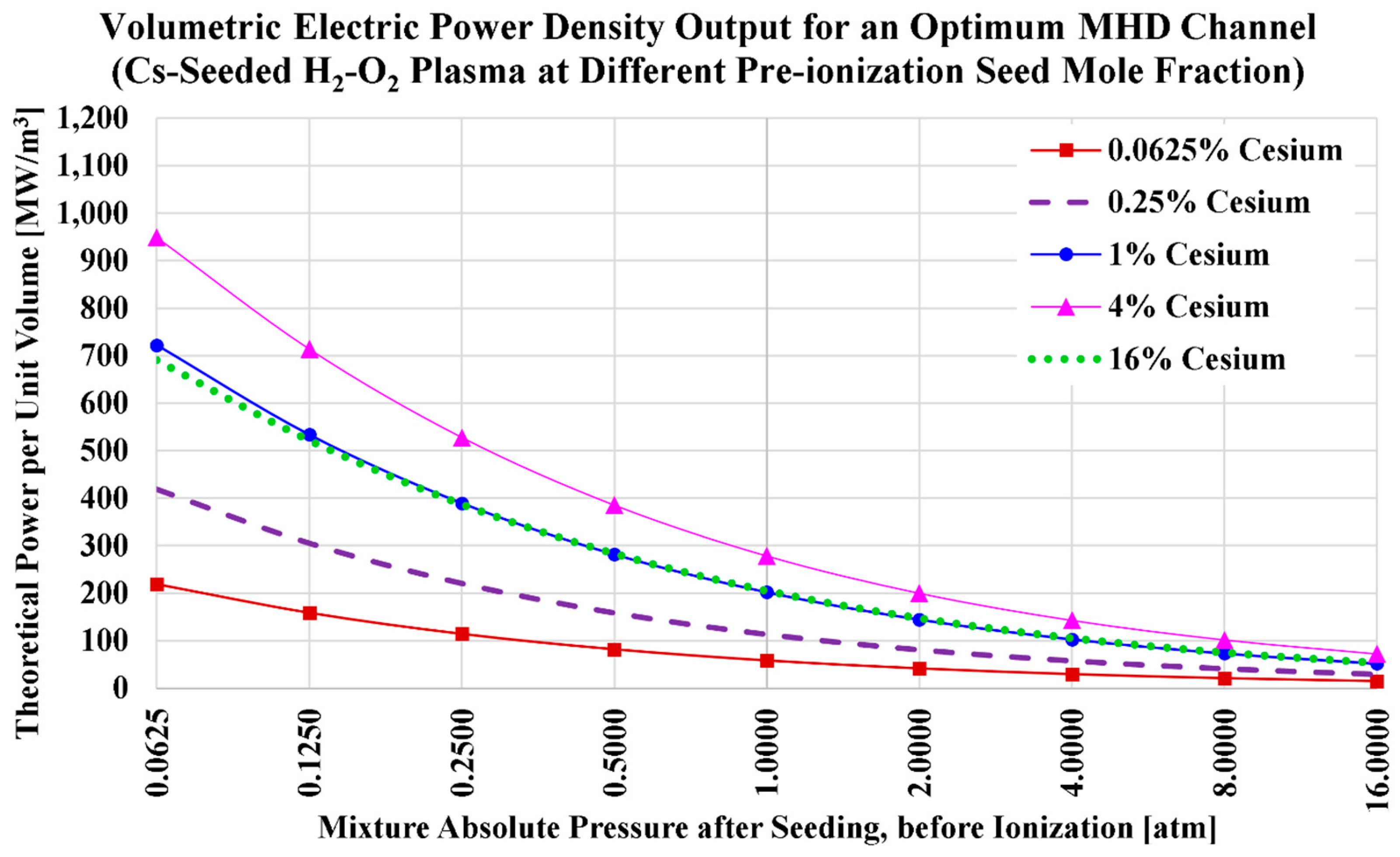
3.4. Cesium Seed and Oxygen Oxidizer
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
References
- Field, D. The most popular element in the universe. Phys. World 1995, 8, 24. [Google Scholar] [CrossRef]
- Goncharuk, V.V.; Goncharuk, D.K. Water is Everywhere. It Holds Everything, Even a Key to Understanding the Universe. D. I. Mendeleev’s Law is the Prototype of the Universe Constitution. J. Water Chem. Technol. 2019, 41, 341–346. [Google Scholar] [CrossRef]
- Barayeu, U.; Sawa, T.; Nishida, M.; Wei, F.-Y.; Motohashi, H.; Akaike, T. Supersulfide biology and translational medicine for disease control. Br. J. Pharmacol. 2025. [Google Scholar] [CrossRef]
- Krebs, R.E. The History and Use of Our Earth’s Chemical Elements: A Reference Guide; Greenwood Press: Westport, CT, USA, 2006; Available online: https://books.google.com.om/books?id=D7LOEAAAQBAJ (accessed on 4 April 2025).
- Ma, Y.H. Palladium Membranes for Hydrogen Separation. In Membranes for Energy Conversion; Peinemann, K.-V., Nunes, S.P., Eds.; John Wiley & Sons: Weinheim, Germany, 2008; pp. 245–261. Available online: https://books.google.com.om/books?id=KCTyy64_IO8C (accessed on 30 March 2025).
- Marzouk, O.A. Performance analysis of shell-and-tube dehydrogenation module. Int. J. Energy Res. 2017, 41, 604–610. [Google Scholar] [CrossRef]
- Vergara, D.; Fernández-Arias, P.; Lampropoulos, G.; Antón-Sancho, Á. Hydrogen Revolution in Europe: Bibliometric Review of Industrial Hydrogen Applications for a Sustainable Future. Energies 2024, 17, 3658. [Google Scholar] [CrossRef]
- Altaf, C.T.; Demir, O.; Colak, T.O.; Karagöz, E.; Kurt, M.; Sankir, N.D.; Sankir, M. Decarbonizing the Industry with Green Hydrogen. In Towards Green Hydrogen Generation; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2024; pp. 1–48. [Google Scholar] [CrossRef]
- Sarkarzadeh, M.; Farsi, M.; Rahimpour, M.R. Modeling and optimization of an industrial hydrogen unit in a crude oil refinery. Int. J. Hydrogen Energy 2019, 44, 10415–10426. [Google Scholar] [CrossRef]
- Moradpoor, I.; Syri, S.; Santasalo-Aarnio, A. Green hydrogen production for oil refining—Finnish case. Renew. Sustain. Energy Rev. 2023, 175, 113159. [Google Scholar] [CrossRef]
- Alves, J.J.; Towler, G.P. Analysis of Refinery Hydrogen Distribution Systems. Ind. Eng. Chem. Res. 2002, 41, 5759–5769. [Google Scholar] [CrossRef]
- Popoola, L.T.; Nwogbu, C.C.; Taura, U.; Asmara, Y.P.; Nwobodo, L.O.; Agbo, A.O. Future prospects towards attaining zero-emission of greenhouse gases from crude oil refinery plants. Clean. Waste Syst. 2025, 11, 100290. [Google Scholar] [CrossRef]
- Cheng, Y.; Zheng, R.; Liu, Z.; Xie, Z. Hydrogen-based industry: A prospective transition pathway toward a low-carbon future. Natl. Sci. Rev. 2023, 10, nwad091. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, J.-F.; Gao, Z.-H.; Chen, S.-Y.; Liu, B.-Y. Review on the challenges and strategies in oil and gas industry’s transition towards carbon neutrality in China. Pet. Sci. 2023, 20, 3931–3944. [Google Scholar] [CrossRef]
- Gass, R.; Li, Z.; Outbib, R.; Jemei, S.; Hissel, D. An advanced 1D physics-based model for PEM hydrogen fuel cells with enhanced overvoltage prediction. Int. J. Hydrogen Energy 2025, 97, 1108–1125. [Google Scholar] [CrossRef]
- Chen, Z.; Shu, C.; Gan, Z.; Cao, J.; Qiu, P.; Sun, X.; Deng, C.; Wu, Y.; Tang, W. Research Progress and Perspectives on Anti-Poisoning Hydrogen Oxidation Reaction Electrocatalysts for Hydrogen Fuel Cells. Small 2025, 21, 2411049. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.H.; Choi, S.S.; Rajakaruna, S. An analysis of the control and operation of a solid oxide fuel-cell power plant in an isolated system. IEEE Trans. Energy Convers. 2005, 20, 381–387. [Google Scholar] [CrossRef]
- Marzouk, O.A. Compilation of Smart Cities Attributes and Quantitative Identification of Mismatch in Rankings. J. Eng. 2022, 2022, 5981551. [Google Scholar] [CrossRef]
- Sun, L.; Wu, G.; Xue, Y.; Shen, J.; Li, D.; Lee, K.Y. Coordinated Control Strategies for Fuel Cell Power Plant in a Microgrid. IEEE Trans. Energy Convers. 2018, 33, 1–9. [Google Scholar] [CrossRef]
- Genovese, M.; Corigliano, O.; Piraino, F.; Fragiacomo, P. E-fuels infrastructures for heavy-duty applications: Case study of a refueling facility based on green hydrogen. Int. J. Hydrogen Energy, 2025; in press. [Google Scholar] [CrossRef]
- Fozer, D.; Owsianiak, M.; Hauschild, M.Z. Quantifying environmental learning and scaling rates for prospective life cycle assessment of e-ammonia production. Renew. Sustain. Energy Rev. 2025, 213, 115481. [Google Scholar] [CrossRef]
- Sun, S.; Jiang, Q.; Zhao, D.; Cao, T.; Sha, H.; Zhang, C.; Song, H.; Da, Z. Ammonia as hydrogen carrier: Advances in ammonia decomposition catalysts for promising hydrogen production. Renew. Sustain. Energy Rev. 2022, 169, 112918. [Google Scholar] [CrossRef]
- Klerke, A.; Christensen, C.H.; Nørskov, J.K.; Vegge, T. Ammonia for hydrogen storage: Challenges and opportunities. J. Mater. Chem. 2008, 18, 2304–2310. [Google Scholar] [CrossRef]
- Marzouk, O.A. Levelized cost of green hydrogen (LCOH) in the Sultanate of Oman using H2A-Lite with polymer electrolyte membrane (PEM) electrolyzers powered by solar photovoltaic (PV) electricity. E3S Web Conf. 2023, 469, 00101. [Google Scholar] [CrossRef]
- Amorim, J.; Baravian, G.; Sultan, G. Absolute density measurements of ammonia synthetized in N2–H2 mixture discharges. Appl. Phys. Lett. 1996, 68, 1915–1917. [Google Scholar] [CrossRef]
- Reuß, M.; Dimos, P.; Léon, A.; Grube, T.; Robinius, M.; Stolten, D. Hydrogen Road Transport Analysis in the Energy System: A Case Study for Germany through 2050. Energies 2021, 14, 3166. [Google Scholar] [CrossRef]
- Marzouk, O.A. Toward More Sustainable Transportation: Green Vehicle Metrics for 2023 and 2024 Model Years. In Intelligent Sustainable Systems; Nagar, A.K., Jat, D.S., Mishra, D.K., Joshi, A., Eds.; Springer Nature: Singapore, 2024; pp. 261–272. [Google Scholar] [CrossRef]
- Dhingra, S.; Sharma, S.; Jaiswal, A.; Chadha, R.; Suneja, G.; Gupta, A. Can hydrogen fuel cell vehicles drive the future of sustainable transportation? An empirical study. Technol. Sustain. 2025, 4, 181–193. [Google Scholar] [CrossRef]
- Marin, G.D.; Naterer, G.F.; Gabriel, K. Rail transportation by hydrogen vs. electrification—Case study for Ontario, Canada, II: Energy supply and distribution. Int. J. Hydrogen Energy 2010, 35, 6097–6107. [Google Scholar] [CrossRef]
- Marzouk, O.A. Growth in the Worldwide Stock of E-Mobility Vehicles (by Technology and by Transport Mode) and the Worldwide Stock of Hydrogen Refueling Stations and Electric Charging Points between 2020 and 2022. In Construction Materials and Their Processing; Trans Tech Publications Ltd.: Wollerau, Switzerland, 2023; pp. 89–96. [Google Scholar] [CrossRef]
- Galimova, T.; Fasihi, M.; Bogdanov, D.; Breyer, C. Impact of international transportation chains on cost of green e-hydrogen: Global cost of hydrogen and consequences for Germany and Finland. Appl. Energy 2023, 347, 121369. [Google Scholar] [CrossRef]
- Marzouk, O.A. Recommended LEED-Compliant Cars, SUVs, Vans, Pickup Trucks, Station Wagons, and Two Seaters for Smart Cities Based on the Environmental Damage Index (EDX) and Green Score. In Innovations in Smart Cities Applications Volume 7; Ben Ahmed, M., Boudhir, A.A., El Meouche, R., Karaș, İ.R., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 123–135. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Huang, X.; Liu, F.; Zhou, F.; Lim, M.K. Uncovering determinants and barriers to hydrogen fuel cell vehicle adoption: Evidence from Chongqing, China. Int. J. Hydrogen Energy 2025, 106, 875–887. [Google Scholar] [CrossRef]
- Bianchi, F.R.; Risso, R.; Cardona, L.; Bove, D.; Cannizzaro, F.; Bonardi, L.; Palmisani, E.; Bosio, B. Feasibility analysis of e-Hydrogen, e-Ammonia and e-Methanol synthesis compared with methane to fuel production. Fuel 2025, 384, 133938. [Google Scholar] [CrossRef]
- Galindo Cifre, P.; Badr, O. Renewable hydrogen utilisation for the production of methanol. Energy Convers. Manag. 2007, 48, 519–527. [Google Scholar] [CrossRef]
- Monnerie, N.; Gan, P.G.; Roeb, M.; Sattler, C. Methanol production using hydrogen from concentrated solar energy. Int. J. Hydrogen Energy 2020, 45, 26117–26125. [Google Scholar] [CrossRef]
- Dalena, F.; Senatore, A.; Marino, A.; Gordano, A.; Basile, M.; Basile, A. Chapter 1—Methanol Production and Applications: An Overview. In Methanol; Basile, A., Dalena, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 3–28. [Google Scholar] [CrossRef]
- Galimova, T.; Fasihi, M.; Bogdanov, D.; Lopez, G.; Breyer, C. Analysis of green e-methanol supply costs: Domestic production in Europe versus imports via pipeline and sea shipping. Renew. Energy 2025, 241, 122336. [Google Scholar] [CrossRef]
- Sillman, J.; Ylä-Kujala, A.; Hyypiä, J.; Kärri, T.; Tuomaala, M.; Soukka, R. Feasibility assessment of e-methanol value chains: Temporal and regional renewable energy, costs, and climate impacts. Appl. Energy 2025, 391, 125887. [Google Scholar] [CrossRef]
- Elmeknassi, Y.; He, W.; Adam, A.; Deng, J.; Lou, Z.; Wang, C.; Chen, L. Performance Analysis of Hydrogen-Powered Gas Turbine Engines: A Parametric Study. In Proceedings of the 2024 7th International Conference on Renewable Energy and Power Engineering (REPE), Beijing, China, 25–27 September 2024; pp. 379–385. [Google Scholar] [CrossRef]
- Chiesa, P.; Lozza, G.; Mazzocchi, L. Using Hydrogen as Gas Turbine Fuel. J. Eng. Gas. Turbines Power 2005, 127, 73–80. [Google Scholar] [CrossRef]
- Stefan, E.; Talic, B.; Larring, Y.; Gruber, A.; Peters, T.A. Materials challenges in hydrogen-fuelled gas turbines. Int. Mater. Rev. 2022, 67, 461–486. [Google Scholar] [CrossRef]
- Nyholm, F.; Toppinen, S.; Saxén, H. Holistic Evaluation Method for Concept-Level Study of Power-to-Liquids Technologies for e-Kerosene Production. Ind. Eng. Chem. Res. 2024, 63, 20264–20286. [Google Scholar] [CrossRef]
- Song, Z.; Zhao, J. Research on the Integrated Development of Nuclear Energy and Aviation Industry Under the Background of “Dual Carbon” Goals. E3S Web Conf. 2024, 573, 03008. [Google Scholar] [CrossRef]
- Marzouk, O.A. Subcritical and supercritical Rankine steam cycles, under elevated temperatures up to 900 °C and absolute pressures up to 400 bara. Adv. Mech. Eng. 2024, 16, 16878132231221065. [Google Scholar] [CrossRef]
- Pacheco, L.S.; Hernández-Gutiérrez, L.E. Advancing Direct Air Capture Technologies: From Carbon Removal to Sustainable Aviation Fuels. In Proceedings of the Copernicus Meetings (EGU General Assembly 2025), Vienna, Austria, 27 April–2 May 2025. [Google Scholar] [CrossRef]
- Gao, R.; Zhang, C.; Jun, K.-W.; Kim, S.K.; Park, H.-G.; Zhao, T.; Wang, L.; Wan, H.; Guan, G. Transformation of CO2 into liquid fuels and synthetic natural gas using green hydrogen: A comparative analysis. Fuel 2021, 291, 120111. [Google Scholar] [CrossRef]
- Quaresma, G.; Magalhães, L.B.; Ferreira, A.F.; Silva, A. E-Kerosene Potential for Commercial Aviation Decarbonization. In Proceedings of the 34th Congress of the International Council of the Aeronautical Sciences (ICAS 2024), Florence, Italy, 9–13 September 2024; ICAS [International Council of the Aeronautical Sciences]: Florence, Italy, 2024. Available online: https://www.icas.org/icas_archive/icas2024/data/papers/icas2024_0680_paper.pdf (accessed on 28 April 2025).
- Nyholm, F.; Saxén, H. Evaluation Method for Power-to-Liquids Concepts for e-Kerosene Production. In Computer Aided Chemical Engineering; Manenti, F., Reklaitis, G.V., Eds.; Elsevier: Amsterdam, The Netherlands, 2024; pp. 3349–3354. [Google Scholar] [CrossRef]
- Ozkan, M.; Narappa, A.B.; Namboodiri, T.; Chai, Y.; Babu, M.; Jennings, J.S.E.; Gao, Y.; Tasneem, S.; Lam, J.; Talluri, K.R.; et al. Forging a sustainable sky: Unveiling the pillars of aviation e-fuel production for carbon emission circularity. iScience 2024, 27, 109154. [Google Scholar] [CrossRef]
- Schomakers, E.-M.; Engelmann, L.; Ziefle, M. Diversity in the acceptance of sustainable aviation fuels: Uncovering varying motivational patterns. Fuel Commun. 2024, 20, 100129. [Google Scholar] [CrossRef]
- De Vries, R.; Wolleswinkel, R.E.; Hoogreef, M.; Vos, R. A New Perspective on Battery-Electric Aviation, Part II: Conceptual Design of a 90-Seater. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024; AIAA [American Institute of Aeronautics and Astronautics]: Orlando, FL, USA, 2024; p. 1490. [Google Scholar] [CrossRef]
- Marzouk, O.A. Urban air mobility and flying cars: Overview, examples, prospects, drawbacks, and solutions. Open Eng. 2022, 12, 662–679. [Google Scholar] [CrossRef]
- Bhapkar, S.; Sain, C.; Kazula, S. Review and Evaluation of Hydrogen and Air Heat Exchangers for Fuel Cell-Powered Electric Aircraft Propulsion. Eng. Proc. 2025, 90, 62. [Google Scholar] [CrossRef]
- Gao, Y.; Jausseme, C.; Huang, Z.; Yang, T. Hydrogen-Powered Aircraft: Hydrogen–electric hybrid propulsion for aviation. IEEE Electrif. Mag. 2022, 10, 17–26. [Google Scholar] [CrossRef]
- Gunasekar, P.; Manigandan, S.; Kumar, T.R.P. Hydrogen as the futuristic fuel for the aviation and aerospace industry—Review. Aircr. Eng. Aerosp. Technol. 2020, 93, 410–416. [Google Scholar] [CrossRef]
- Marzouk, O.A. A two-step computational aeroacoustics method applied to high-speed flows. Noise Control Eng. J. 2008, 56, 396. [Google Scholar] [CrossRef]
- Petrescu, R.V.V.; Machín, A.; Fontánez, K.; Arango, J.C.; Márquez, F.M.; Petrescu, F.I.T. Hydrogen for aircraft power and propulsion. Int. J. Hydrogen Energy 2020, 45, 20740–20764. [Google Scholar] [CrossRef]
- Contreras, A.; Yiğit, S.; Özay, K.; Veziroğlu, T.N. Hydrogen as aviation fuel: A comparison with hydrocarbon fuels. Int. J. Hydrogen Energy 1997, 22, 1053–1060. [Google Scholar] [CrossRef]
- Gerl, B.; Ronovsky-Bodisch, M.; Ferrari, N.; Berens, M. Fundamentals of Innovative Aircraft Heat Exchanger Integration for Hydrogen–Electric Propulsion. Aerospace 2025, 12, 320. [Google Scholar] [CrossRef]
- White, A.S.; Waddington, E.; Merret, J.M.; Ansell, P.J.; Hall, D.K. Trade-Space Assessment of Liquid Hydrogen Propulsion Systems for Electrified Aircraft. J. Aircr. 2025, 62, 270–277. [Google Scholar] [CrossRef]
- Karpuk, S.; Freund, Y.; Hanke-Rauschenbach, R. Potential of Hydrogen Fuel Cell Aircraft for Commercial Applications with Advanced Airframe and Propulsion Technologies. Aerospace 2025, 12, 35. [Google Scholar] [CrossRef]
- Rukini, A.; Rhamdhani, M.A.; Brooks, G.A.; Van den Bulck, A. Metals Production and Metal Oxides Reduction Using Hydrogen: A Review. J. Sustain. Metall. 2022, 8, 1–24. [Google Scholar] [CrossRef]
- Boretti, A. The perspective of hydrogen direct reduction of iron. J. Clean. Prod. 2023, 429, 139585. [Google Scholar] [CrossRef]
- Heidari, A.; Niknahad, N.; Iljana, M.; Fabritius, T. A Review on the Kinetics of Iron Ore Reduction by Hydrogen. Materials 2021, 14, 7540. [Google Scholar] [CrossRef] [PubMed]
- Spreitzer, D.; Schenk, J. Reduction of Iron Oxides with Hydrogen—A Review. Steel Res. Int. 2019, 90, 1900108. [Google Scholar] [CrossRef]
- Chen, Q.; Pan, J.; Guo, Z.; Zhu, D. Optimization of four-component furnace burdens with hydrogen-reduced metallized pellets based on blast furnace performance. Int. J. Hydrogen Energy 2025, 100, 596–607. [Google Scholar] [CrossRef]
- Kar, M.K.; Safarian, J. Producing High Purity Metallic Iron from Bauxite Residue Through Hydrogen Reduction Followed by Flux Smelting. ISIJ Int. 2025, 65, 372–383. [Google Scholar] [CrossRef]
- Adami, B.; Hoffelner, F.; Zarl, M.A.; Schenk, J. Strategic Selection of a Pre-Reduction Reactor for Increased Hydrogen Utilization in Hydrogen Plasma Smelting Reduction. Processes 2025, 13, 420. [Google Scholar] [CrossRef]
- Sun, M.; Pang, K.; Gu, Z.; Shao, S. Analysis of the theory and practice of hydrogen-enriched blast furnace ironmaking. Int. J. Hydrogen Energy 2025, 127, 702–716. [Google Scholar] [CrossRef]
- Xing, Y.; Luo, Z.; Li, H.; Wang, X.; Kou, M.; Wu, S.; Zou, Z.; Zhou, H. Modelling in-furnace phenomena in a hydrogen-rich low-carbon reduction smelting furnace: Influence of blast parameters of hydrogen-rich gas. Appl. Therm. Eng. 2025, 273, 126494. [Google Scholar] [CrossRef]
- Ho, T.; Karri, V. Basic tuning of hydrogen powered car and artificial intelligent prediction of hydrogen engine characteristics. Int. J. Hydrogen Energy 2010, 35, 10004–10012. [Google Scholar] [CrossRef]
- Wróbel, K.; Wróbel, J.; Tokarz, W.; Lach, J.; Podsadni, K.; Czerwiński, A. Hydrogen Internal Combustion Engine Vehicles: A Review. Energies 2022, 15, 8937. [Google Scholar] [CrossRef]
- Swain, M.R.; Pappas, J.M.; Adt, R.R.; Escher, W.J.D. Hydrogen-Fueled Automotive Engine Experimental Testing to Provide an Initial Design-Data Base. In Proceedings of the SAE International Congress and Exposition, Warrendale, PA, USA, 1 February 1981; p. 810350. [Google Scholar] [CrossRef]
- Wang, H.; Li, L.; Huang, J.; Wang, Z.; Wu, S.; Xu, W.; Wang, F.; Hao, L.; Bi, Y. The design and performance tests of customized water-proof welding rods for local-dry underwater welding. Eng. Res. Express 2025. [Google Scholar] [CrossRef]
- Aderouane, F. (Ed.) Materials and Welding. In Design, Construction, and Global Performance Analysis of Offshore Wind Turbines; Springer Nature: Cham, Switzerland, 2025; pp. 15–38. [Google Scholar] [CrossRef]
- Kunar, S.; Mandal, G. Advanced Welding Technologies; John Wiley & Sons: Hoboken, NJ, USA, 2025; ISBN 978-1-394-33190-1. [Google Scholar]
- Suban, M.; Tušek, J.; Uran, M. Use of hydrogen in welding engineering in former times and today. J. Mater. Process. Technol. 2001, 119, 193–198. [Google Scholar] [CrossRef]
- Zhao, Q.; Li, H.; Lv, J.; Liu, X.; Zhang, F.; Jiang, S.; Ma, L.; Wang, C.; Ni, J.; Peng, G. Adhesive-free bonding fiber optic Fabry–Perot pressure sensor based on oxy-hydrogen flame welding and spiral tube. Opt. Commun. 2020, 476, 126307. [Google Scholar] [CrossRef]
- Attah, J.; Mohammed, L.; Nyamful, A.; Donkor, P.; Asamoah, A.; Zainudeen, M.N.; Adjah, J.; Klutse, C.K.; Birikorang, S.A.; Agyemang, F.; et al. Oxy-hydrogen gas as a sustainable fuel for the welding industry: Alternative for oxy-acetylene gas. Clean. Energy Syst. 2024, 9, 100160. [Google Scholar] [CrossRef]
- Arshian, S.; Firoozbakhtian, A.; Salehnia, F.; Naghavi Sheikholeslami, M.; Hamidipanah, Y.; Gilnezhad, J.; Reza Ganjali, M.; Hosseini, M. Ti3C2/Ni/Sm-Based Screen-Printed-Electrode for the ECL Detection of Hydrogen Peroxide as a Milk Preservative. ChemistrySelect 2024, 9, e202304462. [Google Scholar] [CrossRef]
- Alwazeer, D. Consumption of Hydrogen-Treated Foods Provides Nutritional and Health Benefits. In Molecular Hydrogen in Health and Disease; Slezak, J., Kura, B., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 319–337. [Google Scholar] [CrossRef]
- Russell, G.; Nenov, A.; Hancock, J.T. How Hydrogen (H2) Can Support Food Security: From Farm to Fork. Appl. Sci. 2024, 14, 2877. [Google Scholar] [CrossRef]
- Keçebaş, A.; Kayfeci, M. Chapter 1—Hydrogen properties. In Solar Hydrogen Production; Calise, F., D’Accadia, M.D., Santarelli, M., Lanzini, A., Ferrero, D., Eds.; Academic Press: New York, NY, USA, 2019; pp. 3–29. [Google Scholar] [CrossRef]
- Allen, R.R. Hydrogenation. J. Am. Oil Chem. Soc. 1981, 58, 166–169. [Google Scholar] [CrossRef]
- Jovanovic, D.; Radovic, R.; Mares, L.; Stankovic, M.; Markovic, B. Nickel hydrogenation catalyst for tallow hydrogenation and for the selective hydrogenation of sunflower seed oil and soybean oil. Catal. Today 1998, 43, 21–28. [Google Scholar] [CrossRef]
- Anikina, I.D.; Sergeyev, V.V.; Amosov, N.T.; Luchko, M.G. Use of heat pumps in turbogenerator hydrogen cooling systems at thermal power plant. Int. J. Hydrogen Energy 2017, 42, 636–642. [Google Scholar] [CrossRef]
- Hara, S.; Iwami, Y.; Kawasaki, R.; Matsumoto, T.; Shirai, Y.; Shiotsu, M.; Kobayashi, H.; Naruo, Y.; Nonaka, S.; Inatani, Y.; et al. Development of Liquid Hydrogen Cooling System for a Rotor of Superconducting Generator. IEEE Trans. Appl. Supercond. 2021, 31, 5202505. [Google Scholar] [CrossRef]
- Snell, D.S. The hydrogen-cooled turbine generator. Electr. Eng. 1940, 59, 35–50. [Google Scholar] [CrossRef]
- Gray, R.F.; Montgomery, L.; Nelson, R.; Pipkin, J.; Joki-Korpel, S.; Caguiat, F. Designing the cooling systems for the world’s most powerful turbogenerator—Olkiluoto unit 3. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; p. 5. [Google Scholar] [CrossRef]
- Mah, A.X.Y.; Ho, W.S.; Bong, C.P.C.; Hassim, M.H.; Liew, P.Y.; Asli, U.A.; Kamaruddin, M.J.; Chemmangattuvalappil, N.G. Review of hydrogen economy in Malaysia and its way forward. Int. J. Hydrogen Energy 2019, 44, 5661–5675. [Google Scholar] [CrossRef]
- De Rinaldis, S. Green Hydrogen as Industrial Complexes Feedstock and Fuel for Maritime Transport; OnePetro: Richardson, TX, USA, 2021. [Google Scholar]
- Branco, J.B.; Ferreira, A.C.; Gonçalves, A.P.; Soares, C.O.; Almeida Gasche, T. Synthesis of methanol using copper–f block element bimetallic oxides as catalysts and greenhouse gases (CO2, CH4) as feedstock. J. Catal. 2016, 341, 24–32. [Google Scholar] [CrossRef]
- Schwengber, C.A.; Alves, H.J.; Schaffner, R.A.; da Silva, F.A.; Sequinel, R.; Bach, V.R.; Ferracin, R.J. Overview of glycerol reforming for hydrogen production. Renew. Sustain. Energy Rev. 2016, 58, 259–266. [Google Scholar] [CrossRef]
- Marzouk, O.A. Expectations for the Role of Hydrogen and Its Derivatives in Different Sectors Through Analysis of the Four Energy Scenarios: IEA-STEPS, IEA-NZE, IRENA-PES, and IRENA-1.5°C. Energies 2024, 17, 646. [Google Scholar] [CrossRef]
- Espegren, K.; Damman, S.; Pisciella, P.; Graabak, I.; Tomasgard, A. The role of hydrogen in the transition from a petroleum economy to a low-carbon society. Int. J. Hydrogen Energy 2021, 46, 23125–23138. [Google Scholar] [CrossRef]
- Marzouk, O.A. Portrait of the Decarbonization and Renewables Penetration in Oman’s Energy Mix, Motivated by Oman’s National Green Hydrogen Plan. Energies 2024, 17, 4769. [Google Scholar] [CrossRef]
- Marzouk, O.A. Evolution of the (Energy and Atmosphere) credit category in the LEED green buildings rating system for (Building Design and Construction: New Construction), from version 4.0 to version 4.1. J. Infrastruct. Policy Dev. 2024, 8, 5306. [Google Scholar] [CrossRef]
- Marzouk, O.A. Radiant Heat Transfer in Nitrogen-Free Combustion Environments. Int. J. Nonlinear Sci. Numer. Simul. 2018, 19, 175–188. [Google Scholar] [CrossRef]
- Frank, E.D.; Elgowainy, A.; Reddi, K.; Bafana, A. Life-cycle analysis of greenhouse gas emissions from hydrogen delivery: A cost-guided analysis. Int. J. Hydrogen Energy 2021, 46, 22670–22683. [Google Scholar] [CrossRef]
- Marzouk, O.A. Zero Carbon Ready Metrics for a Single-Family Home in the Sultanate of Oman Based on EDGE Certification System for Green Buildings. Sustainability 2023, 15, 13856. [Google Scholar] [CrossRef]
- Xie, T.; Wang, P. Analysis of NO formation in counter-flow premixed hydrogen-air flame. Trans. Can. Soc. Mech. Eng. 2013, 37, 851–859. [Google Scholar] [CrossRef]
- Marzouk, O.A. Tilt sensitivity for a scalable one-hectare photovoltaic power plant composed of parallel racks in Muscat. Cogent Eng. 2022, 9, 2029243. [Google Scholar] [CrossRef]
- Shaner, M.R.; Atwater, H.A.; Lewis, N.S.; McFarland, E.W. A comparative technoeconomic analysis of renewable hydrogen production using solar energy. Energy Environ. Sci. 2016, 9, 2354–2371. [Google Scholar] [CrossRef]
- Marzouk, O.A. Lookup Tables for Power Generation Performance of Photovoltaic Systems Covering 40 Geographic Locations (Wilayats) in the Sultanate of Oman, with and Without Solar Tracking, and General Perspectives About Solar Irradiation. Sustainability 2021, 13, 13209. [Google Scholar] [CrossRef]
- Mostafaeipour, A.; Khayyami, M.; Sedaghat, A.; Mohammadi, K.; Shamshirband, S.; Sehati, M.-A.; Gorakifard, E. Evaluating the wind energy potential for hydrogen production: A case study. Int. J. Hydrogen Energy 2016, 41, 6200–6210. [Google Scholar] [CrossRef]
- Marzouk, O.A. Wind Speed Weibull Model Identification in Oman, and Computed Normalized Annual Energy Production (NAEP) from Wind Turbines Based on Data from Weather Stations. Eng. Rep. 2025, 7, e70089. [Google Scholar] [CrossRef]
- Rezaei, M.; Naghdi-Khozani, N.; Jafari, N. Wind energy utilization for hydrogen production in an underdeveloped country: An economic investigation. Renew. Energy 2020, 147, 1044–1057. [Google Scholar] [CrossRef]
- Marzouk, O.A. Energy Generation Intensity (EGI) of Solar Updraft Tower (SUT) Power Plants Relative to CSP Plants and PV Power Plants Using the New Energy Simulator “Aladdin”. Energies 2024, 17, 405. [Google Scholar] [CrossRef]
- Marzouk, O.A. Summary of the 2023 (1st Edition) Report of TCEP (Tracking Clean Energy Progress) by the International Energy Agency (IEA), and Proposed Process for Computing a Single Aggregate Rating. E3S Web Conf. 2025, 601, 00048. [Google Scholar] [CrossRef]
- Beswick, R.R.; Oliveira, A.M.; Yan, Y. Does the Green Hydrogen Economy Have a Water Problem? ACS Energy Lett. 2021, 6, 3167–3169. [Google Scholar] [CrossRef]
- Marzouk, O.A. Chronologically-Ordered Quantitative Global Targets for the Energy-Emissions-Climate Nexus, from 2021 to 2050. In Proceedings of the 2022 International Conference on Environmental Science and Green Energy (ICESGE), Virtual, 25–27 November 2022; IEEE [Institute of Electrical and Electronics Engineers]: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Marzouk, O.A. Dataset of total emissivity for CO2, H2O, and H2O-CO2 mixtures; over a temperature range of 300–2900 K and a pressure-pathlength range of 0.01–50 atm.m. Data Brief. 2025, 59, 111428. [Google Scholar] [CrossRef] [PubMed]
- Marzouk, O.A. 2030 Ambitions for Hydrogen, Clean Hydrogen, and Green Hydrogen. Eng. Proc. 2023, 56, 14. [Google Scholar] [CrossRef]
- George Davies, W.; Babamohammadi, S.; Yang, Y.; Masoudi Soltani, S. The rise of the machines: A state-of-the-art technical review on process modelling and machine learning within hydrogen production with carbon capture. Gas. Sci. Eng. 2023, 118, 205104. [Google Scholar] [CrossRef]
- Riemer, M.; Duscha, V. Carbon capture in blue hydrogen production is not where it is supposed to be—Evaluating the gap between practical experience and literature estimates. Appl. Energy 2023, 349, 121622. [Google Scholar] [CrossRef]
- Marzouk, O.A. Hydrogen Utilization as a Plasma Source for Magnetohydrodynamic Direct Power Extraction (MHD-DPE). IEEE Access 2024, 12, 167088–167107. [Google Scholar] [CrossRef]
- Sigel, A.; Sigel, H.; Sigel, R.K.O. (Eds.) The Alkali Metal Ions: Their Role for Life; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Akitt, J.W. The Alkali and Alkaline Earth Metals. In Multinuclear NMR; Mason, J., Ed.; Springer: Boston, MA, USA, 1987; pp. 189–220. [Google Scholar] [CrossRef]
- Kennedy, J.J. The Alkali Metal Cesium and Some of Its Salts; ACS Publications: Washington, DC, USA, 2002. [Google Scholar] [CrossRef]
- Messerle, H.K. Magnetohydrodynamic Electrical Power Generation; Wiley: Chichester, UK, 1995. [Google Scholar]
- Angrist, S.W. Direct Energy Conversion, 4th ed.; Allyn and Bacon: Boston, MA, USA, 1982. [Google Scholar]
- Geri, A.; Salvini, A.; Veca, G.M. MHD linear generator modelling. IEEE Trans. Appl. Supercond. 1995, 5, 465–468. [Google Scholar] [CrossRef]
- Zauderer, B.; Tate, E. Electrical characteristics of a linear, nonequilibrium, MHD generator. Proc. IEEE 1968, 56, 1535–1547. [Google Scholar] [CrossRef][Green Version]
- Bünde, R.; Muntenbruch, H.; Raeder, J.; Volk, R.; Zankl, G. MHD Power Generation: Selected Problems of Combustion MHD Generators; Springer: Berlin/Heidelberg, Germany, 1975. [Google Scholar]
- Blackman, V.H.; Jones, M.S., Jr.; Demetriades, A. MHD power generation studies in rectangular channels. In 2nd Symposium on the Engineering Aspects of Magnetohydrodynamics (EAMHD-2); Columbia University Press: New York, NY, USA, 1961; pp. 180–210. [Google Scholar]
- Kayukawa, N. Open-cycle magnetohydrodynamic electrical power generation: A review and future perspectives. Prog. Energy Combust. Sci. 2004, 30, 33–60. [Google Scholar] [CrossRef]
- Marzouk, O.A. Condenser Pressure Influence on Ideal Steam Rankine Power Vapor Cycle Using the Python Extension Package Cantera for Thermodynamics. Eng. Technol. Appl. Sci. Res. 2024, 14, 14069–14078. [Google Scholar] [CrossRef]
- WAESD (Westinghouse Advanced Energy Systems Division). MHD Advanced Power Train; Westinghouse: Pittsburgh, PA, USA, 1985.
- Nimvari, M.E.; Hadidi, A.; Jafarian, A.; Garjasi, N. Analysis of triple combined cycle with MHD generator as a topping cycle. In Proceedings of the 3rd Conference on Thermal Power Plants, New Delhi, India, 18–19 October 2011; pp. 1–5. Available online: https://ieeexplore.ieee.org/abstract/document/6576978 (accessed on 31 March 2025).
- Nichols, L.D. Combined Turbine-Magnetohydrodynamic Brayton Cycle Power System for Space and Ground Use; NASA [United States National Aeronautics and Space Administration]: Cleveland, OH, USA, 1971. Available online: https://books.google.com.om/books?id=WiOTIe5zvBkC (accessed on 31 March 2025).
- Cicconardi, S.P.; Perna, A. Performance Analysis of Integrated Systems Based on MHD Generators. Energy Procedia 2014, 45, 1305–1314. [Google Scholar] [CrossRef]
- Khalili, S.; Jafarian Dehkordi, A.; Giahi, M.H. Investigating the effect of channel angle of a subsonic MHD (Magneto-Hydro-Dynamic) generator on optimum efficiency of a triple combined cycle. Energy 2015, 85, 543–555. [Google Scholar] [CrossRef]
- Esmaeilzadehazimi, M.A.; Manesh, M.H.K.; Heleyleh, B.B.; Modabbaer, H.V. 4E Analysis of Integrated MHD-Combined Cycle. Int. J. Thermodyn. 2019, 22, 219–228. [Google Scholar] [CrossRef]
- Murray, E.M. Time Fluctuations of Temperature in a Magnetohydrodynamic Plasma; Union Carbide Corporation, Nuclear Division: Oak Ridge, TN, USA, 1972. Available online: https://www.osti.gov/servlets/purl/4722548 (accessed on 4 April 2025).
- Park, B.-S.; Usman, M.; Imran, M.; Pesyridis, A. Review of Organic Rankine Cycle experimental data trends. Energy Convers. Manag. 2018, 173, 679–691. [Google Scholar] [CrossRef]
- Miao, Z.; Xu, J.; Yang, X.; Zou, J. Operation and performance of a low temperature organic Rankine cycle. Appl. Therm. Eng. 2015, 75, 1065–1075. [Google Scholar] [CrossRef]
- He, Z.; Zhang, Y.; Dong, S.; Ma, H.; Yu, X.; Zhang, Y.; Ma, X.; Deng, N.; Sheng, Y. Thermodynamic analysis of a low-temperature organic Rankine cycle power plant operating at off-design conditions. Appl. Therm. Eng. 2017, 113, 937–951. [Google Scholar] [CrossRef]
- Esmaeilzadehazimi, M.A.; Khoshgoftar Manesh, M.H.; Majidi, M.; Nourpour, M. Evaluation of a Novel Quadruple Combined Cycle with the Magnetohydrodynamic Generator Based on 6E Analysis. J. Energy Resour. Technol. 2021, 143, 1–28. [Google Scholar] [CrossRef]
- Marzouk, O.A. Adiabatic Flame Temperatures for Oxy-Methane, Oxy-Hydrogen, Air-Methane, and Air-Hydrogen Stoichiometric Combustion Using the NASA CEARUN Tool, GRI-Mech 3.0 Reaction Mechanism, and Cantera Python Package. Eng. Technol. Appl. Sci. Res. 2023, 13, 11437–11444. [Google Scholar] [CrossRef]
- Nabil, T.; Khairat Dawood, M.M. Enabling efficient use of oxy-hydrogen gas (HHO) in selected engineering applications; transportation and sustainable power generation. J. Clean. Prod. 2019, 237, 117798. [Google Scholar] [CrossRef]
- Paparao, J.; Murugan, S. Oxy-hydrogen gas as an alternative fuel for heat and power generation applications—A review. Int. J. Hydrogen Energy 2021, 46, 37705–37735. [Google Scholar] [CrossRef]
- NCBI [National Center for Biotechnology Information] PubChem. Compound Summary for CID 11430, Potassium Carbonate. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/11430 (accessed on 31 March 2025).
- Dixit, N.S.; Venkatramani, N.; Rohatgi, V.K. Measurement of temperature, electrical conductivity and ion density of seeded combustion plasmas. Energy Convers. Manag. 1987, 27, 103–109. [Google Scholar] [CrossRef]
- Avdeev, K.A.; Aksenov, V.S.; Ivanov, V.S.; Medvedev, S.N.; Frolov, S.M.; Frolov, F.S.; Shamshin, I.O. Magnetohydrodynamic effects of heterogeneous spray detonation. Russ. J. Phys. Chem. B 2015, 9, 637–643. [Google Scholar] [CrossRef]
- Lee, K.-T.; Gabriela, S.; Chen, W.-H.; Ong, H.C.; Rajendran, S.; Tran, K.-Q. Co-torrefaction and synergistic effect of spent coffee grounds and tea waste for sustainable waste remediation and renewable energy. Renew. Energy 2024, 233, 121181. [Google Scholar] [CrossRef]
- Tepper, F.; Murchison, A.; Zelenak, J. Thermophysical Properties of Rubidium and Cesium. In Proceedings of the USAF Aerospace Fluids and Lubricants Conference, San Antonio, TX, USA, 16–19 April 1963; Adamczak, R.L., Ed.; Defense Documentation Center for Scientific and Technical Information: Dayton, OH, USA, 1964; pp. 368–387. Available online: https://books.google.com.om/books?id=UWRUAAAAYAAJ (accessed on 31 March 2025).
- Liao, Q.; Tan, Z. Numerical investigations of cold gas dynamic spray with a novel convergent-divergent nozzle. AIP Conf. Proc. 2013, 1558, 2333–2336. [Google Scholar] [CrossRef]
- Marzouk, O.A. The Sod gasdynamics problem as a tool for benchmarking face flux construction in the finite volume method. Sci. Afr. 2020, 10, e00573. [Google Scholar] [CrossRef]
- Deshpande, O.N.; Narappanawar, N. Space optimization through the use of de-laval nozzle and bell nozzle and its theory. In IAENG Transactions on Engineering Sciences; World Scientific: Singapore, 2016; pp. 432–445. [Google Scholar] [CrossRef]
- Kanhukamwe, T.N.; Zincume, P.N. Global Landscape of Photovoltaic Module Manufacturing: A Systematic Literature Review. In Proceedings of the 2024 IEEE International Conference on Engineering, Technology, and Innovation (ICE/ITMC), Madeira Island, Portugal, 24–28 June 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Marzouk, O.A. Facilitating Digital Analysis and Exploration in Solar Energy Science and Technology Through Free Computer Applications. Eng. Proc. 2022, 31, 75. [Google Scholar] [CrossRef]
- Marzouk, O.A. Thermoelectric generators versus photovoltaic solar panels: Power and cost analysis. Edelweiss Appl. Sci. Technol. 2024, 8, 406–428. [Google Scholar] [CrossRef]
- Li, G.; Fan, Y.; Li, Q.; Zheng, Y.; Zhao, D.; Wang, S.; Dong, S.; Guo, W.; Tang, Y. A review on micro combustion powered thermoelectric generator: History, state-of-the-art and challenges to commercialization. Renew. Sustain. Energy Rev. 2025, 207, 114897. [Google Scholar] [CrossRef]
- Chundawat, J.S.; Kumar, A.; Saini, M. Applications of institutionstic and dual hesitant fuzzy numbers in the reliability evaluation of turbogenerators in thermal power plants. Int. J. Inf. Technol. 2025, 1–9. [Google Scholar] [CrossRef]
- Marzouk, O.A. Energy Generation Intensity (EGI) for Parabolic Dish/Engine Concentrated Solar Power in Muscat, Sultanate of Oman. IOP Conf. Ser. Earth Environ. Sci. 2022, 1008, 012013. [Google Scholar] [CrossRef]
- Marzouk, O.A.; Nayfeh, A.H. A Study of the Forces on an Oscillating Cylinder. In Proceedings of the ASME 2007 26th International Conference on Offshore Mechanics and Arctic Engineering (OMAE 2007), San Diego, CA, USA, 10–15 June 2007; ASME [American Society of Mechanical Engineers]: San Diego, CA, USA, 2009; pp. 741–752. [Google Scholar] [CrossRef]
- Marzouk, O.A. One-way and two-way couplings of CFD and structural models and application to the wake-body interaction. Appl. Math. Model. 2011, 35, 1036–1053. [Google Scholar] [CrossRef]
- Panchenko, V.P. Preliminary Analysis of the “Sakhalin” World Largest Pulsed MHD Generator. In Proceedings of the 33rd Plasmadynamics and Lasers Conference, Maui, HI, USA, 20–23 May 2002; AIAA [American Institute of Aeronautics and Astronautics]: Maui, HI, USA, 2002; p. 2147. [Google Scholar] [CrossRef]
- Panchenko, V.P. 55. Preliminary analysis of the “Sakhalin” world largest pulsed MHD generator. In Proceedings of the 4th Workshop on Magnetoplasma Aerodynamics for Aerospace Applications, Moscow, Russia, 20–23 May 2002; pp. 322–331. [Google Scholar]
- Velikhov, E.P.; Pismenny, V.D.; Matveenko, O.G.; Panchenko, V.P.; Yakushev, A.A.; Pisakin, A.V.; Blokh, A.G.; Tkachenko, B.G.; Sergienko, N.M.; Zhukov, B.B.; et al. Pulsed MHD power system “Sakhalin”—The world largest solid propellant fueled MHD generator of 500MWe electric power output. In Proceedings of the 13th International Conference on MHD Electrical Power Generation and High Temperature Technologies, Beijing, China, 12–15 October 1999; pp. 387–398. [Google Scholar]
- Veefkind, A.; Houben, J.W.M.A.; Blom, J.H.; Rietjens, L.H.T. High-power density experiments in a shock-tunnel MHD generator. AIAA J. 1976, 14, 1118–1122. [Google Scholar] [CrossRef]
- Kirkpatrick, A.T. Energy Flows in Engines. Available online: https://www.engr.colostate.edu/~allan/heat_trans/page3/page3.html (accessed on 31 March 2025).
- Hiereth, H.; Prenninger, P. Charging the Internal Combustion Engine; Springer Science & Business Media: Vienna, Austria, 2007. [Google Scholar]
- Chen, H.; Lee, C.H.T. Parametric Sensitivity Analysis and Design Optimization of an Interior Permanent Magnet Synchronous Motor. IEEE Access 2019, 7, 159918–159929. [Google Scholar] [CrossRef]
- Li, J.; Cheng, L.; Wan, N.; Ma, J.; Hu, Y.; Wen, J. Hybrid harvesting of wind and wave energy based on triboelectric-piezoelectric nanogenerators. Sustain. Energy Technol. Assess. 2023, 60, 103466. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, S.; Wang, X.; Huang, X.; Logan, B.E. Separator Characteristics for Increasing Performance of Microbial Fuel Cells. Environ. Sci. Technol. 2009, 43, 8456–8461. [Google Scholar] [CrossRef]
- Kong, X.; Sun, Y.; Li, L.; Li, Y.; Yuan, Z.; Kong, X. Electricity Generation Comparison of Two-Chamber Microbial Fuel Cells with Different Membranes. In Proceedings of the 2010 4th International Conference on Bioinformatics and Biomedical Engineering, Chengdu, China, 18–20 June 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Karra, U.; Manickam, S.S.; McCutcheon, J.R.; Patel, N.; Li, B. Power generation and organics removal from wastewater using activated carbon nanofiber (ACNF) microbial fuel cells (MFCs). Int. J. Hydrogen Energy 2013, 38, 1588–1597. [Google Scholar] [CrossRef]
- Borghi, C.A.; Massarini, A.; Mazzanti, G. Multidimensional models for the analysis of linear MHD generator channel plasma flows. IEEE Trans. Plasma Sci. 1992, 20, 473–476. [Google Scholar] [CrossRef]
- Xue, W.; Miao, L.; Qie, L.; Wang, C.; Li, S.; Wang, J.; Li, J. Gravimetric and volumetric energy densities of lithium-sulfur batteries. Curr. Opin. Electrochem. 2017, 6, 92–99. [Google Scholar] [CrossRef]
- Zhai, T.; Lu, X.; Wang, H.; Wang, G.; Mathis, T.; Liu, T.; Li, C.; Tong, Y.; Li, Y. An Electrochemical Capacitor with Applicable Energy Density of 7.4 Wh/kg at Average Power Density of 3000 W/kg. Nano Lett. 2015, 15, 3189–3194. [Google Scholar] [CrossRef]
- Janovec, M.; Babčan, V.; Kandera, B.; Šajbanová, K.; Škultéty, F.; Halvoň, Ľ. Performance and Weight Parameters Calculation for Hydrogen- and Battery-Powered Aircraft Concepts. Aerospace 2023, 10, 482. [Google Scholar] [CrossRef]
- Blinov, V.N.; Vavilov, I.S.; Kositsin, V.V.; Lukyanchik, A.I.; Ruban, V.I.; Shalay, V.V. Study of power-to-weight ratio of the electrothermal propulsion system of nanosatellite maneuvering satellite platform. J. Phys. Conf. Ser. 2018, 944, 012020. [Google Scholar] [CrossRef]
- Marzouk, O.A. Aerial e-mobility perspective: Anticipated designs and operational capabilities of eVTOL urban air mobility (UAM) aircraft. Edelweiss Appl. Sci. Technol. 2025, 9, 413–442. [Google Scholar] [CrossRef]
- Ma, Y.; Karpuk, S.; Elham, A. Conceptual design and comparative study of strut-braced wing and twin-fuselage aircraft configurations with ultra-high aspect ratio wings. Aerosp. Sci. Technol. 2022, 121, 107395. [Google Scholar] [CrossRef]
- Cinar, G.; Cai, Y.; Chakraborty, I.; Mavris, D.N. Sizing and Optimization of Novel General Aviation Vehicles and Propulsion System Architectures. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018; AIAA [American Institute of Aeronautics and Astronautics]: Atlanta, GA, USA, 2018; p. 3974. [Google Scholar] [CrossRef]
- Mikhaylik, Y.; Kovalev, I.; Xu, J.; Schock, R. Rechargeable Li2S Battery with Specific Energy 350 Wh/kg and Specific Power 3000 W/kg. ECS Trans. 2008, 13, 53. [Google Scholar] [CrossRef]
- Yang, Y.; McDowell, M.T.; Jackson, A.; Cha, J.J.; Hong, S.S.; Cui, Y. New Nanostructured Li2S/Silicon Rechargeable Battery with High Specific Energy. Nano Lett. 2010, 10, 1486–1491. [Google Scholar] [CrossRef]
- Son, Y.; Cha, H.; Jo, C.; Groombridge, A.S.; Lee, T.; Boies, A.; Cho, J.; De Volder, M. Reliable protocols for calculating the specific energy and energy density of Li-Ion batteries. Mater. Today Energy 2021, 21, 100838. [Google Scholar] [CrossRef]
- Park, J.O.; Kim, M.; Kim, J.-H.; Choi, K.H.; Lee, H.C.; Choi, W.; Ma, S.B.; Im, D. A 1000 Wh kg−1 Li–Air battery: Cell design and performance. J. Power Sources 2019, 419, 112–118. [Google Scholar] [CrossRef]
- Seikel, G.R. Coal-Fired Open-Cycle MHD Plants. In The Science and Technology of Coal and Coal Utilization; Cooper, B.R., Ellingson, W.A., Eds.; Springer: Boston, MA, USA, 1984; pp. 307–337. [Google Scholar] [CrossRef]
- Ishikawa, M.; Fujita, M.; Fujita, Y.; Umoto, J. Performance of coal-fired MHD generators with large leakage current. Energy Convers. Manag. 1993, 34, 607–617. [Google Scholar] [CrossRef]
- Marzouk, O.A. Jatropha curcas as Marginal Land Development Crop in the Sultanate of Oman for Producing Biodiesel, Biogas, Biobriquettes, Animal Feed, and Organic Fertilizer. Rev. Agric. Sci. 2020, 8, 109–123. [Google Scholar] [CrossRef]
- Ishikawa, M.; Kyogoku, A.; Umoto, J. Stability of large-scale MHD channels designed for coal-fired MHD power generation. Energy Convers. Manag. 1996, 37, 31–41. [Google Scholar] [CrossRef]
- Marzouk, O.A.; Nayfeh, A.H. Characterization of the flow over a cylinder moving harmonically in the cross-flow direction. Int. J. Non-Linear Mech. 2010, 45, 821–833. [Google Scholar] [CrossRef]
- Sugita, H.; Matsuo, T.; Inui, Y.; Ishikawa, M. Two-dimensional behavior of gas-particle two-phase flow under strong MHD interaction. In Proceedings of the 13th International Conference on MHD Electrical Power Generation and High Temperature Technologies, Beijing, China, 12–15 October 1999; pp. 453–462. [Google Scholar]
- Marzouk, O.A. Direct Numerical Simulations of the Flow Past a Cylinder Moving with Sinusoidal and Nonsinusoidal Profiles. J. Fluids Eng. 2009, 131, 121201. [Google Scholar] [CrossRef]
- Matsuo, T.; Sugita, H.; Ishikawa, M.; Zeigarnik, V.A. Boundary-layer separation and generator performance of self-excited pulsed MHD channel with strong MHD interaction. In Proceedings of the 13th International Conference on MHD Electrical Power Generation and High Temperature Technologies, Beijing, China, 12–15 October 1999; pp. 399–408. [Google Scholar]
- Marzouk, O.A. Contrasting the Cartesian and polar forms of the shedding-induced force vector in response to 12 subharmonic and superharmonic mechanical excitations. Fluid. Dyn. Res. 2010, 42, 035507. [Google Scholar] [CrossRef]
- Marzouk, O.A.; Nayfeh, A.H. Loads on a Harmonically Oscillating Cylinder. In Proceedings of the ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (IDETC-CIE 2007), Las Vegas, NV, USA, 4–7 September 2007; ASME [American Society of Mechanical Engineers]: Las Vegas, NV, USA, 2009; pp. 1755–1774. [Google Scholar] [CrossRef]
- Marzouk, O.A.; Huckaby, E.D. Simulation of a Swirling Gas-Particle Flow Using Different k-Epsilon Models and Particle-Parcel Relationships. Eng. Lett. 2010, 18, 7. [Google Scholar] [CrossRef]
- Sugita, H.; Matsuo, T.; Inui, Y.; Ishikawa, M. Two-dimensional analysis of gas-particle two phase flow in pulsed MHD channel. In Proceedings of the 30th Plasmadynamic and Lasers Conference, Norfolk, VA, USA, 1–28 June 1999; American Institute of Aeronautics and Astronautics: Norfolk, VA, USA, 1999; p. 3483. [Google Scholar] [CrossRef]
- Marzouk, O.A. Flow control using bifrequency motion. Theor. Comput. Fluid. Dyn. 2011, 25, 381–405. [Google Scholar] [CrossRef]
- Hardianto, T.; Sakamoto, N.; Harada, N. Three-Dimensional Flow Analysis in a Faraday-Type MHD Generator. IEEE Trans. Ind. Appl. 2008, 44, 1116–1123. [Google Scholar] [CrossRef]
- Marzouk, O.A.; Nayfeh, A.H. Reduction of the loads on a cylinder undergoing harmonic in-line motion. Phys. Fluids 2009, 21, 083103. [Google Scholar] [CrossRef]
- Hynes, A.J.; Steinberg, M.; Schofield, K. The chemical kinetics and thermodynamics of sodium species in oxygen-rich hydrogen flames. J. Chem. Phys. 1984, 80, 2585–2597. [Google Scholar] [CrossRef]
- Marzouk, O.A. Technical review of radiative-property modeling approaches for gray and nongray radiation, and a recommended optimized WSGGM for CO2/H2O-enriched gases. Results Eng. 2025, 25, 103923. [Google Scholar] [CrossRef]
- Cheng, T.S.; Chao, Y.-C.; Wu, C.-Y.; Li, Y.-H.; Nakamura, Y.; Lee, K.-Y.; Yuan, T.; Leu, T.S. Experimental and numerical investigation of microscale hydrogen diffusion flames. Proc. Combust. Inst. 2005, 30, 2489–2497. [Google Scholar] [CrossRef]
- Aoyagi, M.; Ito, S.; Hashizume, H.; Muroga, T. MHD pressure drop characteristics in a three-surface-multi-layered channel under a strong magnetic field. Fusion. Eng. Des. 2010, 85, 1181–1184. [Google Scholar] [CrossRef]
- Huang, X.; Cao, Y.; Li, J.; Yi, W.; Qu, Y. Enhanced reversible magnetocaloric effect in Ni-Co-Mn-Sb-based magnetic shape memory alloy achieved by Ti substitution for Ni. J. Alloys Compd. 2025, 1010, 178112. [Google Scholar] [CrossRef]
- Hurley, M.E.; Bollineni, R.K.; Donald, A.M.; Flynn, S.; Hamlin, J.J.; Kesler, M.S.; Manuel, M.V.; Meisel, M.W.; Li, L.; Miller, V.M. Microstructural Evolution of Steel During Magnetic Field-Assisted Processing. JOM 2025, 77, 2862–2874. [Google Scholar] [CrossRef]
- Bityurin, V.A.; Borghi, C.A.; Ribani, P.L. High enthalpy extraction numerical experiment in a plasma vane MHD generator. IEEE Trans. Plasma Sci. 1995, 23, 844–851. [Google Scholar] [CrossRef]
- Ishikwa, M.; Yuhara, M.; Fujino, T. Three-dimensional computation of magnetohydrodynamics in a weakly ionized plasma with strong MHD interaction. J. Mater. Process. Technol. 2007, 181, 254–259. [Google Scholar] [CrossRef]
- Ishikawa, M.; Koshiba, Y.; Matsushita, T. Effects of induced magnetic field on large scale pulsed MHD generator with two phase flow. Energy Convers. Manag. 2004, 45, 707–724. [Google Scholar] [CrossRef]
- Ishikawa, M.; Koshiba, Y. 52. Preliminary analysis of large pulsed MHD generator. In Proceedings of the 3th Workshop on Magnetoplasma Aerodynamics for Aerospace Applications, Moscow, Russia, 24–26 April 2001; pp. 276–281. Available online: https://apps.dtic.mil/sti/pdfs/ADA407842.pdf (accessed on 8 February 2025).
- Marzouk, O.A. Detailed and simplified plasma models in combined-cycle magnetohydrodynamic power systems. Int. J. Adv. Appl. Sci. 2023, 10, 96–108. [Google Scholar] [CrossRef]
- Hustad, C.-W.; Coleman, D.L.; Mikus, T. Technology Overview for Integration of an MHD Topping Cycle with the CES Oxyfuel Combustor; CO2-Global. 2009. Available online: https://co2.no/wp-content/uploads/2020/07/MHD_Report-Final.pdf (accessed on 12 June 2011).
- Marzouk, O.A. Evolutionary Computing Applied to Design Optimization. In Proceedings of the ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (IDETC-CIE 2007), Las Vegas, NV, USA, 4–7 September 2007; ASME [American Society of Mechanical Engineers]: Las Vegas, NV, USA, 2009; pp. 995–1003. [Google Scholar] [CrossRef]
- Miller, E.K. Exploring the behavior of a matched load in the time domain. IEEE Antennas Propag. Mag. 2014, 56, 103–111. [Google Scholar] [CrossRef]
- McCune, J. Non-Linear Effects of Fluctuations on MHD Performance. In Proceedings of the 6th Symposium on Engineering Aspects of Magnetohydrodynamics, Pittsburgh, PA, USA, 21–22 April 1965; AIAA [American Institute of Aeronautics and Astronautics]: Pittsburgh, PA, USA, 1965; pp. 89–103. [Google Scholar] [CrossRef]
- Marzouk, O.A. Coupled differential-algebraic equations framework for modeling six-degree-of-freedom flight dynamics of asymmetric fixed-wing aircraft. Int. J. Appl. Adv. Sci. 2025, 12, 30–51. [Google Scholar] [CrossRef]
- Marzouk, O.A. Estimated electric conductivities of thermal plasma for air-fuel combustion and oxy-fuel combustion with potassium or cesium seeding. Heliyon 2024, 10, e31697. [Google Scholar] [CrossRef]
- Frost, L.S. Conductivity of Seeded Atmospheric Pressure Plasmas. J. Appl. Phys. 1961, 32, 2029–2036. [Google Scholar] [CrossRef]
- Raeder, J. Chapter 2—Theory. In MHD Power Generation—Selected Problems of Combustion MHD Generators; Springer: Berlin/Heidelberg, Germany, 1975; pp. 5–85. [Google Scholar]
- Khomkin, A.L.; Shumikhin, A.S. Equation of state and conductivity of aluminum dense vapor plasma. In Proceedings of the 35th EPS Conference on Plasma Physics (2008-Europhysics), Crete, Greece, 9–13 June 2008; pp. 720–723. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=624078677a5a7acac621fa9651ac08e77a1839b9 (accessed on 31 March 2025).
- Ebeling, W.; Fortov, V.E.; Klimontovich, Y.L.; Kovalenko, N.P.; Kraeft, W.D.; Krasny, Y.P.; Kremp, D.; Kulik, P.P.; Riaby, V.A.; Röpke, G.; et al. Transport Properties of Dense Plasmas; Springer: Basel, Switzerland, 2013; Available online: https://books.google.com.om/books?id=xUigBgAAQBAJ (accessed on 31 March 2025).
- Marzouk, O.A. Characteristics of the Flow-Induced Vibration and Forces with 1- and 2-DOF Vibrations and Limiting Solid-to-Fluid Density Ratios. J. Vib. Acoust. 2010, 132, 041013. [Google Scholar] [CrossRef]
- Gavioso, R.M. Determination of the universal gas constant R and other metrological applications of speed of sound measurements. In Recent Advances in Metrology and Fundamental Constants; IOS Press: Amsterdam, Netherlands, 2001; pp. 195–215. [Google Scholar] [CrossRef]
- Marzouk, O.A. Assessment of Three Databases for the NASA Seven-Coefficient Polynomial Fits for Calculating Thermodynamic Properties of Individual Species. Int. J. Aeronaut. Sci. Aerosp. Res. 2018, 5, 150–163. [Google Scholar] [CrossRef]
- Šafarík, P.; Nový, A.; Jícha, D.; Hajšman, M. On the Speed of Sound in Steam. Acta Polytech. 2015, 55, 422–426. [Google Scholar] [CrossRef]
- McBride, B.J.; Zehe, M.J.; Gordon, S. NASA Glenn Coefficients for Calculating Thermodynamic Properties of Individual Species; NASA [United States National Aeronautics and Space Administration]: Cleveland, OH, USA, 2002. Available online: https://ntrs.nasa.gov/api/citations/20020085330/downloads/20020085330.pdf (accessed on 11 October 2011).
- Smirnov, V.N. Calculation of strong-collision dissociation rate constants from NASA thermodynamic polynomials. Int. J. Chem. Kinet. 2020, 52, 559–579. [Google Scholar] [CrossRef]
- Oliva, A.A.; Jemcov, A. Method for Efficient Evaluation of Temperature Using the NASA Polynomials. AIAA J. 2024, 62, 405–408. [Google Scholar] [CrossRef]
- Euclides, H.O.; Barreto, P.R.P. APUAMA: A software tool for reaction rate calculations. J. Mol. Model. 2017, 23, 176. [Google Scholar] [CrossRef]
- Laney, C.B. Computational Gasdynamics, 1st ed.; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar] [CrossRef]
- NIST [United States National Institute of Standards and Technology]; CODATA [Committee on Data for Science and Technology]. Value: Molar Gas Constant. Available online: https://physics.nist.gov/cgi-bin/cuu/Value?r (accessed on 7 May 2022).
- Akasaka, R.; Huber, M.L.; Simoni, L.D.; Lemmon, E.W. A Helmholtz Energy Equation of State for trans-1,1,1,4,4,4-Hexafluoro-2-butene [R-1336mzz(E)] and an Auxiliary Extended Corresponding States Model for the Transport Properties. Int. J. Thermophys. 2023, 44, 50. [Google Scholar] [CrossRef]
- Bespyatov, M.A. Low-Temperature Heat Capacity and Thermodynamic Functions of Europium(III) Heptafluorodimethyloctanedionate. J. Chem. Eng. Data 2023, 68, 3222–3227. [Google Scholar] [CrossRef]
- Linstrom, P.J.; Mallard, W.G. The NIST Chemistry WebBook: A Chemical Data Resource on the Internet. J. Chem. Eng. Data 2001, 46, 1059–1063. [Google Scholar] [CrossRef]
- MacMillan, D. NIST Data Gateway. Ref. Rev. 2012, 26, 43–44. [Google Scholar] [CrossRef]
- Engel, T.; Gasteiger, J. Chemoinformatics: Basic Concepts and Methods; John Wiley & Sons: Weinheim, Germany, 2018; Available online: https://books.google.com.om/books?id=X7paDwAAQBAJ (accessed on 31 March 2025).
- Chan, B. High-Level Quantum Chemistry Reference Heats of Formation for a Large Set of C, H, N, and O Species in the NIST Chemistry Webbook and the Identification and Validation of Reliable Protocols for Their Rapid Computation. J. Phys. Chem. A 2022, 126, 4981–4990. [Google Scholar] [CrossRef] [PubMed]
- NIST [United States National Institute of Standards and Technology]. NIST Chemistry WebBook—Water. 2023. Available online: https://webbook.nist.gov/cgi/cbook.cgi?Name=h2o (accessed on 15 August 2023).
- NIST [United States National Institute of Standards and Technology]. NIST Chemistry WebBook—Nitrogen. 2022. Available online: https://webbook.nist.gov/cgi/cbook.cgi?Name=n2 (accessed on 7 May 2022).
- NIST [United States National Institute of Standards and Technology]. NIST Chemistry WebBook—Cesium. 2023. Available online: https://webbook.nist.gov/cgi/cbook.cgi?Name=cesium (accessed on 15 August 2023).
- NIST [United States National Institute of Standards and Technology]. NIST Chemistry WebBook—Potassium. 2025. Available online: https://webbook.nist.gov/cgi/cbook.cgi?Name=potassium (accessed on 31 March 2025).
- Kuo, K.K. Principles of Combustion, 2nd ed.; John Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion, 2nd ed.; Edwards: Spring Hope, NC, USA, 2005. [Google Scholar]
- Ram, N.K.; Singh, N.R.; Raman, P.; Kumar, A.; Kaushal, P. A detailed experimental analysis of air–steam gasification in a dual fired downdraft biomass gasifier enabling hydrogen enrichment in the producer gas. Energy 2019, 187, 115937. [Google Scholar] [CrossRef]
- Taniguchi, T.; Kawamura, K.; Sakamoto, S.; Tagashira, H. Three-body attachment in oxygen and an air-like nitrogen and oxygen mixture. J. Phys. Appl. Phys. 1982, 15, 1187. [Google Scholar] [CrossRef]
- Elyamani, M.A. The Role of Oxygen-Enriched Air in Sustainable Hydrogen Production and Combustion Performance in Fired Heaters. In Proceedings of the Mediterranean Offshore Conference, Alexandria, Egypt, 20–22 October 2024; OnePetro: Alexandria, Egypt, 2024. [Google Scholar] [CrossRef]
- Mariani, M. Post-combustion CO2: Separation And Stocking. WIT Trans. Ecol. Environ. 2006, 86, 785–791. [Google Scholar]
- Lu, X.; Hu, E.; Li, X.; Ku, J.; Huang, Z. Non-monotonic behaviors of laminar burning velocities of H2/O2/He mixtures at elevated pressures and temperatures. Int. J. Hydrogen Energy 2017, 42, 22036–22045. [Google Scholar] [CrossRef]
- Cooper, C.D.; Naff, W.T.; Compton, R.N. Negative ion properties of p-benzoquinone: Electron affinity and compound states. J. Chem. Phys. 1975, 63, 2752–2757. [Google Scholar] [CrossRef]
- NCBI [National Center for Biotechnology Information] PubChem. Ionization Energy in the Periodic Table of Elements. Available online: https://pubchem.ncbi.nlm.nih.gov/periodic-table/ionization-energy (accessed on 2 April 2025).
- Compton, R.N.; Cooper, C.D. Molecular electron affinities from collisional ionization of cesium. II. SF6 and TeF6. J. Chem. Phys. 1973, 59, 4140–4144. [Google Scholar] [CrossRef]
- Softusvista Unitsconverters. eV/Particle to KJ/mol (Electron Volt Per Particle to KiloJoule Per Mole). Available online: https://www.unitsconverters.com/ru/D-%D0%9A-Millenium/Utu-97-7744 (accessed on 4 April 2025).
- Nizzi, K.E.; Pommerening, C.A.; Sunderlin, L.S. Gas-Phase Thermochemistry of Polyhalide Anions. J. Phys. Chem. A 1998, 102, 7674–7679. [Google Scholar] [CrossRef]
- Gibb, T.C. Principles of Mössbauer Spectroscopy; Science Paperbacks: New York, NY, USA, 1976; Available online: https://books.google.com.om/books?id=6vjtCAAAQBAJ (accessed on 4 April 2025).
- Civiš, S.; Ferus, M.; Kubelík, P.; Jelinek, P.; Chernov, V.E. Potassium spectra in the 700–7000 cm−1 domain: Transitions involving f-, g-, and h-states. Astron. Astrophys. 2012, 541, A125. [Google Scholar] [CrossRef][Green Version]
- Kotarba, A.; Adamski, G.; Sojka, Z.; Djega-Mariadassou, G. Potassium surface stability and electronic promotion in K-NbN0.9O0.1 catalysts. Appl. Surf. Sci. 2000, 161, 105–108. [Google Scholar] [CrossRef]
- Schmidt, L.; Gomer, R. Adsorption of Potassium on Tungsten. J. Chem. Phys. 1965, 42, 3573–3598. [Google Scholar] [CrossRef]
- Englert, B.-G. Statistical Atom: Ionization Energies. Z. Für Naturforschung A 1987, 42, 825–834. [Google Scholar] [CrossRef]
- Crawford, J.R.; Kunz, P.; Yang, H.; Schaffer, P.; Ruth, T.J. e211Rn/e211At and e209At production with intense mass separated Fr ion beams for preclinical 211At-based α-therapy research. Appl. Radiat. Isot. 2017, 122, 222–228. [Google Scholar] [CrossRef]
- RSC [Royal Society of Chemistry]. Francium—Element Information, Properties and Uses. Available online: https://periodic-table.rsc.org/element/87/francium (accessed on 2 April 2025).
- NCBI [National Center for Biotechnology Information] PubChem. Francium (Fr). Available online: https://pubchem.ncbi.nlm.nih.gov/element/87 (accessed on 2 April 2025).
- Venetskii, S. Francium. Metallurgist 1978, 22, 61–65. [Google Scholar] [CrossRef]
- Pocsai, M.A.; Barna, I.F.; Tökési, K. Photoionisation of rubidium in strong laser fields. Eur. Phys. J. D 2019, 73, 74. [Google Scholar] [CrossRef]
- Roman, V.; Kupliauskienė, A.; Borovik, A. Excitation and ionization of outer shells in Rb by electron impact. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 205204. [Google Scholar] [CrossRef]
- RSC [Royal Society of Chemistry]. Rubidium—Element Information, Properties and Uses. Available online: https://periodic-table.rsc.org/element/37/Rubidium (accessed on 2 April 2025).
- Xing, P.; Wang, C.; Chen, Y.; Ma, B. Rubidium extraction from mineral and brine resources: A review. Hydrometallurgy 2021, 203, 105644. [Google Scholar] [CrossRef]
- Sharma, S.K.; Truong, D.Q.; Guo, J.; An, A.K.; Naidu, G.; Deka, B.J. Recovery of rubidium from brine sources utilizing diverse separation technologies. Desalination 2023, 556, 116578. [Google Scholar] [CrossRef]
- Mackay, K.K.; Freund, J.B.; Johnson, H.T. Enhancement of hydrogen microcombustion via field-emission dielectric barrier discharge. Plasma Sources Sci. Technol. 2018, 27, 085007. [Google Scholar] [CrossRef]
- Choi, K.C.; Kim, S.H.; Shin, B.J.; Kang, J.; Choi, K.-Y.; Yoo, E.-H. Effects of Kr,hboxN2, and Ar on Address Discharge Time Lag in AC Plasma-Display Panel with High Xenon Content. IEEE Trans. Electron. Devices 2006, 53, 2410–2413. [Google Scholar] [CrossRef]
- Mohandas, S.; Ramabhadran, R.O.; Kumar, S.S. Theoretical Investigation of a Vital Step in the Gas-Phase Formation of Interstellar Ammonia NH2+ + H2 → NH3+ + H. J. Phys. Chem. A 2020, 124, 8373–8382. [Google Scholar] [CrossRef] [PubMed]
- Pia, M.G.; Seo, H.; Batic, M.; Begalli, M.; Kim, C.H.; Quintieri, L.; Saracco, P. Evaluation of Atomic Electron Binding Energies for Monte Carlo Particle Transport. IEEE Trans. Nucl. Sci. 2011, 58, 3246–3268. [Google Scholar] [CrossRef]
- Wiles, D.M. The Reactions of Active Nitrogen with Phosphine and Hydrogen Chloride. Ph.D. Thesis, Department of Chemistry, McGill University, Montreal, QC, Canada, 1957. Available online: https://escholarship.mcgill.ca/concern/theses/qr46r4819 (accessed on 4 April 2025).
- Mitra, S.K. Atomic Nitrogen in Auroras. Nature 1951, 167, 897. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Kołaski, M.; Lee, H.M.; Kim, K.S. Photoexcitation and Photoionization Dynamics of Water Photolysis. J. Phys. Chem. A 2008, 112, 5502–5508. [Google Scholar] [CrossRef]
- Misaizu, F.; Sanekata, M.; Tsukamoto, K.; Fuke, K.; Iwata, S. Photodissociation of size-selected aquamagnesium (Mg+(H2O)n) ions for n = 1 and 2. J. Phys. Chem. 1992, 96, 8259–8264. [Google Scholar] [CrossRef]
- Wang, C.; Liu, M.; Li, B.; Liu, Y.; Yan, J. Thermodynamic analysis on the transient cycling of coal-fired power plants: Simulation study of a 660 MW supercritical unit. Energy 2017, 122, 505–527. [Google Scholar] [CrossRef]
- Boonnasa, S.; Namprakai, P. Sensitivity analysis for the capacity improvement of a combined cycle power plant (100–600 MW). Appl. Therm. Eng. 2008, 28, 1865–1874. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, G.; Li, B.; Liu, M.; Liu, J. Simulation study on 660 MW coal-fired power plant coupled with a steam ejector to ensure NOx reduction ability. Appl. Therm. Eng. 2017, 111, 550–561. [Google Scholar] [CrossRef]
- Mason, J.E.; Archer, C.L. Baseload electricity from wind via compressed air energy storage (CAES). Renew. Sustain. Energy Rev. 2012, 16, 1099–1109. [Google Scholar] [CrossRef]
- Massarini, A.; Borghi, C.A. Time-dependent quasi-one-dimensional flow models for linear magnetohydrodynamic generator channels. Phys. Fluids B Plasma Phys. 1992, 4, 2823–2829. [Google Scholar] [CrossRef]
- Borghi, C.A.; Cristofolini, A.; Ribani, P.L. Analysis of magneto-plasma dynamic transients in a combustion gas magnetohydrodynamic generator. Phys. Plasmas 1997, 4, 3082–3090. [Google Scholar] [CrossRef]
- Cristofolini, A.; Borghi, C.A. A difference method for the solution of the electrodynamic problem in a magnetohydrodynamic field. IEEE Trans. Magn. 1995, 31, 1749–1752. [Google Scholar] [CrossRef]
- Borghi, C.A.; Massarini, A.; Mazzanti, G.; Ribani, P.L. Steady State Descriptions of MHD Plasma Flows; International Academic Publishers: Lausanne, Switzerland, 1992; pp. 770–775. [Google Scholar]
- Wang, X.; Barnett, A. The Evolving Value of Photovoltaic Module Efficiency. Appl. Sci. 2019, 9, 1227. [Google Scholar] [CrossRef]
- Marzouk, O.A. Land-Use competitiveness of photovoltaic and concentrated solar power technologies near the Tropic of Cancer. Sol. Energy 2022, 243, 103–119. [Google Scholar] [CrossRef]
- Dubey, S.; Sarvaiya, J.N.; Seshadri, B. Temperature Dependent Photovoltaic (PV) Efficiency and Its Effect on PV Production in the World—A Review. Energy Procedia 2013, 33, 311–321. [Google Scholar] [CrossRef]
- Saiki, T.; Takizawa, Y.; Miyahara, K.; Arima, M. Utilizing conductivity of seawater for bioelectric measurement of fish. Sci. Rep. 2020, 10, 16363. [Google Scholar] [CrossRef]
- Saiki, T.; Takizawa, Y.; Murai, K.; Okuno, R.; Arima, M. A novel method for noninvasive bioelectric measurement utilizing conductivity of seawater. Sci. Rep. 2021, 11, 7073. [Google Scholar] [CrossRef]
- Zheng, Z.; Fu, Y.; Liu, K.; Xiao, R.; Wang, X.; Shi, H. Three-stage vertical distribution of seawater conductivity. Sci. Rep. 2018, 8, 9916. [Google Scholar] [CrossRef]
- Zambrano, G.; Riascos, H.; Prieto, P.; Restrepo, E.; Devia, A.; Rincón, C. Optical emission spectroscopy study of r.f. magnetron sputtering discharge used for multilayers thin film deposition. Surf. Coat. Technol. 2003, 172, 144–149. [Google Scholar] [CrossRef]
- Jitschin, W.; Reich, G. Molecular velocity distribution at large Knudsen numbers. J. Vac. Sci. Technol. A 1991, 9, 2752–2756. [Google Scholar] [CrossRef]
- Li, J.; Kuipers, J.A.M. Effect of pressure on gas–solid flow behavior in dense gas-fluidized beds: A discrete particle simulation study. Powder Technol. 2002, 127, 173–184. [Google Scholar] [CrossRef]
- Lynch, G.R.; Dahl, O.I. Approximations to multiple Coulomb scattering. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 1991, 58, 6–10. [Google Scholar] [CrossRef]
- Gámiz, F.; López-Villanueva, J.A.; Jiménez-Tejada, J.A.; Melchor, I.; Palma, A. A comprehensive model for Coulomb scattering in inversion layers. J. Appl. Phys. 1994, 75, 924–934. [Google Scholar] [CrossRef]
- Johnson, W.R.; Weber, T.A.; Mullin, C.J. Coulomb Scattering of Polarized Electrons. Phys. Rev. 1961, 121, 933–939. [Google Scholar] [CrossRef]
- RSC [Royal Society of Chemistry]. Potassium—Element Information, Properties and Uses. Available online: https://periodic-table.rsc.org/element/19/potassium (accessed on 2 April 2025).
- Sarkar, A. Momentum-space properties for the S-states of the valence electron of potassium atom. Eur. Phys. J. D 2022, 76, 118. [Google Scholar] [CrossRef]
- Brown, J.M. A New Limit on Lorentz- and CPT-Violating Neutron Spin Interactions Using a Potassium-Helium Comagnetometer. Ph.D. Thesis, Department of Physics, Princeton University, Princeton, NJ, USA, 2011. Available online: https://www.proquest.com/openview/da8c7ee94b771c5271825badfd66f968/1 (accessed on 3 April 2025).
- Fritzsche, S.; Jänkälä, K.; Huttula, M.; Urpelainen, S.; Aksela, H. Photoelectron satellite structure from the 3d and 4d inner-shell ionization of rubidium and cesium: Role of atomic relaxation. Phys. Rev. A 2008, 78, 032514. [Google Scholar] [CrossRef]
- Webelements. Caesium—Properties of Free Atoms. Available online: https://www.webelements.com/caesium/atoms.html (accessed on 2 April 2025).
- Sherson, J.; Krauter, H.; Olsson, R.K.; Julsgaard, B.; Polzik, E.S. Quantum memory and teleportation using macroscopic gas samples. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 223001. [Google Scholar] [CrossRef]
- Mori, Y.; Ohtake, K.; Yamamoto, M.; Imani, K. Thermodynamic and Electrical Properties of Combustion Gas and Its Plasma: 1st Report, Theoretical Calculation. Bull. JSME 1968, 11, 241–252. [Google Scholar] [CrossRef]
- Marzouk, O.A. Temperature-Dependent Functions of the Electron–Neutral Momentum Transfer Collision Cross Sections of Selected Combustion Plasma Species. Appl. Sci. 2023, 13, 11282. [Google Scholar] [CrossRef]
- Yang, W. A tutorial overview of the angular scattering models of electron–neutral, ion–neutral, neutral–neutral, and Coulomb collisions in Monte Carlo collision modeling on low-temperature plasma. Plasma Sources Sci. Technol. 2024, 33, 023001. [Google Scholar] [CrossRef]
- Banks, P. Collision frequencies and energy transfer electrons. Planet. Space Sci. 1966, 14, 1085–1103. [Google Scholar] [CrossRef]
- Hjärtstam, S.; Andersson, K.; Johnsson, F.; Leckner, B. Combustion characteristics of lignite-fired oxy-fuel flames. Fuel 2009, 88, 2216–2224. [Google Scholar] [CrossRef]
- Bagheri, G.; Ranzi, E.; Pelucchi, M.; Parente, A.; Frassoldati, A.; Faravelli, T. Comprehensive kinetic study of combustion technologies for low environmental impact: MILD and OXY-fuel combustion of methane. Combust. Flame 2020, 212, 142–155. [Google Scholar] [CrossRef]
- Dobó, Z. Heat radiation measurement method for high pressure oxy-fuel combustion. Measurement 2018, 124, 191–196. [Google Scholar] [CrossRef]
- Davidson, R. Methods in Nonlinear Plasma Theory; Elsevier: New York, NY, USA, 2012; Available online: https://books.google.com.om/books?hl=en&lr=&id=8iW0MDOVr0oC (accessed on 28 April 2025).
- Filbet, F.; Negulescu, C.; Yang, C. Numerical study of a nonlinear heat equation for plasma physics. Int. J. Comput. Math. 2012, 89, 1060–1082. [Google Scholar] [CrossRef]
- Marzouk, O.A.; Nayfeh, A.H. New Wake Models with Capability of Capturing Nonlinear Physics. In Proceedings of the ASME 2008 27th International Conference on Offshore Mechanics and Arctic Engineering (OMAE 2008), Estoril, Portugal, 15–20 June 2008; ASME [American Society of Mechanical Engineers]: Estoril, Portugal, 2009; pp. 901–912. [Google Scholar] [CrossRef]
- Kono, M.; Skoric, M. Nonlinear Physics of Plasmas; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010; Available online: https://books.google.com.om/books?hl=en&lr=&id=fHDM99M49xIC (accessed on 28 April 2025).
- Masuda, R.; Matsumoto, M.; Kawasaki, A.; Okuno, Y. Power Generation Characteristics of Disk-Shaped Magnetohydrodynamic Generator Driven by Rotating Detonation. J. Propuls. Power 2025, 41, 125–134. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Z.; Huang, H.; Lu, P. Performance investigations of the two-phase mixer for liquid metal magnetohydrodynamic generator. Theor. Comput. Fluid. Dyn. 2025, 39, 18. [Google Scholar] [CrossRef]
- Chakradhar, K.; Nandagopal, K.; Prashanthi, V.; Parandhama, A.; Somaiah, T.; Thrinath, B.V.S.; Tarakaramu, N.; Rasool, G.; Abduvalieva, D. MHD effect on peristaltic motion of Williamson fluid via porous channel with suction and injection. Partial. Differ. Equ. Appl. Math. 2025, 13, 101103. [Google Scholar] [CrossRef]
- Muehlhauser, J.W. UTSI/CFFF MHD Program Completion and Related Activity (Quarterly Technical Progress Report). 2004. Available online: https://www.osti.gov/servlets/purl/822682 (accessed on 20 September 2023).
- Inoue, I.; Lineberry, J.T.; Ishikawa, M.; Umoto, J. Numerical study of the electrodynamics behavior of the CDIF MHD generator. Energy Convers. Manag. 1998, 39, 785–795. [Google Scholar] [CrossRef]
- Daniel, V.; Lineberry, J.; Wu, Y. Performance evaluations of MHD generator tests at CDIF. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992; AIAA [American Institute of Aeronautics and Astronautics]: Reno, NV, USA, 1992. [Google Scholar] [CrossRef]
- Pian, C.C.P.; Petty, S.W.; Schmitt, E.W.; Farrar, L.C. Prototypic magnetohydrodynamic anode designs and test results. J. Propuls. Power 1995, 11, 1330–1337. [Google Scholar] [CrossRef]
- Norton, O.; Wilson, W. Laser Doppler velocity measurements in the diffuser at CDIF. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992; AIAA [American Institute of Aeronautics and Astronautics]: Reno, NV, USA, 1992. [Google Scholar] [CrossRef]
- Wang, S.-T.; Genens, L.; Elmer, J.; Brown, E.; McHenry, H. Measurements of mechanical properties of superstructures materials for the CFFF syperconducting MHD magnet. IEEE Trans. Magn. 1981, 17, 2308–2311. [Google Scholar] [CrossRef]
- Lineberry, J.; Galanga, F.; Frazier, J. CFFF low mass flow DCW generator operation. In Proceedings of the 24th Aerospace Sciences Meeting, Reno, NV, USA, 6–9 January 1986; AIAA [American Institute of Aeronautics and Astronautics]: Reno, NV, USA, 1986. [Google Scholar] [CrossRef]
- Niemann, R.C.; Wang, S.-T.; Dawson, J.W.; Genens, L.; Smith, R.P.; Turner, L.R.; Gonczy, J.D.; Hoffman, J.; Mataya, K.F.; Smelser, P.; et al. Cryogenic Aspects of the UTSI-CFFF Superconducting Dipole Magnet for MHD Research. In Advances in Cryogenic Engineering; Timmerhaus, K.D., Snyder, H.A., Eds.; Springer: Boston, MA, USA, 1980; pp. 30–38. [Google Scholar] [CrossRef]
- Lee, J. Three-dimensional predictions of reactive turbulent recirculating flow of a cylindrical MHD type combustor. In Proceedings of the 28th Aerospace Sciences Meeting, Reno, NV, USA, 8–11 January 1990; AIAA [American Institute of Aeronautics and Astronautics]: Reno, NV, USA, 1990. [Google Scholar] [CrossRef]
- Bera, T.K. A Magnetohydrodynamic (MHD) Power Generating System: A Technical Review. IOP Conf. Ser. Mater. Sci. Eng. 2020, 955, 012075. [Google Scholar] [CrossRef]
- Ovcharenko, V.A. Commercial Realization of MHD—A Challenge for Superconducting Magnets. In Advances in Cryogenic Engineering; Timmerhaus, K.D., Ed.; Springer: Boston, MA, USA, 1978; pp. 1–8. [Google Scholar] [CrossRef]
- Malghan, V.R. History of MHD power plant development. Energy Convers. Manag. 1996, 37, 569–590. [Google Scholar] [CrossRef]
- Bera, T.K.; Bohre, A.K.; Ahmed, I.; Bhattacharya, A.; Bhowmik, P.S. Magnetohydrodynamic (MHD) Power Generation Systems. In Planning of Hybrid Renewable Energy Systems, Electric Vehicles and Microgrid: Modeling, Control and Optimization; Bohre, A.K., Chaturvedi, P., Kolhe, M.L., Singh, S.N., Eds.; Springer Nature: Singapore, 2022; pp. 905–929. [Google Scholar] [CrossRef]
- Macheret, S.; Shneider, M.; Miles, R. Potential performance of supersonic MHD power generators. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001; AIAA [American Institute of Aeronautics and Astronautics]: Reno, NV, USA, 2001; p. 0795. [Google Scholar] [CrossRef]
- Domínguez-Lozoya, J.C.; Cuevas, S.; Domínguez, D.R.; Ávalos-Zúñiga, R.; Ramos, E. Laboratory Characterization of a Liquid Metal MHD Generator for Ocean Wave Energy Conversion. Sustainability 2021, 13, 4641. [Google Scholar] [CrossRef]
- Ali, H.K.; Braun, R.D. Application of Magnetohydrodynamic Energy Generation to Planetary Entry Vehicles. In Proceedings of the 12th International Energy Conversion Engineering Conference, Cleveland, OH, USA, 28–30 July 2014; AIAA [American Institute of Aeronautics and Astronautics]: Cleveland, OH, USA, 2014; p. 3556. [Google Scholar] [CrossRef][Green Version]
- Panchadar, K.; West, D.; Taylor, J.A.; Krupenkin, T. Mechanical energy harvesting using a liquid metal vortex magnetohydrodynamic generator. Appl. Phys. Lett. 2019, 114, 093901. [Google Scholar] [CrossRef]
- Domínguez-Lozoya, J.C.; Domínguez-Lozoya, D.R.; Cuevas, S.; Ávalos-Zúñiga, R.A. MHD Generation for Sustainable Development, from Thermal to Wave Energy Conversion: Review. Sustainability 2024, 16, 10041. [Google Scholar] [CrossRef]
- Zhao, L.; Peng, A. Review of Conductive Reciprocating Liquid Metal Magnetohydrodynamic Generators. Energies 2025, 18, 959. [Google Scholar] [CrossRef]
- Noda, K.; Kawasaki, A.; Higashino, K. An Experimental Study on Magnetohydrodynamic Power Generation Using a Rotating Detonation Combustor. In Proceedings of the AIAA SCITECH 2025 Forum, Orlando, FL, USA, 6–10 January 2025; AIAA [American Institute of Aeronautics and Astronautics]: Orlando, FL, USA, 2025; p. 203. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, H.; Han, X.; Lu, P. The influence of the gas–liquid metal inlet angles on the performance of a magnetohydrodynamic generator. Chem. Eng. J. 2024, 499, 156316. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, K.; Xu, J.; Jing, W.; Huang, H.; Qin, J. A rapid performance prediction method for Two-Phase liquid metal MHD generators based on Quasi-One-Dimensional model. Therm. Sci. Eng. Prog. 2024, 47, 102258. [Google Scholar] [CrossRef]
- Pacheco, C.C.; Verissimo, G.L.; Colaço, M.J.; Leiroz, A.J.K.; Cruz, M.E.C.; Santos, H.F.L.; DeFilippo, M.; Quirino, T.S. A computational study on square and helical magnetohydrodynamic generators including applications to a combined power cycle. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 604. [Google Scholar] [CrossRef]
- Kimsor, O.; Okuno, Y. Numerical study of plasma behavior in a disk-shaped noble gas MHD generator. Electron. Commun. Jpn. 2024, 107, e12445. [Google Scholar] [CrossRef]
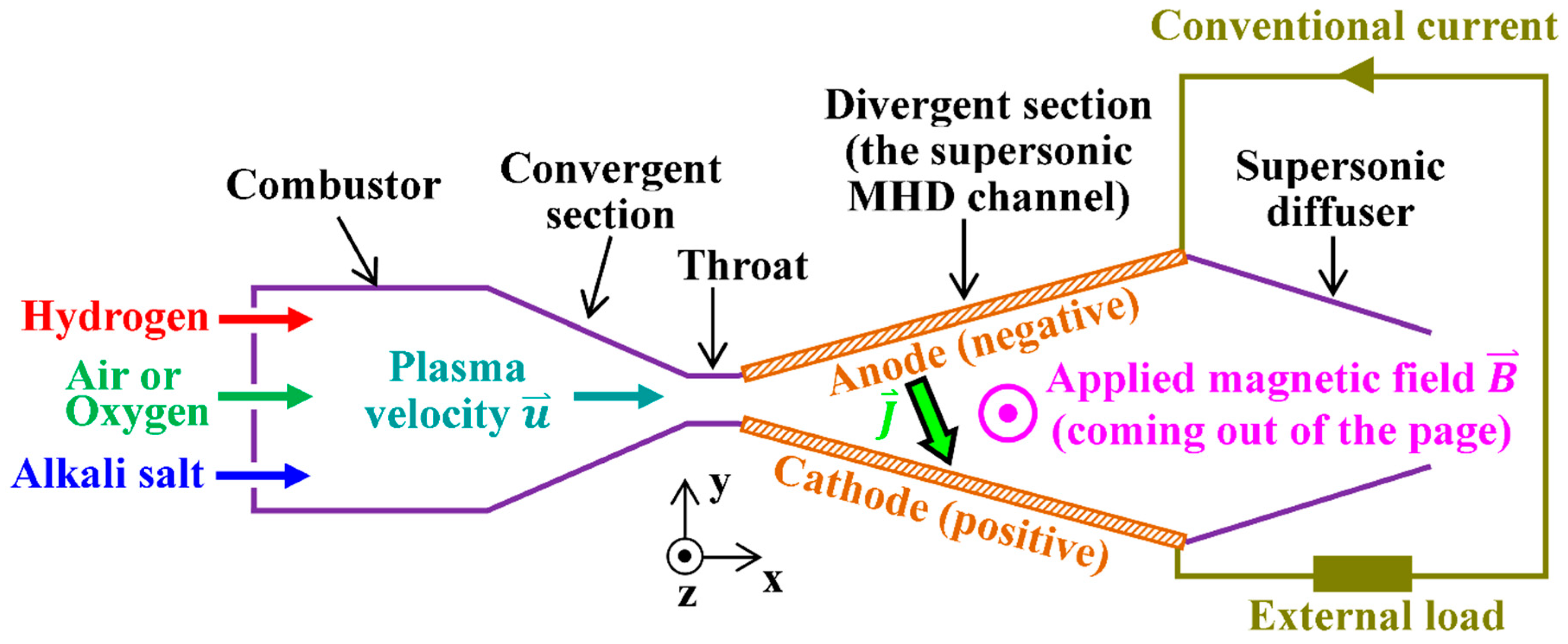
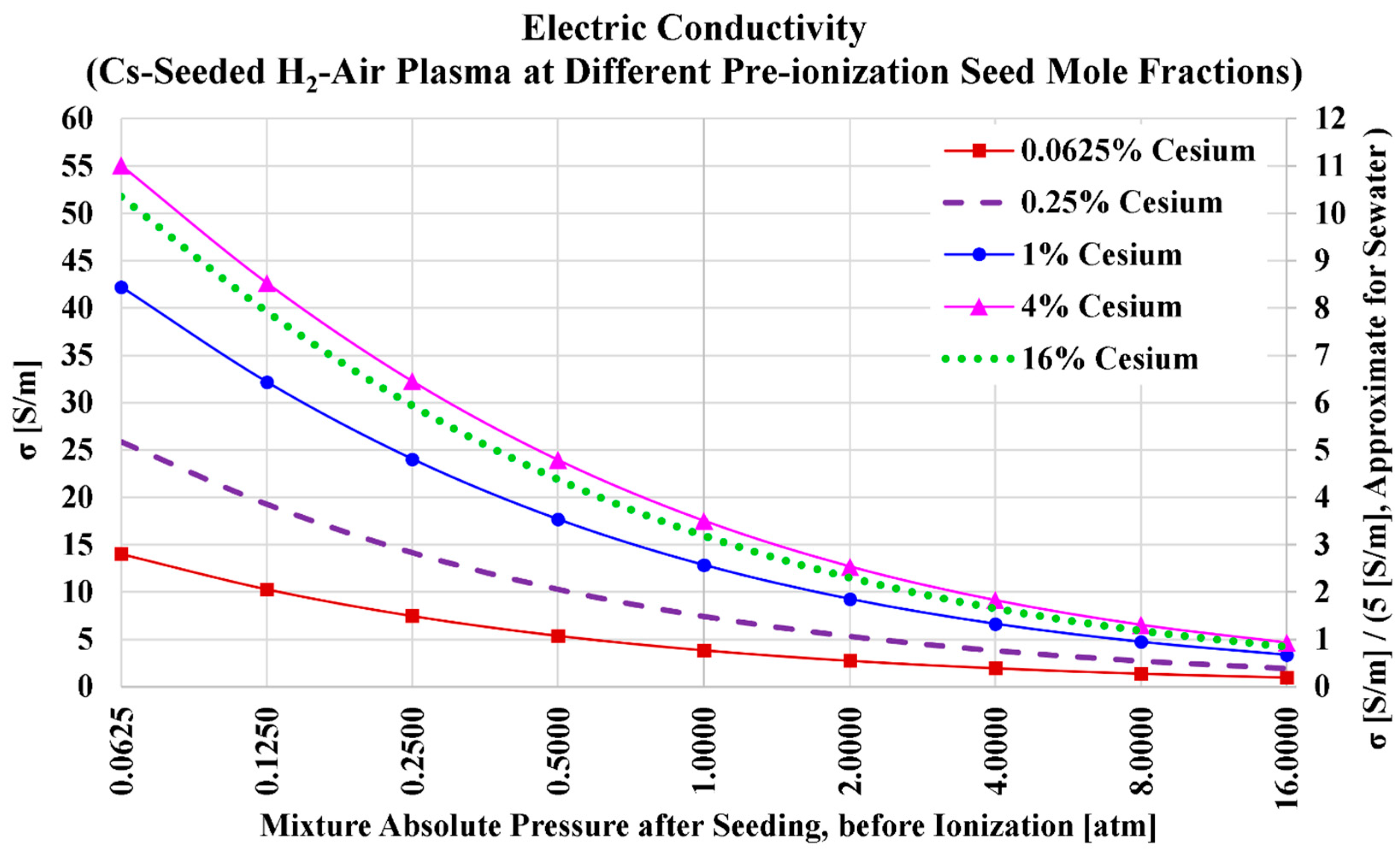
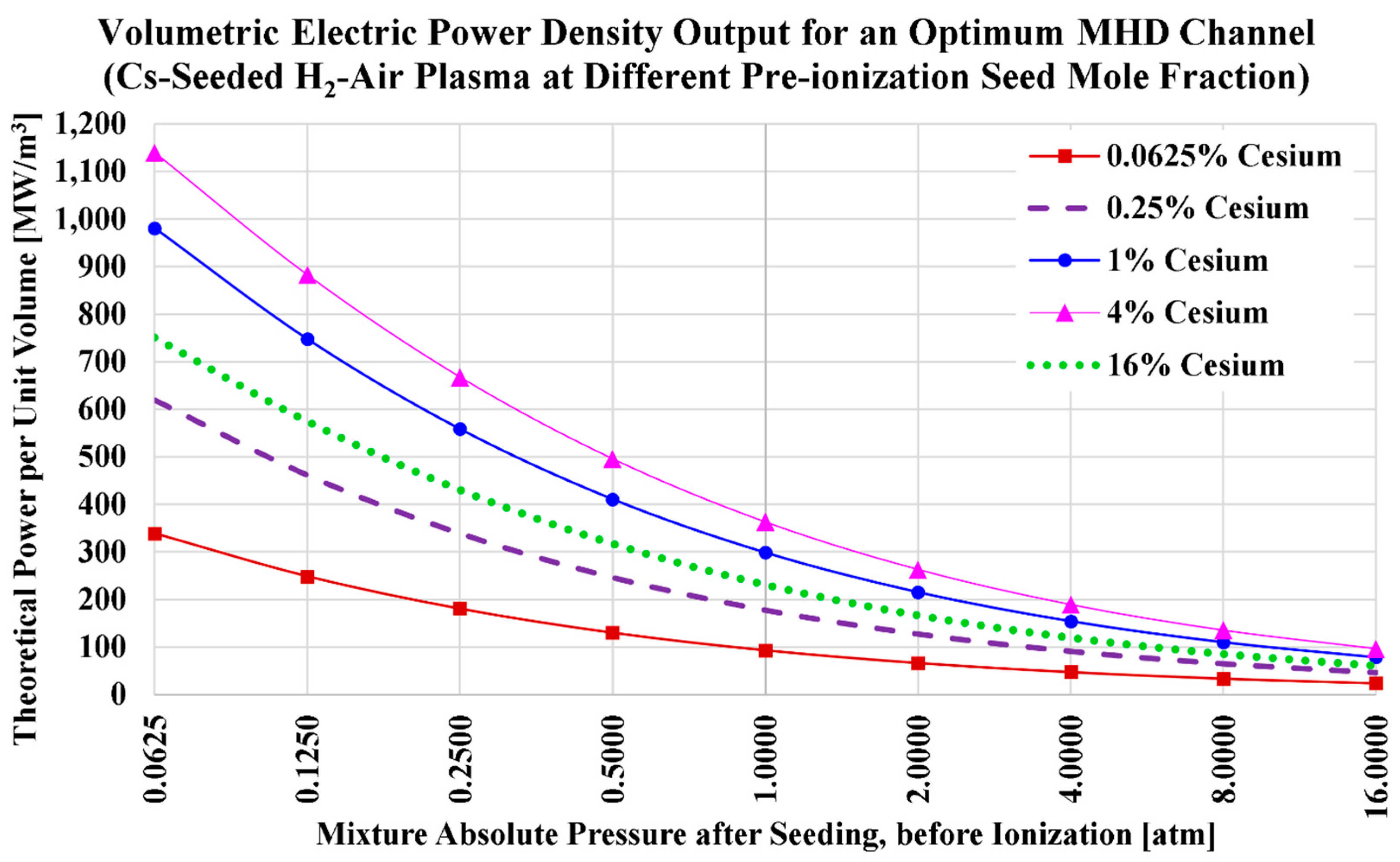
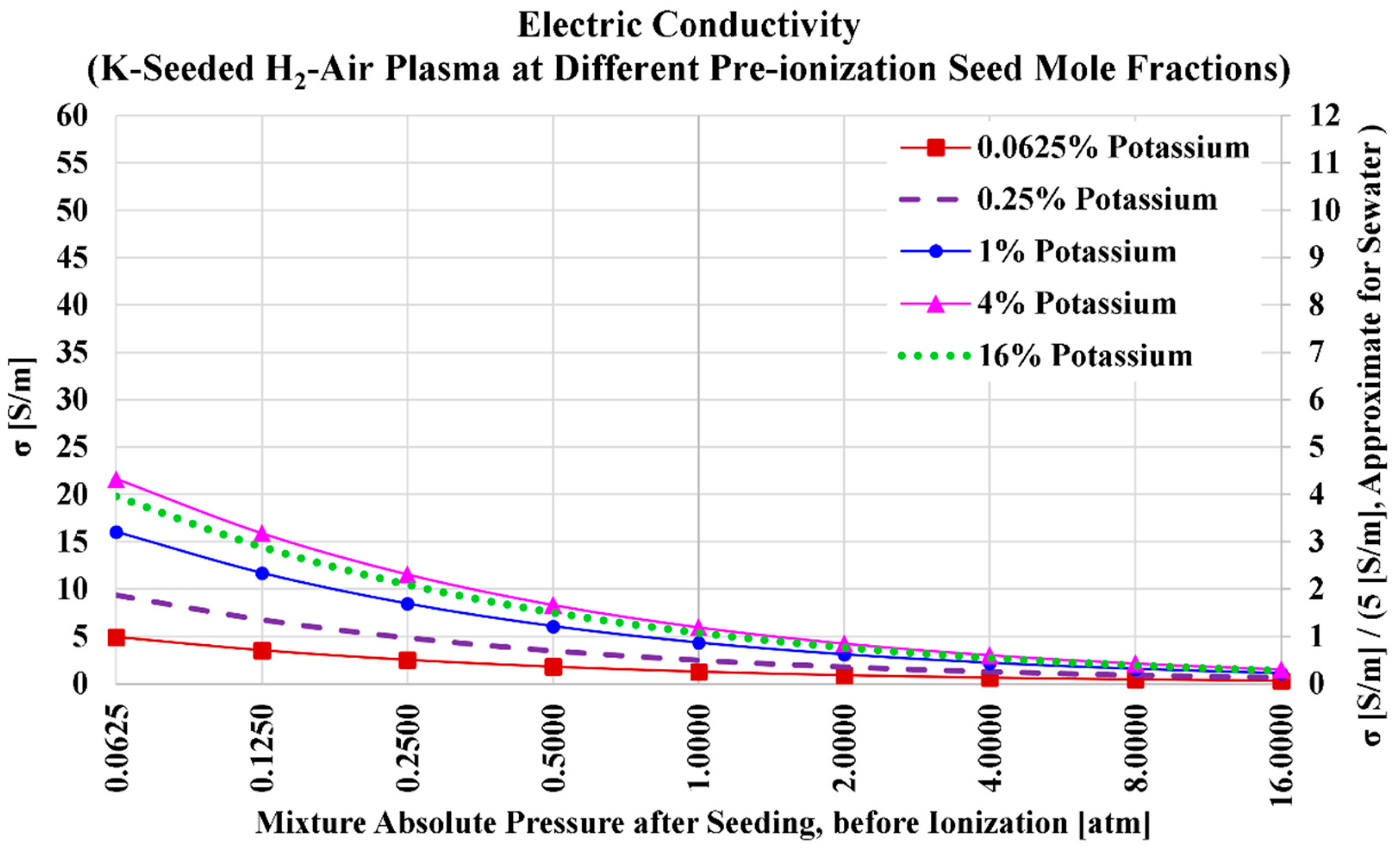

| Serial Number | Characteristics | References |
|---|---|---|
| 1. | Oil refinery | [7,8,9,10,11,12,13,14] |
| 2. | Fuel cell power units | [15,16,17,18,19] |
| 3. | Synthesizing ammonia | [20,21,22,23,24,25] |
| 4. | Electrified-type hydrogen-powered transport | [26,27,28,29,30,31,32,33] |
| 5. | Synthesizing methanol | [34,35,36,37,38,39] |
| 6. | Gas turbines powered by hydrogen or hydrogen-blended gas | [40,41,42] |
| 7. | Synthesizing hydrocarbon fuels | [43,44,45,46,47,48,49,50,51,52] |
| 8. | Aerospace and rocket propulsion | [53,54,55,56,57,58,59,60,61,62] |
| 9. | Reduction processes to extract a metal from its ore | [63,64,65,66,67,68,69,70,71] |
| 10. | Combustion-type hydrogen-powered transport | [72,73,74] |
| 11. | Specialized welding operations | [75,76,77,78,79,80] |
| 12. | Food industry | [81,82,83,84,85,86] |
| 13. | Cooling of turbogenerator winding | [87,88,89,90] |
| 14. | Feedstock for chemical industries | [91,92,93,94] |
| Fixed Parameter | Value | References |
|---|---|---|
| Temperature | 2300 K = 2026.85 °C | [197,198,199] |
| Magnetic-field flux density | 5 T (5 teslas) = 5000 G (50,000 gausses) | [200,201,202,203] |
| Mach number | 2 | [204,205,206] |
| Gaseous Species | Molecular Weight [kg/kmol] | Reference |
|---|---|---|
| Water vapor (H2O) | 18.0153 | [234] |
| Nitrogen (N2) | 28.0134 | [235] |
| Cesium vapor (Cs) | 132.9054519 | [236] |
| Potassium vapor (K) | 39.0983 | [237] |
| Coefficient for (Cp,i) | Species Index (i) | |||
|---|---|---|---|---|
| H2O | N2 | Cs | K | |
| 1.034972096 × 106 | 5.877124060 × 105 | 6.166040900 × 106 | –3.56642236 × 106 | |
| –2.412698562 × 103 | –2.239249073 × 103 | –1.896175522 × 104 | 1.085289825 × 104 | |
| 4.646110780 | 6.066949220 | 2.483229903 × 101 | –1.054134898 × 101 | |
| 2.291998307 × 10–3 | –6.139685500 × 10–4 | –1.251977234 × 10–2 | 8.009801350 × 10–3 | |
| –6.836830480 × 10–7 | 1.491806679 × 10–7 | 3.309017390 × 10–6 | –2.696681041 × 10–6 | |
| 9.426468930 × 10–11 | –1.923105485 × 10–11 | –3.354012020 × 10–10 | 4.715294150 × 10–10 | |
| –4.822380530 × 10–15 | 1.061954386 × 10–15 | 9.626500908 × 10–15 | –2.976897350 × 10–14 | |
| Counter | Varied Quantity | |||
|---|---|---|---|---|
| [atm] | [%] | Seed Metal | Oxidizer | |
| 1. | 0.0625 | 0.0625%, (1/16)% | Cesium (Cs) | Air (79% N2, 21% O2) |
| 2. | 0.125 | 0.25% | Potassium (K) | Oxygen (100% O2) |
| 3. | 0.25 | 1% | ||
| 4. | 0.5 | 4% | ||
| 5. | 1 | 16% | ||
| 6. | 2 | |||
| 7. | 4 | |||
| 8. | 8 | |||
| 9. | 16 | |||
| Property | Different Pre-Ionization Cesium Mole Fraction () | ||||
|---|---|---|---|---|---|
| 0.0625% | 0.25% | 1% | 4% | 16% | |
| [%] | 0.062500% | 0.250000% | 1.000000% | 4.000000% | 16.000000% |
| [%] | 34.688476% | 34.623395% | 34.363068% | 33.321763% | 29.156543% |
| [%] | 65.249024% | 65.126605% | 64.636932% | 62.678237% | 54.843457% |
| [kg/kmol] | 24.611 | 24.814 | 25.627 | 28.878 | 41.881 |
| [J/(kg.K)] | 337.8384 | 335.0721 | 324.4457 | 287.9214 | 198.5258 |
| [-] | 1.243991 | 1.244265 | 1.245365 | 1.249869 | 1.269668 |
| [m/s] | 983.166 | 979.241 | 964.014 | 909.773 | 761.408 |
| [m/s] | 1966.33 | 1958.48 | 1928.03 | 1819.55 | 1522.82 |
| Pressure [atm] | Plasma Electric Conductivity [S/m] (at the Different Cesium Levels) | |||||
|---|---|---|---|---|---|---|
| 0.0625% | 0.25% | 1% | 4% | 6% | 16% | |
| 0.0625 | 14.0116 | 25.8383 | 42.2099 | 55.0610 | 56.0605 | 51.7766 |
| 0.125 | 10.2858 | 19.2426 | 32.1752 | 42.6407 | 43.4010 | 39.6267 |
| 0.25 | 7.4702 | 14.1237 | 24.0379 | 32.2535 | 32.8188 | 29.6901 |
| 0.5 | 5.3830 | 10.2551 | 17.6829 | 23.9483 | 24.3616 | 21.8837 |
| 1 | 3.8573 | 7.3878 | 12.8589 | 17.5335 | 17.8321 | 15.9340 |
| 2 | 2.7530 | 5.2923 | 9.2729 | 12.7050 | 12.9189 | 11.4995 |
| 4 | 1.9593 | 3.7762 | 6.6470 | 9.1379 | 9.2904 | 8.2470 |
| 8 | 1.3917 | 2.6869 | 4.7447 | 6.5378 | 6.6461 | 5.8882 |
| 16 | 0.9871 | 1.9081 | 3.3768 | 4.6603 | 4.7371 | 4.1912 |
| Pressure [atm] | Volumetric Power Density [MW/m3] (at the Different Cesium Levels) | |||||
|---|---|---|---|---|---|---|
| 0.0625% | 0.25% | 1% | 3% | 4% | 16% | |
| 0.0625 | 338.596 | 619.417 | 980.665 | 1146.828 | 1139.332 | 750.427 |
| 0.125 | 248.561 | 461.299 | 747.529 | 886.885 | 882.329 | 574.332 |
| 0.25 | 180.520 | 338.585 | 558.474 | 670.107 | 667.395 | 430.315 |
| 0.5 | 130.082 | 245.844 | 410.828 | 497.150 | 495.543 | 317.173 |
| 1 | 93.213 | 177.106 | 298.752 | 363.771 | 362.806 | 230.940 |
| 2 | 66.527 | 126.871 | 215.438 | 263.484 | 262.894 | 166.669 |
| 4 | 47.347 | 90.526 | 154.430 | 189.454 | 189.083 | 119.528 |
| 8 | 33.631 | 64.413 | 110.234 | 135.521 | 135.281 | 85.341 |
| 16 | 23.854 | 45.743 | 78.453 | 96.591 | 96.432 | 60.745 |
| Property | Different Pre-Ionization Potassium Mole Fraction () | ||||
|---|---|---|---|---|---|
| 0.0625% | 0.25% | 1% | 4% | 16% | |
| [%] | 0.062500% | 0.250000% | 1.000000% | 4.000000% | 16.000000% |
| [%] | 34.688476% | 34.623395% | 34.363068% | 33.321763% | 29.156543% |
| [%] | 65.249024% | 65.126605% | 64.636932% | 62.678237% | 54.843457% |
| [kg/kmol] | 24.552 | 24.579 | 24.689 | 25.125 | 26.872 |
| [J/(kg.K)] | 338.6451 | 338.2691 | 336.7734 | 330.9206 | 309.4112 |
| [-] | 1.243994 | 1.244278 | 1.245418 | 1.250087 | 1.270686 |
| [m/s] | 984.341 | 983.906 | 982.178 | 975.430 | 950.935 |
| [m/s] | 1968.68 | 1967.81 | 1964.36 | 1950.86 | 1901.87 |
| Pressure [atm] | Plasma Electric Conductivity [S/m] (at the Different Potassium Levels) | |||||
|---|---|---|---|---|---|---|
| 0.0625% | 0.25% | 1% | 4% | 6% | 16% | |
| 0.0625 | 4.9217 | 9.3443 | 16.0343 | 21.6201 | 21.9827 | 19.7671 |
| 0.125 | 3.5282 | 6.7405 | 11.6895 | 15.8856 | 16.1504 | 14.4434 |
| 0.25 | 2.5189 | 4.8334 | 8.4459 | 11.5428 | 11.7342 | 10.4518 |
| 0.5 | 1.7931 | 3.4513 | 6.0630 | 8.3195 | 8.4568 | 7.5108 |
| 1 | 1.2739 | 2.4570 | 4.3325 | 5.9617 | 6.0597 | 5.3707 |
| 2 | 0.9037 | 1.7456 | 3.0859 | 4.2546 | 4.3243 | 3.8271 |
| 4 | 0.6405 | 1.2383 | 2.1931 | 3.0277 | 3.0772 | 2.7205 |
| 8 | 0.4536 | 0.8776 | 1.5561 | 2.1502 | 2.1853 | 1.9307 |
| 16 | 0.3211 | 0.6215 | 1.1029 | 1.5250 | 1.5499 | 1.3686 |
| Pressure [atm] | Volumetric Power Density [MW/m3] (at the Different Potassium Levels) | |||||
|---|---|---|---|---|---|---|
| 0.0625% | 0.25% | 1% | 4% | 5% | 16% | |
| 0.0625 | 119.219 | 226.149 | 386.697 | 514.268 | 518.972 | 446.874 |
| 0.125 | 85.464 | 163.132 | 281.914 | 377.864 | 381.364 | 326.521 |
| 0.25 | 61.016 | 116.977 | 203.689 | 274.564 | 277.128 | 236.283 |
| 0.5 | 43.435 | 83.528 | 146.221 | 197.892 | 199.751 | 169.796 |
| 1 | 30.858 | 59.464 | 104.486 | 141.808 | 143.144 | 121.415 |
| 2 | 21.890 | 42.247 | 74.422 | 101.202 | 102.158 | 86.519 |
| 4 | 15.515 | 29.969 | 52.891 | 72.019 | 72.698 | 61.502 |
| 8 | 10.988 | 21.239 | 37.528 | 51.146 | 51.631 | 43.647 |
| 16 | 7.778 | 15.041 | 26.598 | 36.275 | 36.618 | 30.940 |
| Property | Different Pre-Ionization Potassium Mole Fraction () | ||||
|---|---|---|---|---|---|
| 0.0625% | 0.25% | 1% | 4% | 16% | |
| [%] | 0.0625% | 0.25% | 1% | 4% | 16% |
| [%] | 99.9375% | 99.75% | 99% | 96% | 84% |
| [kg/kmol] | 18.028 | 18.068 | 18.226 | 18.859 | 21.389 |
| [J/(kg.K)] | 461.1850 | 460.1760 | 456.1837 | 440.8839 | 388.7337 |
| [-] | 1.183244 | 1.183490 | 1.184479 | 1.188543 | 1.206766 |
| [m/s] | 1120.311 | 1119.201 | 1114.801 | 1097.826 | 1038.727 |
| [m/s] | 2240.62 | 2238.40 | 2229.60 | 2195.65 | 2077.45 |
| Pressure [atm] | Plasma Electric Conductivity [S/m] (at the Different Potassium Levels) | |||||
|---|---|---|---|---|---|---|
| 0.0625% | 0.25% | 1% | 4% | 13% | 16% | |
| 0.0625 | 2.3874 | 4.6735 | 8.6753 | 13.9154 | 16.2537 | 16.1854 |
| 0.125 | 1.7027 | 3.3408 | 6.2385 | 10.0857 | 11.8100 | 11.7558 |
| 0.25 | 1.2112 | 2.3803 | 4.4635 | 7.2563 | 8.5119 | 8.4704 |
| 0.5 | 0.8601 | 1.6920 | 3.1821 | 5.1932 | 6.0993 | 6.0683 |
| 1 | 0.6099 | 1.2008 | 2.2628 | 3.7030 | 4.3527 | 4.3300 |
| 2 | 0.4322 | 0.8513 | 1.6063 | 2.6335 | 3.0974 | 3.0809 |
| 4 | 0.3060 | 0.6030 | 1.1389 | 1.8696 | 2.1997 | 2.1878 |
| 8 | 0.2166 | 0.4269 | 0.8068 | 1.3256 | 1.5601 | 1.5516 |
| 16 | 0.1533 | 0.3021 | 0.5712 | 0.9391 | 1.1054 | 1.0993 |
| Pressure [atm] | Volumetric Power Density [MW/m3] (at the Different Potassium Levels) | |||||
|---|---|---|---|---|---|---|
| 0.0625% | 0.25% | 1% | 4% | 9% | 16% | |
| 0.0625 | 74.910 | 146.352 | 269.538 | 419.279 | 458.894 | 436.583 |
| 0.125 | 53.426 | 104.618 | 193.827 | 303.888 | 333.446 | 317.099 |
| 0.25 | 38.004 | 74.540 | 138.679 | 218.636 | 240.334 | 228.479 |
| 0.5 | 26.988 | 52.985 | 98.866 | 156.474 | 172.221 | 163.685 |
| 1 | 19.137 | 37.603 | 70.304 | 111.573 | 122.907 | 116.797 |
| 2 | 13.561 | 26.659 | 49.907 | 79.349 | 87.463 | 83.104 |
| 4 | 9.601 | 18.883 | 35.385 | 56.332 | 62.116 | 59.013 |
| 8 | 6.796 | 13.368 | 25.067 | 39.941 | 44.054 | 41.853 |
| 16 | 4.810 | 9.460 | 17.747 | 28.296 | 31.215 | 29.652 |
| Property | Different Pre-Ionization Cesium Mole Fraction () | ||||
|---|---|---|---|---|---|
| 0.0625% | 0.25% | 1% | 4% | 16% | |
| [%] | 0.0625% | 0.25% | 1% | 4% | 16% |
| [%] | 99.9375% | 99.75% | 99% | 96% | 84% |
| [kg/kmol] | 18.087 | 18.303 | 19.164 | 22.611 | 36.398 |
| [J/(kg.K)] | 459.6900 | 454.2795 | 433.8539 | 367.7191 | 228.4336 |
| [-] | 1.183242 | 1.183482 | 1.184449 | 1.188419 | 1.206172 |
| [m/s] | 1118.493 | 1112.004 | 1087.161 | 1002.552 | 796.065 |
| [m/s] | 2236.99 | 2224.01 | 2174.32 | 2005.10 | 1592.13 |
| Pressure [atm] | Plasma Electric Conductivity [S/m] (at the Different Cesium Levels) | |||||
|---|---|---|---|---|---|---|
| 0.0625% | 0.25% | 1% | 4% | 13% | 16% | |
| 0.0625 | 6.9878 | 13.5501 | 24.4282 | 37.7620 | 43.6710 | 43.5831 |
| 0.125 | 5.0633 | 9.8700 | 18.0514 | 28.4084 | 33.0271 | 32.9308 |
| 0.25 | 3.6427 | 7.1273 | 13.1716 | 21.0071 | 24.5184 | 24.4295 |
| 0.5 | 2.6073 | 5.1146 | 9.5223 | 15.3342 | 17.9480 | 17.8732 |
| 1 | 1.8595 | 3.6539 | 6.8382 | 11.0877 | 13.0034 | 12.9440 |
| 2 | 1.3227 | 2.6023 | 4.8876 | 7.9629 | 9.3514 | 9.3060 |
| 4 | 0.9392 | 1.8492 | 3.4818 | 5.6913 | 6.6899 | 6.6560 |
| 8 | 0.6661 | 1.3121 | 2.4746 | 4.0541 | 4.7684 | 4.7435 |
| 16 | 0.4719 | 0.9300 | 1.7559 | 2.8812 | 3.3901 | 3.3721 |
| Pressure [atm] | Volumetric Power Density [MW/m3] (at the Different Cesium Levels) | |||||
|---|---|---|---|---|---|---|
| 0.0625% | 0.25% | 1% | 4% | 5% | 16% | |
| 0.0625 | 218.548 | 418.885 | 721.804 | 948.874 | 947.117 | 690.486 |
| 0.125 | 158.358 | 305.119 | 533.382 | 713.839 | 714.060 | 521.722 |
| 0.25 | 113.928 | 220.332 | 389.194 | 527.861 | 528.886 | 387.036 |
| 0.5 | 81.545 | 158.112 | 281.365 | 385.314 | 386.524 | 283.165 |
| 1 | 58.157 | 112.956 | 202.055 | 278.609 | 279.721 | 205.072 |
| 2 | 41.368 | 80.447 | 144.419 | 200.090 | 201.008 | 147.435 |
| 4 | 29.374 | 57.166 | 102.880 | 143.010 | 143.725 | 105.451 |
| 8 | 20.833 | 40.562 | 73.119 | 101.870 | 102.409 | 75.151 |
| 16 | 14.759 | 28.750 | 51.883 | 72.398 | 72.793 | 53.424 |
| Reference | Comparison with Our Study |
|---|---|
| [309] | The study in this reference is limited to potassium seeding and does not explore the effect of using cesium seeding (which we did). |
| [310] | The study in this reference uses liquid metal as a working fluid for magnetohydrodynamic power generators, not hydrogen (which we used). |
| [311] | The study in this reference describes a specific flow problem and a special channel that is porous. The exact fluid type is not specified, making the study have probable great theoretical value but not necessarily applicable to commercial magnetohydrodynamic power generation (which we considered). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marzouk, O.A. Power Density and Thermochemical Properties of Hydrogen Magnetohydrodynamic (H2MHD) Generators at Different Pressures, Seed Types, Seed Levels, and Oxidizers. Hydrogen 2025, 6, 31. https://doi.org/10.3390/hydrogen6020031
Marzouk OA. Power Density and Thermochemical Properties of Hydrogen Magnetohydrodynamic (H2MHD) Generators at Different Pressures, Seed Types, Seed Levels, and Oxidizers. Hydrogen. 2025; 6(2):31. https://doi.org/10.3390/hydrogen6020031
Chicago/Turabian StyleMarzouk, Osama A. 2025. "Power Density and Thermochemical Properties of Hydrogen Magnetohydrodynamic (H2MHD) Generators at Different Pressures, Seed Types, Seed Levels, and Oxidizers" Hydrogen 6, no. 2: 31. https://doi.org/10.3390/hydrogen6020031
APA StyleMarzouk, O. A. (2025). Power Density and Thermochemical Properties of Hydrogen Magnetohydrodynamic (H2MHD) Generators at Different Pressures, Seed Types, Seed Levels, and Oxidizers. Hydrogen, 6(2), 31. https://doi.org/10.3390/hydrogen6020031







