Techno-Economic Feasibility of Fuel Cell Vehicle-to-Grid Fast Frequency Control in Non-Interconnected Islands
Abstract
1. Introduction
2. Description of the Proposed Concept: Fuel-Cell-to-Grid Fast Frequency Control
Description of FCEV Frequency Control Algorithm
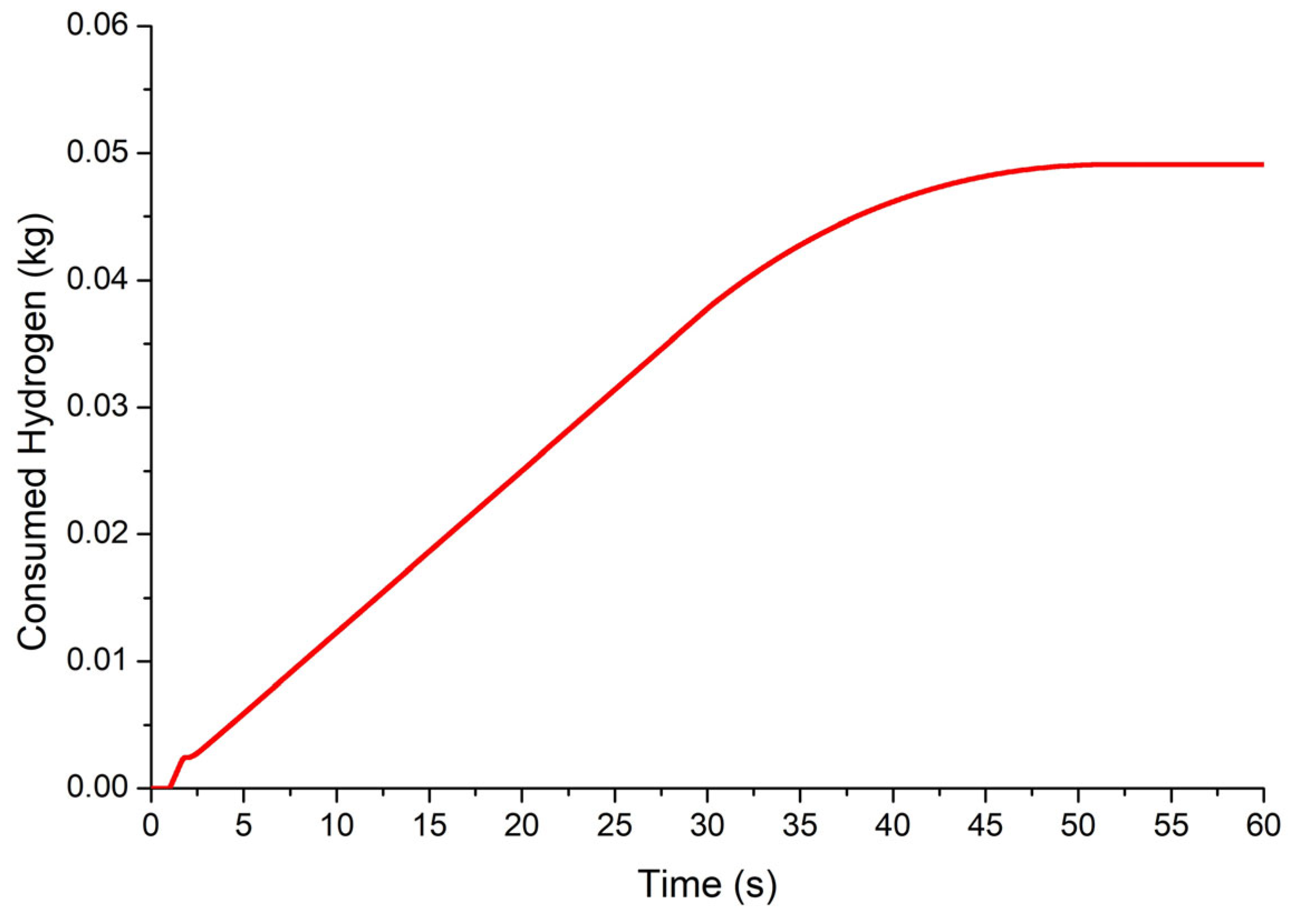
3. Case Study
- ▪
- Scenario 1: The network includes three (3) gas turbines. The disturbance involves a rapid 27 MW drop in wind power over 2 s, simulating the output reduction in a 50-MW wind farm when wind speed decreases from 14 m/s to 10.8 m/s. This wind power variation is modeled in Figure 3 via the input .
- ▪
- Scenario 2: The disturbance is identical to Scenario 1. However, only two (2) gas turbines are connected, resulting in reduced system inertia, highlighting the impact of lower inertia on frequency stability.
- ▪
- Scenario 3: The network consists of three (3) gas turbines. The disturbance is a sudden outage of a large 20 MW wind farm, potentially caused by a fault.
- A.
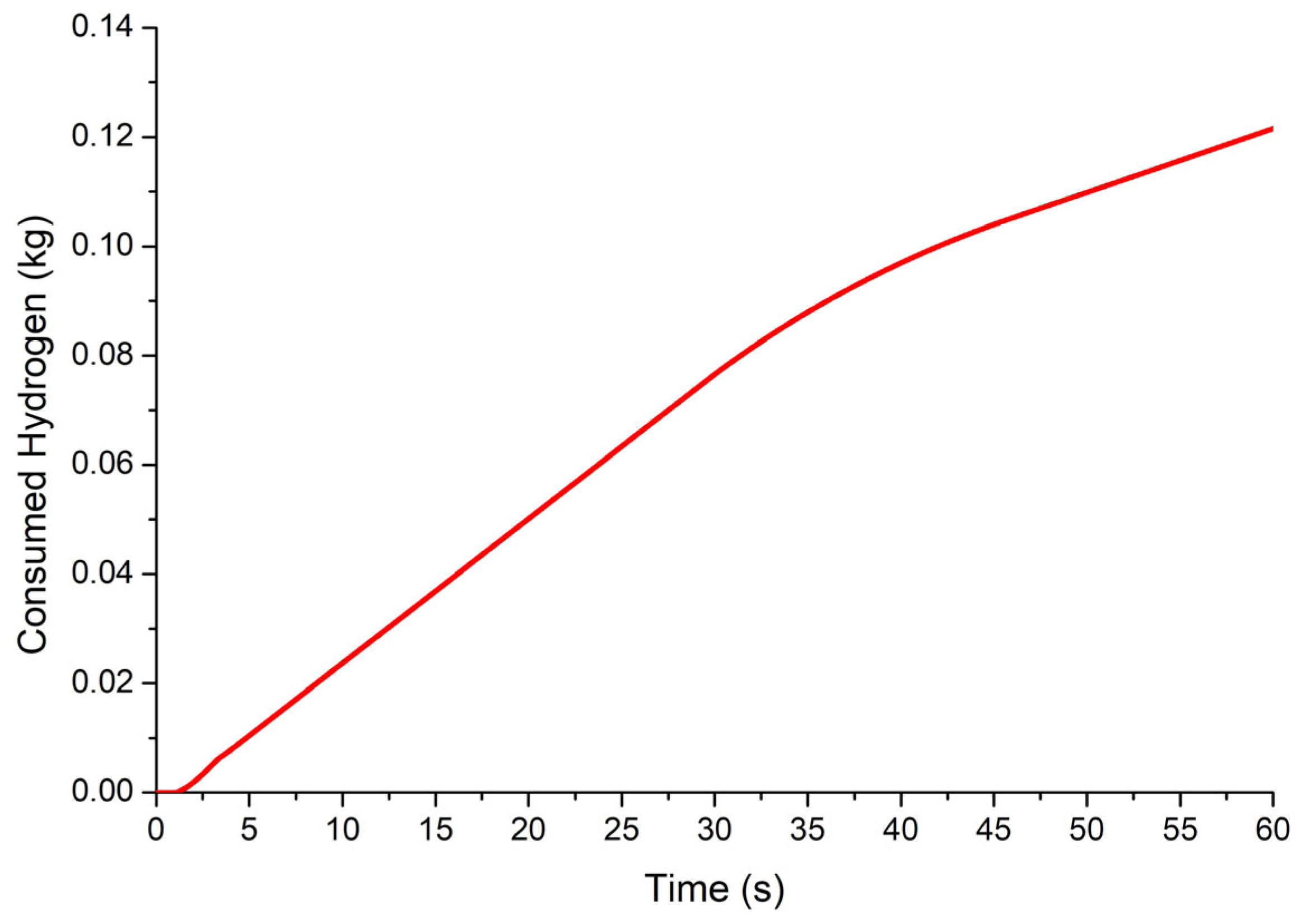
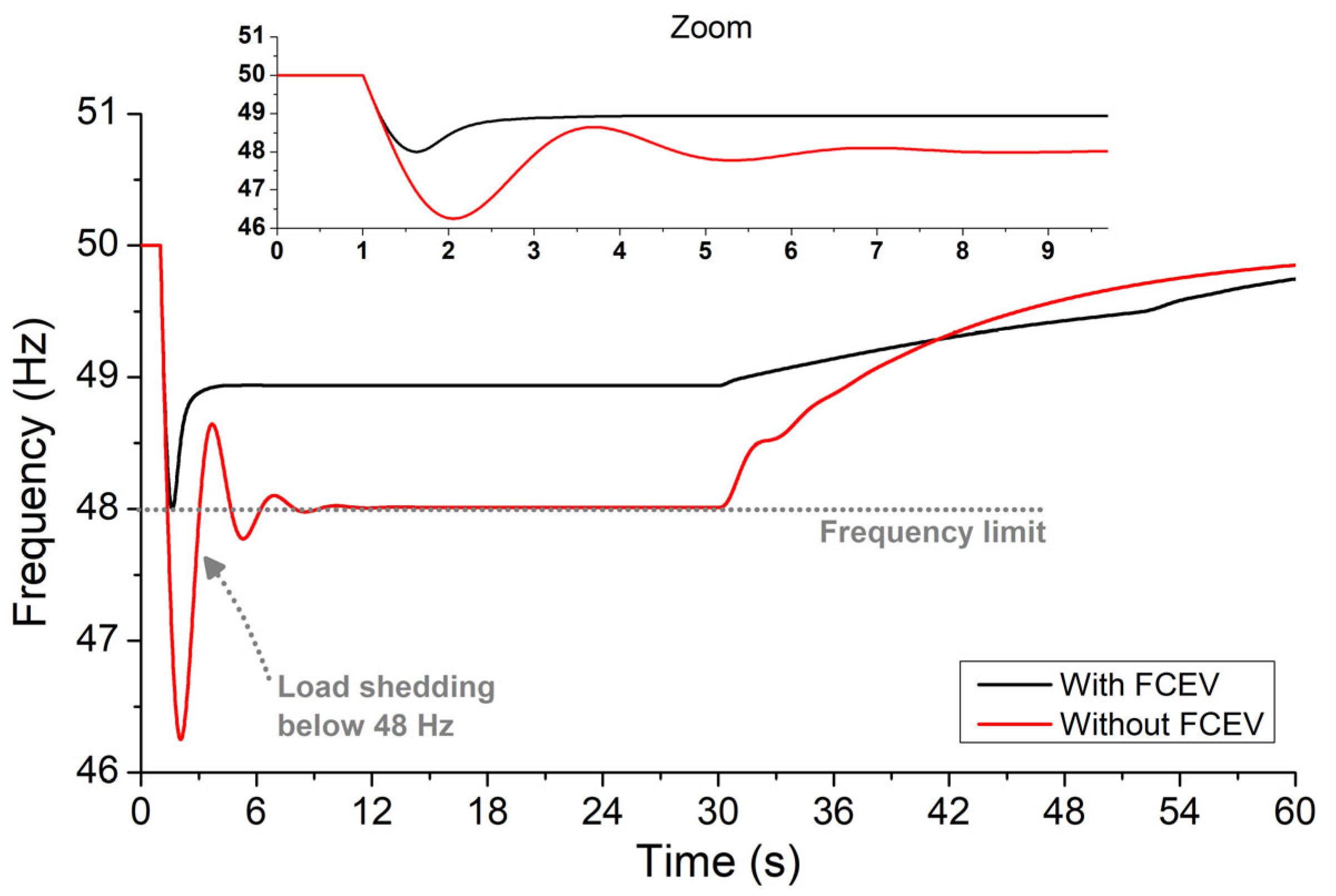
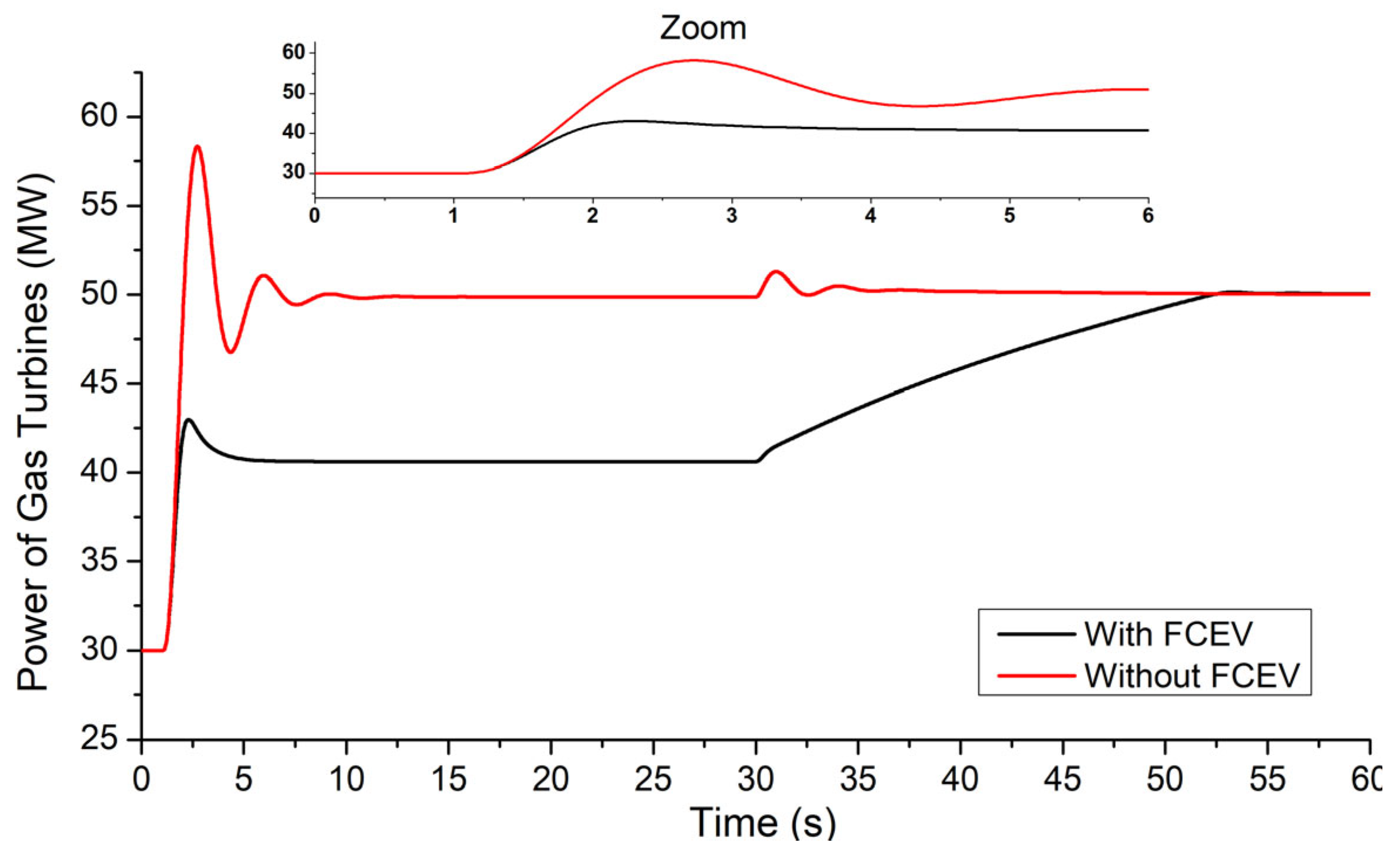
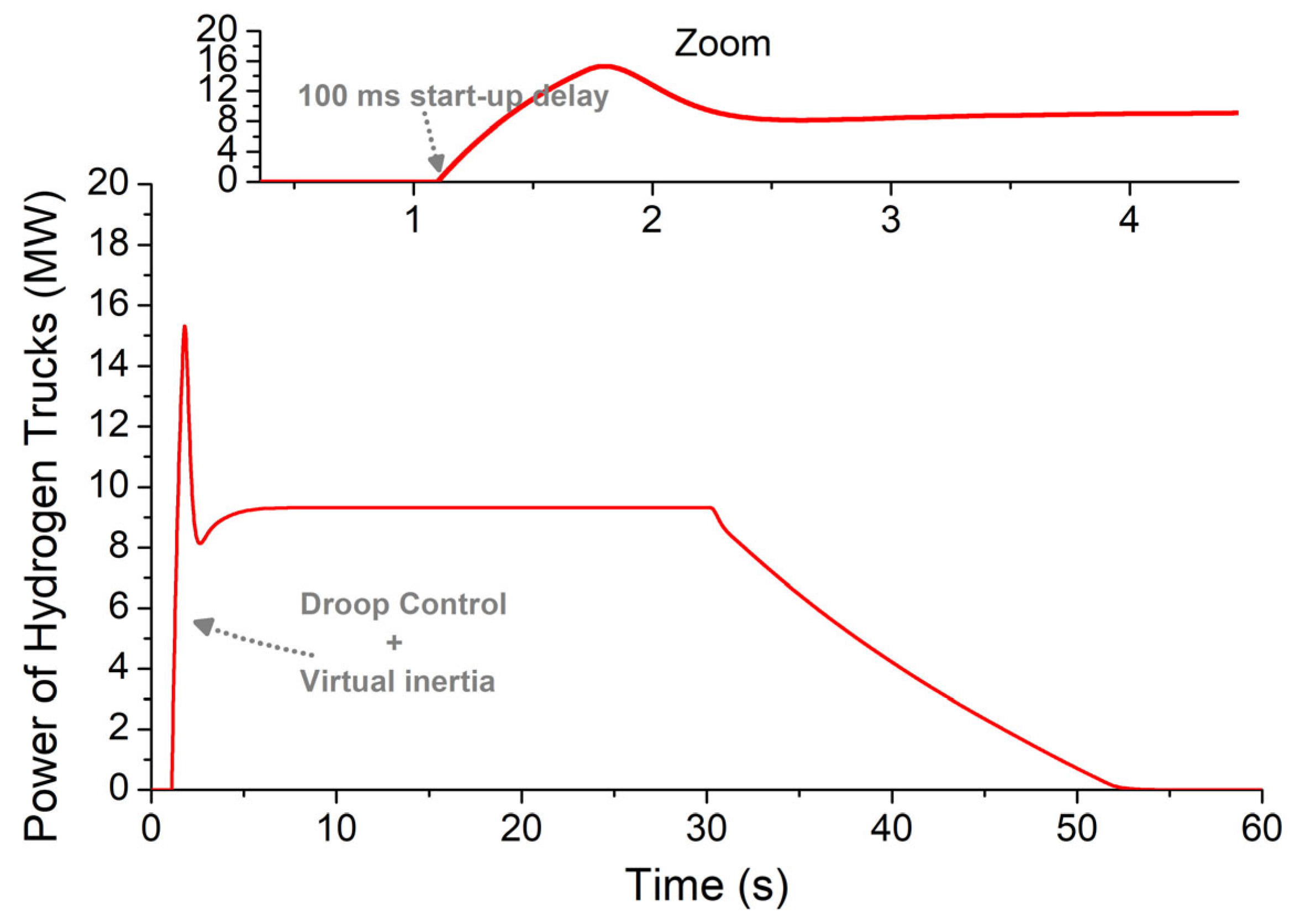
- Simulation Results: Scenario 1
- B.
- Simulation Results: Scenario 2
- C.
- Simulation Results: Scenario 3
4. Discussion
- ✓
- Frequency Threshold: The FCEV response is triggered when the frequency drops below 49.5 Hz.
- ✓
- Droop Slope: , where represents the maximum power provided by the FCEV.
- ✓
- Maximum Reaction Delay: The response delay should be less than 100 ms.
- ✓
- Ramp-Up Time: The ramp-up time from 0 to is recommended to be less than 2 s.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| FCEV | Fuel cell electric vehicle |
| FC | Fuel cell |
| DC | Direct current |
| NII | Non-interconnected island |
| BESS | Battery energy storage system |
| RES | Renewable energy source |
| AC | Alternating current |
| ESS | Energy storage system |
| EV | Electric vehicle |
| V2G | Vehicle-to-grid |
| BEV | Battery electric vehicle |
| PV | Photovoltaic |
| FCEV2G | Fuel cell electric vehicle-to-grid |
| CSO | Competitive swarm optimization |
| ICA | Imperialist competitive algorithm |
| BEV2G | Battery electric vehicle-to-grid |
| G2V | Grid-to-vehicle |
| VI | Virtual inertia |
| IBDG | Inverter-based distributed generator |
| ROCOF | Rate of change of frequency |
| CAPEX | Capital expenditure |
| Variables | |
| Total active power output of FCEV | |
| Virtual inertia component of FCEV active power output | |
| Droop control power component active power output | |
| Power ramp-up function | |
| Equivalent inertia of the island | |
| System base power (total power of thermal generators) | |
| Wind power variation | |
| Load variations | |
| Renewable energy source variations | |
| Start-up delay | |
References
- Katsaprakakis, D. Hybrid power plants in non-interconnected insular systems. Appl. Energy 2016, 164, 268–283. [Google Scholar] [CrossRef]
- Katsaprakakis, D.; Dakanali, I.; Condaxakis, C.; Christakis, D. Comparing electricity storage technologies for small insular grids. Appl. Energy 2019, 251, 84–89. [Google Scholar] [CrossRef]
- Pombo, D.V.; Martinez-Rico, J.; Marczinkowski, H.M. Towards 100% renewable islands in 2040 via generation expansion planning: The case of São Vicente, Cape Verde. Appl. Energy 2022, 315, 118869. [Google Scholar] [CrossRef]
- Pompodakis, E.E.; Kryonidis, G.C.; Karapidakis, E.S. Volt/Var control and energy management in non-interconnected insular networks with multiple hybrid power plants. Appl. Energy 2023, 331, 120427. [Google Scholar] [CrossRef]
- Sarasúaa, J.I.; Lucas, G.M.; Lafoz, M. Analysis of alternative frequency control schemes for increasing renewable energy penetration in El Hierro Island power system. Int. J. Electr. Power Energy Syst. 2019, 113, 807–823. [Google Scholar] [CrossRef]
- Cheng, Y.; Azizipanah-Abarghooee, R.; Azizi, S.; Ding, L.; Terzija, V. Smart frequency control in low inertia energy systems based on frequency response techniques: A review. Appl. Energy 2020, 279, 115798. [Google Scholar] [CrossRef]
- Margaris, I.D.; Papathanassiou, S.A.; Hatziargyriou, N.D.; Hansen, A.D.; Sorensen, P. Frequency control in autonomous power systems with high wind power penetration. IEEE Trans. Sustain. Energy 2012, 3, 189–199. [Google Scholar] [CrossRef]
- Alqahtani, S.; Shaher, A.; Garada, A.; Cipcigan, L. Impact of the High Penetration of Renewable Energy Sources on the Frequency Stability of the Saudi Grid. Electronics 2023, 12, 1470. [Google Scholar] [CrossRef]
- Pompodakis, E.; Orfanoudakis, G.; Katsigiannis, G.; Tsikalakis, A.; Kryonidis, G.; Karapidakis, E.S. Investigating Frequency Stability Challenges in Non-Interconnected Renewable-Rich Islands. In Proceedings of the UPEC 2024, Cardiff, UK, 2–6 September 2024. [Google Scholar]
- Nguyen-Huu, T.A.; Van Nguyen, T.; Hur, K.; Shim, J.W. Coordinated control of a hybrid energy storage system for improving the capability of frequency regulation and state-of-charge management. Energies 2020, 13, 6304. [Google Scholar] [CrossRef]
- Khalilisenobari, R.; Wu, M. Optimal participation of price-maker battery energy storage systems in energy and ancillary services markets considering degradation cost. Int. J. Electr. Power Energy Syst. 2022, 138, 107924. [Google Scholar] [CrossRef]
- Alam, M.S.; Chowdhury, T.A.; Dhar, A.; Al-Ismail, F.S.; Choudhury, M.S.H.; Shafiullah, M.; Hossain, M.I.; Hossain, M.A.; Ullah, A.; Rahman, S.M. Solar and Wind Energy Integrated System Frequency Control: A Critical Review on Recent Developments. Energies 2023, 16, 812. [Google Scholar] [CrossRef]
- Robledo, C.B.; Poorte, M.J.; Mathijssen, H.H.M.; van der Veen, R.A.C.; van Wijk, A.J.M. Fuel cell electric vehicle-to-grid feasibility: A technical analysis of aggregated units offering frequency reserves. In Intelligent Integrated Energy Systems: The PowerWeb Program at TU Delft; Palensky, P., Cvetkovi’c, M., Keviczky, T., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 167–194. [Google Scholar]
- Lee, C.-Y.; Jang, J.-W.; Lee, M.-K. Willingness to accept values for vehicle-togrid service in South Korea. Transp. Res. Part D Transp. Environ. 2020, 87, 102487. [Google Scholar] [CrossRef]
- Oceano, A.; Rodella, G.; Rizzo, R.; Di Noia, L.P.; Brusaglino, G. Grid balancing support through Electric Vehicles mobile storage. In Proceedings of the 2020 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Sorrento, Italy, 24–26 June 2020; pp. 108–113. [Google Scholar]
- Solanke, T.U.; Ramachandaramurthy, V.K.; Yong, J.Y.; Pasupuleti, J.; Kasinathan, P.; Rajagopalan, A. A review of strategic charging–discharging control of gridconnected electric vehicles. J. Energy Storage 2020, 28, 101193. [Google Scholar] [CrossRef]
- Forrest, K.E.; Tarroja, B.; Zhang, L.; Shaffer, B.; Samuelsen, S. Charging a renewable future: The impact of electric vehicle charging intelligence on energy storage requirements to meet renewable portfolio standards. J. Power Sources 2016, 336, 63–74. [Google Scholar] [CrossRef]
- van der Kam, M.; van Sark, W. Smart charging of electric vehicles with photovoltaic power and vehicle-to-grid technology in a microgrid; a case study. Appl. Energy 2015, 152, 20–30. [Google Scholar] [CrossRef]
- Hyundai Nexo. Available online: https://www.hyundaiusa.com/us/en/vehicles/nexo (accessed on 1 November 2024).
- Toyota Mirai. Available online: https://mag.toyota.co.uk/toyota-mirai-technical-specifications-vs-fchv-adv/ (accessed on 1 November 2024).
- Honda Clarity. Available online: https://automobiles.honda.com/honda-automobiles/home/clarity-fuel-cell (accessed on 1 November 2024).
- Mercedes-Benz. Available online: https://group.mercedes-benz.com/documents/sustainability/product/daimler-environmental-check-lifecycle-compact-glc-f-cell-en.pdf (accessed on 1 November 2024).
- Kathimerini. Available online: https://www.ekathimerini.com/economy/1209162/hydrogen-powered-bus-tested-in-central-athens-route/ (accessed on 19 August 2024). (In Greek).
- European Commission; Joint Research Centre; Bravo Diaz, L.; Boillot, L. Historical Analysis of Clean Hydrogen JU Fuel Cell Electric Vehicles, Buses and Refueling Infrastructure Projects; Publications Office of the European Union: Luxembourg, 2024; Available online: https://data.europa.eu/doi/10.2760/892745 (accessed on 1 November 2024).
- Lipman, T.E.; Edwards, J.L.; Kammen, D.M. Economic Implications of Net Metering for Stationary and Motor Vehicle Fuel Cell Systems in California; University of California Energy Institute: Berkeley, CA, USA, 2002. [Google Scholar]
- Kempton, W.; Tomic, J.; Letendre, S.; Brooks, A.; Lipman, T. Vehicle-to-Grid Power: Battery, Hybrid, and Fuel Cell Vehicles as Resources for Distributed Electric Power in California; University of California: Davis, CA, USA, 2001; Volume IUCD-ITS-R. [Google Scholar]
- Williams, B.D.; Kurani, K.S. Commercializing light-duty plug-in/plug-out hydrogenfuel-cell vehicles: “Mobile Electricity” technologies and opportunities. J. Power Sources 2007, 166, 549–566. [Google Scholar] [CrossRef]
- Lipman, T.E.; Edwards, J.L.; Kammen, D.M. Fuel cell system economics: Comparing the costs of generating power with stationary and motor vehicle PEM fuel cell systems. Energy Policy 2004, 32, 101–125. [Google Scholar] [CrossRef]
- Kissock, J.K. Combined heat and power for buildings using fuel-cell cars. In Proceedings of the 1998 International Solar Energy Conference, Albuquerque, NM, USA, 14–17 June 1998; pp. 121–132. [Google Scholar]
- Alavi, F.; Park Lee, E.; van de Wouw, N.; De Schutter, B.; Lukszo, Z. Fuel cell cars in a microgrid for synergies between hydrogen and electricity networks. Appl. Energy 2017, 192, 296–304. [Google Scholar] [CrossRef]
- Cao, S. Comparison of the energy and environmental impact by integrating a H2 vehicle and an electric vehicle into a zero-energy building. Energy Convers. Manag. 2016, 123, 153–173. [Google Scholar] [CrossRef]
- Cao, S.; Alanne, K. Technical feasibility of a hybrid on-site H2 and renewable energy system for a zero-energy building with a H2 vehicle. Appl. Energy 2015, 158, 568–583. [Google Scholar] [CrossRef]
- Garmsiri, S.; Koohi-Fayegh, S.; Rosen, M.A.; Smith, G.R. Integration of transportation energy processes with a net zero energy community using captured waste hydrogen from electrochemical plants. Int. J. Hydrogen Energy 2016, 41, 8337–8346. [Google Scholar] [CrossRef]
- Oldenbroek, V.; Verhoef, L.A.; Van Wijk, A.J.M. Fuel cell electric vehicle as a power plant: Fully renewable integrated transport and energy system design and analysis for smart city areas. Int. J. Hydrogen Energy 2017, 42, 8166–8196. [Google Scholar] [CrossRef]
- Robledo, C.B.; Oldenbroek, V.; Abbruzzese, F.; van Wijk, A.J.M. Integrating a hydrogen fuel cell electric vehicle with vehicle-to-grid technology, photovoltaic power and a residential building. Appl. Energy 2018, 215, 615–629. [Google Scholar] [CrossRef]
- İnci, M. Technoeconomic Analysis of Fuel Cell Vehicle-to-Grid (FCV2G) System Supported by Photovoltaic Energy. Energy Technol. 2023, 11, 2201162. [Google Scholar] [CrossRef]
- Qian, F.; Gao, W.; Yang, Y.; Yu, D. Economic optimization and potential analysis of fuel cell vehicle-to-grid (FCV2G) system with large-scale buildings. Energy Convers. Manag. 2020, 205, 112463. [Google Scholar] [CrossRef]
- Li, H.; Sun, B.; Hao, J.; Zhao, J.; Li, J.; Khakichi, A. Economical planning of fuel cell vehicle-to-grid integrated green buildings with a new hybrid optimization algorithm. Int. J. Hydrogen Energy 2022, 47, 8514–8531. [Google Scholar] [CrossRef]
- İnci, M.; Buyuk, M.; Savrun, M.M.; Demir, M.H. Design and analysis of fuel cell vehicle-to-grid (FCV2G) system with high voltage conversion interface for sustainable energy production. Sustain. Cities Soc. 2021, 67, 102753. [Google Scholar] [CrossRef]
- İnci, M. Connecting multiple vehicular PEM fuel cells to electrical power grid as alternative energy sources: A Case Study. Int. J. Hydrogen Energy 2024, 52, 1035–1051. [Google Scholar] [CrossRef]
- Savrun, M.M.; Inci, M.; Buyuk, M. Design and analysis of a high energy efficient multi-port dc-dc converter interface for fuel cell/battery electric vehicle-to-home (V2H) system. J. Energy Storage 2022, 45, 103755. [Google Scholar] [CrossRef]
- Oldenbroek, V.; Hamoen, V.; Alva, S.; Robledo, C.; Verhoef, L.; van Wijk, A. Fuel cell electric vehicle-to-grid: Experimental feasibility and operational performance as balancing power plant. Fuel Cell 2018, 18, 649–662. [Google Scholar] [CrossRef]
- Pompodakis, E.E.; Kryonidis, G.C.; Karapidakis, E.S. Optimizing the installation of hybrid power plants in non-interconnected islands. J. Energy Storage 2023, 74, 109511. [Google Scholar] [CrossRef]
- Karapidakis, E.; Kalogerakis, C.; Pompodakis, E. Sustainable Power Generation Expansion in Island Systems with Extensive RES and Energy Storage. Inventions 2023, 8, 127. [Google Scholar] [CrossRef]
- Ahmed, A.; Pompodakis, E.E.; Katsigiannis, Y.; Karapidakis, E.S. Optimizing the Installation of a Centralized Green Hydrogen Production Facility in the Island of Crete, Greece. Energies 2024, 17, 1924. [Google Scholar] [CrossRef]
- Huang, C.; Zong, Y.; You, S.; Træholt, C. Analytical Modeling and Control of Grid-Scale Alkaline Electrolyzer Plant for Frequency Support in Wind-Dominated Electricity-Hydrogen Systems. IEEE Trans. Sustain. Energy 2023, 14, 217–232. [Google Scholar] [CrossRef]
- Toyota Fuel Cell Modules. Available online: https://www.toyota-europe.com/content/dam/toyota/tme/assets-without-cars/2022/image/lifestyle/brands-and-services/toyota-fuel-cell/fuel-cell-business/011931_Fuel_Cell_A5_portrait_WEB_P.pdf (accessed on 1 November 2024).
- Bignell, W.; Saffron, H.; Nguyen, T.T.; Humpage, W.D. Effects of machine inertia constants on system transient stability. Electr. Power Syst. Res. 1999, 51, 153–165. [Google Scholar] [CrossRef]
- Fernandez-Guillam, A.; Gómez-Lázaro, E.; Muljadi, E.; Molina-García, Á. Power systems with high renewable energy sources: A review of inertia and frequency control strategies over time. Renew. Sustain. Energy Rev. 2019, 115, 109369. [Google Scholar]
- H2 MOBILITY Deutschland GmbH & Co. KG. Available online: https://h2.live/en/fuelcell-cars/h2-trucks/ (accessed on 1 November 2024).
- Guillamon, A.F.; Muljadi, E.; García, A.M. Frequency control studies: A review of power system, conventional and renewable generation unit modeling. Electr. Power Syst. Res. 2022, 211, 108191. [Google Scholar]
- Nikiforow, K.; Pennanen, J.; Ihonen, J.; Uski, S.; Koski, P. Power ramp rate capabilities of a 5 kW proton exchange membrane fuel cell system with discrete ejector control. J. Power Sources 2018, 381, 30–37. [Google Scholar] [CrossRef]
- Alshehri, F.; Suárez, V.G.; Torres, J.L.R.; Perilla, A.; van der Meijden, M.A.M.M. Modelling and evaluation of PEM hydrogen technologies for frequency ancillary services in future multi-energy sustainable power systems. Heliyon 2019, 5, e01396. [Google Scholar] [CrossRef]
- Technology Assessment of a Fuel Cell Vehicle: 2017, Toyota Mirai. Available online: https://publications.anl.gov/anlpubs/2018/06/144774.pdf (accessed on 2 November 2024).
- Pompodakis, E.E.; Orfanoudakis, G.I.; Katsigiannis, Y.A.; Karapidakis, E.S. Hydrogen Production from Wave Power Farms to Refuel Hydrogen-Powered Ships in the Mediterranean Sea. Hydrogen 2024, 5, 494–518. [Google Scholar] [CrossRef]
- Vengatesan, S.; Jayakumar, A.; Sadasivuni, K.K. FCEV vs. BEV—A short overview on identifying the key contributors to affordable & clean energy (SDG-7). Energy Strategy Rev. 2024, 53, 101380. [Google Scholar]
- Jayakumar, A.; Chalmers, A.; Lie, T.T. Review of prospects for adoption of fuel cell electric vehicles in New Zealand. IET Electr. Syst. Transp. 2017, 7, 259–266. [Google Scholar] [CrossRef]
- Pompodakis, E.E.; Ahmed, A.; Orfanoudakis, G.I.; Karapidakis, E.S. Optimization of Residential Hydrogen Facilities with Waste Heat Recovery: Economic Feasibility across Various European Cities. Processes 2024, 12, 1933. [Google Scholar] [CrossRef]
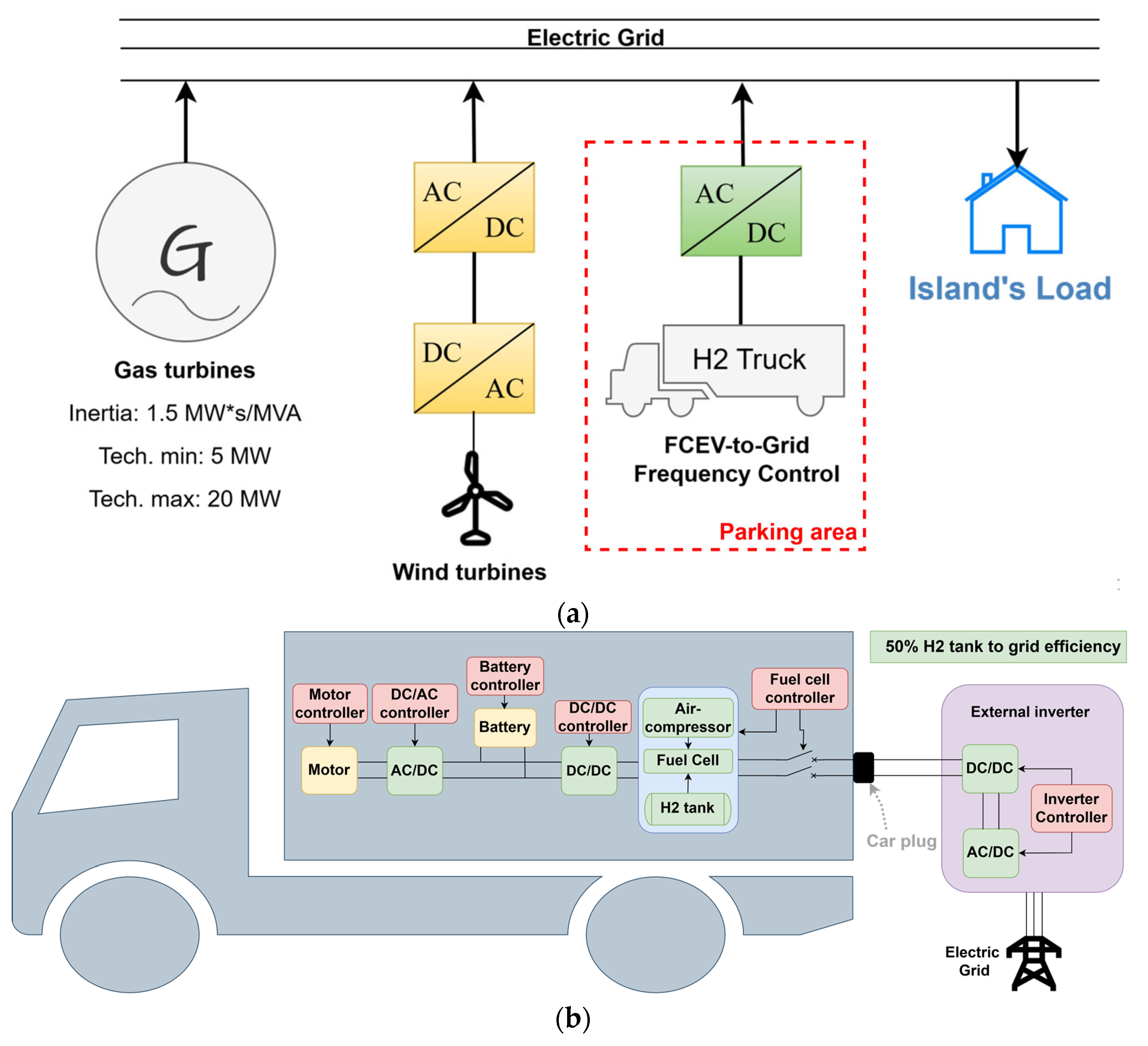
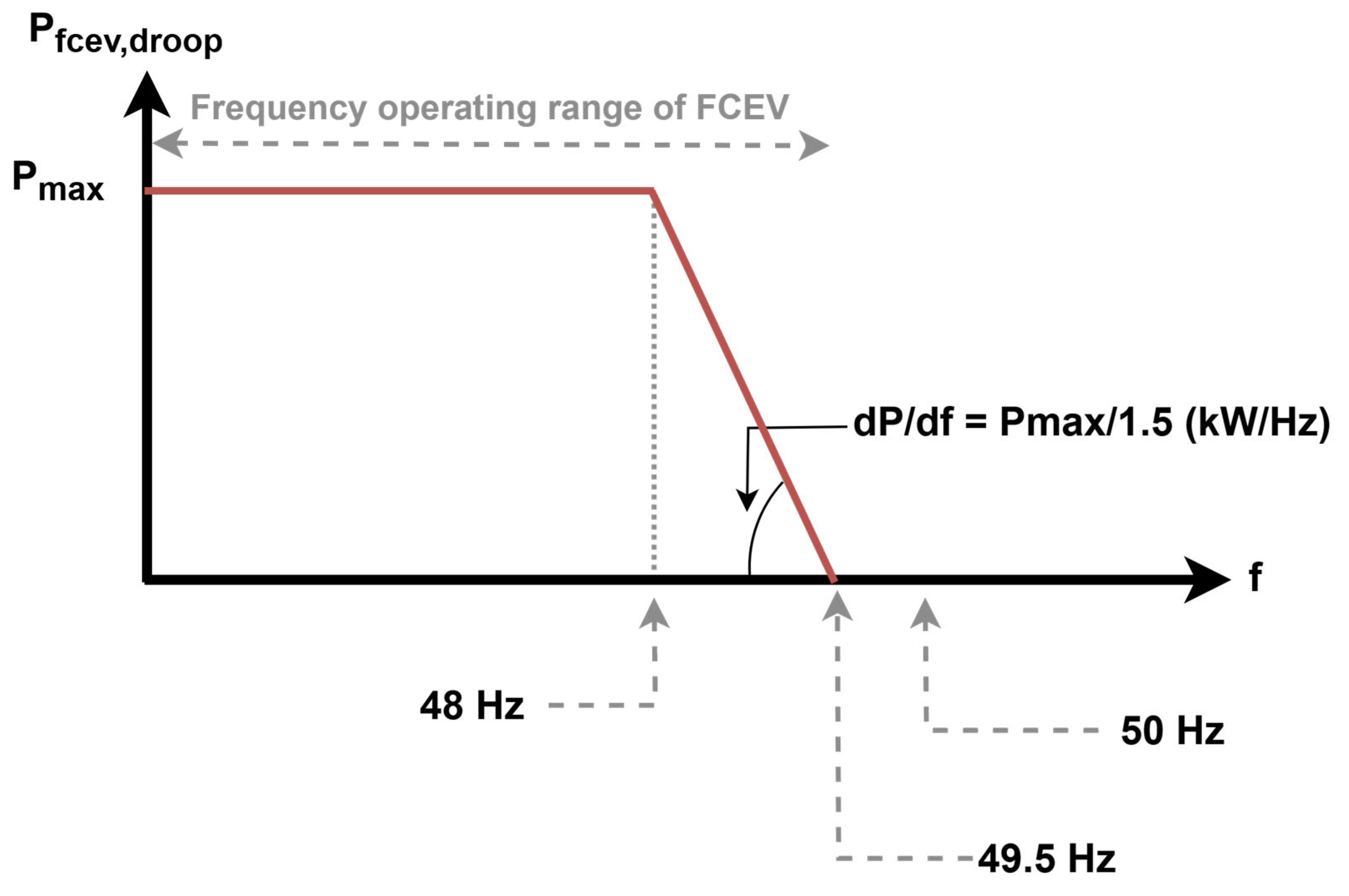
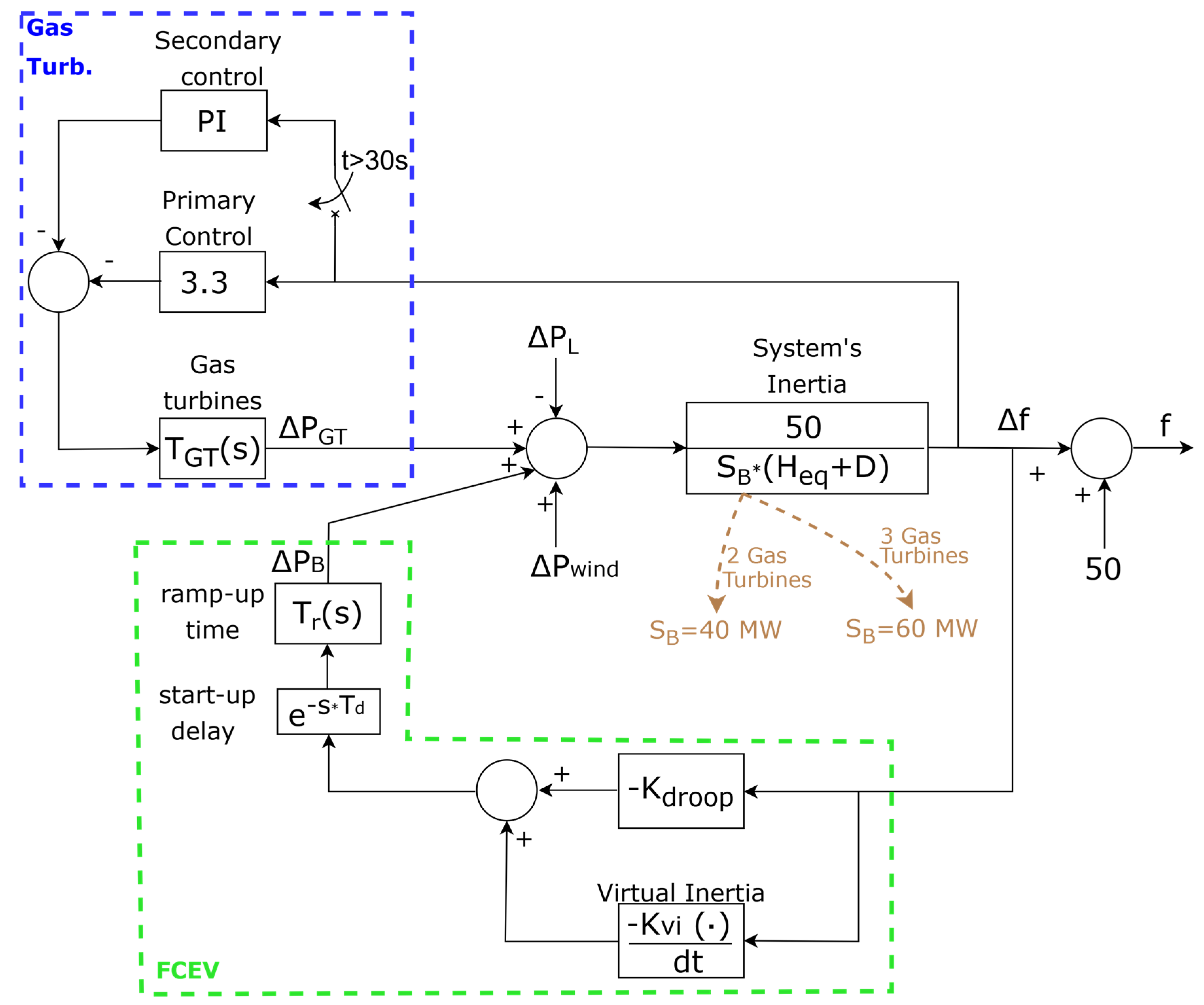
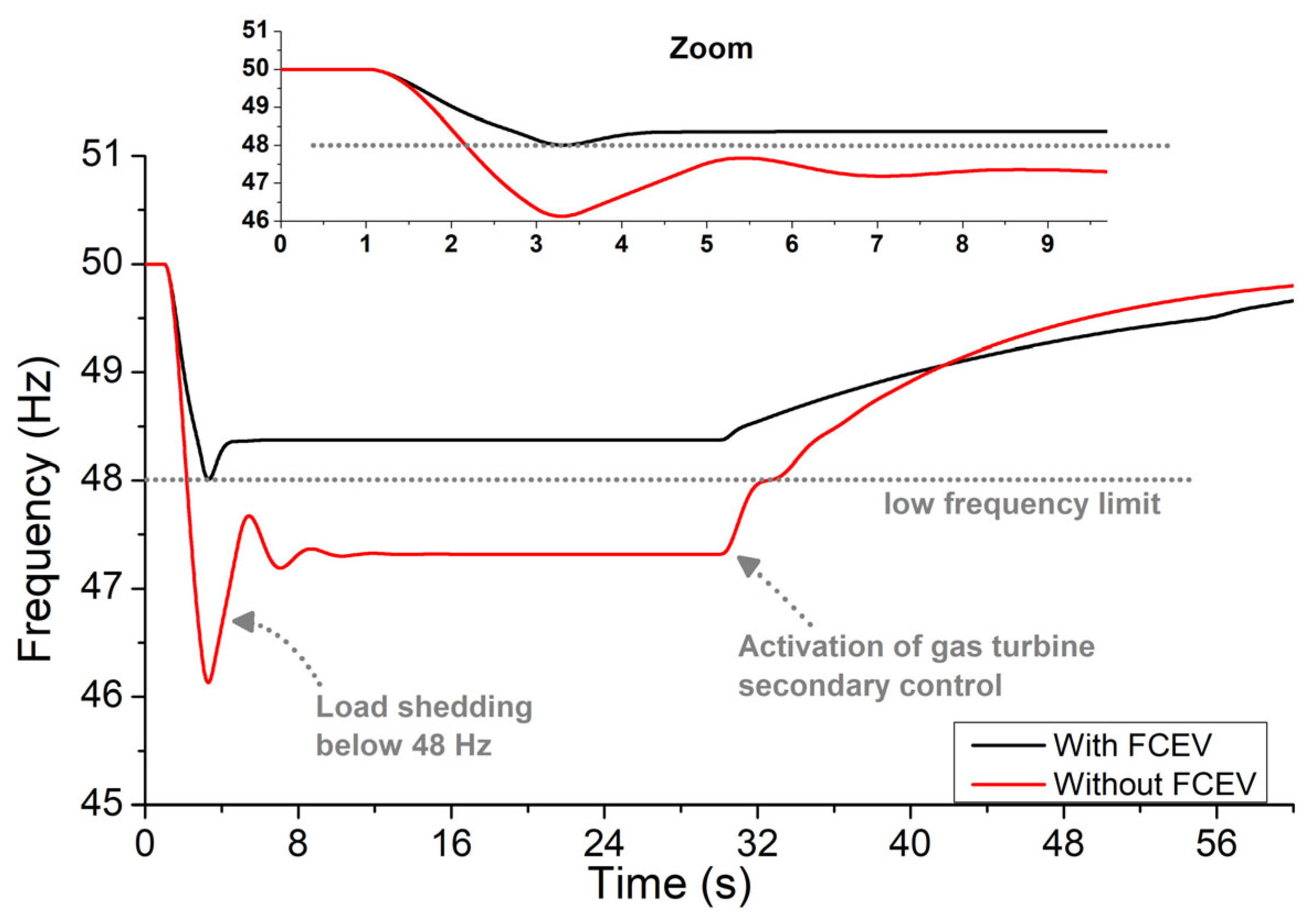

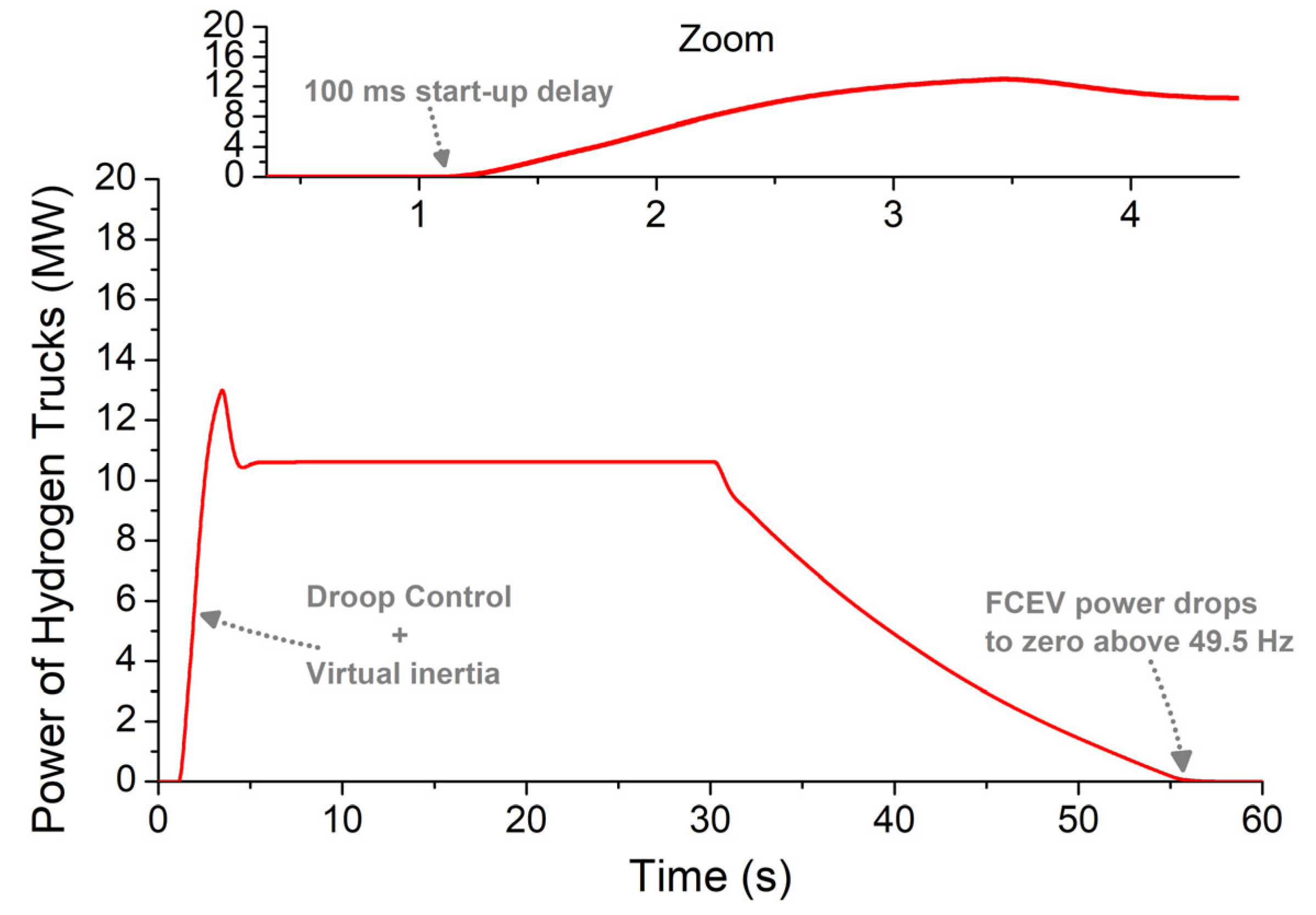

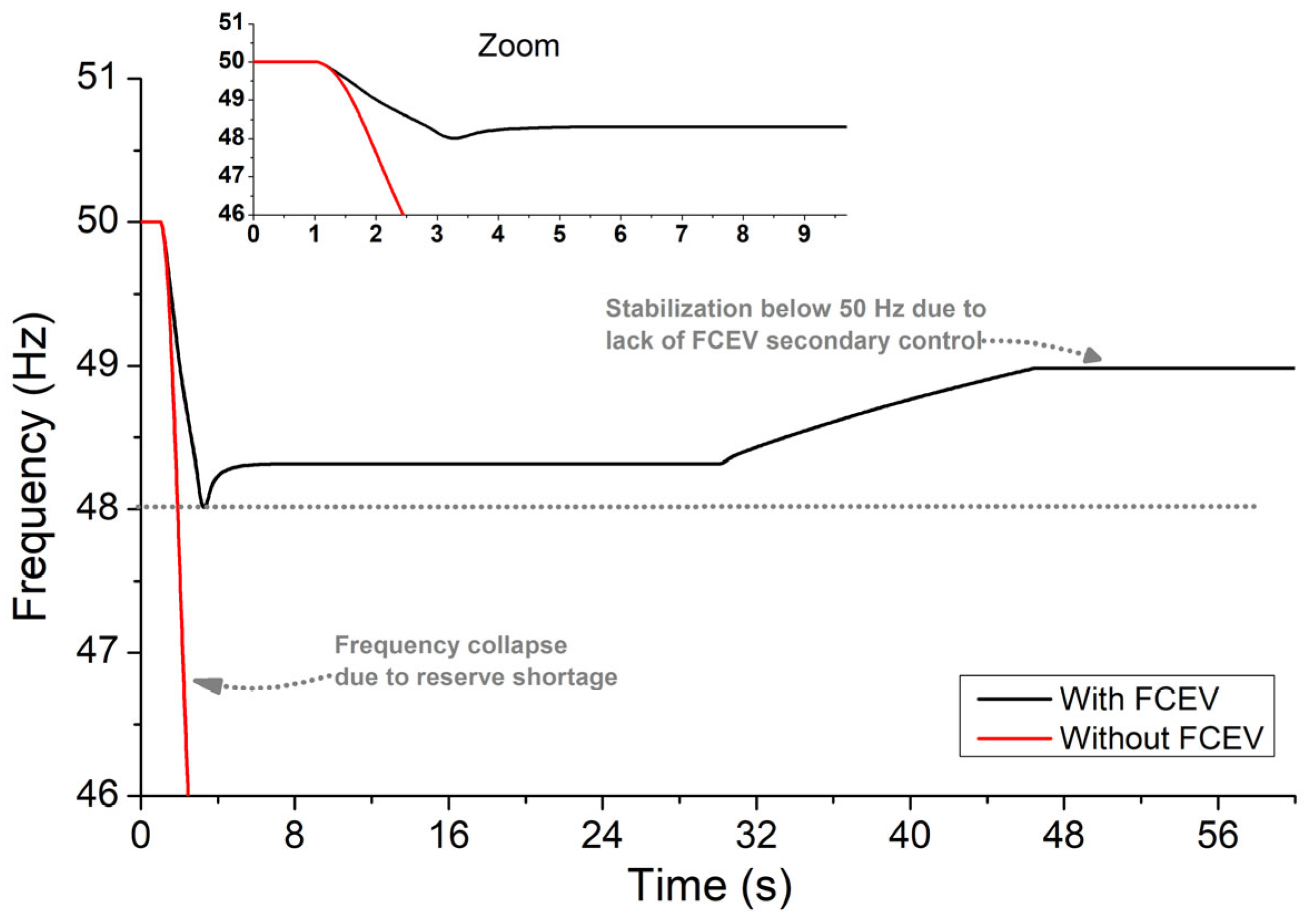
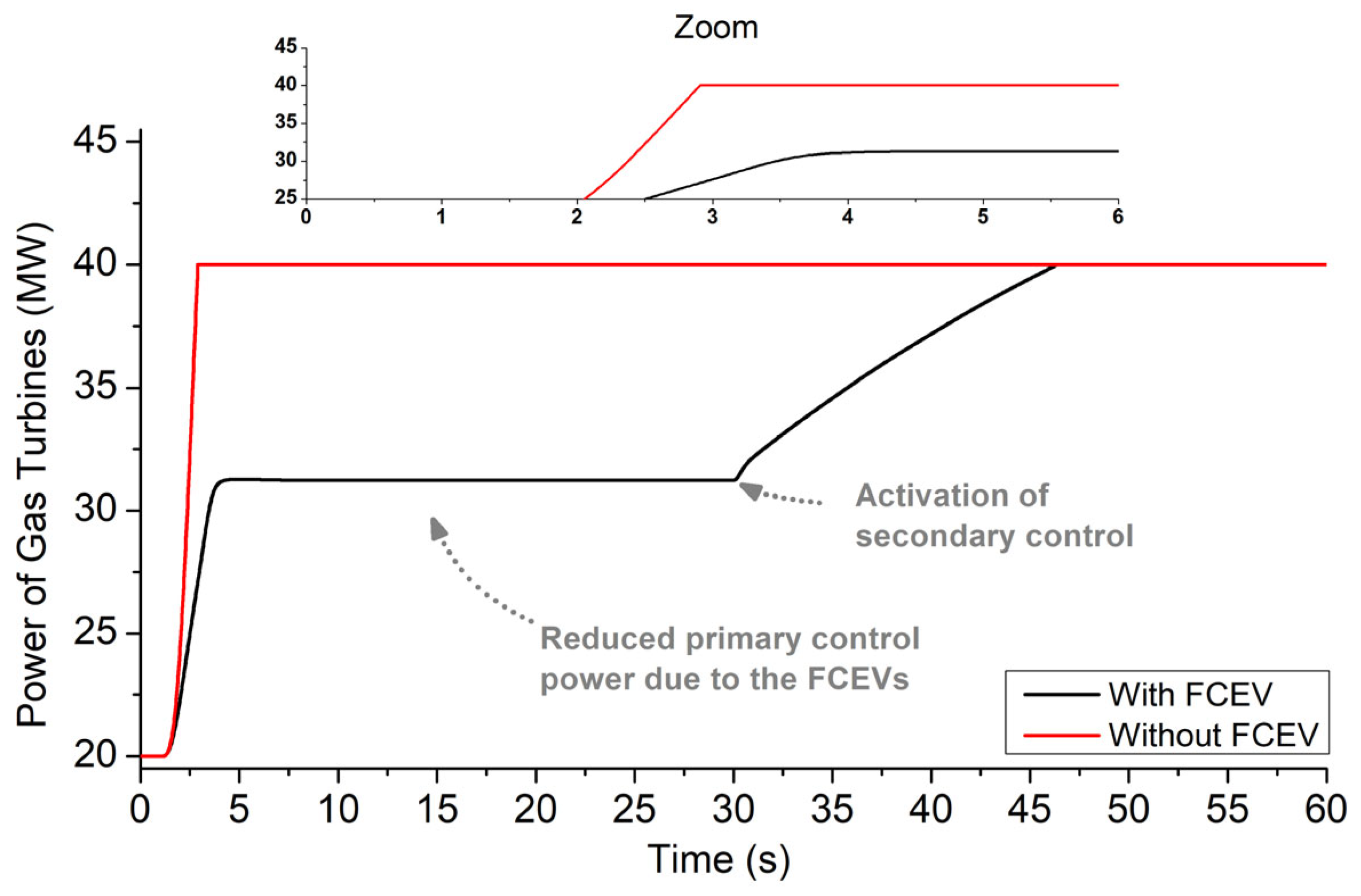
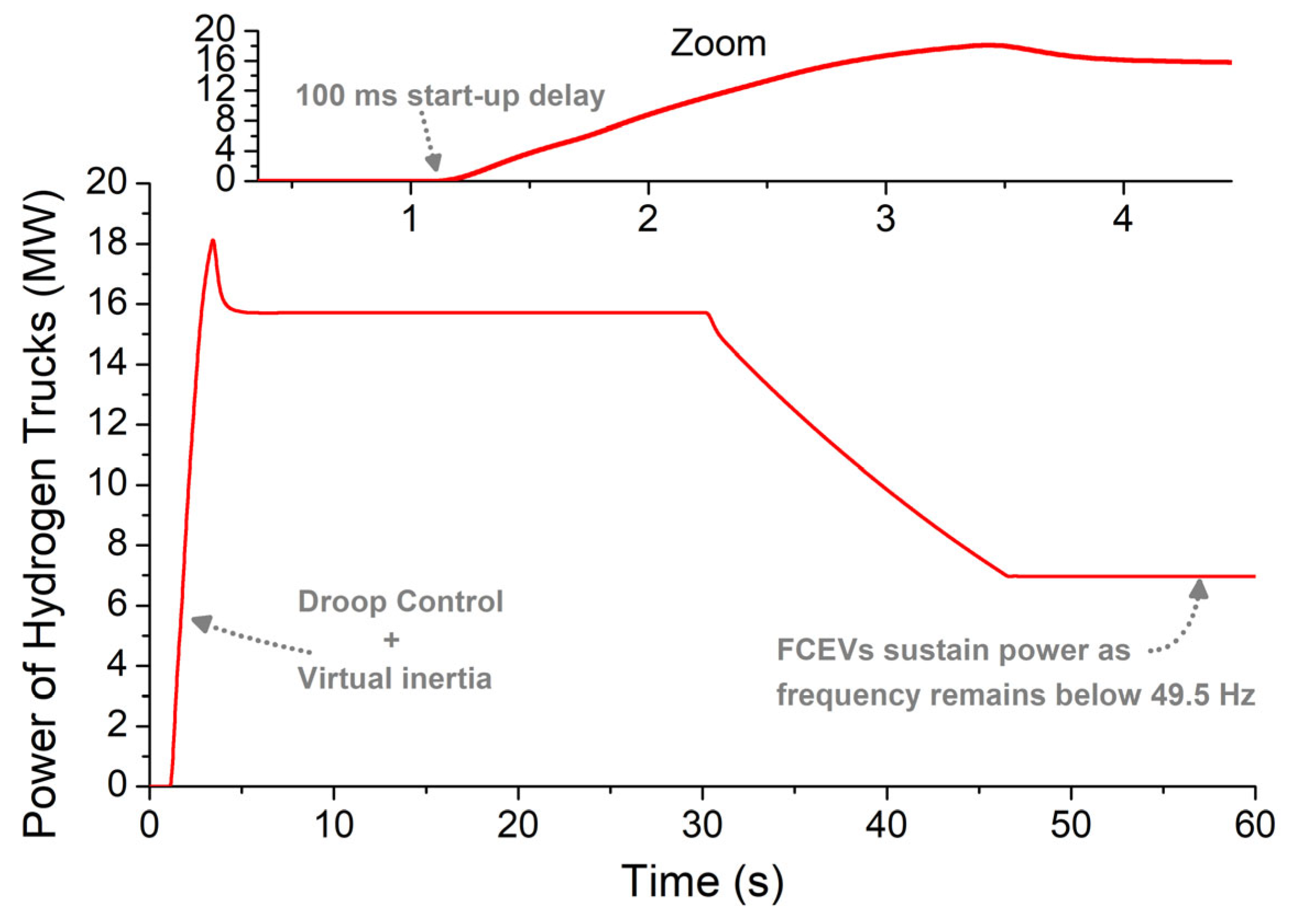
| Block | Parameter | Value |
| Gas turbine | See Figure 4 of [51] | |
| Technical minimum–maximum | 5–20 MW | |
| Droop control | 3.3 MW/Hz | |
| Secondary control | Activation at 30 sec | |
| Electric Network | Nominal Power | 100 MW (island the size of Rhode, Greece) |
| 1.5 [7,48,49] (Figure 8 of [49]) | ||
| D | 0.05 [51] | |
| 40 MVA (2 gas turbines) 60 MVA (3 gas turbines) | ||
| FCEV | Start-up delay () | 100 ms |
| Ramp-up time | 2 s [47,50,52,53] | |
| 200 kW (per truck) [50,54] | ||
| 0.0001 | ||
| Efficiency | 50% [50,54] | |
| Load | 0 | |
| RESs | Scenario 1: Scenario 2: Scenario 3: |
| FCEVs | Consumption per disturbance per vehicle | 0.1 kg H2 |
| Number of disturbances per day | 3 | |
| Cost of hydrogen | 5 EUR/kg | |
| Number of vehicles | 100 | |
| Total annual cost | 150 EUR/day or 54,750 EUR/year | |
| Grid-scale battery | Levelized CAPEX | 100,000 EUR/MW |
| Capacity | 10 MW | |
| Capital recovery factor | 0.13 | |
| Annualized CAPEX | 130,000 EUR/year | |
| Electricity consumption | 500 kWh/day | |
| Levelized electricity cost | 0.15 EUR/kWh | |
| Annual electricity cost | 75 EUR/day or 27,375 EUR/year | |
| Total annual cost | 157,375 EUR/year |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Christos, T.; Pompodakis, E.E.; Orfanoudakis, G.I. Techno-Economic Feasibility of Fuel Cell Vehicle-to-Grid Fast Frequency Control in Non-Interconnected Islands. Hydrogen 2025, 6, 1. https://doi.org/10.3390/hydrogen6010001
Christos T, Pompodakis EE, Orfanoudakis GI. Techno-Economic Feasibility of Fuel Cell Vehicle-to-Grid Fast Frequency Control in Non-Interconnected Islands. Hydrogen. 2025; 6(1):1. https://doi.org/10.3390/hydrogen6010001
Chicago/Turabian StyleChristos, Tziotas, Evangelos E. Pompodakis, and Georgios I. Orfanoudakis. 2025. "Techno-Economic Feasibility of Fuel Cell Vehicle-to-Grid Fast Frequency Control in Non-Interconnected Islands" Hydrogen 6, no. 1: 1. https://doi.org/10.3390/hydrogen6010001
APA StyleChristos, T., Pompodakis, E. E., & Orfanoudakis, G. I. (2025). Techno-Economic Feasibility of Fuel Cell Vehicle-to-Grid Fast Frequency Control in Non-Interconnected Islands. Hydrogen, 6(1), 1. https://doi.org/10.3390/hydrogen6010001







