A Technical Study on an Integrated Closed-Loop Solid Oxide Fuel Cell and Ammonia Decomposition System for Marine Application
Abstract
1. Introduction
2. Methodology
2.1. Electrochemical Reaction
2.2. Mass and Heat Transfer Equation
2.3. Evaluation Metric
- The 0D model is applied to ammonia cracking and SOFC systems.
- Only the static condition is evaluated and discussed.
- Assuming that all cells behave the same in the stack, a single-cell modular SOFC is used to represent the stack by considering the number of cells either in series and/or parallel arrangement. This would help simplify the assessment of the SOFC’s performance and capacity.
- The temperature difference within the electrolyte structure (anode and cathode electrolyte) is negligible.
- The transfer of heat between the electrolyte structure, the external surroundings, and between the SOFCs and ammonia crackers is not considered.
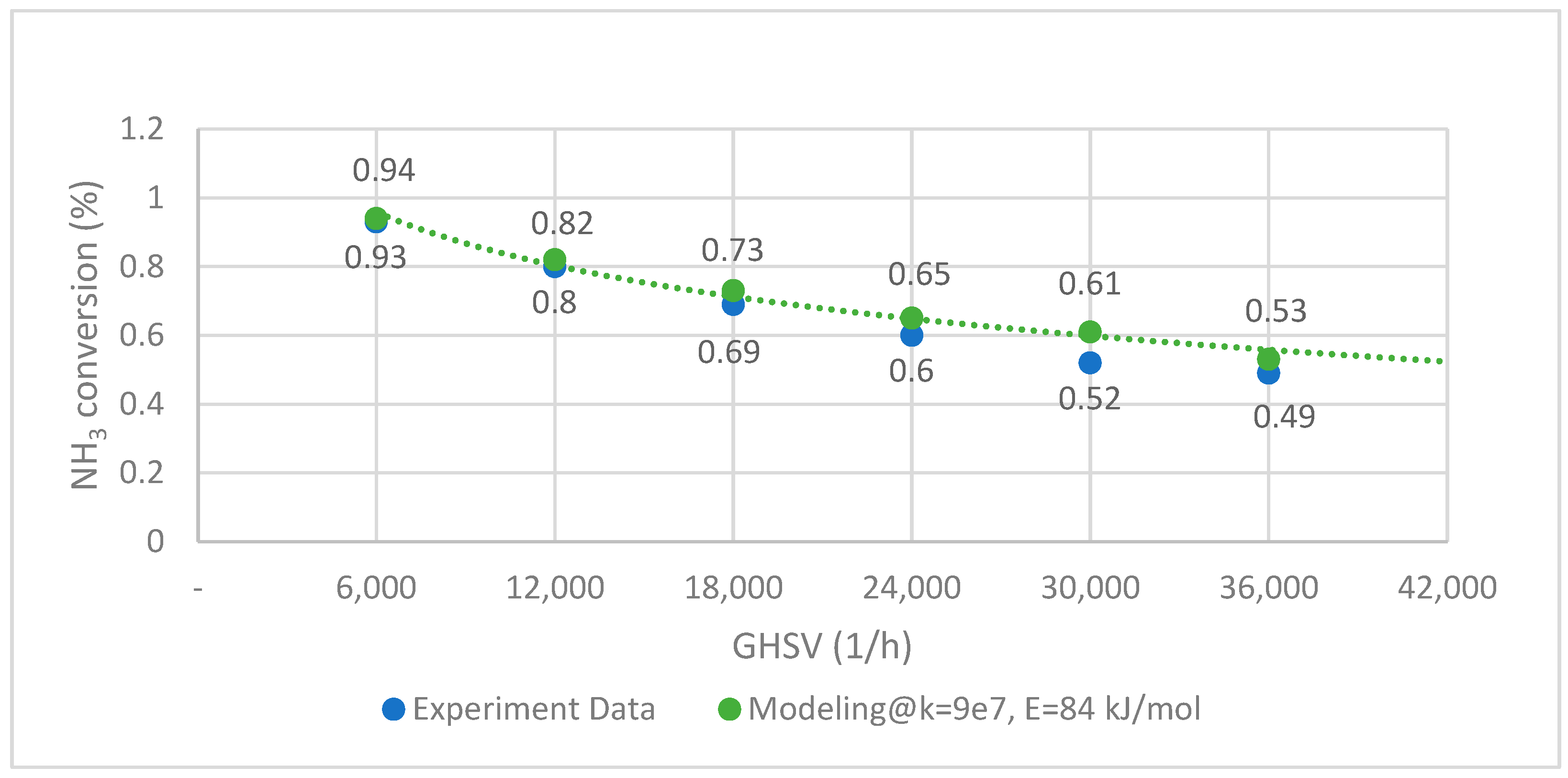
3. Validation
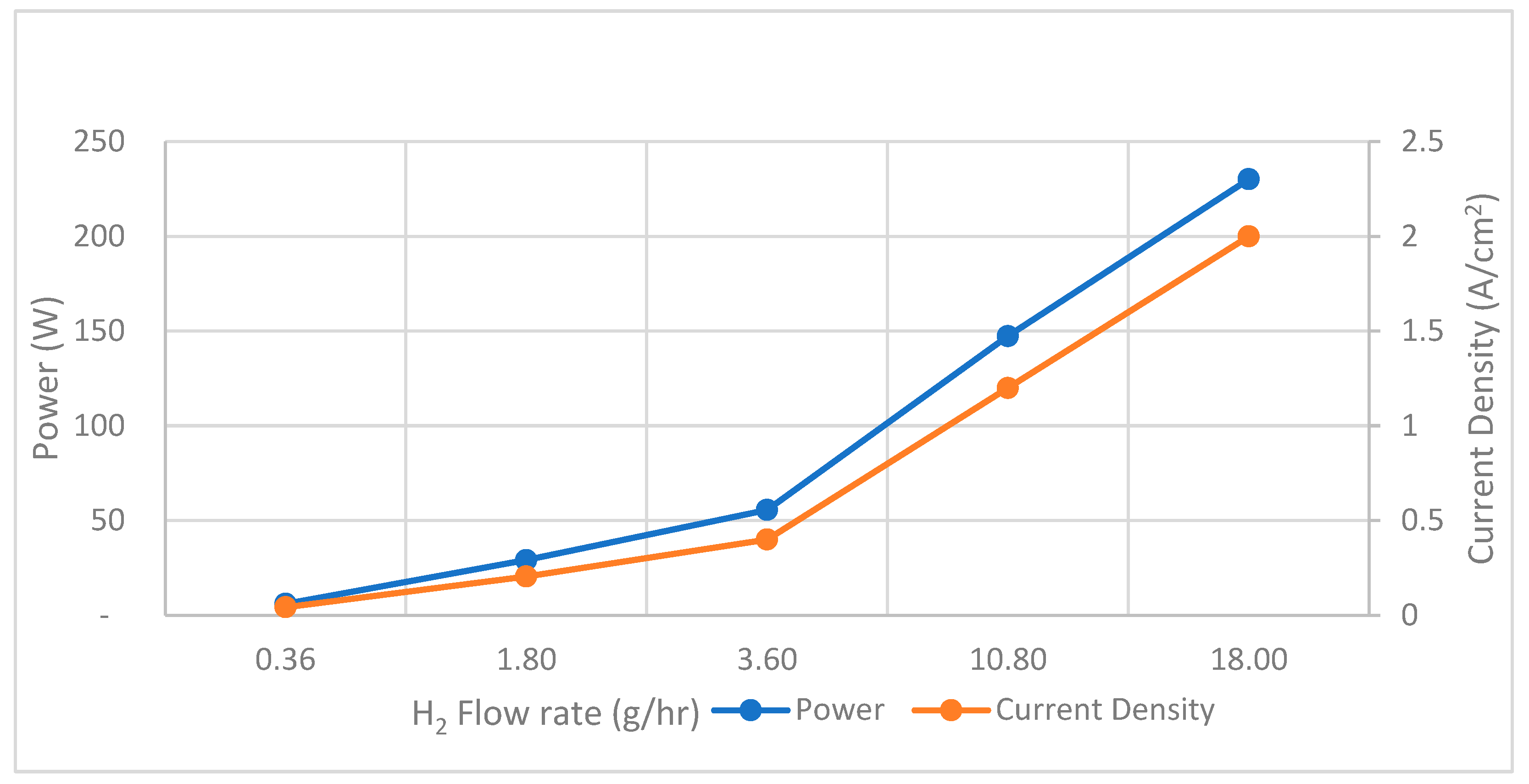
4. Result Evaluation and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Specific heat capacity for electrolyte, kJ/kg-K | |
| Specific heat capacity for the anode, kJ/kg-K | |
| Specific heat capacity for the cathode, kJ/kg-K | |
| Activation energy of the reaction | |
| Energy of activation | |
| Total energy in the anode, kJ | |
| Total energy in the cathode, kJ | |
| F | Faraday constant, kJ/mol |
| Gibbs free energy, J/mol | |
| H | Height of channel, mm |
| Enthalpy of , kJ/kg | |
| Enthalpy of , kJ/kg | |
| Enthalpy of , kJ/kg | |
| Enthalpy of , kJ/kg | |
| Enthalpy of O2− | |
| Enthalpy of the O2− species crossing electrolyte, kJ/kg | |
| I | Current generated from the fuel cell through the electrochemical reaction from electrons |
| Component, e.g., H+, O2− | |
| J | Electrode current density, A/cm2 |
| Number of reactions | |
| Exchange current density, A/cm2 | |
| k | Thermal conductivity coefficient of the material, W/mK |
| Ko | Pre-exponential factor |
| Pre-exponential factor of the activation losses | |
| L | Length of single FC anode, m |
| Mass of electrolyte, kg | |
| Mass of anode, kg | |
| Mass of cathode, kg | |
| Mass flow rate in, kg/s | |
| Mass flow rate out, kg/s | |
| Mass flow rate in, kg/s | |
| Mass flow rate out, kg/s | |
| Mass flow rate in, kg/s | |
| Mass flow rate out, kg/s | |
| Mass flow rate of component i, kg/s | |
| Mass flow rate of component O2, kg/s | |
| Molecular weight of in-stream (including O2 and N2) entering the cathode side, kg/kmol | |
| Molecular weight of component i, kg/kmol | |
| Molecular weight of component O2, kg/kmol | |
| No. of mol of O2 entering the cathode side | |
| No. of mass fraction of hydrogen in the anode | |
| The power produced by the fuel cell, W | |
| Pressure of H2, bar | |
| Pressure of N2, bar | |
| Pressure of NH3, bar | |
| Partial pressure generated by the water in the anode, Pa | |
| Partial pressure generated by H2 in the anode, Pa | |
| Partial pressure generated by O2 in the anode, Pa | |
| Partial pressure generated by the water in triple phase boundary, Pa | |
| Partial pressure generated by H2 in triple phase boundary, Pa | |
| Partial pressure generated by O2 in triple phase boundary, Pa | |
| Partial pressure generated by O2 in the cathode, Pa | |
| Heat transfer rate from SOFC to ammonia cracker, kJ/s | |
| R | Universal gas constant, kJ/mol/K |
| RNH3 | Reaction rate in % |
| Rate of the electrochemical reaction of hydrogen | |
| Temperature for anode, K | |
| Temperature for the cathode, K | |
| Overall temperature for ammonia cracker, K | |
| Temperature for electrolytes, K | |
| Overall temperature for SOFC, K | |
| Temperature for electrode, K | |
| Temperature at anode, K | |
| Temperature at cathode, K | |
| Time, s | |
| Tortuosity of membrane between anode and electrolyte | |
| Tortuosity of membrane between cathode and electrolyte | |
| Tortuosity of membrane cross electrolyte | |
| V | Voltage generated from the fuel cell through the electrochemical reaction from electrons |
| Activation voltage losses, V | |
| Total cell voltage produced, V | |
| Open circuit voltage, V | |
| Ohmic voltage losses, V | |
| Voltage losses due to mass transport, V | |
| W | Width of single FC anode, m |
| Mass fraction for hydrogen at the anode | |
| Greek letters | |
| transfer coefficient | |
| Emissivity | |
| Stefan–Boltzmann constant, 5.67 × 10−8 J/(s × m2)/K4 | |
| Conductivity of the anode electrolyte layer | |
| Conductivity of the cathode electrolyte layer | |
| Conductivity of the electrolyte layer | |
| Heat transfer coefficient for the cathode, kJ/(s × m2 × K) | |
| Heat transfer coefficient for the anode, kJ/(s × m2 × K) | |
| Air excess ratio | |
| Heat transfer coefficient for SOFC, kJ/(s × m2 × K) | |
| Enthalpy of reaction 1 process, e.g., energy consumed from O2− to form H2O, J/mol | |
| Cell efficiency |
References
- Pompodakis, E.E.; Orfanoudakis, G.I.; Katsigiannis, Y.A.; Karapidakis, E.S. Hydrogen Production from Wave Power Farms to Refuel Hydrogen-Powered Ships in the Mediterranean Sea. Hydrogen 2024, 5, 494–518. [Google Scholar] [CrossRef]
- Chen, P.S.-L.; Fan, H.; Enshaei, H.; Zhang, W.; Shi, W.; Abdussamie, N.; Miwa, T.; Qu, Z.; Yang, Z. Opportunities and Challenges of Hydrogen Ports: An Empirical Study in Australia and Japan. Hydrogen 2024, 5, 436–458. [Google Scholar] [CrossRef]
- Inal, O.B.; Zincir, B.; Deniz, C. Investigation on the Decarbonization of Shipping: An Approach to Hydrogen and Ammonia. Int. J. Hydrogen Energy 2022, 47, 19888–19900. [Google Scholar] [CrossRef]
- Sørensen, R.D.; Berning, T. A Computational Fluid Dynamics Analysis of Hydrogen Leakage and Nitrogen Purging of a Solid Oxide Fuel Cell Stack. Hydrogen 2023, 4, 917–931. [Google Scholar] [CrossRef]
- Wartsila.com. Experience Wärtsilä 25 Ammonia, 4-Stroke Engine for Marine Applications. Available online: https://www.wartsila.com/marine/wartsila-25-ammonia (accessed on 25 July 2024).
- Elkafas, A.G.; Rivarolo, M.; Gadducci, E.; Magistri, L.; Massardo, A.F. Fuel Cell Systems for Maritime: A Review of Research Development, Commercial Products, Applications, and Perspectives. Processes 2022, 11, 97. [Google Scholar] [CrossRef]
- Xing, H.; Stuart, C.; Spence, S.; Chen, H. Fuel Cell Power Systems for Maritime Applications: Progress and Perspectives. Sustainability 2021, 13, 1213. [Google Scholar] [CrossRef]
- Jeerh, G.; Zhang, M.; Tao, S. Recent Progress in Ammonia Fuel Cells and Their Potential Applications. J. Mater. Chem. A 2020, 9, 727–752. [Google Scholar] [CrossRef]
- Ammonia Cracker. Available online: https://samgasprojects.com/detail/ammonia-cracker.html (accessed on 25 July 2024).
- Wang, Z.; Dong, B.; Yin, J.; Li, M.; Ji, Y.; Han, F. Towards a Marine Green Power System Architecture: Integrating Hydrogen and Ammonia as Zero-Carbon Fuels for Sustainable Shipping. Int. J. Hydrogen Energy 2024, 50, 1069–1087. [Google Scholar] [CrossRef]
- Welaya, Y.M.; El Gohary, M.M.; Ammar, N.R. A Comparison between Fuel Cells and Other Alternatives for Marine Electric Power Generation. Int. J. Nav. Arch. Ocean Eng. 2011, 3, 141–149. [Google Scholar] [CrossRef]
- Benet, Á.; Villalba-Herreros, A.; D’amore-Domenech, R.; Leo, T.J. Knowledge Gaps in Fuel Cell-Based Maritime Hybrid Power Plants and Alternative Fuels. J. Power Sources 2022, 548, 232066. [Google Scholar] [CrossRef]
- Díaz-de-Baldasano, M.C.; Mateos, F.J.; Núñez-Rivas, L.R.; Leo, T.J. Conceptual Design of Offshore Platform Supply Vessel Based on Hybrid Diesel Generator-Fuel Cell Power Plant. Appl. Energy 2014, 116, 91–100. [Google Scholar] [CrossRef]
- Di Ilio, G.; Bionda, A.; Ponzini, R.; Salvadore, F.; Cigolotti, V.; Minutillo, M.; Georgopoulou, C.; Mahos, K. Towards the Design of a Hydrogen-Powered Ferry for Cleaner Passenger Transport. Int. J. Hydrogen Energy 2024. In Press. [Google Scholar] [CrossRef]
- Dall’armi, C.; Micheli, D.; Taccani, R. Comparison of Different Plant Layouts and Fuel Storage Solutions for Fuel Cells Utilization on a Small Ferry. Int. J. Hydrogen Energy 2021, 46, 13878–13897. [Google Scholar] [CrossRef]
- Babatunde, O.M.; Akintayo, B.D.; Emezirinwune, M.U.; Olanrewaju, O.A. Environmental Impact Assessment of a 1 kW Proton-Exchange Membrane Fuel Cell: A Mid-Point and End-Point Analysis. Hydrogen 2024, 5, 352–373. [Google Scholar] [CrossRef]
- McKinlay, C.J.; Turnock, S.R.; Hudson, D.A. Route to Zero Emission Shipping: Hydrogen, Ammonia or Methanol? Int. J. Hydrogen Energy 2021, 46, 28282–28297. [Google Scholar] [CrossRef]
- Lamari, F.; Weinberger, B.; Langlois, P.; Fruchart, D. Instances of Safety-Related Advances in Hydrogen as Regards Its Gaseous Transport and Buffer Storage and Its Solid-State Storage. Hydrogen 2024, 5, 387–402. [Google Scholar] [CrossRef]
- Matveev, K.I.; Leachman, J.W. The Effect of Liquid Hydrogen Tank Size on Self-Pressurization and Constant-Pressure Venting. Hydrogen 2023, 4, 444–455. [Google Scholar] [CrossRef]
- Energy.gov. Comparison of Fuel Cell Technologies. Available online: https://www.energy.gov/eere/fuelcells/comparison-fuel-cell-technologies (accessed on 25 July 2024).
- Nanadegani, F.S.; Sunden, B. Review of Exergy and Energy Analysis of Fuel Cells. Int. J. Hydrogen Energy 2023, 48, 32875–32942. [Google Scholar] [CrossRef]
- Bielefeld, N.M.; Sørensen, R.D.; Jørgensen, M.; Kure, K.; Berning, T. A One-Dimensional Computational Model to Identify Operating Conditions and Cathode Flow Channel Dimensions for a Proton Exchange Membrane Fuel Cell. Hydrogen 2024, 5, 624–643. [Google Scholar] [CrossRef]
- Dudek, M.; Raźniak, A.; Markowski, J.; Danchak, L.; Dudek, P. The Energy Efficiency of an Extended Range Unit Involving a Polymer Exchange Membrane Fuel Cell Stack. E3S Web Conf. 2024, 551, 01010. [Google Scholar] [CrossRef]
- Tawalbeh, M.; Alarab, S.; Al-Othman, A.; Javed, R.M.N. The Operating Parameters, Structural Composition, and Fuel Sustainability Aspects of PEM Fuel Cells: A Mini Review. Fuels 2022, 3, 449–474. [Google Scholar] [CrossRef]
- Singh, M.; Zappa, D.; Comini, E. Solid Oxide Fuel Cell: Decade of Progress, Future Perspectives and Challenges. Int. J. Hydrogen Energy 2021, 46, 27643–27674. [Google Scholar] [CrossRef]
- Tellez-Cruz, M.M.; Escorihuela, J.; Solorza-Feria, O.; Compañ, V. Proton Exchange Membrane Fuel Cells (PEMFCs): Advances and Challenges. Polymers 2021, 13, 3064. [Google Scholar] [CrossRef]
- Micoli, L.; Coppola, T.; Turco, M. A Case Study of a Solid Oxide Fuel Cell Plant on Board a Cruise Ship. J. Mar. Sci. Appl. 2021, 20, 524–533. [Google Scholar] [CrossRef]
- Ilbas, M.; Kumuk, B.; Alemu, M.A.; Arslan, B. Numerical Investigation of a Direct Ammonia Tubular Solid Oxide Fuel Cell in Comparison with Hydrogen. Int. J. Hydrogen Energy 2020, 45, 35108–35117. [Google Scholar] [CrossRef]
- Stambouli, A.B.; Traversa, E. Fuel Cells, an Alternative to Standard Sources of Energy. Renew. Sustain. Energy Rev. 2002, 6, 295–304. [Google Scholar] [CrossRef]
- Yilmaz, F.; Ozturk, M. Design and Modeling of an Integrated Combined Plant with SOFC for Hydrogen and Ammonia Generation. Int. J. Hydrogen Energy 2022, 47, 31911–31926. [Google Scholar] [CrossRef]
- Kamara, K.P.; Merlin, G.; Bamba, G.; Druart, F.; Deseure, J. Simulation of Biogas Conversion Using Porous Solid Oxide Electrochemical Cells: Virtual Prototyping. Hydrogen 2022, 3, 488–500. [Google Scholar] [CrossRef]
- Peppas, A.; Kottaridis, S.; Politi, C.; Angelopoulos, P.M.; Taxiarchou, M. Multi-Model Assessment for Secondary Smelting Decarbonisation: The Role of Hydrogen in the Clean Energy Transition. Hydrogen 2023, 4, 103–119. [Google Scholar] [CrossRef]
- Ni, M.; Leung, M.K.H.; Leung, D.Y.C. Ammonia-Fed Solid Oxide Fuel Cells for Power Generation-A Review. Int. J. Energy Res. 2009, 33, 943–959. [Google Scholar] [CrossRef]
- Duong, P.A.; Ryu, B.; Kim, C.; Lee, J.; Kang, H. Energy and Exergy Analysis of an Ammonia Fuel Cell Integrated System for Marine Vessels. Energies 2022, 15, 3331. [Google Scholar] [CrossRef]
- Quach, T.-Q.; Giap, V.-T.; Lee, D.K.; Pineda, I.T.; Ahn, K.Y. Parametric Study of a High-Performance Ammonia-Fed SOFC Standalone System. J. Mech. Sci. Technol. 2022, 36, 3193–3201. [Google Scholar] [CrossRef]
- Cinti, G.; Liso, V.; Araya, S.S. Design Improvements for Ammonia-Fed SOFC Systems through Power Rating, Cascade Design and Fuel Recirculation. Int. J. Hydrogen Energy 2023, 48, 15269–15279. [Google Scholar] [CrossRef]
- Salogni, A.; Colonna, P. Modeling of Solid Oxide Fuel Cells for Dynamic Simulations of Integrated Systems. Appl. Therm. Eng. 2009, 30, 464–477. [Google Scholar] [CrossRef]
- Tabassum, H.; Mukherjee, S.; Chen, J.; Holiharimanana, D.; Karakalos, S.; Yang, X.; Hwang, S.; Zhang, T.; Lu, B.; Chen, M.; et al. Hydrogen Generation via Ammonia Decomposition on Highly Efficient and Stable Ru-Free Catalysts: Approaching Complete Conversion at 450 °C. Energy Environ. Sci. 2022, 15, 4190–4200. [Google Scholar] [CrossRef]
- Xu, Y.-W.; Wu, X.-L.; Zhong, X.; Zhao, D.; Fu, J.; Jiang, J.; Deng, Z.; Fu, X.; Li, X. Development of Solid Oxide Fuel Cell and Battery Hybrid Power Generation System. Int. J. Hydrogen Energy 2020, 45, 8899–8914. [Google Scholar] [CrossRef]
- MarineLink. Why Ammonia Is the Fuel of the Future for Maritime Shipping. Available online: https://www.marinelink.com/news/why-ammonia-fuel-future-maritime-shipping-506822 (accessed on 27 July 2023).
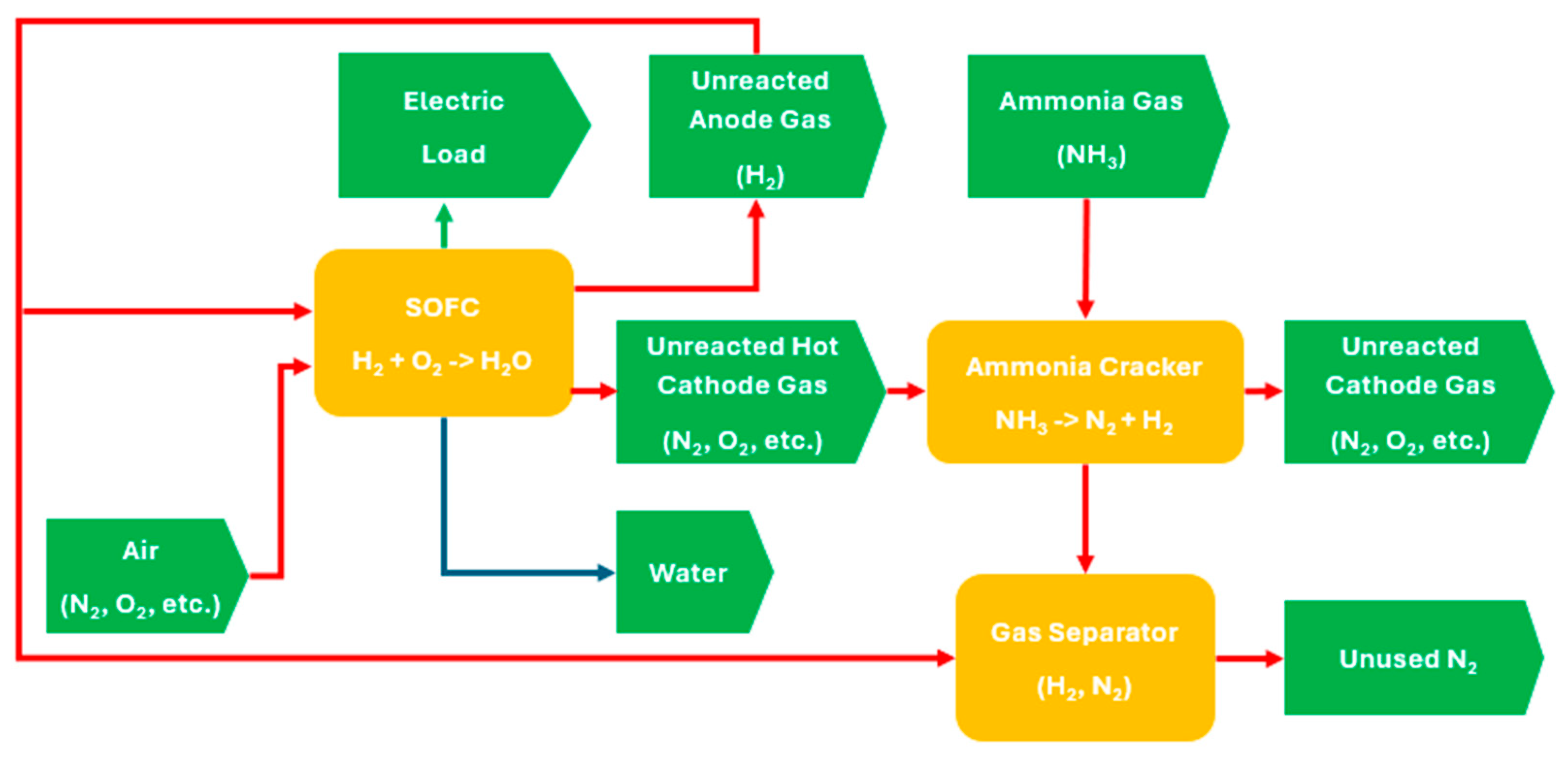





| Component | Input Parameter | Reaction/Process | Output Parameter |
|---|---|---|---|
| Ammonia Cracker |
|
|
|
|
|
| |
| Gas Separator |
|
|
|
| SOFCs |
|
|
|
| Parameter | Value | Unit |
|---|---|---|
| Cell Area | 0.15 × 0.15 | m2 |
| Inlet Fuel (H2) Flow Rate | 1 × 10−3 | g/s |
| Gas Inlet Pressure | 1 | Bar |
| Gas Inlet Temperature | 600 | K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Miao, B.; Chan, S.H. A Technical Study on an Integrated Closed-Loop Solid Oxide Fuel Cell and Ammonia Decomposition System for Marine Application. Hydrogen 2024, 5, 723-736. https://doi.org/10.3390/hydrogen5040038
Wu S, Miao B, Chan SH. A Technical Study on an Integrated Closed-Loop Solid Oxide Fuel Cell and Ammonia Decomposition System for Marine Application. Hydrogen. 2024; 5(4):723-736. https://doi.org/10.3390/hydrogen5040038
Chicago/Turabian StyleWu, Shengwei, Bin Miao, and Siew Hwa Chan. 2024. "A Technical Study on an Integrated Closed-Loop Solid Oxide Fuel Cell and Ammonia Decomposition System for Marine Application" Hydrogen 5, no. 4: 723-736. https://doi.org/10.3390/hydrogen5040038
APA StyleWu, S., Miao, B., & Chan, S. H. (2024). A Technical Study on an Integrated Closed-Loop Solid Oxide Fuel Cell and Ammonia Decomposition System for Marine Application. Hydrogen, 5(4), 723-736. https://doi.org/10.3390/hydrogen5040038






