Abstract
Boil-off losses occur when gaseous hydrogen has to be released from a cryogenic tank due to liquid hydrogen evaporating. These are a substantial drawback for all areas in which liquid hydrogen is discussed as a potential fuel to limit the climate impact. Especially boil-off losses during fuelling are one of the most significant source of losses along the liquid hydrogen pathway. To analyse and minimize such losses, simulations of the filling process are performed with the simulation tool “EcoSimPro”. The simulations are validated with an analytical solution. The results show that boil-off losses can be significantly reduced by pre-cooling the cryogenic tank with liquid nitrogen. This method is most effective for relatively small tanks that could be used e.g., in small air crafts or air taxis.
1. Introduction
The topic of hydrogen has developed very dynamically in recent years and has gained new momentum, especially with the publication of the “National Hydrogen Strategy” in Germany [1] and the “Hydrogen Strategy” of the European Union [2]. In the wake of this new momentum, there are currently many ideas and projects that want to lay out and test demonstrators from all areas of mobility (aviation, shipping, automotive). Particularly in aviation, the possible benefits are immense as the switch to hydrogen fuel could reduce its climate impact substantially [3]. While liquid hydrogen powered unmanned air vehicles (UAVs) exist [4], liquid hydrogen passenger aircraft are only in the first stages of development [5]. Air taxis could serve as a demonstrator of liquid hydrogen technology and an intermediate step between UAVs and larger passenger aircraft.
At the Institute of Space Propulsion of the German Aerospace Center (DLR), amongst other research areas, liquid hydrogen rocket engines are simulated and optimized with the tool “EcoSimPro” [6,7,8].
Cryogenic hydrogen is a challenging fuel to handle, because it has to be stored at about 20 K (−253 C) to remain liquid. Heat input from the environment into a cryogenic tank leads to hydrogen evaporating, which increases the pressure. When the maximum tank pressure is reached, gaseous hydrogen has to be vented to the environment to limit the pressure rise. To analyse this boil-off, especially for future large-scale storage and transport applications, many numerical models were developed [9,10]. This development lead among other things to so called zero-boil off methods where the gaseous hydrogen is e.g., re-liquefied and thus boil-off completely prevented [11,12]. Another source of boil-off occurs during transfer from one tank to another. This is because of the large temperature difference between the cryogenic fuel and the walls of the tank that is being fuelled. This problem becomes more dominant for smaller tanks, because of their worse volume-surface-ratio. Additionally these kind of tanks usually have a less efficient insulation and are filled and emptied more often. The boil-off losses during fuelling are presumably the most significant source of losses along the liquid hydrogen () pathway [13]. Since hydrogen production and liquefaction are energy intensive and expensive, it is desirable to reduce boil-off losses as much as possible. This effect was modelled and discussed e.g., by Petitpas, however there is still no general solution or recommendation to that problem [9,13,14].
Pre-cooling the cryotank with liquid nitrogen before fuelling reduces the temperature difference between the walls of the cryotank and the liquid hydrogen. It therefore could be a method to reduce boil-off losses during the fuelling process. Whether this reduction is significant and how much liquid nitrogen is needed for pre-cooling is investigated in this study. The problem of nitrogen freezing at temperature as well as other practical or economical aspects of this method are not considered. This study should be viewed as a preparation for further considerations on the pre-cooling method.
The investigation is done numerically with the simulation tool “EcoSimPro” and validated with an analytical solution of the problem.
2. Materials and methods
2.1. EcoSimPro
EcoSimPro is used used for many different applications including digital twins of process plants, aircraft engines and rockets, engineering for the design of products, health monitoring, optimization and virtual commissioning. It is used for modeling 0D or 1D multidisciplinary continuous-discrete systems and any kind of system based on differential-algebraic equations (DAE) and discrete events [15,16,17]. EcoSimPro includes an object-oriented programming language and a Graphical User Interface. There are many different simulation toolkits including toolkits for space applications, aeronautics, power, hydro, cryogenics and fusion energy. The toolkit used to build the “Fuelling Model” is the European Space Propulsion System Simulation (ESPSS) toolkit, which is the standard tool of the European Space Agency and European industry for propulsion simulation. It also includes a complete database of fluids to be used as propellants, pressurizing fluids or other applications. The ESPSS toolkit is used to simulate complex fluid systems under transient or steady conditions and optimization of these systems.
2.2. Fuelling Model
The Fuelling Model that can be seen in Figure 1 consists of a liquid hydrogen tank (cryotank), its insulation and the insulation-air interface, a pressure relief fluid line, a fuelling fluid line and a mass flow controller.
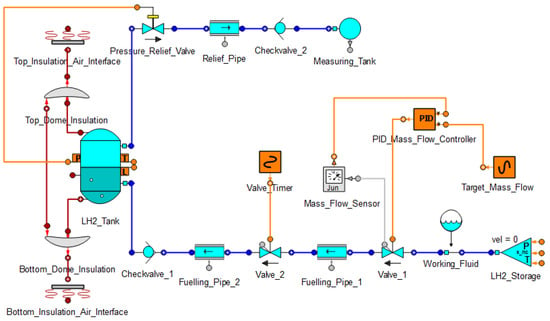
Figure 1.
Fuelling Model (created in EcoSimPro).
The pressure relief line contains the pressure relief valve, which is set to open at the maximum cryotank pressure, a pipe, a check valve and a measuring tank. This tank measures how much gas goes through the pressure relief line, thus quantifying boil-off losses. The fuelling line consists of a check valve to make sure the fluid only flows into the cryotank, two pipes, two valves, a component to define the fluid inside the line and the storage boundary condition. Valve 1 is used as a mass flow control valve and is controlled by the PID mass flow controller. It measures the mass flow and compares this value to the target mass flow. Valve 2 is open during the fuelling process and closes when the cryotank is full. The insulation of the cryotank is made of vacuum insulated panels (VIP). This is a thin, high-performing insulation material consisting of a rigid, highly-porous core and a gas-tight outer envelope which is evacuated and sealed. This results in a thermal conductivity of 0.006 W/mK, which is about 5 times lower than polyurethane foam.
Since the pressure in the storage boundary condition is set higher than the target pressure of the cryotank, no pump is needed in the fuelling line.
2.2.1. Mesh Study
In numerical simulations, the discretization or meshing of a model is the process of dividing a geometry into a finite number of elements for numerical analysis. It determines the accuracy of the simulation, but also the computing effort. A compromise has to be found, taking these opposing requirements into account. For the Fuelling Model, the discretization of the cryotank wall has the largest impact on the simulation results.
The cryotank wall is split into two hemispherical domes, separated by a thin cylindrical part. Contrary to the exemplary discretization shown in Figure 2, there is only one node for the liquid and gas volume respectively. This is recommended if thermal stratification in the liquid or gas sides is not necessary to be calculated [18]. Each dome consists of 50 nodes in the vertical direction and 3 radial nodes, totalling 150 nodes for each dome. The discretization in the vertical direction is closely reviewed, due to its effect on the boiling rate of the hydrogen. As the cryotank is filled, the liquid level rises, meaning the liquid comes into contact with the next vertical wall node. Since this node has not yet been cooled by the liquid hydrogen, it now transmits its heat to the hydrogen, increasing the hydrogen boiling rate. This effect can be reduced by increasing the number of vertical nodes. In Figure 3 the boiling rate is compared for 20, 50 and 100 vertical nodes for each dome.
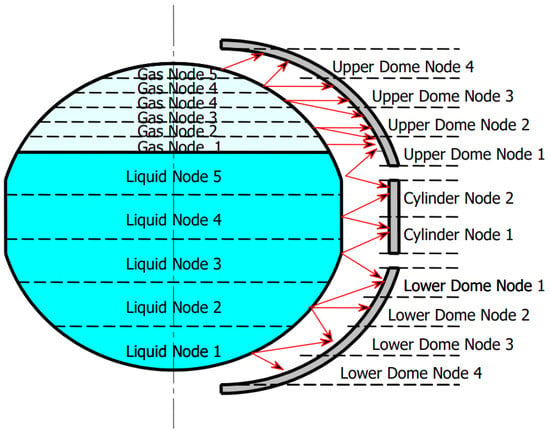
Figure 2.
Cryotank exemplary fluid and wall discretization.
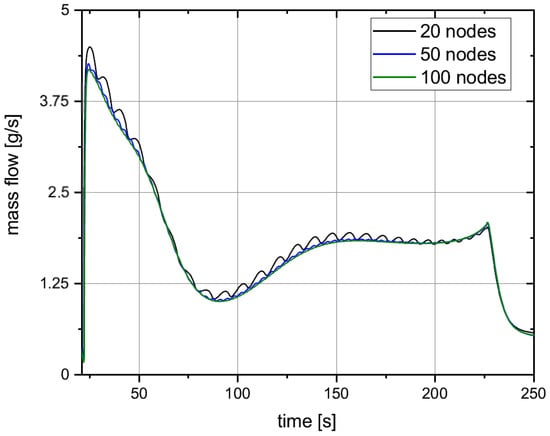
Figure 3.
Boiling rate during fuelling for 20, 50 and 100 vertical nodes.
The boiling rate in the case of 50 vertical wall nodes is significantly smoother than for 20 nodes. The boiling rate for 100 vertical nodes is slightly smoother than for 50 nodes, but the computing effort increased significantly. For that reason, 50 vertical nodes is chosen for the final version of the Fuelling Model, as it represents a good compromise between accuracy and computational recources.
2.2.2. Boundary and Initial Conditions

Table 1.
Selected boundary conditions of the Fuelling Model.

Table 2.
Selected initial conditions of the Fuelling Model.
The cylindrical part of the cryotank is set to be 0.001 m high, meaning the cryotank is nearly spherical. In the following simulations, the initial cryotank fill level is set to 5% and the initial liquid temperature is set to 20 K, because otherwise all of the liquid evaporates before the liquid hydrogen from the fuelling line reaches the cryotank, thus leading to a termination of the simulation.
2.3. Analytical Validation
To validate the simulation results, boil-off losses are calculated analytically. Minimum and maximum expected boil-off losses as well as a more realistic mean value are calculated, using simplified thermodynamic formulas. The maximum boil-off losses (Equation (1)) are calculated by dividing the heat that needs to be removed from the cryotank by the vaporization enthalpy of hydrogen.
The underlying assumption in that case is that the evaporated hydrogen leaves the cryotank without absorbing any additional heat. That means it does not increase its temperature after evaporation. Since this approach overestimates the boil-off losses, these are the maximum expected boil-off losses. consists of multiple components (Equation (2)).
These represent the heat that needs to be removed from the cryotank walls (Equation (3)), the insulation (Equation (4)) and the gas inside the cryotank (Equation (5)). Each of those components is calculated by multiplying with its heat capacity and mass m.
The mass of the gas inside the cryotank before fuelling is provided by the Fuelling Model. The mass of the cryotank wall and insulation is calculated in Equation (6) using the radius r of the cryotank, the density of the material and the thickness t.
The minimum boil-off losses (Equation (7)) are calculated by extending Equation (1). Instead of assuming that no additional heat is absorbed by the gaseous hydrogen leaving the cryotank, it is assumed that it leaves the cryotank at the starting temperature of the cryotank. Since the temperature of the cryotank decreases quickly after liquid hydrogen enters, this assumption will underestimate boil-off losses.
That means we now have an upper and lower boundary for boil-off losses, meaning if the simulation results are correct, they should be within those boundaries. As a third value, a mean value for boil-off losses is calculated (Equation (8)). In this case, the gaseous hydrogen absorbs heat before leaving the cryotank, but only half as much, as for the minimum boil-off losses.
Two different cryotank wall materials are considered. These are the stainless steel alloy 304L (SS) and the aluminium alloy 5083-O (AL). Both are chosen for their satisfactory properties at cryogenic temperatures. Materials data from the National Institute of Standards and Technology (NIST) is used. To compare how much cooling the cryotank with liquid nitrogen reduces boil-off losses, these are calculated for two cases. Either the cryotank is not pre-cooled and thus has an initial temperature of 293 K or it is pre-cooled with , which results in an initial temperature of 94 K. This is the boiling point of at 5 bar. Additionally, the required mass to pre-cool the cryotank is calculated the same way as the hydrogen boil-off losses and presented in Figure 4. The insulation thickness of 50 mm is chosen to reduce boil-off due to heat flux from the environment after the tank is full. The temperature difference of the insulation before fuelling and after fuelling is approximated by calculating the mean temperature of the insulation before fuelling and after the fuelling process for the standard fuelling process and the pre-cooling method. The results are listed in Table 3.
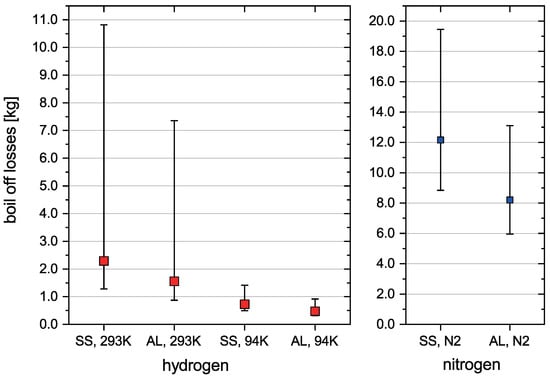
Figure 4.
Boil-off losses for hydrogen and nitrogen (analytical validation).

Table 3.
Approximation of .
The heat capacities of steel, aluminium, hydrogen and nitrogen are dependant on their temperature, however for the simplified analytical validation average heat capacities are used in the calculations. These values are chosen depending on the starting and final temperature of the material. For aluminium, this process is shown in Figure 5. For the temperature interval 27–94 K (green line in Figure 5), the heat capacity is much lower than for the other intervals.
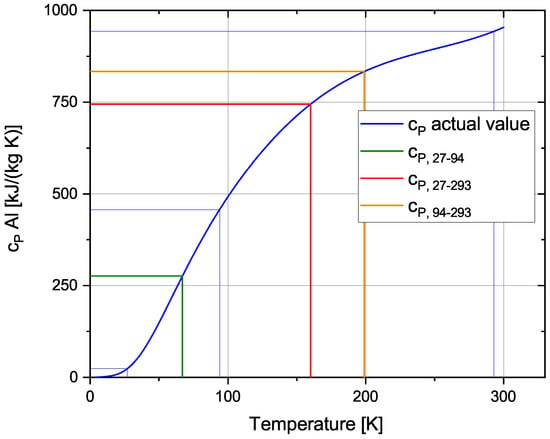
Figure 5.
Average heat capacity for different temperature intervals.
The values chosen for each temperature interval are displayed in Table 4.

Table 4.
Constants and variables used in the analytical validation.
3. Results
In the following sections, the results of the analytical validation and the simulation results of the Fuelling Model are presented separately.
3.1. Analytical Validation Results
Figure 4 shows the boil-off losses for the two different cryotank materials. The symbols represent the mean boil-off losses, the error bars represent the calculated minimum and maximum values. It was assumed stainless steel and aluminium wall material and an initial cryotank temperature 293 K and 94 K. right part of the diagram represents the amount of liquid nitrogen, that is needed to pre-cool the cryotank from 293 K to 94 K.
The differences between minimum and maximum boil-off losses are higher for 293 K initial cryotank temperature than for 94 K. This is because the between initial and final temperature of the cryotank is higher. That means the difference between denominator in Equation (7) and in Equation (1) is comparatively higher for 293 K than for 94 K. That results in larger uncertainties for the 293 K case. Another observation is that the mean boil-off values are closer to the minimum than to the maximum boil-off values. Additionally, the boil-off values for AL are smaller than for SS, since both tanks have the same thickness, which results in a lower mass and thus lower total heat capacity for the aluminium tank.
In regards to the question whether pre-cooling the cryotank reduces boil-off losses, the analytical validation clearly shows lower boil-off losses for the pre-cooled cryotank with 94 K initial temperature than for 293 K initial temperature. The reduction in boil-off losses ranges from a factor of 2.7 when considering the minimum boil-off losses to a factor of 8, considering the maximum boil-off losses.
3.2. Fuelling Model Results
The results of the simulations that are performed for the Fuelling Model are presented below. Specifically, the pressure inside the cryogenic tank and the mass flow through the pressure relief valve for the different cryotank materials and initial temperatures, are compared. Additionally, the total boil-off losses during fuelling are presented in Table 5. A pre-cooling simulation is carried out, to verify whether the tank cools down with the calculated amount of . Here, the wall temperature over the pre-cooling process is plotted.

Table 5.
Boil-off losses Fuelling Model.
Figure 6 shows the pressure inside the cryogenic tank during the fuelling process for the different cases.
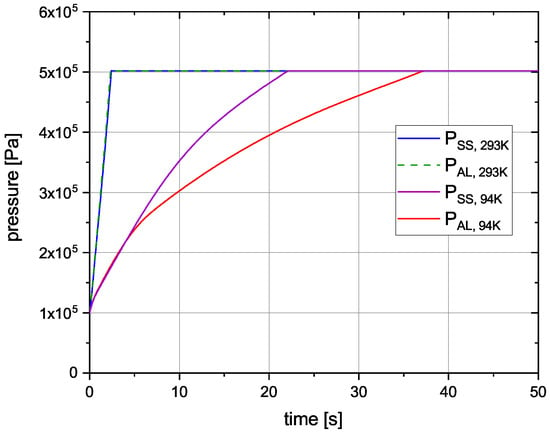
Figure 6.
Pressure inside cryogenic tank.
The pressure rises quickly from 1 to 5 bar, due to evaporating. Since takes up about 851 times more volume than , the pressure increases rapidly. As it reaches the maximum cryotank pressure of 5 bar, the pressure relief valve opens and is vented into the environment. The pressure increase happens more slowly for the initial temperature of 94 K. While the increase for stainless steel happens faster for 94 K initial temperature, the pressure increase for 293 K is equally fast for both materials.
In Figure 7 the mass flow through the pressure relief valve during the fuelling process is shown. For all curves, the mass flow spikes initially when the valve opens. This spike is higher for 293 K initial cryotank temperature. Another spike occurs when the cryotank is full and the fuelling valve closes. The mass flow curves for the 94 K initial condition look similar, with the stainless steel curve starting a bit earlier due to the pressure increasing faster (Figure 6). While the mass flow for the 94 K curves increases during fuelling, it decreases for the 293 K curves. The area under each curve represents the total boil-off losses during the fuelling process, shown in Table 5.
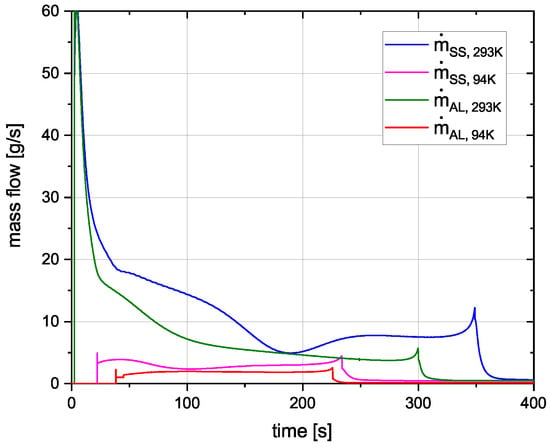
Figure 7.
Mass flow through pressure relief valve.
The simulations of the Fuelling Model show that a pre-cooled cryotank reduces boil-off losses. The reduction factor is 6.4 for stainless steel and 7.6 for aluminium.
To validate whether the tank can be cooled down to the desired temperature with the pre-cooling method, a pre-cooling simulation is conducted. The tank wall material for this simulation is SS 304L. A mass flow of 0.01 kg/s over 1900 s is chosen, totalling 19 kg of . This is near the maximum boil-off value calculated in the analytical validation for SS 304L.
In Figure 8 the tank wall temperature is plotted over time. While a detailed look at the pre-cooling method still has to follow, it shows that the tank can be cooled down to the required temperature with the calculated amounts of .
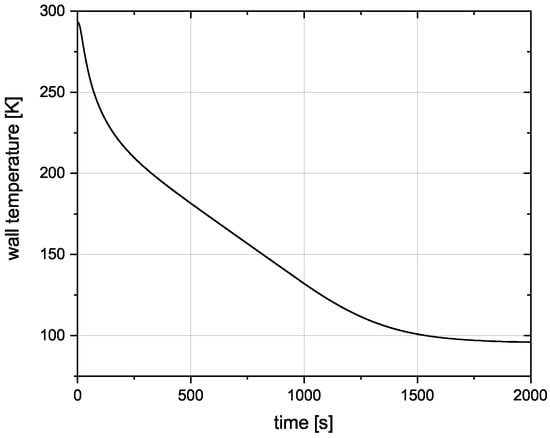
Figure 8.
Temperature of the tank wall during the pre-cooling process.
4. Sensitivity Study
A sensitivity study is performed to increase the applicability of the results to different use cases. The parameters “Tank size”, “Tank geometry”, “Mass flow” and “Insulation thickness” are varied in the simulations to understand their influence on boil-off losses and the applicability of the pre-cooling method. The boil-off losses for the standard fuelling process and the pre-cooling method are then calculated and compared to the “reference case”. The reference case is the -Tank that was discussed in the other chapters of this work, including the corresponding mass flow and insulation thickness.
4.1. Tank Size
While in a sensitivity study, only one parameter at a time should be varied, this procedure is not practical for the variation of the tank size. For the different tank sizes, the mass flow is also varied accordingly to ensure meaningful filling times. For example, a 30 m radius tank can not be filled with the reference case mass flow, as the boil-off rate for such a tank is higher than this mass flow. In Table 6 the tank sizes are assigned certain mass flows and corresponding filling times are calculated. The filling times are not constant, because for different tank sizes, meaningful filling times vary. Using the 30 m radius tank as an example once again, it is evident, that such a tank will not be filled in 150 s as the 0.1 m radius tank.

Table 6.
Tank sizes and corresponding mass flows and filling times.
In Figure 9 the relative boil-off losses for the different tank sizes are depicted. Relative boil-off losses are calculated by dividing the boil-off losses with the total fuel mass, which is different for each tank size. While the red points represent the relative boil-off losses for the standard fuelling process, the blue points represent the relative boil-off losses for the pre-cooling method. Thus for each tank size, the reduction of the boil-off losses by applying the pre-cooling method can be interpreted. Relative boil-off losses are decreasing with increasing tank size, because the volume and thus hydrogen fuel mass increases with the power of three, while the tank wall mass increases with the power of two. Thus, to cool down the tank wall, a lower percentage of hydrogen must be evaporated for larger tanks. It is evident, that the pre-cooling method is more effective, the smaller the tank is. While for a 1 m radius tank, the boil-off losses can still be reduced from 10% to 2%, which arguably is still significant, for a 3 m tank, the boil-off losses are not reduced significantly. This is an important finding, because it shows the application limits of the pre-cooling method.
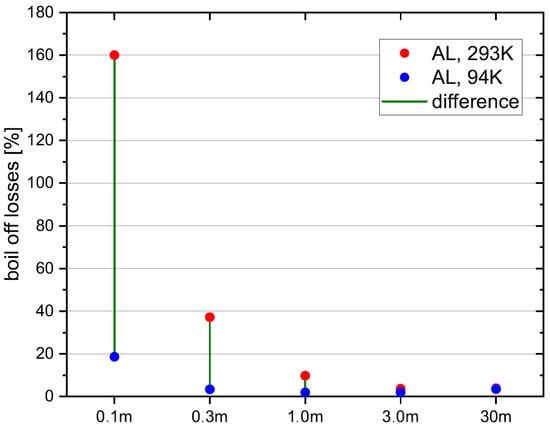
Figure 9.
Relvative boil-off losses for different tank sizes.
4.2. Tank Geometry
To study the effect of the tank geometry on the boil-off losses, the radius and length of the cylindrical section of the -tank are varied while the volume remains constant. The simulated tank geometries are shown in Table 7 and the results of the simulations are displayed in Figure 10.

Table 7.
Simulated tank geometries.
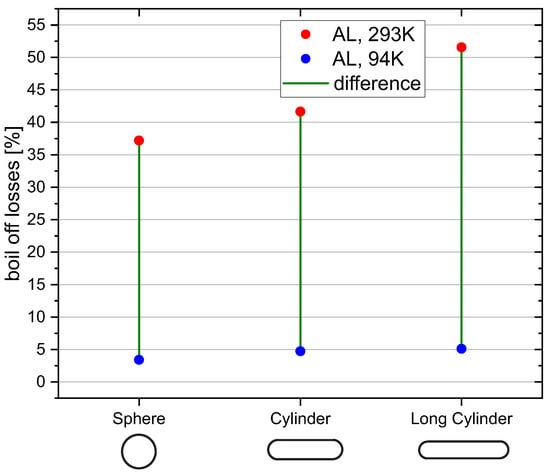
Figure 10.
Relvative boil-off losses for different tank geometries.
The results indicate that boil-off losses increase for more cylindrical tank geometries. A cylinder has a larger surface-area-to-volume ratio than a sphere, leading to a larger tank wall mass, which has to be cooled down. This results in higher boil-off losses the more stretched the cylinder becomes. Since the difference in boil-off losses between K and 94 K increases for more cylindrical geometries, the pre-cooling method is more effective for those geometries compared to a spherical tank. This finding is relevant, because cylindrical tanks are used in many applications as in rockets or air planes due to their more efficient usage of storage space.
4.3. Mass Flow
For the mass flow sensitivity study the reference case tank is used and five different mass flows are simulated (Table 8).

Table 8.
Simulated mass flows.
The resulting boil-off losses are shown in Figure 11. Boil-off losses compared to the reference case are higher for the 0.1× and 0.2× mass flows. This could be explained by the longer filling time and thus higher heat input from the environment. This trend however does not continue for the 5× and 10× mass flows. Here the boil-off losses for the standard fuelling process increase slightly, while the boil-off losses for the pre-cooling method do not. The reasons for the increase from 1× to 5× are not clear and should be further examined. Compared to the results of the tank size variation, the parameter mass flow does not seem to have as strong of an influence on the applicability of the pre-cooling method. The boil-off off losses can be reduced significantly for all the simulated mass flows. If however, the mass flow is really small, it could be the case, that the heat stored by the walls of the tank becomes insignificant, compared to the heat input from the environment over the filling process, thus making the pre-cooling method less effective. That means it is more effective, the shorter the filling time is.
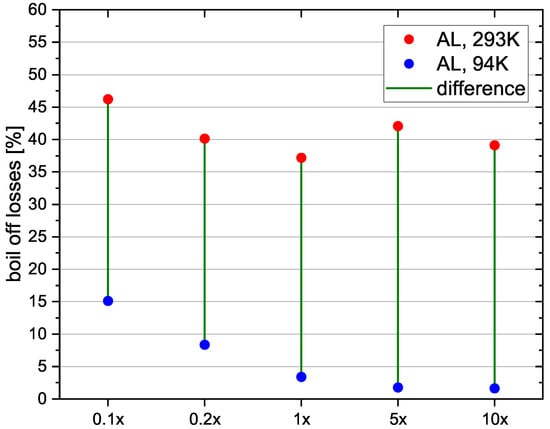
Figure 11.
Relvative boil-off losses for different mass flows.
4.4. Insulation thickness
The reference tank is used once again and the thickness of the insulation consisting of vacuum insulated panels is varied to study its effect on the boil-off losses. In Table 9, the different insulation thicknesses are shown.

Table 9.
Variation of insulation thickness.
The results of the simulations (Figure 12) show that boil-off losses are higher for a lower insulation thickness, due to higher heat flux from the environment during the fuelling process. The reduction of the boil-off losses by using the pre-cooling method is similar for all simulated insulation thicknesses. Thus its influence on the applicability of the pre-cooling method is not significant.
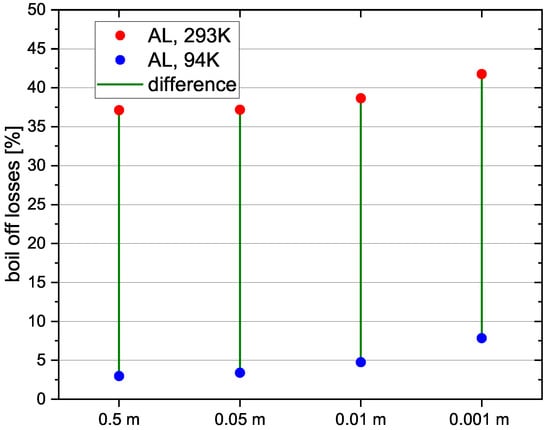
Figure 12.
Relvative boil-off losses for different insulation thickness.
5. Discussion
Along the pathway, boil-off losses during transfer from one tank to another are presumably the most significant source of losses [13]. Since hydrogen production and liquefaction are energy intensive and expensive, it is desirable to reduce boil-off losses as much as possible.
As can be seen in Figure 13, the results of both the simulation and the analytical validation show a significant reduction in boil-off losses if the cryotank is pre-cooled and the results of the simulation are within the boundaries of the analytical validation. The reduction factor ranges from 2.7 to 8 for the analytical validation and from 6.3 to 7.6 for the simulation. By putting the boil-off losses of the simulation in relation to the total fuel mass, the results can be more easily interpreted. In that case, the boil-off losses are reduced significantly from 38–60% of the total fuel mass to 5–9%.
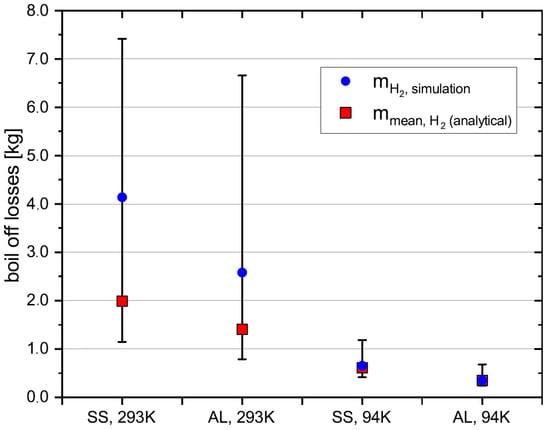
Figure 13.
Comparison of the results of the simulation and the analytical validation.
The results of the sensitivity study show that the parameter tank size has the greatest influence on the applicability of the pre-cooling method. Its effectiveness increases with decreasing tank size. The parameter tank geometry has a moderate influence, the pre-cooling method is more effective for more cylindrical geometries. The parameters mass flow and insulation thickness have a small impact on the resulting boil-off losses.
To study, whether pre-cooling the receiving tank with makes economic sense, the boil-off losses have to be taken into account, as well as the price of both and . The boil-off losses during pre-cooling are approximately 4.5 times higher than the losses for 293 K initial temperature. Thus in a first approximation, as long as the price per kg of is more than 4.5 times higher than the price of , pre-cooling makes economic sense. Since the price of might decrease with respect to the price of this development should be taken into account.
Since nitrogen freezes at temperatures, it is not practical to directly fuel into the tank after pre-cooling. This study had been made as preparational work for the implementation of the pre-cooling method. These include considerations such as indirect pre-cooling of the tank from outside or usage of available cold boil-off gases.
6. Conclusions
In this study, the hydrogen boil-off losses that occur during a fuelling process are investigated numerically and validated analytically. More specifically, the question whether these can be significantly reduced by pre-cooling the cryogenic tank with liquid nitrogen, is answered.
The results show that boil-off losses during fuelling can be reduced significantly from 2.58–4.14 kg (38–60% of the total fuel mass) to 0.34–0.65 kg (5–9%) by pre-cooling the cryogenic tank with liquid nitrogen. To validate the numerical results of the “Fuelling Model”, experimental data is necessary. Additionally, different approaches to reduce boil-off losses during fuelling must be compared to each other. These include capturing and either re-liquefying the boiled-off hydrogen or using it to produce electricity, filling the cryotank from the top [13] or lowering the temperature of the incoming by using a sub-cooler.
Additional research should also focus on the economic aspects as well as the practicality of the pre-cooling method.
Author Contributions
Conceptualization, F.G.-T. and J.H.; methodology, F.G.-T.; software, F.G.-T.; validation, F.G.-T. and J.H.; formal analysis, F.G.-T.; writing—original draft preparation, F.G.-T.; writing—review and editing, F.G.-T. and J.H.; visualization, F.G.-T. and J.H.; supervision, J.H. and D.L.; project administration, J.H. and D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Federal Ministry for Economic Affairs and Energy. The National Hydrogen Strategy; Federal Ministry for Economic Affairs and Energy: Berlin, Germany, 2020. [Google Scholar]
- European Comission. A Hydrogen Strategy for a Climate-Neutral Europe; European Comission: Brussels, Belgium, 2020.
- McKinsey & Company. Hydrogen-Powered Aviation; McKinsey & Company: New York, NY, USA, 2020. [Google Scholar]
- Stroman, R.O.; Schuette, M.W.; Swider-Lyons, K.; Rodgers, J.A.; Edwards, D.J. Liquid hydrogen fuel system design and demonstration in a small long endurance air vehicle. Int. J. Hydrogen Energy 2014, 39, 11279–11290. [Google Scholar] [CrossRef]
- Airbus. Airbus Reveals New Zero-Emission Concept Aircraft. 2020. Available online: https://www.airbus.com/newsroom/press-releases/en/2020/09/airbus-reveals-new-zeroemission-concept-aircraft.html (accessed on 3 August 2021).
- Dresia, K.; Waxenegger-Wilfing, G.; dos Santos Hahn, R.; Deeken, J.; Oschwald, M. Nonlinear Control of an Expander-Bleed Rocket Engine using Reinforcement Learning. In Proceedings of the 7th Space Propulsion Conference 2020+1, Virtual Conference, 17–19 March 2021. [Google Scholar]
- Schmierer, C.; Kobald, M.; Steelant, J.; Schlechtriem, S. Hybrid Propulsion for a Moon Sample Return Mission. In Proceedings of the 6th Space Propulsion Conference, Seville, Spain, 14–18 May 2018. [Google Scholar]
- Bombardieri, C.; Traudt, T.; Manfletti, C. Modeling Fluid Transient Phenomena in LRE Feedlines. In Proceedings of the 5th Space Propulsion Conference, Rome, Italy, 2–6 May 2016. [Google Scholar]
- Ghafri, S.Z.A.; Swanger, A.; Jusko, V.; Siahvashi, A.; Perez, F.; Johns, M.L.; May, E.F. Modelling of Liquid Hydrogen Boil-Off. Energies 2022, 3, 1149. [Google Scholar] [CrossRef]
- Kalanidhi, A. Boil-off in long-term stored liquid hydrogen. Int. J. Hydrogen Energy 1988, 13, 311–313. [Google Scholar] [CrossRef]
- Notardonato, W.U.; Swanger, A.M.; Fesmire, J.E.; Jumper, K.M.; Johnson, W.L.; Tomsik, T.M. Zero boil-off methods for large-scale liquid hydrogen tanksusing integrated refrigeration and storage. In Proceedings of the Cryogenic Engineering Conference (CEC) 2017, Madison, WI, USA, 9–13 July 2017. [Google Scholar] [CrossRef]
- Haberbusch, M.S.; Stochl, R.J.; Culler, A.J. Thermally optimized zero boil-off densified cryogen storage system for space. Cryogenics 2004, 44, 485–491. [Google Scholar] [CrossRef]
- Petitpas, G. Boil-Off Losses along LH2 Pathway; Technical Report; Lawrence Livermore National Lab. (LLNL): Livermore, CA, USA, 2018. [Google Scholar]
- Petitpas, G. Simulation of boil-off losses during transfer at a LH2 based hydrogen refueling station. Int. J. Hydrogen Energy 2018, 43, 21451–21463. [Google Scholar] [CrossRef]
- Bradu, B.; Vinuela, E.B.; Gayet, P. Example of cryogenic process simulation using EcosimPro: LHC beam screen cooling circuits. Cryogenics 2013, 53, 45–50. [Google Scholar] [CrossRef]
- Gregori, C.; Torres, A.; Pérez, R.; Kaya, T. LHP Modeling with EcosimPro and Experimental Validation; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2005. [Google Scholar]
- Díaz, S.P. Modelling and simulation of an industrial steam boiler with Ecosimpro. In Proceedings of the 1st Meeting of EcosimPro Users, UNED, Madrid, Spain, 3–4 May 2001; pp. 1–10. [Google Scholar]
- Agrupados, E. ESPSS EcosimPro Libraries User Manual; ESA: Paris, France, 2017; Volume 1. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).