Abstract
The engineering correlations for assessment of hazard distance defined by a size of fireball after either liquid hydrogen spill combustion or high-pressure hydrogen tank rupture in a fire in the open atmosphere (both for stand-alone and under-vehicle tanks) are presented. The term “fireball size” is used for the maximum horizontal size of a fireball that is different from the term “fireball diameter” applied to spherical or semi-spherical shape fireballs. There are different reasons for a fireball to deviate from a spherical shape, e.g., in case of tank rupture under a vehicle, the non-instantaneous opening of tank walls, etc. Two conservative correlations are built using theoretical analysis, numerical simulations, and experimental data available in the literature. The theoretical model for hydrogen fireball size assumes complete isobaric combustion of hydrogen in air and presumes its hemispherical shape as observed in the experiments and the simulations for tank rupturing at the ground level. The dependence of the fireball size on hydrogen mass and fireball’s diameter-to-height ratio is discussed. The correlation for liquid hydrogen release fireball is based on the experiments by Zabetakis (1964). The correlations can be applied as engineering tools to access hazard distances for scenarios of liquid or gaseous hydrogen storage tank rupture in a fire in the open atmosphere.
1. Introduction
International standard “ISO 19880-1. Gaseous hydrogen—Fueling stations. Part 1” [1] defines hazard distance as the distance from the hazard to a determined physical effect value that can lead to a range of harm to people, equipment, or environment. Hazard distance can be used as an input to quantitative risk assessment (determination of the quantitative or qualitative value of risk related to a specific situation and a recognized threat/hazard) to estimate, for example, the risk of injury or fatality to people, e.g., via probit functions. This study focuses on hazard distance defined by the maximum size of the fireball created by the combustion of gaseous or liquid hydrogen released from a storage tank.
The harm to people and damage to buildings after rupture of a pressurized tank with flammable substance in a fire can be assessed by pressure effects of the blast wave, i.e., pressure and impulse, and thermal effects of the fireball, i.e., high temperature and radiative heat flux. Three characteristic temperature thresholds are suggested as criteria for thermal hazard: 70 °C—“no harm” limit; 115 °C—pain limit for 5 min exposure; 309 °C—third degree burns for a 20 s exposure (“death” limit) [2]. The harm from radiative heat flux can be estimated either directly by the value of heat flux or through the thermal doze. The thermal heat flux thresholds are [3]: 1.6 kW/m2—“no-harm” for long exposures; 4–5 kW/m2—“pain” for 20 s exposure (first-degree burn); 9.5 kW/m2—second-degree burn after 20 s; 12.5–15 kW/m2—first-degree burn after 10 s or 1% lethality in 1 min; 25 kW/m2—significant injury in 10 s or 100% lethality in 1 min; and 35–37.5 kW/m2—1% lethality in 10 s. The thermal dose is calculated as I3/4t [3], where I is the radiative heat flux (kW/m2) and t is the duration of exposure to the radiation (s). Thermal doses in infrared spectrum in a range 80–130 (kW/m2)4/3s result in first-degree burns, 240–730 (kW/m2)4/3s—in second-degree burns, and 870–2640 (kW/m2)4/3s—in third-degree burns [3].
To underpin the deployment of hydrogen systems and infrastructure, there is a need in engineering tools to assess the hazard distances for scenarios of hydrogen storage tank rupture in a fire, including a hazard distance defined by the fireball.
Experimental data on fireball size are very limited. Two fire tests on the rupture of gaseous storage tanks were performed in the USA [4,5,6]. The first of two fire tests involved a stand-alone Type IV hydrogen storage tank 72.4 L (initial storage pressure 34.3 MPa, surrounding temperature 300 K, the stored hydrogen mass calculated using Abel-Noble EoS was 1.64 kg). The propane burner had a heat release rate (HRR) = 350 kW (specific heat release rate (HRR/A) = 1.63 MW/m2). The Type IV tank ruptured after 6 min 27 s of fire exposure. At the moment of rupture, the pressure and temperature inside the tank raised to 35.7 MPa and 312 K, respectively. The fireball diameter varied “only slightly” between images from high-speed visible range and infra-red video-cameras [5]. In both experiments the fireball durations, as determined from the IR camera images, were about 4.5 s [7]. The dynamics of fireball for the first test with a stand-alone tank was later studied numerically in [8]. The model was successfully validated against available experimental fireball size and shape at 45 ms after the tank rupture. Then, the validated model was used to study dynamics of the fireball, whose maximum diameter reached about 16.5 m at 2 s after the tank rupture. The simulated fireball had a hemispherical shape.
The second fire test was carried out with compressed hydrogen Type III tank installed under a typical sport utility vehicle (SUV) [6,7]. The tank had a slightly larger volume of 88 L, initial pressure 31.8 MPa, and temperature 304 K (presuming it was equal to the ambient temperature). The total mass of hydrogen in the tank was equal to 1.89 kg. The burner HRR was equal 265 kW (HRR/A = 0.65 MW/m2). The tank failed after 12 min 18 s of fire exposure, i.e., almost twice later compared to the stand-alone tank due to lower HRR/A. The maximum fireball size was estimated from the high-speed video-camera in experiments as 24 m and from the infra-red camera as 24.4 m (see Figure 1a). The fireball had a flattened rather than hemispherical shape due to the presence of vehicle over the ruptured tank.

Figure 1.
Fireball tests: (a) Under-vehicle Type III tank at initial pressure 31.8 MPa (1.89 kg) [7]; (b) stand-alone Type IV tank at initial pressure 70.23 MPa (1.37 kg). Reproduced with permission from [9], JSAE, 2006; (c) stand-alone Type III tank at initial pressure 35 MPa (3.9 kg) with a partial opening during rupture in a fire. Reproduced with permission from [10], Elsevier, 2018; (d) visible flames after ignition of 7.8 L liquefied hydrogen (LH2) spill in motion during 0.3–0.56 s [11].
Two other tests on the rupture of gaseous hydrogen tanks in a fire were conducted in Japan [9] on tanks with nominal working pressure (NWP) 70 MPa following protocol ISO 11439 [12]. Test 1 was carried out with a Type IV tank of 35 L having initial pressure 70.23 MPa, temperature 281 K, and hydrogen mass 1.37 kg. The tank ruptured after 21 min 21 s of fire exposure. The last recorded pressure in the tank before the rupture was 94.54 MPa. Test 2 was performed with a Type III tank of 36 L with initial pressure 70.69 MPa, initial temperature 282 K, and 1.406 kg of hydrogen. This tank ruptured 10 min 54 s after exposure to the fire. The pressure measured just before the tank burst was 99.47 MPa. Both tests resulted in a fireball with a diameter of approximately 18 m as reported in the paper [9]. The fireball had a somewhat flattened shape (see Figure 1b).
Two more tests with compressed hydrogen Type III tanks rupture in a fire and the consequences of their explosions are described by Shen et al. [10]. The rupture in each case was caused presumably by the failure of thermally activated pressure release device (TPRD) to vent tank content [10]. Both tanks had internal volume 165 L and were filled with hydrogen at NWP 35 MPa. The initial temperature was not reported, though, presuming it was 293 K, the hydrogen inventory should have been 3.9 kg. It is worth mentioning that in the first test “the temperature and pressure of the tank increased marginally” before the rupture, while in the second test the inner pressure in the tank reached 43.73 MPa just before the tank rupture. The authors reported a fireball diameter as low as 7–8 m for this comparatively large hydrogen mass [10]. However, the snapshot in Figure 1c shows that instead of the entire instantaneous tank rupture, only one dome was detached and the tank was flying like a rocket with still burning hydrogen in the wake of the “rocket”. Thus, only a fraction of stored hydrogen mass participated in the initial fireball combustion. This explains the comparatively small size of the fireball registered in these experiments.
In 1964, Zabetakis published probably the earliest correlation for height and width of a fireball of liquid hydrogen [11]. The fireballs after release, rapid vaporization, and ignition of liquid hydrogen in the range from 2.8 L to 89 L were investigated. Figure 1d shows a motion sequence of visible flames resulted from 7.8 L spill of LH2 experiment [11] from 0.3 to 0.56 s time. The delay time between spillage and ignition was in the range 0–16 sec. The combustion process for shorter ignition delays was qualitatively similar to typical boiling liquid expanding vapor explosion (BLEVE) with flush evaporation of released boiling liquid. For longer ignition delays, the combustion was more similar to hydrogen-air deflagration. Zabetakis [11] argued that the experimental data are fairly well represented by the following equation (here and later the mass in correlations is in kilograms and distances are in meters):
In 1977, Fay and Lewis [13], and in 1978 Hardee et al. [14], suggested that the fireball diameter for non-premixed vapor-cloud combustion should scale with mass of fuel in power one third, i.e., , assuming that fireball represents the volume of combustion products of released fuel. This apparent assumption is adopted in this study as well. The theoretical dependence of spherical fireball diameter on fuel mass, i.e., , is different from the correlation by Zabetakis, where fireball size was correlated with the fuel mass as .
In 1978, Hasegawa and Sato published an empirical correlation for propane BLEVE at pressures MPa [15] which was modified in 1982 by Moorhouse and Pritchard using the experimental results of Hasegawa and Sato [16] as:
The empirical correlation for fireball diameter for rocket propellants proposed by Hord in 1978 [17] provided an even larger diameter of a fireball:
In 1981, Roberts [18] presented a correlation for the diameter of fireball resulting from propane BLEVEs, which resulted in fireball diameter slightly above but close to that by Hasegawa and Sato [15] and Moorhouse and Pritchard [16]:
In 1995, Dorofeev et al. [19] demonstrated that the dependence applies to fireballs of different combustion types. Large-scale experiments on fireball formation and thermal effects from deflagrations and detonations of 0.1–100 tons of industrial fuels, namely, gasoline, kerosene, and diesel, were performed [19]. The fireball started to rise from the ground forming the mushroom shape 1–2 s after ignition. The derived in [19] correlation is:
In 1996, the experiments on propane-air detonation by Dorofeev et al. [20] resulted in a larger fireball diameter compared to reported previously for propane correlations by Roberts [18], Hasegawa and Sato [15], and Moorhouse and Pritchard [16]:
Dorofeev et al. [19] concluded that fireball diameter for detonations was larger than for relatively slower deflagrations studied by other authors.
The correlation (4) was validated against experiments with releases of propane up to 422 kg and fireball formation time up to 4 s from the start of the release. Roberts [18] also summarized models, where fireball was considered as a sphere having the mass of fuel and air in stoichiometric composition, and density of combustion products at adiabatic flame temperature. Thus, Roberts’s correlation is derived from the assumption of thermal expansion of combustion products of the stoichiometric propane-air mixture at the adiabatic temperature K when the expansion ratio is . Though Roberts argued that theoretically, this fireball diameter is not the largest possible, he concluded that his correlation “provides a reasonable representation of the available data” over a large range of a released amount of fuel and conditions [18].
It is worth noting that when the approach of Roberts [18] is applied for the analysis of fireball after hydrogen tank rupture in a fire (in the assumptions of adiabatic flame temperature K and expansion ratio [21]) it leads to the fireball diameter which is practically the same as the correlation (3).
In 2005, Zalosh and Weyandt commented that existing correlations for fireball size developed for hydrocarbons are slightly conservative when applied to hydrogen fireballs [5]. However, in 2019, Li claimed that the correlation by Roberts “appears to be also applicable to hydrogen” [22]. Thus, this study aims to clarify validity of the above claims and to derive the correlations for gaseous and liquid hydrogen fireball size based on the described above correlations and available experimental data. It should be underlined that the diameter of a spherical fireball and the maximum size of real conditions fireball for the same hydrogen mass can differ significantly and this should be accounted for performing hydrogen safety engineering.
2. Validation Experiments
Table 1 presents experimental data on fireball diameter resulted from ruptures of high-pressure gaseous hydrogen tanks.

Table 1.
High-pressure hydrogen tank rupture experiments.
Experimental fireball diameters demonstrate significant scatter that should be commented on. For example, test [4] gives a diameter about two times larger compared to test [10] while the hydrogen mass in this test is 2.4 times smaller. This is due to the experimentally observed “non-instantaneous” rupture of the tank (see Figure 1c) and thus the partial release of hydrogen from the tank during detachment of only one dome at the moment of tank failure in a fire to create an initial fireball. Simulated fireball size after rupturing of stand-alone tanks with a close mass in tests [4] and [9] have close size, i.e., 14 ± 2 m for 1.64 kg and 11 ± 1 m for 1.367 kg respectively. However, the experimental maximum size of the fireball of 18 m in tests [9] is higher the fireball size 11 ± 1 m obtained in CFD simulations of the same test in [8]. This is due to the flattened shape of a fireball in the experiment while it is rather a hemispherical shape in simulations because of the presence of obstacles and probably peculiarities of non-instantaneous tank opening during the rupture. The largest fireball size of 24 m is registered in the experiment with 1.87 kg tank rupture under the vehicle [6]. The geometry played a key role in the flattened shape of the fireball. This must be accounted for in the development of the correlation for the maximum fireball size.
Table 2 shows experimental data by Zabetakis [11] used to build the correlation for liquefied hydrogen (LH2) spill fireball size.

Table 2.
LH2 spill experiments [11].
Comparison of similar hydrogen inventories in Table 1 and Table 2 shows that within the experimentally studied range of a similar hydrogen mass, a high-pressure tank rupture test provides somewhat larger fireball compare to a LH2 spill test. For instance, a hemispherical fireball of a high-pressure tank rupture with 1.64 kg of hydrogen [4] has a diameter of 14 ± 2 m (Table 1), while the maximum fireball size from spilt 1.65 kg of LH2 is about 12 m [11] (Table 2). In this case of relatively small inventory, the difference may be considered negligible taking into account that fireball diameter of the spherical fireball is = 1.26 times smaller than hemispherical fireball (for the same mass of hydrogen). This, however, contradicts the results of functional dependence in correlation by Zabetakis [1], which should result in larger maximum size of LH2 spill fireballs compared to the fireballs of fuel-air mixtures where its maximum diameter is proportional to fuel mass in power (), . This observation is discussed Section 4 below.
3. Gaseous Hydrogen Tank Rupture in a Fire
In 2015, a theoretical model of fireball diameter after high-pressure hydrogen tank rupture in a fire in the open atmosphere at ground level was published [23]. The model accounted for the observed in experiments’ hemispherical rather than spherical shape of a fireball [4]. The hemispherical fireball shape was confirmed later by three-dimensional (3D) simulations [8]. Similar to previous studies, the model assumes that the hemispherical fireball is filled with products of complete combustion of hydrogen released into the air.
Hydrogen mass in a storage tank of volume is calculated using the Abel-Noble EoS for real gas as:
The volume of released hydrogen after expansion to atmospheric pressure and temperature is and the volume of air required to completely burn this hydrogen is (m3). The hemispherical fireball diameter is then , where the volume of combustion products is and the expansion coefficient of products for adiabatic stoichiometric combustion of hydrogen in the air is 6.85 [21]. This leads to the volume of combustion products and theoretical hemispherical fireball diameter:
It can be shown that the diameter of the hemisphere is by = 1.26 times larger than the diameter of the sphere of the same volume. Thus, the correlation for a spherical fireball would be which is slightly below the diameter calculated by the correlation for rocket propellants with the coefficient 7.93 and a slightly lower degree for the mass term, Equation (3) [17].
It is worth mentioning here the conclusions of Dorofeev et al. [20] that the coefficient in the correlation for fireball diameter for the same fuel is larger for detonation compared to fireball diameter resulting from BLEVE or deflagration. This could be due to several reasons, e.g., the larger momentum of combustion products behind the detonation wave, higher temperature of detonation products, etc. The similar reasoning could be applied to expectations to have a larger correlation coefficient for fireballs after high-pressure hydrogen tank rupture in a fire compared to combustion of a cold cloud after an LH2 spillage.
Figure 2 combines available experimental and simulated results on the fireball size from high-pressure hydrogen tank rupture in the open atmosphere as a function of hydrogen mass presented in Table 1. The figure shows experimental and simulated data by symbols and presents the theoretical correlation (7) for the hemispherical fireball diameter for stand-alone tank rupture in a fire in the open atmosphere (dashed line). The filled diamond symbol in Figure 2 represents the under-vehicle tank rupture in a fire experiment [6]. This experiment demonstrates that the presence of the vehicle increases the maximum fireball size compared to a stand-alone tank rupture. This experiment was used to “calibrate” the conservative correlation, which was derived using the theoretical dependence , and requirement to match this largest reliably obtained size of a fireball of 24 m from the under-vehicle tank rupture test. The conservative correlation for fireball size from a high-pressure tank rupture in a fire recommended for use in hydrogen safety engineering is:
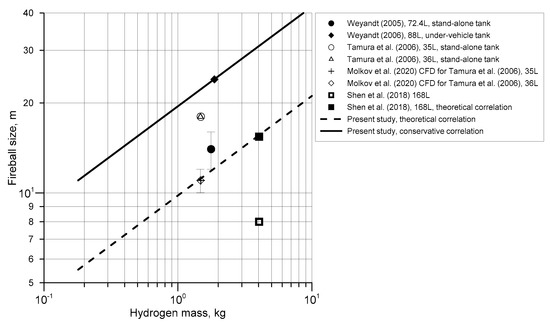
Figure 2.
Conservative correlation for the maximum hydrogen fireball size (solid line), Equation (8), and the theoretical correlation for the diameter of hemispherical fireball (dashed line), Equation (7).
The correlation is presented in Figure 2 by solid line.
The maximum experimental fireball diameter 18 m reported by Tamura et al. [9] for two stand-alone tank tests (open circle and open triangle symbols) is above the theoretical correlation for hemispherical shape fireball of 10.9−11.0 m and obtained numerically fireball size of practically equal to the theoretical value of 11 ± 1 m (cross and open diamond symbols). The larger fireball size registered in the experiments can be explained by the fact that it was not hemispherical and rather flattened with horizontal size larger than the height.
Experimental data by Shen et al. [10], shown in Figure 2 by open square symbol, were affected by the non-instantaneous partial release of hydrogen during tank failure at dome area that was followed by jetting of hydrogen from the dome, resulting in reduced hydrogen mass which contributed to the development of a primary fireball. According to the theoretical correlation in Equation (7), the instantaneous release of the total 3.9 kg of hydrogen from the tank would result in hemispherical fireball diameter of 15.4 m shown in Figure 2 by filled square symbol. The amount of hydrogen required to create an 8 m-diameter fireball was estimated using the theoretical correlation Equation (7) as 0.54 kg.
Data for stand-alone tank test by Weyandt [4] (filled circle) are above the theoretical correlation for hemispherical fireballs. This is, in addition to two tests by Tamura et al. [9] and the under-vehicle test by Weyandt [6], another experimental indication that in real life the fireball shape may be distorted (e.g., flattened) providing larger hazard distance compared to that found from assumption of hemispherical fireball shape.
3.1. Effect of Fireball Shape on Hazard Distance
The mass of instantaneously released hydrogen defines, in general, the volume of combustion products. This volume has a minimum size when it is spherical, slightly larger (by = 1.26 times) when it is hemispherical, and it can be significantly larger if it is longer in one direction, e.g., diameter, and shorter in another direction, e.g., height. The last describes situations like that with the tank rupture under a vehicle in the fire test [6].
The experiments have evidenced that fireball shape in real conditions, e.g., for tank rupture in a fire under a vehicle, can be different from spherical or hemispherical. Figure 1b shows the fireball in the experiment by Tamura et al. [9] where the ratio of fireball width to height is about 3 (though not at the moment when the fireball reached its largest size). In this view, the hemispherical fireball may be considered as having width to height ratio 2, while a spherical fireball has a ratio of 1. Experimental figures do not give opportunity to have a detailed three-dimensional view of the fireball shape, which may be flattened, elongated, or uneven in some other way, providing for a significantly different maximum fireball size observed in a test from that calculated following theoretical correlation in Equation (7).
For the fixed volume of combustion products and the assumption that fireball has flattened (“pancake”) shape with diameter and height , the maximum size of the fireball (i.e., fireball diameter) is , or, using the expression for combustion products volume discussed above,
Figure 3 compares maximum hemispherical fireball size, i.e., fireball diameter as per Equation (7), with maximum diameter of flattened fireballs having diameter to height ratios and 30, as well as with diameter of spherical fireball from combustion of equal hydrogen mass. Fireball diameter for the ratio nearly coincides with diameter of hemispherical fireball having very close maximum size to height ratio . The dependence for provides the largest fireball size for a given hydrogen mass, while the spherical fireball results, naturally, in the smallest fireball diameter. The data from under vehicle tank rupture test by Weyandt [6] and from study by Tamura et al. [9] are also indicated in Figure 3, giving a potential explanation for unexpectedly large fireball sizes observed in these experiments. Fireball diameter in the experiment by Weyandt [6] reached 24 m, which corresponds to fireball width to height ratio given hydrogen mass 1.87 kg. For hydrogen mass 1.367 kg in the experiment by Tamura [9], the fireball size 18 m was obtained with diameter to height ratio
. Both
ratios are way above value 2, suggesting that the fireballs’ development could result in their flattened shape and much larger hazard distances. In the experiment by Weyandt [6], the fireball was clearly affected by presence of the car body above the tank, which should result in predominantly horizontal hydrogen propagation and hence fireball development along the ground, too. The experiment by Tamura et al. [9] was conducted in an open atmosphere and the flattened fireball shape could be result of some other factors, e.g., non-instantaneous tank rupture.
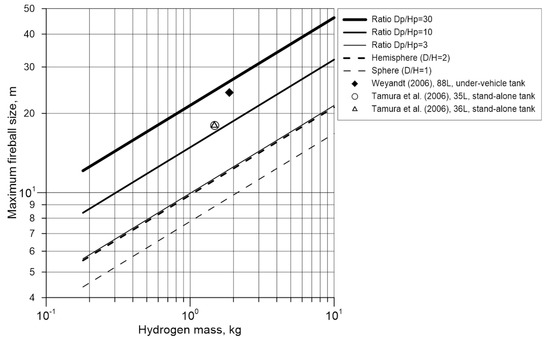
Figure 3.
Maximum fireball size for different width to height ratios in comparison with experimental data by Weyandt [6] and Tamura et al. [9].
3.2. Effect of Temperature, Radiative Heat Flux, and Thermal Dose on Hazard Distance
To estimate the effect of radiative heat transfer on simulated fireball size, two CFD simulations of the stand-alone tank rupture test by Weyandt [4] were performed—with and without radiative heat transfer modelling. The presence of radiation in the model decreased the fireball size by about 20%.
For the simulation with radiative heat transfer, the eddy dissipation concept (EDC)-based model [8] was coupled with discrete ordinates (DO) radiation model [24] to enable prediction of hazard distance based on thermal doze harm criteria [3]. Planck mean absorption coefficient of water vapor was modeled following [25] as . Calculation of Planck mean absorption coefficient was realized via User Defined Function functionality of ANSYS Fluent software employed in this study as the CFD engine. Polar and azimuthal angles were resolved by 5 solid angles with each solid angle further resolved by 3 × 3 pixels divisions.
Figure 4 shows thermal doses with distance from the tank accumulated in the time interval 0.15–2.8 s. The horizontal dashed line shows the “first-degree burn” threshold defined by the thermal doze 80 (kW/m2)4/3 s [3]. The “second-degree burns” threshold 240 (kW/m2)4/3 s [3] was not reached even after 2.8 s of fireball simulation. Though in simulations the fireball existed up to about 4 s, increase of exposure time beyond 1.8 s practically does not result in increase of the thermal doze. The fireball itself also presents thermal hazard, i.e., temperature. The vertical solid line in Figure 4 shows maximum fireball radius 7 m recorded in experiment [4]. The hazard distance defined by fireball size exceeds the hazard distance defined by thermal dose during the whole fireball development period.
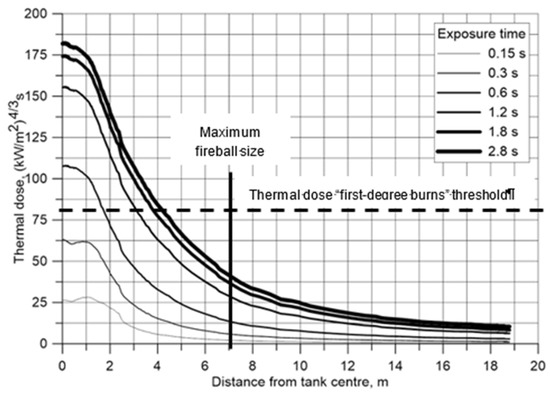
Figure 4.
Comparison of hazard distances for tank rupture test by Weyandt [4]: simulated radiation thermal dose and temperature hazard associated with maximum fireball size.
4. Fireball of Ignited LH2 Hydrogen Spill
Figure 5 compares experimental data from Table 2 by Zabetakis [11] on fireball size from liquid hydrogen spills with available correlations. In the original correlation by Zabetakis [11], the fireball size is proportional to the square root of hydrogen mass, . The authors believe that when the experimental data by Zabetakis is scaled with hydrogen mass in power , the “best-fit” correlation of experimental fireball diameter becomes
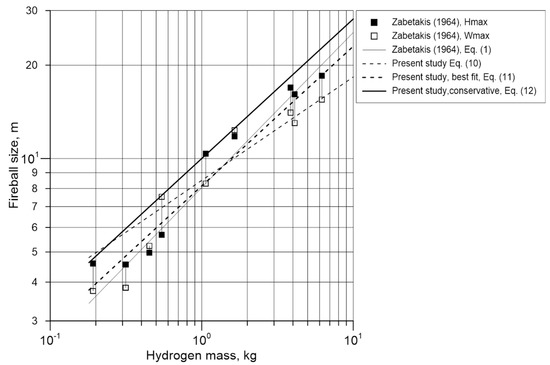
Figure 5.
Comparison of experimental data by Zabetakis [11] on fireball size from LH2 spills in open atmosphere with available correlations: original correlation by Zabetakis [11] Equation (1), analytically based correlation
Equation (10), the best fit correlation Equation (11), and conservative fit correlation Equation (12).
The proportionality coefficient 8.5 in Equation (10) is larger than the proportionality coefficient 7.24 in Equation (5) obtained by Dorofeev et al. [19] for the detonation of industrial fuels (diesel, kerosene, gasoline) meaning LH2 spill fireballs are larger than those for hydrocarbon clouds detonations. It also exceeds the value of the largest coefficient between the reviewed fireball size correlations—coefficient 7.93 in Equation (3) proposed by Hord. Thus, the correlations obtained for hydrocarbon fireballs are not applicable to hydrogen safety engineering.
Another surprising observation from Figure 5 is that the analytically based Equation (10), where maximum fireball diameter is proportional to hydrogen mass in power (i.e., ), does not describe experimental data well. This may be explained by a relatively long combustion time for fireballs developing at subsonic speeds. Such fireballs are affected by buoyancy and air entrainment and tend to take mushroom shape (Figure 1d), which is far from the assumption of even three-dimensional expansion of combustion products underlying theoretical dependence on fuel mass in power . Another potential explanation is the long ignition delay time (up to 16 s) in some of experiments [11], also allowing for buoyancy and entrainment to affect hydrogen cloud formation. Both considerations may explain the highlighted earlier discrepancy between larger fireball size observed for small hydrogen masses in Table 1 despite generally larger fireball dimensions expected from experimentally based correlation by Zabetakis, Equation (1). Indeed, small spills of LH2 are likely to flash-evaporate in a short time, which is not sufficient for buoyancy force to affect hydrogen-air cloud. Tank rupture, quite in accordance with observations following from Dorofeev et al. [19], will provide a larger fireball due to explosive, supersonic hydrogen expansion in this case. On the contrary, large LH2 quantities require substantial evaporation time, sufficient for buoyancy forces to take effect and contribute to hydrogen mixing.
The authors developed their own best fit correlation for experimental data by Zabetakis (not constrained by power index ), which formally resulted in expression
The coefficient of determination for this correlation is , which is marginally better than that for the original correlation by Zabetakis, . This suggests that the original correlation was not the best fit, but a rather practical approximation of the best fit.
To obtain the conservative fit correlation for fireballs from LH2 spills, Equation (11) was adjusted to eliminate underprediction of all experimental data by Zabetakis, i.e., to match fireball size 10.37 m from the spill of 1.06 kg LH2 in Table 2:
The conservative fit dependence Equation (12) is shown in Figure 5 by a thick solid line.
5. Conclusions
The significance of the present study is in development of practical tools—best-fit and conservative-fit correlations—for assessment of fireball thermal hazards arising from rupture of gaseous hydrogen tanks and liquified hydrogen spills in open spaces. The correlations are expected to be used in the framework of hydrogen safety engineering and hydrogen applications development.
The originality of the performed research is in conducting for the first-time analysis of fireball size from high-pressure gaseous hydrogen tank ruptures. The analytically based model for fireball volume was used to correlate fireball size with hydrogen mass in power 1/3. The model assumes hemispherical fireball shape and stoichiometric combustion of released hydrogen with air. The model substantiated development of original best-fit and conservative fit correlations for hydrogen tank rupture fireballs. The experimentally observed scatter of fireball sizes when correlated against hydrogen mass was analyzed. It was demonstrated that non-uniform expansion and mixing of hydrogen due to external obstruction or non-instantaneous tank wall opening increases the hazard distance.
Maximum size of fireballs from the liquified hydrogen spills best correlates against hydrogen mass with power index about 1/2. The authors inspected the original correlation by Zabetakis (1964) and proposed its more accurate formulation as well as a conservative-fit version. It was suggested that the slower evaporation, burning, and expansion of liquified hydrogen spills is affected by buoyancy and air entrainment, and assumption of spherical or hemispherical fireball shape is not applicable in this case.
The rigor of this work is in the systematic overview and analysis of the published work on fireballs from gaseous hydrogen tank ruptures and liquified spills. The available data on hydrogen fireball sizes were presented together with results of previous modeling efforts. It was revealed that despite previous claims, fireballs from rupture of high-pressure hydrogen tanks and liquified hydrogen spills are generally larger than those from hydrocarbon fuels. The earlier correlations for maximum size of fireballs from hydrocarbon fuel deflagrations and detonations are not applicable for hydrogen fireballs considered in the present study.
Author Contributions
Conceptualization: D.M., V.M., V.S., and M.K.; methodology: V.M., D.M., M.K., and V.S.; software: V.S.; validation: V.S. and M.K.; formal analysis: D.M., V.S., V.M., and M.K.; investigation: V.S., D.M., V.M., and M.K.; data curation: V.S., M.K., D.M., and V.M.; writing—original draft preparation: V.S. and D.M.; writing—review and editing, V.M., D.M., and V.S.; visualization: V.S., V.M., and D.M.; supervision: V.M.; project administration: V.M.; funding acquisition: V.M. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the Project “HYLANTIC”–EAPA_204/2016 which is co-financed by the European Regional Development Fund in the framework of the Interreg Atlantic program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are publicly available in the cited references.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Acronyms | |
| BLEVE | Boiling liquid expanding vapor explosion |
| EoS | Equation of state |
| GTR#13 | The Global Technical Regulation No.13 |
| LH2 | Liquified hydrogen |
| HRR | Heat release rate (kW) |
| HRR/A | Specific heat release rate (kW/m2) |
| NWP | Nominal working pressure |
| SUV | Sport utility vehicle |
| TPRD | Thermally activated pressure relief device |
| Greeks | |
| ρ | Mixture density (kg/m3) |
| Latins | |
| A | Burner area |
| ap | Planck mean absorption coefficient of water (m·atm)−1 |
| b = 0.007691 | Hydrogen co-volume constant (m3/kg) |
| D | Fireball diameter (m) |
| H | Fireball height (m) |
| I | Radiative heat flux (kW/m2) |
| k | Proportionality coefficient in Equation (10), |
| M | Molecular mass (kg/kmol) |
| m | Mass (kg) |
| p | Pressure (Pa) |
| R | Fireball radius (m) |
| T | Temperature (K) |
| t | Time (s) |
| V | Volume, tank volume (m3) |
| W | Fireball maximum size (width) (m) |
| Xw | Water mole fraction (-) |
| Subscripts | |
| bf | Best fit |
| b | Burnt mixture |
| c | Conservative |
| H2 | Hydrogen |
| hms | Hemisphere |
| max | Maximum |
| p | “Pancake” (flattened) fireball shape |
| s | Surrounding |
| sph | Spherical |
| u | Unburnt mixture |
References
- ISO. ISO/DIS 19880-1. TI Organization for Standardization I. Gaseous Hydrogen-Fuelling Stations, Part 1: General Requirements; ISO: Geneva, Switzerland, 2018. [Google Scholar]
- Molkov, V.; Saffers, J.B. Hydrogen jet flames. Int. J. Hydrog. Energy 2013, 38, 8141–8158. [Google Scholar] [CrossRef]
- LaChance, J.; Tchouvelev, A.; Engebo, A. Development of uniform harm criteria for use in quantitative risk analysis of the hydrogen infrastructure. Int. J. Hydrog. Energy 2011, 36, 2381–2388. [Google Scholar] [CrossRef]
- Weyandt, N. Analysis of Induced Catastrophic Failure of A 5000 psig Type IV Hydrogen Cylinder; Southwest Research Institute report for the Motor Vehicle Fire Research Institute: Charlottesville, VA, USA, 2005. [Google Scholar]
- Zalosh, R.; Weyandt, N. Hydrogen Fuel Tank Fire Exposure Burst Test. SAE Trans. 2005, 114, 2338–2343. [Google Scholar] [CrossRef]
- Weyandt, N. Vehicle Bonfire to Induce Catastrophic Failure of a 5000-Psig Hydrogen Cylinder Installed on a Typical SUV; Southwest Research Institute Report; Motor Vehicle Fire Research Institute: Charlottesville, VA, USA, 2006. [Google Scholar]
- Zalosh, R. Blast waves and fireballs generated by hydrogen fuel tank rupture during fire exposure. In Proceedings of the 5th International Seminar on Fire and Explosion Hazards, University of Edinburgh, Edinburgh, UK, 23–27 April 2007. [Google Scholar]
- Molkov, V.V.; Cirrone, D.M.C.; Shentsov, V.; Dery, W.; Kim, W.; Makarov, D. Dynamics of blast wave and fireball after hydrogen tank rupture in a fire in the open atmosphere. Int. J. Hydrog. Energy 2021, 46, 4644–4665. [Google Scholar] [CrossRef]
- Tamura, Y.; Takahashi, M.; Maeda, Y.; Mitsuishi, H.; Suzuki, J.; Watanabe, S. Fire exposure burst test of 70 MPa automobile high-pressure hydrogen cylinders. In Proceedings of the Society of Automotive Engineers of Japan Annual Autumn Congress, Sapporo, Japan, 28 September 2006. [Google Scholar]
- Shen, C.; Ma, L.; Huang, G.; Wu, Y.; Zheng, J.; Liu, Y.; Hu, J. Consequence assessment of high-pressure hydrogen storage tank rupture during fire test. J. Loss Prev. Process. Ind. 2018, 55, 223–231. [Google Scholar] [CrossRef]
- Zabetakis, M.G. Flammability Characteristics of Combustible Gases and Vapors; Bureau of Mines: Pittsburgh, PA, USA, 1964. [CrossRef]
- ISO. ISO 11439. Gas Cylinders–High Pressure Cylinders for the On-Board Storage of Natural Gas as a Fuel for Automotive Vehicles; ISO: Geneva, Switzerland, 2000. [Google Scholar]
- Fay, J.A.; Lewis, D.H. Unsteady burning of unconfined fuel vapor clouds. Symp. (Int.) Combust. 1977, 16, 1397–1405. [Google Scholar] [CrossRef]
- Hardee, H.C.; Lee, D.O.; Benedick, W.B. Thermal Hazard from LNG Fireballs. Combust. Sci. Technol. 1978, 17, 189–197. [Google Scholar] [CrossRef]
- Hasegawa, K.; Sato, K. Experimental Investigation of the Unconfined Vapour-Cloud Explosions of Hydrocarbons; Fire Research Institute, Fire Defense Agency: Tokyo, Japan, 1978. [Google Scholar]
- Moorhouse, J.; Pritchard, M.J. Thermal Radiation Hazards from Large Pool Fires and Fireballs: A Literature Review; British Gas Corporation, Research Midlands Research Station: Solihull, UK, 1982; p. 33. [Google Scholar]
- Hord, J. Is hydrogen a safe fuel? Int. J. Hydrogen Energy 1978, 3, 157–176. [Google Scholar] [CrossRef]
- Roberts, A.F. Thermal radiation hazards from releases of LPG from pressurised storage. Fire Saf. J. 1981, 4, 197–212. [Google Scholar] [CrossRef]
- Dorofeev, S.; Sidorov, V.; Efimenko, A.; Kochurko, A.; Kuznetsov, M.; Chaivanov, B.; Matsukov, D.; Pereverzev, A.; Avenyan, V. Fireballs from deflagration and detonation of heterogeneous fuel-rich clouds. Fire Saf. J. 1995, 25, 323–336. [Google Scholar] [CrossRef]
- Dorofeev, S.B.; Sidorov, V.P.; Kuznetsov, M.S.; Dvoinishnikov, A.E.; Alekseev, V.I.; Efimenko, A.A. Air blast and heat radiation from fuel-rich mixture detonations. Shock Waves 1996, 6, 21–28. [Google Scholar] [CrossRef]
- Molkov, V. Fundamentals of Hydrogen Safety Engineering. Available online: https://bookboon.com/en/fundamentals-of-hydrogen-safety-engineering-i-ebook (accessed on 4 January 2021).
- Li, Y.Z. Study of fire and explosion hazards of alternative fuel vehicles in tunnels. Fire Saf. J. 2019, 110, 102871. [Google Scholar] [CrossRef]
- Molkov, V.; Kashkarov, S. Blast wave from a high-pressure gas tank rupture in a fire: Stand-alone and under-vehicle hydrogen tanks. Int. J. Hydrogen Energy 2015, 40, 12581–12603. [Google Scholar] [CrossRef]
- Murthy, J.Y.; Mathur, S.R. Finite volume method for radiative heat transfer using unstructured meshes. J. Thermophys. Heat Transf. 1998, 12, 313–321. [Google Scholar] [CrossRef]
- Yan, L.; Yue, G.; He, B. Development of an absorption coefficient calculation method potential for combustion and gasification simulations. Int. J. Heat Mass Transf. 2015, 91, 1069–1077. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).