Is the Tea Bag Index (TBI) Useful for Comparing Decomposition Rates among Soils?
Abstract
1. Introduction
2. Materials and Methods
2.1. Incubation Study
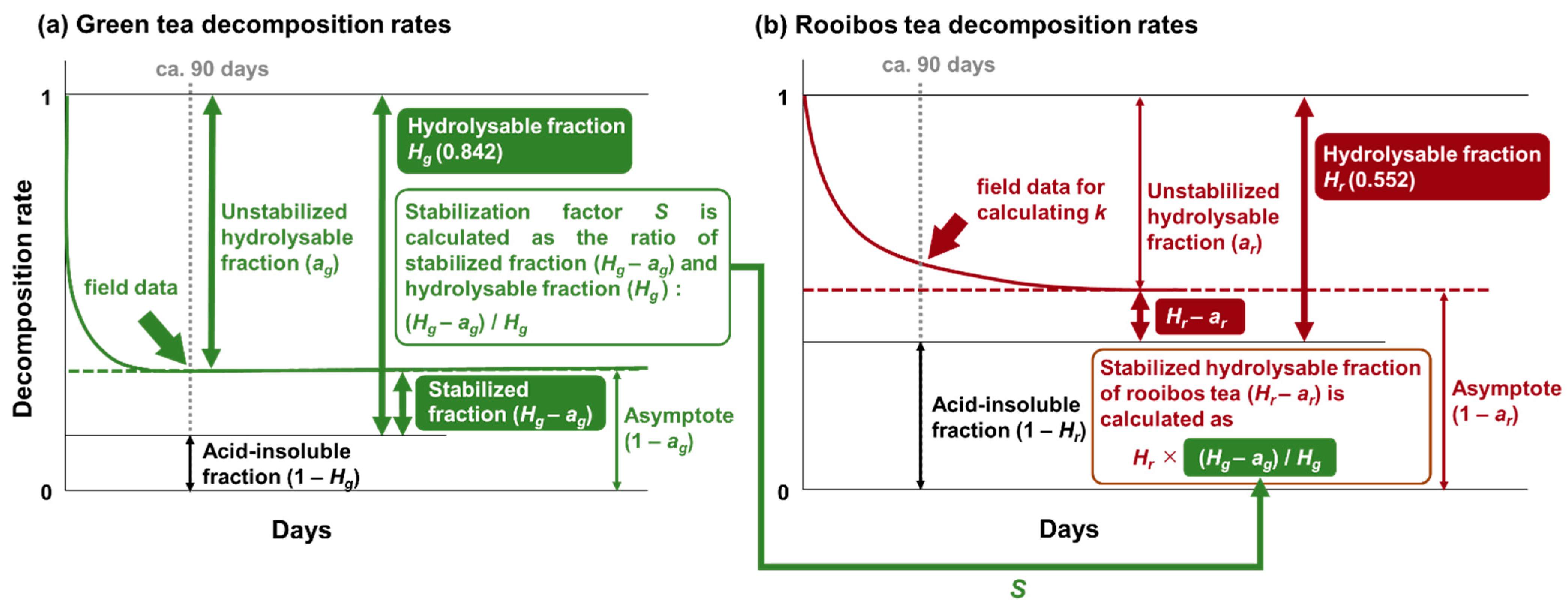
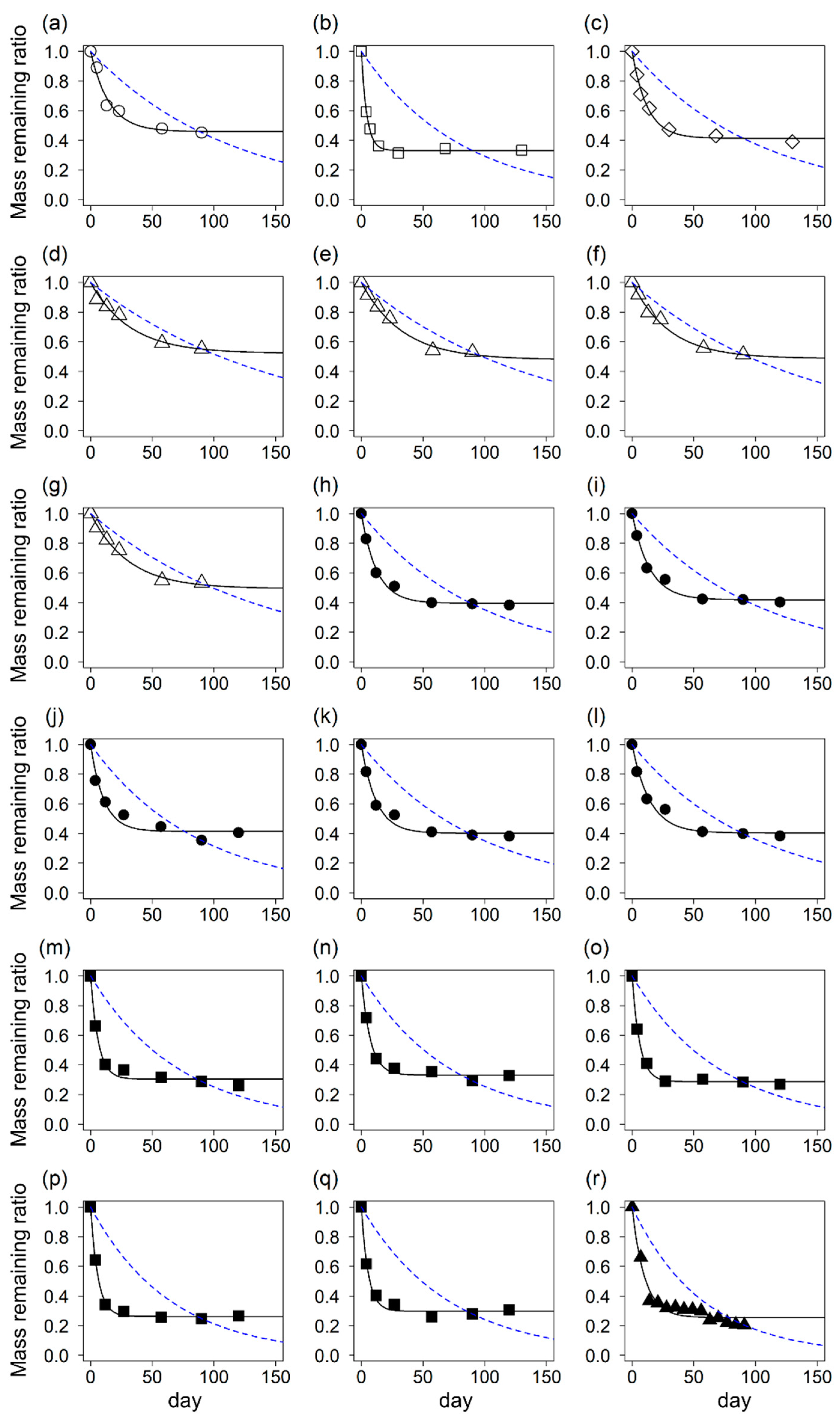
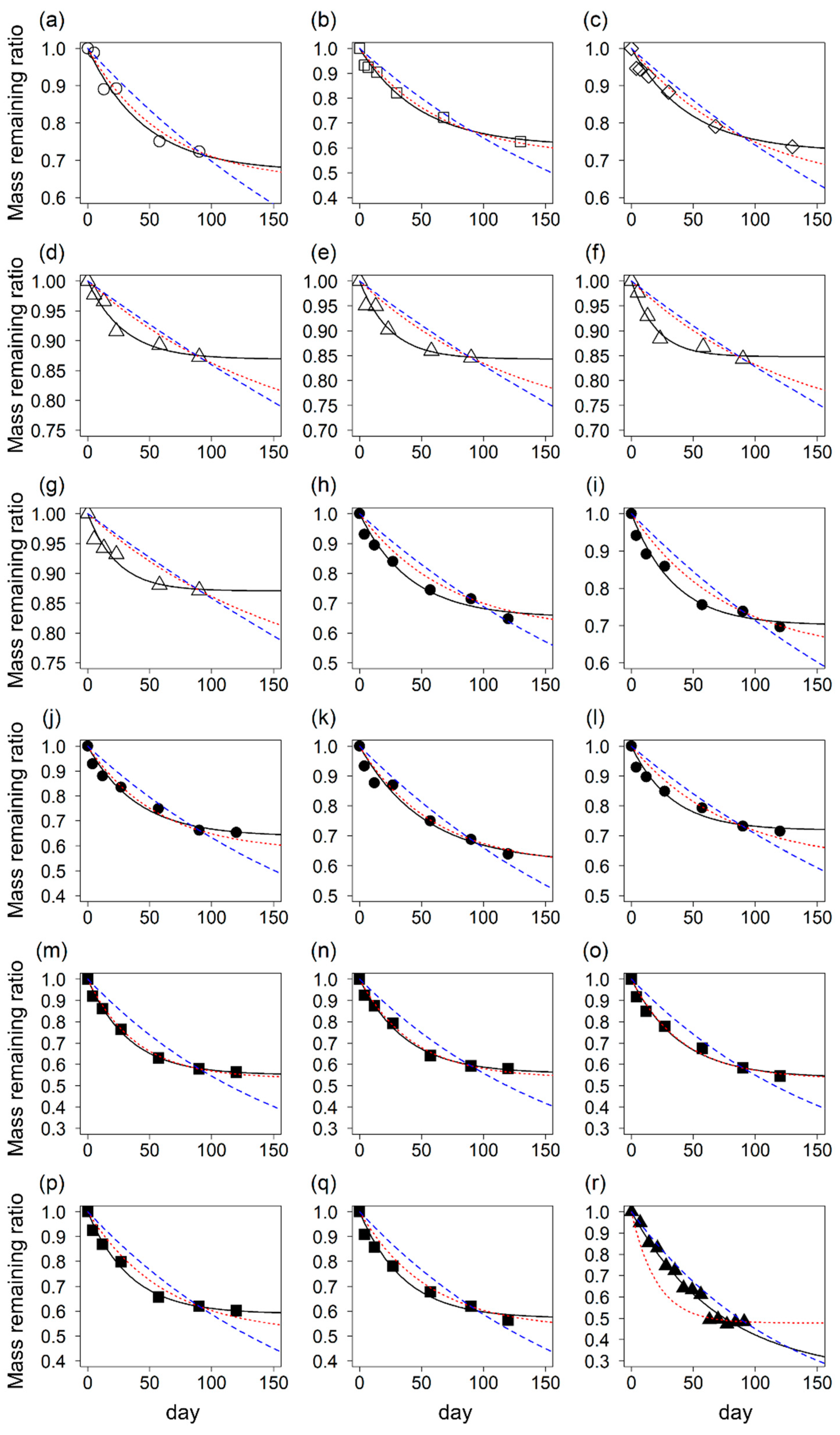
2.2. Determination of k_TBI, S_TBI, k_Fitting, and S_Fitting
2.3. Data Collection from the Literature
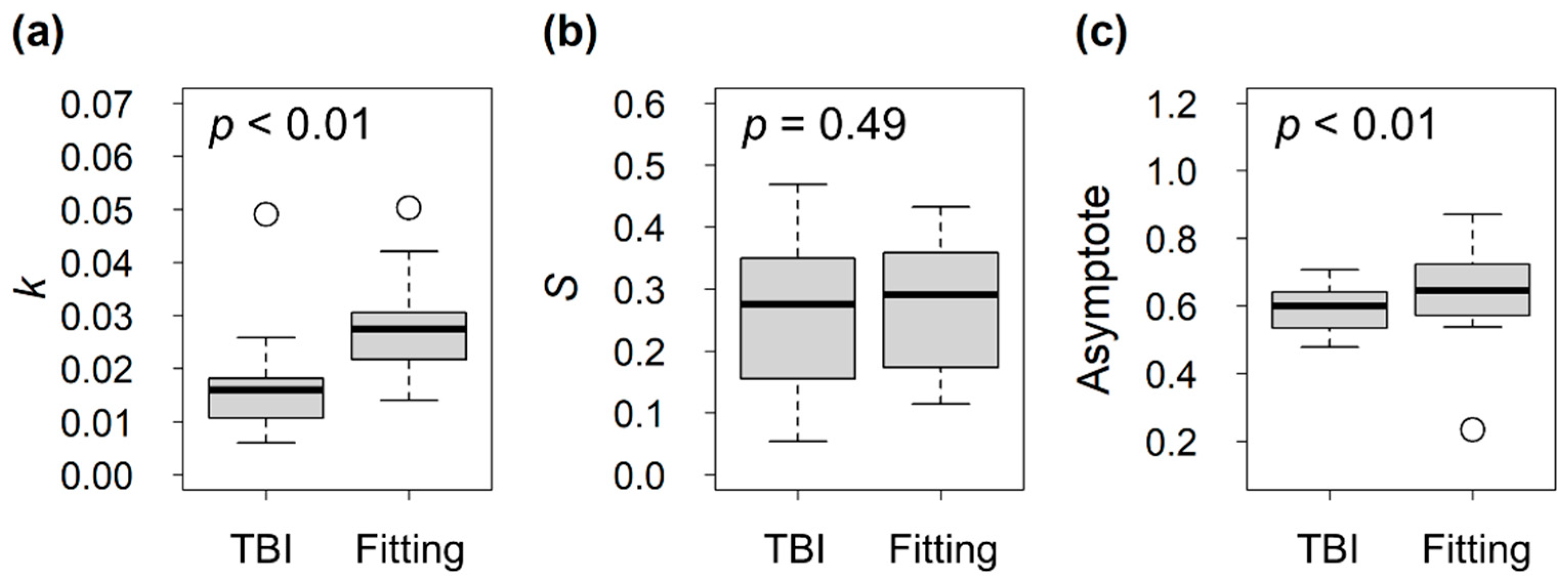
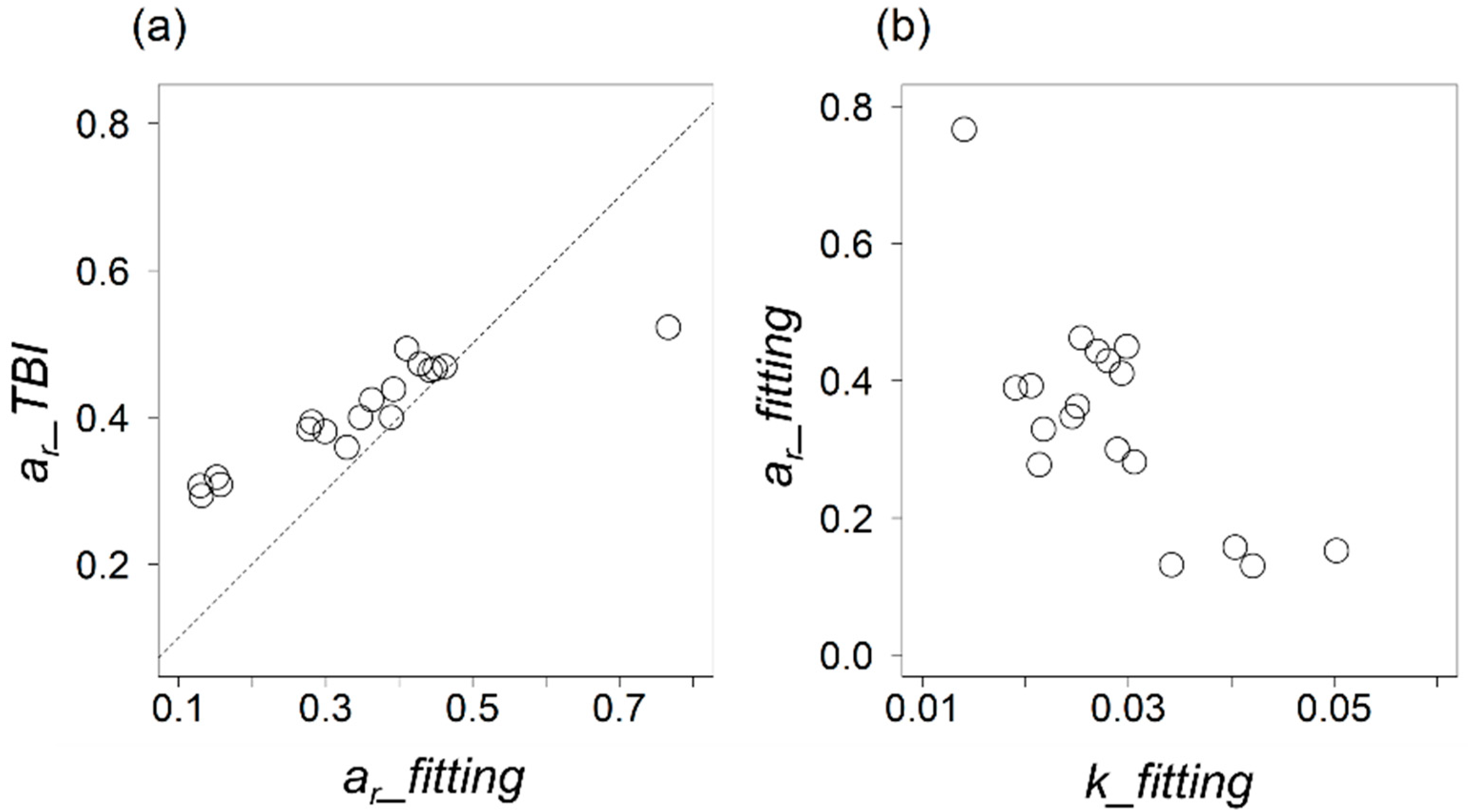
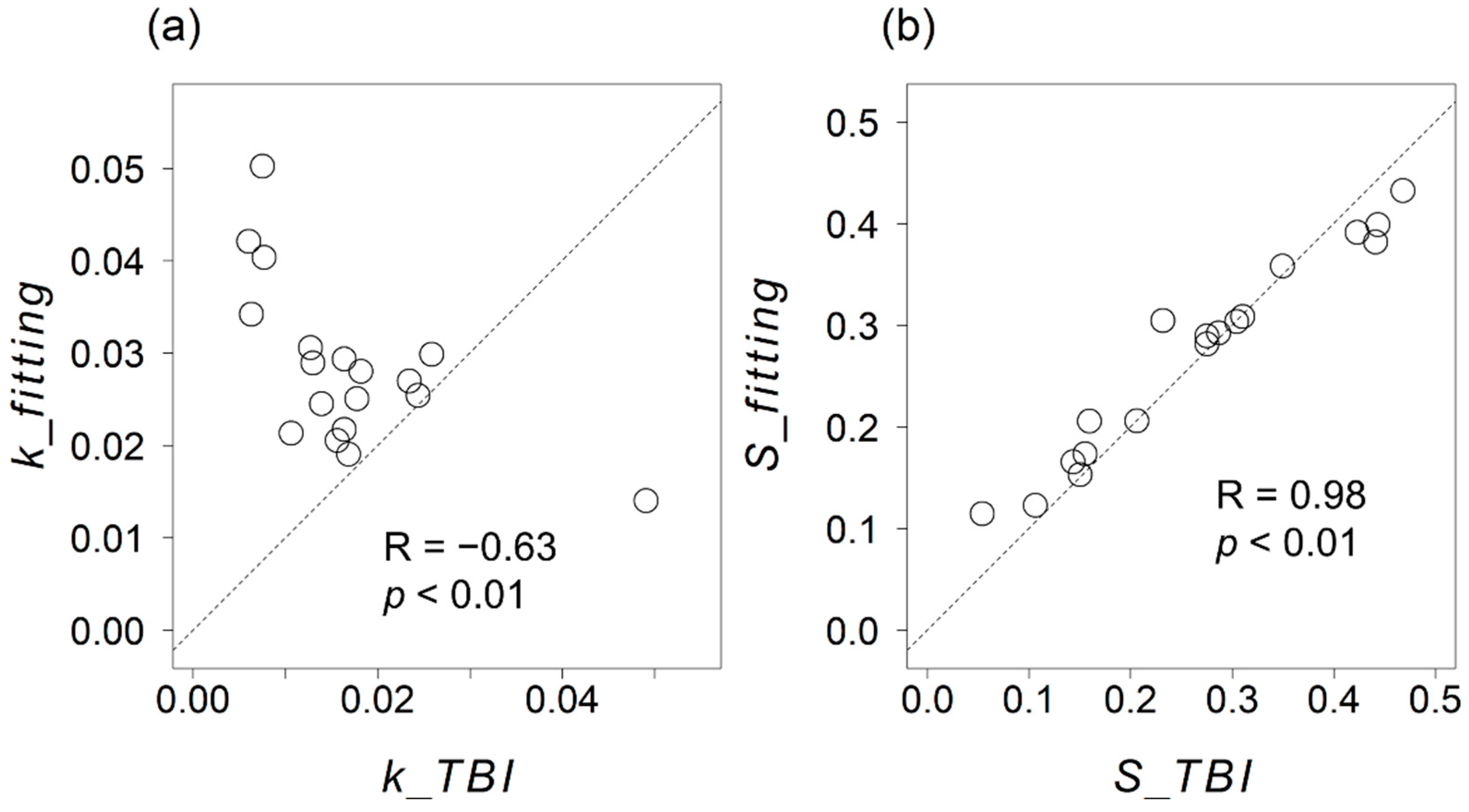
3. Results and Discussion
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Knorr, M.; Frey, S.; Curtis, P. Nitrogen additions and litter decomposition: A meta analysys. Ecology 2005, 86, 3252–3257. [Google Scholar] [CrossRef]
- Keuskamp, J.A.; Dingemans, B.J.J.; Lehtinen, T.; Sarneel, J.M.; Hefting, M.M. Tea Bag Index: A novel approach to collect uniform decomposition data across ecosystems. Methods Ecol. Evol. 2013, 4, 1070–1075. [Google Scholar] [CrossRef]
- Petraglia, A.; Cacciatori, C.; Chelli, S.; Fenu, G.; Calderisi, G.; Gargano, D.; Abeli, T.; Orsenigo, S.; Carbognani, M. Litter decomposition: Effects of temperature driven by soil moisture and vegetation type. Plant Soil 2019, 435, 187–200. [Google Scholar] [CrossRef]
- Fujii, S.; Mori, A.S.; Koide, D.; Makoto, K.; Matsuoka, S.; Osono, T.; Isbell, F. Disentangling relationships between plant diversity and decomposition processes under forest restoration. J. Appl. Ecol. 2017, 54, 80–90. [Google Scholar] [CrossRef]
- Fanin, N.; Bezaud, S.; Sarneel, J.M.; Cecchini, S.; Nicolas, M.; Augusto, L. Relative Importance of Climate, Soil and Plant Functional Traits During the Early Decomposition Stage of Standardized Litter. Ecosystems 2020, 23, 1004–1018. [Google Scholar] [CrossRef]
- Fung, T.K.; Richards, D.R.; Leong, R.A.T.; Ghosh, S.; Tan, C.W.J.; Drillet, Z.; Leong, K.L.; Edwards, P.J. Litter decomposition and infiltration capacities in soils of different tropical urban land covers. Urban Ecosyst. 2022, 25, 21–34. [Google Scholar] [CrossRef]
- Mori, T. Validation of the Tea Bag Index as a standard approach for assessing organic matter decomposition: A laboratory incubation experiment. Ecol. Indic. 2022, 141, 109077. [Google Scholar] [CrossRef]
- Mori, T.; Aoyagi, R.; Taga, H.; Sakai, Y. Effects of water content and mesh size on tea bag decomposition. Ecologies 2021, 2, 175–186. [Google Scholar] [CrossRef]
- Mori, T.; Ishizuka, S.; Konda, R.; Wicaksono, A.; Heriyanto, J.; Hardjono, A.; Ohta, S. Effects of phosphorus addition on N2O emissions from an Acacia mangium soil in relatively aerobic condition. Tropics 2016, 25, 117–125. [Google Scholar] [CrossRef]
- Duddigan, S.; Shaw, L.J.; Alexander, P.D.; Collins, C.D.; Society, R.H. Chemical Underpinning of the Tea Bag Index: An Examination of the Decomposition of Tea Leaves. Appl. Environ. Soil Sci. 2020, 2020, 6085180. [Google Scholar] [CrossRef]
- Mori, T. Can Nonwoven Tea Bags Be Used to Determine the Tea Bag Index? Ecologies 2022, 3, 175–182. [Google Scholar] [CrossRef]
- Mori, T. Tea Bags—Standard Materials for Testing Impacts of Nitrogen Addition on Litter Decomposition in Aquatic Ecosystems? Nitrogen 2021, 2, 259–267. [Google Scholar] [CrossRef]
- Mori, T.; Ono, K.; Sakai, Y. Testing the Tea Bag Index as a potential indicator for assessing litter decomposition in aquatic ecosystems. bioRxiv 2021. [Google Scholar] [CrossRef]
- Seelen, L.M.S.; Flaim, G.; Keuskamp, J.; Teurlincx, S.; Arias Font, R.; Tolunay, D.; Fránková, M.; Šumberová, K.; Temponeras, M.; Lenhardt, M. An affordable and reliable assessment of aquatic decomposition: Tailoring the Tea Bag Index to surface waters. Water Res. 2019, 151, 31–43. [Google Scholar] [CrossRef] [PubMed]
- Teo, A.; Kristensen, N.P.; Keuskamp, J.A.; Evans, T.A.; Foo, M.; Chisholm, R.A. Validation and extension of the Tea Bag Index to collect decomposition data from termite-rich ecosystems. Pedobiologia 2020, 80, 150639. [Google Scholar] [CrossRef]
- Tummers, B. DataThief III. 2006. Available online: http://datathief.org/ (accessed on 9 November 2022).
- R Core Team. R: A Language and Environment for Statistical Computing; Statistical, R Foundation for Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 28 May 2022).
- Mori, T.; Nakamura, R.; Aoyagi, R. Risk of misinterpreting the Tea Bag Index: Field observations and a random simulation. Ecol. Res. 2022, 37, 381–389. [Google Scholar] [CrossRef]
- Mori, T.; Hashimoto, T.; Sakai, Y. Evaluating the tea bag method as a potential tool for detecting the effects of added nutrients and their interactions with climate on litter decomposition. bioRxiv 2021. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mori, T. Is the Tea Bag Index (TBI) Useful for Comparing Decomposition Rates among Soils? Ecologies 2022, 3, 521-529. https://doi.org/10.3390/ecologies3040038
Mori T. Is the Tea Bag Index (TBI) Useful for Comparing Decomposition Rates among Soils? Ecologies. 2022; 3(4):521-529. https://doi.org/10.3390/ecologies3040038
Chicago/Turabian StyleMori, Taiki. 2022. "Is the Tea Bag Index (TBI) Useful for Comparing Decomposition Rates among Soils?" Ecologies 3, no. 4: 521-529. https://doi.org/10.3390/ecologies3040038
APA StyleMori, T. (2022). Is the Tea Bag Index (TBI) Useful for Comparing Decomposition Rates among Soils? Ecologies, 3(4), 521-529. https://doi.org/10.3390/ecologies3040038





