Exploring Therapeutic Dynamics: Mathematical Modeling and Analysis of Type 2 Diabetes Incorporating Metformin Dynamics
Abstract
1. Introduction
1.1. Overview of Type 2 Diabetes Models
1.2. Motivations, Contributions, and Objectives
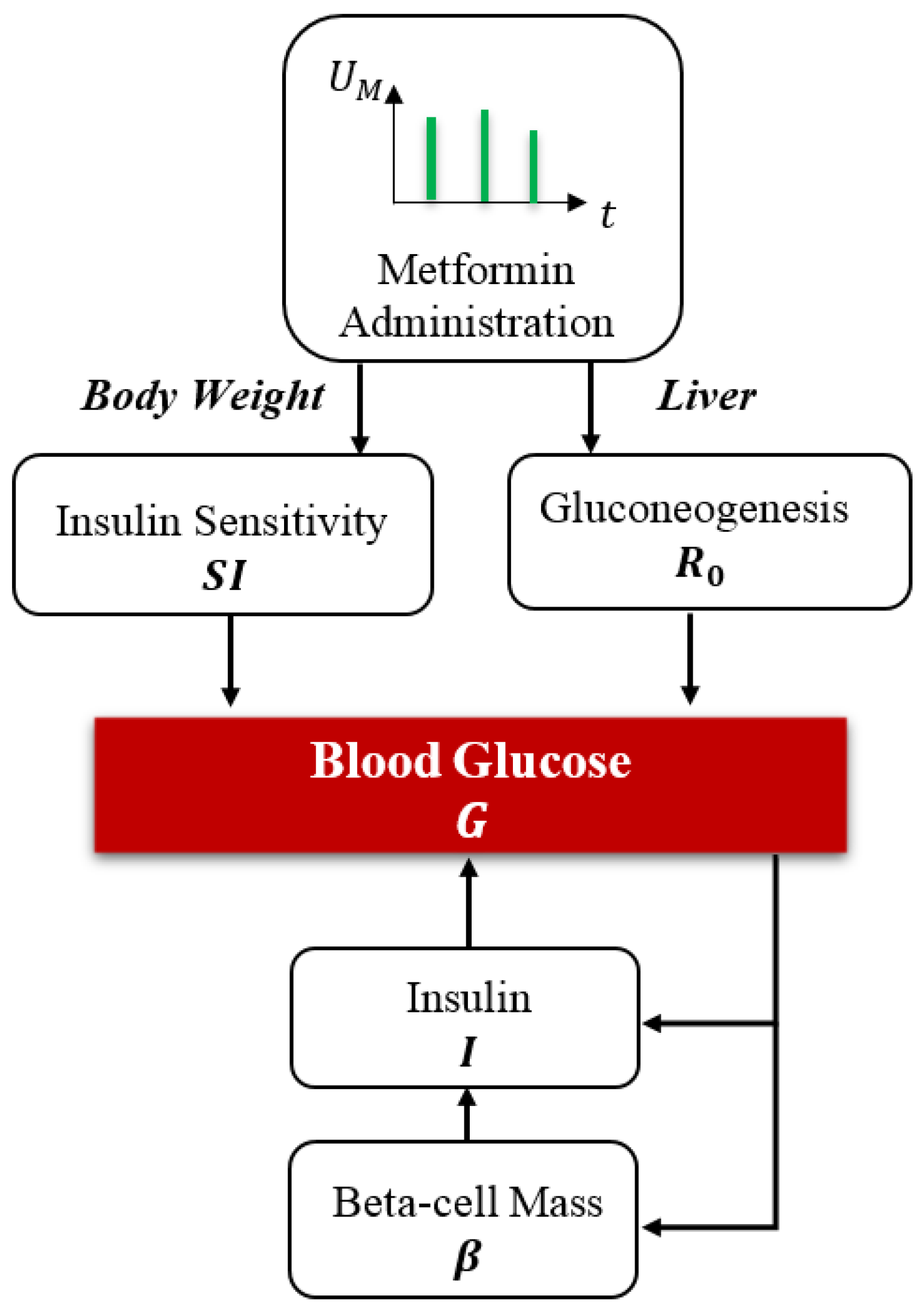
- Integration of Metformin into Glucose-Insulin Dynamics: Explicit incorporation of metformin into the classical BIG model as a continuous-state variable, enabling detailed examination of its impact on insulin sensitivity, hepatic glucose suppression, and glucose utilization. This inclusion captures the dual pharmacodynamic role of metformin in both hepatic and peripheral glucose regulation, enhancing the model’s capability to represent therapeutic interventions.
- Development of a Control-Oriented Mathematical Model: Creation of a simplified yet analytically rigorous framework that enhances interpretability and applicability in both control-theoretic studies and clinical practice, contrasting with complex, high-dimensional models. The model supports the simulation of diverse metformin dosing profiles and allows for treatment scenario testing, aligning closely with real-world pharmacological practice.
- Comprehensive Well-Posedness and Global Boundedness Analysis: Rigorous demonstration of the model’s mathematical well-posedness under biologically reasonable constraints, including local Lipschitz continuity, invariance of the non-negative orthant, and global boundedness, thereby confirming the existence, uniqueness, and biological relevance of solutions.
- Global Stability and Bifurcation Analysis: Application of Lyapunov stability methods to confirm the robustness of equilibrium states under realistic conditions and identification of saddle-node bifurcations that mark transitions from homeostasis to pathological states, thereby linking glucose regulation dynamics with the pharmacological effects of metformin. This analysis provides novel theoretical insights into how treatment-driven parameters such as metformin concentration modulate the stability landscape of glucose regulation.
- Identification of Critical Parameter Thresholds: Determination of parameter ranges crucial for maintaining glucose homeostasis, highlighting the balance between glucose production () and utilization (). Identifying these thresholds provides insights into physiological transitions between health and disease states.
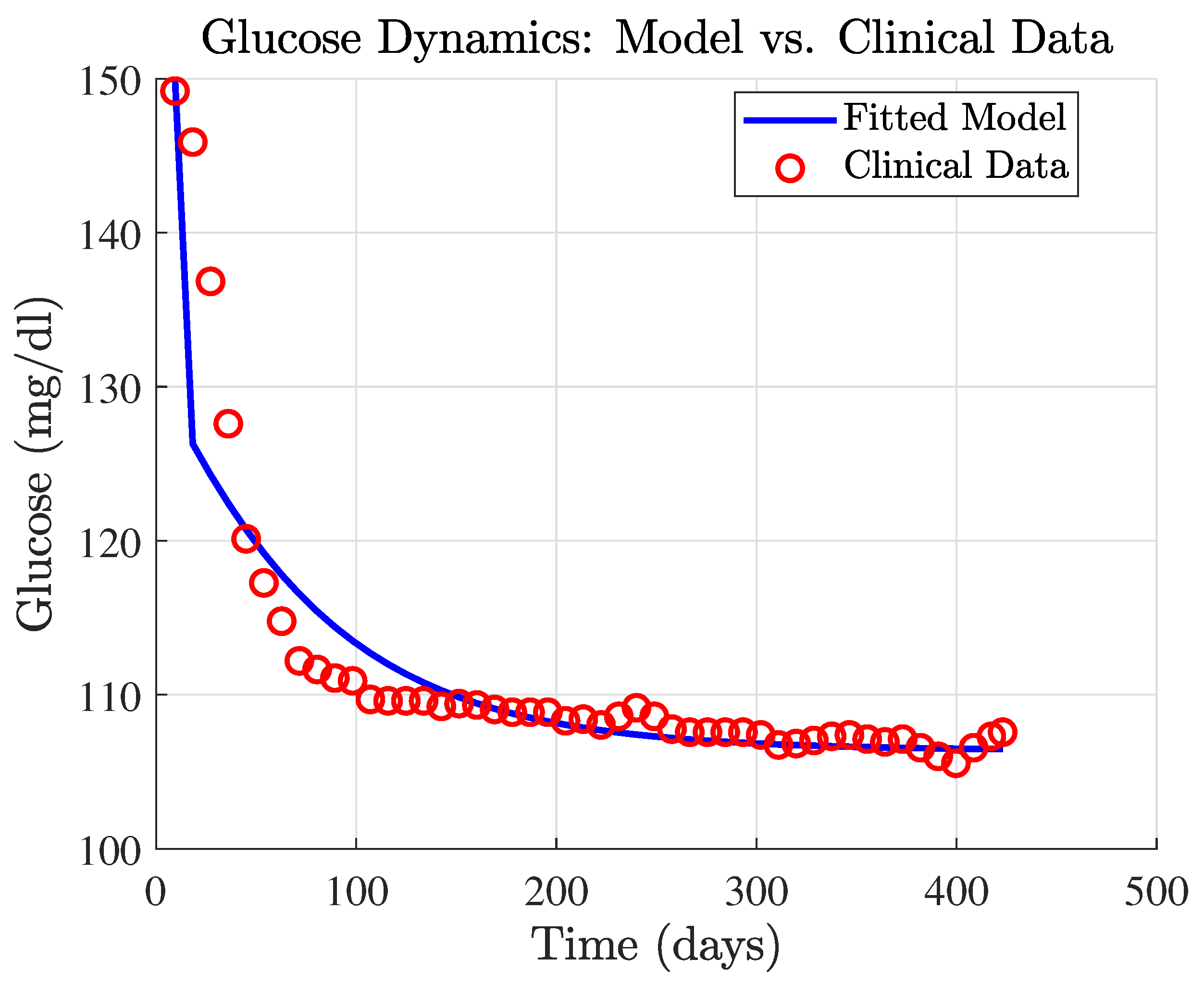
- Long-Term Treatment Scenario Simulations: Evaluation of various dosing strategies and pharmacokinetic scenarios through simulations, enhancing personalized therapeutic decision-making for effective long-term glycemic management. These simulations are supported by parameter sensitivity studies and validated using clinical data, reinforcing the model’s relevance and predictive capability.
2. Materials and Methods
2.1. Beta Cell-Insulin-Glucose Dynamics and Metformin
2.2. Insulin-Glucose Homeostasis
2.3. The BIG Model
- G is the blood glucose concentration,
- is the net glucose production rate at zero glucose,
- is the glucose uptake rate at zero insulin,
- represents insulin sensitivity,
- I is the blood insulin concentration,
- is the maximum insulin secretion rate,
- K is the insulin clearance rate (hepatic, renal, and receptor-mediated uptake),
- B is the beta-cell mass,
- is the baseline beta-cell apoptosis rate,
- and are coefficients for glucose-dependent beta-cell proliferation and death, respectively,
- c is the rate of insulin sensitivity degradation.
2.4. Metformin’s Role in Glycemic Regulation in T2DM
2.5. The Metformin-Integrated BIG Model
2.6. Well-Posedness and Boundedness
2.7. Lipschitz Continuity
- For :
- For :
- For :
- For :
- For :
2.8. Existence and Uniqueness
- For : Equation has the explicit solution . If , then for all .
- For : The equation with has the solution:If , then for all .
- For B: If , then , so for all t. If , then for small . If B ever reaches 0 at some time , then , so B cannot become negative.
- For I: If , then (assuming ), so I cannot become negative. If , then for small . If I ever reaches 0 at some time , then , so I cannot become negative.
- For G: A similar analysis shows that G cannot become negative if .
2.9. Boundedness and Global Existence
- For : The explicit solution gives:
- For : Using the variation of constants formula with the bounded input :As , is bounded by .
- For : When G is sufficiently large, specifically if (assuming ), then . This creates an upper bound:
- For : The term is bounded between 0 and 1. If , then . With bounded by some , we have:
- For : If and G are sufficiently large, specifically if , then . With bounded, is also bounded.
2.10. Continuous Dependence
2.11. Well-Posedness
- Existence and Uniqueness: For any non-negative initial condition, there exists a unique solution.
- Global Existence: Solutions exist for all and remain bounded.
- Continuous Dependence: Solutions depend continuously on initial conditions and parameters.
2.12. Stability Analysis
2.13. Equilibrium Points
2.14. Characterization of Equilibrium Points
2.14.1. Equilibrium Point
2.14.2. Potential Additional Equilibrium Points
2.15. Local Stability Analysis
2.15.1. Linearization Around Equilibrium Points
2.15.2. Stability of Equilibrium Point
2.15.3. Stability Conditions for Equilibrium Point
2.15.4. Potential Additional Equilibrium Points
- 1.
- The Jacobian matrix evaluated at has one zero eigenvalue and four strictly negative eigenvalues. Thus, is non-hyperbolic, with a one-dimensional center subspace in the B-direction.
- 2.
- By the Center Manifold Theorem, there exists a one-dimensional center manifold passing through , locally expressible as:where is the first-order expansion coefficient.
- 3.
- The reduced dynamics on is given by:
- 4.
- The sign of determines the local stability of the equilibrium point:
- If , then and is locally asymptotically stable;
- If , then and is unstable;
- If , higher-order terms must be considered.
3. Results
3.1. Mathematical Results
- Subsystem The equation has the explicit solution . For , as , regardless of the initial condition. Therefore, the subsystem is globally asymptotically stable with equilibrium .
- Subsystem With , the equation becomes approximately for large t. For , as , regardless of the initial condition. Therefore, the subsystem is also globally asymptotically stable with equilibrium .
- B-I-G SubsystemWith and for large t, we have:
3.1.1. Lyapunov Function Approach
3.1.2. Long-Term Behavior Analysis
- The equilibrium is locally asymptotically stable.
- For the B equation: .
- With , we have when .
- Therefore, as .
- With , we have as .
- The equilibrium appears to be globally asymptotically stable in this case.
- The equilibrium is unstable.
- For the B equation: .
- With , we have when .
- grows without bound, which is biologically unrealistic.
- This suggests model limitations or the existence of other equilibria not captured in our analysis.
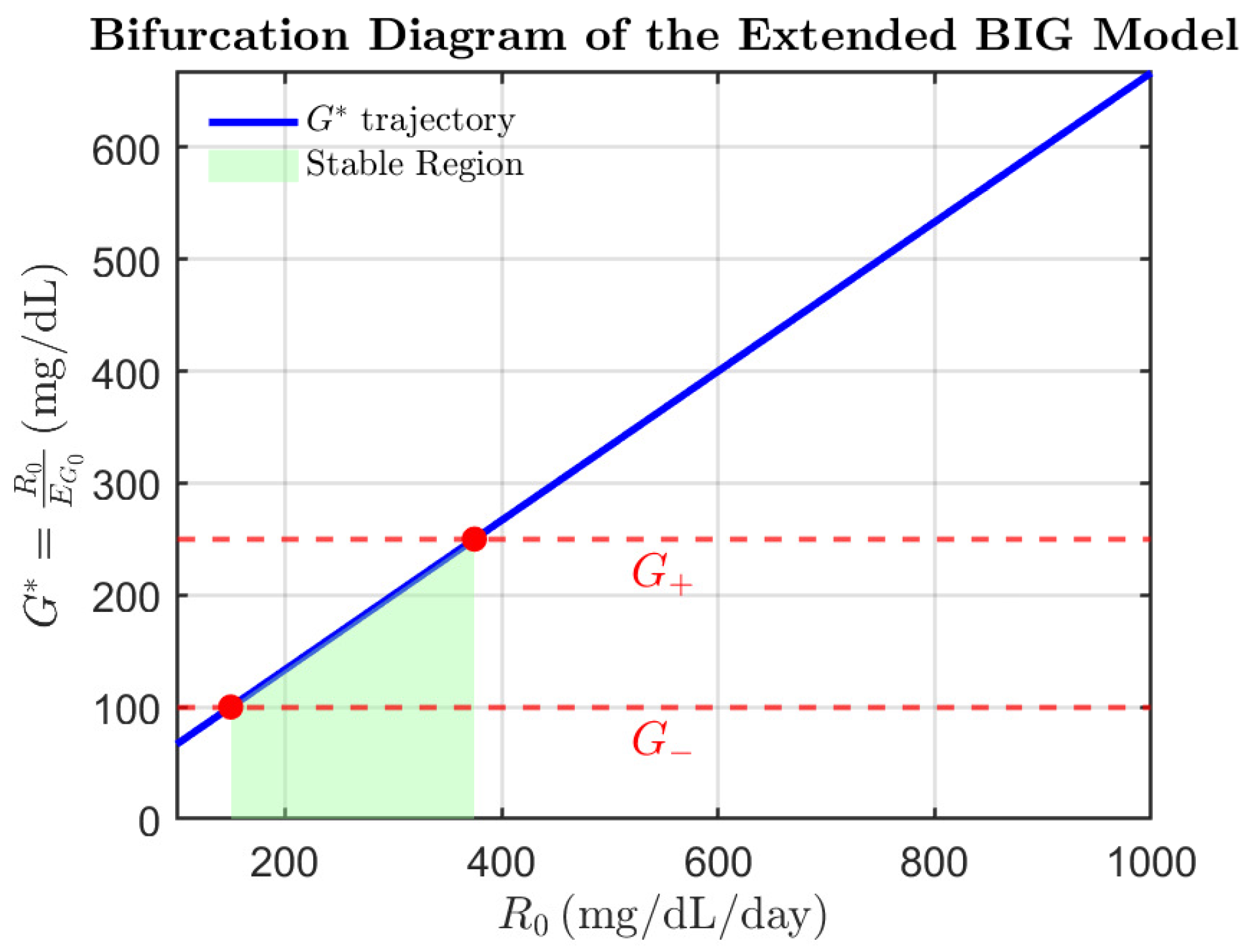
3.1.3. Bifurcation Analysis
- One eigenvalue of the Jacobian becomes zero.
- The equilibrium point changes stability.
- In the case where or , the equilibrium point is non-hyperbolic.
- The dynamics on the center manifold typically exhibit saddle-node bifurcation behavior.
3.1.4. Summary of Stability and Bifurcation Analysis
- Equilibrium Point:
- Asymptotically stable if .
- Unstable if or (if positive).
- This represents a state with no insulin and no beta-cells, where glucose is at a baseline level.
- Global Stability:
- The system components and always converge to 0 globally.
- For the G-I-B subsystem, global stability depends on the relationship between and the roots of .
- When , the equilibrium appears to be globally asymptotically stable.
- Bifurcations:
- The system undergoes saddle-node bifurcations when is equal to or .
- These bifurcations represent critical transitions in the system’s dynamics.
3.1.5. Biological Implications: Stability Analysis
- Stability Criterion: When , i.e., , the system converges to the asymptotically stable equilibrium characterized by vanishing beta-cell mass. In contrast, if , the equilibrium becomes unstable, and the system may transition toward unbounded growth or oscillatory dynamics. This outcome is consistent with the results of our bifurcation and Lyapunov-based analysis but recasts the condition within a more intuitive, threshold-based epidemiological framework.
3.1.6. Biological Implications: Bifurcation
3.2. Computational Results
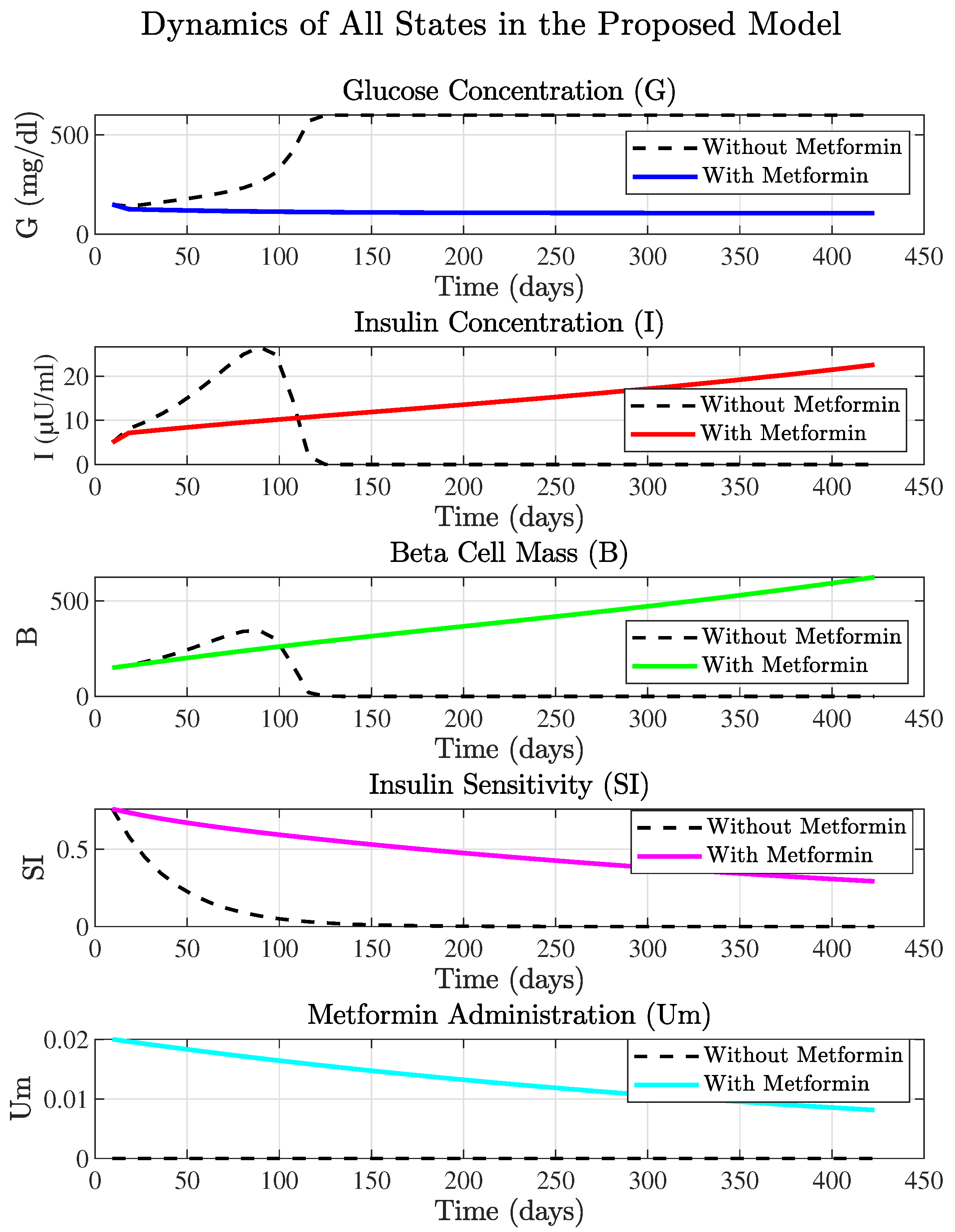
3.2.1. The Metformin-Integrated Model States Analysis
3.2.2. Metformin Parameter Tuning
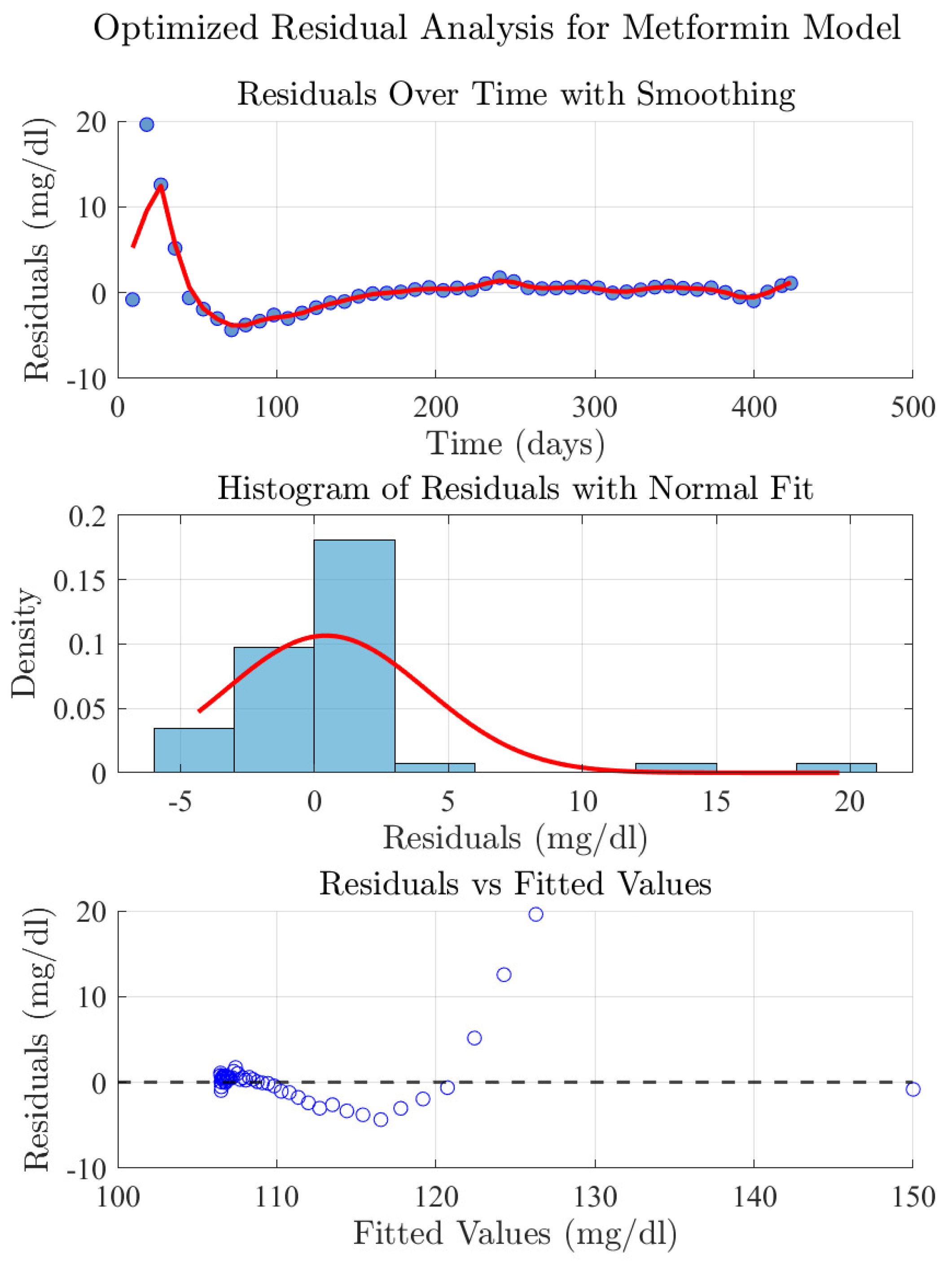
3.2.3. Residual Analysis of the Metformin Model
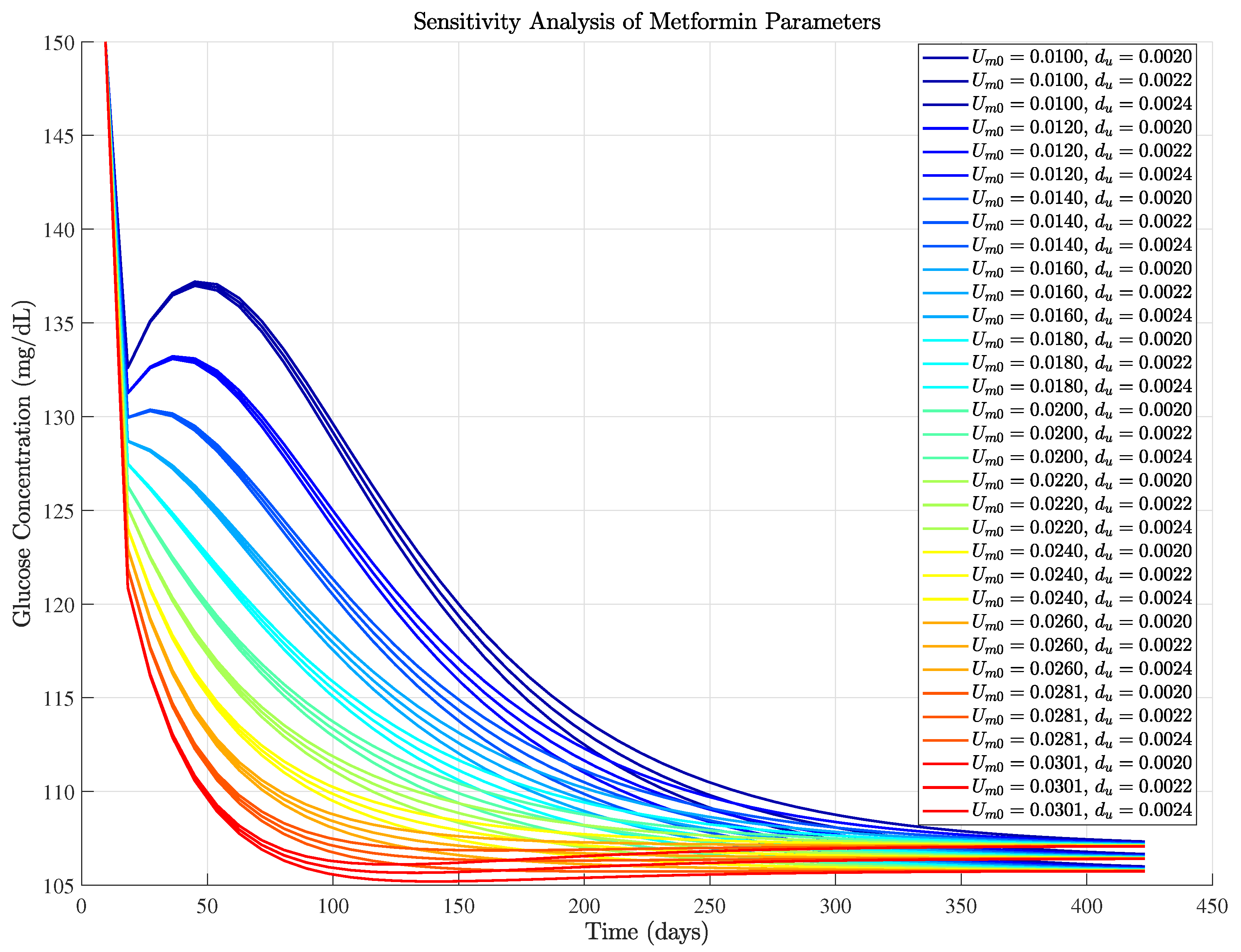
3.2.4. Sensitivity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Lu, X.; Xie, Q.; Pan, X.; Zhang, R.; Zhang, X.; Peng, G.; Zhang, Y.; Shen, S.; Tong, N. Type 2 diabetes mellitus in adults: Pathogenesis, prevention and therapy. Signal Transduct. Target. Ther. 2024, 9, 262. [Google Scholar] [CrossRef]
- Safiri, S.; Karamzad, N.; Kaufman, J.S.; Bell, A.W.; Nejadghaderi, S.A.; Sullman, M.J.; Moradi-Lakeh, M.; Collins, G.; Kolahi, A.A. Prevalence, deaths and disability-adjusted-life-years (DALYs) due to type 2 diabetes and its attributable risk factors in 204 countries and territories, 1990–2019: Results from the global burden of disease study 2019. Front. Endocrinol. 2022, 13, 838027. [Google Scholar] [CrossRef] [PubMed]
- Perng, W.; Conway, R.; Mayer-Davis, E.; Dabelea, D. Youth-onset type 2 diabetes: The epidemiology of an awakening epidemic. Diabetes Care 2023, 46, 490–499. [Google Scholar] [CrossRef] [PubMed]
- Aikaeli, F.; Njim, T.; Gissing, S.; Moyo, F.; Alam, U.; Mfinanga, S.G.; Okebe, J.; Ramaiya, K.; Webb, E.L.; Jaffar, S.; et al. Prevalence of microvascular and macrovascular complications of diabetes in newly diagnosed type 2 diabetes in low-and-middle-income countries: A systematic review and meta-analysis. PLoS Glob. Public Health 2022, 2, e0000599. [Google Scholar] [CrossRef] [PubMed]
- Pop-Busui, R.; Januzzi, J.L.; Bruemmer, D.; Butalia, S.; Green, J.B.; Horton, W.B.; Knight, C.; Levi, M.; Rasouli, N.; Richardson, C.R. Heart failure: An underappreciated complication of diabetes. A consensus report of the American Diabetes Association. Diabetes Care 2022, 45, 1670–1690. [Google Scholar] [CrossRef]
- Cohrs, C.M.; Panzer, J.K.; Drotar, D.M.; Enos, S.J.; Kipke, N.; Chen, C.; Bozsak, R.; Schoniger, E.; Ehehalt, F.; Distler, M.; et al. Dysfunction of Persisting beta Cells Is a Key Feature of Early Type 2 Diabetes Pathogenesis. Cell Rep. 2020, 31, 107469. [Google Scholar] [CrossRef]
- Lv, C.; Sun, Y.; Zhang, Z.Y.; Aboelela, Z.; Qiu, X.; Meng, Z.X. Beta-cell dynamics in type 2 diabetes and in dietary and exercise interventions. J. Mol. Cell Biol. 2022, 14, mjac046. [Google Scholar] [CrossRef]
- Huang, H.; Lorenz, B.R.; Zelmanovitz, P.H.; Chan, C.B. Metformin preserves β-cell compensation in insulin secretion and mass expansion in prediabetic nile rats. Int. J. Mol. Sci. 2021, 22, 421. [Google Scholar] [CrossRef]
- Forslund, K.; Hildebrand, F.; Nielsen, T.; Falony, G.; Le Chatelier, E.; Sunagawa, S.; Prifti, E.; Vieira-Silva, S.; Gudmundsdottir, V.; Krogh Pedersen, H. Disentangling type 2 diabetes and metformin treatment signatures in the human gut microbiota. Nature 2015, 528, 262–266. [Google Scholar] [CrossRef]
- Marchetti, P.; Del Guerra, S.; Marselli, L.; Lupi, R.; Masini, M.; Pollera, M.; Bugliani, M.; Boggi, U.; Vistoli, F.; Mosca, F.; et al. Pancreatic islets from type 2 diabetic patients have functional defects and increased apoptosis that are ameliorated by metformin. J. Clin. Endocrinol. Metab. 2004, 89, 5535–5541. [Google Scholar] [CrossRef]
- López-Palau, N.E.; Olais-Govea, J.M. Mathematical model of blood glucose dynamics by emulating the pathophysiology of glucose metabolism in type 2 diabetes mellitus. Sci. Rep. 2020, 10, 12697. [Google Scholar] [CrossRef]
- Nazirun, N.N.N.; Wahab, A.A.; Selamat, A.; Fujita, H.; Krejcar, O.; Kuča, K.; Seng, G.H. Prediction Models for Type 2 Diabetes Progression: A Systematic Review. IEEE Access 2024, 12, 161595–161619. [Google Scholar] [CrossRef]
- Murphree, D.H.; Arabmakki, E.; Ngufor, C.; Storlie, C.B.; McCoy, R.G. Stacked classifiers for individualized prediction of glycemic control following initiation of metformin therapy in type 2 diabetes. Comput. Biol. Med. 2018, 103, 109–115. [Google Scholar] [CrossRef] [PubMed]
- Villikudathil, A.T.; McGuigan, D.H.; English, A. Exploring metformin monotherapy response in Type-2 diabetes: Computational insights through clinical, genomic, and proteomic markers using machine learning algorithms. Comput. Biol. Med. 2024, 171, 108106. [Google Scholar] [CrossRef] [PubMed]
- Chae, J.W.; Baek, I.H.; Lee, B.Y.; Cho, S.K.; Kwon, K.I. Population PK/PD analysis of metformin using the signal transduction model. Br. J. Clin. Pharmacol. 2012, 74, 815–823. [Google Scholar] [CrossRef]
- Zake, D.M.; Kurlovics, J.; Zaharenko, L.; Komasilovs, V.; Klovins, J.; Stalidzans, E. Physiologically based metformin pharmacokinetics model of mice and scale-up to humans for the estimation of concentrations in various tissues. PLoS ONE 2021, 16, e0249594. [Google Scholar] [CrossRef]
- Long, J.; Fang, Q.; Shi, Z.; Miao, Z.; Yan, D. Integrated biomarker profiling for predicting the response of type 2 diabetes to metformin. Diabetes Obes. Metab. 2024, 26, 3439–3447. [Google Scholar] [CrossRef]
- Mirzaee, A.; Dehghani, M.; Mohammadi, M. Optimal impulsive blood glucose control through multiple injections. Chaos Solitons Fractals 2021, 152, 111326. [Google Scholar] [CrossRef]
- Mirzaee, A.; Dehghani, M.; Abolpour, R.; Mohammadi, M.; Sadabadi, M.S. Robust Optimal Impulsive Blood Glucose Control Exploiting a Direct Searching Algorithm. IEEE Sens. J. 2023, 23, 3183–3193. [Google Scholar] [CrossRef]
- Bergman, R. Origins and History of the Minimal Model of Glucose Regulation. Front. Endocrinol. 2021, 11, 583016. [Google Scholar] [CrossRef]
- Topp, B.; Promislow, K.; Devries, G.; Miura, R.M.; Finegood, D.T. A model of β-cell mass, insulin, and glucose kinetics: Pathways to diabetes. J. Theor. Biol. 2000, 206, 605–619. [Google Scholar] [CrossRef]
- Boxonov, Z.; Rozikov, U. Stability analysis of a three-dimensional system of Topp model with diabetes. arXiv 2024, arXiv:2405.00323. [Google Scholar] [CrossRef]
- Subramanian, V.; Bagger, J.I.; Harihar, V.; Holst, J.J.; Knop, F.K.; Villsboll, T. An Extended Minimal Model of OGTT: Estimation of Alpha- and Beta-Cell Dysfunction, Insulin Resistance, and the Incretin Effect. Am. J.-Physiol.-Endocrinol. Metab. 2024, 326, E182–E205. [Google Scholar] [CrossRef] [PubMed]
- Farahmand, B.; Dehghani, M.; Vafamand, N.; Mirzaee, A.; Boostani, R.; Pieper, J.K. Robust nonlinear control of blood glucose in diabetic patients subject to model uncertainties. ISA Trans. 2023, 133, 353–368. [Google Scholar] [CrossRef] [PubMed]
- Pompa, M.; Panunzi, S.; Borri, A.; De Gaetano, A. A comparison among three maximal mathematical models of the glucose-insulin system. PLoS ONE 2021, 16, e0257789. [Google Scholar] [CrossRef] [PubMed]
- Banzi, W.; Kambutse, I.; Dusabejambo, V.; Rutaganda, E.; Minani, F.; Niyobuhungiro, J.; Mpinganzima, L.; Ntaganda, J.M. Mathematical Modelling of Glucose-Insulin System and Test of Abnormalities of Type 2 Diabetic Patients. Int. J. Math. Math. Sci. 2021, 2021, 6660177. [Google Scholar] [CrossRef]
- Visentin, R.; Schiavon, M.; Bonet, J.; Riz, M.; Wagenhuber, B.; Dalla Man, C. Tailoring the Padova Type 2 Diabetes Simulator for Treatment Guidance in Target Populations. IEEE Trans. Biomed. Eng. 2024, 71, 1780–1788. [Google Scholar] [CrossRef]
- Visentin, R.; Cobelli, C.; Dalla Man, C. The Padova Type 2 Diabetes Simulator from Triple-Tracer Single-Meal Studies: In Silico Trials Also Possible in Rare but Not-So-Rare Individuals. Diabetes Technol. Ther. 2020, 22, 892–903. [Google Scholar] [CrossRef]
- Galicia-Garcia, U.; Benito-Vicente, A.; Jebari, S.; Larrea-Sebal, A.; Siddiqi, H.; Uribe, K.B.; Ostolaza, H.; Martín, C. Pathophysiology of Type 2 Diabetes Mellitus. Int. J. Mol. Sci. 2020, 21, 6275. [Google Scholar] [CrossRef]
- Rena, G.; Hardie, D.G.; Pearson, E.R. The mechanisms of action of metformin. Diabetologia 2017, 60, 1577–1585. [Google Scholar] [CrossRef]
- Foretz, M.; Guigas, B.; Viollet, B. Understanding the glucoregulatory mechanisms of metformin in type 2 diabetes mellitus. Nat. Rev. Endocrinol. 2019, 15, 569–589. [Google Scholar] [CrossRef]
- Hirst, J.A.; Farmer, A.J.; Ali, R.; Roberts, N.W.; Stevens, R.J. Quantifying the Effect of Metformin Treatment and Dose on Glycemic Control. Diabetes Care 2012, 35, 446–454. [Google Scholar] [CrossRef] [PubMed]
- Ray, R.; Haq, A.U.; Chaudhry, R.; Burra, S.; Batool, A.; Masmoum, M.D.; Ullah, I. Efficacy of Metformin in Weight Management and Glycemic Control in Type 2 Diabetes: An Updated Systematic Review and Meta-Analysis. J. Adv. Med. Med. Res. 2024, 36, 225–239. [Google Scholar] [CrossRef]
- Sanchez-Rangel, E.; Inzucchi, S. Metformin: Clinical use in type 2 diabetes. Diabetologia 2017, 60, 1586–1593. [Google Scholar] [CrossRef]
- He, D.; Han, H.; Fu, X.; Liu, A.; Zhan, Y.; Qiu, H.; Ma, L.; Zhang, X.; Wang, X. Metformin Reduces Blood Glucose in Treatment-Naive Type 2 Diabetes by Altering the Gut Microbiome. Can. J. Diabetes 2021, 46, 150–156. [Google Scholar] [CrossRef]
- Winter, W.D.; DeJongh, J.; Post, T.; Ploeger, B.; Urquhart, R.; Moules, I.; Eckland, D.; Danhof, M. A mechanism-based disease progression model for comparison of long-term effects of pioglitazone, metformin and gliclazide on disease processes underlying type 2 diabetes mellitus. J. Pharmacokinet. Pharmacodyn. 2006, 33, 313–343. [Google Scholar] [CrossRef]
| Parameter | Value | Units |
|---|---|---|
| 1.44 | d−1 | |
| 864 | mg·dL−1·d−1 | |
| 43.2 | μU·mL−1·d−1 | |
| 20,000 | mg2·dL−2 | |
| K | 432 | d−1 |
| 0.06 | d−1 | |
| mg−1·dL·d−1 | ||
| mg−2·dL2·d−1 | ||
| c | d−1 | |
| 1 | μU−1·mL·d−2 | |
| d−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirzaee, A.; Yarahmadian, S. Exploring Therapeutic Dynamics: Mathematical Modeling and Analysis of Type 2 Diabetes Incorporating Metformin Dynamics. Biophysica 2025, 5, 37. https://doi.org/10.3390/biophysica5030037
Mirzaee A, Yarahmadian S. Exploring Therapeutic Dynamics: Mathematical Modeling and Analysis of Type 2 Diabetes Incorporating Metformin Dynamics. Biophysica. 2025; 5(3):37. https://doi.org/10.3390/biophysica5030037
Chicago/Turabian StyleMirzaee, Alireza, and Shantia Yarahmadian. 2025. "Exploring Therapeutic Dynamics: Mathematical Modeling and Analysis of Type 2 Diabetes Incorporating Metformin Dynamics" Biophysica 5, no. 3: 37. https://doi.org/10.3390/biophysica5030037
APA StyleMirzaee, A., & Yarahmadian, S. (2025). Exploring Therapeutic Dynamics: Mathematical Modeling and Analysis of Type 2 Diabetes Incorporating Metformin Dynamics. Biophysica, 5(3), 37. https://doi.org/10.3390/biophysica5030037






