Abstract
Caenorhabditis elegans is among the most important model organisms. It has been extensively studied from the perspective of life and biomedical sciences. However, no model of growth and metabolism of C. elegans is available in the literature that is based on biothermodynamics and bioenergetics. Such a model would provide insight into growth and metabolism of C. elegans from the perspective of the fundamental laws of nature. In this research, a chemical and thermodynamic characterization of C. elegans is performed, with the determination of empirical formulas, thermodynamic properties of living matter, reactions of biosynthesis, catabolism and metabolism, thermodynamic properties of biosynthesis, catabolism and metabolism, and phenomenological coefficients. Based on the determined properties, a model of the growth and metabolism of C. elegans is developed. The model is used to discuss the metabolism of C. elegans from the aspect of physical chemistry.
1. Introduction
Caenorhabditis elegans is an important model organism for research in genetics [1], aging [2], immunology [3], neurology [4], pharmacy [5] and many other fields of life and biomedical sciences [6,7]. The properties that make C. elegans a good model organism are easy cultivation, small nutritional and growth requirements, and rapid and simple reproduction [6]. Moreover, Caenorhabditis elegans is among the best studied organisms from the perspective of biology [3,7]. Macromolecular composition of C. elegans is available in the literature [8,9], as well as an analysis of its growth and metabolism from the perspective of chemical kinetics [8,9]. However, no biothermodynamic and bioenergetic models of the growth and metabolism of C. elegans are available in the literature. Such models would provide deeper insight into the growth and metabolism of C. elegans from the perspective of the fundamental laws of nature.
Biothermodynamics and bioenergetics are interdisciplinary fields at the interface of biology, chemistry, physics, and engineering [10,11]. Their aim is to analyze organisms and life processes based on the fundamental laws of physics and chemistry [10,11]. Biothermodynamic analysis has been extensively applied to growth and metabolism of microorganisms, including bacteria [12,13,14,15,16], yeast [15,17,18], filamentous fungi [14,15], unicellular algae [15,19,20], and viruses [21,22,23,24]. Moreover, biothermodynamics has been applied in the analysis of growth, metabolism, and competition of plants [25,26,27].
Biothermodynamics and bioenergetics have been applied with great success in engineering and analysis of pathogen–host interactions. Biothermodynamics is a very valuable tool for the development of biotechnological processes [28,29], like the design of bioreactors [30,31] and biorefineries [32,33]. Moreover, thermodynamics is important for research in environmental sciences [34,35] and soil research [36,37]. Furthermore, biothermodynamics and bioenergetics have been applied to study interactions between organisms, like the virus–host interactions [38,39] and bacteria–host interactions [22]. This approach was able to give insight into the interactions of SARS-CoV-2 with its host organism [40,41,42,43] and COVID-19 epidemiology [44,45]. However, very few models of animal growth and metabolism exist that are based on biothermodynamics and bioenergetics [46].
Biothermodynamics is widely used in the development of mechanistic models of microbial metabolism. Every microorganism species has a characteristic empirical formula and thermodynamic properties (enthalpy, entropy, Gibbs energy) of living matter [15,16,17]. Biothermodynamic models of microbial metabolism are based on metabolism (growth) reactions, which show how nutrients are converted into new living matter and catabolic products by organisms [47,48,49]. The general form of a metabolism reaction is
(Nutrients) → (Living matter) + (Additional products)
Metabolism reactions lead to changes in thermodynamic properties, called thermodynamic properties of metabolism (growth) [16,17,50]. Gibbs energy of metabolism is the driving force of metabolism and multiplication of microorganisms [10,12,47]. This is why Gibbs energy can be used to predict the energetic efficiency of metabolism and growth rate [11,51,52]. Equations were developed to calculate the Gibbs energy of metabolism based on the composition of nutrients [53,54]. Gibbs energy can also be used to analyze interactions between organisms, like infection and competition [55,56].
Attempts were made to extend biothermodynamic models of growth and metabolism to multicellular organisms. Growth and metabolism of plants and algae were analyzed using growth reactions [19,27]. Growth reactions of plants have a similar form to those of microorganisms, but the nutrients are CO2, water, and inorganic ions, while the additional product is oxygen [19,57]. The driving force for growth and metabolism of organisms is Gibbs energy [10,19]. Gibbs energy expenditure was used to analyze competition between plants [26]. Moreover, biothermodynamic models were used to discuss the growth and stress resistance of plants [25,58,59]. Furthermore, a mechanistic model of animal growth and metabolism was reported for the fish species Anguilla anguilla (European eel) [46] and the insect Bombyx mori (domestic silk moth) [60]. However, very little data on the chemical and thermodynamic properties of animal species are available in the literature. Chemical and thermodynamic data are important since they are the basis for biothermodynamic analysis.
Nonequilibrium thermodynamics is an important tool for the development of mechanistic models of growth and metabolism [47,52,61]. Phenomenological equations are a part of nonequilibrium thermodynamics, which allow for calculating rates of processes based on their driving force [52,61]. The driving force of chemical reactions is the Gibbs energy change [52,61]. Metabolism is a chemical process that consists of catabolism and biosynthesis [47,52]. Catabolism and biosynthesis are chemical processes with reaction rates and Gibbs energy changes ΔbsG and ΔcatG, respectively [47,52]. The biosynthesis phenomenological equation allows us to find the rate of biosynthesis, rbs, based on Gibbs energies of biosynthesis, ΔbsG, and catabolism, ΔcatG,
where LBB and LBC are phenomenological coefficients [47,52]. LBB is the biosynthesis–biosynthesis phenomenological coefficient, which shows how the Gibbs energy of biosynthesis influences the biosynthesis rate [47,52]. LBC is the biosynthesis–catabolism coupling phenomenological coefficient, which shows how the Gibbs energy of catabolism influences the biosynthesis rate [47,52]. The LBC phenomenological coefficient shows how the energy released by degradation of nutrients in catabolism drives the formation of new living matter in biosynthesis [47,52].
In this research, a model of growth and metabolism will be developed for C. elegans, based on biothermodynamics and bioenergetics. Caenorhabditis elegans was chosen due to its importance as a model organism in life sciences. Caenorhabditis elegans is a small, free-living soil nematode (roundworm) that lives in many parts of the world and feeds on microorganisms like bacteria [7,62]. An adult C. elegans organism consists of about 1000 somatic cells [63]. It is unsegmented, with a cylindrical body shape [64].
After they hatch from eggs, C. elegans larvae develop into adult organisms [65,66,67]. The development can proceed through four larval stages (L1–L4) in favorable environments [68,69,70] or through the Dauer stage in unfavorable environments [71,72,73]. Under conditions when nutrients are abundant and the environment is not overcrowded, C. elegans development proceeds through four larval stages [74,75,76]. At each stage, specific changes occur in the morphology of the organism [77,78,79]. Under this pathway, the development process takes several days [80,81,82]. The development process requires energy, which is obtained from nutrients [8,83,84]. In cases when nutrients are limited or the environment is overcrowded, the larvae develop through the Dauer stage [73,85,86]. The Dauer stage is optimized for exploration of new environments in search of food sources [87,88,89]. Dauer larvae do not feed or grow, but they are highly motile [90,91,92]. Since Dauer larvae do not feed, the pharyngeal pumping is ceased to conserve energy [93,94]. Their entire organism is covered by a thick cuticle, which also covers the mouth and improves resistance to environmental stress [95,96,97]. Also, special enzymes are produced that protect against environmental stress [98]. The organisms also become more compact [74,99]. During the Dauer stage, all energy needed for metabolism comes from the intestinal and hypodermal lipid stores [100,101,102]. When Dauer larvae find a favorable environment, they continue their development into the adult stage [73,103,104].
The goal of this paper is to perform a chemical and thermodynamic characterization of C. elegans. The properties that will be calculated include the empirical formula, biosynthesis reaction, catabolism reaction, metabolism reaction, thermodynamic properties (enthalpy, entropy, Gibbs energy) of living matter, biosynthesis, catabolism, and metabolism, as well as phenomenological coefficients. Based on these properties, a mechanistic model of growth and metabolism of C. elegans will be developed based on biothermodynamics and bioenergetics. The developed model will be used to analyze the growth and metabolism of C. elegans from the perspective of the fundamental laws of nature.
2. Methods
2.1. Data Sources
The genetic sequence of C. elegans was taken from the NCBI database [105,106], under the accession numbers: BX284601.5 for chromosome I, BX284602.5 for chromosome II, BX284603.4 for chromosome III, BX284604.4 for chromosome IV, BX284605.5 for chromosome V, and BX284606.5 for chromosome X. The genetic sequence of E. coli was taken from the NCBI database [105,106], under the accession number U00096.3.
The macromolecular composition of Caenorhabditis elegans is 60% proteins, 20% lipids, 6.5% nucleic acids, and 6% carbohydrates [8,9]. The macromolecular composition of Escherichia coli is 55% protein, 7–9% lipids, 23% nucleic acids, and 6% carbohydrates [8,63,107].
The empirical formulas of the macromolecular constituents are: proteins CH1.59O0.32N0.26S0.007 (or C100H159N26O32S0.7), lipids CH1.92O0.12 (or C51H98O6), and carbohydrates CH2O [108]. The empirical formulas of the nucleic acids of C. elegans and E. coli were determined with the atom counting method, as described below.
The metabolic heat rate of C. elegans is 28 µW/mg-wet-wt (microwatts per milligram of wet weight) [109,110]. The water content of C. elegans tissues is 80% [111]. The biosynthesis rate of C. elegans is 1.375 C-mol/C-mol day (or 1.59 × 10−5 C-mol/C-mol s; the units mean: C-moles of new living matter formed for each existing C-mole of living matter per second) [112].
2.2. Chemical and Empirical Formulas of Nucleic Acids
Chemical and empirical formulas of nucleic acids of C. elegans and E. coli were determined with the atom counting method, based on the genetic sequences, as described in [113,114,115]. The atom counting method is a computational method for the determination of molecular formulas, empirical formulas, and molar masses of macromolecules and macromolecular assemblies, like nucleic acids, proteins, virus particles, etc. [113,114,115]. The atom counting method is applied using a computer program [113,114]. The inputs are genetic sequences, protein sequences, and particle morphology [113,114]. Nucleic acids and proteins are biopolymers composed of nucleotide and amino acid monomer residues [116,117,118]. Every monomer residue has a well-defined molecular formula [119,120]. The molecular formula of the entire biopolymer is the sum of atoms coming from all the monomer residues. This is why in the atom counting method, the program goes along the genetic and protein sequences and adds atoms coming from the monomer residues [113,114,115]. This gives the molecular formula of the entire nucleic acid or protein [113,114,115]. Molecular formulas have the general form CmCHmHOmONmNPmPSmS, where mC, mH, mO, mN, mP, and mS are the numbers of C, H, O, N, P, and S atoms in the molecular formula. The empirical formulas are calculated from molecular formulas with the equation nJ = mJ/mC, where nJ is the number of atoms of element J in the empirical formula, mJ is the number of atoms of element J in the molecular formula, and mJ is the number of carbon atoms in the molecular formula. Empirical formulas have the general form CnCHnHOnONnNPnPSnS, where nC, nH, nO, nN, nP, and nS are the numbers of C, H, O, N, P, and S atoms in the empirical formula. This gives the molecular and empirical formulas of biopolymers like nucleic acids and proteins.
Multiple biopolymers can form a macromolecular assembly [121,122]. This is why in the case of macromolecular assemblies, the numbers of atoms that come from every biopolymer are multiplied by the number of copies of the biopolymer. If the macromolecular assembly contains lipids, the numbers of atoms that come from lipids are calculated based on particle morphology [113,114,115]. Summation of all the atoms that come from the constituents of a macromolecular assembly gives its molecular formula [113,114,115]. The molecular formula is then used to calculate the empirical formula as described above [113,114,115]. The atom counting method calculates molecular and empirical formulas of macromolecules and macromolecular assemblies that are in good agreement with experimental results [113,114,115].
2.3. Empirical Formulas of Living Matter
Empirical formulas of living matter of C. elegans and E. coli were determined using the molecular composition method, as described in [113]. The molecular composition method uses a macromolecular composition of living matter as input. The macromolecular composition comes in the form of mass fractions of the macromolecular components of living matter. These are first converted into mole fractions of macromolecular components through the equation
where xX is the mole fraction of macromolecular component X, wX and wY represent the mass fractions of macromolecular components X and Y, respectively, while Mr(X) and Mr(Y) represent the molar masses of the empirical formulas of molecular components X and Y, respectively. The summation is over all Y macromolecular components that constitute living matter. The mole fractions of macromolecular components are used to find the empirical formula of living matter using the equation
where nJ is the number of atoms of element J in the empirical formula of living matter, and nJ(X) is the number of atoms of element J in the empirical formula of macromolecular component X. The summation is over all X macromolecular components that constitute the living matter.
2.4. Thermodynamic Properties of Living Matter
Empirical formulas were used to predict standard thermodynamic properties of living matter using predictive biothermodynamic models. The Patel–Erickson–Battley model was used, which combines the Patel–Erickson equation to find enthalpy and the Battley equation to find entropy.
The Patel–Erickson equation gives the standard enthalpy of combustion of living matter, based on its empirical formula [17,123]. It has the form
where ΔCHm0 is the standard enthalpy of combustion of living matter and E is the number of electrons transferred to oxygen during its complete combustion, also known as the degree of reduction [17,123]. E can be found from the empirical formula using the equation
where nJ is the number of atoms of element J in the empirical formula of living matter [17,123].
ΔCHm0 is then converted into the standard enthalpy of formation, ΔfHm0, of living matter through Hess’ law [15,17]. ΔCHm0 is defined as the enthalpy change for the reaction of complete oxidation of organic matter by oxygen.
CnCHnHOnONnNPnPSnS + (nC + ¼ nH + 1¼ nP + 1½ nS − ½ nO) O2 → nC CO2 + ½ nH H2O + ½ nN N2 + ¼ nP P4O10 + nS SO3
Standard enthalpies of formation of all the inorganic compounds in this reaction are known [124,125]. Thus, Hess’ law can be applied to calculate ΔfHm0, of living matter, through the equation [15,124,125]
The Battley equation can be used to find standard molar entropy of living matter, Sm0, from its empirical formula [126,127]. The Battley equation has the form
where Sm0(bio) is standard molar entropy of living matter, Sm0(J) standard molar entropy of element J in its standard state, aJ number of atoms of element J in its standard state, and nJ number of atoms of element J in the empirical formula of living matter [126,127]. The summation is over all J elements constituting the living matter [126,127]. For example, the standard state of hydrogen is H2, with an entropy of 130.684 J/mol K and aH = 2 [124].
The Battley equation can also be modified to give the standard entropy of formation, ΔfS0, of living matter [15,126]. In that case, it takes the form
ΔfSm0 is then combined with ΔfHm0 to find the standard Gibbs energy of formation, ΔfGm0, of living matter using the equation
where T is temperature.
The Patel–Erickson–Battley model was applied to calculate thermodynamic properties of a wide range of biological substances, which include biopolymers, cells, tissues, and organisms [15,127,128,129]. It was used to calculate thermodynamic properties of macromolecules [115,130] and macromolecular assemblies [60,114]. Moreover, the Patel–Erickson–Battley approach was applied to find thermodynamic properties of soil organic matter and gave results in good agreement with experiment [131,132]. The Patel–Erickson–Battley model was applied to microorganisms, which included bacteria, yeast, filamentous fungi, and algae [15,16,22,127,128,129]. The Patel–Erickson–Battley model was used to calculate thermodynamic properties of multicellular organisms, which include living matter of plants [133], fish species Anguilla anguilla (European eel) [46], insect Bombyx mori (domestic silk moth) [60], and human tissues [134]. The uncertainty in the standard enthalpy of combustion predicted with the Patel–Erickson equation is 5.36% [15]. The uncertainty in standard molar entropy predicted with the Battley equation is 19.7% or less [126].
2.5. Biosynthesis, Catabolism, and Metabolism Reactions and Thermodynamic Properties
Biosynthesis reactions are macromolecular equations that describe the conversion of nutrients by organisms into new living matter [29,50,119]. They are sometimes called anabolic reactions [11,29,119]. Each biosynthesis reaction consists of nutrients as reactants, living matter as the main product of biosynthesis, and additional biosynthesis products. Every nutrient taken by the organism from the environment contributes one or more elements to the formation of new living matter [135]. In the biosynthesis reaction of C. elegans, living matter of E. coli (the carbon and energy source) is converted into living matter of C. elegans, the main product of growth. Excess nitrogen, sulfur, and phosphorus are released as ammonium, sulfate, and hydrogen phosphate ions. The general biosynthesis reaction of C. elegans has the form
where (E. coli) represents the empirical formula of living matter of E. coli and (C. elegans) represents the empirical formula of living matter of C. elegans. The living matter of E. coli represents the source of carbon, nitrogen, phosphorus, and sulfur. The main product of growth is the living matter of C. elegans. The ions NH4+, SO42−, and HPO42− are additional biosynthesis products that remove excess nitrogen, sulfur, and phosphorus. H2CO3 and HCO3− form a bicarbonate buffer that maintains the pH constant. O2 takes the excess electrons produced by the oxidation of nutrients. It will disappear from the product side when the catabolic reaction is added. The convention with positive stoichiometric coefficients for products and negative stoichiometric coefficients for reactants is used [124,125].
(E. coli) + H2CO3 (aq) + H2O (l) → (C. elegans) + NH4+ (aq) + SO42− (aq) + HCO3− (aq) + HPO42− (aq) + O2 (g)
Catabolism reactions describe the degradation of nutrients by organisms into simple catabolic products to provide energy that drives the metabolism [11,29,50,119]. A catabolism reaction contains nutrients and the electron acceptor as reactants and, on the product side, catabolic waste products [11,29,50]. The general catabolism reaction for C. elegans has the form
where (E. coli) represents the empirical formula of living matter of E. coli, which is the energy source. No new living matter is produced in the catabolism reaction [11,29,50]. O2 is the electron acceptor. The catabolic waste products are CO2 and the ions NH4+, SO42−, and HPO42−, which remove excess carbon, hydrogen, nitrogen, sulfur, and phosphorus. H2CO3 and HCO3− form a bicarbonate buffer that maintains the pH constant.
(E. coli) + H2CO3 (aq) + O2 (g) → NH4+ (aq) + SO42− (aq) + HCO3− (aq) + HPO42− (aq) + H2O (l) + CO2 (aq)
Biosynthesis and catabolism are the main components of metabolism [29,50]. Thus, the biosynthesis and catabolism reactions are combined to obtain the metabolism reaction. This is accomplished with Hess’s law [124,125]. The catabolism reaction is multiplied by the ratio of the catabolism rate, rcat, and biosynthesis rate, rbs [136]. Then, it is added to the biosynthesis reaction [136]. Therefore, the metabolism reaction of C. elegans has the general form
where (E. coli) and (C. elegans) represent the empirical formulas of living matter of E. coli and C. elegans, respectively.
(E. coli) + H2CO3 (aq) + O2 (g) → (C. elegans) + NH4+ (aq) + SO42− (aq) + HCO3− (aq) + HPO42− (aq) + H2O (l) + CO2 (aq)
Once the biosynthesis, catabolism and metabolism reactions, and stoichiometric coefficients are known, their thermodynamic properties can be determined. This is accomplished through Hess’s law [124,125]. Standard thermodynamic properties of reaction r are given by the equations
where ΔrH0, ΔrS0, and ΔrG0 are standard enthalpy, entropy, and Gibbs energy of reaction r, respectively; νX is the stoichiometric coefficient of substance X in reaction r; ΔfH0(X) is standard enthalpy of formation of substance X; Sm0(X) is standard molar entropy of substance X; and ΔfG0(X) standard Gibbs energy of substance X [124,125]. The summation is over all X substances that react in reaction r [124,125]. The convention with positive stoichiometric coefficients for products and negative stoichiometric coefficients for reactants is used [124,125].
ΔrH0, ΔrS0, and ΔrG0 of biosynthesis, catabolism, and metabolism are standard changes in the thermodynamic properties of enthalpy, entropy, and Gibbs energy [124,125]. This means that they represent changes for processes where the initial and final substances are in their standard states [124,125]. The standard state of a substance at a specified temperature is its pure form at 1 bar [124,125]. The temperature used in this research is 25 °C (298.15 K). However, under biological conditions, the substances are not in their pure forms but are mixed. This means that the actual values of thermodynamic properties are not identical to their standard values. The differences between actual and standard thermodynamic properties were analyzed in [137]. The difference between the standard and actual Gibbs energy of biosynthesis is between 22% and 25% [137]. Gibbs energies of catabolism and metabolism have much higher values, and for them, mixing results in only a minor correction [137]. Therefore, even though the actual values of thermodynamic properties are more accurate, standard values can be used for analysis in most cases, except when the values of Gibbs energies of catabolism, biosynthesis, and metabolism are very low (below 10 kJ/C-mol).
2.6. Kinetic Properties of Biosynthesis, Catabolism, and Metabolism
Heat rates of catabolism, biosynthesis and metabolism were calculated based on the metabolic rate, Rm, and biosynthesis rate, rbs, combined with the molar mass of the empirical formula, Mr, water content of tissues, ww, and standard enthalpy of catabolism, ΔbsH0. The metabolic rate was used to find the metabolism heat rate, , using the equation
where Rm is the metabolic rate, Mr molar mass of the empirical formula of living matter, and ww water content of tissues of C. elegans. The biosynthesis rate, rbs, was used to find the biosynthesis heat rate, , using the equation
where ΔbsH0 is standard enthalpy of biosynthesis [46,138,139]. From the biosynthesis heat rate and metabolism heat rate, the catabolism heat rate, , was calculated using the equation [46]
The catabolism heat rate was used to find the catabolism rate, rcat, with the equation
where ΔcatH0 is standard enthalpy of catabolism [46,138,139].
2.7. Phenomenological Equations and Coefficients
The kinetic and thermodynamic parameters are united through the framework of nonequilibrium thermodynamics. This is achieved using phenomenological equations. Phenomenological equations give rates of processes based on their physical driving forces [11,52,61]. The physical driving force of chemical reactions is Gibbs energy [11,52,61]. Gibbs energy of a chemical reaction can be used to find its affinity [52]. This is performed using the equation
where T is temperature, while Ai and ΔiG are affinity and Gibbs energy of reaction i, respectively [52]. This equation was used to find biosynthesis affinity, Abs, and catabolism affinity, Acat, based on their Gibbs energies.
If a system performs multiple chemical reactions simultaneously, the rate of every reaction can be found using the phenomenological equation
where ri is the rate of reaction i, Lij is the phenomenological coefficient between reactions i and j, while Aj is the affinity of reaction j [52]. The summation is over all j chemical reactions that the system performs [52].
In our case, we have a system with two reactions—biosynthesis and catabolism. Thus, the phenomenological equations take the form
where rbs and rcat are the rates of the biosynthesis and catabolism reactions, respectively, while Abs and Acat are the affinities (driving forces) of biosynthesis and catabolism reactions, respectively [11,52]. LBB, LCC, and LBC are the phenomenological coefficients [11,52]. LBB describes the influence of the biosynthesis driving force on biosynthesis rate [11,52]. LCC describes the influence of catabolism driving force on catabolism rate [11,52]. LBC is called the coupling coefficient since it describes the influence of catabolism on biosynthesis and vice versa [11,52].
Under complete coupling between biosynthesis and catabolism, the coupling coefficient can be found through the equation [11]
Finally, when Equations (22)–(24) can be combined and solved for LBB and LCC. This gives
Equations (26)–(28) were used to find the LBB, LCC, and LBC.
2.8. Changes in Environmental Conditions
The mechanistic model developed above assumes abundant nutrients and optimal temperature for growth and metabolism. Changes in nutrient availability and temperature can lead to changes in growth rate. The influence of temperature on thermodynamic properties of living matter, catabolism, biosynthesis, and metabolism can be taken into account with heat capacity. Heat capacity of living matter can be calculated with the Hurst–Harrison model
where C0p,m is the standard molar heat capacity at constant pressure, nJ is the number of atoms of element J in the empirical formula, while cJ is the contribution of element J to heat capacity [140,141]. C0p,m can be used to calculate the standard reaction heat capacity, ΔrCp0, of living matter with Hess’s law
where C0p,m(X) standard molar heat capacity at constant pressure of substance X that participates in the reaction and νX is the stoichiometric coefficient of substance X [124,125]. The reaction heat capacity can be used to calculate changes in standard reaction enthalpy with Kirchhoff’s law
where ΔrH0(T1) and ΔrH0(T2) are standard reaction enthalpies at temperatures T1 and T2, respectively [124,125]. This equation can be applied to catabolism, biosynthesis, and metabolism reactions. Moreover, the dependence of reaction Gibbs energy with temperature can be found with the Gibbs–Helmholtz equation
where ΔrG0(T1) and ΔrG0(T2) are standard reaction Gibbs energies at temperatures T1 and T2, respectively [124,125]. These equations can be applied to biosynthesis, catabolism, and metabolism reactions.
Changes in reaction Gibbs energy due to changes in nutrient concentrations can be taken into account with the equation
where ΔrG is reaction Gibbs energy, ΔrG0 standard reaction Gibbs energy, R universal gas constant, T temperature, and Q reaction quotient [124,125]. This equation shows how the reaction Gibbs energy changes with concentrations of reactants and products, which is summarized by the reaction quotient. The reaction quotient is given by the equation
where aj and νj are activity and stoichiometric coefficient of substance j, respectively [124,125].
3. Results
Table 1 shows the molecular formulas of nucleic acids of Caenorhabditis elegans and Escherichia coli. For C. elegans, molecular formulas were calculated for all six chromosomes (I, II, III, IV, V, and X), while for E. coli, the molecular formula was calculated for the entire circular DNA molecule. The molecular formulas were calculated with the atom counting method based on genetic sequences, as described in [113]. Chromosome I of C. elegans has the molecular formula C2.96×108H3.71×108O1.81×108N1.11×108P3.01×107 and a molar mass of 9311 MDa. Chromosome II of C. elegans has the molecular formula C3.00×108H3.76×108O1.83×108N1.12×108P3.06×107 and a molar mass of 9439 MDa. Chromosome III of C. elegans has the molecular formula C2.71×108H3.40×108O1.65×108N1.01×108P2.76×107 and a molar mass of 8515 MDa. Chromosome IV of C. elegans has the molecular formula C3.44×108H4.31×108O2.10×108N1.29×108P3.50×107 and a molar mass of 10,807 MDa. Chromosome V of C. elegans has the molecular formula C4.11×108H5.16×108O2.51×108N1.54×108P4.18×107 and a molar mass of 12,926 MDa. Chromosome X of C. elegans has the molecular formula C3.48×108H4.37×108O2.13×108N1.30×108P3.54×107 and a molar mass of 10,946 MDa. The circular DNA of E. coli has the molecular formula C9.05×107H1.14×108O5.57×107N3.48×107P9.28×106; and a molar mass of 2868 MDa.

Table 1.
Molecular formulas of nucleic acids of C. elegans and E. coli. The molecular formulas have the general form CmCHmHOmONmNPmP, where mC, mH, mO, mN, and mP are the numbers of C, H, O, N, and P atoms in the molecular formula, respectively.
Table 2 gives empirical formulas of the living matter of C. elegans and E. coli. The empirical formulas of living matter were calculated with the molecular composition method, as described in [113]. An empirical formula (also known as the unit carbon formula or C-mole formula) shows the number of atoms of constituent elements of living matter per carbon atom [15,48]. Living matter of E. coli is characterized by the empirical formula CH1.5919O0.3842N0.2361P0.019264S0.004408, which has a molar mass of 23.81 g/C-mol. Living matter of C. elegans is characterized by the empirical formula CH1.6898O0.3062N0.1775P0.004866S0.004297, which has a molar mass of 21.39 g/C-mol.

Table 2.
Empirical formulas of living matter of E. coli and C. elegans. The empirical formulas have the general form CnCHnHOnONnNPnPSnS, where nC, nH, nO, nN, nP, and nS are the numbers of C, H, O, N, P, and S atoms in the empirical formula, respectively.
Table 3 presents thermodynamic properties of living matter of E. coli and C. elegans. These include standard enthalpy of formation, ΔfH0, standard molar entropy, Sm0, and standard Gibbs energy of formation, ΔfG0. Thermodynamic properties of living matter were calculated with the Patel–Erickson model [17,123] and the Battley model [127,136]. For living matter of E. coli, standard enthalpy of formation is −87.52 kJ/C-mol, standard molar entropy is 32.25 J/C-mol K, and standard Gibbs energy of formation is −45.71 kJ/C-mol. For living matter of C. elegans, standard enthalpy of formation is −70.50 kJ/C-mol, standard molar entropy is 30.79 J/C-mol K, and standard Gibbs energy of formation is −30.58 kJ/C-mol.

Table 3.
Thermodynamic properties of living matter of E. coli and C. elegans: standard enthalpy of formation, ΔfH0, standard molar entropy, Sm0, and standard Gibbs energy of formation, ΔfG0.
Table 4 shows the stoichiometries of biosynthesis, catabolism, and metabolism of C. elegans. The biosynthesis, catabolism, and metabolism reactions were formulated based on the empirical formulas of living matter of C. elegans and E. coli from Table 2. Stoichiometric coefficients of the reactants are negative, while those of the products are positive.

Table 4.
Stoichiometries of biosynthesis (anabolism), catabolism, and metabolism of C. elegans: stoichiometric coefficients in the biosynthesis reaction, νbs, stoichiometric coefficients in the catabolism reaction, νcat, and stoichiometric coefficients in the metabolism reaction, νmet. The stoichiometric coefficients of reactants are negative, while the stoichiometric coefficients of products are positive.
Table 5 presents thermodynamic properties of biosynthesis, catabolism, and metabolism of C. elegans. The determined standard reaction enthalpies, ΔrH0, include standard enthalpy of biosynthesis, ΔbsH0, standard enthalpy of catabolism, ΔcatH0, and standard enthalpy of metabolism, ΔmetH0. The determined standard reaction entropies, ΔrS0, include standard entropy of biosynthesis, ΔbsS0, standard entropy of catabolism, ΔcatS0, and standard entropy of metabolism, ΔmetS0. The determined standard reaction Gibbs energies, ΔrG0, include the standard Gibbs energy of biosynthesis, ΔbsG0, the standard Gibbs energy of catabolism, ΔcatG0, and the standard Gibbs energy of metabolism, ΔmetG0. These properties were determined based on the reaction stoichiometries from Table 4 and thermodynamic properties of living matter from Table 3, using Hess’s law, as described in [124,125]. For the biosynthesis of C. elegans, the standard enthalpy of biosynthesis is 36.08 kJ/C-mol, the standard entropy of biosynthesis is 9.68 J/C-mol K, and the standard Gibbs energy of biosynthesis is 33.37 kJ/C-mol. For the catabolism of C. elegans, the standard enthalpy of catabolism is −501.80 kJ/C-mol, the standard entropy of catabolism is −94.58 J/C-mol K, and the standard Gibbs energy of catabolism is −473.29 kJ/C-mol. For the metabolism of C. elegans, the standard enthalpy of metabolism is −188.15 kJ/C-mol, the standard entropy of metabolism is −32.58 J/C-mol K, and the standard Gibbs energy of metabolism is −178.12 kJ/C-mol.

Table 5.
Thermodynamic properties of biosynthesis (anabolism), catabolism, and metabolism of C. elegans: standard reaction enthalpy, ΔrH0, standard reaction entropy, ΔrS0, and standard reaction Gibbs energy, ΔrG0.
Table 6 presents the kinetic properties of biosynthesis, catabolism, and metabolism reactions of C. elegans. The determined properties include metabolism heat rate, , biosynthesis heat rate, , catabolism heat rate, , and catabolism rate, rcat. They were determined as described in [138,139]. The metabolism heat rate of C. elegans is −2.99 × 10−3 kJ/mol s. The biosynthesis heat rate of C. elegans is 5.74 × 10−4 kJ/mol s. The catabolism heat rate of C. elegans is −3.57 × 10−3 kJ/mol s. The catabolism rate of C. elegans is 7.11 × 10−6 C-mol/C-mol s.

Table 6.
Kinetic properties of metabolism, biosynthesis (anabolism), and catabolism of C. elegans: metabolism heat rate, , biosynthesis heat rate, , catabolism heat rate, , biosynthesis rate, rbs, and catabolism rate, rcat. The rbs value was taken from [112].
Table 7 gives phenomenological coefficients and reaction affinities of biosynthesis and catabolism of C. elegans. These include catabolism affinity, Acat, biosynthesis affinity, Abs, catabolism-catabolism phenomenological coefficient, LCC, biosynthesis–biosynthesis phenomenological coefficient, LCC, and catabolism–biosynthesis phenomenological coefficient, LCB. They were determined using nonequilibrium thermodynamics, as described in [11,52]. The catabolism affinity of C. elegans is 1.587 kJ/mol K. The biosynthesis affinity of C. elegans is −0.112 kJ/mol K. The catabolism–catabolism phenomenological coefficient is 5.319 × 10−6 C-mol K/kJ s. The biosynthesis–biosynthesis phenomenological coefficient is 2.664 × 10−5 C-mol K/kJ s. The catabolism–biosynthesis phenomenological (coupling) coefficient is 1.190 × 10−5 C-mol K/kJ s.

Table 7.
Phenomenological coefficients of catabolism and biosynthesis of C. elegans: catabolism affinity, Acat, biosynthesis affinity, Abs, catabolism–catabolism phenomenological coefficient, LCC, biosynthesis–biosynthesis phenomenological coefficient, LCC, and catabolism–biosynthesis phenomenological coefficient, LCB.
4. Discussion
Organisms represent growing open biothermodynamic systems [142,143,144]. As a system, an organism consists of a certain amount of substance (living matter) separated from its environment [10,14,16,46]. This system interacts with its environment, which includes other organisms. These interactions represent biothermodynamic processes, like metabolism, growth, and competition [11,12,15,16,29]. Therefore, organisms and the processes they perform can be analyzed using the laws of chemistry and thermodynamics. This provides a basis for the development of mechanistic models based on biothermodynamics and bioenergetics, which can help better understand organisms.
This study focuses on Caenorhabditis elegans, a widely used model organism in life sciences. Chemical composition (empirical formula) and thermodynamic properties of the living matter of C. elegans were determined for the first time. Moreover, they were compared to empirical formulas and thermodynamic properties of the fish species Anguilla anguilla and the insect Bombyx mori. The differences in chemical and thermodynamic properties were discussed from the perspective of the lifecycles of the organisms. Growth and metabolism of C. elegans were also discussed from the perspective of chemistry and thermodynamics. A mechanistic model of growth and metabolism of C. elegans was developed based on biothermodynamics and bioenergetics. This model provides a deeper insight into the growth, metabolism, and evolution of C. elegans from the perspective of the fundamental laws of nature.
4.1. Chemical and Thermodynamic Properties of Living Matter of C. elegans
The empirical formula of C. elegans is given in Table 2. Empirical formulas are of particular importance for the determination of biosynthesis and metabolism (growth) reactions, as will be discussed below. The empirical formula of C. elegans living matter is CH1.6898O0.3062N0.1775P0.004866S0.004297. To compare, the empirical formula of Anguilla anguilla (European eel) in the yellow phase is CH1.753O0.220N0.132S0.004 [46]. Empirical formula of Bombyx mori (domestic silk moth) larvae is CH1.6803O0.2815N0.1903S0.005122 [60]. Therefore, every animal species has a characteristic empirical formula, different than those of other species.
Based on the empirical formulas, the thermodynamic properties of the living matter of C. elegans were determined and are shown in Table 3. Gibbs energy of formation of C. elegans is −30.58 kJ/C-mol. Gibbs energies of formation have been determined for living matter of other animal species: −15.00 kJ/C-mol for yellow A. anguilla [46], −8.65 kJ/C-mol for silver A. anguilla [46], and −24.12 kJ/C-mol for B. mori [60]. Gibbs energies of formation of the analyzed animal species are shown in Figure 1.
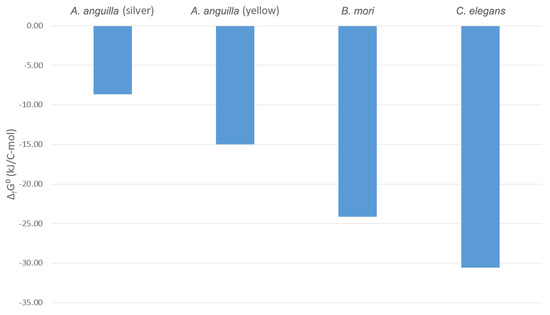
Figure 1.
Usable energy content of animal species. Standard Gibbs energies of formation, ΔfG0, are shown for Anguilla anguilla in the yellow and silver phases of its lifecycle, Bombyx mori (domestic silk moth) larvae, and C. elegans. The ΔfG0 values for the yellow A. anguilla, silver A. anguilla, and B. mori were taken from [46,60].
Figure 1 shows that the Gibbs energies of formation of yellow and silver A. anguilla are greater (less negative) than those of C. elegans. This means that A. anguilla has a higher usable energy content than C. elegans. The reason for this is the lifecycle of A. anguilla, which covers a very large area through which eels migrate. It begins with eel larvae, which hatch in the western Atlantic, in the Sargasso Sea [145,146,147]. The eels are then carried by the Gulf Stream to the coasts of Europe where they settle in rivers and lakes as glass eels [148,149,150]. There, they turn into yellow eels, which feed and grow [151,152,153]. After that, they become mature as silver eels, which migrate through the Atlantic to the Sargasso Sea where they spawn [154,155,156]. During the migration, the silver eels do not feed and must, therefore, rely on energy stored in their tissues [157]. This is why the usable energy content of their tissues is very high, which is shown by their high Gibbs energies of formation.
B. mori also has a higher (less negative) Gibbs energy of formation than C. elegans (Figure 1). This means that B. mori tissues have a high usable energy content. The high usable energy content of B. mori can be explained by its lifecycle. Eggs of B. mori hatch into larvae, which feed and grow [158,159,160]. After that, the larvae enter the pupal phase, in which they form a cocoon made of raw silk in which they molt into adult moths [161,162,163]. While in the pupal phase inside the cocoon, the larvae cannot feed and must use energy stored in their tissues to molt [164,165,166]. This means that tissues of B. mori must store large amounts of usable energy and, therefore, have a high Gibbs energy of formation.
Comparative analysis of the lifecycles of animal species C. elegans, A. Anguilla, and B. mori showed that the lifecycles of animal species influence their morphological properties, which determine their biothermodynamic properties. The long migration of A. anguilla through the Atlantic without opportunities to feed requires large amounts of energy that must be stored in its tissues and is reflected in its high usable energy content. The need for metamorphosis of B. mori in a cocoon without feeding also requires large amounts of energy, which makes its tissue energy content high. Therefore, organisms have evolved tissue compositions with different usable energy contents as an adaptation to efficiently perform their lifecycles.
4.2. Energy Content of Animals, Plants, and Microorganisms
Figure 2 shows thermodynamic properties of living matter of subcellular microorganisms, unicellular microorganisms, plant multicellular organisms, and animal multicellular organisms. Subcellular organisms are represented by viruses. Unicellular microorganisms belong to bacteria, fungi, and algae. Multicellular organisms are represented by plants and animals: humans, Anguilla anguilla (European eel) in the yellow phase of its lifecycle, Anguilla anguilla in the silver phase, and Caenorhabditis elegans. Figure 2a shows standard enthalpies of formation. From Figure 2a, it can be seen that the standard enthalpy of formation, ΔfH0, of living matter of C. elegans is the closest to that of other animals (humans, yellow A. anguilla, and silver A. anguilla). Moreover, it can be seen that animals have a less negative (higher) standard enthalpy of formation than microorganisms, which themselves have a less negative standard enthalpy of formation than plants. This means that the total energy content of animals is greater than that of microorganisms, which is greater than that of plants.
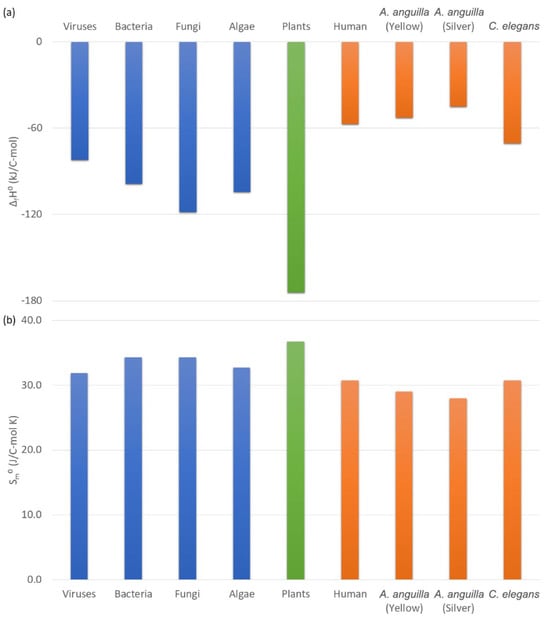
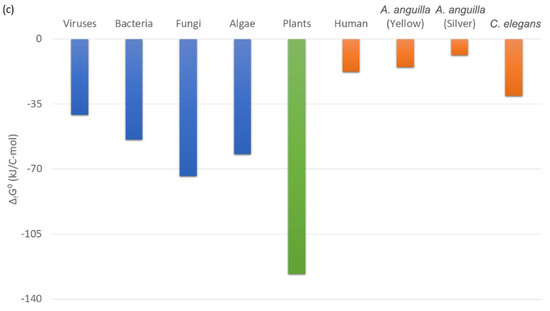
Figure 2.
Thermodynamic properties of living matter of organisms. This figure shows (a) standard enthalpy of formation, ΔfH0, (b) standard molar entropy, Sm0, and (c) standard Gibbs energy of formation, ΔfG0, for several classes of organisms: subcellular (viruses), unicellular (bacteria, fungi, and algae), multicellular plants, and multicellular animals (human, A. anguilla yellow stage, A. anguilla silver stage, and C. elegans).
Figure 2b shows standard molar entropies of living matter of microorganisms, plants, and animals. Standard molar entropy of C. elegans is the closest to that of other animals (humans and A. anguilla). Figure 2b also shows that standard molar entropies of animals are lower than those of microorganisms, which are lower than those of plants. This means that the unusable energy content of animals is lower than that of microorganisms, which is lower than that of plants.
Figure 2c shows standard Gibbs energies of formation of living matter of microorganisms, plants, and animals. Gibbs energies of formation of animals (human, yellow A. anguilla, silver A. anguilla, and C. elegans) are less negative (greater) than those of microorganisms, which are less negative than for plants. This means that the usable energy content of animals is greater than that of microorganisms, which is greater than that of plants.
4.3. Thermodynamic Properties of Catabolism, Biosynthesis, and Metabolism
Living matter of organisms is formed in the processes of growth and metabolism. Metabolism is a chemical process that can be represented by a macrochemical equation called the metabolism reaction [11,17,29]. The metabolism reaction can further be divided into the biosynthesis (anabolism) and catabolism reactions [11,17,29]. Biosynthesis, catabolism, and metabolism reactions of C. elegans are given in Table 4. These reactions can be analyzed using the laws of chemical thermodynamics to find their thermodynamic properties [11,17,29]. Thermodynamic properties of biosynthesis, catabolism, and metabolism are given in Table 5.
The processes of biosynthesis and catabolism are schematically presented in Figure 3. Nutrients are the starting point for biosynthesis and catabolism. In biosynthesis, the nutrients are used to produce new living matter. The usable energy content of the newly produced C. elegans living matter is a little higher than that of the nutrient E. coli cells. This is why Gibbs energy of biosynthesis is slightly positive ΔbsG0 = 33.37 kJ/C-mol (Table 5). The usable energy content of the catabolic products is much lower than that of the nutrients. This is why Gibbs energy of catabolism is negative ΔcatG0 = −473.29 kJ/C-mol (Table 5).
Figure 3.
A schematic representation of biosynthesis and catabolism reactions. In biosynthesis, the nutrient E. coli cells are converted into new living matter of C. elegans. In catabolism, nutrients are degraded into catabolic products. The nutrients are distributed between biosynthesis and catabolism. The height on the scheme represents usable energy content. The difference in usable energy content between new living matter and nutrients is the Gibbs energy of biosynthesis. The difference in usable energy content between catabolic products and nutrients is the Gibbs energy of catabolism.
In the biosynthesis reaction, the living matter of E. coli, the carbon and energy source, is converted into the living matter of C. elegans, the main biosynthesis product, and additional biosynthesis products that take excess nitrogen, sulfur, and phosphorus. The biosynthesis reaction of C. elegans is
where CH1.5919O0.3842N0.2361P0.019264S0.004408 is the empirical formula of living matter of E. coli, and CH1.6898O0.3062N0.1775P0.004866S0.004297 is the empirical formula of living matter of C. elegans (Table 4).
CH1.5919O0.3842N0.2361P0.019264S0.004408 + 0.02954 H2CO3 (aq) + 0.15845 H2O (l) → CH1.6898O0.3062N0.1775P0.004866S0.004297 + 0.05856 NH4+ (aq) + 0.00011 SO42− (aq) + 0.02954 HCO3− (aq) + 0.01440 HPO42− (aq) + 0.08921 O2 (g)
From Table 5, the standard enthalpy of biosynthesis of C. elegans is 36.08 kJ/C-mol. The positive enthalpy change for the biosynthesis reaction means that enthalpy does not contribute favorably toward the feasibility of the biosynthesis reaction. Even though it is positive, the enthalpy change of the biosynthesis reaction is not great (e.g., compared to the catabolism reaction, which is −501.80 kJ/C-mol). The reason for this is that the main source of food for C. elegans is E. coli cells. This means that in the biosynthesis reaction, the living matter of E. coli is converted into the living matter of C. elegans. However, both living matter of E. coli and C. elegans consist of similar classes of molecules (i.e., proteins, lipids, nucleic acids, carbohydrates, etc.) [119]. All these molecules are made mostly of C, H, N, O, P, and S atoms bound by covalent bonds (e.g., C-H, C-O, C=O, C-N, O-H, N-H, etc.) [119]. Since there is no great change in the types of bonds between the atoms, there is no great release or absorption of energy during the biosynthesis processes [124,125]. This is why the enthalpy change of the biosynthesis process is not great.
The standard entropy of biosynthesis is 9.68 J/C-mol K. This means that, even though it is small, the entropy change contributes favorably toward the feasibility of the biosynthesis reaction. Standard Gibbs energy of biosynthesis is 33.37 kJ/C-mol. It is positive due to the positive enthalpy change. The positive Gibbs energy of biosynthesis implies that the biosynthesis process is not spontaneous and, therefore, is not thermodynamically feasible unless it is coupled with another process that is spontaneous.
In the catabolism reaction, the living matter of E. coli is degraded into simple catabolic products to release energy needed for the metabolism of C. elegans. The catabolism reaction of C. elegans is (Table 4)
CH1.5919O0.3842N0.2361P0.019264S0.004408 + 0.18871 H2CO3 (aq) + 1.05954 O2 (g) → 0.23606 NH4+ (aq) + 0.00441 SO42− (aq) + 0.18871 HCO3− (aq) + 0.01926 HPO42− (aq) + 0.40859 H2O (l) + CO2 (aq)
The standard enthalpy of catabolism of C. elegans is highly negative, −501.80 kJ/C-mol (Table 5). The highly negative Gibbs energy change contributes very favorably to the feasibility of catabolism. The highly negative enthalpy originates from the large amount of energy released when nutrients are oxidized by oxygen. The main source of energy for C. elegans is the E. coli cells that it feeds on, which have the empirical formula CH1.5919O0.3842N0.2361P0.019264S0.004408. During catabolism, the types of bonds between the elements from living matter change. Elements with lower electronegativity (C, H, P, and S) bind to oxygen to form oxides and give their valence electrons to oxygen. The acceptance of electrons by the highly electronegative oxygen atoms releases a large amount of energy [17,123]. This is why the catabolism reaction is highly exothermic and, therefore, has a highly negative enthalpy change.
The standard entropy of catabolism is negative, −94.58 J/C-mol K. The negative entropy change contributes unfavorably to the feasibility of catabolism. However, the highly negative enthalpy component is dominant in the catabolism reaction and results in a highly negative Gibbs energy of catabolism: −473.29 kJ/C-mol. Due to the highly negative Gibbs energy change, the catabolism reaction is spontaneous and has a great driving force.
The catabolism and biosynthesis reactions together form the metabolism reaction. Figure 4 shows Gibbs energies of biosynthesis, catabolism, and metabolism. In the metabolism reaction, the living matter of E. coli is partly degraded into simple catabolic products to release energy, while the rest is used as the substrate to produce new living matter of C. elegans. Gibbs energy of metabolism is negative because a part of the substrate is degraded in catabolism, which has a highly negative Gibbs energy. The metabolism reaction of C. elegans is (Table 4)
1.44685 CH1.5919O0.3842N0.2361P0.019264S0.004408 + 0.11386 H2CO3 (aq) + 0.38424 O2 (g) → CH1.6898O0.3062N0.1775P0.004866S0.004297 + 0.16404 NH4+ (aq) + 0.00208 SO42− (aq) + 0.11386 HCO3− (aq) + 0.02301 HPO42− (aq) + 0.02412 H2O (l) + 0.44685 CO2 (aq)
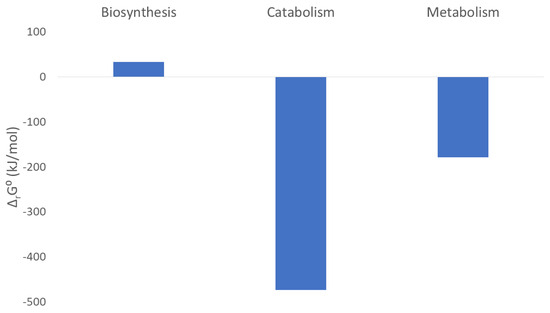
Figure 4.
Gibbs energies of biosynthesis, catabolism, and metabolism.
As shown in Table 5, the standard enthalpy of metabolism is −188.15 kJ/C-mol. The negative enthalpy change contributes favorably to the feasibility of metabolism. It originates from the highly negative enthalpy change of the catabolism reaction, which overcomes the slightly positive enthalpy of biosynthesis. The standard entropy of metabolism is −32.58 J/C-mol K. The negative value means that the entropy change contributes unfavorably to the feasibility of the metabolism reaction. The negative entropy of metabolism comes from the negative entropy of catabolism, which dominates over the slightly positive entropy of biosynthesis.
Standard Gibbs energy of metabolism is −178.12 kJ/C-mol (Table 5). The negative Gibbs energy value means that the metabolism of C. elegans as a chemical process is spontaneous and feasible. Therefore, the biosynthesis process has a positive Gibbs energy change (33.37 kJ/C-mol), which means that alone, it is not feasible. However, biosynthesis is coupled with catabolism, which has a highly negative Gibbs energy change (−473.29 kJ/C-mol). This results in a negative Gibbs energy of metabolism, which makes the growth and metabolism of C. elegans possible (Figure 4).
The carbon and energy source for the growth and metabolism of C. elegans is the E. coli cells. The nutrients for metabolism are distributed between catabolism and biosynthesis. Part of the nutrients are degraded in catabolism to release energy, while the rest is used to produce new living matter in biosynthesis. Every organism must achieve a balance between the catabolism and biosynthesis processes [10,29]. If all the nutrients were used for biosynthesis, growth would have been highly efficient since the nutrients would be incorporated into new living matter [10,29]. However, this would leave no nutrients for catabolism, and the driving force would not be sufficient for the metabolism to proceed [10,29]. On the other hand, if all the nutrients were sent into catabolism, a lot of energy would be available and the metabolism would proceed very rapidly, according to the phenomenological equations [10,29]. However, this would leave no nutrients for the production of new living matter in biosynthesis, and there would be no growth [10,29]. Therefore, a balance must be made between catabolism and biosynthesis to allow enough nutrients to go into biosynthesis for biomass production and still release energy in catabolism [10,29]. As shown in Table 4, the metabolism reaction takes 1.44685 C-moles of nutrient E. coli cells to produce 1 C-mol of new living matter of C. elegans. This means that the 69.1% C-moles from the nutrients are incorporated into new living matter in biosynthesis, while the remaining 30.9% C-moles are degraded in catabolism to release energy. This allows most of the nutrients to be converted into living matter, while a small part is degraded to release energy.
The coupling between catabolism and biosynthesis can be analyzed using phenomenological equations. Phenomenological equations belong to nonequilibrium thermodynamics and show how rates of processes depend on their driving forces [11,52]. For chemical reactions, phenomenological equations show how reaction rates depend on reaction Gibbs energies [11,52]. The biosynthesis phenomenological equation shows how the biosynthesis rate depends on the Gibbs energy of biosynthesis and the Gibbs energy of catabolism:
where rbs is the biosynthesis rate, ΔcatG Gibbs energy of catabolism, ΔbsG Gibbs energy of biosynthesis, T temperature, LCB catabolism–biosynthesis coupling phenomenological coefficient, and LBB biosynthesis–biosynthesis phenomenological coefficient [11,46,52]. The biosynthesis rate of C. elegans is given in Table 6, while the phenomenological coefficients LBB and LCB are given in Table 7. The phenomenological coefficients LBB and LCB are both positive. This means that, due to the negative signs before the Gibbs energy changes in the parentheses, more negative Gibbs energies of catabolism and biosynthesis imply a greater biosynthesis rate. In the second term on the right, Gibbs energy of biosynthesis is positive and would not be able to drive the biosynthesis process alone (with a positive Gibbs energy change, the reaction rate would be negative and the reaction would proceed in reverse). However, due to the highly negative Gibbs energy of catabolism, the second term on the right is much greater than the first term. Thus, the first term dominates, and the biosynthesis rate is positive, which makes biosynthesis possible.
Gibbs energies of catabolism and biosynthesis have also been reported for the fish species Anguilla anguilla (European eel) [46]. Gibbs energy of biosynthesis for yellow A. anguilla is 74.84 kJ/C-mol, while its Gibbs energy of catabolism is −466.62 kJ/C-mol [46]. The positive Gibbs energy of biosynthesis means that in A. anguilla, like in C. elegans, the biosynthesis process is not spontaneous. This means that in both A. anguilla and C. elegans, the highly negative Gibbs energies of catabolism provide the driving force for growth and metabolism. Gibbs energy of biosynthesis of A. anguilla (74.84 kJ/C-mol) is different than that of C. elegans (33.37 kJ/C-mol). This can be explained by the differences in the diets and chemical compositions of these organisms. Anguilla anguilla feeds on small aquatic animals [167], while C. elegans feeds on bacteria [168]. The different diets lead to different carbon and energy sources. Moreover, the empirical formulas (chemical compositions) of living matter of C. elegans and A. anguilla are different, due to different morphologies. Therefore, the different diets and chemical compositions of C. elegans and A. anguilla lead to different biosynthesis reactions, which result in different Gibbs energies of biosynthesis. Gibbs energies of catabolism of C. elegans (−473.29 kJ/C-mol) and A. anguilla (−466.62 kJ/C-mol) are slightly different, which is a consequence of the different diets (carbon and energy sources of these organisms).
4.4. Multicellular vs. Unicellular Organisms
Gibbs energy is the driving force of growth and metabolism for microorganisms [10,11,12] and multicellular organisms [46,60]. Moreover, as was discussed above with C. elegans, A. anguilla, and B. mori, organisms have evolved different Gibbs energy contents of their tissues as an adaptation for their lifecycles. This is why it is interesting to discuss the evolution of organisms from the perspective of the Gibbs energy of metabolic processes.
Gibbs energies of metabolism of the multicellular organism C. elegans and microorganisms are shown in Figure 5. Gibbs energies of metabolism of many microorganism species have been reported in the literature [12,29,54] and are between −250 and −500 kJ/C-mol, under favorable aerobic conditions [29]. Under less favorable anaerobic conditions, Gibbs energies of metabolism of microorganisms are between −240 and −340 kJ/C-mol [29]. On the other hand, the Gibbs energy of metabolism of the multicellular organism C. elegans is −178.12 kJ/C-mol (Table 5). Therefore, the Gibbs energy of metabolism of the multicellular organism C. elegans is less negative than that of microorganisms. This means that the metabolism of C. elegans dissipates much less useful energy than that of microorganisms.
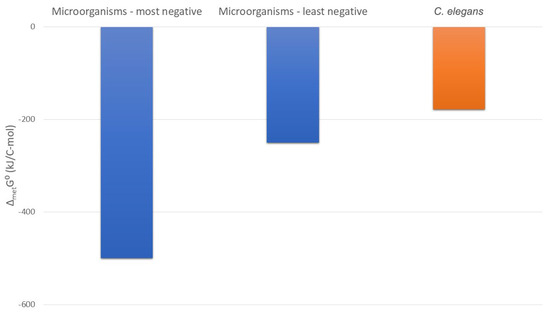
Figure 5.
Usable energy expenditure in the metabolism of microorganisms and C. elegans. This figure shows standard Gibbs energies of metabolism, ΔmetG0, which represent the driving force of metabolism, but also its usable energy expenditure. The most negative and the least negative values ΔmetG0 of microorganisms are presented, as well as ΔmetG0 of C. elegans.
The degree of reduction of the nutrients, ES, on which C. elegans feeds can be found using the equation
where nC,S, nH,S, nO,S, nN,S, nP,S, and nS,S represent the numbers of C, H, O, N, P, and S atoms in the substrate [17]. The E. coli cells on which C. elegans feeds have the empirical formula CH1.5919O0.3842N0.2361P0.019264S0.004408 (Table 2). This means that ES = 4.95 for C. elegans. The substrate degree of reduction is a measure of its energy content [17,48] and can be used to find the Gibbs energy of metabolism of microorganisms, using the equations [54]
Since 4.95 > 4.67, Equation (41) applies and ΔmetG0 is −437.57 kJ/C-mol. This means that if microorganisms were feeding on a substrate with the same energy content as that on which C. elegans feeds, they would have a Gibbs energy of metabolism of −437.57 kJ/C-mol. However, for C. elegans, ΔmetG0 is only −178.12 kJ/C-mol (Table 5). Therefore, the Gibbs energy of metabolism of C. elegans is about 2.5 times less negative than that of microorganisms that feed on the same substrate.
The less negative Gibbs energy of metabolism means that C. elegans has a lower driving force of metabolism and growth than microorganisms. However, except for being the driving force of metabolism, the Gibbs energy of metabolism also represents the usable energy expenditure by the metabolism [11,29]. The less negative Gibbs energy of metabolism implies that C. elegans dissipates less usable energy for its metabolism. This means that the metabolism of the multicellular C. elegans is more energetically efficient than that of microorganisms. This is in agreement with the much greater multiplication rate of microorganisms. Bacteria can divide every 30 min under favorable conditions for growth [135], while C. elegans grows much more slowly [112]. The faster multiplication implies a greater biosynthesis rate. The greater biosynthesis rate means, according to the biosynthesis phenomenological equation, a more negative Gibbs energy of metabolism.
The metabolism of the multicellular organism C. elegans is in a thermodynamically much more efficient mode than that of microorganisms. It has a lower biosynthesis rate, but it also dissipates less Gibbs energy than microorganisms. On the other hand, microorganisms multiply much faster and also dissipate much more energy. This might indicate different metabolic strategies. The strategy of microorganisms is to multiply rapidly, at the cost of dissipation of large amounts of usable energy. This mode of growth should be favorable under conditions when nutrients are plentiful. Microorganisms are surrounded by other microorganisms, with which they must compete for energy [135]. If different microorganism species compete for nutrients and energy, it is favorable for a microorganism to use the nutrients and energy as fast as possible, even if the efficiency of their utilization is lower [135]. In that case, it uses more of the nutrients for its own metabolism and leaves less for the competing microorganisms [135]. That way, it can outcompete its rival microorganisms [135]. The large driving force and fast multiplication rate of microorganisms might be a physical explanation for this. On the other hand, multicellular organisms grow much more slowly, but they are more energetically efficient. This more efficient mode of metabolism could be advantageous when nutrients and energy are not abundantly available. The energy limitation implies a lower biosynthesis rate, according to the biosynthesis phenomenological equation. Therefore, the Gibbs energies of metabolism and growth rates of microorganisms and multicellular organisms might indicate different metabolic strategies.
The more efficient metabolic strategy might have contributed to the appearance of multicellularity through evolution. Individual microbial cells might be a very efficient mode of life when nutrients and energy are available in large amounts. The energy can be dissipated in great amounts to provide the driving force for rapid microbial multiplication. This is why microorganisms under favorable conditions can afford to have a Gibbs energy of metabolism of −500 kJ/C-mol and multiply every 30 min. However, when nutrients and energy are not plentiful, they must be saved. The multicellular mode allows for a much more energetically efficient metabolism. The multicellular C. elegans can grow with a Gibbs energy of metabolism of just −178.12 kJ/C-mol.
This argument is also supported by the case of the slime mold Dictyostelium discoideum. The cells of D. discoideum exist as unicellular organisms when nutrients and energy are abundant [169,170]. However, when they become scarce, the unicellular organisms unite into a multicellular organism, which then migrates to a place with more nutrients and energy [169,170]. Therefore, unicellular organisms are the dominant form under abundant energy conditions, while the multicellular form is dominant under low energy conditions, which can be explained by the lower energy consumption of multicellular organisms.
4.5. Future Development
This research presents a mechanistic model of growth and metabolism of C. elegans, based on chemical and nonequilibrium thermodynamics. The model was used to discuss the metabolism and evolution of C. elegans from the perspective of energy and fundamental laws of nature. The model shows that the chemical composition of the organism (empirical formula) determines its thermodynamic properties of biosynthesis, which represent the driving force and determine the rates of growth and metabolism. This implies that by changing the empirical formula of an organism, it is possible to affect its growth and metabolism rates. This means that the model allows us to predict the influence of the chemical properties of an organism on their biological properties. Therefore, the results of this research can be applied in the future in metabolic engineering to optimize the growth and metabolism of organisms by changes in their chemical composition.
The development of mechanistic models of growth and metabolism is also important in research on interactions of organisms, like competition [16,55]. Metabolic processes of organisms represent chemical reactions [29,119]. In these reactions, nutrients represent the reactants [29,119]. In case we have several organism species that live in an environment and consume similar nutrients, their metabolic reactions share the same reactants. Since the nutrients are limited, the metabolic reactions of organisms are competitive. These chemical reactions are led by a driving force—Gibbs energy [29,52]. This means that the reaction with the most negative Gibbs energy proceeds at the greatest rate, consumes the greatest amount of nutrients, and dominates [16,55]. Therefore, based on metabolic reactions and Gibbs energies, it is possible to develop models of interactions of organisms. This is important for environmental sciences since it would provide deeper insight into the role of energy in interactions of organisms and develop models of how energy and nutrients available in the environment affect organism and their interactions.
Biothermodynamic research on biological structures, metabolism, and interactions between organisms is a highly interesting topic with applications in many fields of science and engineering [10,61,141]. However, the research in the field is limited by the amount of available data on chemical and thermodynamic properties of organisms and their metabolism. Collecting more data on chemical and thermodynamic properties of C. elegans would help improve the biothermodynamic model of C. elegans metabolism and growth.
In this research, a mechanistic model of the growth and metabolism of C. elegans was developed. To extend the model to other organisms, more data will be needed on chemical composition, thermodynamic properties of living matter, and metabolic rates and growth rates of organisms. To overcome this limitation, further research will be needed, especially in the fields of biochemistry, molecular biology, and biophysics.
5. Conclusions
The empirical formula of living matter of Caenorhabditis elegans is CH1.6898O0.3062N0.1775P0.004866S0.004297, while its standard Gibbs energy of formation of living matter is −30.58 kJ/C-mol. These are different from the empirical formulas and Gibbs energies of other organisms. Therefore, every animal species is characterized by a specific empirical formula and thermodynamic properties of living matter.
Comparative analysis of the lifecycles of animal species C. elegans, A. anguilla, and B. mori showed that the lifecycles of animal species influence their morphological properties, which determine their biothermodynamic properties. Animal species that must perform intense metabolic activity for prolonged periods without access to food (A. anguilla and B. mori) must store large amounts of energy in their tissues. Due to this, their tissues have a high usable energy content and, therefore, a high Gibbs energy of formation.
The physical driving forces of growth (Gibbs energies of metabolism) and growth rates were compared for microorganisms and C. elegans, a multicellular organism. It was found that the driving force for the growth of C. elegans (−178.12 kJ/C-mol) is much lower than that of microorganisms (−250 to −500 kJ/C-mol). This means that the growth of C. elegans is much more energetically efficient. On the other hand, the growth rate of C. elegans was found to be much lower than that of microorganisms. This is in good agreement with the lower physical driving force of growth of C. elegans, according to the phenomenological equations. This might indicate that C. elegans and microorganisms use different metabolic strategies. Microorganisms dissipate large amounts of energy and multiply rapidly, while C. elegans dissipates much less energy and multiplies more slowly. This is why the greater metabolic efficiency could have contributed to the evolution of multicellular organisms from microorganisms, under conditions when energy and nutrients were limited.
The mechanistic model proposed in this research shows how the chemical composition of the organism influences its Gibbs energy, which is the driving force of metabolism and influences growth rate. This means that the model can show how changes in the chemical composition of the organism influence its metabolism and growth rate. This is why the development of biothemodynamic models of growth and metabolism can contribute to research in metabolic engineering.
The proposed model also shows how nutrients are used to produce biomass and release energy that drives metabolism. This is important in studies on the interactions of organisms. Nutrients are reactants in metabolism reactions. If several species of organisms compete for nutrients, then their metabolism reactions share the same reactants. Since the amount of nutrients in an environment is limited, the metabolic reactions of the species are competitive chemical reactions. The driving force of chemical reactions is Gibbs energy, which influences reaction rates. This means that phenomenological equations can be used to analyze the competition between metabolic reactions of different species of organisms. This means that the development of biothermodynamic models of metabolism can contribute to research on interactions of organisms in environmental sciences.
Author Contributions
M.E.P.: conceptualization, methodology, software, validation, formal analysis, investigation, data curation, writing—original draft, writing—review and editing, visualization; supervision M.P.: validation, formal analysis, investigation, data curation, writing—original draft, writing—review and editing; visualization. D.P.: validation; resources; writing—review and editing; supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ministry of Science, Technological Development and Innovation of the Republic of Serbia grant number 451-03-136/2025-03/200026.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
This work was supported by the Ministry of Science, Technological Development and Innovation of the Republic of Serbia (Grant No. 451-03-136/2025-03/200026).
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Abs | Biosynthesis affinity |
| Acat | Catabolism affinity |
| Ai | Affinity of reaction i |
| aJ | Number of atoms of element J in its standard state |
| E | Degree of reduction |
| LBB | Biosynthesis–biosynthesis phenomenological coefficient |
| LBC | Biosynthesis–catabolism coupling phenomenological coefficient |
| LBB | Catabolism–catabolism phenomenological coefficient |
| Lij | The phenomenological coefficient between reactions i and j |
| Mr(X) | Molar mass of the empirical formula of molecular components X |
| Mr | Molar mass of the empirical formula of living matter |
| nJ | Number of atoms of element J in the empirical formula |
| Biosynthesis heat rate | |
| Catabolism heat rate | |
| Metabolism heat rate | |
| Rm | Metabolic rate |
| rbs | Biosynthesis rate |
| rcat | Catabolism rate |
| ri | Rate of reaction i |
| Sm0 | Standard molar entropy |
| T | Temperature |
| xX | Mole fraction of macromolecular component X |
| wX | Mass fraction of macromolecular component X |
| ww | Water content of tissues |
| ΔbsG0 | Standard Gibbs energy of biosynthesis |
| ΔbsH0 | Standard enthalpy of biosynthesis |
| ΔbsS0 | Standard entropy of biosynthesis |
| ΔCHm0 | Standard enthalpy of combustion |
| ΔcatG0 | Standard Gibbs energy of catabolism |
| ΔcatH0 | Standard enthalpy of catabolism |
| ΔcatS0 | Standard entropy of catabolism |
| ΔmetG0 | Standard Gibbs energy of metabolism |
| ΔmetH0 | Standard enthalpy of metabolism |
| ΔmetS0 | Standard entropy of metabolism |
| ΔrG0 | Standard reaction Gibbs energy |
| ΔrH0 | Standard reaction enthalpy |
| ΔrS0 | Standard reaction entropy |
| νX | Stoichiometric coefficient of substance X |
References
- Riddle, D.L.; Blumenthal, T.; Meyer, B.J. (Eds.) Section I, The Biological Model. In C. elegans II, 2nd ed.; Cold Spring Harbor Laboratory Press: Long Island, NY, USA, 1997. Available online: https://www.ncbi.nlm.nih.gov/books/NBK20086/ (accessed on 4 May 2025).
- Zhang, S.; Li, F.; Zhou, T.; Wang, G.; Li, Z. Caenorhabditis elegans as a Useful Model for Studying Aging Mutations. Front. Endocrinol. 2020, 11, 554994. [Google Scholar] [CrossRef] [PubMed]
- Marsh, E.K.; May, R.C. Caenorhabditis elegans, a Model Organism for Investigating Immunity. Appl. Environ. Microbiol. 2012, 78, 2075–2081. [Google Scholar] [CrossRef] [PubMed]
- Roussos, A.; Kitopoulou, K.; Borbolis, F.; Palikaras, K. Caenorhabditis elegans as a Model System to Study Human Neurodegenerative Disorders. Biomolecules 2023, 13, 478. [Google Scholar] [CrossRef] [PubMed]
- Kaletta, T.; Hengartner, M.O. Finding function in novel targets: C. elegans as a model organism. Nat. Rev. Drug Discov. 2006, 5, 387–399. [Google Scholar] [CrossRef]
- Meneely, P.M.; Dahlberg, C.L.; Rose, J.K. Working with Worms: Caenorhabditis elegans as a Model Organism. Curr. Protoc. Essent. Lab. Tech. 2019, 19, e35. [Google Scholar] [CrossRef]
- Frézal, L.; Félix, M.-A. C. elegans outside the Petri dish. eLife 2015, 4, e05849. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Zečić, A.; Dhondt, I.; Braeckman, B.P. The nutritional requirements of Caenorhabditis elegans. Genes Nutr. 2019, 14, 15. [Google Scholar] [CrossRef]
- Yilmaz, L.S.; Walhout, A.J. A Caenorhabditis elegans Genome-Scale Metabolic Network Model. Cell Syst. 2016, 2, 297–311. [Google Scholar] [CrossRef]
- Assael, M.J.; Maitland, G.C.; Maskow, T.; von Stockar, U.; Wakeham, W.A.; Will, S. Commonly Asked Questions in Thermodynamics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2022; ISBN 9780367338916. [Google Scholar] [CrossRef]
- Von Stockar, U. Live cells as open non-equilibrium systems. In Biothermodynamics: The Role of Thermodynamics in Biochemical Engineering; Stockar, U., Ed.; EPFL Press: Lausanne, Switzerland, 2013. [Google Scholar]
- Von Stockar, U.; Liu, J.-S. Does microbial life always feed on negative entropy? Thermodynamic analysis of microbial growth. Biochim. Biophys. Acta (BBA)–Bioenerg. 1999, 1412, 191–211. [Google Scholar] [CrossRef]
- Battley, E.H. On the enthalpy of formation of Escherichia coli K-12 cells. Biotechnol. Bioeng. 1992, 39, 5–12. [Google Scholar] [CrossRef]
- Popovic, M.; Stenning, G.B.; Göttlein, A.; Minceva, M. Elemental composition, heat capacity from 2 to 300 K and derived thermodynamic functions of 5 microorganism species. J. Biotechnol. 2021, 331, 99–107. [Google Scholar] [CrossRef] [PubMed]
- Popovic, M. Thermodynamic properties of microorganisms: Determination and analysis of enthalpy, entropy, and Gibbs free energy of biomass, cells and colonies of 32 microorganism species. Heliyon 2019, 5, e01950. [Google Scholar] [CrossRef] [PubMed]
- Popovic, M.; Šekularac, G.; Stevanović, M. Thermodynamics of microbial consortia: Enthalpies and Gibbs energies of microorganism live matter and macromolecules of E. coli, G. oxydans, P. fluorescens, S. thermophilus and P. chrysogenum. J. Biotechnol. 2024, 379, 6–17. [Google Scholar] [CrossRef]
- Battley, E.H. The development of direct and indirect methods for the study of the thermodynamics of microbial growth. Thermochim. Acta 1998, 309, 17–37. [Google Scholar] [CrossRef]
- Teh, K.-Y.; Lutz, A.E. Thermodynamic analysis of fermentation and anaerobic growth of baker’s yeast for ethanol production. J. Biotechnol. 2010, 147, 80–87. [Google Scholar] [CrossRef]
- Patiño, R.; Janssen, M.; von Stockar, U. A study of the growth for the microalgaChlorella vulgaris by photo-bio-calorimetry and other on-line and off-line techniques. Biotechnol. Bioeng. 2007, 96, 757–767. [Google Scholar] [CrossRef]
- Janssen, M.; Patiño, R.; von Stockar, U. Application of bench-scale biocalorimetry to photoautotrophic cultures. Thermochim. Acta 2005, 435, 18–27. [Google Scholar] [CrossRef]
- Popovic, M. Biothermodynamics of Viruses from Absolute Zero (1950) to Virothermodynamics (2022). Vaccines 2022, 10, 2112. [Google Scholar] [CrossRef]
- Popović, M.E.; Stevanović, M.; Pavlović, M.P. Return of the forgotten nightmare: Bordetella pertussis uses a more negative Gibbs energy of metabolism to outcompete its host organism. Microb. Risk Anal. 2024, 26, 100292. [Google Scholar] [CrossRef]
- Popović, M.E.; Šekularac, G. The wind of change: Gibbs energy of binding and infectivity evolution of Omicron BA.2.86 Pirola, EG.5.1, XBB.1.16 Arcturus, CH.1.1 and BN.1 variants of SARS-CoV-2. Microb. Risk Anal. 2024, 26, 100290. [Google Scholar] [CrossRef]
- Popović, M.E.; Šekularac, G.; Mihailović, M. Like a summer storm: Biothermodynamic analysis of Rotavirus A—Empirical formula, biosynthesis reaction and driving force of virus multiplication and antigen-receptor binding. Microb. Risk Anal. 2024, 26, 100291. [Google Scholar] [CrossRef]
- Dragicevic, V.; Sredojevic, S. Thermodynamics of Seed and Plant Growth. Thermodynamics—Systems in Equilibrium and Non-Equilibrium; InTech: London, UK, 2011. [Google Scholar] [CrossRef]
- Dragičević, V.; Simić, M.; Brankov, M. Energy Distribution between Maize and Weeds. In 15. International Conference on Fundamental and Applied Aspects of Physical Chemistry, Belgrade, Serbia, 20–24 September 2021. Godine-Book of Abstracts; Society of Physical Chemists of Serbia: Belgrade, Serbia, 2021; Volume 2, pp. 681–684. Available online: https://rik.mrizp.rs/handle/123456789/1049 (accessed on 4 May 2025).
- Sabater, B.; Skene, K.R. Editorial: Plant Thermodynamics. Front. Plant Sci. 2022, 13, 932245. [Google Scholar] [CrossRef] [PubMed]
- Von Stockar, U.; Maskow, T.; Liu, J.; Marison, I.W.; Patiño, R. Thermodynamics of microbial growth and metabolism: An analysis of the current situation. J. Biotechnol. 2006, 121, 517–533. [Google Scholar] [CrossRef]
- Von Stockar, U. Biothermodynamics of live cells: A tool for biotechnology and biochemical engineering. J. Non-Equilib. Thermodyn. 2010, 35, 415–475. [Google Scholar] [CrossRef]
- Maskow, T.; Paufler, S. What does calorimetry and thermodynamics of living cells tell us? Methods 2015, 76, 3–10. [Google Scholar] [CrossRef]
- Von Stockar, U.; van der Wielen, L.A. Thermodynamics in biochemical engineering. J. Biotechnol. 1997, 59, 25–37. [Google Scholar] [CrossRef]
- Milão, R.d.F.D.; Carminati, H.B.; Araújo, O.d.Q.F.; de Medeiros, J.L. Thermodynamic, financial and resource assessments of a large-scale sugarcane-biorefinery: Prelude of full bioenergy carbon capture and storage scenario. Renew. Sustain. Energy Rev. 2019, 113, 109251. [Google Scholar] [CrossRef]
- Golberg, A.; Vitkin, E.; Linshiz, G.; Khan, S.A.; Hillson, N.J.; Yakhini, Z.; Yarmush, M.L. Proposed design of distributed macroalgal biorefineries: Thermodynamics, bioconversion technology, and sustainability implications for developing economies. Biofuels Bioprod. Biorefining 2014, 8, 67–82. [Google Scholar] [CrossRef]
- Nielsen, S.N.; Müller, F.; Marques, J.C.; Bastianoni, S.; Jørgensen, S.E. Thermodynamics in Ecology—An Introductory Review. Entropy 2020, 22, 820. [Google Scholar] [CrossRef]
- Jorgensen, S.E. Thermodynamics and Ecological Modelling; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Barros, N. Thermodynamics of soil microbial metabolism: Applications and functions. Appl. Sci. 2021, 11, 4962. [Google Scholar] [CrossRef]
- Barros, N.; Rodríguez-Añon, J.A.; Proupín, J.; Pérez-Cruzado, C. The effect of extreme temperatures on soil organic matter decomposition from Atlantic oak forest ecosystems. iScience 2021, 24, 103527. [Google Scholar] [CrossRef] [PubMed]
- Popović, M.E.; Stevanovic, M.; Mihailovic, M. Breaking news: Empirical formulas, molar masses, biosynthesis reactions, and thermodynamic properties of virus particles, biosynthesis and binding of Omicron JN.1 variant of SARS-CoV-2. J. Serbian Chem. Soc. 2024, 89, 305–320. [Google Scholar] [CrossRef]
- Popovic, M. Why doesn’t Ebola virus cause pandemics like SARS-CoV-2? Microb. Risk Anal. 2022, 22, 100236. [Google Scholar] [CrossRef]
- Lucia, U.; Grisolia, G.; Deisboeck, T.S. Thermodynamics and SARS-CoV-2: Neurological effects in post-COVID 19 syndrome. Atti Della Accad. Peloritana dei Pericolanti 2021, 99, A3. [Google Scholar] [CrossRef]
- Lucia, U.; Grisolia, G.; Deisboeck, T.S. Seebeck-like effect in SARS-CoV-2 bio-thermodynamics. Atti Della Accad. Peloritana dei Pericolanti-Cl. di Sci. Fis. Matematiche e Naturali 2020, 98, 6. [Google Scholar] [CrossRef]
- Özilgen, M.; Yilmaz, B. COVID-19 disease causes an energy supply deficit in a patient. Int. J. Energy Res. 2021, 45, 1157–1160. [Google Scholar] [CrossRef]
- Yilmaz, B.; Ercan, S.; Akduman, S.; Özilgen, M. Energetic and exergetic costs of COVID-19 infection on the body of a patient. Int. J. Exergy 2020, 32, 314–327. [Google Scholar] [CrossRef]
- Lucia, U.; Deisboeck, T.S.; Grisolia, G. Entropy-Based Pandemics Forecasting. Front. Phys. 2020, 8, 274. [Google Scholar] [CrossRef]
- Kaniadakis, G.; Baldi, M.M.; Deisboeck, T.S.; Grisolia, G.; Hristopulos, D.T.; Scarfone, A.M.; Sparavigna, A.; Wada, T.; Lucia, U. The κ-statistics approach to epidemiology. Sci. Rep. 2020, 10, 19949. [Google Scholar] [CrossRef]
- Popović, M.E. Animal bioenergetics: Thermodynamic and kinetic analysis of growth and metabolism of Anguilla anguilla. Zoology 2024, 163, 126158. [Google Scholar] [CrossRef]
- Von Stockar, U. Biothermodynamics of live cells: Energy dissipation and heat generation in cellular structures. In Biothermodynamics: The Role of Thermodynamics in Biochemical Engineering; Stockar, U., Ed.; EPFL Press: Lausanne, Switzerland, 2013. [Google Scholar]
- Battley, E.H. The thermodynamics of microbial growth. In Handbook of Thermal Analysis and Calorimetry, From Macromolecules to Man; Kemp, E.B., Ed.; Elsevier: Amsterdam, The Netherlands, 1999; Volume 4, pp. 219–235. [Google Scholar] [CrossRef]
- Sandler, S.I. Chemical, Biochemical, and Engineering Thermodynamics, 5th ed.; Wiley: Hoboken, NJ, USA, 2017; ISBN 978-1-119-32128-6. [Google Scholar]
- Battley, E.H. A theoretical study of the thermodynamics of microbial growth using Saccharomyces cerevisiae and a different free energy equation. Q. Rev. Biol. 2013, 88, 69–96. [Google Scholar] [CrossRef] [PubMed]
- Von Stockar, U.; Marison, I. The definition of energetic growth efficiencies for aerobic and anaerobic microbial growth and their determination by calorimetry and by other means. Thermochim. Acta 1993, 229, 157–172. [Google Scholar] [CrossRef]
- Dermirel, Y. Nonequilibrium Thermodynamics: Transport and Rate Processes in Physical, Chemical and Biological Systems, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2007; ISBN 9780444595812. [Google Scholar]
- Heijnen, J.J.; Van Dijken, J.P. In search of a thermodynamic description of biomass yields for the chemotrophic growth of microorganisms. Biotechnol. Bioeng. 1992, 39, 833–858. [Google Scholar] [CrossRef]
- Liu, J.-S.; Vojinović, V.; Patiño, R.; Maskow, T.; von Stockar, U. A comparison of various Gibbs energy dissipation correlations for predicting microbial growth yields. Thermochim. Acta 2007, 458, 38–46. [Google Scholar] [CrossRef]
- Popović, M.E.; Tadić, V. (R)evolution of Viruses: Introduction to biothermodynamics of viruses. Virology 2025, 603, 110319. [Google Scholar] [CrossRef]
- Popović, M.E.; Stevanović, M.; Tadić, V. Biothermodynamic analysis of the Dengue virus: Empirical formulas, biosynthesis reactions and thermodynamic properties of antigen-receptor binding and biosynthesis. Microb. Risk Anal. 2024, 27, 100326. [Google Scholar] [CrossRef]
- Temme, A.A.; Liu, J.C.; Cornwell, W.K.; Aerts, R.; Cornelissen, J.H. Hungry and thirsty: Effects of CO2 and limited water availability on plant performance. Flora 2019, 254, 188–193. [Google Scholar] [CrossRef]
- Dragičević, V. Thermodynamics of Abiotic Stress and Stress Tolerance of Cultivated Plants; InTech: London, UK, 2015. [Google Scholar] [CrossRef][Green Version]
- Barbacci, A.; Magnenet, V.; Lahaye, M. Thermodynamical journey in plant biology. Front. Plant Sci. 2015, 6, 481. [Google Scholar] [CrossRef][Green Version]
- Popović, M.E.; Pantovic-Pavlovic, M.; Sekularac, G. Chemical and thermodynamic properties of Bombyx mori (domestic silk moth): Empirical formula, driving force, and biosynthesis, catabolism and metabolism reactions. Therm. Sci. 2023, 27, 4893–4910. [Google Scholar] [CrossRef]
- Balmer, R.T. Modern Engineering Thermodynamics; Academic Press: Cambridge, MA, USA, 2010. [Google Scholar] [CrossRef]
- Komura, T.; Takemoto, A.; Kosaka, H.; Suzuki, T.; Nishikawa, Y. Prolonged Lifespan, Improved Perception, and Enhanced Host Defense of Caenorhabditis elegans by Lactococcus cremoris subsp. cremoris. Microbiol. Spectr. 2022, 10, e0045421. [Google Scholar] [CrossRef]
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell, 5th ed.; Garland Science: New York, NY, USA, 2008. [Google Scholar]
- Strange, K. An Overview of C. elegans Biology. In C. elegans. Methods in Molecular Biology; Strange, K., Ed.; Humana Press: Totowa, NJ, USA, 2006; Volume 351. [Google Scholar] [CrossRef]
- El-Bawab, F. Chapter 9—Phylum Nematoda. In Invertebrate Embryology and Reproduction; El-Bawab, F., Ed.; Academic Press: Amsterdam, The Netherlands, 2020; pp. 422–470. ISBN 9780128141144. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Li, P.; Zhou, Q.; Zheng, X.; Gu, Q. Caenorhabditis elegans: A nature present for advanced food science. Curr. Opin. Food Sci. 2023, 49, 100971. [Google Scholar] [CrossRef]
- Scharf, A.; Pohl, F.; Egan, B.M.; Kocsisova, Z.; Kornfeld, K. Reproductive Aging in Caenorhabditis elegans: From Molecules to Ecology. Front. Cell Dev. Biol. 2021, 9, 718522. [Google Scholar] [CrossRef] [PubMed]
- Filina, O.; Demirbas, B.; Haagmans, R.; van Zon, J.S. Temporal scaling in C. elegans larval development. Proc. Natl. Acad. Sci. USA 2022, 119, e2123110119. [Google Scholar] [CrossRef] [PubMed]
- Rougvie, A.E.; Moss, E.G. Chapter Six—Developmental Transitions in C. elegans Larval Stages. In Current Topics in Developmental Biology; Rougvie, A.E., O’Connor, M.B., Eds.; Academic Press: Amsterdam, The Netherlands, 2013; pp. 153–180. ISBN 9780123969682. [Google Scholar] [CrossRef]
- Uppaluri, S.; Brangwynne, C.P. A size threshold governs Caenorhabditis elegans developmental progression. Proc. R. Soc. B Biol. Sci. 2015, 282, 20151283. [Google Scholar] [CrossRef]
- Tennessen, J.M.; Opperman, K.J.; Rougvie, A.E. The C. elegans developmental timing protein LIN-42 regulates diapause in response to environmental cues. Development 2010, 137, 3501–3511. [Google Scholar] [CrossRef]
- Mata-Cabana, A.; Pérez-Nieto, C.; Olmedo, M. Nutritional control of postembryonic development progression and arrest in Caenorhabditis elegans. Adv. Genet. 2021, 107, 33–87. [Google Scholar] [CrossRef]
- Fielenbach, N.; Antebi, A. C. elegans dauer formation and the molecular basis of plasticity. Genes Dev. 2008, 22, 2149–2165. [Google Scholar] [CrossRef]
- Bodkhe, R.; Trang, K.; Hammond, S.; Jung, D.K.; Shapira, M. Emergence of dauer larvae in Caenorhabditis elegans disrupts continuity of host-microbiome interactions. FEMS Microbiol. Ecol. 2024, 100, fiae149. [Google Scholar] [CrossRef]
- Binti, S.; Melinda, R.V.; Joseph, B.B.; Edeen, P.T.; Miller, S.D.; Fay, D.S. A life cycle alteration can correct molting defects in Caenorhabditis elegans. Dev. Biol. 2022, 483, 143–156. [Google Scholar] [CrossRef]
- Harvey, S.C.; Shorto, A.; E Viney, M. Quantitative genetic analysis of life-history traits of Caenorhabditis elegans in stressful environments. BMC Evol. Biol. 2008, 8, 15. [Google Scholar] [CrossRef]
- Gritti, N.; Kienle, S.; Filina, O.; van Zon, J.S. Long-term time-lapse microscopy of C. elegans post-embryonic development. Nat. Commun. 2016, 7, 12500. [Google Scholar] [CrossRef] [PubMed]
- Pasquinelli, A.E.; Ruvkun, G. Control of developmental timing by Micrornas and their targets. Annu. Rev. Cell Dev. Biol. 2002, 18, 495–513. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Guan, G.; Ho, V.W.S.; Wong, M.-K.; Chan, L.-Y.; Tang, C.; Zhao, Z.; Yan, H. Establishment of a morphological atlas of the Caenorhabditis elegans embryo using deep-learning-based 4D segmentation. Nat. Commun. 2020, 11, 6254. [Google Scholar] [CrossRef]
- Patil, G.; van Zon, J.S. Timers, variability, and body-wide coordination: C. elegans as a model system for whole-animal developmental timing. Curr. Opin. Genet. Dev. 2024, 85, 102172. [Google Scholar] [CrossRef]
- Zhang, L.; Gualberto, D.G.; Guo, X.; Correa, P.; Jee, C.; Garcia, L.R. TMC-1 attenuates C. elegans development and sexual behaviour in a chemically defined food environment. Nat. Commun. 2015, 6, 6345. [Google Scholar] [CrossRef]
- Braendle, C.; Paaby, A. Life history in Caenorhabditis elegans: From molecular genetics to evolutionary ecology. Genetics 2024, 228, iyae151. [Google Scholar] [CrossRef]
- Rashid, S.; Wong, C.; Roy, R. Developmental plasticity and the response to nutrient stress in Caenorhabditis elegans. Dev. Biol. 2021, 475, 265–276. [Google Scholar] [CrossRef]
- Cao, X.; Xie, Y.; Yang, H.; Sun, P.; Xue, B.; Garcia, L.R.; Zhang, L. EAT-2 attenuates C. elegans development via metabolic remodeling in a chemically defined food environment. Cell. Mol. Life Sci. 2023, 80, 205. [Google Scholar] [CrossRef]
- Arnold, K.R.; Rose, M.R.; Avise, J.C. Genetic association between dauer metabolic arrest and increased lifespan. In Conceptual Breakthroughs-Conceptual Breakthroughs in the Evolutionary Biology of Aging; Arnold, K.R., Rose, M.R., Avise, J.C., Eds.; Academic Press: Cambridge, MA, USA, 1993; pp. 169–171. ISBN 9780128215456. [Google Scholar] [CrossRef]
- Hammerschmith, E.W.; Woodruff, G.C.; Moser, K.A.; Johnson, E.; Phillips, P.C. Opposing directions of stage-specific body shape change in a close relative of C. elegans. BMC Zool. 2022, 7, 38. [Google Scholar] [CrossRef]
- Pradhan, S.; Quilez, S.; Homer, K.; Hendricks, M. Environmental Programming of Adult Foraging Behavior in C. elegans. Curr. Biol. 2019, 29, 2867–2879.e4. [Google Scholar] [CrossRef]
- Androwski, R.J.; Flatt, K.M.; Schroeder, N.E. Phenotypic plasticity and remodeling in the stress-induced Caenorhabditis elegans dauer. Wiley Interdiscip. Rev. Dev. Biol. 2017, 6, e278. [Google Scholar] [CrossRef] [PubMed]
- Haley, J.A.; Chalasani, S.H. C. elegans foraging as a model for understanding the neuronal basis of decision-making. Cell. Mol. Life Sci. 2024, 81, 252. [Google Scholar] [CrossRef] [PubMed]
- Baugh, L.R. To grow or not to grow: Nutritional control of development during Caenorhabditis elegans L1 arrest. Genetics 2013, 194, 539–555. [Google Scholar] [CrossRef]
- Golden, J.W.; Riddle, D.L. The Caenorhabditis elegans dauer larva: Developmental effects of pheromone, food, and temperature. Dev. Biol. 1984, 102, 368–378. [Google Scholar] [CrossRef]
- Kaul, T.K.; Rodrigues, P.R.; Ogungbe, I.V.; Kapahi, P.; Gill, M.S. Bacterial Fatty Acids Enhance Recovery from the Dauer Larva in Caenorhabditis elegans. PLoS ONE 2014, 9, e86979. [Google Scholar] [CrossRef]
- Hu, P.J. Dauer. In WormBook: The Online Review of C. elegans Biology; 2007; pp. 1–19. Available online: http://www.wormbook.org/chapters/www_dauer/dauer.html (accessed on 4 May 2025).
- Dalton, H.M.; Curran, S.P. Hypodermal responses to protein synthesis inhibition induce systemic developmental arrest and AMPK-dependent survival in Caenorhabditis elegans. PLoS Genet. 2018, 14, e1007520. [Google Scholar] [CrossRef]
- Lee, K.E.; Cho, J.H.; Song, H.-O. Calumenin, a Ca2+ Binding Protein, Is Required for Dauer Formation in Caenorhabditis elegans. Biology 2023, 12, 464. [Google Scholar] [CrossRef]
- Britz, S.; Markert, S.M.; Witvliet, D.; Steyer, A.M.; Tröger, S.; Mulcahy, B.; Kollmannsberger, P.; Schwab, Y.; Zhen, M.; Stigloher, C. Structural Analysis of the Caenorhabditis elegans Dauer Larval Anterior Sensilla by Focused Ion Beam-Scanning Electron Microscopy. Front. Neuroanat. 2021, 15, 732520. [Google Scholar] [CrossRef]
- Vlaar, L.E.; Bertran, A.; Rahimi, M.; Dong, L.; Kammenga, J.E.; Helder, J.; Goverse, A.; Bouwmeester, H.J. On the role of dauer in the adaptation of nematodes to a parasitic lifestyle. Parasites Vectors 2021, 14, 554. [Google Scholar] [CrossRef]
- Erkut, C.; Vasilj, A.; Boland, S.; Habermann, B.; Shevchenko, A.; Kurzchalia, T.V. Molecular strategies of the Caenorhabditis elegans dauer larva to survive extreme desiccation. PLoS ONE 2013, 8, e82473. [Google Scholar] [CrossRef]
- Kim, K.; Gade, V.R.; Kurzchalia, T.V.; Guck, J. Quantitative imaging of Caenorhabditis elegans dauer larvae during cryptobiotic transition. Biophys. J. 2022, 121, 1219. [Google Scholar] [CrossRef] [PubMed]
- Narbonne, P.; Roy, R. Caenorhabditis elegans dauers need LKB1/AMPK to ration lipid reserves and ensure long-term survival. Nature 2009, 457, 210–214. [Google Scholar] [CrossRef] [PubMed]
- Burnell, A.M.; Houthoofd, K.; O’Hanlon, K.; Vanfleteren, J.R. Alternate metabolism during the dauer stage of the nematode Caenorhabditis elegans. Exp. Gerontol. 2005, 40, 850–856. [Google Scholar] [CrossRef] [PubMed]
- Jia, R.; Zhang, J.; Jia, K. Neuroendocrine regulation of fat metabolism by autophagy gene atg-18 in C.elegans dauer larvae. FEBS Open Bio 2019, 9, 1623–1631. [Google Scholar] [CrossRef]
- Rottiers, V.; Motola, D.L.; Gerisch, B.; Cummins, C.L.; Nishiwaki, K.; Mangelsdorf, D.J.; Antebi, A. Hormonal control of C. elegans dauer formation and life span by a Rieske-like oxygenase. Dev. Cell 2006, 10, 473–482. [Google Scholar] [CrossRef]
- Ewald, C.Y.; Castillo-Quan, J.I.; Blackwell, T.K. Untangling Longevity, Dauer, and Healthspan in Caenorhabditis elegans Insulin/IGF-1-Signalling. Gerontology 2018, 64, 96–104. [Google Scholar] [CrossRef]
- NCBI. NCBI Database [Online] National Center for Biotechnology Information. 2024. Available online: https://www.ncbi.nlm.nih.gov/ (accessed on 7 March 2024).
- Sayers, E.W.; Bolton, E.E.; Brister, J.R.; Canese, K.; Chan, J.; Comeau, D.C.; Connor, R.; Funk, K.; Kelly, C.; Kim, S. Database resources of the national center for biotechnology information. Nucleic Acids Res. 2022, 50, D20–D26. [Google Scholar] [CrossRef]
- Bremer, H.; Dennis, P.P. Modulation of Chemical Composition and Other Parameters of the Cell at Different Exponential Growth Rates. EcoSal Plus 2008, 3. [Google Scholar] [CrossRef]
- Wang, Z.-m.; Ma, R.; Pierson, R.N.; Heymsfield, S.B. Five-Level Model: Reconstruction of Body Weight at Atomic, Molecular, Cellular, and Tissue-System Levels from Neutron Activation Analysis. In Human Body Composition. Basic Life Sciences; Ellis, K.J., Eastman, J.D., Eds.; Springer: Boston, MA, USA, 1993; Volume 60. [Google Scholar] [CrossRef]
- Van Voorhies, W.A. The influence of metabolic rate on longevity in the nematode Caenorhabditis elegans. Aging Cell 2002, 1, 91–101. [Google Scholar] [CrossRef]
- Van Voorhies, W.A. Metabolism and aging in the nematode Caenorhabditis elegans. Free. Radic. Biol. Med. 2002, 33, 587–596. [Google Scholar] [CrossRef]
- Baasch, T.; Reichert, P.; Lakämper, S.; Vertti-Quintero, N.; Hack, G.; i Solvas, X.C.; Demello, A.; Gunawan, R.; Dual, J. Acoustic Compressibility of Caenorhabditis elegans. Biophys. J. 2018, 115, 1817–1825. [Google Scholar] [CrossRef] [PubMed]
- Muschiol, D.; Schroeder, F.; Traunspurger, W. Life cycle and population growth rate of Caenorhabditis elegans studied by a new method. BMC Ecol. 2009, 9, 14. [Google Scholar] [CrossRef] [PubMed]
- Popovic, M. Atom counting method for determining elemental composition of viruses and its applications in biothermodynamics and environmental science. Comput. Biol. Chem. 2022, 96, 107621. [Google Scholar] [CrossRef] [PubMed]
- Popovic, M.; Šekularac, G. Death from the Nile: Empirical formula, molar mass, biosynthesis reaction and Gibbs energy of biosynthesis of the West Nile virus. Microb. Risk Anal. 2023, 25, 100281. [Google Scholar] [CrossRef]
- Popović, M.E.; Stevanović, M.; Pavlović, M.P. Biothermodynamics of hemoglobin and red blood cells: Analysis of structure and evolution of hemoglobin and red blood cells, based on molecular and empirical formulas, biosynthesis reactions, and thermodynamic properties of formation and biosynthesis. J. Mol. Evol. 2024, 92, 776–798. [Google Scholar] [CrossRef]
- Wang, F.F.; Li, P.; Chu, H.C.; Lo, P.K. Nucleic Acids and Their Analogues for Biomedical Applications. Biosensors 2022, 12, 93. [Google Scholar] [CrossRef]
- Pakornpadungsit, P.; Smitthipong, W.; Chworos, A. Self-assembly nucleic acid-based biopolymers: Learn from the nature. J. Polym. Res. 2018, 25, 45. [Google Scholar] [CrossRef]
- Numata, K. How to define and study structural proteins as biopolymer materials. Polym. J. 2020, 52, 1043–1056. [Google Scholar] [CrossRef]
- Berg, J.M.; Tymoczko, J.L.; Stryer, L. Biochemistry, 5th ed.; Freeman: New York, NY, USA, 2002; ISBN-13: 978-0716746843. [Google Scholar]
- Nelson, D.L.; Cox, M.M. Lehninger Principles of Biochemistry, 6th ed.; W.H. Freeman: New York, NY, USA, 2012; ISBN-13 978-1429234146. [Google Scholar]
- Sali, A.; Chiu, W. Macromolecular assemblies highlighted. Structure 2005, 13, 339–341. [Google Scholar] [CrossRef]
- Alber, F.; Förster, F.; Korkin, D.; Topf, M.; Sali, A. Integrating diverse data for structure determination of macromolecular assemblies. Annu. Rev. Biochem. 2008, 77, 443–477. [Google Scholar] [CrossRef][Green Version]
- Patel, S.A.; Erickson, L.E. Estimation of heats of combustion of biomass from elemental analysis using available electron concepts. Biotechnol. Bioeng. 1981, 23, 2051–2067. [Google Scholar] [CrossRef]
- Atkins, P.W.; de Paula, J. Physical Chemistry for the Life Sciences, 2nd ed.; W.H. Freeman and Company: New York, NY, USA, 2011; ISBN-13: 978-1429231145. [Google Scholar]
- Atkins, P.W.; de Paula, J. Physical Chemistry: Thermodynamics, Structure, and Change, 10th ed.; W.H. Freeman and Company: New York, NY, USA, 2014; ISBN-13: 978-1429290197. [Google Scholar]
- Battley, E.H. An empirical method for estimating the entropy of formation and the absolute entropy of dried microbial biomass for use in studies on the thermodynamics of microbial growth. Thermochim. Acta 1999, 326, 7–15. [Google Scholar] [CrossRef]
- Battley, E.H.; Stone, J.R. A comparison of values for the entropy and the entropy of formation of selected organic substances of biological importance in the solid state, as determined experimentally or calculated empirically. Thermochim. Acta 2000, 349, 153–161. [Google Scholar] [CrossRef]
- Battley, E.H. Calculation of the heat of growth of Escherichia coli K-12 on succinic acid. Biotechnol. Bioeng. 1991, 37, 334–343. [Google Scholar] [CrossRef]
- Battley, E.H. An alternate method of calculating the heat of growth of Escherichia coli K-12 on succinic acid. Biotechnol. Bioeng. 1991, 38, 480–492. [Google Scholar] [CrossRef]
- Popovic, M.; Tadić, V.; Mihailović, M. From genotype to phenotype with biothermodynamics: Empirical formulas, biosynthesis reactions and thermodynamic properties of preproinsulin, proinsulin and insulin molecules. J. Biomol. Struct. Dyn. 2023, 42, 10388–10400. [Google Scholar] [CrossRef]
- Barros, N.; Popovic, M.; Molina-Valero, J.; Lestido-Cardama, Y.; Pérez-Cruzado, C. Unravelling the thermodynamic properties of soil ecosystems in mature beech forests. Sci. Rep. 2024, 14, 16644. [Google Scholar] [CrossRef]
- Barros, N.; Popovic, M.; Pérez-Cruzado, C. Complete thermodynamic characterization of the soil organic matter from forest ecosystems. In Proceedings of the EGU General Assembly 2023, Vienna, Austria, 24–28 April 2023. EGU23-1389. [Google Scholar] [CrossRef]
- Popovic, M.; Minceva, M. Standard Thermodynamic properties, biosynthesis rates, and the driving force of growth of five agricultural plants. Front. Plant Sci. 2021, 12, 871. [Google Scholar] [CrossRef]
- Popovic, M.E.; Minceva, M. Thermodynamic properties of human tissues. Therm. Sci. 2020, 24, 4115–4133. [Google Scholar] [CrossRef]
- Riedel, S.; Morse, S.; Mietzner, T.; Miller, S. Jawetz, Melnick & Adelbergs Medical Microbiology, 28th ed.; McGraw-Hill Education: New York, NY, USA, 2019; ISBN 978-1260012026. [Google Scholar]
- Popovic, M. SARS-CoV-2 strain wars continues: Chemical and thermodynamic characterization of live matter and biosynthesis of Omicron BN.1, CH.1.1 and XBC variants. Microb. Risk Anal. 2023, 24, 100260. [Google Scholar] [CrossRef]
- Popović, M.E. Thermodynamics of Bacteria-phage Interactions T4 and Lambda Bacteriophages, and E. coli can Coexist in Natural Ecosystems due to the Ratio of their Gibbs Energies of Biosynthesis. Therm. Sci. 2023, 27, 411–431. [Google Scholar] [CrossRef]
- Privalov, P.L. Microcalorimetry of Macromolecules: The Physical Basis of Biological Structures; John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 978-1-118-10451-4. [Google Scholar]
- Sarge, S.M.; Höhne, G.W.; Hemminger, W. Calorimetry: Fundamentals, Instrumentation and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2014; ISBN 978-3-527-32761-4. [Google Scholar]
- Hurst, J.E.; Harrison, B.K. Estimation of liquid and solid heat capacities using a modified Kopp’s rule. Chem. Eng. Commun. 1992, 112, 21–30. [Google Scholar] [CrossRef]
- Ozilgen, M.; Sorguven Oner, E. Biothermodynamics: Principles and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Von Bertalanffy, L. General System Theory: Foundations, Development, Applications; George Braziller Inc.: New York, NY, USA, 1971; ISBN-13: 978-0807604533. [Google Scholar]
- Von Bertalanffy, L. The theory of open systems in physics and biology. Science 1950, 111, 23–29. [Google Scholar] [CrossRef] [PubMed]
- Popovic, M. Living organisms from Prigogine’s perspective: An opportunity to introduce students to biological entropy balance. J. Biol. Educ. 2017, 52, 294–300. [Google Scholar] [CrossRef]
- Ciccotti, E.; Betulla Morello, E. European eel in the Mediterranean Sea–Outcomes of the GFCM Research Programme; Studies and Reviews No. 103 (General Fisheries Commission for the Mediterranean); FAO: Rome, Italy, 2023. [Google Scholar]
- Hanel, R.; Marohn, L.; Westerberg, H. No new evidence for an Atlantic eels spawning area outside the Sargasso Sea. Sci. Rep. 2022, 12, 11778. [Google Scholar] [CrossRef]
- Deelder, C.L. Synopsis of Biological Data on the eel, Anguilla Anguilla (Linnaeus, 1758). FAO Fisheries Synopsis (80, Rev. 1); FAO: Rome, Italy, 1984; p. 73. ISBN 92-5-102166-X. Available online: https://www.fao.org/inland-fisheries/topic/detail/fr/c/1150088/ (accessed on 4 May 2025).
- Naisbett-Jones, L.C.; Putman, N.F.; Stephenson, J.F.; Ladak, S.; Young, K.A. A Magnetic Map Leads Juvenile European Eels to the Gulf Stream. Curr. Biol. 2017, 27, 1236–1240. [Google Scholar] [CrossRef]
- Lagarde, R.; Peyre, J.; Amilhat, E.; Bourrin, F.; Prellwitz, F.; Perrault, A.; Simon, G.; Faliex, E. Phenology and environmental drivers of glass eel entrance in a Mediterranean lagoon. ICES J. Mar. Sci. 2022, 79, 2107–2116. [Google Scholar] [CrossRef]
- Milosevic, D.; Mrdak, D.; Pesic, A.; Ikica, Z.; Kovacevic, A. Migration wawes and stage of pigmentation of glass eels from river Bojana (Montenegro). Agric. For. 2022, 68, 103–110. [Google Scholar] [CrossRef]
- Itakura, H. Behavior. In Eel Science Fisheries Science Series; Tsukamoto, K., Kuroki, M., Watanabe, S., Eds.; Springer: Singapore, 2023. [Google Scholar] [CrossRef]
- De Leo, G.A.; Gatto, M. Trends in vital rates of the European eel: Evidence for density dependence? Ecol. Appl. 1996, 6, 1281–1294. [Google Scholar] [CrossRef]
- Bauchot, M.-L. Anguillidae. In Fishes of the North-Eastern Atlantic and the Mediterranean; Whitehead, P.J.P., Bauchot, M.-L., Hureau, J.-C., Nielsen, J., Tortonese, E., Eds.; UNESCO: Paris, France, 1986; Volume 2, pp. 535–536. [Google Scholar]
- Acou, A.; Boury, P.; Laffaille, P.; Crivelli, A.J.; Feunteun, E. Towards a standardized characterization of the potentially migrating silver European eel (Anguilla anguilla L.). Arch. Hydrobiol. 2005, 164, 237–255. [Google Scholar] [CrossRef]
- Wright, R.M.; Piper, A.T.; Aarestrup, K.; Azevedo, J.M.N.; Cowan, G.; Don, A.; Gollock, M.; Ramallo, S.R.; Velterop, R.; Walker, A.; et al. First direct evidence of adult European eels migrating to their breeding place in the Sargasso Sea. Sci. Rep. 2022, 12, 15362. [Google Scholar] [CrossRef] [PubMed]
- Berry, L.; Brookes, D.; Walker, B. The problem of the migration of the European eel (Anguilla anguilla). Sci. Prog. (1933) 1972, 60, 465–485. Available online: https://www.jstor.org/stable/43420191 (accessed on 4 May 2025).
- Cresci, A.; Durif, C.M.; Paris, C.B.; Shema, S.D.; Skiftesvik, A.B.; Browman, H.I. Glass eels (Anguilla anguilla) imprint the magnetic direction of tidal currents from their juvenile estuaries. Commun. Biol. 2018, 2, 366. [Google Scholar] [CrossRef] [PubMed]
- Konala, N.; Abburi, P.; Bovillac, V.R.; Mamillapalli, A. The effect of bovine milk on the growth of Bombyx mori. J. Insect Sci. 2013, 13, 98. [Google Scholar] [CrossRef]
- He, Z.; Fang, Y.; Li, D.-C.; Chen, D.-S.; Wu, F. Effect of Lactic Acid Supplementation on the Growth and Reproduction of Bombyx mori (Lepidopteria: Bombycidae). J. Insect Sci. 2021, 21, 7. [Google Scholar] [CrossRef]
- Dai, M.; Feng, P.; Mao, T.; Gu, H.; Bian, D.; Sun, H.; Li, F.; Wei, J.; Li, B. Study of compensatory growth based on different nutrition conditions of Bombyx mori. J. Asia-Pac. Entomol. 2022, 25, 101948. [Google Scholar] [CrossRef]
- Tassoni, L.; Cappellozza, S.; Zotte, A.D.; Belluco, S.; Antonelli, P.; Marzoli, F.; Saviane, A. Nutritional Composition of Bombyx mori Pupae: A Systematic Review. Insects 2022, 13, 644. [Google Scholar] [CrossRef]
- Blossman-Myer, B.; Burggren, W.W. The silk cocoon of the silkworm, Bombyx mori: Macro structure and its influence on transmural diffusion of oxygen and water vapor. Comp. Biochem. Physiol. Part A Mol. Integr. Physiol. 2010, 155, 259–263. [Google Scholar] [CrossRef]
- Muramatsu, D.; Kinjoh, T.; Shinoda, T.; Hiruma, K. The role of 20-hydroxyecdysone and juvenile hormone in pupal commitment of the epidermis of the silkworm, Bombyx mori. Mech. Dev. 2008, 125, 411–420. [Google Scholar] [CrossRef]
- Tomotake, H.; Katagiri, M.; Yamato, M. Silkworm pupae (Bombyx mori) are new sources of high quality protein and lipid. J. Nutr. Sci. Vitaminol. 2010, 56, 446–448. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhou, S.; Duan, H.; Wang, J.; Yan, W. Silkworm Pupae: A Functional Food with Health Benefits for Humans. Foods 2022, 11, 1594. [Google Scholar] [CrossRef] [PubMed]
- Herman, R.A.; Yan, C.-H.; Wang, J.-Z.; Xun, X.-M.; Wu, C.-K.; Li, Z.-N.; Ayepa, E.; You, S.; Gong, L.-C.; Wang, J. Insight into the silkworm pupae: Modification technologies and functionality of the protein and lipids. Trends Food Sci. Technol. 2022, 129, 408–420. [Google Scholar] [CrossRef]
- Cresci, A. A comprehensive hypothesis on the migration of European glass eels (Anguilla anguilla). Biol. Rev. Camb. Philos. Soc. 2020, 95, 1273–1286. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Holdorf, A.D.; Walhout, A.J. C. elegans and its bacterial diet as a model for systems-level understanding of host–microbiota interactions. Curr. Opin. Biotechnol. 2017, 46, 74–80. [Google Scholar] [CrossRef]
- Willard, S.S.; Devreotes, P.N. Signaling pathways mediating chemotaxis in the social amoeba, Dictyostelium discoideum. Eur. J. Cell Biol. 2006, 85, 897–904. [Google Scholar] [CrossRef]
- Katoh, M.; Chen, G.; Roberge, E.; Shaulsky, G.; Kuspa, A. Developmental Commitment in Dictyostelium discoideum. Eukaryot. Cell 2007, 6, 2038–2045. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).