Resonance for Life: Metabolism and Social Interactions in Bacterial Communities
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
- Calculation of the energy, , and potential, , of each agent. It is performed according to the following formula:where is the geometrical distance between the nodes .
- Establishing connections between nodes. Each agent creates a link with other agents that have a lower potential. This step constructs the network.
- Distribution of the resources (sensing charges) among the agents. This occurs with a higher probability; the higher the total energy, the closer the energy of the agents involved, and the lower the productivity index. Through the links, resources (sensing charges) are transferred and assimilated with the assigned assimilation rate σ (σ is in the range [0, 1]) [19].
- Reproduction/migration. Each agent with a charge higher than min divides itself in equal parts (binary fission), and the daughter agent occupies the lowest potential position among the eight nearest neighbors. Agents with a charge lower than min move to the lowest potential position among the eight nearest neighbors. A larger than 1 value of the fitness of the colony indicates that the initial nucleus of agents has grown [21].
- Production of public goods. When a link is established, it is assigned an effective resistance [19]. This resistance measures the difficulty of transferring information between agents, and depends on factors such as distance, , and the propensity to produce public goods (α); it increases as this propensity decreases. Additionally, the resistance value decreases as the amount of charge distributed across the landscape and the productivity index increases.
3. Results
3.1. Metabolic Origin of the Social Behaviors
3.2. QS Mediation Between Different Behaviors
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Parsek, M.R.; Greenberg, E.P. Sociomicrobiology: The connections between quorum sensing and biofilms. Trends Microbiol. 2005, 13, 27–33. [Google Scholar] [PubMed]
- Ravasz, E.; Barabási, A.L. Hierarchical organization in complex networks. Phys. Rev. E 2003, 67, 026112. [Google Scholar]
- Redhead, D.; Power, E.A. Social hierarchies and social networks in humans. Philos. Trans. B 2022, 377, 20200440. [Google Scholar] [CrossRef]
- Nealson, K.H.; Hastings, J.W. Bacterial bioluminescence: Its control and ecological significance. Microbiol. Rev. 1979, 43, 496–518. [Google Scholar] [PubMed]
- Miller, M.B.; Bassler, B.L. Quorum sensing in bacteria. Annu. Rev. Microbiol. 2001, 55, 165–199. [Google Scholar] [PubMed]
- Bassler, B.L.; Losick, R. Bacterially speaking. Cell 2006, 125, 237–246. [Google Scholar]
- Abisado, R.G.; Benomar, S.; Klaus, J.R.; Dandekar, A.A.; Chandler, J.R. Bacterial quorum sensing and microbial community interactions. MBio 2008, 9, 10–1128. [Google Scholar]
- Ayrapetyan, M.; Williams, T.C.; Oliver, J.D. Interspecific quorum sensing mediates the resuscitation of viable but nonculturable vibrios. Appl. Environ. Microbiol. 2014, 80, 2478–2483. [Google Scholar]
- Bari, S.N.; Roky, M.K.; Mohiuddin, M.; Kamruzzaman, M.; Mekalanos, J.J.; Faruque, S.M. Quorum-sensing autoinducers resuscitate dormant Vibrio cholerae in environmental water samples. Proc. Natl. Acad. Sci. USA 2013, 110, 9926–9931. [Google Scholar]
- Personnic, N.; Striednig, B.; Hilbi, H. Quorum sensing controls persistence, resuscitation, and virulence of Legionella subpopulations in biofilms. ISME J. 2021, 15, 196–210. [Google Scholar]
- Dandekar, A.A.; Chugani, S.; Greenberg, E.P. Bacterial quorum sensing and metabolic incentives to cooperate. Science 2012, 338, 264–266. [Google Scholar] [CrossRef] [PubMed]
- Bruger, E.L.; Waters, C.M. Bacterial quorum sensing stabilizes cooperation by optimizing growth strategies. Appl. Environ. Microb. 2016, 82, 6498–6506. [Google Scholar] [CrossRef] [PubMed]
- Bruger, E.L.; Waters, C.M. Maximizing growth yield and dispersal via quorum sensing promotes cooperation in Vibrio bacteria. Appl. Environ. Microb. 2018, 84, e00402-18. [Google Scholar] [CrossRef]
- Bruger, E.L.; Snyder, D.J.; Cooper, V.S.; Waters, C.M. Quorum sensing provides a molecular mechanism for evolution to tune and maintain investment in cooperation. ISME J. 2021, 15, 1236–1247. [Google Scholar] [CrossRef] [PubMed]
- Smalley, N.E.; An, D.; Parsek, M.R.; Chandler, J.R.; Dandekar, A.A. Quorum sensing protects Pseudomonas aeruginosa against cheating by other species in a laboratory coculture model. J. Bacteriol. 2015, 197, 3154–3159. [Google Scholar] [CrossRef]
- Zhao, K.; Liu, L.; Chen, X.; Huang, T.; Du, L.; Lin, J.; Yuan, Y.; Zhou, Y.; Yue, B.; Wei, K.; et al. Behavioral heterogeneity in quorum sensing can stabilize social cooperation in microbial populations. BMC Biol. 2019, 17, 1–15. [Google Scholar] [CrossRef]
- Miller, S.D.; Haddock, S.H.; Straka, W.C., III; Seaman, C.J.; Combs, C.L.; Wang, M.; Shi, W.; Nam, S. Honing in on bioluminescent milky seas from space. Sci. Rep. 2021, 11, 15443. [Google Scholar] [CrossRef]
- Wilhelm, M.J.; Gh, M.S.; Wu, T.; Li, Y.; Chang, C.M.; Ma, J.; Dai, H.L. Determination of bacterial surface charge density via saturation of adsorbed ions. Biophys. J. 2021, 120, 2461–2470. [Google Scholar] [CrossRef]
- Alfinito, E.; Cesaria, M.; Beccaria, M. Did Maxwell dream of electrical bacteria? Biophysica 2022, 2, 281–291. [Google Scholar] [CrossRef]
- Alfinito, E.; Beccaria, M.; Cesaria, M. Cooperation in bioluminescence: Understanding the role of autoinducers by a stochastic random resistor model. Eur. Phys. J. E 2023, 46, 94. [Google Scholar] [CrossRef]
- Alfinito, E.; Beccaria, M. Competitive Distribution of Public Goods: The Role of Quorum Sensing in the Development of Bacteria Colonies. Biophysica 2024, 4, 327–339. [Google Scholar] [CrossRef]
- Dudley, S.A. Discovering cooperative traits in crop plants. PLoS Biol. 2022, 20, e3001892. [Google Scholar]
- Henke, J.M.; Bassler, B.L. Bacterial social engagements. Trends Cell Biol. 2004, 14, 648–656. [Google Scholar] [CrossRef]
- Bruger, E.; Waters, C. Sharing the sandbox: Evolutionary mechanisms that maintain bacterial cooperation. F1000Research 2015, 4, F1000-Faculty. [Google Scholar]
- Ben-Jacob, E. Social behavior of bacteria: From physics to complex organization. Eur. Phys. J. B 2008, 65, 315–322. [Google Scholar] [CrossRef]
- Coyte, K.Z.; Rakoff-Nahoum, S. Understanding competition and cooperation within the mammalian gut microbiome. Curr. Biol. 2019, 29, R538–R544. [Google Scholar] [PubMed]
- Michaelis, C.; Grohmann, E. Horizontal gene transfer of antibiotic resistance genes in biofilms. Antibiotics 2023, 12, 328. [Google Scholar] [CrossRef]
- Fourcade, Y. Fine-tuning niche models matters in invasion ecology. A lesson from the land planarian Obama nungara. Ecol. Model 2021, 457, 109686. [Google Scholar]
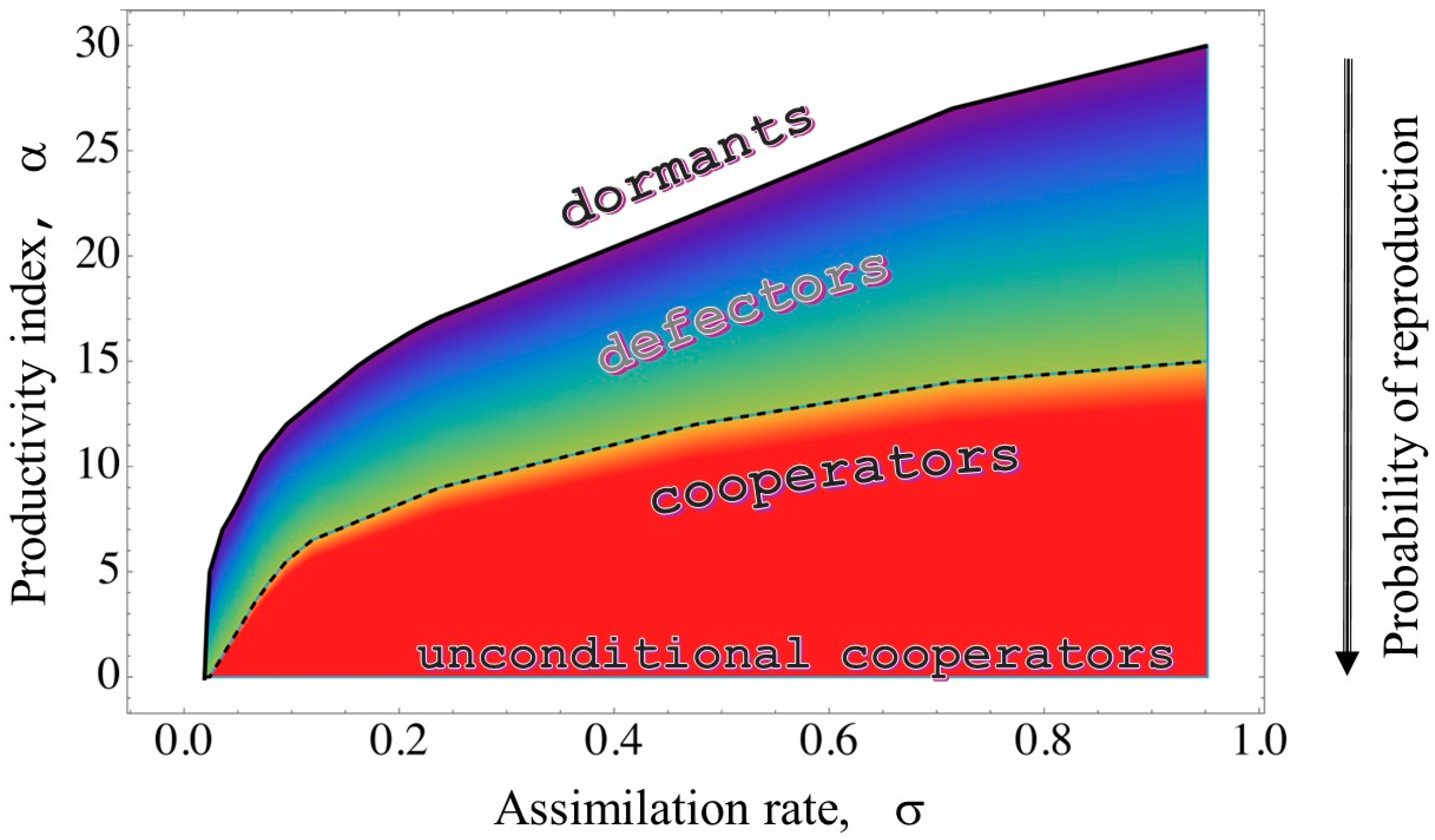
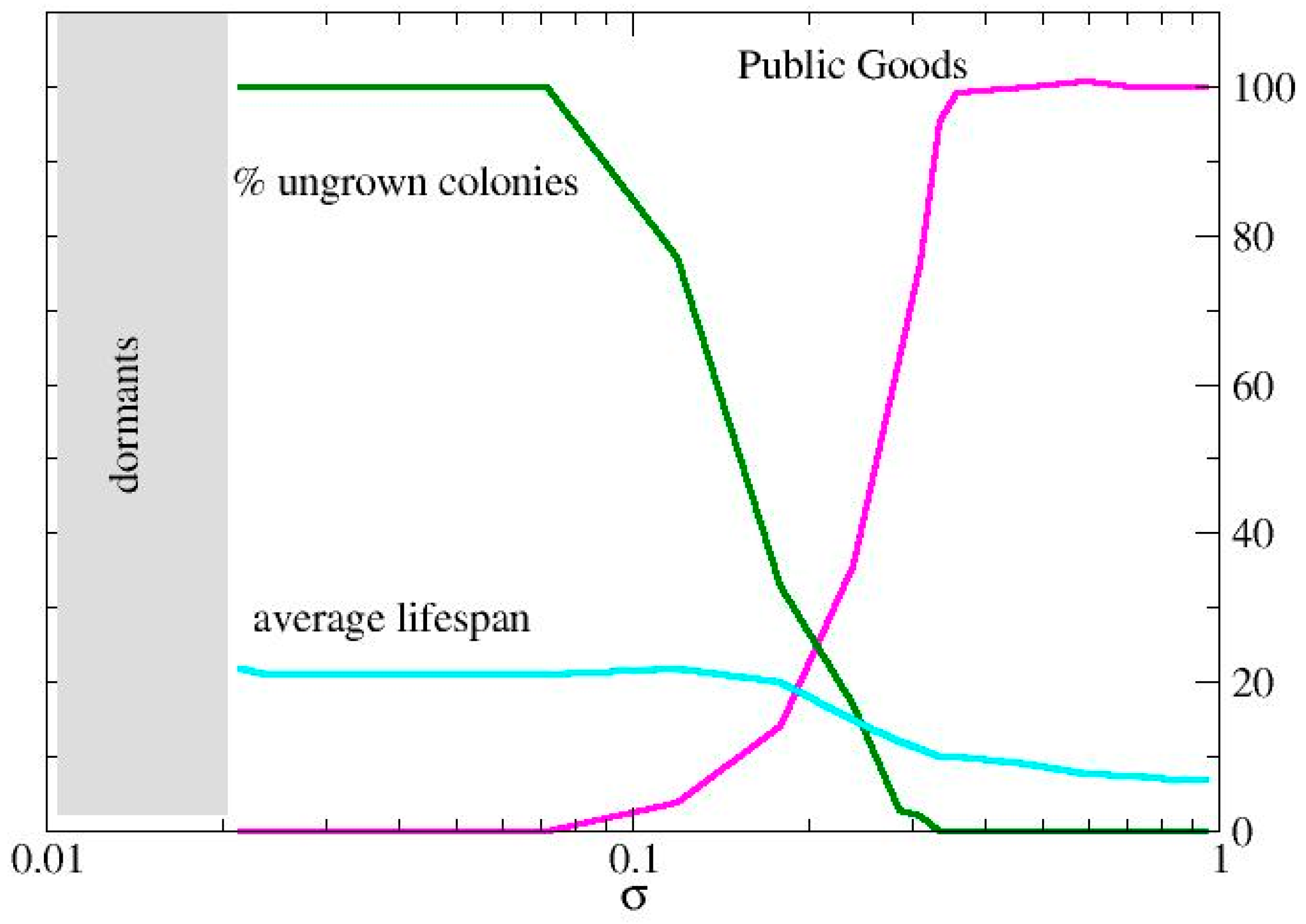
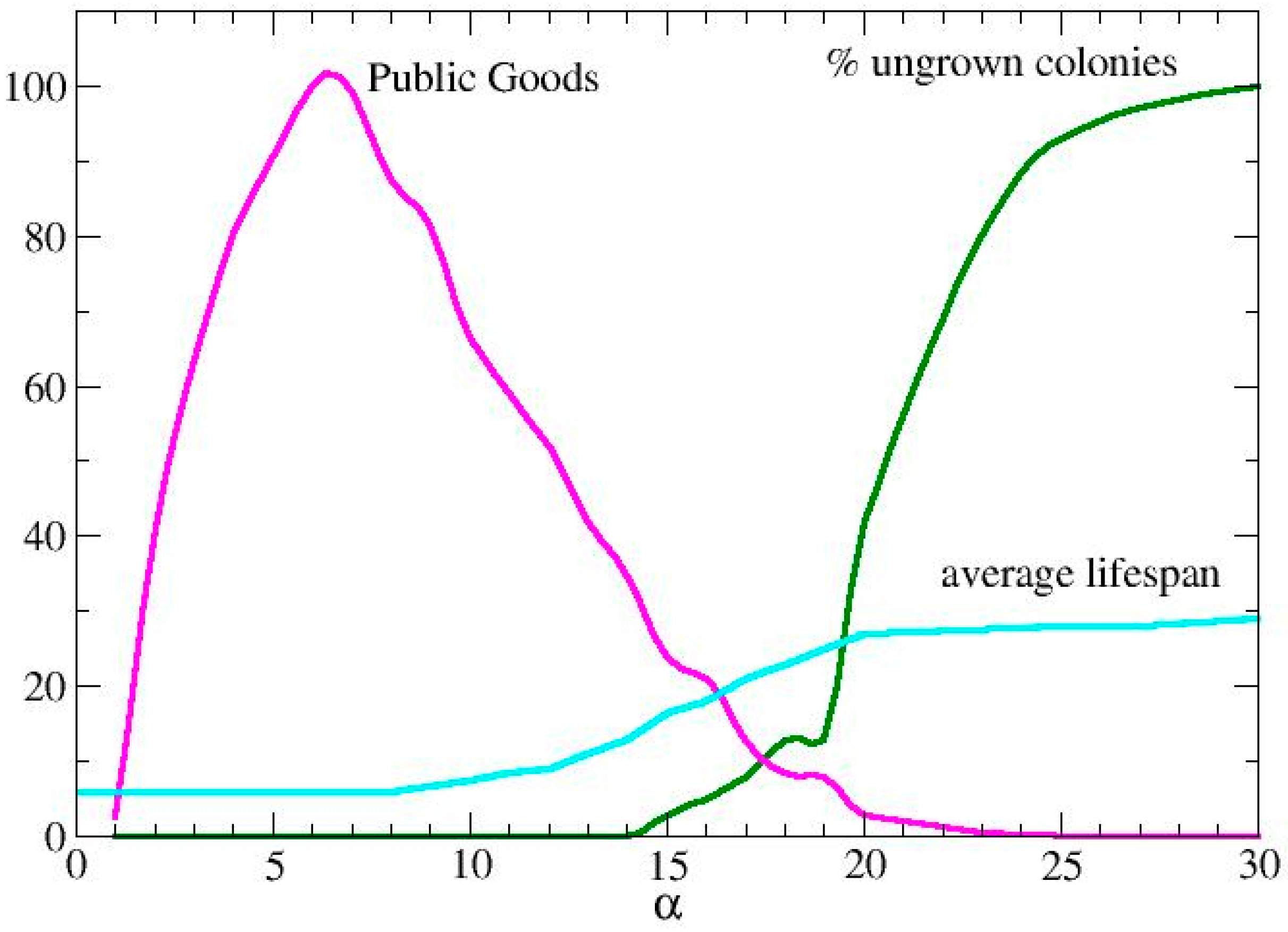
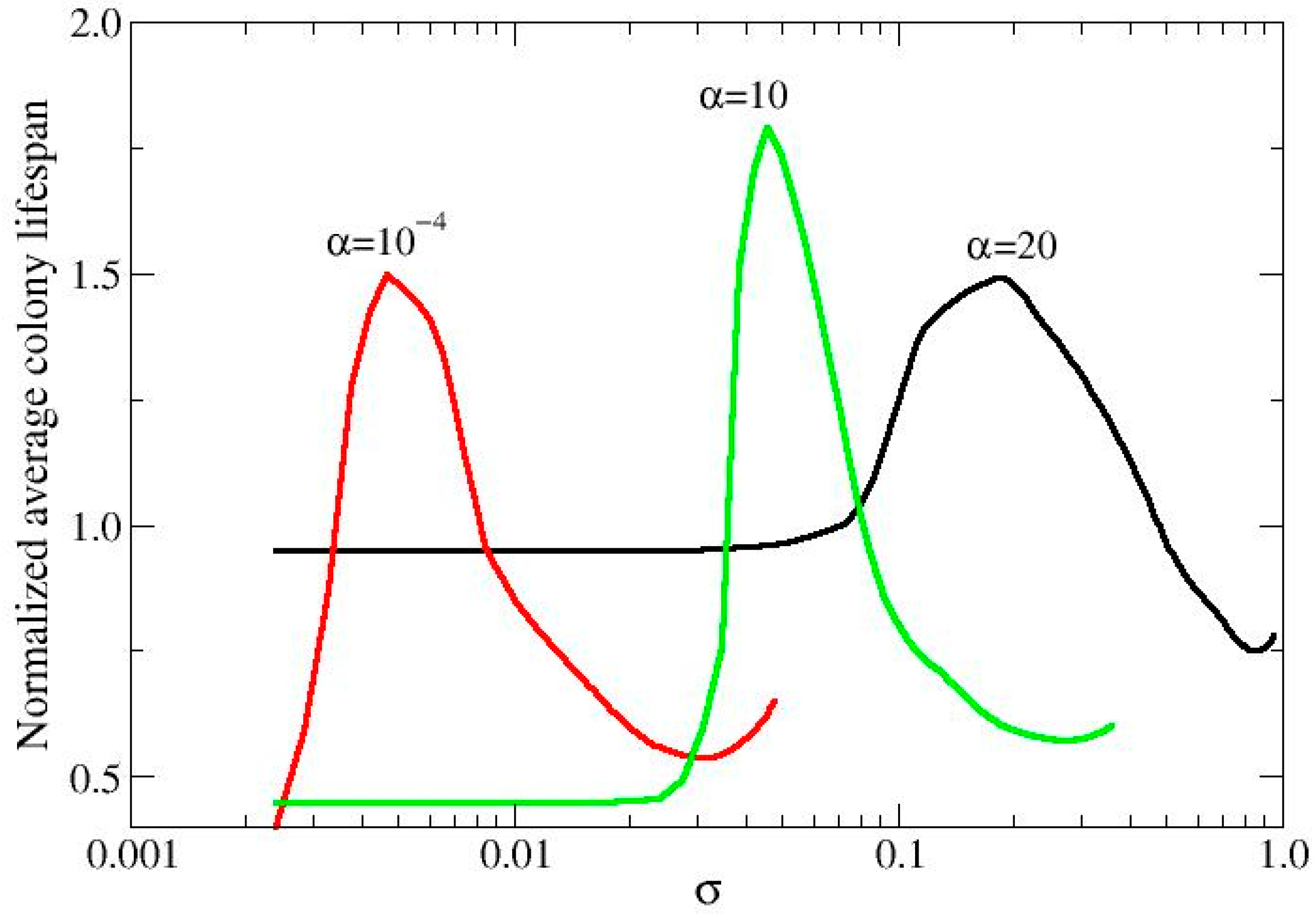
| Social Trait | Probability of Reproduction | PG Production |
|---|---|---|
| dormant | 0 | Zero |
| cooperators | 1 | Maximal |
| unconditional cooperators | 1 | From modest to high |
| defectors | 1 | From modest to low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alfinito, E.; Beccaria, M. Resonance for Life: Metabolism and Social Interactions in Bacterial Communities. Biophysica 2025, 5, 12. https://doi.org/10.3390/biophysica5020012
Alfinito E, Beccaria M. Resonance for Life: Metabolism and Social Interactions in Bacterial Communities. Biophysica. 2025; 5(2):12. https://doi.org/10.3390/biophysica5020012
Chicago/Turabian StyleAlfinito, Eleonora, and Matteo Beccaria. 2025. "Resonance for Life: Metabolism and Social Interactions in Bacterial Communities" Biophysica 5, no. 2: 12. https://doi.org/10.3390/biophysica5020012
APA StyleAlfinito, E., & Beccaria, M. (2025). Resonance for Life: Metabolism and Social Interactions in Bacterial Communities. Biophysica, 5(2), 12. https://doi.org/10.3390/biophysica5020012







