Cellular Compartmentalization as a Physical Regulatory Mechanism of Signaling Pathways
Abstract
1. Introduction
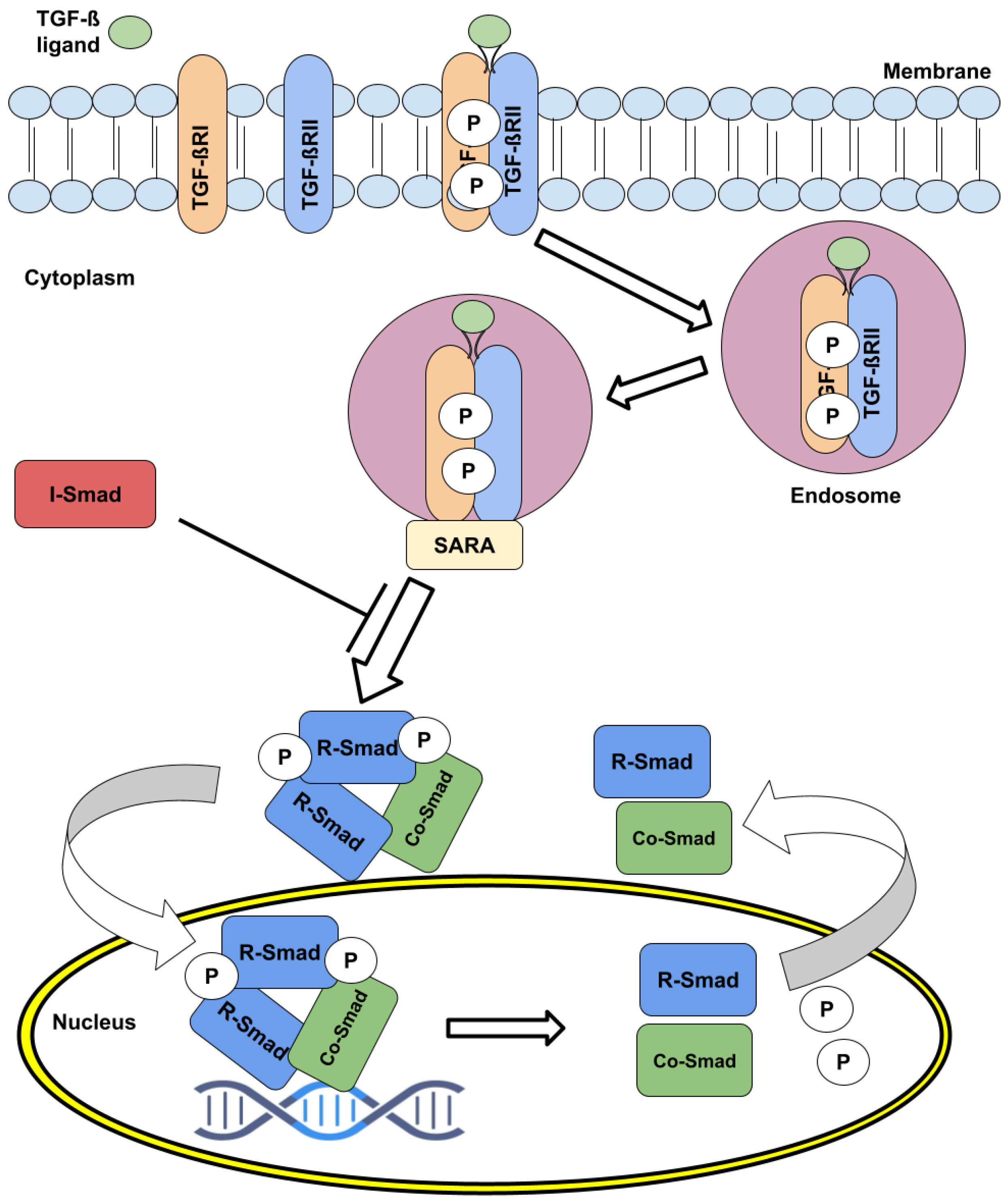
2. The TGF- Pathway Signaling Dynamics and Regulation
3. R-Smad Nucleocytoplasmatic Shuttling as a Modulation of Signal Transduction
4. Dynamics and Regulation of Export and Import of the R-Smads
5. Taking Advantage of Nucleoplasmatic Shuttling to Study the TGF- Pathway
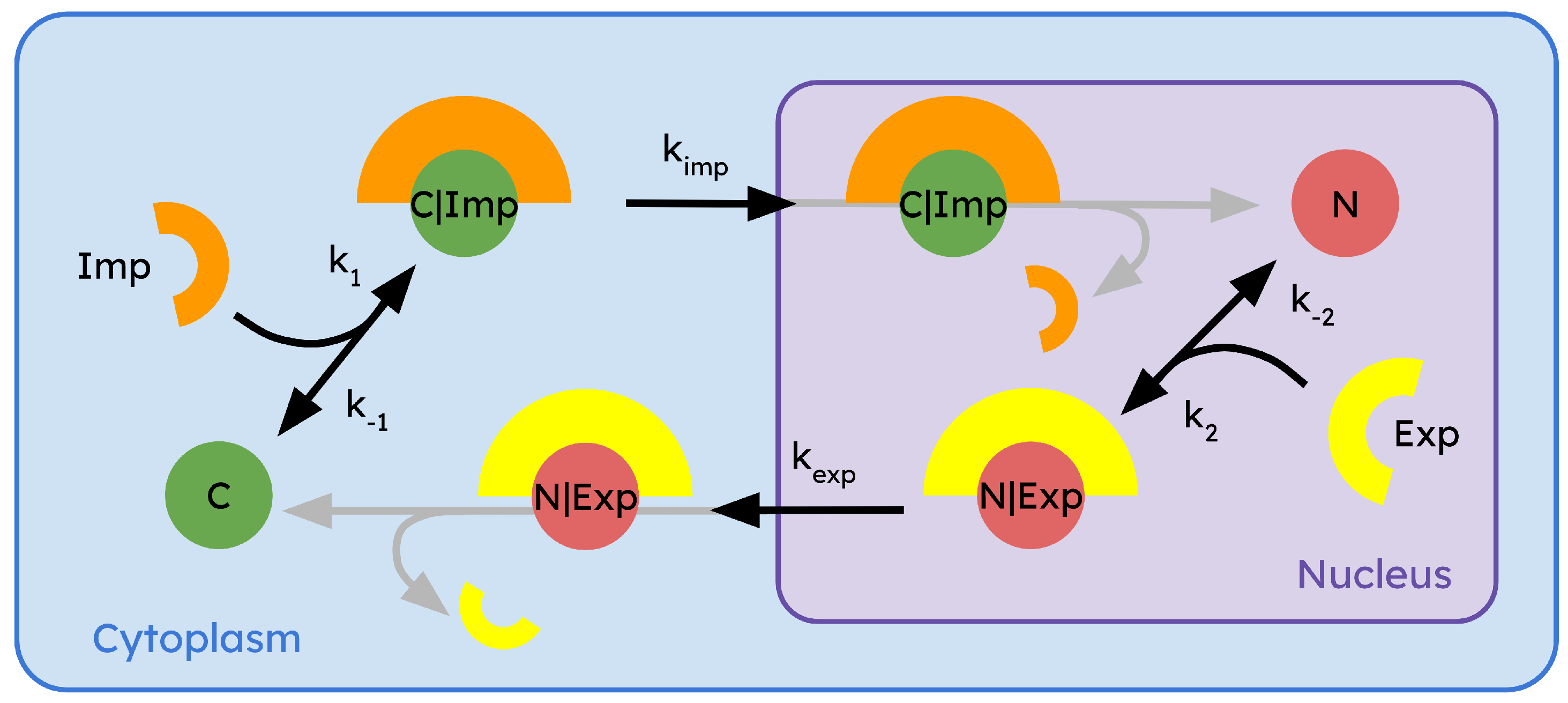
6. Mathematical Modeling of Regulatory Compartmentalization
6.1. Using the Mass Action Law to Model a Biological System
6.2. Simplification Using the Mass Conservation Law
6.3. Nondimensionalization of the Model
6.4. Pseudo-Steady-State Approximation
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Heldin, C.H.; Moustakas, A. Signaling Receptors for TGF-beta Family Members. Cold Spring Harb. Perspect. Biol. 2016, 8, a022053. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Q.; Xiao, X.; Qiu, Y.; Xu, Z.; Chen, C.; Chong, B.; Zhao, X.; Hai, S.; Li, S.; An, Z.; et al. Protein posttranslational modifications in health and diseases: Functions, regulatory mechanisms, and therapeutic implications. MedComm 2023, 4, e261. [Google Scholar] [CrossRef] [PubMed]
- Matschinsky, F.M. Editorial: Ebb and Tide of Glucokinase. Int. J. Exp. Diabetes Res. 2001, 2, 168–171. [Google Scholar] [PubMed]
- Jetton, T.L.; Shiota, M.; Knobel, S.M.; Piston, D.W.; Cherrington, A.D.; Magnuson, M.A. Substrate-induced Nuclear Export and Peripheral Compartmentalization of Hepatic Glucokinase Correlates with Glycogen Deposition. J. Diabetes Res. 2001, 2, 173–186. [Google Scholar] [CrossRef]
- Erb, T.J.; Zarzycki, J. A short history of RubisCO: The rise and fall (?) of Nature’s predominant CO2 fixing enzyme. Curr. Opin. Biotechnol. 2018, 49, 100–107. [Google Scholar] [CrossRef]
- Amritkar, K.; Cuevas-Zuviría, B.; Kacar, B. Ancestral structure prediction reveals the conformational impact of the RuBisCO small subunit across time. bioRxiv 2024. [Google Scholar] [CrossRef]
- George, C.; Brittain, S.G. A rapid method for quantifying cytoplasmic versus nuclear localization in endogenous peripheral blood leukocytes by conventional flow cytometry. Cytom. Part A 2017, 91, 351–363. [Google Scholar] [CrossRef][Green Version]
- Oliver, J.D. ERp57 Functions as a Subunit of Specific Complexes Formed with the ER Lectins Calreticulin and Calnexin. Mol. Biol. Cell 1999, 10, 2573–2582. [Google Scholar] [CrossRef]
- Kimura, T. ERp57 binds competitively to protein disulfide isomerase and calreticulin. Biochem. Biophys. Res. Commun. 2005, 331, 224–230. [Google Scholar] [CrossRef]
- Grillo, C. DNA-binding Activity of the ERp57 C-terminal Domain Is Related to a Redox-dependent Conformational Change. J. Biol. Chem. 2007, 282, 10299–10310. [Google Scholar] [CrossRef]
- Jeong Sook Kim-Han, K.L.O. Cell Stress Induced by the Parkinsonian Mimetic, 6-Hydroxydopamine, is Concurrent with Oxidation of the Chaperone, ERp57, and Aggresome Formation. Antioxid. Redox Signal. 2007, 9, 2255–2264. [Google Scholar] [CrossRef] [PubMed]
- Grindel, B.J. Tumor necrosis factor-α treatment of HepG2 cells mobilizes a cytoplasmic pool of ERp57/1,25D3-MARRS to the nucleus. J. Cell. Biochem. 2011, 112, 2606–2615. [Google Scholar] [CrossRef] [PubMed]
- Scott, M.S. Refining Protein Subcellular Localization. PLoS Comput. Biol. 2005, 1, e66. [Google Scholar] [CrossRef] [PubMed]
- Rajesh Nair, B.R. Protein Subcellular Localization Prediction Using Artificial Intelligence Technology. Methods Mol. Biol. 2008, 484, 435–463. [Google Scholar] [CrossRef]
- Mien-Chie Hung, W.L. Protein localization in disease and therapy. J. Cell Sci. 2011, 124, 3381–3392. [Google Scholar] [CrossRef]
- Binder, J.X. COMPARTMENTS: Unification and visualization of protein subcellular localization evidence. Database 2014, 2014, bau012. [Google Scholar] [CrossRef]
- Ruiz-Herrero, T.; Estrada, J.; Guantes, R.; Miguez, D.G. A Tunable Coarse-Grained Model for Ligand-Receptor Interaction. PLoS Comput. Biol. 2013, 9, e1003274. [Google Scholar] [CrossRef]
- Doldán-Martelli, V.; Míguez, D.G. Synergistic Interaction between Selective Drugs in Cell Populations Models. PLoS ONE 2015, 10, e0117558. [Google Scholar] [CrossRef]
- Doldán-Martelli, V.; Guantes, R.; Míguez, D.G. A mathematical model for the rational design of chimeric ligands in selective drug therapies. CPT Pharmacomet. Syst. Pharmacol. 2013, 2, e26. [Google Scholar] [CrossRef]
- Míguez, D.G. The role of asymmetric binding in ligand-receptor systems with 1:2 interaction ratio. Biophys. Chem. 2010, 148, 74–81. [Google Scholar] [CrossRef]
- Xu, X.; Zheng, L.; Yuan, Q.; Zhen, G.; Crane, J.L.; Zhou, X.; Cao, X. Transforming growth factor-β in stem cells and tissue homeostasis. Bone Res. 2018, 6, 2. [Google Scholar] [CrossRef] [PubMed]
- Papanikolaou, S.; Vourda, A.; Syggelos, S.; Gyftopoulos, K. Cell Plasticity and Prostate Cancer: The Role of Epithelial–Mesenchymal Transition in Tumor Progression, Invasion, Metastasis and Cancer Therapy Resistance. Cancers 2021, 13, 2795. [Google Scholar] [CrossRef] [PubMed]
- Derynck, R.; Budi, E.H. Specificity, versatility, and control of TGF-beta family signaling. Sci. Signal. 2019, 12, eaav5183. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z.; Fan, T.; Xiao, C.; Tian, H.; Zheng, Y.; Li, C.; He, J. TGF-beta signaling in health, disease and therapeutics. Signal Transduct. Target. Ther. 2024, 9, 61. [Google Scholar] [CrossRef]
- Goebel, E.J.; Hart, K.N.; McCoy, J.C.; Thompson, T.B. Structural biology of the TGFβ family. Exp. Biol. Med. 2019, 244, 1530–1546. [Google Scholar] [CrossRef]
- Tzavlaki, K.; Moustakas, A. TGF-beta Signaling. Biomolecules 2020, 10, 487. [Google Scholar] [CrossRef]
- Huang, T.; David, L.; Mendoza, V.; Yang, Y.; De, K.; Sun, L.; Fang, X.; Wrana, J.L.; Hinck, A.P. TGF-β signalling is mediated by two autonomously functioning TBRI:TBRII pairs. EMBO J. 2011, 30, 1263–1276. [Google Scholar] [CrossRef]
- Mitchell, H.; Choudhury, A.; Pagano, R.E.; Leof, E.B. Ligand-dependent and -independent Transforming Growth Factor-β Receptor Recycling Regulated by Clathrin-mediated Endocytosis and Rab11. Mol. Biol. Cell 2004, 15, 4166–4178. [Google Scholar] [CrossRef]
- Derynck, R.; Zhang, Y.E. Smad-dependent and Smad-independent pathways in TGF-β family signalling. Nature 2003, 425, 577–584. [Google Scholar] [CrossRef]
- Kim, M.S.; Jin, W. TrkB-Induced Inhibition of R-SMAD/SMAD4 Activation is Essential for TGF-beta-Mediated Tumor Suppressor Activity. Cancers 2020, 12, 1048. [Google Scholar] [CrossRef]
- Budi, E.H.; Duan, D.; Derynck, R. Transforming Growth Factor-β Receptors and Smads: Regulatory Complexity and Functional Versatility. Trends Cell Biol. 2017, 27, 658–672. [Google Scholar] [CrossRef] [PubMed]
- Miyazawa, K.; Miyazono, K. Regulation of TGF-beta Family Signaling by Inhibitory Smads. Cold Spring Harb. Perspect. Biol. 2017, 9, a022095. [Google Scholar] [CrossRef] [PubMed]
- Aykul, S.; Maust, J.; Thamilselvan, V.; Floer, M.; Martinez-Hackert, E. Smad2/3 Activation Regulates Smad1/5/8 Signaling via a Negative Feedback Loop to Inhibit 3T3-L1 Adipogenesis. Int. J. Mol. Sci. 2021, 22, 8472. [Google Scholar] [CrossRef] [PubMed]
- Baburajendran, N.; Jauch, R.; Tan, C.Y.Z.; Narasimhan, K.; Kolatkar, P.R. Structural basis for the cooperative DNA recognition by Smad4 MH1 dimers. Nucleic Acids Res. 2011, 39, 8213–8222. [Google Scholar] [CrossRef]
- Xin, X.; Cheng, X.; Zeng, F.; Xu, Q.; Hou, L. The Role of TGF-beta/SMAD Signaling in Hepatocellular Carcinoma: From Mechanism to Therapy and Prognosis. Int. J. Biol. Sci. 2024, 20, 1436–1451. [Google Scholar] [CrossRef]
- Hata, A.; Chen, Y.G. TGF-beta Signaling from Receptors to Smads. Cold Spring Harb. Perspect. Biol. 2016, 8, a022061. [Google Scholar] [CrossRef]
- Xu, F.; Liu, C.; Zhou, D.; Zhang, L. TGF-beta/SMAD Pathway and Its Regulation in Hepatic Fibrosis. J. Histochem. Cytochem. 2016, 64, 157–167. [Google Scholar] [CrossRef]
- Bai, H.; Lester, G.M.; Petishnok, L.; Dean, D. Cytoplasmic transport and nuclear import of plasmid DNA. Biosci. Rep. 2017, 37, BSR20160616. [Google Scholar] [CrossRef]
- Schmierer, B.; Hill, C.S. Kinetic Analysis of Smad Nucleocytoplasmic Shuttling Reveals a Mechanism for Transforming Growth Factor β-Dependent Nuclear Accumulation of Smads. Mol. Cell. Biol. 2005, 25, 9845–9858. [Google Scholar] [CrossRef]
- Hill, C.S. Nucleocytoplasmic shuttling of Smad proteins. Cell Res. 2009, 19, 36–46. [Google Scholar] [CrossRef]
- Otsuka, S.; Ellenberg, J. Mechanisms of nuclear pore complex assembly—Two different ways of building one molecular machine. FEBS Lett. 2018, 592, 475–488. [Google Scholar] [CrossRef] [PubMed]
- Paci, G.; Caria, J.; Lemke, E.A. Cargo transport through the nuclear pore complex at a glance. J. Cell Sci. 2021, 134, jcs247874. [Google Scholar] [CrossRef] [PubMed]
- Timney, B.L.; Raveh, B.; Mironska, R.; Trivedi, J.M.; Kim, S.J.; Russel, D.; Wente, S.R.; Sali, A.; Rout, M.P. Simple rules for passive diffusion through the nuclear pore complex. J. Cell Biol. 2016, 215, 57–76. [Google Scholar] [CrossRef] [PubMed]
- Oka, M.; Yoneda, Y. Importin α: Functions as a nuclear transport factor and beyond. Proc. Jpn. Acad. Ser. B 2018, 94, 259–274. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Guo, L.; Chen, L.; Gong, B.; Jia, D.; Sun, Q. Nuclear transport proteins: Structure, function and disease relevance. Signal Transduct. Target. Ther. 2023, 8, 425. [Google Scholar] [CrossRef]
- Kurisaki, A.; Kose, S.; Yoneda, Y.; Heldin, C.H.; Moustakas, A. Transforming Growth Factor-β Induces Nuclear Import of Smad3 in an Importin-β1 and Ran-dependent Manner. Mol. Biol. Cell 2001, 12, 1079–1091. [Google Scholar] [CrossRef]
- Chen, X.; Xu, L. Mechanism and Regulation of Nucleocytoplasmic Trafficking of Smad. Cell Biosci. 2011, 1, 40. [Google Scholar] [CrossRef]
- Kırlı, K.; Karaca, S.; Dehne, H.J.; Samwer, M.; Pan, K.T.; Lenz, C.; Urlaub, H.; Görlich, D. A deep proteomics perspective on CRM1-mediated nuclear export and nucleocytoplasmic partitioning. eLife 2015, 4, e11466. [Google Scholar] [CrossRef]
- Abdel Mouti, M.; Pauklin, S. TGFB1/INHBA Homodimer/Nodal-SMAD2/3 Signaling Network: A Pivotal Molecular Target in PDAC Treatment. Mol. Ther. 2021, 29, 920–936. [Google Scholar] [CrossRef]
- Watanabe, M.; Masuyama, N.; Fukuda, M.; Nishida, E. Regulation of intracellular dynamics of Smad4 by its leucine-rich nuclear export signal. EMBO Rep. 2000, 1, 176–182. [Google Scholar] [CrossRef]
- Dai, F.; Lin, X.; Chang, C.; Feng, X.H. Nuclear Export of Smad2 and Smad3 by RanBP3 Facilitates Termination of TGF-β Signaling. Dev. Cell 2009, 16, 345–357. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Kang, Y.; Çöl, S.; Massagué, J. Smad2 Nucleocytoplasmic Shuttling by Nucleoporins CAN/Nup214 and Nup153 Feeds TGFβ Signaling Complexes in the Cytoplasm and Nucleus. Mol. Cell 2002, 10, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Kofler, M.; Kapus, A. Nuclear Import and Export of YAP and TAZ. Cancers 2023, 15, 4956. [Google Scholar] [CrossRef] [PubMed]
- Kurisaki, A.; Kurisaki, K.; Kowanetz, M.; Sugino, H.; Yoneda, Y.; Heldin, C.H.; Moustakas, A. The Mechanism of Nuclear Export of Smad3 Involves Exportin 4 and Ran. Mol. Cell. Biol. 2006, 26, 1318–1332. [Google Scholar] [CrossRef]
- Song, R.; Tikoo, S.; Jain, R.; Pinello, N.; Au, A.Y.M.; Nagarajah, R.; Porse, B.; Rasko, J.E.J.; Wong, J.J.-L. Dynamic intron retention modulates gene expression in the monocytic differentiation pathway. Immunology 2022, 165, 274–286. [Google Scholar] [CrossRef]
- Pierreux, C.E.; Nicolás, F.J.; Hill, C.S. Transforming Growth Factor β-Independent Shuttling of Smad4 between the Cytoplasm and Nucleus. Mol. Cell. Biol. 2000, 20, 9041–9054. [Google Scholar] [CrossRef]
- Zou, M.L.; Chen, Z.H.; Teng, Y.Y.; Liu, S.Y.; Jia, Y.; Zhang, K.W.; Sun, Z.L.; Wu, J.J.; Yuan, Z.D.; Feng, Y.; et al. The Smad Dependent TGF-beta and BMP Signaling Pathway in Bone Remodeling and Therapies. Front. Mol. Biosci. 2021, 8, 593310. [Google Scholar] [CrossRef]
- Warmflash, A.; Zhang, Q.; Sorre, B.; Vonica, A.; Brivanlou, A.H. Dynamics of TGF-beta signaling reveal adaptive and pulsatile behaviors reflected in the nuclear localization of transcription factor Smad4. Proc. Natl. Acad. Sci. USA 2012, 109, E1947–E1956. [Google Scholar] [CrossRef]
- Li, Y.; Luo, W.; Yang, W. Nuclear Transport and Accumulation of Smad Proteins Studied by Single-Molecule Microscopy. Biophys. J. 2018, 114, 2243–2251. [Google Scholar] [CrossRef]
- Nicolás, F.J.; De Bosscher, K.; Schmierer, B.; Hill, C.S. Analysis of Smad nucleocytoplasmic shuttling in living cells. J. Cell Sci. 2004, 117, 4113–4125. [Google Scholar] [CrossRef]
- Zi, Z.; Feng, Z.; Chapnick, D.A.; Dahl, M.; Deng, D.; Klipp, E.; Moustakas, A.; Liu, X. Quantitative analysis of transient and sustained transforming growth factor-β signaling dynamics. Mol. Syst. Biol. 2011, 7, 492. [Google Scholar] [CrossRef] [PubMed]
- Sorre, B.; Warmflash, A.; Brivanlou, A.; Siggia, E. Encoding of Temporal Signals by the TGF-β Pathway and Implications for Embryonic Patterning. Dev. Cell 2014, 30, 334–342. [Google Scholar] [CrossRef] [PubMed]
- Frick, C.L.; Yarka, C.; Nunns, H.; Goentoro, L. Sensing relative signal in the Tgf-β/Smad pathway. Proc. Natl. Acad. Sci. USA 2017, 114, E2975–E2982. [Google Scholar] [CrossRef] [PubMed]
- Kretzschmar, M.; Doody, J.; Timokhina, I.; Massague, J. A mechanism of repression of TGFbeta/Smad signaling by oncogenic Ras. Genes Dev. 1999, 13, 804–816. [Google Scholar] [CrossRef]
- Míguez, D.G.; Gil-Guiñón, E.; Pons, S.; Martí, E. Smad2 and Smad3 cooperate and antagonize simultaneously in vertebrate neurogenesis. J. Cell Sci. 2013, 126, 5335–5343. [Google Scholar] [CrossRef]
- Sanz, A.L.; Míguez, D.G. Dual R-Smads interplay in the regulation of vertebrate neurogenesis. Neurogenesis 2014, 1, e29529. [Google Scholar] [CrossRef][Green Version]
- Schmierer, B.; Tournier, A.L.; Bates, P.A.; Hill, C.S. Mathematical modeling identifies Smad nucleocytoplasmic shuttling as a dynamic signal-interpreting system. Proc. Natl. Acad. Sci. USA 2008, 105, 6608–6613. [Google Scholar] [CrossRef]
- Khatibi, S.; Zhu, H.J.; Wagner, J.; Tan, C.W.; Burgess, A.W. Mathematical model of TGF- beta signalling: Feedback coupling is consistent with signal switching. BMC Syst. Biol. 2017, 11, 48. [Google Scholar] [CrossRef]
- Chen, W.W.; Niepel, M.; Sorger, P.K. Classic and contemporary approaches to modeling biochemical reactions. Genes Dev. 2010, 24, 1861–1875. [Google Scholar] [CrossRef]
- Hangos, K.M.; Szederkényi, G. Mass action realizations of reaction kinetic system models on various time scales. J. Phys. Conf. Ser. 2011, 268, 012009. [Google Scholar] [CrossRef]
- Guldberg, C.M.; Waage, P. Ueber die chemische Affinität. 1. Einleitung. J. Prakt. Chem. 1879, 19, 69–114. [Google Scholar] [CrossRef]
- Berthollet, C.L. Essai de Statique Chimique; A Paris: Chez Firmin Didot …; Nabu Press: New York, NY, USA, 1803. [Google Scholar]
- Van’T Hoff, J.H. Die Grenzebene, ein Beitrag zur Kenntniss der Esterbildung. Ber. Dtsch. Chem. Ges. 1877, 10, 669–678. [Google Scholar] [CrossRef]
- Weiss, L. A simple demonstration of the law of conservation of mass. J. Chem. Educ. 1943, 20, 579. [Google Scholar] [CrossRef]
- Schummer, J. The Philosophy of Chemistry. In Philosophy of Chemistry: Synthesis of a New Discipline; Baird, D., Scerri, E., McIntyre, L., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 19–39. [Google Scholar] [CrossRef]
- Míguez, D.G.; Satnoianu, R.; Muñuzuri, A. Experimental steady pattern formation in reaction-diffusion-advection systems. Phys. Rev. E 2006, 73, 25201. [Google Scholar] [CrossRef] [PubMed]
- Míguez, D.G.; Izús, G.; Muñuzuri, A. Robustness and stability of flow-and-diffusion structures. Phys. Rev. E 2006, 73, 016207. [Google Scholar] [CrossRef]
- Pierre Madl, P.R. Quantum Electrodynamics Coherence and Hormesis: Foundations of Quantum Biology. Int. J. Mol. Sci. 2023, 24, 14003. [Google Scholar] [CrossRef]
- Renati, P. Reframing Some Methods in Life Sciences: Relationship and Causation in Living Matter. Cut. Edge Res. Biol. 2023, 8, 127–194. [Google Scholar] [CrossRef]
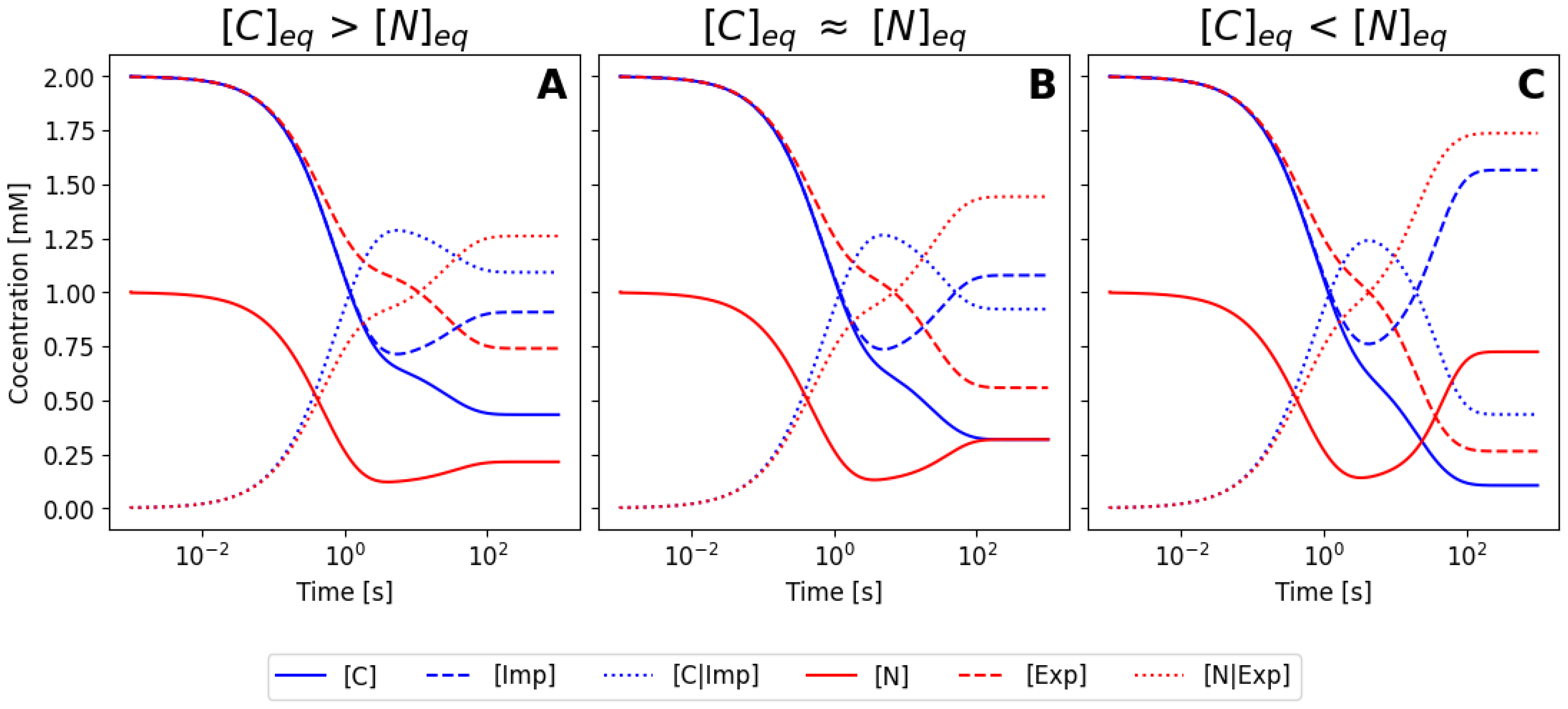
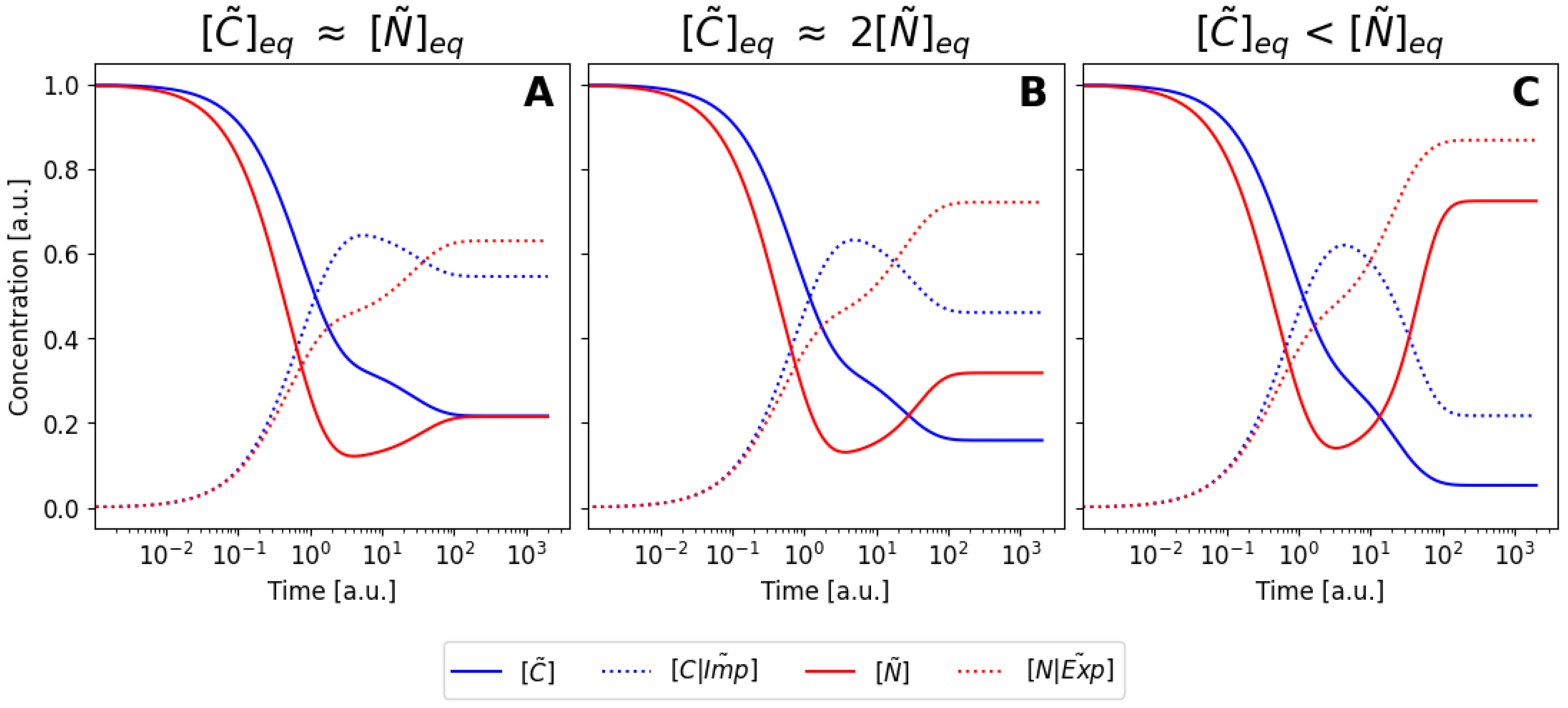

| Rate | Set 1 | Set 2 | Set 3 | Set 4 |
|---|---|---|---|---|
| 500 (M·s)−1 | 500 (M·s)−1 | 500 (M·s)−1 | 50 (M·s)−1 | |
| 0.15 s−1 | 0.15 s−1 | 0.15 s−1 | 1.5 s−1 | |
| 0.03 (M·s)−1 | 0.036 (M·s)−1 | 0.04 (M·s)−1 | 0.03 (M·s)−1 | |
| 1000 s−1 | 1000 s−1 | 1000 s−1 | 1 s−1 | |
| 0.1 s−1 | 0.1 s−1 | 0.1 s−1 | 0.3 s−1 | |
| 0.026 s−1 | 0.023 s−1 | 0.01 s−1 | 0.3 s−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fayad, A.N.; Mazo-Durán, D.; Míguez, D.G. Cellular Compartmentalization as a Physical Regulatory Mechanism of Signaling Pathways. Biophysica 2024, 4, 634-650. https://doi.org/10.3390/biophysica4040042
Fayad AN, Mazo-Durán D, Míguez DG. Cellular Compartmentalization as a Physical Regulatory Mechanism of Signaling Pathways. Biophysica. 2024; 4(4):634-650. https://doi.org/10.3390/biophysica4040042
Chicago/Turabian StyleFayad, Ahmed N., Diego Mazo-Durán, and David G. Míguez. 2024. "Cellular Compartmentalization as a Physical Regulatory Mechanism of Signaling Pathways" Biophysica 4, no. 4: 634-650. https://doi.org/10.3390/biophysica4040042
APA StyleFayad, A. N., Mazo-Durán, D., & Míguez, D. G. (2024). Cellular Compartmentalization as a Physical Regulatory Mechanism of Signaling Pathways. Biophysica, 4(4), 634-650. https://doi.org/10.3390/biophysica4040042







