Biophysical Modeling of Cardiac Cells: From Ion Channels to Tissue
Abstract
1. Introduction
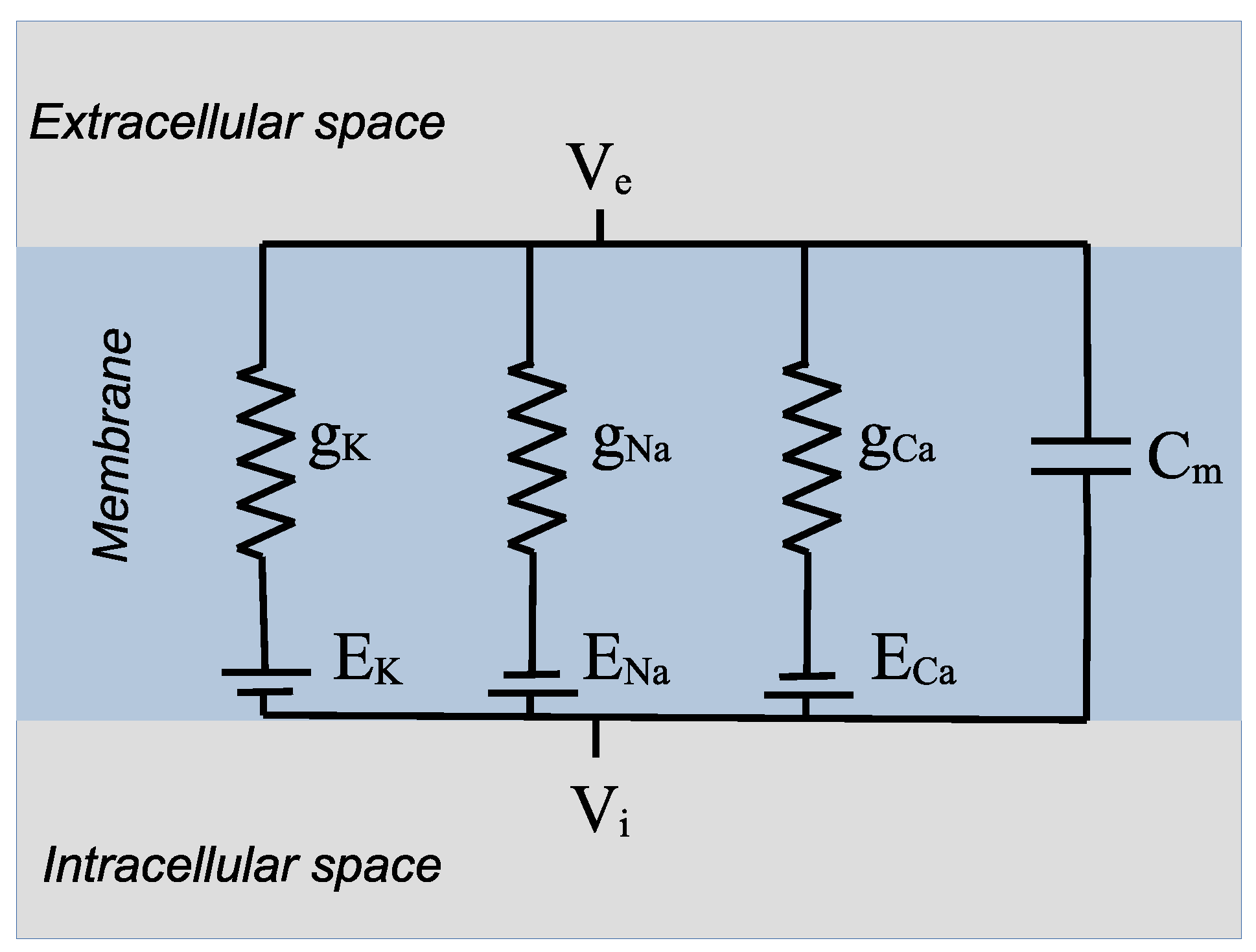
2. Description of Ion Channels
2.1. Sodium Channels
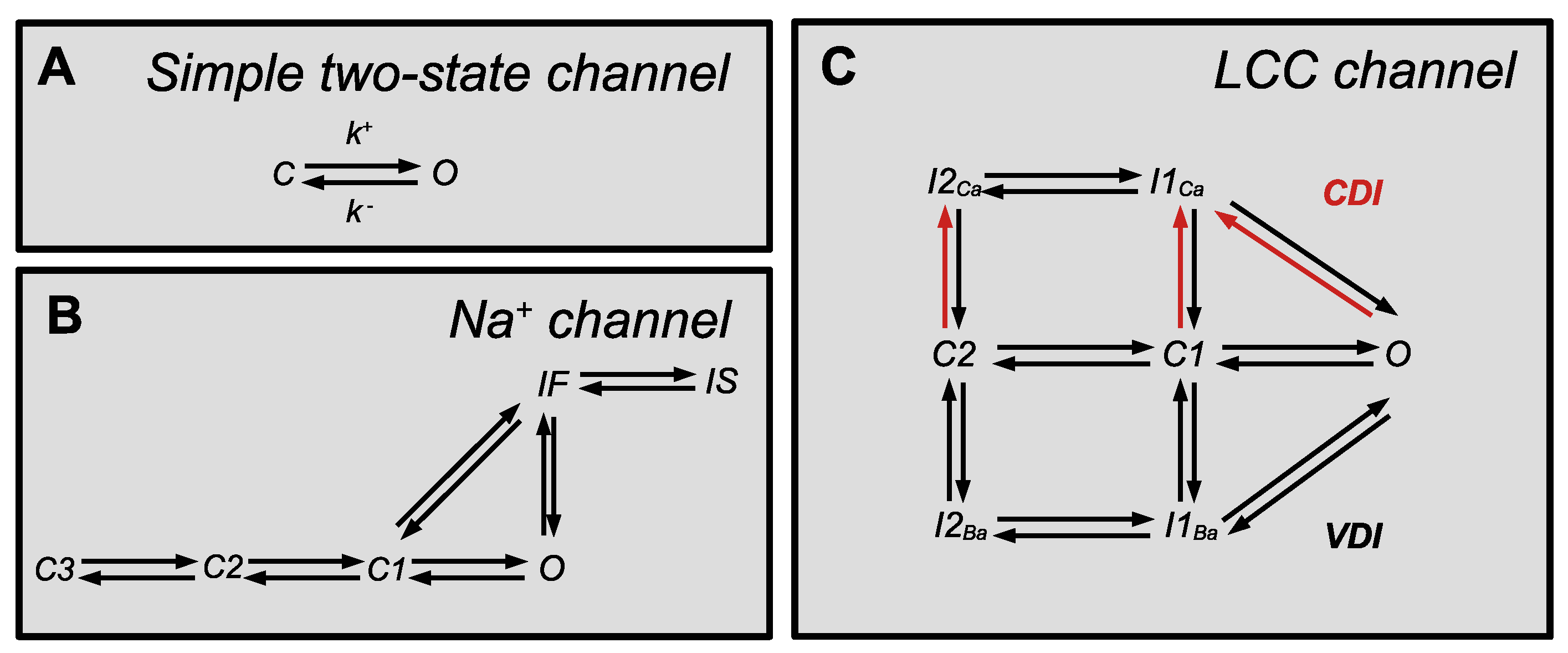
2.2. Potassium Channels
2.3. Calcium Channels
2.4. Pumps and Exchangers
3. Models of Intracellular Ca2+ Dynamics
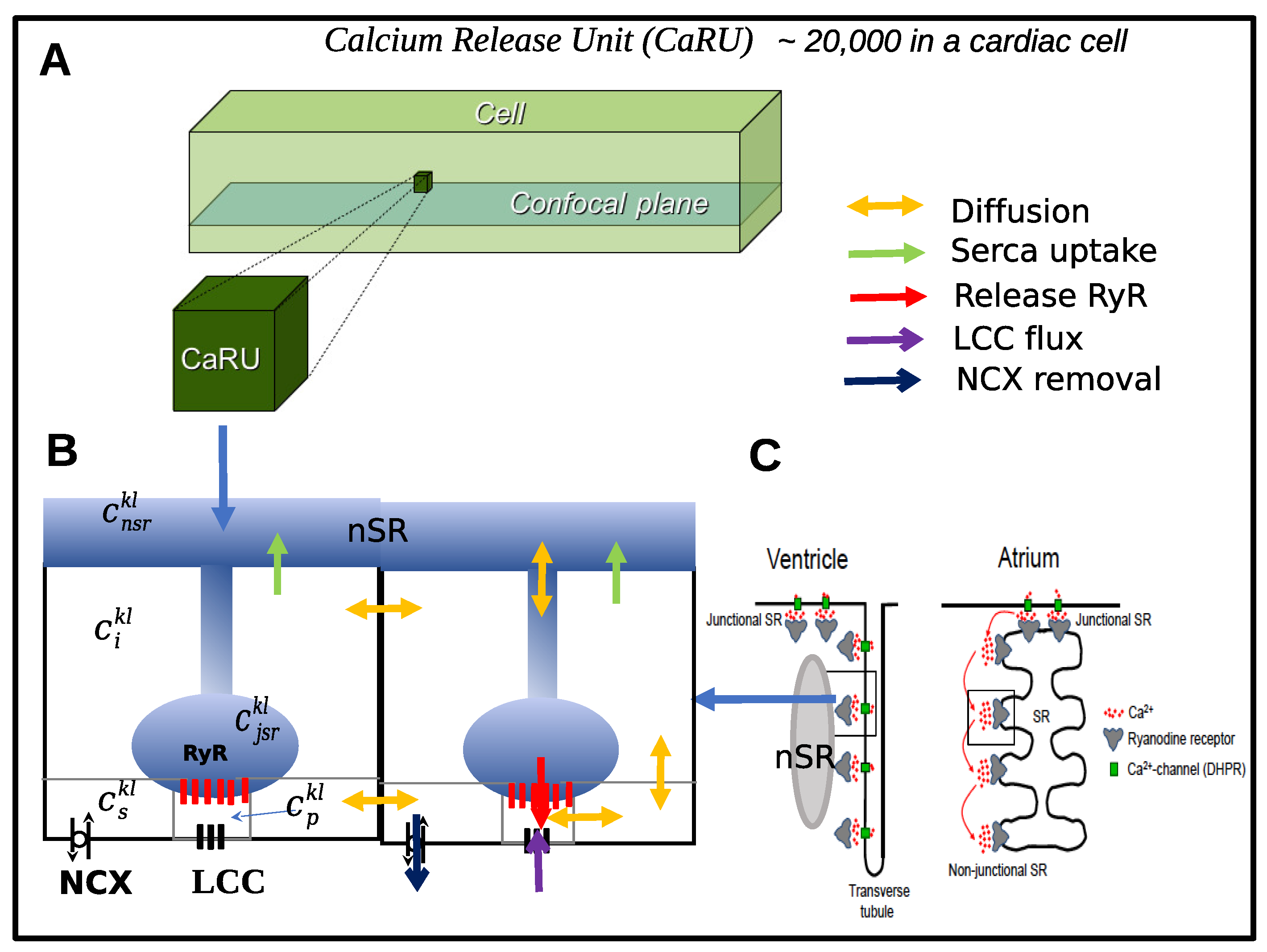
3.1. Models at the Submicron Scale
3.2. Models at the Micron Scale
3.3. Scaling-Up Subcellular Models
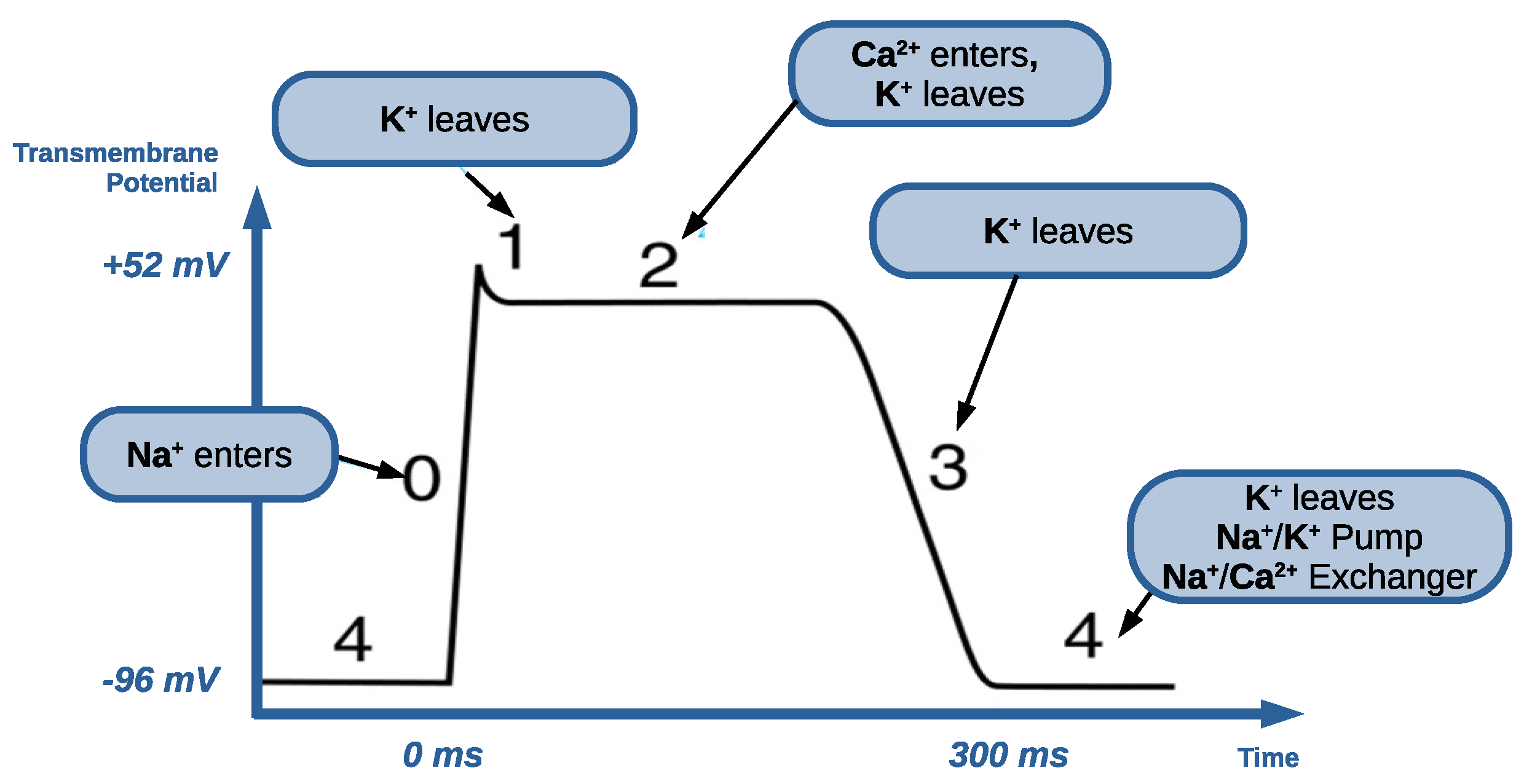
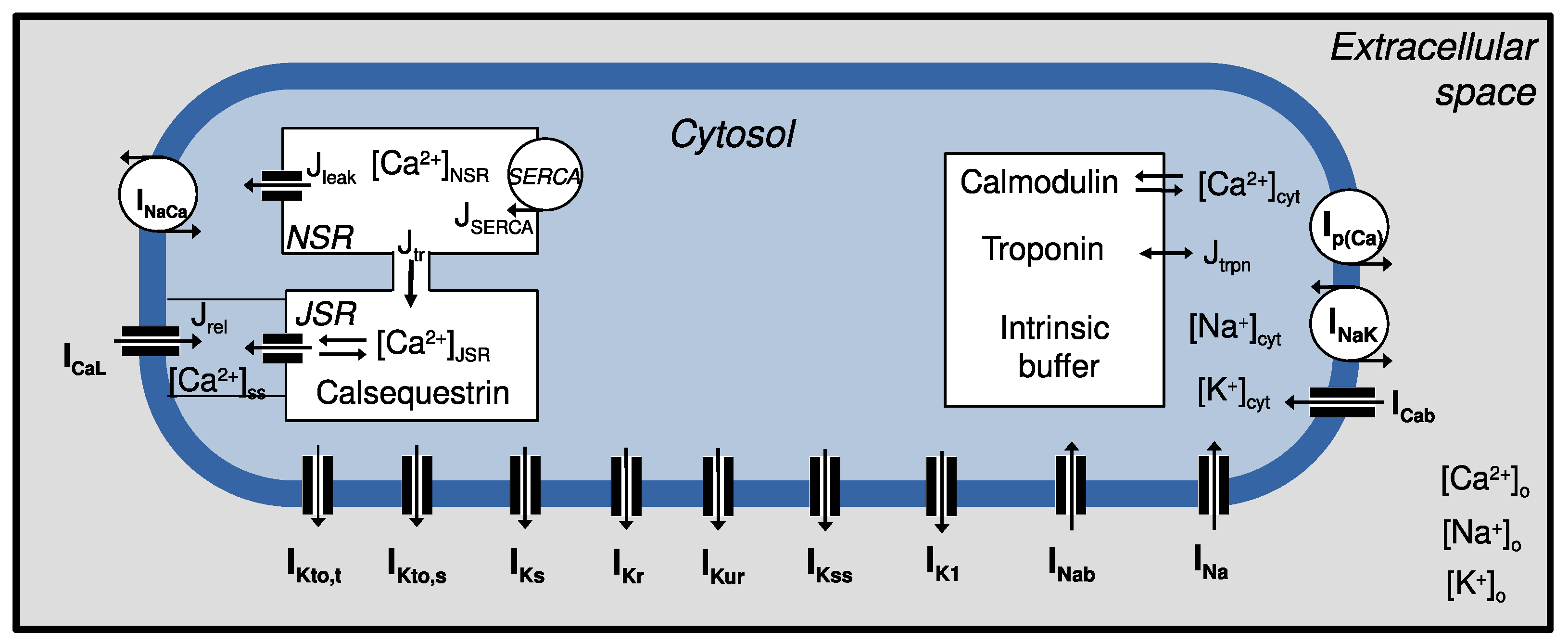
4. Cardiac Cell Models
4.1. Action Potential Dysfunctions
4.1.1. Channelopathies
4.1.2. EADs and DADs
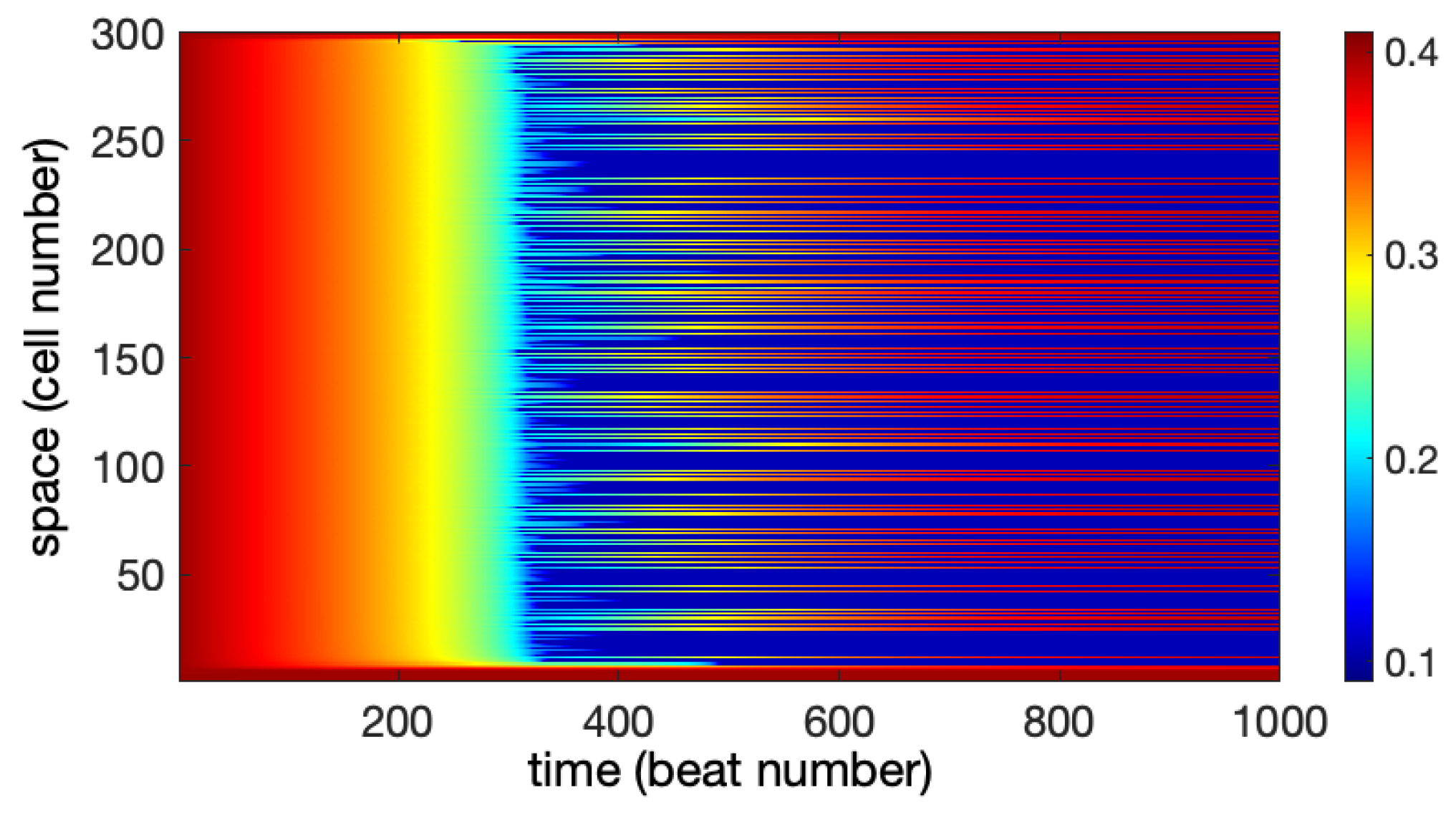
4.1.3. Alternans
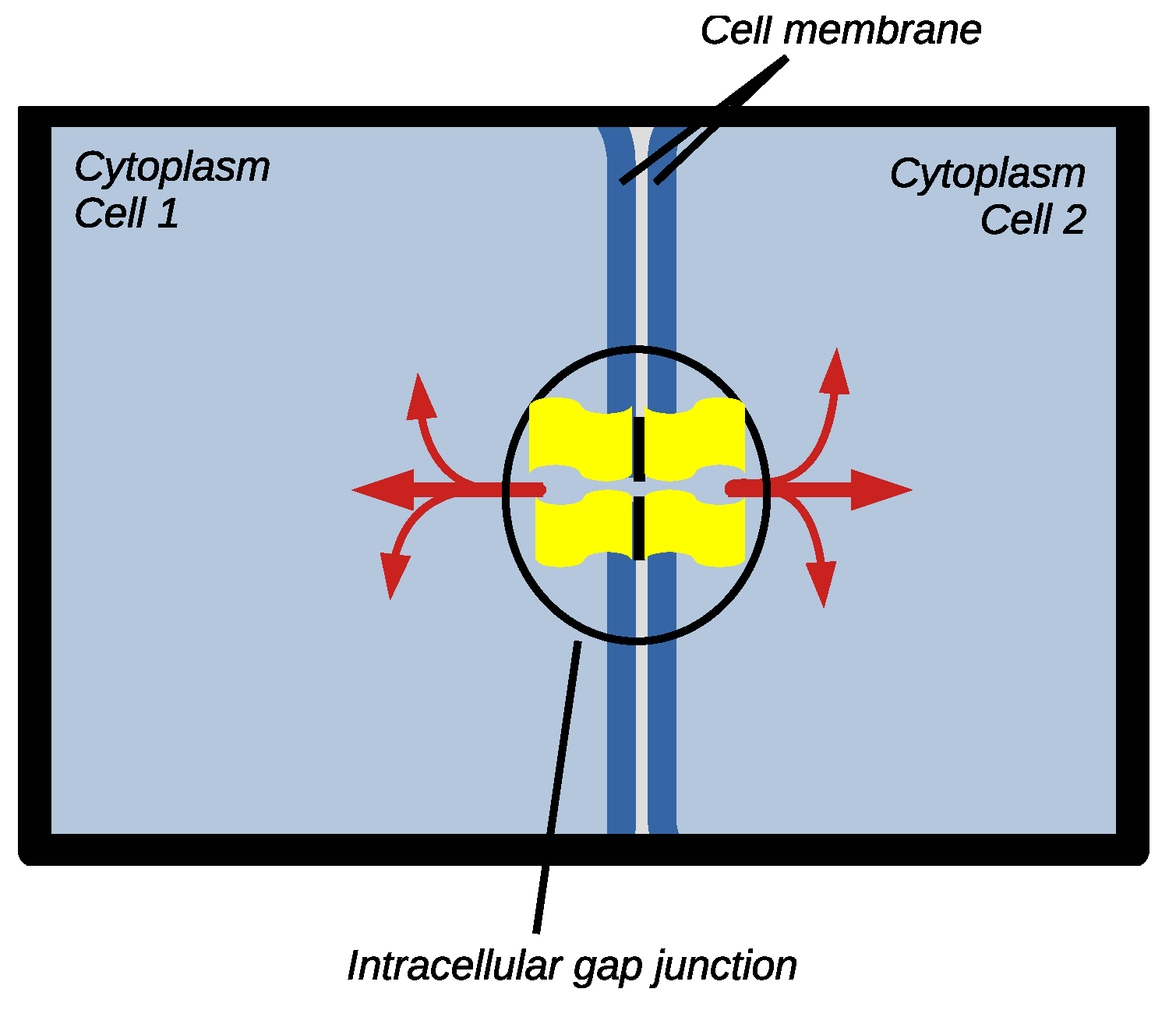
5. Intercellular Coupling
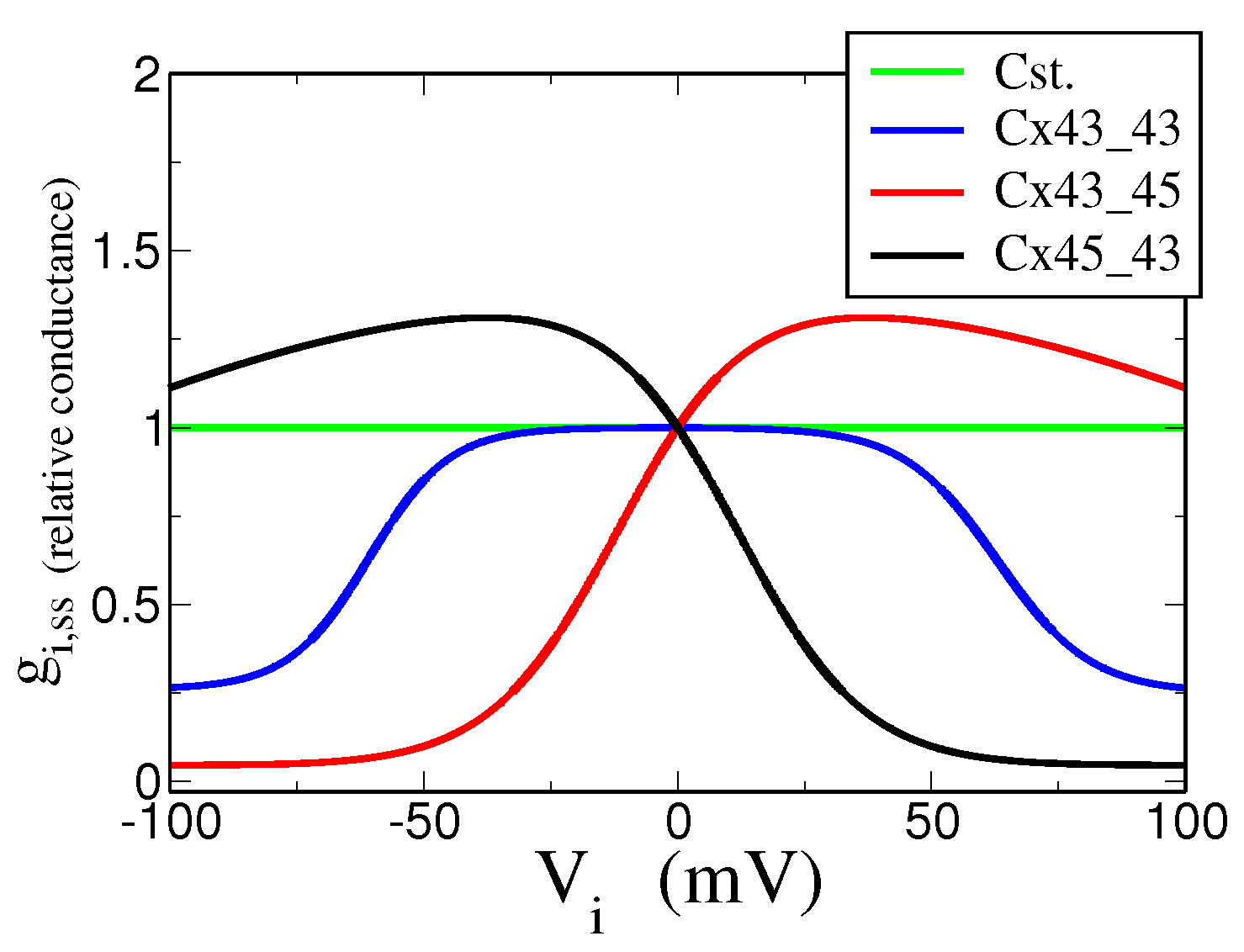
5.1. Experimental Data and Stochastic Model
5.2. Dynamical Model
5.3. Modeling Studies of GJ Dynamics in Cardiac Tissue
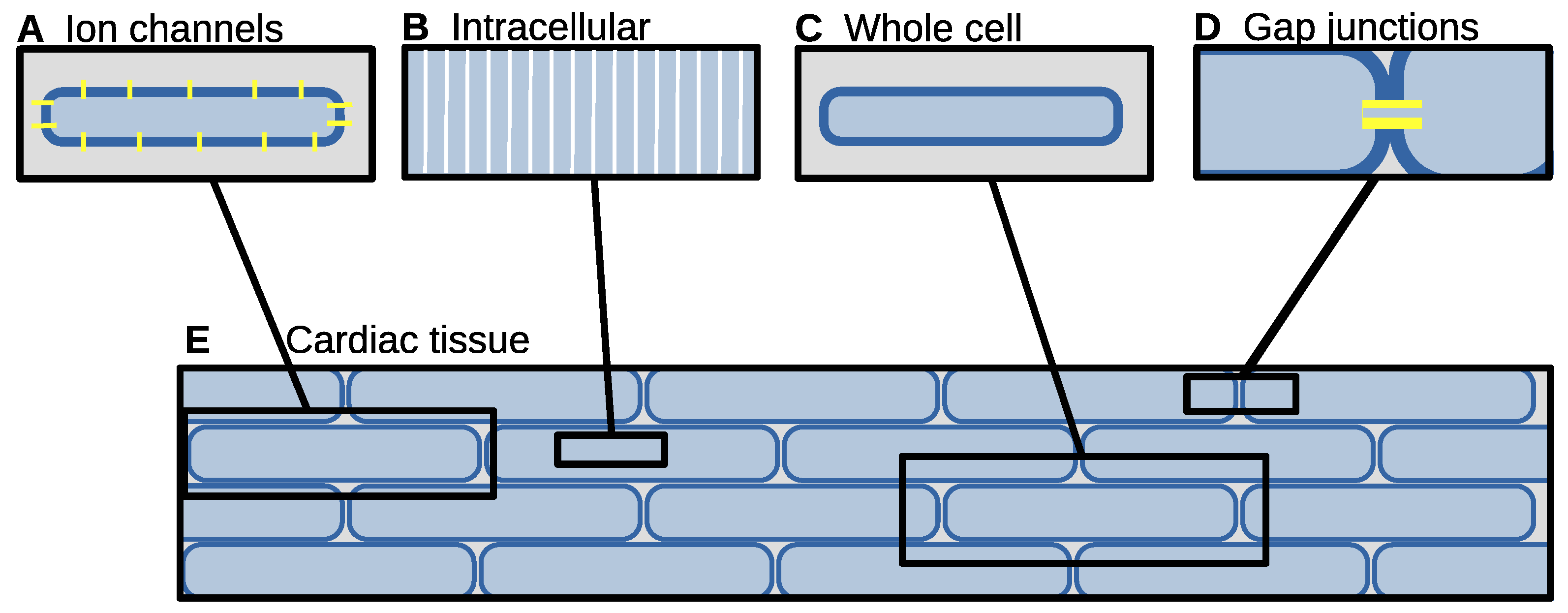
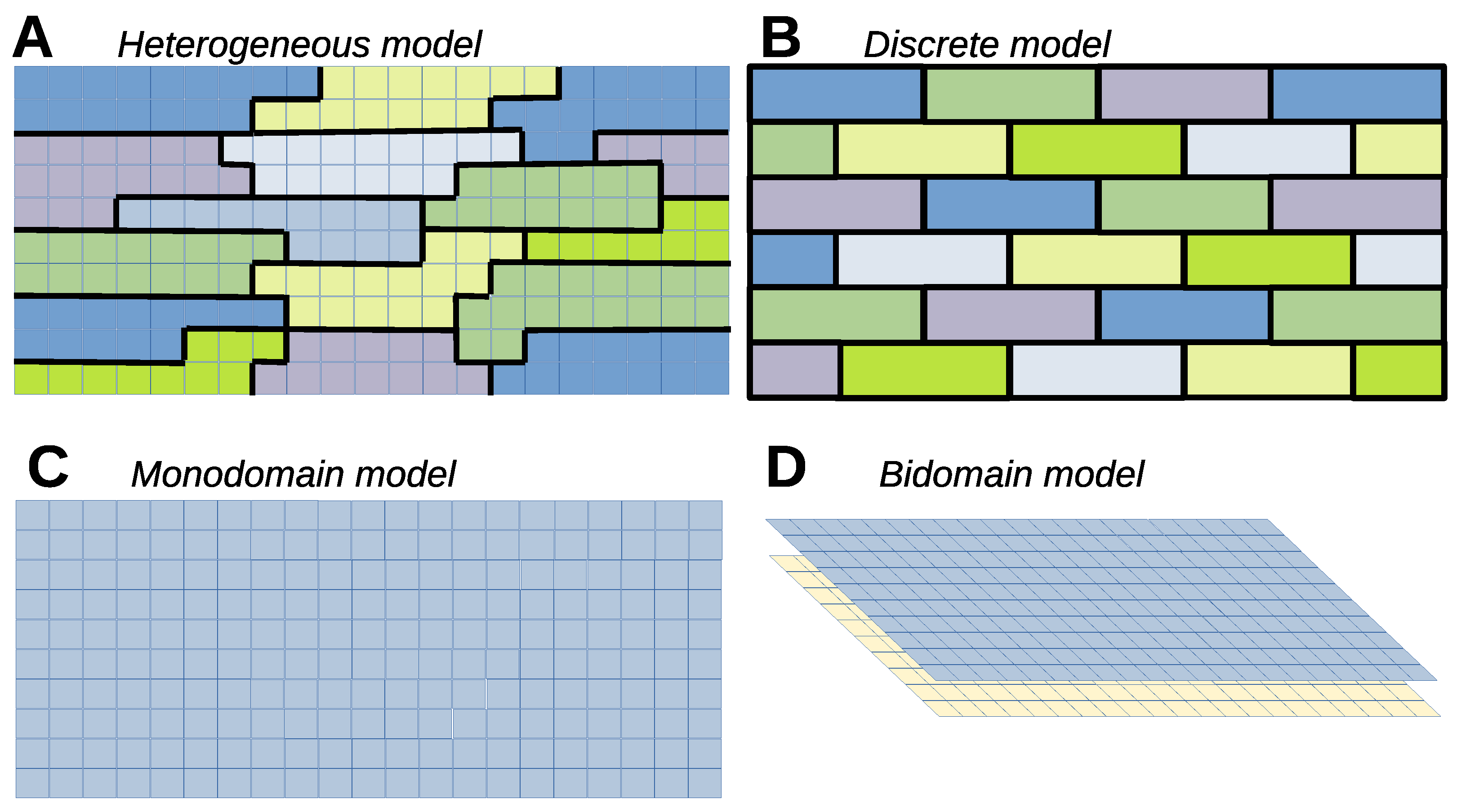
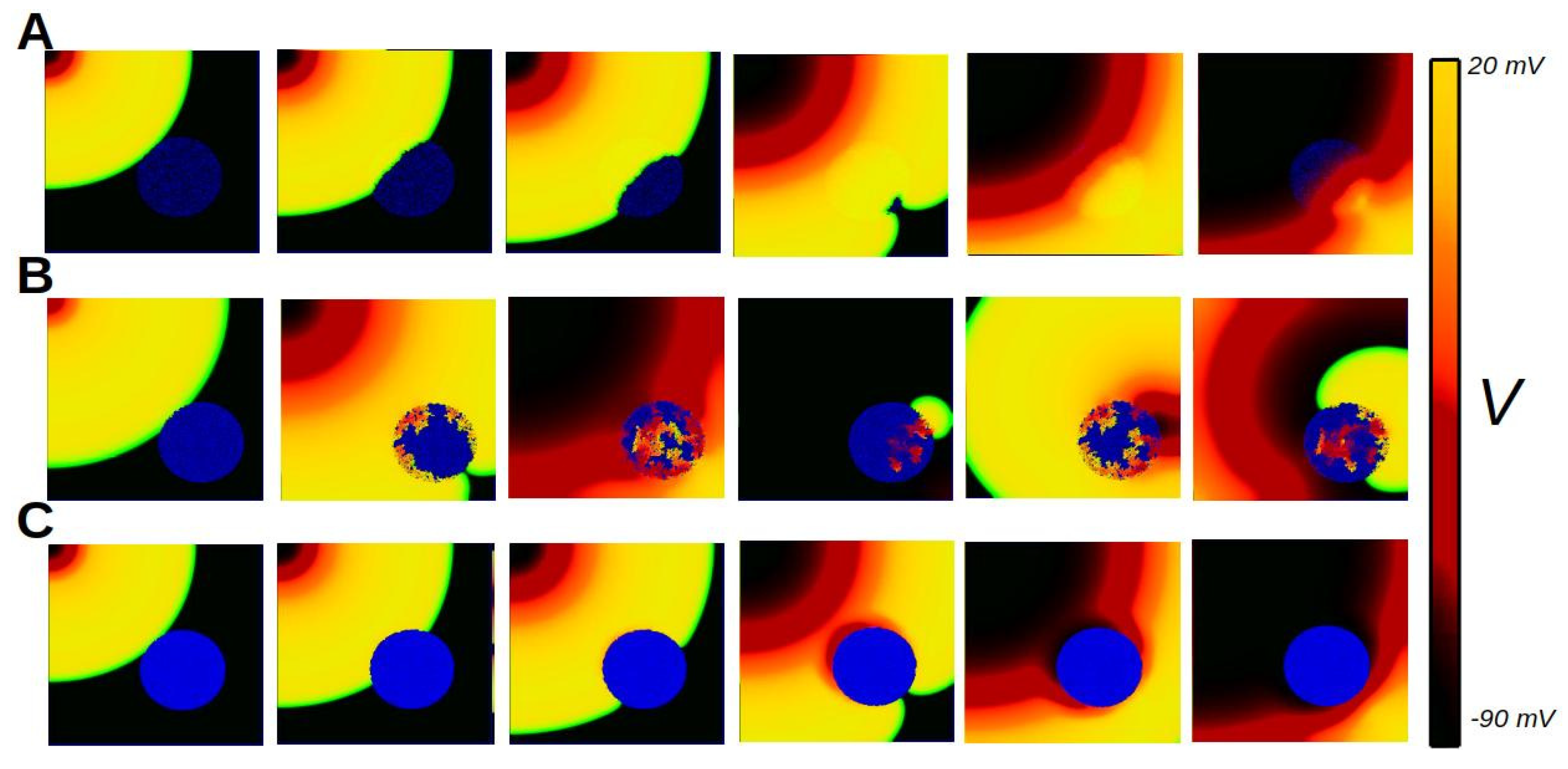
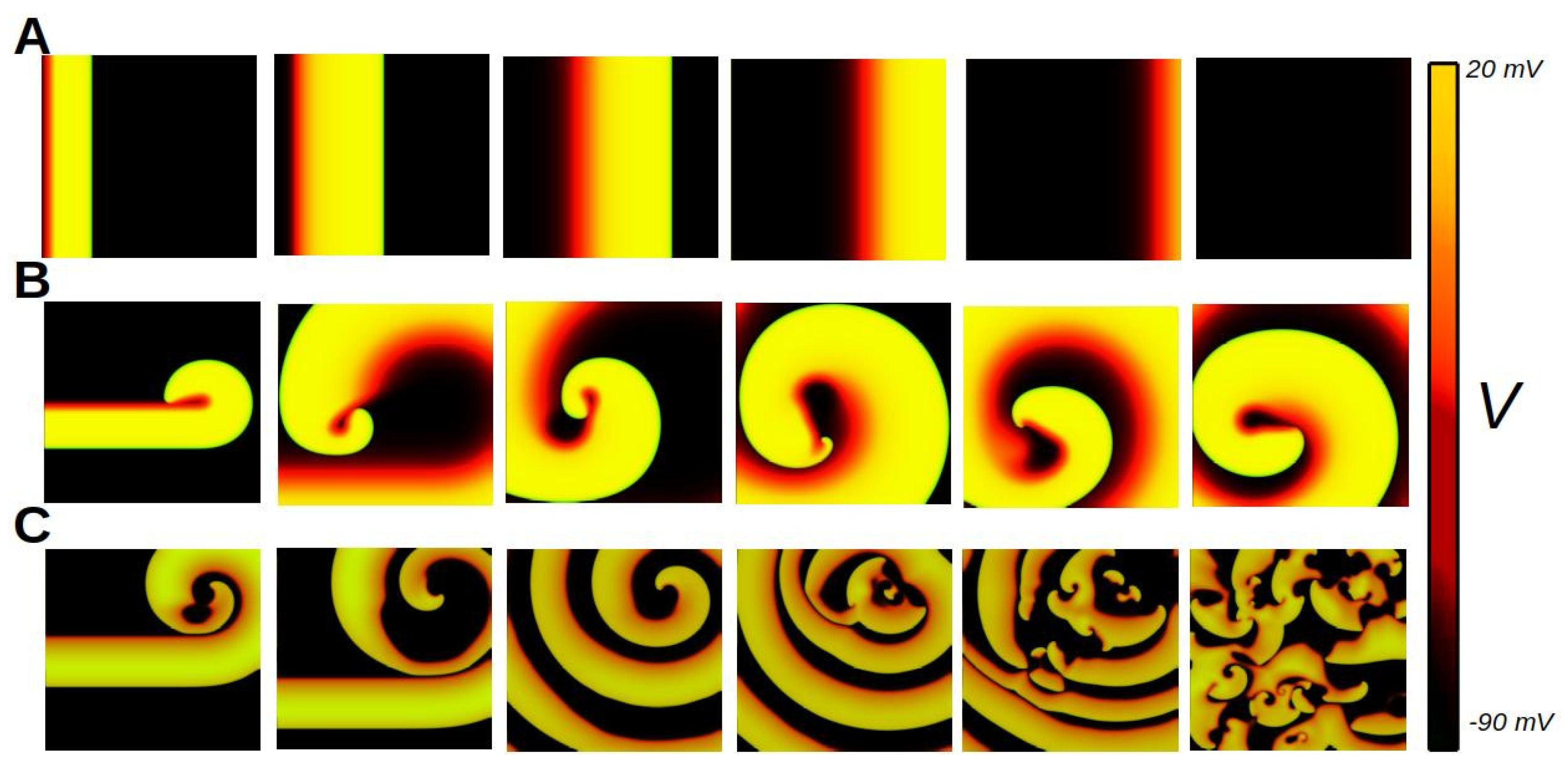
6. Biophysics of Cardiac Tissue
6.1. Heterogeneous Model
6.2. Heterogeneous Cell Model, Continuous Extracellular Potential
6.3. Discrete Model
6.4. Continuous Monodomain Model
6.5. Bidomain Model
6.6. Tridomain Model
6.7. Anisotropy of Cardiac Tissue
7. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lozano, R.; Naghavi, M.; Foreman, K.; Lim, S.; Shibuya, K.; Aboyans, V.; Abraham, J.; Adair, T.; Aggarwal, R.; Ahn, S.Y.; et al. Global and regional mortality from 235 causes of death for 20 age groups in 1990 and 2010: A systematic analysis for the Global Burden of Disease Study 2010. Lancet 2012, 380, 2095–2128. [Google Scholar] [CrossRef] [PubMed]
- Mathers, C.D.; Boerma, T.; Ma Fat, D. Global and regional causes of death. Br. Med. Bull. 2009, 92, 7–32. [Google Scholar] [CrossRef]
- Mendis, S.; Puska, P.; Norrving, B.E.; World Health Organization. Global Atlas on Cardiovascular Disease Prevention and Control; World Health Organization: Geneva, Switzerland, 2011. [Google Scholar]
- Timmis, A.; Aboyans, V.; Vardas, P.; Townsend, N.; Torbica, A.; Kavousi, M.; Boriani, G.; Huculeci, R.; Kazakiewicz, D.; Scherr, D.; et al. European society of cardiology: The 2023 atlas of cardiovascular disease statistics. Eur. Heart J. 2024, 45, 4019–4062. [Google Scholar] [CrossRef] [PubMed]
- Malmivuo, J.; Plonsey, R. Bioelectromagnetism: Principles and Applications of Bioelectric and Biomagnetic Fields; Oxford University Press: Oxford, MA, USA, 1995. [Google Scholar]
- Zipes, D.P.; Jalife, J.; Stevenson, W.G. Cardiac Electrophysiology: From Cell to Bedside E-Book; Elsevier Health Sciences: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Bigger, J.T., Jr.; Dresdale, R.J.; Heissenbuttel, R.H.; Weld, F.M.; Wit, A.L. Ventricular arrhythmias in ischemic heart disease: Mechanism, prevalence, significance, and management. Prog. Cardiovasc. Dis. 1977, 19, 255–300. [Google Scholar] [CrossRef] [PubMed]
- Arutunyan, A.; Swift, L.M.; Sarvazyan, N. Initiation and propagation of ectopic waves: Insights from an in vitro model of ischemia-reperfusion injury. Am. J. Physiol.-Heart Circ. Physiol. 2002, 283, H741–H749. [Google Scholar] [CrossRef] [PubMed]
- Clusin, W.T. Calcium and cardiac arrhythmias: DADs, EADs, and alternans. Crit. Rev. Clin. Lab. Sci. 2003, 40, 337–375. [Google Scholar] [CrossRef] [PubMed]
- Wehrens, X.H.; Lehnart, S.E.; Marks, A.R. Intracellular calcium release and cardiac disease. Annu. Rev. Physiol. 2005, 67, 69–98. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Liao, Z.; Grandi, E.; Shiferaw, Y.; Bers, D.M. Slow [Na] i changes and positive feedback between membrane potential and [Ca] i underlie intermittent early afterdepolarizations and arrhythmias. Circ. Arrhythmia Electrophysiol. 2015, 8, 1472–1480. [Google Scholar] [CrossRef]
- Oliveira, R.S.; Alonso, S.; Campos, F.O.; Rocha, B.M.; Fernandes, J.F.; Kuehne, T.; Dos Santos, R.W. Ectopic beats arise from micro-reentries near infarct regions in simulations of a patient-specific heart model. Sci. Rep. 2018, 8, 16392. [Google Scholar] [CrossRef]
- Arevalo, H.; Plank, G.; Helm, P.; Halperin, H.; Trayanova, N. Tachycardia in post-infarction hearts: Insights from 3D image-based ventricular models. PLoS ONE 2013, 8, e68872. [Google Scholar] [CrossRef]
- Trayanova, N. Defibrillation of the heart: Insights into mechanisms from modelling studies. Exp. Physiol. 2006, 91, 323–337. [Google Scholar] [CrossRef] [PubMed]
- Colman, M.A.; Alvarez-Lacalle, E.; Echebarria, B.; Sato, D.; Sutanto, H.; Heijman, J. Multi-scale computational modeling of spatial calcium handling from nanodomain to whole-heart: Overview and perspectives. Front. Physiol. 2022, 13, 836622. [Google Scholar] [CrossRef]
- Chen, W.; Wasserstrom, J.A.; Shiferaw, Y. Role of coupled gating between cardiac ryanodine receptors in the genesis of triggered arrhythmias. Am. J. Physiol.-Heart Circ. Physiol. 2009, 297, H171–H180. [Google Scholar] [CrossRef]
- Heijman, J.; Voigt, N.; Nattel, S.; Dobrev, D. Calcium handling and atrial fibrillation. Wien. Med. Wochenschr. 2012, 162, 287–291. [Google Scholar] [CrossRef] [PubMed]
- Hove-Madsen, L.; Llach, A.; Bayes-Genís, A.; Roura, S.; Font, E.R.; Arís, A.; Cinca, J. Atrial fibrillation is associated with increased spontaneous calcium release from the sarcoplasmic reticulum in human atrial myocytes. Circulation 2004, 110, 1358–1363. [Google Scholar] [CrossRef] [PubMed]
- Shiferaw, Y.; Aistrup, G.L.; Louch, W.E.; Wasserstrom, J. Remodeling promotes proarrhythmic disruption of calcium homeostasis in failing atrial myocytes. Biophys. J. 2020, 118, 476–491. [Google Scholar] [CrossRef] [PubMed]
- Niederer, S.A.; Lumens, J.; Trayanova, N.A. Computational models in cardiology. Nat. Rev. Cardiol. 2019, 16, 100–111. [Google Scholar] [CrossRef] [PubMed]
- Clayton, R.; Bernus, O.; Cherry, E.; Dierckx, H.; Fenton, F.H.; Mirabella, L.; Panfilov, A.V.; Sachse, F.B.; Seemann, G.; Zhang, H. Models of cardiac tissue electrophysiology: Progress, challenges and open questions. Prog. Biophys. Mol. Biol. 2011, 104, 22–48. [Google Scholar] [CrossRef]
- Rappel, W.J. The physics of heart rhythm disorders. Phys. Rep. 2022, 978, 1–45. [Google Scholar] [CrossRef] [PubMed]
- Karma, A. Physics of cardiac arrhythmogenesis. Annu. Rev. Condens. Matter Phys. 2013, 4, 313–337. [Google Scholar] [CrossRef]
- Alonso, S.; Bär, M.; Echebarria, B. Nonlinear physics of electrical wave propagation in the heart: A review. Rep. Prog. Phys. 2016, 79, 096601. [Google Scholar] [CrossRef] [PubMed]
- Beeler, G., Jr.; Reuter, H. Voltage clamp experiments on ventricular myocardial fibres. J. Physiol. 1970, 207, 165–190. [Google Scholar] [CrossRef] [PubMed]
- Deck, K.; Kern, R.; Trautwein, W. Voltage clamp technique in mammalian cardiac fibres. Pflüger’s Archiv für die gesamte Physiologie des Menschen und der Tiere 1964, 280, 50–62. [Google Scholar] [CrossRef]
- Bragard, J.R.; Camara, O.; Echebarria, B.; Giorda, L.G.; Pueyo, E.; Saiz, J.; Sebastian, R.; Soudah, E.; Vazquez, M. Cardiac computational modelling. Rev. Espa Nola De Cardiol. (Engl. Ed.) 2021, 74, 65–71. [Google Scholar] [CrossRef]
- Noble, D. Modeling the heart–from genes to cells to the whole organ. Science 2002, 295, 1678–1682. [Google Scholar] [CrossRef] [PubMed]
- Trayanova, N.A.; Rice, J.J. Cardiac electromechanical models: From cell to organ. Front. Physiol. 2011, 2, 43. [Google Scholar] [CrossRef] [PubMed]
- Qu, Z.; Garfinkel, A.; Weiss, J.N.; Nivala, M. Multi-scale modeling in biology: How to bridge the gaps between scales? Prog. Biophys. Mol. Biol. 2011, 107, 21–31. [Google Scholar] [CrossRef]
- Kekenes-Huskey, P.M.; Liao, T.; Gillette, A.K.; Hake, J.E.; Zhang, Y.; Michailova, A.P.; McCulloch, A.D.; McCammon, J.A. Molecular and subcellular-scale modeling of nucleotide diffusion in the cardiac myofilament lattice. Biophys. J. 2013, 105, 2130–2140. [Google Scholar] [CrossRef] [PubMed]
- McCulloch, A.D. Systems biophysics: Multiscale biophysical modeling of organ systems. Biophys. J. 2016, 110, 1023–1027. [Google Scholar] [CrossRef]
- Quarteroni, A.; Lassila, T.; Rossi, S.; Ruiz-Baier, R. Integrated heart—Coupling multiscale and multiphysics models for the simulation of the cardiac function. Comput. Methods Appl. Mech. Eng. 2017, 314, 345–407. [Google Scholar] [CrossRef]
- Chabiniok, R.; Wang, V.Y.; Hadjicharalambous, M.; Asner, L.; Lee, J.; Sermesant, M.; Kuhl, E.; Young, A.A.; Moireau, P.; Nash, M.P.; et al. Multiphysics and multiscale modelling, data–model fusion and integration of organ physiology in the clinic: Ventricular cardiac mechanics. Interface Focus 2016, 6, 20150083. [Google Scholar] [CrossRef]
- Keynes, R.D.; Aidley, D.J.; Huang, C.L.H. Nerve and Muscle; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Keener, J.; Sneyd, J. Mathematical Physiology; Springer: New York, NY, USA, 1998. [Google Scholar]
- Sachse, F.B. Computational Cardiology: Modeling of Anatomy, Electrophysiology, and Mechanics; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Winfree, A. A spatial scale factor for electrophysiological models of myocardium. Prog. Biophys. Mol. Biol. 1998, 69, 185–203. [Google Scholar] [CrossRef] [PubMed]
- Lawley, S.D.; Keener, J.P. Electrodiffusive flux through a stochastically gated ion channel. SIAM J. Appl. Math. 2019, 79, 551–571. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500. [Google Scholar] [CrossRef] [PubMed]
- Keener, J.P. Invariant manifold reductions for Markovian ion channel dynamics. J. Math. Biol. 2009, 58, 447–457. [Google Scholar] [CrossRef]
- Smith, G.D. Modeling the stochastic gating of ion channels. In Computational Cell Biology; Springer: Berlin/Heidelberg, Germany, 2002; pp. 285–319. [Google Scholar]
- Schmandt, N.T.; Galán, R.F. Stochastic-Shielding Approximation of Markov Chains and Its Application to Efficiently Simulate Random Ion-Channel Gating. Phys. Rev. Lett. 2012, 109, 118101. [Google Scholar] [CrossRef] [PubMed]
- Anderson, D.F.; Ermentrout, B.; Thomas, P.J. Stochastic representations of ion channel kinetics and exact stochastic simulation of neuronal dynamics. J. Comput. Neurosci. 2015, 38, 67–82. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Ramírez-Piscina, L.; Sancho, J.M. Physical properties of voltage gated pores. Eur. Phys. J. B 2018, 91, 1–9. [Google Scholar] [CrossRef]
- Ramírez-Piscina, L. Subconductance states in a semimicroscopic model for a tetrameric pore. Phys. Rev. E 2024, 109, 044402. [Google Scholar] [CrossRef] [PubMed]
- Maffeo, C.; Bhattacharya, S.; Yoo, J.; Wells, D.; Aksimentiev, A. Modeling and simulation of ion channels. Chem. Rev. 2012, 112, 6250–6284. [Google Scholar] [CrossRef] [PubMed]
- Beeler, G.W.; Reuter, H. Reconstruction of the action potential of ventricular myocardial fibres. J. Physiol. 1977, 268, 177–210. [Google Scholar] [CrossRef]
- Luo, C.H.; Rudy, Y. A model of the ventricular cardiac action potential. Depolarization, repolarization, and their interaction. Circ. Res. 1991, 68, 1501–1526. [Google Scholar] [CrossRef] [PubMed]
- Clancy, C.E.; Rudy, Y. Linking a genetic defect to its cellular phenotype in a cardiac arrhythmia. Nature 1999, 400, 566–569. [Google Scholar] [CrossRef]
- Clancy, C.E.; Rudy, Y. Na+ channel mutation that causes both Brugada and long-QT syndrome phenotypes: A simulation study of mechanism. Circulation 2002, 105, 1208–1213. [Google Scholar] [CrossRef] [PubMed]
- Mahajan, A.; Shiferaw, Y.; Sato, D.; Baher, A.; Olcese, R.; Xie, L.H.; Yang, M.J.; Chen, P.S.; Restrepo, J.G.; Karma, A.; et al. A rabbit ventricular action potential model replicating cardiac dynamics at rapid heart rates. Biophys. J. 2008, 94, 392–410. [Google Scholar] [CrossRef]
- Zhang, X.D.; Lieu, D.K.; Chiamvimonvat, N. Small-conductance Ca2+-activated K+ channels and cardiac arrhythmias. Heart Rhythm 2015, 12, 1845–1851. [Google Scholar] [CrossRef] [PubMed]
- Sato, D.; Dixon, R.E.; Santana, L.F.; Navedo, M.F. A model for cooperative gating of L-type Ca2+ channels and its effects on cardiac alternans dynamics. PLoS Comput. Biol. 2018, 14, e1005906. [Google Scholar] [CrossRef]
- Novaes, G.M.; Alvarez-Lacalle, E.; Muñoz, S.A.; Dos Santos, R.W. An ensemble of parameters from a robust Markov-based model reproduces L-type calcium currents from different human cardiac myocytes. PLoS ONE 2022, 17, e0266233. [Google Scholar] [CrossRef] [PubMed]
- Mullins, L. A mechanism for Na/Ca transport. J. Gen. Physiol. 1977, 70, 681–695. [Google Scholar] [CrossRef]
- Chu, L.; Greenstein, J.L.; Winslow, R.L. Modeling Na+-Ca2+ exchange in the heart: Allosteric activation, spatial localization, sparks and excitation-contraction coupling. J. Mol. Cell. Cardiol. 2016, 99, 174–187. [Google Scholar] [CrossRef]
- Campbell, A.K. Intracellular Calcium; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Hancock, J.T. Cell Signalling; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Bers, D. Excitation-Contraction Coupling and Cardiac Contractile Force; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; Volume 237. [Google Scholar]
- Kaestner, L. Calcium Signalling: Approaches and Findings in the Heart and Blood; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Parmacek, M.S.; Solaro, R.J. Biology of the troponin complex in cardiac myocytes. Prog. Cardiovasc. Dis. 2004, 47, 159–176. [Google Scholar] [CrossRef] [PubMed]
- Dibb, K.; Graham, H.; Venetucci, L.; Eisner, D.; Trafford, A. Analysis of cellular calcium fluxes in cardiac muscle to understand calcium homeostasis in the heart. Cell Calcium 2007, 42, 503–512. [Google Scholar] [CrossRef]
- Conesa, D.; Echebarria, B.; Peñaranda, A.; Cantalapiedra, I.R.; Shiferaw, Y.; Alvarez-Lacalle, E. Two-variable nullcline analysis of ionic general equilibrium predicts calcium homeostasis in ventricular myocytes. PLoS Comput. Biol. 2020, 16, e1007572. [Google Scholar] [CrossRef] [PubMed]
- Soeller, C.; Crossman, D.; Gilbert, R.; Cannell, M.B. Analysis of ryanodine receptor clusters in rat and human cardiac myocytes. Proc. Natl. Acad. Sci. USA 2007, 104, 14958–14963. [Google Scholar] [CrossRef]
- Hou, Y.; Bai, J.; Shen, X.; de Langen, O.; Li, A.; Lal, S.; Dos Remedios, C.G.; Baddeley, D.; Ruygrok, P.N.; Soeller, C.; et al. Nanoscale organisation of ryanodine receptors and junctophilin-2 in the failing human heart. Front. Physiol. 2021, 12, 724372. [Google Scholar] [CrossRef]
- Baddeley, D.; Jayasinghe, I.; Lam, L.; Rossberger, S.; Cannell, M.B.; Soeller, C. Optical single-channel resolution imaging of the ryanodine receptor distribution in rat cardiac myocytes. Proc. Natl. Acad. Sci. USA 2009, 106, 22275–22280. [Google Scholar] [CrossRef]
- Sheard, T.M.; Hurley, M.E.; Colyer, J.; White, E.; Norman, R.; Pervolaraki, E.; Narayanasamy, K.K.; Hou, Y.; Kirton, H.M.; Yang, Z.; et al. Three-dimensional and chemical mapping of intracellular signaling nanodomains in health and disease with enhanced expansion microscopy. ACS Nano 2019, 13, 2143–2157. [Google Scholar] [CrossRef]
- Chen, H.; Valle, G.; Furlan, S.; Nani, A.; Gyorke, S.; Fill, M.; Volpe, P. Mechanism of calsequestrin regulation of single cardiac ryanodine receptor in normal and pathological conditions. J. Gen. Physiol. 2013, 142, 127–136. [Google Scholar] [CrossRef]
- Wei, J.; Yao, J.; Belke, D.; Guo, W.; Zhong, X.; Sun, B.; Wang, R.; Paul Estillore, J.; Vallmitjana, A.; Benitez, R.; et al. Ca2+-CaM dependent inactivation of RyR2 underlies Ca2+ alternans in intact heart. Circ. Res. 2021, 128, e63–e83. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Tian, X.; Wang, R.; Fill, M.; Chen, S.W. Abnormal termination of Ca2+ release is a common defect of RyR2 mutations associated with cardiomyopathies. Circ. Res. 2012, 110, 968–977. [Google Scholar] [CrossRef] [PubMed]
- Cannell, M.B.; Kong, C.H. Local control in cardiac E–C coupling. J. Mol. Cell. Cardiol. 2012, 52, 298–303. [Google Scholar] [CrossRef] [PubMed]
- Van Petegem, F. Ryanodine receptors: Structure and function. J. Biol. Chem. 2012, 287, 31624–31632. [Google Scholar] [CrossRef] [PubMed]
- Sheard, T.M.; Hurley, M.E.; Smith, A.J.; Colyer, J.; White, E.; Jayasinghe, I. Three-dimensional visualization of the cardiac ryanodine receptor clusters and the molecular-scale fraying of dyads. Philos. Trans. R. Soc. B 2022, 377, 20210316. [Google Scholar] [CrossRef]
- Maleckar, M.M.; Edwards, A.G.; Louch, W.E.; Lines, G.T. Studying dyadic structure–function relationships: A review of current modeling approaches and new insights into Ca2+ (mis) handling. Clin. Med. Insights Cardiol. 2017, 11, 1179546817698602. [Google Scholar] [CrossRef] [PubMed]
- Hong, T.; Shaw, R.M. Cardiac T-tubule microanatomy and function. Physiol. Rev. 2017, 97, 227–252. [Google Scholar] [CrossRef] [PubMed]
- Richards, M.A.; Clarke, J.D.; Saravanan, P.; Voigt, N.; Dobrev, D.; Eisner, D.A.; Trafford, A.W.; Dibb, K.M. Transverse tubules are a common feature in large mammalian atrial myocytes including human. Am. J. Physiol.-Heart Circ. Physiol. 2011, 301, H1996–H2005. [Google Scholar] [CrossRef] [PubMed]
- Benitah, J.P.; Perrier, R.; Mercadier, J.J.; Pereira, L.; Gómez, A.M. RyR2 and calcium release in heart failure. Front. Physiol. 2021, 12, 734210. [Google Scholar] [CrossRef] [PubMed]
- Marchena, M.; Echebarria, B. Computational model of calcium signaling in cardiac atrial cells at the submicron scale. Front. Physiol. 2018, 9, 1760. [Google Scholar] [CrossRef]
- Marchena, M.; Echebarria, B. Influence of the tubular network on the characteristics of calcium transients in cardiac myocytes. PLoS ONE 2020, 15, e0231056. [Google Scholar] [CrossRef] [PubMed]
- Marchena, M.; Echebarria, B.; Shiferaw, Y.; Alvarez-Lacalle, E. Buffering and total calcium levels determine the presence of oscillatory regimes in cardiac cells. PLoS Comput. Biol. 2020, 16, e1007728. [Google Scholar] [CrossRef] [PubMed]
- Falcke, M. On the role of stochastic channel behavior in intracellular Ca2+ dynamics. Biophys. J. 2003, 84, 42–56. [Google Scholar] [CrossRef] [PubMed]
- Weber, C.R.; Piacentino III, V.; Ginsburg, K.S.; Houser, S.R.; Bers, D.M. Na+-Ca2+ exchange current and submembrane [Ca2+] during the cardiac action potential. Circ. Res. 2002, 90, 182–189. [Google Scholar] [CrossRef]
- Chen, W.; Aistrup, G.; Wasserstrom, J.A.; Shiferaw, Y. A mathematical model of spontaneous calcium release in cardiac myocytes. Am. J. Physiol.-Heart Circ. Physiol. 2011, 300, H1794–H1805. [Google Scholar] [CrossRef] [PubMed]
- Colman, M.A.; Pinali, C.; Trafford, A.W.; Zhang, H.; Kitmitto, A. A computational model of spatio-temporal cardiac intracellular calcium handling with realistic structure and spatial flux distribution from sarcoplasmic reticulum and t-tubule reconstructions. PLoS Comput. Biol. 2017, 13, e1005714. [Google Scholar] [CrossRef] [PubMed]
- Nivala, M.; de Lange, E.; Rovetti, R.; Qu, Z. Computational modeling and numerical methods for spatiotemporal calcium cycling in ventricular myocytes. Front. Physiol. 2012, 3, 114. [Google Scholar] [CrossRef] [PubMed]
- Sutanto, H.; Van Sloun, B.; Schönleitner, P.; Van Zandvoort, M.A.; Antoons, G.; Heijman, J. The subcellular distribution of ryanodine receptors and L-type Ca2+ channels modulates Ca2+-transient properties and spontaneous Ca2+-release events in atrial cardiomyocytes. Front. Physiol. 2018, 9, 1108. [Google Scholar] [CrossRef] [PubMed]
- Noble, D. A modification of the Hodgkin—Huxley equations applicable to Purkinje fibre action and pacemaker potentials. J. Physiol. 1962, 160, 317. [Google Scholar] [CrossRef] [PubMed]
- Luo, C.h.; Rudy, Y. A dynamic model of the cardiac ventricular action potential. I. Simulations of ionic currents and concentration changes. Circ. Res. 1994, 74, 1071–1096. [Google Scholar] [CrossRef] [PubMed]
- Winslow, R.L.; Rice, J.; Jafri, S.; Marban, E.; O’Rourke, B. Mechanisms of altered excitation-contraction coupling in canine tachycardia-induced heart failure, II: Model studies. Circ. Res. 1999, 84, 571–586. [Google Scholar] [CrossRef]
- Shannon, T.R.; Wang, F.; Puglisi, J.; Weber, C.; Bers, D.M. A mathematical treatment of integrated Ca dynamics within the ventricular myocyte. Biophys. J. 2004, 87, 3351–3371. [Google Scholar] [CrossRef] [PubMed]
- Bondarenko, V.E.; Szigeti, G.P.; Bett, G.C.; Kim, S.J.; Rasmusson, R.L. Computer model of action potential of mouse ventricular myocytes. Am. J. Physiol.-Heart Circ. Physiol. 2004, 287, H1378–H1403. [Google Scholar] [CrossRef] [PubMed]
- Priebe, L.; Beuckelmann, D.J. Simulation study of cellular electric properties in heart failure. Circ. Res. 1998, 82, 1206–1223. [Google Scholar] [CrossRef]
- Ten Tusscher, K.H.; Noble, D.; Noble, P.J.; Panfilov, A.V. A model for human ventricular tissue. Am. J. Physiol.-Heart Circ. Physiol. 2004, 286, H1573–H1589. [Google Scholar] [CrossRef] [PubMed]
- Iyer, V.; Mazhari, R.; Winslow, R.L. A computational model of the human left-ventricular epicardial myocyte. Biophys. J. 2004, 87, 1507–1525. [Google Scholar] [CrossRef] [PubMed]
- Nygren, A.; Fiset, C.; Firek, L.; Clark, J.W.; Lindblad, D.S.; Clark, R.B.; Giles, W.R. Mathematical model of an adult human atrial cell: The role of K+ currents in repolarization. Circ. Res. 1998, 82, 63–81. [Google Scholar] [CrossRef] [PubMed]
- Courtemanche, M.; Ramirez, R.J.; Nattel, S. Ionic mechanisms underlying human atrial action potential properties: Insights from a mathematical model. Am. J. Physiol.-Heart Circ. Physiol. 1998, 275, H301–H321. [Google Scholar] [CrossRef] [PubMed]
- Noble, D.; Noble, S. A model of sino-atrial node electrical activity based on a modification of the DiFrancesco-Noble (1984) equations. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1984, 222, 295–304. [Google Scholar]
- Walker, M.A.; Gurev, V.; Rice, J.J.; Greenstein, J.L.; Winslow, R.L. Estimating the probabilities of rare arrhythmic events in multiscale computational models of cardiac cells and tissue. PLoS Comput. Biol. 2017, 13, e1005783. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Ni, H.; Morotti, S.; Smith, C.E.; Sato, D.; Louch, W.E.; Edwards, A.G.; Grandi, E. Mechanisms of spontaneous Ca2+ release-mediated arrhythmia in a novel 3D human atrial myocyte model: I. Transverse-axial tubule variation. J. Physiol. 2023, 601, 2655–2683. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.B.; de Lange, E.; Garfinkel, A.; Weiss, J.N.; Qu, Z. Delayed afterdepolarizations generate both triggers and a vulnerable substrate promoting reentry in cardiac tissue. Heart Rhythm 2015, 12, 2115–2124. [Google Scholar] [CrossRef] [PubMed]
- Colman, M.A.; Perez Alday, E.A.; Holden, A.V.; Benson, A.P. Trigger vs. substrate: Multi-dimensional modulation of QT-prolongation associated arrhythmic dynamics by a hERG channel activator. Front. Physiol. 2017, 8, 757. [Google Scholar] [CrossRef]
- Williams, G.S.; Huertas, M.A.; Sobie, E.A.; Jafri, M.S.; Smith, G.D. A probability density approach to modeling local control of calcium-induced calcium release in cardiac myocytes. Biophys. J. 2007, 92, 2311–2328. [Google Scholar] [CrossRef]
- Fenton, F.; Karma, A. Vortex dynamics in three-dimensional continuous myocardium with fiber rotation: Filament instability and fibrillation. Chaos Interdiscip. J. Nonlinear Sci. 1998, 8, 20–47. [Google Scholar] [CrossRef] [PubMed]
- Bueno-Orovio, A.; Cherry, E.M.; Fenton, F.H. Minimal model for human ventricular action potentials in tissue. J. Theor. Biol. 2008, 253, 544–560. [Google Scholar] [CrossRef] [PubMed]
- Peñaranda, A.; Cantalapiedra, I.R.; Bragard, J.; Echebarria, B. Cardiac dynamics: A simplified model for action potential propagation. Theor. Biol. Med Model. 2012, 9, 1–18. [Google Scholar] [CrossRef]
- Aliev, R.R.; Panfilov, A.V. A simple two-variable model of cardiac excitation. Chaos Solitons Fractals 1996, 7, 293–301. [Google Scholar] [CrossRef]
- Karma, A. Spiral breakup in model equations of action potential propagation in cardiac tissue. Phys. Rev. Lett. 1993, 71, 1103. [Google Scholar] [CrossRef]
- Mitchell, C.C.; Schaeffer, D.G. A two-current model for the dynamics of cardiac membrane. Bull. Math. Biol. 2003, 65, 767–793. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Kirsch, G.E.; Zhang, D.; Brugada, R.; Brugada, J.; Brugada, P.; Potenza, D.; Moya, A.; Borggrefe, M.; Breithardt, G.; et al. Genetic basis and molecular mechanism for idiopathic ventricular fibrillation. Nature 1998, 392, 293–296. [Google Scholar] [CrossRef] [PubMed]
- Wilde, A.A.; Antzelevitch, C.; Borggrefe, M.; Brugada, J.; Brugada, R.; Brugada, P.; Corrado, D.; Hauer, R.N.; Kass, R.S.; Nademanee, K.; et al. Proposed diagnostic criteria for the Brugada syndrome: Consensus report. Circulation 2002, 106, 2514–2519. [Google Scholar] [CrossRef] [PubMed]
- Antzelevitch, C. Role of spatial dispersion of repolarization in inherited and acquired sudden cardiac death syndromes. Am. J. Physiol.-Heart Circ. Physiol. 2007, 293, H2024–H2038. [Google Scholar] [CrossRef]
- Tran, D.X.; Sato, D.; Yochelis, A.; Weiss, J.N.; Garfinkel, A.; Qu, Z. Bifurcation and chaos in a model of cardiac early afterdepolarizations. Phys. Rev. Lett. 2009, 102, 258103. [Google Scholar] [CrossRef] [PubMed]
- Barrio, R.; Martínez, M.Á.; Serrano, S.; Pueyo, E. Dynamical mechanism for generation of arrhythmogenic early afterdepolarizations in cardiac myocytes: Insights from in silico electrophysiological models. Phys. Rev. E 2022, 106, 024402. [Google Scholar] [CrossRef] [PubMed]
- Barrio, R.; Martínez, M.; Pueyo, E.; Serrano, S. Dynamical analysis of early afterdepolarization patterns in a biophysically detailed cardiac model. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 073137. [Google Scholar] [CrossRef]
- Campos, F.O.; Shiferaw, Y.; Prassl, A.J.; Boyle, P.M.; Vigmond, E.J.; Plank, G. Stochastic spontaneous calcium release events trigger premature ventricular complexes by overcoming electrotonic load. Cardiovasc. Res. 2015, 107, 175–183. [Google Scholar] [CrossRef] [PubMed]
- Weiss, J.N.; Karma, A.; Shiferaw, Y.; Chen, P.S.; Garfinkel, A.; Qu, Z. From pulsus to pulseless: The saga of cardiac alternans. Circ. Res. 2006, 98, 1244–1253. [Google Scholar] [CrossRef] [PubMed]
- Nolasco, J.; Dahlen, R.W. A graphic method for the study of alternation in cardiac action potentials. J. Appl. Physiol. 1968, 25, 191–196. [Google Scholar] [CrossRef] [PubMed]
- Fox, J.J.; Bodenschatz, E.; Gilmour, R.F., Jr. Period-doubling instability and memory in cardiac tissue. Phys. Rev. Lett. 2002, 89, 138101. [Google Scholar] [CrossRef] [PubMed]
- Echebarria, B.; Karma, A. Instability and spatiotemporal dynamics of alternans in paced cardiac tissue. Phys. Rev. Lett. 2002, 88, 208101. [Google Scholar] [CrossRef]
- Shiferaw, Y.; Watanabe, M.; Garfinkel, A.; Weiss, J.; Karma, A. Model of intracellular calcium cycling in ventricular myocytes. Biophys. J. 2003, 85, 3666–3686. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Lacalle, E.; Cantalapiedra, I.R.; Penaranda, A.; Cinca, J.; Hove-Madsen, L.; Echebarria, B. Dependency of calcium alternans on ryanodine receptor refractoriness. PLoS ONE 2013, 8, e55042. [Google Scholar] [CrossRef]
- Picht, E.; DeSantiago, J.; Blatter, L.A.; Bers, D.M. Cardiac alternans do not rely on diastolic sarcoplasmic reticulum calcium content fluctuations. Circ. Res. 2006, 99, 740–748. [Google Scholar] [CrossRef]
- Lugo, C.A.; Cantalapiedra, I.R.; Peñaranda, A.; Hove-Madsen, L.; Echebarria, B. Are SR Ca content fluctuations or SR refractoriness the key to atrial cardiac alternans?: Insights from a human atrial model. Am. J. Physiol.-Heart Circ. Physiol. 2014, 306, H1540–H1552. [Google Scholar] [CrossRef] [PubMed]
- Cantalapiedra, I.R.; Alvarez-Lacalle, E.; Peñaranda, A.; Echebarria, B. Minimal model for calcium alternans due to SR release refractoriness. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 093928. [Google Scholar] [CrossRef]
- Alvarez-Lacalle, E.; Echebarria, B.; Spalding, J.; Shiferaw, Y. Calcium alternans is due to an order-disorder phase transition in cardiac cells. Phys. Rev. Lett. 2015, 114, 108101. [Google Scholar] [CrossRef] [PubMed]
- Shiferaw, Y.; Karma, A. Turing instability mediated by voltage and calcium diffusion in paced cardiac cells. Proc. Natl. Acad. Sci. USA 2006, 103, 5670–5675. [Google Scholar] [CrossRef] [PubMed]
- Vogel, R.; Weingart, R. Mathematical model of vertebrate gap junctions derived from electrical measurements on homotypic and heterotypic channels. J. Physiol. 1998, 510, 177189. [Google Scholar] [CrossRef] [PubMed]
- Desplantez, T.; Halliday, D.; Dupont, E.; Weingart, R. Cardiac connexins Cx43 and Cx45: Formation of diverse gap junction channels with diverse electrical properties. Pflugers Arch. 2004, 448, 363–375. [Google Scholar] [CrossRef]
- Desplantez, T.; Dupont, E.; Severs, N.; Weingart, R. Gap junction channels and cardiac impulse propagation. J. Memb. Biol. 2007, 218, 13–28. [Google Scholar] [CrossRef]
- Willy, G.Y.; Yue, B.; Aoyama, H.; Kim, N.K.; Cameron, J.A.; Chen, H.; Bai, D. Junctional delay, frequency, and direction-dependent uncoupling of human heterotypic Cx45/Cx43 gap junction channels. J. Mol. Cell. Cardiol. 2017, 111, 17–26. [Google Scholar]
- Santos-Miranda, A.; Noureldin, M.; Bai, D. Effects of temperature on transjunctional voltage-dependent gating kinetics in Cx45 and Cx40 gap junction channels. J. Mol. Cell. Cardiol. 2019, 127, 185–193. [Google Scholar] [CrossRef]
- Spray, D.; Harris, A.; Bennett, M. Equilibrium properties of a voltage-dependent junctional conductance. J. Gen. Physiol. 1981, 77, 77–93. [Google Scholar] [CrossRef] [PubMed]
- Spray, D.; Harris, A.; Bennett, M. Gap junctional conductance is a simple and sensitive function of intracellular pH. Science 1981, 211, 712–715. [Google Scholar] [CrossRef] [PubMed]
- Harris, A.; Spray, D.; Bennett, M. Kinetic properties of a voltage-dependent junctional conductance. J. Gen. Physiol. 1981, 77, 95–117. [Google Scholar] [CrossRef]
- Chen-Izu, Y.; Moreno, A.; Spangler, R. Opposing gates model for voltage gating of gap junction channels. Am. J. Physiol. Cell Physiol. 2001, 281, C1604–C1613. [Google Scholar] [CrossRef]
- Paulauskas, N.; Pranevicius, M.; Bukauskas, F. A stochastic four-state model of contingent gating of gap junction channels containing two fast gates sensitive to transjunctional voltage. Biophys. J. 2009, 96, 3936–3948. [Google Scholar] [CrossRef] [PubMed]
- Paulauskas, N.; Pranevicius, M.; Bukauskas, F. Stochastic 16-state model of voltage gating of gap-junction channels enclosing fast and slow gate. Biophys. J. 2012, 102, 2471–2480. [Google Scholar] [CrossRef]
- Snipas, M.; Kraujalis, T.; Paulauskas, N.; Maciunas, K.; Bukauskas, F.F. Stochastic Model of Gap Junctions Exhibiting Rectification and Multiple Closed States of Slow Gates. Biophys. J. 2016, 110, 1322–1333. [Google Scholar] [CrossRef]
- Hand, P.E.; Griffith, B.E. Adaptive multiscale model for simulating cardiac conduction. Proc. Natl. Acad. Sci. USA 2010, 107, 14603–14608. [Google Scholar] [CrossRef] [PubMed]
- Costa, C.M.; Silva, P.A.A.; dos Santos, R.W. Mind the Gap: A Semicontinuum Model for Discrete Electrical Propagation in Cardiac Tissue. IEEE Trans. Biomed. Eng. 2016, 63, 765–774. [Google Scholar] [PubMed]
- Qu, Z. Network dynamics in cardiac electrophysiology. In Systems Biology of Metabolic and Signaling Networks; Springer: Berlin/Heidelberg, Germany, 2014; pp. 243–260. [Google Scholar]
- Lin, X.; Crye, M.; Veenstra, R.D. Regulation of connexin43 gap junctional conductance by ventricular action potentials. Circ. Res. 2003, 93, e63–e73. [Google Scholar] [CrossRef]
- Santos-Miranda, A.; Chen, H.; Chen, R.C.; Odoko-Ishimoto, M.; Aoyama, H.; Bai, D. The amino terminal domain plays an important role in transjunctional voltage-dependent gating kinetics of Cx45 gap junctions. J. Mol. Cell. Cardiol. 2020, 143, 71–84. [Google Scholar] [CrossRef] [PubMed]
- Hawks, C.; Elorza, J.; Wittt, A.; Laroze, D.; Cantalapiedra, I.R.; Penaranda, A.; Echebarria, B.; Bragard, J. Gap Junction Dynamics Induces Localized Conductance Bistability in Cardiac Tissue. Int. J. Bifurc. Chaos 2019, 29, 1930021. [Google Scholar] [CrossRef]
- Bragard, J.; Witt, A.; Hawks, C.; Elorza, J.; Cantalapiedra, I.R.; Penaranda, A.; Echebarria, B. Conductance heterogeneities induced by multistability in the dynamics of coupled gap junctions. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 073144. [Google Scholar] [CrossRef] [PubMed]
- Cantalapiedra, I.R.; Penaranda, A.; Echebarria, B. Propagation malfunctions due to gap junction dysregulation. In Proceedings of the Computing in Cardiology 2014, Cambridge, MA, USA, 7–10 September 2014; pp. 1045–1048. [Google Scholar]
- Hawks, C.; Elorza, J.; Echebarria, B.; Cantalapiedra, I.R.; Peñaranda, A.; Bragard, J. Influence of gap junction dynamics on the stability of reentrant waves in cardiac tissue. In Proceedings of the 2015 Computing in Cardiology Conference (CinC), Nice, France, 6–9 September 2015; pp. 437–440. [Google Scholar]
- Henriquez, A.; Vogel, R.; Muller-Borer, B.; Henriquez, C.; Weingart, R.; Cascio, W. Influence of dynamic gap junction resistance on impulse propagation in ventricular myocardium: A computer simulation study. Biophys. J. 2001, 81, 2112–2121. [Google Scholar] [CrossRef]
- Maciunas, K.; Snipas, M.; Kraujalis, T.; Kraujalienė, L.; Panfilov, A.V. The role of the Cx43/Cx45 gap junction voltage gating on wave propagation and arrhythmogenic activity in cardiac tissue. Sci. Rep. 2023, 13, 14863. [Google Scholar] [CrossRef] [PubMed]
- Gaudesius, G.; Miragoli, M.; Thomas, S.P.; Rohr, S. Coupling of cardiac electrical activity over extended distances by fibroblasts of cardiac origin. Circ. Res. 2003, 93, 421–428. [Google Scholar] [CrossRef]
- Ongstad, E.; Kohl, P. Fibroblast–myocyte coupling in the heart: Potential relevance for therapeutic interventions. J. Mol. Cell. Cardiol. 2016, 91, 238–246. [Google Scholar] [CrossRef]
- Bazhutina, A.; Balakina-Vikulova, N.A.; Kursanov, A.; Solovyova, O.; Panfilov, A.; Katsnelson, L.B. Mathematical modelling of the mechano-electric coupling in the human cardiomyocyte electrically connected with fibroblasts. Prog. Biophys. Mol. Biol. 2021, 159, 46–57. [Google Scholar] [CrossRef]
- Chilton, L.; Giles, W.R.; Smith, G.L. Evidence of intercellular coupling between co-cultured adult rabbit ventricular myocytes and myofibroblasts. J. Physiol. 2007, 583, 225–236. [Google Scholar] [CrossRef] [PubMed]
- Vasquez, C.; Mohandas, P.; Louie, K.L.; Benamer, N.; Bapat, A.C.; Morley, G.E. Enhanced fibroblast–myocyte interactions in response to cardiac injury. Circ. Res. 2010, 107, 1011–1020. [Google Scholar] [CrossRef]
- Li, Y.; Asfour, H.; Bursac, N. Age-dependent functional crosstalk between cardiac fibroblasts and cardiomyocytes in a 3D engineered cardiac tissue. Acta Biomater. 2017, 55, 120–130. [Google Scholar] [CrossRef] [PubMed]
- Quinn, T.A.; Camelliti, P.; Rog-Zielinska, E.A.; Siedlecka, U.; Poggioli, T.; O’Toole, E.T.; Knöpfel, T.; Kohl, P. Electrotonic coupling of excitable and nonexcitable cells in the heart revealed by optogenetics. Proc. Natl. Acad. Sci. USA 2016, 113, 14852–14857. [Google Scholar] [CrossRef]
- Xie, Y.; Garfinkel, A.; Weiss, J.N.; Qu, Z. Cardiac alternans induced by fibroblast-myocyte coupling: Mechanistic insights from computational models. Am. J. Physiol.-Heart Circ. Physiol. 2009, 297, H775–H784. [Google Scholar] [CrossRef] [PubMed]
- Jacquemet, V.; Henriquez, C.S. Modelling cardiac fibroblasts: Interactions with myocytes and their impact on impulse propagation. Europace 2007, 9, vi29–vi37. [Google Scholar] [CrossRef] [PubMed]
- Sachse, F.B.; Moreno, A.P.; Abildskov, J. Electrophysiological modeling of fibroblasts and their interaction with myocytes. Ann. Biomed. Eng. 2008, 36, 41–56. [Google Scholar] [CrossRef] [PubMed]
- Hubbard, M.L.; Henriquez, C.S. A microstructural model of reentry arising from focal breakthrough at sites of source-load mismatch in a central region of slow conduction. Am. J. Physiol.-Heart Circ. Physiol. 2014, 306, H1341–H1352. [Google Scholar] [CrossRef] [PubMed]
- Jacquemet, V.; Henriquez, C.S. Loading effect of fibroblast-myocyte coupling on resting potential, impulse propagation, and repolarization: Insights from a microstructure model. Am. J. Physiol.-Heart Circ. Physiol. 2008, 294, H2040–H2052. [Google Scholar] [CrossRef]
- Spach, M.S.; Heidlage, J.F.; Dolber, P.C.; Barr, R.C. Electrophysiological effects of remodeling cardiac gap junctions and cell size: Experimental and model studies of normal cardiac growth. Circ. Res. 2000, 86, 302–311. [Google Scholar] [CrossRef] [PubMed]
- Gouvêa de Barros, B.; Sachetto Oliveira, R.; Meira, W., Jr.; Lobosco, M.; Weber dos Santos, R. Simulations of Complex and Microscopic Models of Cardiac Electrophysiology Powered by Multi-GPU Platforms. Comput. Math. Methods Med. 2012, 2012, 824569. [Google Scholar] [CrossRef] [PubMed]
- Prudat, Y.; Kucera, J.P. Nonlinear behaviour of conduction and block in cardiac tissue with heterogeneous expression of connexin 43. J. Mol. Cell. Cardiol. 2014, 76, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Gouvêa de Barros, B.; Weber dos Santos, R.; Lobosco, M.; Alonso, S. Simulation of ectopic pacemakers in the heart: Multiple ectopic beats generated by reentry inside fibrotic regions. BioMed Res. Int. 2015, 2015, 713058. [Google Scholar] [CrossRef]
- Tveito, A.; Jæger, K.H.; Kuchta, M.; Mardal, K.A.; Rognes, M.E. A cell-based framework for numerical modeling of electrical conduction in cardiac tissue. Front. Phys. 2017, 5, 48. [Google Scholar] [CrossRef]
- Jæger, K.H.; Edwards, A.G.; Giles, W.R.; Tveito, A. From millimeters to micrometers; re-introducing myocytes in models of cardiac electrophysiology. Front. Physiol. 2021, 12, 763584. [Google Scholar] [CrossRef] [PubMed]
- Alonso, S.; Bär, M. Reentry near the percolation threshold in a heterogeneous discrete model for cardiac tissue. Phys. Rev. Lett. 2013, 110, 158101. [Google Scholar] [CrossRef]
- Oliveira, R.S.; de Barros, B.G.; Gomes, J.M.; Lobosco, M.; Alonso, S.; Bär, M.; dos Santos, R.W. Reactive interstitial and reparative fibrosis as substrates for cardiac ectopic pacemakers and reentries. In Proceedings of the Bioinformatics and Biomedical Engineering: 4th International Conference, IWBBIO 2016, Granada, Spain, 20–22 April 2016; Proceedings 4. Springer: Berlin/Heidelberg, Germany, 2016; pp. 346–357. [Google Scholar]
- Cherry, E.M.; Ehrlich, J.R.; Nattel, S.; Fenton, F.H. Pulmonary vein reentry—Properties and size matter: Insights from a computational analysis. Heart Rhythm 2007, 4, 1553–1562. [Google Scholar] [CrossRef]
- Panfilov, A. Spiral breakup in an array of coupled cells: The role of the intercellular conductance. Phys. Rev. Lett. 2002, 88, 118101. [Google Scholar] [CrossRef] [PubMed]
- Jæger, K.H.; Tveito, A. Efficient, cell-based simulations of cardiac electrophysiology; The Kirchhoff Network Model (KNM). NPJ Syst. Biol. Appl. 2023, 9, 25. [Google Scholar] [CrossRef]
- Mora, M.T.; Gomez, J.F.; Morley, G.; Ferrero, J.M.; Trenor, B. Mechanistic investigation of Ca2+ alternans in human heart failure and its modulation by fibroblasts. PLoS ONE 2019, 14, e0217993. [Google Scholar] [CrossRef] [PubMed]
- Ten Tusscher, K.; Panfilov, A. Influence of nonexcitable cells on spiral breakup in two-dimensional and three-dimensional excitable media. Phys. Rev. E 2003, 68, 062902. [Google Scholar] [CrossRef] [PubMed]
- Alonso, S.; Bär, M. Reentry produced by small-scale heterogeneities in a discrete model of cardiac tissue. J. Phys. Conf. Ser. 2016, 727, 012002. [Google Scholar] [CrossRef]
- Alonso, S.; Dos Santos, R.W.; Bär, M. Reentry and ectopic pacemakers emerge in a three-dimensional model for a slab of cardiac tissue with diffuse microfibrosis near the percolation threshold. PLoS ONE 2016, 11, e0166972. [Google Scholar] [CrossRef] [PubMed]
- Sachetto, R.; Alonso, S.; Dos Santos, R.W. Killing many birds with two stones: Hypoxia and fibrosis can generate ectopic beats in a human ventricular model. Front. Physiol. 2018, 9, 764. [Google Scholar] [CrossRef] [PubMed]
- Qu, Z.; Xie, F.; Garfinkel, A.; Weiss, J.N. Origins of spiral wave meander and breakup in a two-dimensional cardiac tissue model. Ann. Biomed. Eng. 2000, 28, 755–771. [Google Scholar] [CrossRef]
- Panfilov, A.V. Spiral breakup as a model of ventricular fibrillation. Chaos Interdiscip. J. Nonlinear Sci. 1998, 8, 57–64. [Google Scholar] [CrossRef]
- Pastore, J.M.; Girouard, S.D.; Laurita, K.R.; Akar, F.G.; Rosenbaum, D.S. Mechanism linking T-wave alternans to the genesis of cardiac fibrillation. Circulation 1999, 99, 1385–1394. [Google Scholar] [CrossRef] [PubMed]
- Brahmajothi, M.V.; Campbell, D.L.; Rasmusson, R.L.; Morales, M.J.; Trimmer, J.S.; Nerbonne, J.M.; Strauss, H.C. Distinct transient outward potassium current (Ito) phenotypes and distribution of fast-inactivating potassium channel alpha subunits in ferret left ventricular myocytes. J. Gen. Physiol. 1999, 113, 581–600. [Google Scholar] [CrossRef] [PubMed]
- Cantalapiedra, I.R.; Peñaranda, A.; Echebarria, B.; Bragard, J. Phase-2 reentry in cardiac tissue: Role of the slow calcium pulse. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2010, 82, 011907. [Google Scholar] [CrossRef] [PubMed]
- Penaranda, A.; Cantalapiedra, I.R.; Echebarria, B. Slow pulse due to calcium current induces phase-2 reentry in heterogeneous tissue. In Proceedings of the 2010 Computing in Cardiology, Belfast, UK, 26–29 September 2010; pp. 661–664. [Google Scholar]
- Alonso, S.; Panfilov, A.V. Negative filament tension in the Luo-Rudy model of cardiac tissue. Chaos Interdiscip. J. Nonlinear Sci. 2007, 17, 015102. [Google Scholar] [CrossRef]
- Alonso, S.; Bär, M.; Panfilov, A.V. Negative tension of scroll wave filaments and turbulence in three-dimensional excitable media and application in cardiac dynamics. Bull. Math. Biol. 2013, 75, 1351–1376. [Google Scholar] [CrossRef] [PubMed]
- Echebarria, B.; Hakim, V.; Henry, H. Nonequilibrium ribbon model of twisted scroll waves. Phys. Rev. Lett. 2006, 96, 098301. [Google Scholar] [CrossRef]
- Fenton, F.H.; Luther, S.; Cherry, E.M.; Otani, N.F.; Krinsky, V.; Pumir, A.; Bodenschatz, E.; Gilmour, R.F., Jr. Termination of atrial fibrillation using pulsed low-energy far-field stimulation. Circulation 2009, 120, 467–476. [Google Scholar] [CrossRef] [PubMed]
- Luther, S.; Fenton, F.H.; Kornreich, B.G.; Squires, A.; Bittihn, P.; Hornung, D.; Zabel, M.; Flanders, J.; Gladuli, A.; Campoy, L.; et al. Low-energy control of electrical turbulence in the heart. Nature 2011, 475, 235–239. [Google Scholar] [CrossRef] [PubMed]
- Buran, P.; Bär, M.; Alonso, S.; Niedermayer, T. Control of electrical turbulence by periodic excitation of cardiac tissue. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 113110. [Google Scholar] [CrossRef]
- dos Santos, R.W.; Plank, G.; Bauer, S.; Vigmond, E.J. Parallel multigrid preconditioner for the cardiac bidomain model. IEEE Trans. Biomed. Eng. 2004, 51, 1960–1968. [Google Scholar]
- Potse, M.; Dubé, B.; Richer, J.; Vinet, A.; Gulrajani, R.M. A comparison of monodomain and bidomain reaction-diffusion models for action potential propagation in the human heart. IEEE Trans. Biomed. Eng. 2006, 53, 2425–2435. [Google Scholar] [CrossRef] [PubMed]
- Jæger, K.H.; Tveito, A. Deriving the bidomain model of cardiac electrophysiology from a cell-based model; properties and comparisons. Front. Physiol. 2022, 12, 811029. [Google Scholar] [CrossRef] [PubMed]
- Jæger, K.H.; Trotter, J.D.; Cai, X.; Arevalo, H.; Tveito, A. Evaluating computational efforts and physiological resolution of mathematical models of cardiac tissue. Sci. Rep. 2024, 14, 16954. [Google Scholar] [CrossRef] [PubMed]
- Bragard, J.; Šimić, A.; Laroze, D.; Elorza, J. Advantage of four-electrode over two-electrode defibrillators. Phys. Rev. E 2015, 92, 062919. [Google Scholar] [CrossRef] [PubMed]
- Sachse, F.B.; Moreno, A.; Seemann, G.; Abildskov, J. A model of electrical conduction in cardiac tissue including fibroblasts. Ann. Biomed. Eng. 2009, 37, 874–889. [Google Scholar] [CrossRef] [PubMed]
- Bragard, J.; Sankarankutty, A.C.; Sachse, F.B. Extended bidomain modeling of defibrillation: Quantifying virtual electrode strengths in fibrotic myocardium. Front. Physiol. 2019, 10, 337. [Google Scholar] [CrossRef]
- Sánchez, J.; Gomez, J.F.; Martinez-Mateu, L.; Romero, L.; Saiz, J.; Trenor, B. Heterogeneous effects of fibroblast-myocyte coupling in different regions of the human atria under conditions of atrial fibrillation. Front. Physiol. 2019, 10, 847. [Google Scholar] [CrossRef]
- Caldwell, B.J.; Trew, M.L.; Sands, G.B.; Hooks, D.A.; LeGrice, I.J.; Smaill, B.H. Three distinct directions of intramural activation reveal nonuniform side-to-side electrical coupling of ventricular myocytes. Circ. Arrhythmia Electrophysiol. 2009, 2, 433–440. [Google Scholar] [CrossRef] [PubMed]
- Penland, R.C.; Harrild, D.M.; Henriquez, C.S. Modeling impulse propagation and extracellular potential distributions in anisotropic cardiac tissue using a finite volume element discretization. Comput. Vis. Sci. 2002, 4, 215–226. [Google Scholar] [CrossRef]
- Tobón, C.; Ruiz-Villa, C.A.; Heidenreich, E.; Romero, L.; Hornero, F.; Saiz, J. A three-dimensional human atrial model with fiber orientation. Electrograms and arrhythmic activation patterns relationship. PLoS ONE 2013, 8, e50883. [Google Scholar] [CrossRef]
- Panfilov, A.V.; Keener, J.P. Re-entry in three-dimensional Fitzhugh-Nagumo medium with rotational anisotropy. Phys. D Nonlinear Phenom. 1995, 84, 545–552. [Google Scholar] [CrossRef]
- Gil, D.; Aris, R.; Borras, A.; Ramírez, E.; Sebastian, R.; Vazquez, M. Influence of fiber connectivity in simulations of cardiac biomechanics. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 63–72. [Google Scholar] [CrossRef]
- Nordsletten, D.; Niederer, S.; Nash, M.; Hunter, P.; Smith, N. Coupling multi-physics models to cardiac mechanics. Prog. Biophys. Mol. Biol. 2011, 104, 77–88. [Google Scholar] [CrossRef]
- Bradley, C.; Bowery, A.; Britten, R.; Budelmann, V.; Camara, O.; Christie, R.; Cookson, A.; Frangi, A.F.; Gamage, T.B.; Heidlauf, T.; et al. OpenCMISS: A multi-physics & multi-scale computational infrastructure for the VPH/Physiome project. Prog. Biophys. Mol. Biol. 2011, 107, 32–47. [Google Scholar]
- Corrias, A.; Jie, X.; Romero, L.; Bishop, M.; Bernabeu, M.; Pueyo, E.; Rodriguez, B. Arrhythmic risk biomarkers for the assessment of drug cardiotoxicity: From experiments to computer simulations. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 3001–3025. [Google Scholar] [CrossRef] [PubMed]
- Zemzemi, N.; Bernabeu, M.O.; Saiz, J.; Cooper, J.; Pathmanathan, P.; Mirams, G.R.; Pitt-Francis, J.; Rodriguez, B. Computational assessment of drug-induced effects on the electrocardiogram: From ion channel to body surface potentials. Br. J. Pharmacol. 2013, 168, 718–733. [Google Scholar] [CrossRef] [PubMed]
- Lafortune, P.; Arís, R.; Vázquez, M.; Houzeaux, G. Coupled electromechanical model of the heart: Parallel finite element formulation. Int. J. Numer. Methods Biomed. Eng. 2012, 28, 72–86. [Google Scholar] [CrossRef] [PubMed]
- Santiago, A.; Aguado-Sierra, J.; Zavala-Aké, M.; Doste-Beltran, R.; Gómez, S.; Arís, R.; Cajas, J.C.; Casoni, E.; Vázquez, M. Fully coupled fluid-electro-mechanical model of the human heart for supercomputers. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e3140. [Google Scholar] [CrossRef] [PubMed]
- Doste, R.; Soto-Iglesias, D.; Bernardino, G.; Alcaine, A.; Sebastian, R.; Giffard-Roisin, S.; Sermesant, M.; Berruezo, A.; Sanchez-Quintana, D.; Camara, O. A rule-based method to model myocardial fiber orientation in cardiac biventricular geometries with outflow tracts. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3185. [Google Scholar] [CrossRef] [PubMed]
- Smith, N.; de Vecchi, A.; McCormick, M.; Nordsletten, D.; Camara, O.; Frangi, A.F.; Delingette, H.; Sermesant, M.; Relan, J.; Ayache, N.; et al. euHeart: Personalized and integrated cardiac care using patient-specific cardiovascular modelling. Interface Focus 2011, 1, 349–364. [Google Scholar] [CrossRef] [PubMed]
- Krishnamurthy, A.; Villongco, C.T.; Chuang, J.; Frank, L.R.; Nigam, V.; Belezzuoli, E.; Stark, P.; Krummen, D.E.; Narayan, S.; Omens, J.H.; et al. Patient-specific models of cardiac biomechanics. J. Comput. Phys. 2013, 244, 4–21. [Google Scholar] [CrossRef] [PubMed]
- Taylor, C.A.; Figueroa, C. Patient-specific modeling of cardiovascular mechanics. Annu. Rev. Biomed. Eng. 2009, 11, 109–134. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Perez, A.; Sebastian, R.; Izquierdo, M.; Ruiz, R.; Bishop, M.; Ferrero, J.M. Personalized cardiac computational models: From clinical data to simulation of infarct-related ventricular tachycardia. Front. Physiol. 2019, 10, 580. [Google Scholar] [CrossRef]
- Niederer, S.A.; Sacks, M.S.; Girolami, M.; Willcox, K. Scaling digital twins from the artisanal to the industrial. Nat. Comput. Sci. 2021, 1, 313–320. [Google Scholar] [CrossRef]
- Corral-Acero, J.; Margara, F.; Marciniak, M.; Rodero, C.; Loncaric, F.; Feng, Y.; Gilbert, A.; Fernandes, J.F.; Bukhari, H.A.; Wajdan, A.; et al. The ‘Digital Twin’to enable the vision of precision cardiology. Eur. Heart J. 2020, 41, 4556–4564. [Google Scholar] [CrossRef] [PubMed]
- Guidi, G.; Pettenati, M.C.; Miniati, R.; Iadanza, E. Random forest for automatic assessment of heart failure severity in a telemonitoring scenario. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 3230–3233. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alonso, S.; Alvarez-Lacalle, E.; Bragard, J.; Echebarria, B. Biophysical Modeling of Cardiac Cells: From Ion Channels to Tissue. Biophysica 2025, 5, 5. https://doi.org/10.3390/biophysica5010005
Alonso S, Alvarez-Lacalle E, Bragard J, Echebarria B. Biophysical Modeling of Cardiac Cells: From Ion Channels to Tissue. Biophysica. 2025; 5(1):5. https://doi.org/10.3390/biophysica5010005
Chicago/Turabian StyleAlonso, Sergio, Enrique Alvarez-Lacalle, Jean Bragard, and Blas Echebarria. 2025. "Biophysical Modeling of Cardiac Cells: From Ion Channels to Tissue" Biophysica 5, no. 1: 5. https://doi.org/10.3390/biophysica5010005
APA StyleAlonso, S., Alvarez-Lacalle, E., Bragard, J., & Echebarria, B. (2025). Biophysical Modeling of Cardiac Cells: From Ion Channels to Tissue. Biophysica, 5(1), 5. https://doi.org/10.3390/biophysica5010005





