Next Article in Journal
In Silico Design of Novel Piperazine-Based mTORC1 Inhibitors Through DFT, QSAR and ADME Investigations
Next Article in Special Issue
Re-Examination of the Sel’kov Model of Glycolysis and Its Symmetry-Breaking Instability Due to the Impact of Diffusion with Implications for Cancer Imitation Caused by the Warburg Effect
Previous Article in Journal
Modulatory Impact of Tefluthrin, Telmisartan, and KB-R7943 on Voltage-Gated Na+ Currents
Previous Article in Special Issue
Modeling Thermal Effects of Pulsating Currents in Human Tissues: How to Prevent Necrosis
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Biophysica
Volume 4
Issue 4
10.3390/biophysica4040033
biophysica-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Is Water the Engine of Protein Folding?

by
Marco Campanile
1 and
Giuseppe Graziano
2,*
1
Department of Chemical Sciences, University of Naples Federico II, Via Cintia, 80126 Naples, Italy
2
Department of Science and Technology, University of Sannio, Via Francesco de Sanctis, 82100 Benevento, Italy
*
Author to whom correspondence should be addressed.
Biophysica 2024, 4(4), 507-516; https://doi.org/10.3390/biophysica4040033
Submission received: 14 September 2024 / Revised: 3 October 2024 / Accepted: 15 October 2024 / Published: 16 October 2024
(This article belongs to the Collection Feature Papers in Biophysics)
Browse Figures
Versions Notes

Abstract

:
No one can dismiss the fundamental role played by water in several important biochemical processes, including the folding of globular proteins. The so-called hydrophobic effect is the theoretical construct to rationalize how water molecules stabilize the folded state. However, over the years, analyses have been published that lead to the conclusion that water destabilizes the folded state. The aim of the present work is to state that the gain in translational entropy of water molecules (due to the decrease in water-accessible surface area associated with folding) is the driving force behind protein folding.

1. Introduction

According to the famous and influential review article published by Walter Kauzmann in 1959 [1], the hydrophobic effect must play a major role in the folding of polypeptide chains and in the conformational stability of the folded state in water and aqueous solutions. The idea is that nonpolar side chains, to avoid unfavorable contact with water molecules, cluster together to produce a nonpolar core, resembling an organic liquid (i.e., the oil drop model). Kauzmann’s explanation was based on the values of the Gibbs free energy change of transfer for hydrocarbon species from an organic liquid to water, which proved to be largely positive and entropy-dominated [2]. This entropy dominance was attributed to the special ability of water molecules to form ordered 3D structures to host nonpolar species, which cannot be involved in H-bonds. Kauzmann’s classic explanation ascribes water the fundamental role of overcoming the large conformational entropy loss associated with the internal rotation degrees of freedom of the polypeptide chain, and to transition from the huge ensemble of denatured and swollen conformations to the few that are associated with the folded state. The hydrophobic effect is usually described as a water-mediated attraction. Kauzmann’s classic explanation was widely accepted at the time and is still considered valid [3,4,5]. Although there are several problems with it (as will be clarified below), the main idea that water is the engine of protein folding is correct. Therefore, it was a surprise to read the following title of an article recently published in Protein Science [6]: “Water-mediated interactions destabilize proteins”. This title is the simple consequence of an erroneous division of the relevant thermodynamic quantities and points out the need to define a correct statistical mechanical model for the folding–unfolding transition of polypeptide chains in water. It is also important to recognize that in the past similar situations have occurred [7,8,9,10,11]. Measured macroscopic thermodynamic quantities are path-independent state functions and cannot provide, by themselves, any molecular level description. To overcome this limitation, a specific path must be defined. However, the same physical process could be described by different paths, each one leading to a different set of thermodynamic quantities. Therefore, the selection of a proper statistical mechanical model is necessary to define a path whose steps are physically meaningful [12,13,14]. For instance, it was rapidly recognized on analyzing the protein structures solved by means of X-ray crystallography that their average volume packing density is around 0.72 [15,16] (i.e., the volume packing density is given by the ratio of the volume occupied by all the atoms constituting the protein to the volume of the envelope containing the whole protein molecule in the folded state). The latter value implies that the folded state resembles a solid, not an organic liquid (the volume packing density of the hexagonal close packing structure is 0.74, whereas that of common organic liquids is around 0.5 [16]). This picture is supported by the measured values of the adiabatic compressibility of several globular proteins dissolved in aqueous solutions [17,18]; also, the heat capacity of folded proteins is comparable to that of crystalline solids made up of organic molecules with a chemical composition closely similar to that of proteins [19,20]. In fact, Schrödinger considered globular proteins as “aperiodic crystals” [21], while Liquori proposed to consider them as “crystal molecules” [22]. Thus, the search for an organic liquid mimicking the interior of globular proteins has been unsuccessful because the premise (i.e., the oil drop model) is not correct [23,24,25].

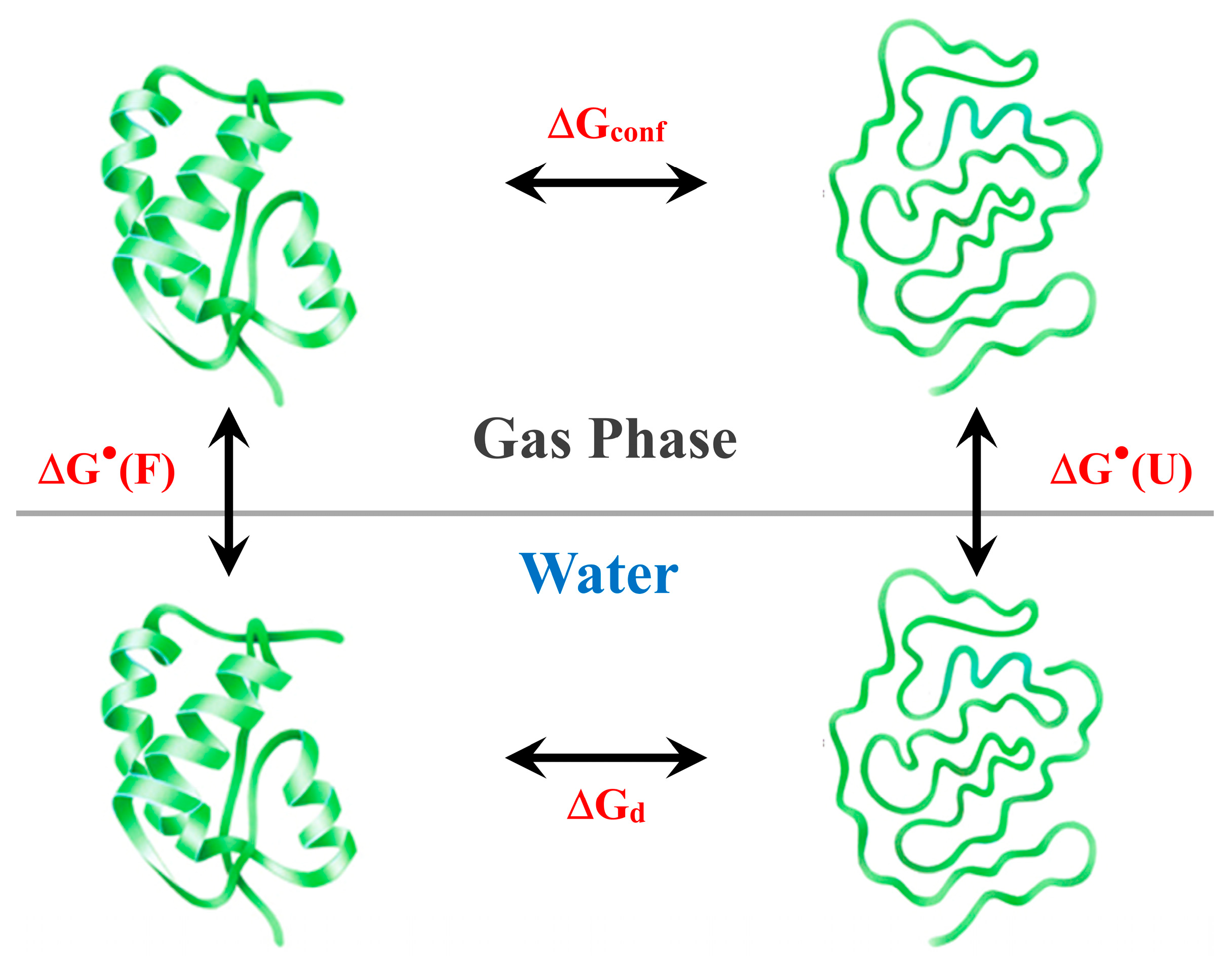
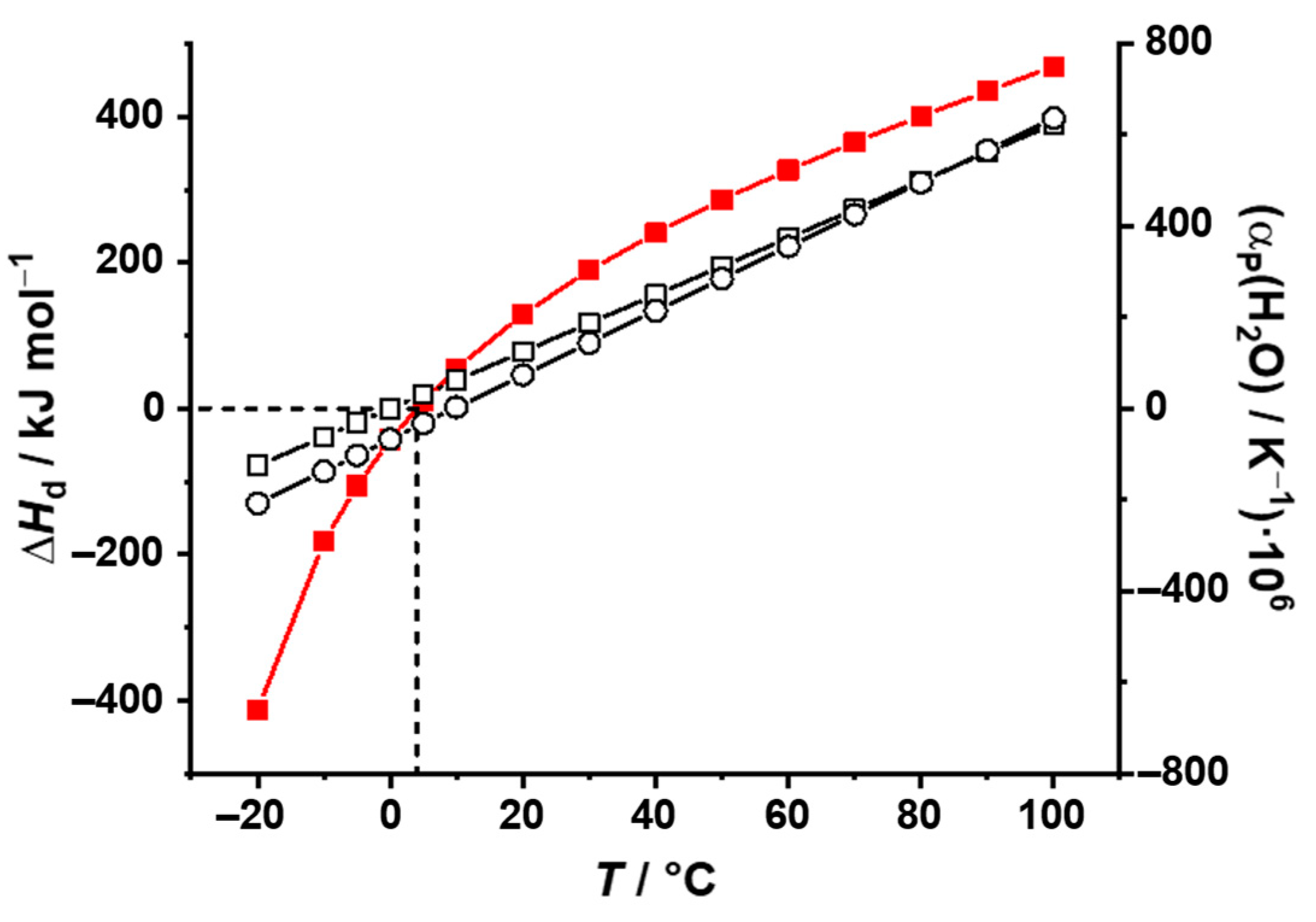
2. General Analysis

The present treatment starts from the words written by Sumi and Imamura (the authors of the Protein Science article [6]) in the first sentence of their Abstract: “Proteins are folded to avoid exposure of the nonpolar groups to water because water-mediated interactions between nonpolar groups are a promising factor in the thermodynamic stabilities of protein”. The last two sentences of their article are the following: “the present study on GCN4-p1 demonstrates that the water-mediated interactions of the total and nonpolar part contribution destabilize the protein. This work will boost change in the current paradigm that proteins are stabilized by avoiding exposure of the nonpolar groups to water” [6]. Accepting these sentences literally, one should conclude that all the nonpolar groups of a polypeptide chain are buried in the interior of the folded state. This is absolutely not true because proteins are heteropolymers, and the chain connectivity renders such a complete segregation impossible: all the nonpolar moieties are inside the globular structure to avoid the contact with water, and all the polar moieties are outside, on the surface of the globule, to make contacts with water molecules (consider also that the backbone consists of both nonpolar groups and the strongly polar peptide groups). Complete segregation holds for micelles, not for globular proteins. Chothia and colleagues, by performing detailed analyses of protein 3D structures [26,27], determined that the average composition is the following: (a) buried surface, (62 ± 1)% nonpolar, (31 ± 2)% polar, and (7 ± 2)% charged; (b) accessible surface, (56 ± 4)% nonpolar, (26 ± 4)% polar, and (18 ± 5)% charged. These results have recently been verified and confirmed [28]. On this point, Alan Cooper wrote, “when I look inside of a protein structure, it does not look particularly “hydrophobic”, certainly not to the extent that one sees inside a detergent micelle, for example. Yes, there are more nonpolar groups inside, but maybe not so many as one might expect, and with every amino acid side chain, polar or otherwise, there comes the polar amide backbone” [29]. Buried and accessible surfaces are similar in chemical nature, and more than fifty percent of the accessible surface of folded structures is made up of nonpolar groups, and more than a third of the buried surface is made up of the sum of polar and charged groups. These numbers are the simple consequence of the heteropolymeric nature of globular proteins and underscore that group additivity approaches cannot properly describe the conformational stability of such fine-tuned macromolecules quantitatively [30]. In other words, a globular protein is not the sum of a certain number of chemically different side chains, because the latter are covalently linked to the polypeptide chain and are not independent of each other [31]. Group additivity cannot hold for globular proteins. Thus, the hydration thermodynamics of the folded and unfolded states cannot be obtained as the sum of group contributions (even when the latter are weighted for their water accessible surface area, WASA [15]). The folded state must be treated as a unique object (and the same must hold for the unfolded state, using an object of a different shape). The question becomes the following: how detailed does the object need to be in order to reliably describe the folded state? The answer to this question depends on the process to describe, in this case the interaction of water molecules with the folded and unfolded states. It is necessary to adopt precise definitions to derive meaningful quantities. The folding–unfolding transition can be fruitfully analyzed by means of the following thermodynamic cycle, shown in Figure 1, that consists of the following steps: unfolding in water and unfolding in the ideal gas phase, followed by hydration of the folded state and hydration of the unfolded state.
Following the statistical mechanical analysis performed by Arieh Ben-Naim [32], hydration must refer to the transfer of a solute molecule from a fixed position in the gas phase to a fixed position in water. In all liquids, the molecules are very close together, and it is necessary to create, at a fixed position, a void space—a cavity—whose size is appropriate to host the solute molecule [33,34,35] (i.e., cavity creation may appear to be an unnecessary construct; actually, it is the simplest theoretical manner to account for the basic fact that each molecule has its own body, and so two molecules cannot occupy the same space at the same time). In any liquid, cavity creation is associated with a Gibbs free energy cost, ΔGc, whose magnitude increases upon raising the liquid number density [36]. To create a cavity at a fixed position while keeping the temperature and pressure constant, the liquid volume has to increase by the van der Waals volume, VvdW, of the cavity. There is a further and fundamental consequence. The centers of liquid molecules should at most lie on the solvent accessible surface area of the cavity (i.e., cavity WASA if the liquid is water), if the latter must be void (look carefully at Figure 2) [37].
The cavity presence leads to a solvent-excluded volume effect which affects all the liquid molecules since they are in continuous translational motion (note that the equipartition theorem holds for the kinetic energy of the molecules in real liquids [38]). The solvent-excluded volume effect is operative in any liquid; its magnitude is particularly large in water due to its high number density [36], and does not depend on the polar or nonpolar chemical nature of the solute molecule (i.e., it can be considered a geometric effect). A statistical mechanical theory of hydration, based on these ideas, works well in rationalizing both the poor solubility of hydrocarbons and the good solubility of alcohols in water [39], and the large negative entropy change occurring in both cases [40]. Cavity creation always leads to a decrease in the translational entropy of liquid molecules due to the drop in the accessible configurational space. This holds for any liquids, and is exaggerated in water due to its high number density that arises from the small size of water molecules [36]. Such a general mechanism for the entropy reduction associated with hydration has nothing to do with the claimed increase in tetrahedral structural order for the formation of something resembling icebergs or clathrates [40]. The existence of such ordered structures is not possible in a liquid phase; indeed, they have never been observed [41,42,43]. This is a weak point in the classic Kauzmann explanation. It is true that the hydration entropy loss is due to water molecules, although not to an increase in their tetrahedral order but rather to a loss in their translational entropy.
A further point needs clarification. The above reasoning indicates that, keeping the temperature and pressure fixed, ΔGc must scale with the cavity WASA, and so a dependence on cavity shape has to emerge [36,37]. Indeed, fixing the cavity VvdW and changing the cavity shape from a sphere to a family of thinner and longer prolate spherocylinders, the ΔGc magnitude increases [37,44]. This was verified by means of both classic scaled particle theory (SPT) calculations [44,45] and computer simulations in detailed water models [46,47,48]. Such a result has a direct consequence for the conformational stability of globular proteins. Experimental measurements have firmly established the following: (a) the difference in molecular volume between the folded and unfolded states is so small as to be neglected at 1 atm [49,50,51]; (b) there is a large WASA increase associated with unfolding [15,26]. The latter indicates that there is a large increase in the magnitude of the solvent-excluded volume effect associated with protein unfolding. Water molecules lose much more translational entropy when the protein is unfolded than when the protein is folded [52]. Of course, looking at the inverse process, one can state that the folding of polypeptide chains leads to a large gain in the translational entropy of water molecules. The latter is the folding driving force, and water molecules are the engine of the process. It has been shown that, since the WASA change upon unfolding plays the main role, simple geometric objects, such as a sphere modeling the folded state and a prolate spherocylinder modeling the unfolded state (the two objects have the same VvdW, but very different WASA; see Figure 2), can lead to reliable values for the Gibbs free energy decrease caused by the decrease in the magnitude of the solvent-excluded volume effect upon the folding of the polypeptide chain [53,54] (note that the use of simple geometric objects to model the states of globular proteins is supported by the success of the tube model developed by Maritan and colleagues [55,56]). The magnitude of the latter can be large enough to overcome the loss in conformational entropy of the polypeptide chain, ensuring the thermodynamic stability of the folded state. It is useful to provide a numerical example. A polypeptide chain of 76 residues (corresponding to the protein ubiquitin) has VvdW = 7790 Å3 (i.e., the average VvdW of a residue in native structures is 102.5 Å3 [57]); the corresponding folded state is a sphere of 12.3 Å radius. A series of prolate spherocylinders, all having the above VvdW, can describe conformations belonging to the unfolded ensemble, or better, can be used to “model” the folding process. The geometric features of these objects are listed in Table 1, together with the classic SPT-ΔGc values, calculated at 20 °C and 1 atm, in a hard sphere fluid having the experimental density of water and particle diameter σ(H2O) = 2.8 Å (i.e., the distance corresponding to the first maximum of the oxygen–oxygen radial distribution function of water at room temperature [58]).
In Figure 3, the SPT-ΔGc values are reported as a function of the cavity WASA (panel A), and of the cavity cylindrical length (panel B).
The first plot confirms this dependence on the cavity shape and WASA; the second one confirms the large Gibbs free energy decrease associated with the chain collapse and resembles a side of the funnel that should guide protein folding [59,60]. The ΔGc decrease upon folding has a magnitude larger than that associated with the conformational entropy loss; the latter can be roughly estimated by considering an equal and temperature-independent contribution of 19 J K−1molres−1 for all the residues, as suggested by the results of large-scale computer simulations [61]. For a protein of 76 residues, like ubiquitin, the quantity T⋅Nres⋅ΔSconf = 423.3 kJ mol−1, at 20 °C and 1 atm, proves to be smaller than the ΔGc difference between the sphere and the penultimate spherocylinder listed in Table 1, amounting to 522.4 kJ mol−1. For the same couple of cavities, performing the classic SPT calculations in an organic liquid, such as carbon tetrachloride, using its experimental density at 20 °C and 1 atm and the particle diameter σ(CCl4) = 5.37 Å [53], results in ΔΔGc = 755.5 − 434.7 = 320.8 kJ mol−1; the latter value is smaller than the T⋅Nres⋅ΔSconf contribution reported above. This clarifies that the magnitude of the solvent-excluded volume effect in CCl4 would not be enough to overwhelm the loss in conformational entropy of the polypeptide chain. The large magnitude of the solvent-excluded volume effect is one of the reasons that renders water “special” for protein folding [53], together with its tetrahedral, 2-donor, and 2-acceptor H-bonding capabilities.
To conclude, it is necessary to account for a last contribution to the folding process [52,53,54]: the direct energetic attractions between water molecules and the folded state and those between water molecules and the unfolded state; and finally, the difference in intramolecular energetic attractions between the folded and unfolded states (see the caption of Figure 1, and note that there is no real difference between internal energy and enthalpy in the case of condensed states of matter). The calculation of this energetic contribution is a formidable task. Nevertheless, several pieces of evidence indicate that, in water, the sum of the three terms should be close to zero [54]. For instance, the large decrease in the number of intermolecular protein–water H-bonds upon folding is almost entirely compensated for by the intra-protein H-bonds existing in the secondary structure elements of the folded state. According to George Rose [62,63,64], an H-bond satisfaction principle holds that a peptide group must be involved in H-bonds with water molecules or with other protein groups; otherwise, the folded state would not be stable. A similar situation holds for the other weak attractive energetic interactions. However, some authors, such as Sumi and Imamura [6]—even though they used a thermodynamic cycle similar to that shown in Figure 1—decided to add the protein–water energetic attractions to the water-mediated contributions; consequently, the role of the entropic solvent-excluded volume effect is masked, and the role of intra-protein energetic attractions seems to be dominant in the overall Gibbs free energy balance. It is not correct to look only at the contribution of the intra-protein energetic attractions, as this favors the folded state for sure; it is necessary to look at the overall balance of the energetic attractions—those with water molecules and the intra-protein interactions in the two states—and to isolate the entropic contribution of water.
The idea that the sum of the three energetic terms should be close to zero may appear strange because DSC measurements have indicated that the temperature-induced unfolding of small globular proteins is an endothermic and cooperative process, resembling the melting of a “crystal molecule” [65,66,67]. However, this resemblance should not be taken literally, as is emphasized by the temperature dependence of the denaturation enthalpy change, ΔHd (note that the sum of the three energetic terms considered above does not correspond to ΔHd, because the latter also accounts for the water reorganization upon unfolding; see below). The latter quantity is largely positive at the denaturation temperature of the protein, decreases markedly on lowering the temperature, is zero at a temperature labelled TH, and becomes negative on further lowering the temperature [68]. This trend cannot be associated with a melting process; rather, it must be attributed to the reorganization of water–water H-bonds upon unfolding [52,53,54]. Both the folded and unfolded states are surrounded by a first hydration shell of water molecules; however, the first hydration shell of the unfolded state is markedly larger in size than that of the folded state as a consequence of the WASA increase associated with unfolding [15,26]. Therefore, protein unfolding causes not only the destruction of the tertiary and secondary structures of the folded state, but also the passage of a large number of water molecules from the bulk to the first hydration shell. There is a strong coupling between these two sub-processes, leading to a cooperativity close to that of a first-order phase transition. At room temperature and above, the water molecules in the first hydration shell, on average, are involved in less H-bonds compared to those in the bulk [43], and so the enlargement of the hydration shell is endothermic. In this respect, it is worth noting the following: (a) the analysis of unfolding thermodynamic data for a set of 115 globular proteins led to an average value of <TH> = (277.5 ± 25.0) K [54]; (b) the latter value has a special meaning because it practically corresponds to the temperature of maximum density, TMD, of water, where the isobaric thermal expansion coefficient is equal to zero, αP(H2O) = 0 at TMD = 277 K [69]; and (c) the reorganization of water–water H-bonds is proportional to αP(H2O) [54], as emphasized by the application of classic SPT to real liquids, pioneered by Pierotti [45]. This is confirmed by a comparison between the temperature dependence of ΔHd for a protein of 76 residues, calculated using the average thermodynamic values obtained from two different datasets—by Robertson and Murphy [70] and Sawle and Ghosh [71]—and that of αP(H2O), as illustrated in Figure 4.
This implies that the dominant contribution in ΔHd comes from the reorganization of water–water H-bonds associated with protein unfolding [54], and should not significantly affect the conformational stability of globular proteins due to the nearly complete enthalpy–entropy compensation characterizing this water reorganization [43,72,73].
It is worth noting that other scientists have developed theoretical and computational approaches whose outcomes confirm that water is the engine of protein folding, and the main contribution is due to the gain in translational entropy of water molecules, caused by the decrease in the solvent-excluded volume associated with folding [74,75,76,77,78,79].

3. Conclusions

The approaches calculating hydration thermodynamics by means of group additivity contributions cannot account for the solvent-excluded volume effect caused in water (and in all liquids) by the presence of the folded state and the unfolded state, respectively, of a globular protein. It should be clear that the solvent-excluded volume effect is non-additive by definition. In fact, the decrease in translational entropy of liquid molecules produced by a large object with a given shape cannot be obtained by summing the effects caused by a certain number of small and quasi-spherical groups, whose total van der Waals volume corresponds to that of the large object. For instance, a sphere with radius rc = 12.3 Å and VvdW = 7790 Å3 can be considered the sum of 10 smaller spheres, each having VvdW = 7790/10 = 779 Å3, rc = 5.71 Å and WASA = 635 Å2. The classic SPT-ΔGc to create such a spherical cavity in water amounts to 166 kJ mol−1, at 20 °C and 1 atm; it is evident that 10 times 166 kJ mol−1 is not equal to the classic SPT-ΔGc to create in water the spherical cavity with rc = 12.3 Å; the same is also true for the WASA values (refer to the numbers listed in the first row of Table 1). A similar situation emerges by considering small spheres, each having VvdW = 7790/20 = 389.5 Å3, rc = 4.53 Å and WASA = 442 Å2. These numerical examples should help convince readers that additivity approaches fail to recognize the role played by water molecules, leading to the wrong conclusion that water destabilizes the folded state of globular proteins. In contrast, it is necessary to recognize the need to consider the solvent-excluded volume effect associated with the presence of a solute molecule in water, its relationship with the translational entropy of water molecules, and the decrease in its magnitude when a polypeptide chain folds. Following this path, the conclusion is that water is the engine of protein folding.

Author Contributions

Conceptualization, G.G.; methodology, M.C. and G.G.; validation, M.C. and G.G.; writing—original draft preparation, M.C. and G.G.; writing—review and editing, M.C. and G.G.; supervision, G.G.; project administration, G.G.; funding acquisition, G.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Università degli Studi del Sannio, FRA 2023.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Kauzmann, W. Some Factors in the Interpretation of Protein Denaturation. In Advances in Protein Chemistry; Elsevier: Amsterdam, The Netherlands, 1959; Volume 14, pp. 1–63. ISBN 978-0-12-034214-3. [Google Scholar]
  2. Dill, K.A. Dominant Forces in Protein Folding. Biochemistry 1990, 29, 7133–7155. [Google Scholar] [CrossRef] [PubMed]
  3. Blokzijl, W.; Engberts, J.B.F.N. Hydrophobic Effects. Opinions and Facts. Angew. Chem. Int. Ed. Engl. 1993, 32, 1545–1579. [Google Scholar] [CrossRef]
  4. Southall, N.T.; Dill, K.A.; Haymet, A.D.J. A View of the Hydrophobic Effect. J. Phys. Chem. B 2002, 106, 521–533. [Google Scholar] [CrossRef]
  5. Ball, P. Water as an Active Constituent in Cell Biology. Chem. Rev. 2008, 108, 74–108. [Google Scholar] [CrossRef]
  6. Sumi, T.; Imamura, H. WATER-MEDIATED Interactions Destabilize Proteins. Protein Sci. 2021, 30, 2132–2143. [Google Scholar] [CrossRef]
  7. Murphy, K.P.; Privalov, P.L.; Gill, S.J. Common Features of Protein Unfolding and Dissolution of Hydrophobic Compounds. Science 1990, 247, 559–561. [Google Scholar] [CrossRef]
  8. Herzfeld, J. Understanding Hydrophobic Behavior. Science 1991, 253, 88. [Google Scholar] [CrossRef]
  9. Muller, N. Does Hydrophobic Hydration Destabilize Protein Native Structures? Trends Biochem. Sci. 1992, 17, 459–463. [Google Scholar] [CrossRef]
  10. Oobatake, M.; Ooi, T. Hydration and Heat Stability Effects on Protein Unfolding. Prog. Biophys. Mol. Biol. 1993, 59, 237–284. [Google Scholar] [CrossRef]
  11. Makhatadze, G.I.; Privalov, P.L. Energetics of Protein Structure. In Advances in Protein Chemistry; Elsevier: Amsterdam, The Netherlands, 1995; Volume 47, pp. 307–425. ISBN 978-0-12-034247-1. [Google Scholar]
  12. Smith, P.E.; Van Gunsteren, W.F. When Are Free Energy Components Meaningful? J. Phys. Chem. 1994, 98, 13735–13740. [Google Scholar] [CrossRef]
  13. Mark, A.E.; Van Gunsteren, W.F. Decomposition of the Free Energy of a System in Terms of Specific Interactions. J. Mol. Biol. 1994, 240, 167–176. [Google Scholar] [CrossRef] [PubMed]
  14. Boresch, S.; Karplus, M. The Meaning of Component Analysis: Decomposition of the Free Energy in Terms of Specific Interactions. J. Mol. Biol. 1995, 254, 801–807. [Google Scholar] [CrossRef] [PubMed]
  15. Lee, B.; Richards, F.M. The Interpretation of Protein Structures: Estimation of Static Accessibility. J. Mol. Biol. 1971, 55, 379-IN4. [Google Scholar] [CrossRef]
  16. Richards, F.M.; Lim, W.A. An Analysis of Packing in the Protein Folding Problem. Quart. Rev. Biophys. 1993, 26, 423–498. [Google Scholar] [CrossRef] [PubMed]
  17. Gekko, K.; Noguchi, H. Compressibility of Globular Proteins in Water at 25. Degree. C. J. Phys. Chem. 1979, 83, 2706–2714. [Google Scholar] [CrossRef]
  18. Kharakoz, D.P. Protein Compressibility, Dynamics, and Pressure. Biophys. J. 2000, 79, 511–525. [Google Scholar] [CrossRef]
  19. Cooper, A. Thermodynamic Fluctuations in Protein Molecules. Proc. Natl. Acad. Sci. USA 1976, 73, 2740–2741. [Google Scholar] [CrossRef]
  20. Cooper, A. Heat Capacity of Hydrogen-Bonded Networks: An Alternative View of Protein Folding Thermodynamics. Biophys. Chem. 2000, 85, 25–39. [Google Scholar] [CrossRef]
  21. Schrödinger, E.; Penrose, R. What Is Life?: With Mind and Matter and Autobiographical Sketches, 1st ed.; Cambridge University Press: Cambridge, UK, 1992; ISBN 978-0-521-42708-1. [Google Scholar]
  22. Liquori, A.M. The Stereochemical Code and the Logic of a Protein Molecule. Quart. Rev. Biophys. 1969, 2, 65–92. [Google Scholar] [CrossRef]
  23. Nozaki, Y.; Tanford, C. The Solubility of Amino Acids and Two Glycine Peptides in Aqueous Ethanol and Dioxane Solutions. J. Biol. Chem. 1971, 246, 2211–2217. [Google Scholar] [CrossRef]
  24. Damodaran, S.; Song, K.B. The Role of Solvent Polarity in the Free Energy of Transfer of Amino Acid Side Chains from Water to Organic Solvents. J. Biol. Chem. 1986, 261, 7220–7222. [Google Scholar] [CrossRef] [PubMed]
  25. Andrew Karplus, P. Hydrophobicity Regained. Protein Sci. 1997, 6, 1302–1307. [Google Scholar] [CrossRef] [PubMed]
  26. Miller, S.; Janin, J.; Lesk, A.M.; Chothia, C. Interior and Surface of Monomeric Proteins. J. Mol. Biol. 1987, 196, 641–656. [Google Scholar] [CrossRef] [PubMed]
  27. Harpaz, Y.; Gerstein, M.; Chothia, C. Volume Changes on Protein Folding. Structure 1994, 2, 641–649. [Google Scholar] [CrossRef] [PubMed]
  28. Merlino, A.; Pontillo, N.; Graziano, G. A Driving Force for Polypeptide and Protein Collapse. Phys. Chem. Chem. Phys. 2017, 19, 751–756. [Google Scholar] [CrossRef]
  29. Cooper, A. Protein Heat Capacity: An Anomaly That Maybe Never Was. J. Phys. Chem. Lett. 2010, 1, 3298–3304. [Google Scholar] [CrossRef]
  30. Dill, K.A. Additivity Principles in Biochemistry. J. Biol. Chem. 1997, 272, 701–704. [Google Scholar] [CrossRef]
  31. Dill, K.A. Polymer Principles and Protein Folding. Protein Sci. 1999, 8, 1166–1180. [Google Scholar] [CrossRef]
  32. Ben-Naim, A. Solvation Thermodynamics; Springer: Boston, MA, USA, 1987; ISBN 978-1-4757-6552-6. [Google Scholar]
  33. Lee, B. A Procedure for Calculating Thermodynamic Functions of Cavity Formation from the Pure Solvent Simulation Data. J. Chem. Phys. 1985, 83, 2421–2425. [Google Scholar] [CrossRef]
  34. Pohorille, A.; Pratt, L.R. Cavities in Molecular Liquids and the Theory of Hydrophobic Solubilities. J. Am. Chem. Soc. 1990, 112, 5066–5074. [Google Scholar] [CrossRef]
  35. Tomasi, J.; Persico, M. Molecular Interactions in Solution: An Overview of Methods Based on Continuous Distributions of the Solvent. Chem. Rev. 1994, 94, 2027–2094. [Google Scholar] [CrossRef]
  36. Graziano, G. Scaled Particle Theory Study of the Length Scale Dependence of Cavity Thermodynamics in Different Liquids. J. Phys. Chem. B 2006, 110, 11421–11426. [Google Scholar] [CrossRef] [PubMed]
  37. Graziano, G. Dimerization Thermodynamics of Large Hydrophobic Plates: A Scaled Particle Theory Study. J. Phys. Chem. B 2009, 113, 11232–11239. [Google Scholar] [CrossRef]
  38. McQuarrie, D.A. Statistical Mechanics; Harper’s Chemistry Series; Harper & Row: New York, NY, USA, 1976; ISBN 978-0-06-044366-5. [Google Scholar]
  39. Graziano, G. Contrasting the Hydration Thermodynamics of Methane and Methanol. Phys. Chem. Chem. Phys. 2019, 21, 21418–21430. [Google Scholar] [CrossRef] [PubMed]
  40. Bologna, A.; Graziano, G. Remarks on the Hydration Entropy of Polar and Nonpolar Species. J. Mol. Liq. 2023, 391, 123437. [Google Scholar] [CrossRef]
  41. Soper, A.K.; Finney, J.L. Hydration of Methanol in Aqueous Solution. Phys. Rev. Lett. 1993, 71, 4346–4349. [Google Scholar] [CrossRef]
  42. Buchanan, P.; Aldiwan, N.; Soper, A.K.; Creek, J.L.; Koh, C.A. Decreased Structure on Dissolving Methane in Water. Chem. Phys. Lett. 2005, 415, 89–93. [Google Scholar] [CrossRef]
  43. Graziano, G. Structural Order in the Hydration Shell of Nonpolar Groups versus That in Bulk Water. ChemPhysChem 2024, 25, e202400102. [Google Scholar] [CrossRef]
  44. Graziano, G. The Gibbs Energy Cost of Cavity Creation Depends on Geometry. J. Mol. Liq. 2015, 211, 1047–1051. [Google Scholar] [CrossRef]
  45. Pierotti, R.A. A Scaled Particle Theory of Aqueous and Nonaqueous Solutions. Chem. Rev. 1976, 76, 717–726. [Google Scholar] [CrossRef]
  46. Wallqvist, A.; Berne, B.J. Molecular Dynamics Study of the Dependence of Water Solvation Free Energy on Solute Curvature and Surface Area. J. Phys. Chem. 1995, 99, 2885–2892. [Google Scholar] [CrossRef]
  47. Patel, A.J.; Varilly, P.; Chandler, D.; Garde, S. Quantifying Density Fluctuations in Volumes of All Shapes and Sizes Using Indirect Umbrella Sampling. J. Stat. Phys. 2011, 145, 265–275. [Google Scholar] [CrossRef] [PubMed]
  48. Sosso, G.C.; Caravati, S.; Rotskoff, G.; Vaikuntanathan, S.; Hassanali, A. On the Role of Nonspherical Cavities in Short Length-Scale Density Fluctuations in Water. J. Phys. Chem. A 2017, 121, 370–380. [Google Scholar] [CrossRef] [PubMed]
  49. Royer, C.A. Revisiting Volume Changes in Pressure-Induced Protein Unfolding. Biochim. Biophys. Acta (BBA) Protein Struct. Mol. Enzymol. 2002, 1595, 201–209. [Google Scholar] [CrossRef]
  50. Chalikian, T.V. Volumetric Properties of Proteins. Annu. Rev. Biophys. Biomol. Struct. 2003, 32, 207–235. [Google Scholar] [CrossRef]
  51. Chen, C.R.; Makhatadze, G.I. Molecular Determinant of the Effects of Hydrostatic Pressure on Protein Folding Stability. Nat. Commun. 2017, 8, 14561. [Google Scholar] [CrossRef]
  52. Graziano, G. On the Molecular Origin of Cold Denaturation of Globular Proteins. Phys. Chem. Chem. Phys. 2010, 12, 14245. [Google Scholar] [CrossRef]
  53. Graziano, G. On the Mechanism of Cold Denaturation. Phys. Chem. Chem. Phys. 2014, 16, 21755–21767. [Google Scholar] [CrossRef]
  54. Pica, A.; Graziano, G. Shedding Light on the Extra Thermal Stability of Thermophilic Proteins. Biopolymers 2016, 105, 856–863. [Google Scholar] [CrossRef]
  55. Maritan, A.; Micheletti, C.; Trovato, A.; Banavar, J.R. Optimal Shapes of Compact Strings. Nature 2000, 406, 287–290. [Google Scholar] [CrossRef]
  56. Banavar, J.R.; Maritan, A. Physics of Proteins. Annu. Rev. Biophys. Biomol. Struct. 2007, 36, 261–280. [Google Scholar] [CrossRef] [PubMed]
  57. Liquori, A.M.; Sadun, C. Close Packing of Amino Acid Residues in Globular Proteins: Specific Volume and Site Binding of Water Molecules. Int. J. Biol. Macromol. 1981, 3, 56–59. [Google Scholar] [CrossRef]
  58. Head-Gordon, T.; Hura, G. Water Structure from Scattering Experiments and Simulation. Chem. Rev. 2002, 102, 2651–2670. [Google Scholar] [CrossRef] [PubMed]
  59. Dill, K.A.; Chan, H.S. From Levinthal to Pathways to Funnels. Nat. Struct. Biol. 1997, 4, 10–19. [Google Scholar] [CrossRef] [PubMed]
  60. Wolynes, P.G. Evolution, Energy Landscapes and the Paradoxes of Protein Folding. Biochimie 2015, 119, 218–230. [Google Scholar] [CrossRef]
  61. Baxa, M.C.; Haddadian, E.J.; Jumper, J.M.; Freed, K.F.; Sosnick, T.R. Loss of Conformational Entropy in Protein Folding Calculated Using Realistic Ensembles and Its Implications for NMR-Based Calculations. Proc. Natl. Acad. Sci. USA 2014, 111, 15396–15401. [Google Scholar] [CrossRef]
  62. Gong, H.; Porter, L.L.; Rose, G.D. Counting Peptide-water Hydrogen Bonds in Unfolded Proteins. Protein Sci. 2011, 20, 417–427. [Google Scholar] [CrossRef]
  63. Rose, G.D. Reframing the Protein Folding Problem: Entropy as Organizer. Biochemistry 2021, 60, 3753–3761. [Google Scholar] [CrossRef]
  64. Rose, G.D. Protein Folding—Seeing Is Deceiving. Protein Sci. 2021, 30, 1606–1616. [Google Scholar] [CrossRef]
  65. Privalov, P.L. Stability of Proteins Small Globular Proteins. In Advances in Protein Chemistry; Elsevier: Amsterdam, The Netherlands, 1979; Volume 33, pp. 167–241. ISBN 978-0-12-034233-4. [Google Scholar]
  66. Privalou, P.L. Thermodynamic Problems of Protein Structure. Annu. Rev. Biophys. Biophys. Chem. 1989, 18, 47–69. [Google Scholar] [CrossRef]
  67. Kaya, H.; Chan, H.S. Polymer Principles of Protein Calorimetric Two-State Cooperativity. Proteins 2000, 40, 637–661. [Google Scholar] [CrossRef] [PubMed]
  68. Becktel, W.J.; Schellman, J.A. Protein Stability Curves. Biopolymers 1987, 26, 1859–1877. [Google Scholar] [CrossRef]
  69. Kell, G.S. Density, Thermal Expansivity, and Compressibility of Liquid Water from 0.Deg. to 150.Deg.. Correlations and Tables for Atmospheric Pressure and Saturation Reviewed and Expressed on 1968 Temperature Scale. J. Chem. Eng. Data 1975, 20, 97–105. [Google Scholar] [CrossRef]
  70. Robertson, A.D.; Murphy, K.P. Protein Structure and the Energetics of Protein Stability. Chem. Rev. 1997, 97, 1251–1268. [Google Scholar] [CrossRef] [PubMed]
  71. Sawle, L.; Ghosh, K. How Do Thermophilic Proteins and Proteomes Withstand High Temperature? Biophys. J. 2011, 101, 217–227. [Google Scholar] [CrossRef] [PubMed]
  72. Lee, B. Enthalpy-Entropy Compensation in the Thermodynamics of Hydrophobicity. Biophys. Chem. 1994, 51, 271–278. [Google Scholar] [CrossRef] [PubMed]
  73. Dunitz, J.D. Win Some, Lose Some: Enthalpy-Entropy Compensation in Weak Intermolecular Interactions. Chem. Biol. 1995, 2, 709–712. [Google Scholar] [CrossRef]
  74. Harano, Y.; Kinoshita, M. Translational-Entropy Gain of Solvent upon Protein Folding. Biophys. J. 2005, 89, 2701–2710. [Google Scholar] [CrossRef]
  75. Kinoshita, M. A New Theoretical Approach to Biological Self-Assembly. Biophys. Rev. 2013, 5, 283–293. [Google Scholar] [CrossRef]
  76. Kinoshita, M. Importance of Translational Entropy of Water in Biological Self-Assembly Processes like Protein Folding. Int. J. Mol. Sci. 2009, 10, 1064–1080. [Google Scholar] [CrossRef]
  77. Maruyama, Y.; Harano, Y. Does Water Drive Protein Folding? Chem. Phys. Lett. 2013, 581, 85–90. [Google Scholar] [CrossRef]
  78. Kamo, F.; Ishizuka, R.; Matubayasi, N. Correlation Analysis for Heat Denaturation of Trp-cage Miniprotein with Explicit Solvent. Protein Sci. 2016, 25, 56–66. [Google Scholar] [CrossRef]
  79. Tokunaga, Y.; Yamamori, Y.; Matubayasi, N. Probabilistic Analysis for Identifying the Driving Force of Protein Folding. J. Chem. Phys. 2018, 148, 125101. [Google Scholar] [CrossRef] [PubMed]
Biophysica 04 00033 g001
Figure 1. Schematic representation of the thermodynamic cycle describing the folding–unfolding transition of a protein. ΔG●(F) and ΔG●(U) are the Gibbs free energy changes associated with the hydration of the folded and unfolded states, respectively. ΔGd and ΔGconf are the Gibbs free energy changes for the unfolding of the protein in water and in the gas phase, respectively. According to the thermodynamic cycle, the denaturation Gibbs free energy change is given by the following: ΔGd = ΔGconf + ΔG●(U) − ΔG●(F) (1). Considering that hydration consists of cavity creation and switching on solute-water energetic attractions, Equation (1) becomes ΔGd = ΔE(intra) − T⋅ΔSconf + ΔGc(U) + Ea(U-water) − ΔGc(F) − Ea(F-water) (2). This can be rearranged to ΔGd = [ΔGc(U) − ΔGc(F)] − T⋅ΔSconf + [Ea(U-water) − Ea(F-water) + ΔE(intra)] (3). Equation (3) has the merit of grouping together the terms due to (a) the translational entropy of water molecules—which comes from the difference in solvent-excluded volume effect associated with the change in cavity shape—(b) the conformational entropy of the chain, and (c) the protein-water and intra-protein energetic attractions. See the text for details.
Figure 1. Schematic representation of the thermodynamic cycle describing the folding–unfolding transition of a protein. ΔG●(F) and ΔG●(U) are the Gibbs free energy changes associated with the hydration of the folded and unfolded states, respectively. ΔGd and ΔGconf are the Gibbs free energy changes for the unfolding of the protein in water and in the gas phase, respectively. According to the thermodynamic cycle, the denaturation Gibbs free energy change is given by the following: ΔGd = ΔGconf + ΔG●(U) − ΔG●(F) (1). Considering that hydration consists of cavity creation and switching on solute-water energetic attractions, Equation (1) becomes ΔGd = ΔE(intra) − T⋅ΔSconf + ΔGc(U) + Ea(U-water) − ΔGc(F) − Ea(F-water) (2). This can be rearranged to ΔGd = [ΔGc(U) − ΔGc(F)] − T⋅ΔSconf + [Ea(U-water) − Ea(F-water) + ΔE(intra)] (3). Equation (3) has the merit of grouping together the terms due to (a) the translational entropy of water molecules—which comes from the difference in solvent-excluded volume effect associated with the change in cavity shape—(b) the conformational entropy of the chain, and (c) the protein-water and intra-protein energetic attractions. See the text for details.
Biophysica 04 00033 g001
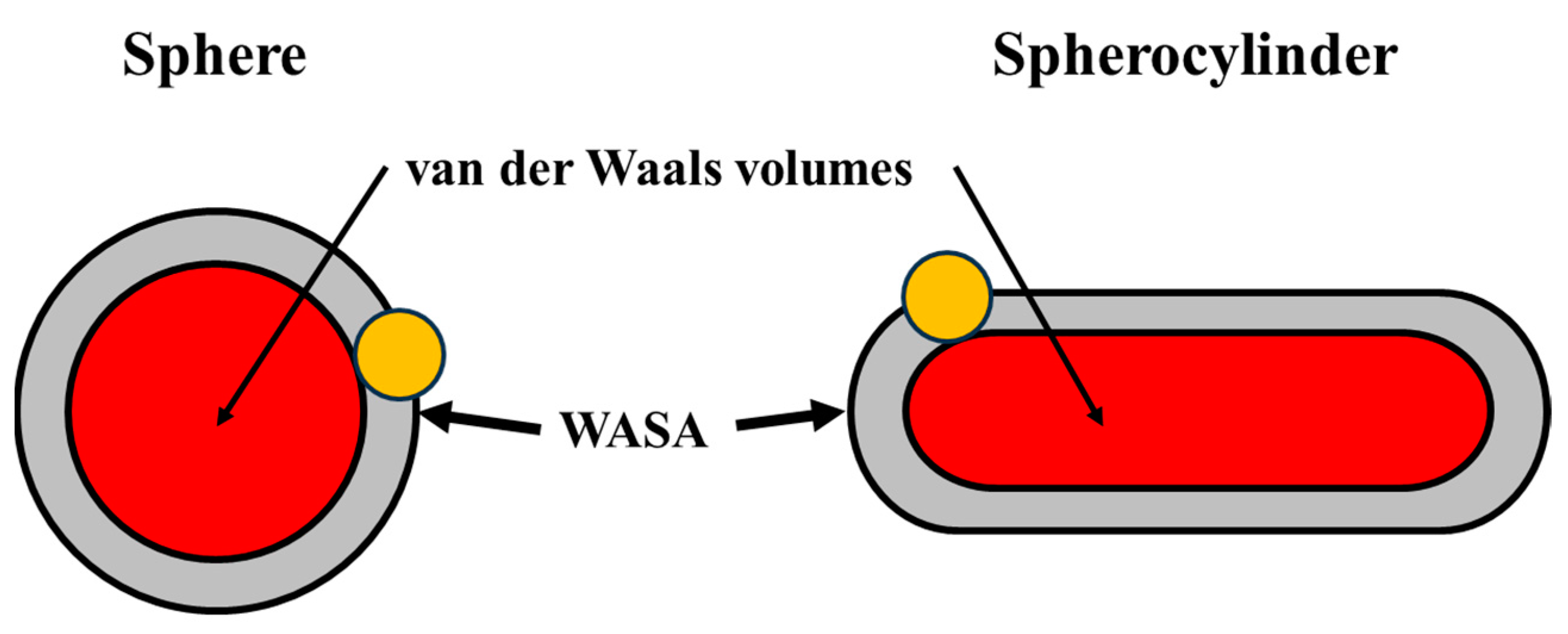
Biophysica 04 00033 g002
Figure 2. Schematic 2D representation of the van der Waals volume, VvdW, and the Water Accessible Surface Area, WASA, of a sphere and a prolate spherocylinder, the two objects chosen to represent the folded and the unfolded states, respectively, of a globular protein. The yellow sphere represents a water molecule that, rolling on the surface of the inner sphere or the inner spherocylinder, defines their WASA. The two objects must have the same VvdW to model the globular protein states; in the picture, they are not to scale.
Figure 2. Schematic 2D representation of the van der Waals volume, VvdW, and the Water Accessible Surface Area, WASA, of a sphere and a prolate spherocylinder, the two objects chosen to represent the folded and the unfolded states, respectively, of a globular protein. The yellow sphere represents a water molecule that, rolling on the surface of the inner sphere or the inner spherocylinder, defines their WASA. The two objects must have the same VvdW to model the globular protein states; in the picture, they are not to scale.
Biophysica 04 00033 g002
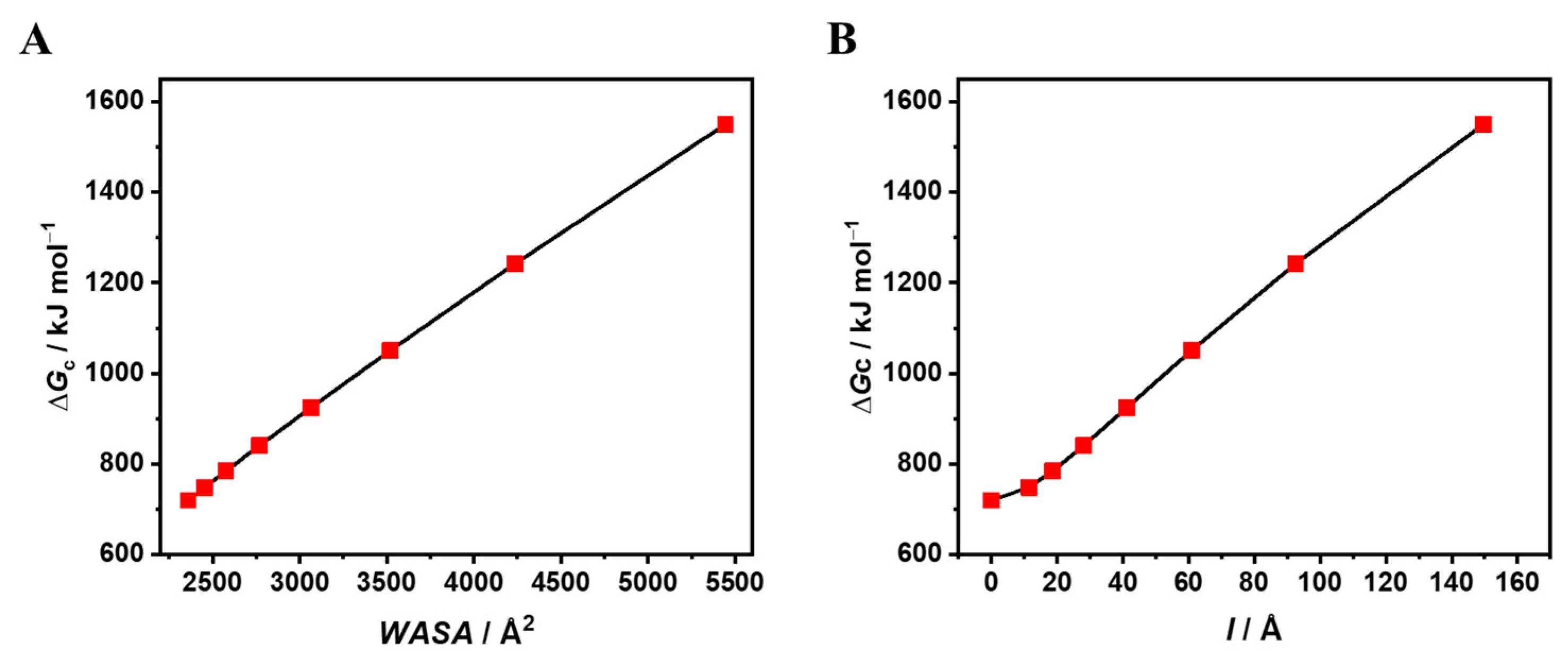
Biophysica 04 00033 g003
Figure 3. Plots of the ΔGc values calculated by means of classic SPT relationships, at 20 °C and 1 atm, as a function of (A) WASA and (B) cylindrical length (l). Red squares indicate the calculated data points. Black curves were added as a guide for the eye.
Figure 3. Plots of the ΔGc values calculated by means of classic SPT relationships, at 20 °C and 1 atm, as a function of (A) WASA and (B) cylindrical length (l). Red squares indicate the calculated data points. Black curves were added as a guide for the eye.
Biophysica 04 00033 g003
Biophysica 04 00033 g004
Figure 4. Temperature dependence of ΔHd for a protein with 76 residues, calculated using thermodynamic values from the datasets of Robertson and Murphy (black line with empty circles) and Sawle and Ghosh (black line with empty squares). The temperature dependence of αP(H2O) is also reported (red curve and red squares). The intersection between the dashed black lines indicates the temperature of maximum density of water, TMD = 4 °C.
Figure 4. Temperature dependence of ΔHd for a protein with 76 residues, calculated using thermodynamic values from the datasets of Robertson and Murphy (black line with empty circles) and Sawle and Ghosh (black line with empty squares). The temperature dependence of αP(H2O) is also reported (red curve and red squares). The intersection between the dashed black lines indicates the temperature of maximum density of water, TMD = 4 °C.
Biophysica 04 00033 g004
Table 1. Classic SPT-ΔGc values to create prolate spherocylindrical cavities, at 20 °C and 1 atm, in a hard sphere fluid having the experimental density of water and particle diameter σ(H2O) = 2.8 Å. By fixing the cavity VvdW to that of a sphere of 12.3 Å radius, ΔGc values were calculated on increasing the cylindrical length-to-radius ratio (l/a). The values of the spherical cavity are reported in the first row.
Table 1. Classic SPT-ΔGc values to create prolate spherocylindrical cavities, at 20 °C and 1 atm, in a hard sphere fluid having the experimental density of water and particle diameter σ(H2O) = 2.8 Å. By fixing the cavity VvdW to that of a sphere of 12.3 Å radius, ΔGc values were calculated on increasing the cylindrical length-to-radius ratio (l/a). The values of the spherical cavity are reported in the first row.
a
Å		l
Å		VvdW
Å3		WASA
Å2		ΔGc
kJ mol−1		ΔGc/WASA
J mol−1 Å−2
12.3/77902359719.8305.1
10.011.4677902454748.6305.1
9.018.6177902575784.6304.7
8.028.0777902768840.7303.7
7.041.2777903065925.2301.9
6.060.88779035191050.9298.6
5.092.51779042351242.2293.3
4.0149.65779054441550.1284.7
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Campanile, M.; Graziano, G. Is Water the Engine of Protein Folding? Biophysica 2024, 4, 507-516. https://doi.org/10.3390/biophysica4040033

AMA Style

Campanile M, Graziano G. Is Water the Engine of Protein Folding? Biophysica. 2024; 4(4):507-516. https://doi.org/10.3390/biophysica4040033

Chicago/Turabian Style

Campanile, Marco, and Giuseppe Graziano. 2024. "Is Water the Engine of Protein Folding?" Biophysica 4, no. 4: 507-516. https://doi.org/10.3390/biophysica4040033

APA Style

Campanile, M., & Graziano, G. (2024). Is Water the Engine of Protein Folding? Biophysica, 4(4), 507-516. https://doi.org/10.3390/biophysica4040033

Article Metrics

Back to TopTop