Modulatory Impact of Tefluthrin, Telmisartan, and KB-R7943 on Voltage-Gated Na+ Currents
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals, Reagents, and Solutions Used in This Study
2.2. Cell Preparation
2.3. Electrophysiological Measurements
2.4. Data Recordings
2.5. Curve-Fitting Procedures for INa Inactivation Time Course
2.6. Statistical Analyses
2.7. Computer Simulations
2.8. Numerical Simulation Technique Employed in This Study
3. Results
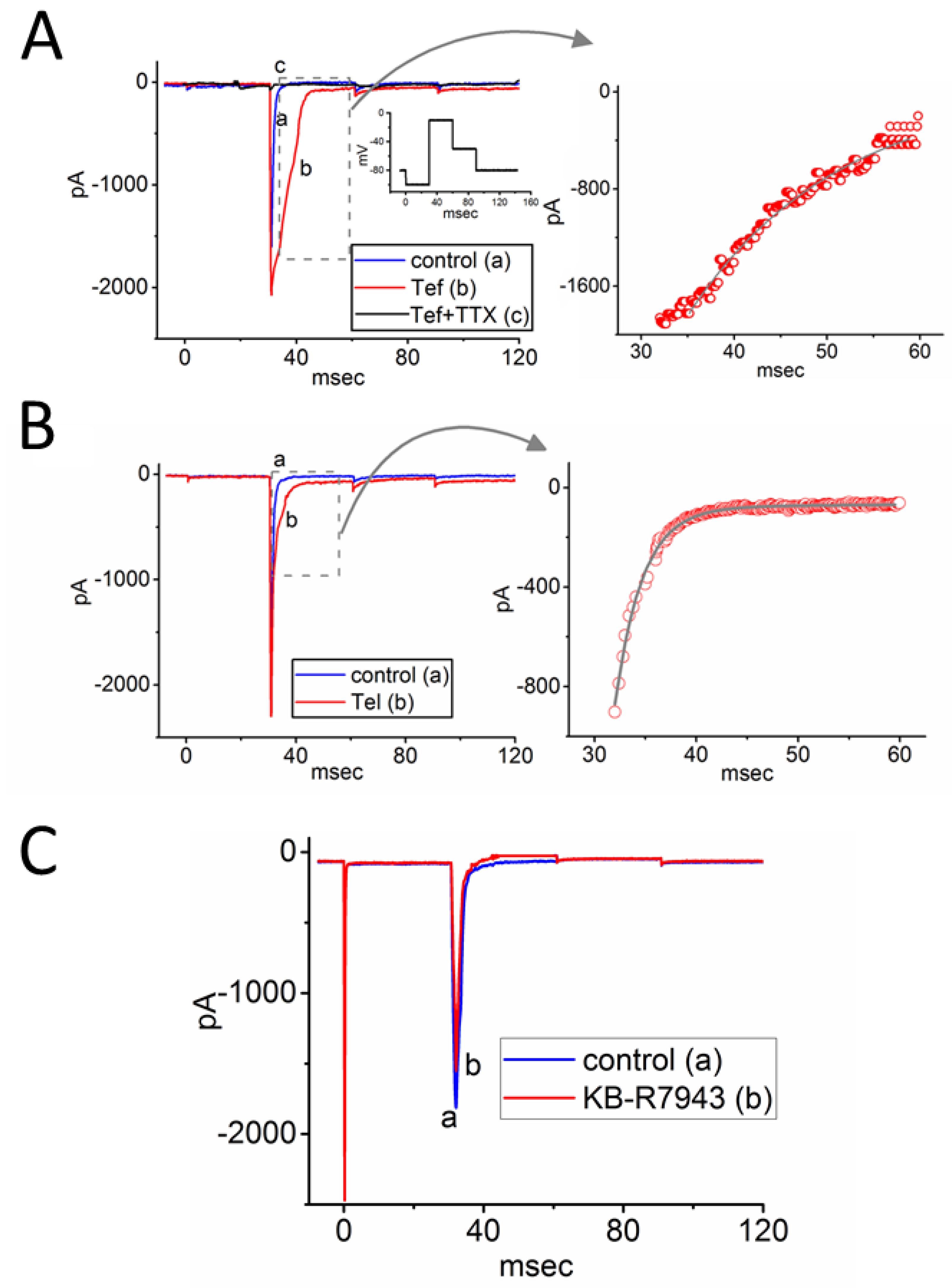
3.1. Effects of Either Tef, Tel, or KB-R7943 on INa Measured from Rat DRG Neurons
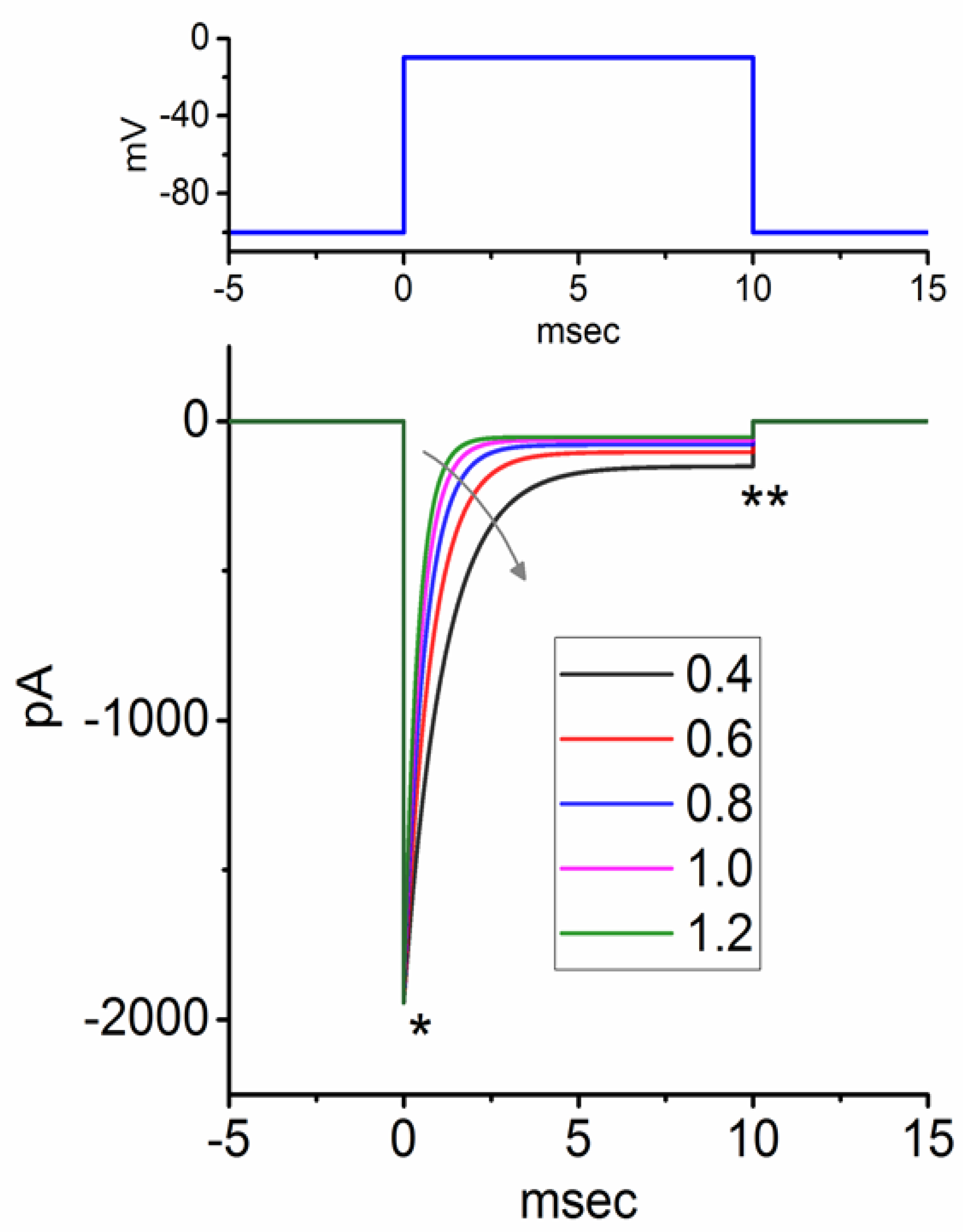
3.2. Simulated INa Traces Created from a Modified HH Model
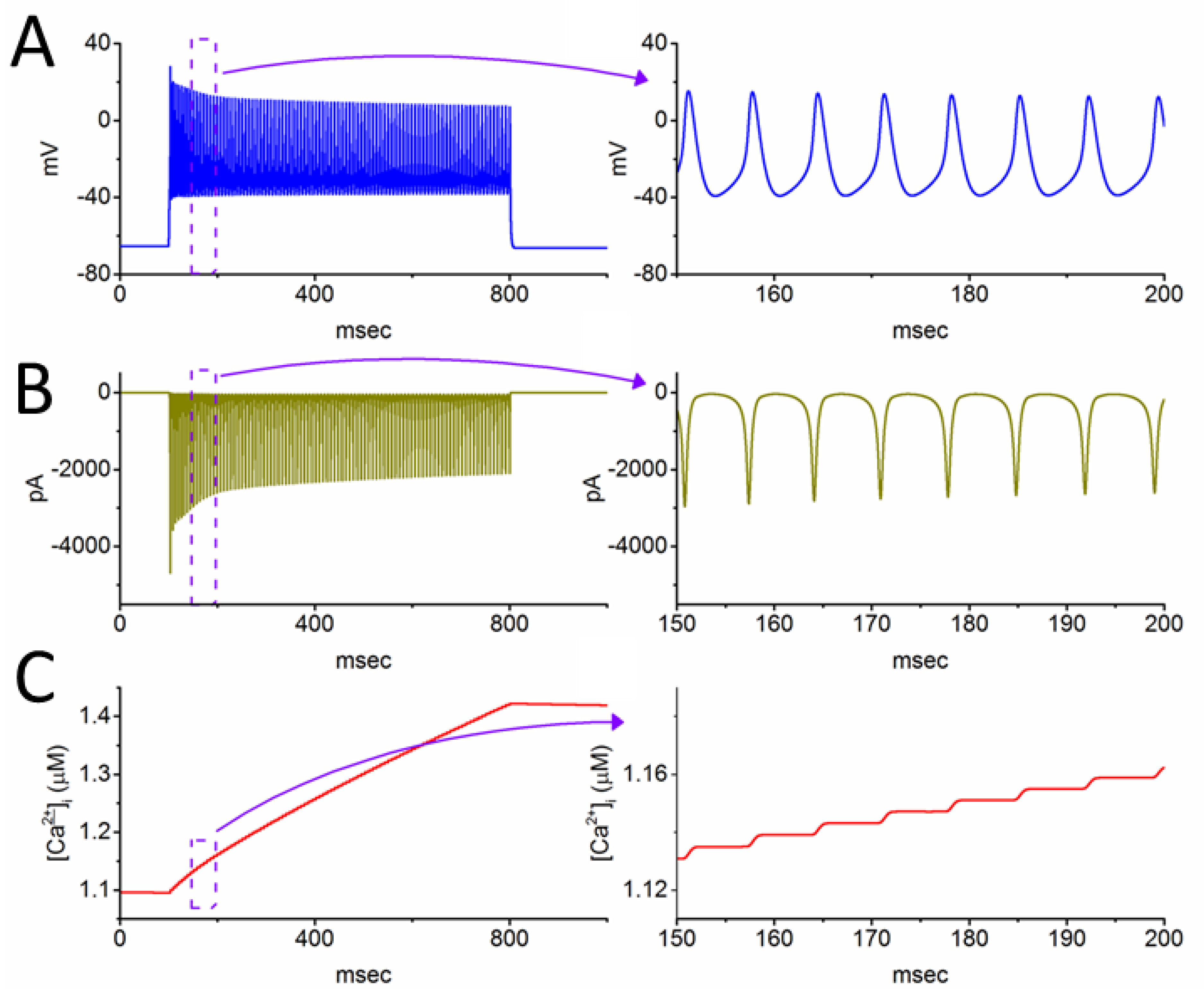
3.3. Changes of Membrane Potential Caused by Different Value of
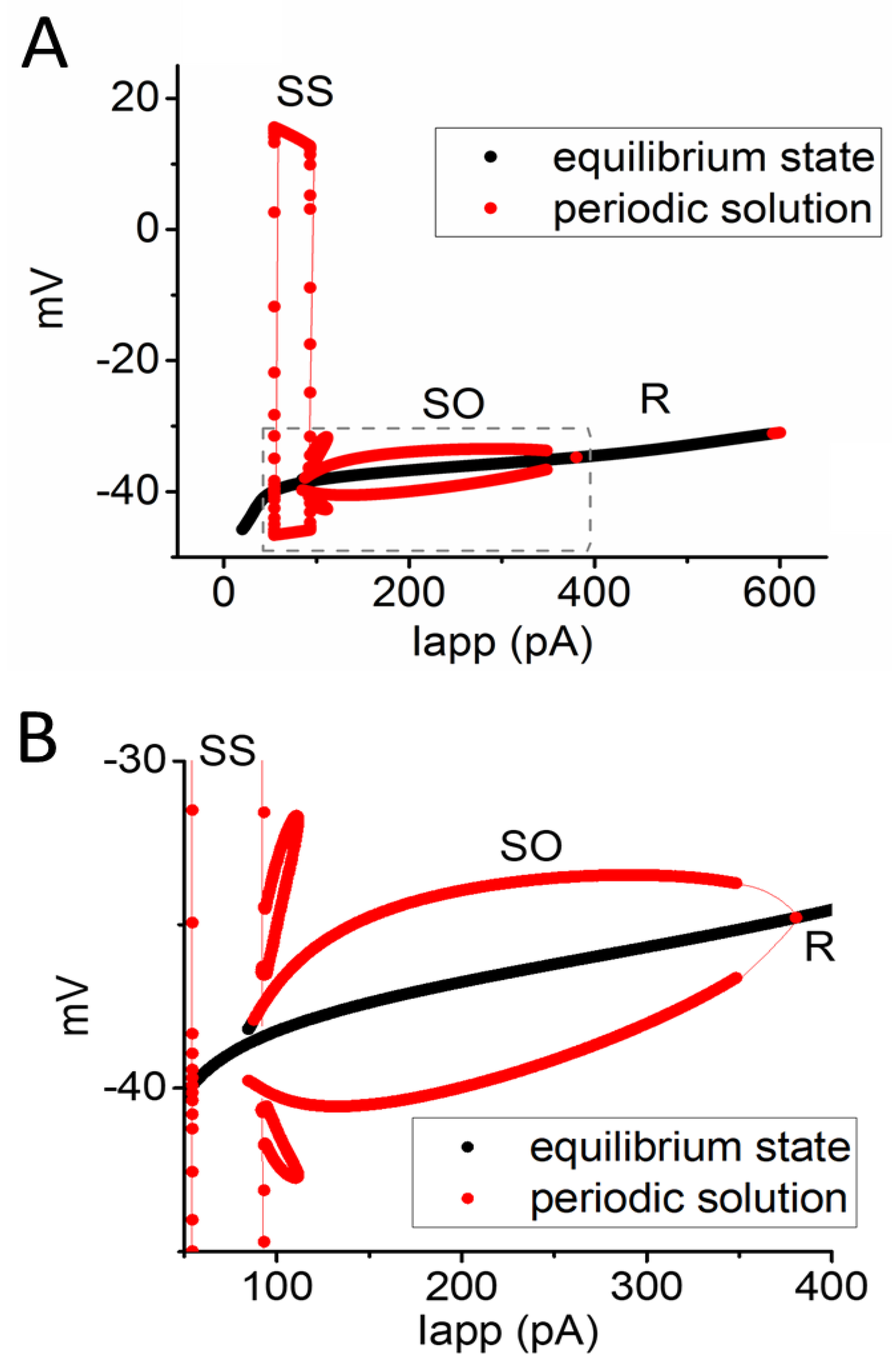
3.4. Relationship of Changes in Steady-State Membrane Potential vs. the Iapp Value
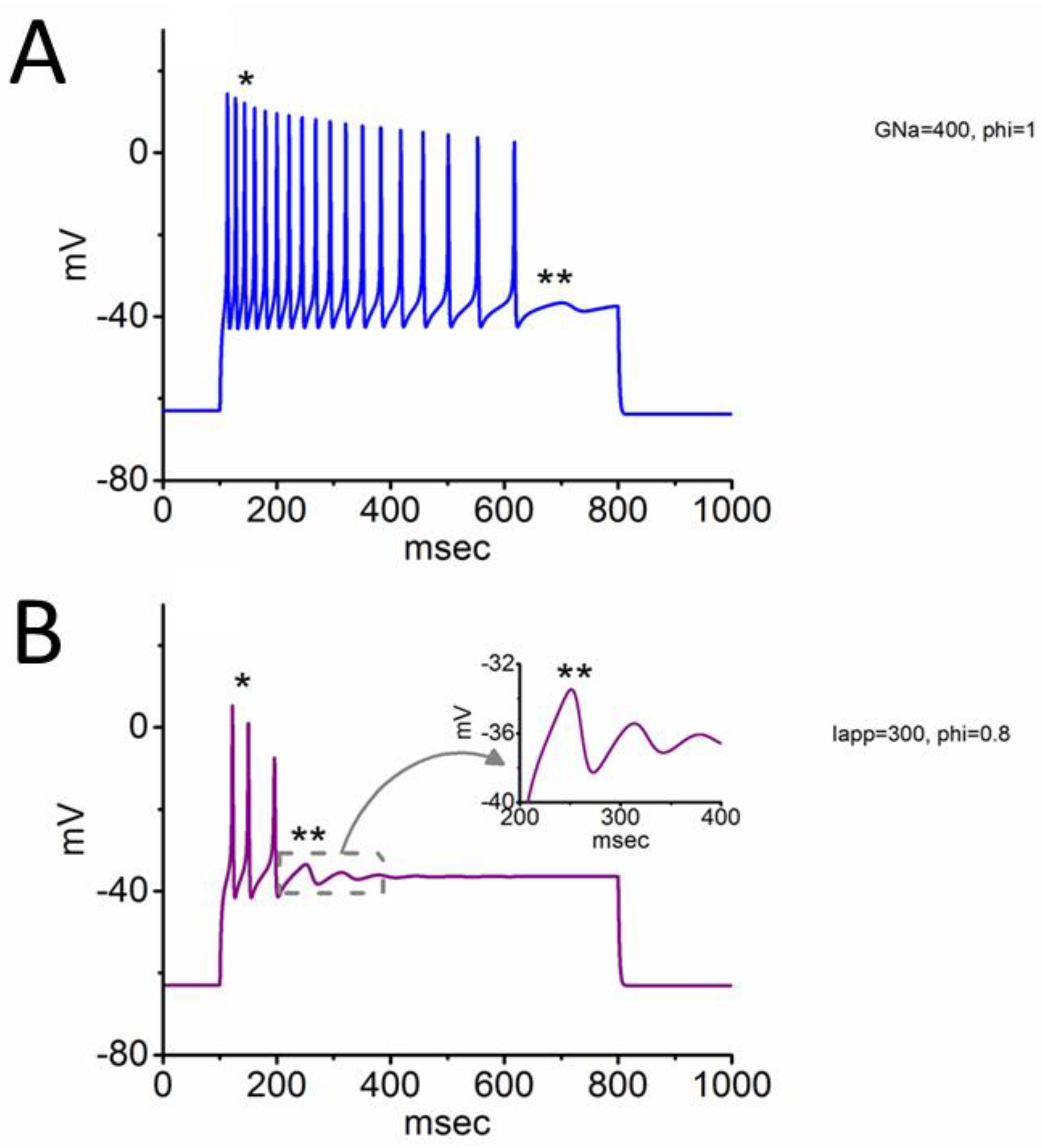
3.5. Further Modifications on Changes in Membrane Potential with the Increasing Iapp Value with a Fixed Value of 0.8
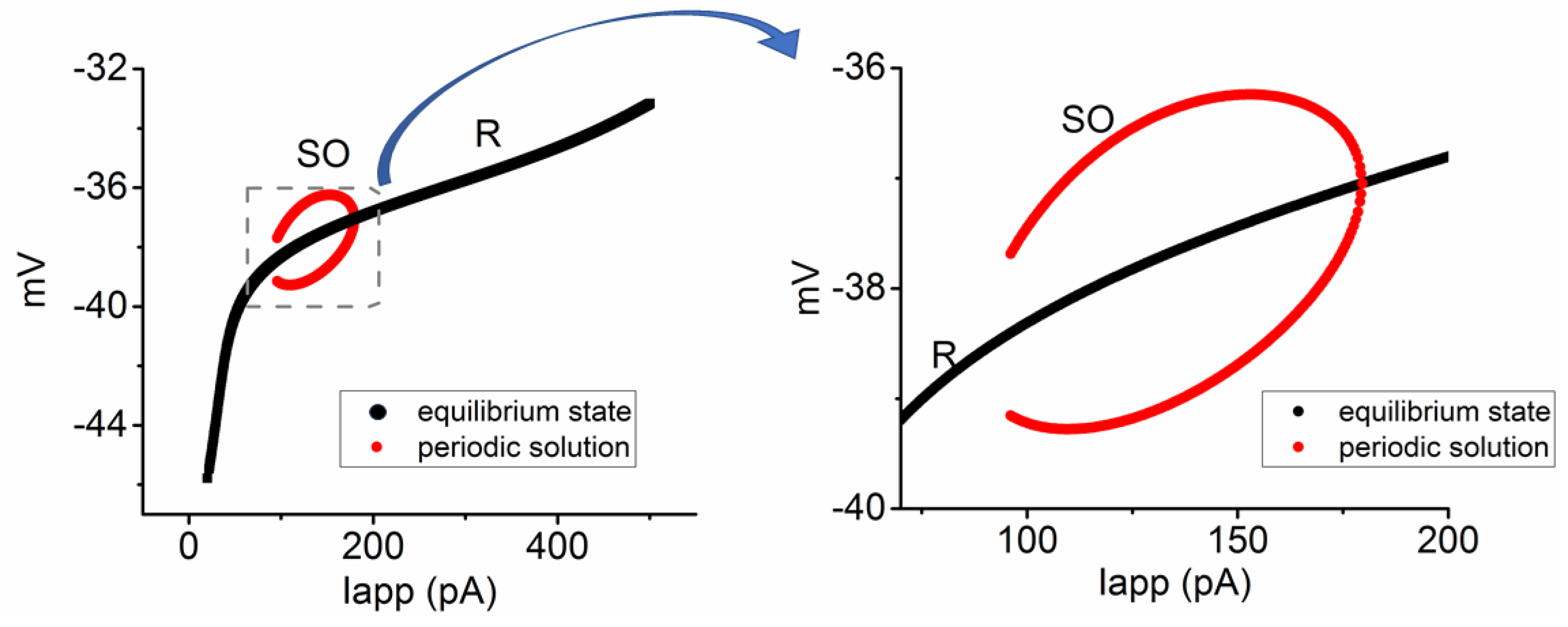
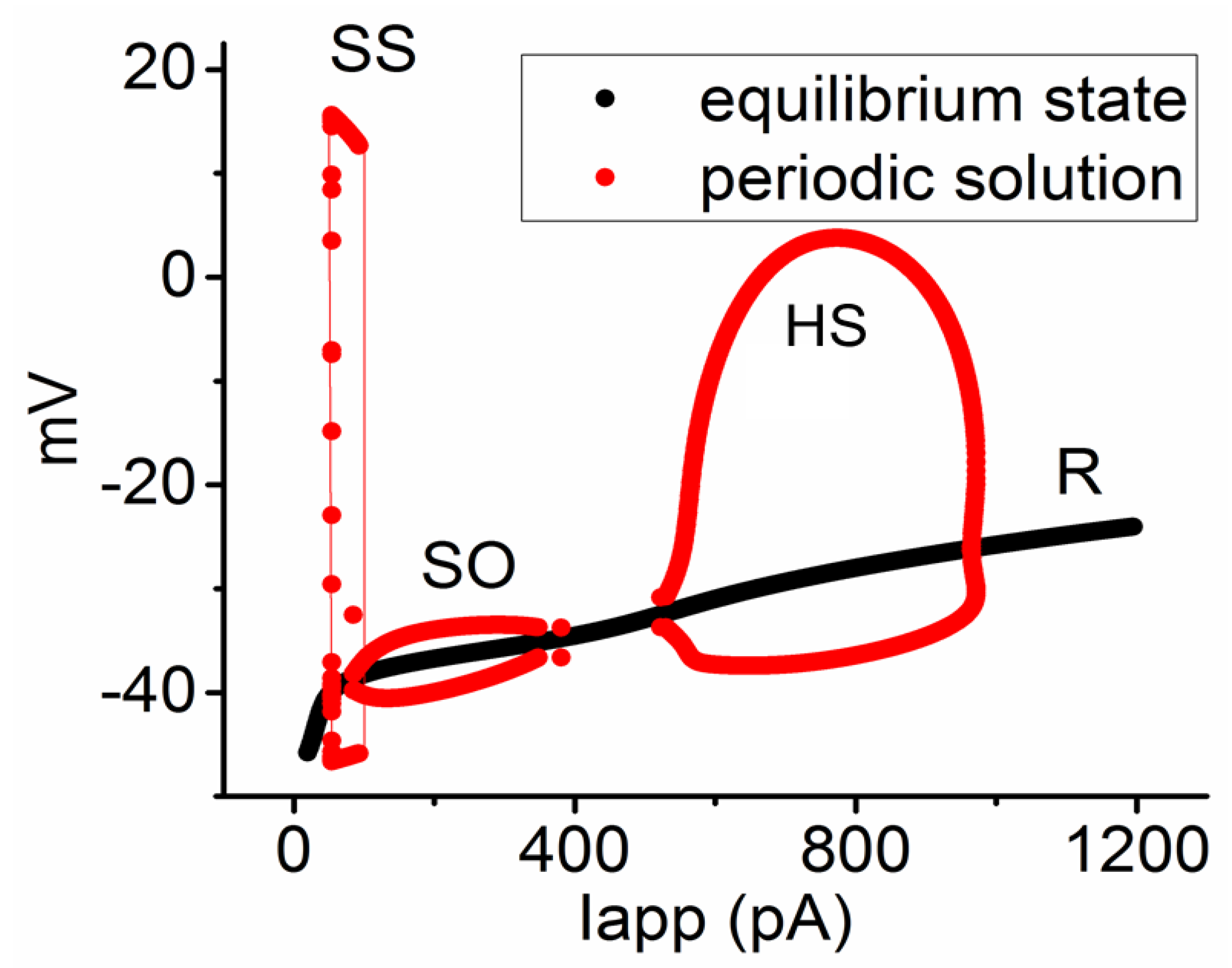
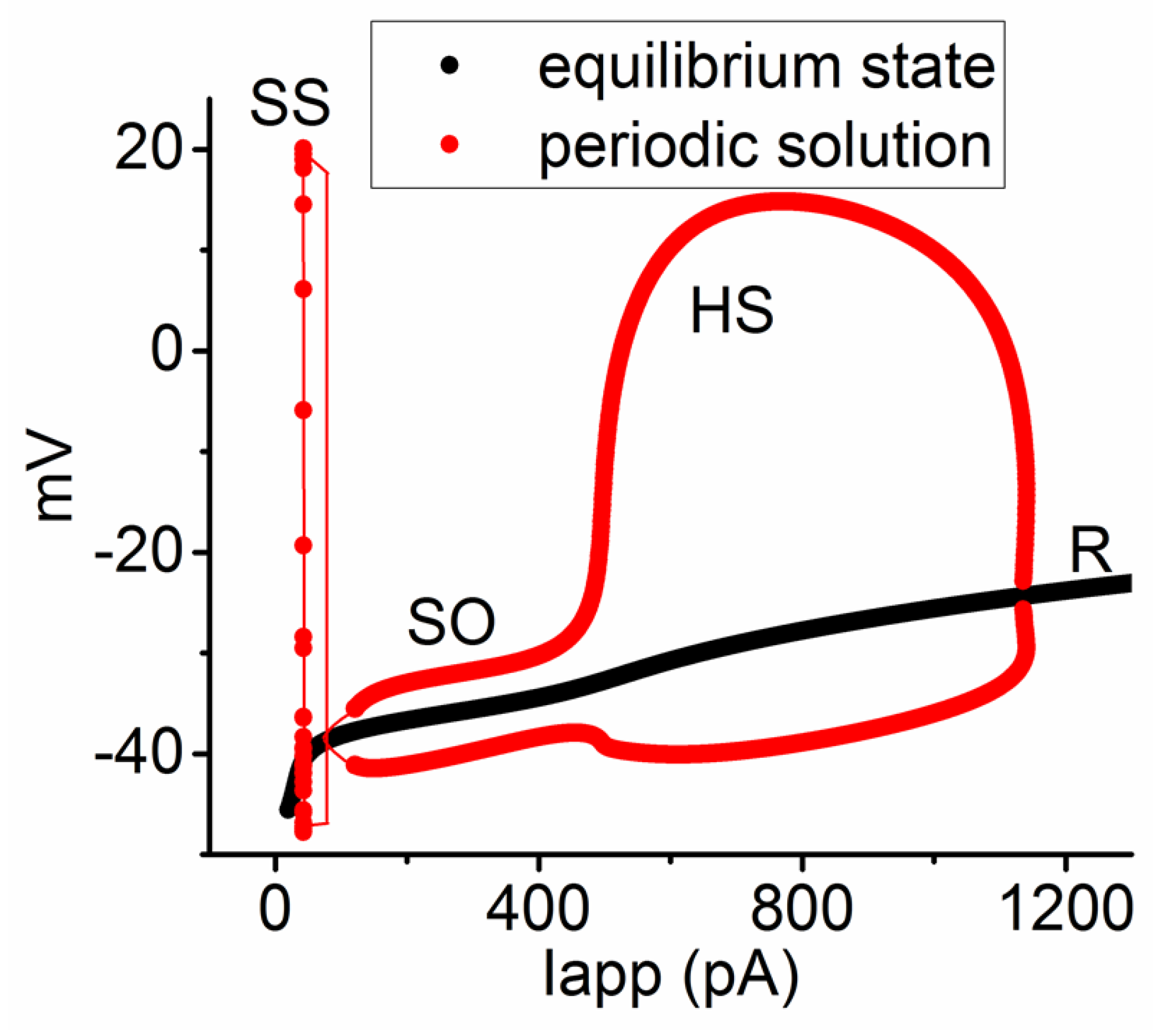
3.6. Bifurcation Analysis on the Relationship between Iapp and Membrane Potential at the Range between 0 and 1200 pA
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Catterall, W.A. Voltage-gated sodium channels at 60: Structure, function and pathophysiology. J. Physiol. 2012, 590, 2577–2589. [Google Scholar] [CrossRef] [PubMed]
- De Lera Ruiz, M.; Kraus, R.L. Voltage-Gated Sodium Channels: Structure, Function, Pharmacology, and Clinical Indications. J. Med. Chem. 2015, 58, 7093–7118. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Zhou, Q.; Pan, X.; Li, Z.; Wu, J.; Yan, N. Structure of a eukaryotic voltage-gated sodium channel at near-atomic resolution. Science 2017, 355, eaal4326. [Google Scholar] [CrossRef]
- Bennett, D.L.; Clark, A.J.; Huang, J.; Waxman, S.G.; Dib-Hajj, S.D. The Role of Voltage-Gated Sodium Channels in Pain Signaling. Physiol. Rev. 2019, 99, 1079–1151. [Google Scholar] [CrossRef] [PubMed]
- Taddese, A.; Bean, B.P. Subthreshold Sodium Current from Rapidly Inactivating Sodium Channels Drives Spontaneous Firing of Tuberomammillary Neurons. Neuron 2002, 33, 587–600. [Google Scholar] [CrossRef]
- Carter, B.C.; Bean, B.P. Incomplete Inactivation and Rapid Recovery of Voltage-Dependent Sodium Channels During High-Frequency Firing in Cerebellar Purkinje Neurons. J. Neurophysiol. 2011, 105, 860–871. [Google Scholar] [CrossRef]
- Huang, C.-W.; Hung, T.-Y.; Wu, S.-N. The inhibitory actions by lacosamide, a functionalized amino acid, on voltage-gated Na+ currents. Neuroscience 2015, 287, 125–136. [Google Scholar] [CrossRef]
- So, E.C.; Wu, S.-N.; Lo, Y.-C.; Su, K. Differential regulation of tefluthrin and telmisartan on the gating charges of INa activation and inactivation as well as on resurgent and persistent INa in a pituitary cell line (GH3). Toxicol. Lett. 2018, 285, 104–112. [Google Scholar] [CrossRef]
- Lin, M.-H.; Lin, J.-F.; Yu, M.-C.; Wu, S.-N.; Wu, C.-L.; Cho, H.-Y. Characterization in Potent Modulation on Voltage-Gated Na+ Current Exerted by Deltamethrin, a Pyrethroid Insecticide. Int. J. Mol. Sci. 2022, 23, 14733. [Google Scholar] [CrossRef]
- Jiang, N.; Nutter, T.J.; Cooper, B.Y. Molecular and cellular influences of permethrin on mammalian nociceptors at physiological temperatures. NeuroToxicology 2013, 37, 207–219. [Google Scholar] [CrossRef]
- Silwal, P.M.; Adhikari, R.; Yadav, B.M.; Sah, S.K.M.; Bhatt, A.; Basnet, S.M. Lambda-cyhalothrin ingestion: An infrequent yet concerning presentation of pyrethroid poisoning. Ann. Med. Surg. 2023, 85, 5250–5254. [Google Scholar] [CrossRef] [PubMed]
- Hegazy, N.; Rezq, S.; Fahmy, A. Renin-angiotensin system blockade modulates both the peripheral and central components of neuropathic pain in rats: Role of calcitonin gene–related peptide, substance P and nitric oxide. Basic Clin. Pharmacol. Toxicol. 2020, 127, 451–460. [Google Scholar] [CrossRef] [PubMed]
- Schweighofer, N.; Doya, K.; Kawato, M.; Davoine, F.; Curti, S.; Hakimian, S.; Norris, S.A.; Greger, B.; Keating, J.G.; Anderson, C.H.; et al. Electrophysiological properties of inferior olive neurons: A compartmental model. J. Neurophysiol. 1999, 82, 804–817. [Google Scholar] [CrossRef] [PubMed]
- Amran, S.; Homma, N.; Hashimoto, K. Pharmacology of KB-R7943: A Na+–Ca2+ exchange inhibitor. Cardiovasc. Drug Rev. 2003, 21, 255–276. [Google Scholar] [CrossRef]
- Huang, Y.; Wen, L.-L.; Xie, J.-D.; Ouyang, H.-D.; Chen, D.-T.; Zeng, W.-A. Antinociceptive effectiveness of the inhibition of NCX reverse-mode action in rodent neuropathic pain model. Mol. Pain 2019, 15, 1744806919864511. [Google Scholar] [CrossRef]
- Andreeva-Gateva, P.; Hristov, M.; Strokova-Stoilova, M.; Ivanova, N.; Sabit, Z.; Surcheva, S.; Beliakov, M.; Karakashev, G.; Sukhov, I.; Belinskaya, D.; et al. Therapeutic potential of orally applied KB-R7943 in streptozotocin-induced neuropathy in rats. Heliyon 2024, 10, e27367. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Miraucourt, L.S.; Qiu, H.; Sharif-Naeini, R.; Khadra, A. Modulation of SK Channels via Calcium Buffering Tunes Intrinsic Excitability of Parvalbumin Interneurons in Neuropathic Pain: A Computational and Experimental Investigation. J. Neurosci. 2023, 43, 5608–5622. [Google Scholar] [CrossRef]
- White, J.; Budde, T.; Kay, A. A bifurcation analysis of neuronal subthreshold oscillations. Biophys. J. 1995, 69, 1203–1217. [Google Scholar] [CrossRef]
- Enns-Ruttan, J.S.; Miura, R.M. Spontaneous Secondary Spiking in Excitable Cells. J. Theor. Biol. 2000, 205, 181–199. [Google Scholar] [CrossRef]
- Chang, T.-T.; Yang, C.-J.; Lee, Y.-C.; Wu, S.-N. Stimulatory Action of Telmisartan, an Antagonist of Angiotensin II Receptor, on Voltage-Gated Na^+ Current: Experimental and Theoretical Studies. Chin. J. Physiol. 2018, 61, 1–13. [Google Scholar] [CrossRef]
- Wu, S.-N.; Yu, M.-C. Inhibition of Voltage-Gated Na+ Currents Exerted by KB-R7943 (2-[2-[4-(4-nitrobenzyloxy)phenyl]ethyl]isothiourea), an Inhibitor of Na+-Ca2+ Exchanging Process. Int. J. Mol. Sci. 2023, 24, 1805. [Google Scholar] [CrossRef] [PubMed]
- Brown, A.M. A modeling study predicts the presence of voltage gated Ca2+ channels on myelinated central axons. Comput. Methods Programs Biomed. 2002, 71, 25–31. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.-N.; So, E.C.; Liao, Y.-K.; Huang, Y.-M. Reversal by ranolazine of doxorubicin-induced prolongation in the inactivation of late sodium current in rat dorsal root ganglion neurons. Pain Med. 2015, 16, 1032–1034. [Google Scholar] [CrossRef]
- Ghovanloo, M.-R.; Tyagi, S.; Zhao, P.; Effraim, P.R.; Dib-Hajj, S.D.; Waxman, S.G. Sodium currents in naïve mouse dorsal root ganglion neurons: No major differences between sexes. Channels 2023, 18, 2289256. [Google Scholar] [CrossRef]
- Traub, R.D.; Miles, R. Multiple Modes of Neuronal Population Activity Emerge after Modifying Specific Synapses in a Model of the CA3 Region of the Hippocampus. Ann. N. Y. Acad. Sci. 1991, 627, 277–290. [Google Scholar] [CrossRef]
- Winslow, R.L. Bifurcation analysis of nonlinear retinal horizontal cell models. I. Properties of isolated cells. J. Neurophysiol. 1989, 62, 738–749. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.-N. Simulations of the cardiac action potential based on the Hodgkin-Huxley kinetics with the use of Microsoft Excel spreadsheets. Chin. J. Physiol. 2004, 47, 15–22. [Google Scholar]
- Chen, B.-S. Effects of Transient Receptor Potential-Like Current on the Firing Pattern of Action Potentials in the Hodgkin-Huxley Neuron during Exposure to Sinusoidal External Voltage. Chin. J. Physiol. 2010, 53, 423–429. [Google Scholar] [CrossRef] [PubMed]
- Chiesa, N.; Rosati, B.; Arcangeli, A.; Olivotto, M.; Wanke, E. A Novel Role for HERG K+ Channels: Spike-Frequency Adaptation. J. Physiol. 1997, 501, 313–318. [Google Scholar] [CrossRef]
- Wu, S.; Yeh, C.; Huang, H.; So, E.C.; Lo, Y. Electrophysiological characterization of sodium-activated potassium channels in NG108-15 and NSC-34 motor neuron-like cells. Acta Physiol. 2012, 206, 120–134. [Google Scholar] [CrossRef]
- A Navarro, M.; Salari, A.; Lin, J.L.; Cowan, L.M.; Penington, N.J.; Milescu, M.; Milescu, L.S. Sodium channels implement a molecular leaky integrator that detects action potentials and regulates neuronal firing. eLife 2020, 9, e54940. [Google Scholar] [CrossRef] [PubMed]
- Schröder, U.H.; Breder, J.; Sabelhaus, C.F.; Reymann, K.G. The novel Na+/Ca2+ exchange inhibitor KB-R7943 protects CA1 neurons in rat hippocampal slices against hypoxic/hypoglycemic injury. Neuropharmacology 1999, 38, 319–321. [Google Scholar] [CrossRef] [PubMed]
- Roy, M.; Narahashi, T. Differential properties of tetrodotoxin-sensitive and tetrodotoxin- resistant sodium channels in rat dorsal root ganglion neurons. J. Neurosci. 1992, 12, 2104–2111. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.M.; Kim, H.I.; Shin, Y.K.; Lee, C.S.; Park, M.; Song, J.-H. Diclofenac inhibition of sodium currents in rat dorsal root ganglion neurons. Brain Res. 2003, 992, 120–127. [Google Scholar] [CrossRef] [PubMed]
- Szulczyk, B.; Pasierski, M.; Gawlak, M. Prefrontal cortex pyramidal neurons express functional Nav1.8 tetrodotoxin-resistant sodium currents. Clin. Exp. Pharmacol. Physiol. 2021, 49, 350–359. [Google Scholar] [CrossRef]
- Kim, H.K.; Youm, J.B.; Lee, S.R.; Lim, S.E.; Ko, T.H.; Long, L.T.; Nilius, B.; Won, D.N.; Noh, J.-H.; Ko, K.S.; et al. The angiotensin receptor blocker and PPAR-γ agonist, telmisartan, delays inactivation of voltage-gated sodium channel in rat heart: Novel mechanism of drug action. Pflügers Arch. Eur. J. Physiol. 2012, 464, 631–643. [Google Scholar] [CrossRef]
- Chang, W.; Wu, S. Activation of voltage-gated sodium current and inhibition of erg-mediated potassium current caused by telmisartan, an antagonist of angiotensin II type-1 receptor, in HL-1 atrial cardiomyocytes. Clin. Exp. Pharmacol. Physiol. 2018, 45, 797–807. [Google Scholar] [CrossRef]
- Lai, M.-C.; Wu, S.-N.; Huang, C.-W. Telmisartan, an Antagonist of Angiotensin II Receptors, Accentuates Voltage-Gated Na+ Currents and Hippocampal Neuronal Excitability. Front. Neurosci. 2020, 14, 902. [Google Scholar] [CrossRef]
- Lu, T.-L.; Wu, S.-N. Investigating the Impact of Selective Modulators on the Renin–Angiotensin–Aldosterone System: Unraveling Their Off-Target Perturbations of Transmembrane Ionic Currents. Int. J. Mol. Sci. 2023, 24, 14007. [Google Scholar] [CrossRef]
- Gould, H.J.; Soignier, R.D.; Cho, S.R.; Hernandez, C.; Diamond, I.; Taylor, B.K.; Paul, D. Ranolazine Attenuates Mechanical Allodynia Associated with Demyelination Injury. Pain Med. 2014, 15, 1771–1780. [Google Scholar] [CrossRef]
- Gould, H.J.; Diamond, I. Ranolazine: A potential treatment for refractory neuropathic pain. J. Neurol. Sci. 2016, 369, 310–311. [Google Scholar] [CrossRef] [PubMed]
- Castellanos, A.; Andres, A.; Bernal, L.; Callejo, G.; Comes, N.; Gual, A.; Giblin, J.P.; Roza, C.; Gasull, X. Pyrethroids inhibit K2P channels and activate sensory neurons: Basis of insecticide-induced paraesthesias. Pain 2017, 159, 92–105. [Google Scholar] [CrossRef] [PubMed]
- Karádi, D.; Galambos, A.R.; Lakatos, P.P.; Apenberg, J.; Abbood, S.K.; Balogh, M.; Kiraly, K.; Riba, P.; Essmat, N.; Szucs, E.; et al. Telmisartan Is a Promising Agent for Managing Neuropathic Pain and Delaying Opioid Analgesic Tolerance in Rats. Int. J. Mol. Sci. 2023, 24, 7970. [Google Scholar] [CrossRef] [PubMed]
- Klemic, K.G.; Kirsch, G.E.; Jones, S.W. U-Type Inactivation of Kv3.1 and Shaker Potassium Channels. Biophys. J. 2001, 81, 814–826. [Google Scholar] [CrossRef] [PubMed]
- Lin, M.-W.; Wang, Y.-J.; Liu, S.-I.; Lin, A.-A.; Lo, Y.-C.; Wu, S.-N. Characterization of aconitine-induced block of delayed rectifier K+ current in differentiated NG108-15 neuronal cells. Neuropharmacology 2008, 54, 912–923. [Google Scholar] [CrossRef]
- Wang, Y.-J.; Lin, M.-W.; Lin, A.-A.; Peng, H.; Wu, S.-N. Evidence for state-dependent block of DPI 201-106, a synthetic inhibitor of Na+ channel inactivation, on delayed-rectifier K+ current in pituitary tumor (GH3) cells. Acta Physiol. Pol. 2008, 59, 409–423. [Google Scholar]
- Wu, S.-N.; Chen, B.-S.; Lin, M.-W.; Liu, Y.-C. Contribution of slowly inactivating potassium current to delayed firing of action potentials in NG108-15 neuronal cells: Experimental and theoretical studies. J. Theor. Biol. 2008, 252, 711–721. [Google Scholar] [CrossRef]
- Hsiao, H.-T.; Wang, J.C.-F.; Wu, S.-N. Inhibitory Effectiveness in Delayed-Rectifier Potassium Current Caused by Vortioxetine, Known to Be a Novel Antidepressant. Biomedicines 2022, 10, 1318. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, D.; Darwish, Y.; Fu, X.; Trussell, L.O.; Huang, H. KCNQ Channels Enable Reliable Presynaptic Spiking and Synaptic Transmission at High Frequency. J. Neurosci. 2022, 42, 3305–3315. [Google Scholar] [CrossRef]
- Woolf, C.J.; Ma, Q. Nociceptors—Noxious Stimulus Detectors. Neuron 2007, 55, 353–364. [Google Scholar] [CrossRef]
- Nascimento de Lima, A.P.; Zhang, H.; Chen, L.; Effraim, P.R.; Gomis-Perez, C.; Cheng, X.; Huang, J.; Waxman, S.G.; Dib-Hajj, S.D. Nav1.8 in small dorsal root ganglion neurons contributes to vincristine-induced mechanical allodynia. Brain 2024, 147, 3157–3170. [Google Scholar] [CrossRef] [PubMed]
- Fukuoka, T.; Kobayashi, K.; Noguchi, K. Laminae-specific distribution of alpha-subunits of voltage-gated sodium channels in the adult rat spinal cord. Neuroscience 2010, 169, 994–1006. [Google Scholar] [CrossRef]
- Petitjean, H.; Pawlowski, S.A.; Fraine, S.L.; Sharif, B.; Hamad, D.; Fatima, T.; Berg, J.; Brown, C.M.; Jan, L.-Y.; Ribeiro-Da-Silva, A.; et al. Dorsal Horn Parvalbumin Neurons Are Gate-Keepers of Touch-Evoked Pain after Nerve Injury. Cell Rep. 2015, 13, 1246–1257. [Google Scholar] [CrossRef] [PubMed]
- Gradwell, M.A.; Boyle, K.A.; Browne, T.J.; Bell, A.M.; Leonardo, J.; Reyes, F.S.P.; Dickie, A.C.; Smith, K.M.; Callister, R.J.; Dayas, C.V.; et al. Diversity of inhibitory and excitatory parvalbumin interneuron circuits in the dorsal horn. Pain 2021, 163, e432–e452. [Google Scholar] [CrossRef] [PubMed]
- Stangier, J.; Schmid, J.; Türck, D.; Switek, H.; Verhagen, A.; Peeters, P.A.; van Marle, S.P.; Tamminga, W.J.; Sollie, F.A.; Jonkman, J.H. Absorption, metabolism, and excretion of intravenously and orally administered [14C]telmisartan in healthy volunteers. J. Clin. Pharmacol. 2000, 40, 1312–1322. [Google Scholar] [CrossRef] [PubMed]
- Miyata, A.; Zipes, D.P.; Hall, S.; Rubart, M. KB-R7943 Prevents Acute, Atrial Fibrillation–Induced Shortening of Atrial Refractoriness in Anesthetized Dogs. Circulation 2002, 106, 1410–1419. [Google Scholar] [CrossRef]
- Wu, S.-N.; Wu, Y.-H.; Chen, B.-S.; Lo, Y.-C.; Liu, Y.-C. Underlying mechanism of actions of tefluthrin, a pyrethroid insecticide, on voltage-gated ion currents and on action currents in pituitary tumor (GH3) cells and GnRH-secreting (GT1-7) neurons. Toxicology 2009, 258, 70–77. [Google Scholar] [CrossRef]

| Symbol or Parameter | Description * | Value |
|---|---|---|
| Cm | Membrane capacitance (pF) | 30 |
| gNa | Maximum Na+ current conductance (nS) | 300 |
| gCa | Maximum Ca2+ current conductance (nS) | 8 |
| gK1 | Maximum KV1 current conductance (nS) | 15 |
| gK3 | Maximum KV3 current conductance (nS) | 180 |
| gSK | Maximum SK K+ current conductance (nS) | 10 |
| gleak | Maximum leak current conductance (nS) | 8 |
| VNa | Na+ reversal potential (mV) | 58 |
| VK | K+ reversal potential (mV) | −80 |
| VCa | Ca2+ reversal potential (mV) | 68 |
| VLeak | Reversal potential for leak current (mV) | −50 |
| γ | Ca2+ recovery rate (ms−1) | 0.01 |
| kSK | Ca2+ sensitivity of SK channel (μM) | 0.8 |
| A | Cell surface area (μm2) | 3000 |
| Adjustable βh-inactivation parameter of h gating variable (dimensionless) | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.-Y.; Huang, Y.-B.; Wu, C.-L.; Wu, S.-N. Modulatory Impact of Tefluthrin, Telmisartan, and KB-R7943 on Voltage-Gated Na+ Currents. Biophysica 2024, 4, 488-506. https://doi.org/10.3390/biophysica4040032
Huang H-Y, Huang Y-B, Wu C-L, Wu S-N. Modulatory Impact of Tefluthrin, Telmisartan, and KB-R7943 on Voltage-Gated Na+ Currents. Biophysica. 2024; 4(4):488-506. https://doi.org/10.3390/biophysica4040032
Chicago/Turabian StyleHuang, Hsun-Yu, Yi-Bo Huang, Chao-Liang Wu, and Sheng-Nan Wu. 2024. "Modulatory Impact of Tefluthrin, Telmisartan, and KB-R7943 on Voltage-Gated Na+ Currents" Biophysica 4, no. 4: 488-506. https://doi.org/10.3390/biophysica4040032
APA StyleHuang, H.-Y., Huang, Y.-B., Wu, C.-L., & Wu, S.-N. (2024). Modulatory Impact of Tefluthrin, Telmisartan, and KB-R7943 on Voltage-Gated Na+ Currents. Biophysica, 4(4), 488-506. https://doi.org/10.3390/biophysica4040032





