Abstract
Statistically significant violations of the Clauser–Horne–Shimony–Holt (CHSH) inequality are the “gold standard” test for quantum entanglement between spatially separated systems. Here, we report an experimental design that implements a CHSH test between bioelectric state variables for a human subject and bioelectric and/or biochemical state variables for cultured human cells in vitro. While we were unable to obtain evidence for entanglement with this design, observing only classical correlation, we report lessons learned and suggest possible avenues for future studies.
1. Introduction
Since its first observation by Aspect et al. in 1982 [1], quantum entanglement between spatially separated systems has become a well-established physical phenomenon [2,3] that serves as the basis for multiple quantum communication, security, and computing technologies [4,5,6,7]. Formally, a state (using the Dirac notation) of a composite quantum system is separable if it factors, i.e., if ; otherwise, it is entangled. Whether a state factors depends on the choice of Hilbert-space basis used to describe it, and hence, on the choice of observables used to characterize it experimentally. Whether entanglement can be observed or accessed as a resource in a given physical situation is, therefore, dependent on both the formal and the experimental methods employed [8,9,10,11,12].
On the theoretical side, entanglement between fundamental processes of information exchange is increasingly being proposed to underlie the structure of spacetime itself [13,14,15,16,17,18]. Such models challenge the idea that entangled systems are “spatially separated”; in particular, they require a distinction between the laboratory reference frame in which systems are observed and any spatial reference frame attributed to the systems themselves. One response to this situation is the “ER = EPR” hypothesis that entangled states are equivalent to Einstein–Rosen (ER) bridges, i.e., to topological connections or “wormholes” between otherwise-distinct regions of spacetime [19]. This hypothesis cannot at present be experimentally tested [20]; however, it has proven theoretically productive, particularly in black-hole physics. If ER = EPR is correct, entangled systems may appear to have spatially separated components when measured in a laboratory reference frame, but nonetheless, have no “internal” spatial separation.
While the idea that living systems employ quantum coherence, and, therefore, entanglement, as an information processing resource was proposed by Schrödinger as early as 1944 [21], searches for entanglement effects in living systems were initially considered to be infeasible due to the scale of expected decoherence effects [22]. Empirical work over the past two decades has, however, yielded considerable evidence for entanglement at the macromolecular scale [23,24,25], although the interpretation of these results remains controversial [26,27,28]. Internal use of entanglement as a computational resource by individual cells is consistent with their measured energy budgets, which, in both prokaryotes and eukaryotes, are orders of magnitude smaller than expected for purely classical information processing [29]. It is also consistent with recent observations of long-range electrodynamic coherence between macromolecules in a cell-like in vitro environment [30].
Entanglement effects can be expected to be even more difficult to demonstrate at the multicellular scale. Lee et al. [31] have approached this problem by abandoning physiological conditions, cooling a tardigrade (Ramazzottius varieornatus) to cryogenic temperatures and demonstrating entanglement between the frozen—but later revived—tardigrade and two qubits implemented micro-electronically. Such methods clearly will not work for entanglement searches in multi-neuron circuits or whole brains, and hence, will not work for testing “quantum brain” theories, of which the OrchOR theory of Hameroff and Penrose [32,33] is the most prominent. A direct approach to this question has been taken by Kerskens and López Pérez [34], who employed nuclear magnetic resonance (NMR) of bulk water in the brain as an entanglement witness to detect whole-brain scale coherence.
It has long been suggested that human perception, decision making, or other aspects of cognition may involve quantum processes [35,36,37,38,39], leading to the development of quantum decision theories [40,41,42]. Motivated by these ideas, psychological methods have also been used to search for entanglement. A large “quantum cognition” literature has claimed to demonstrate entanglement effects via the indirect method of psychological testing of awake human subjects [43]; however, many of these studies have been shown to be statistically flawed [44]. Indeed, it is the difficulty of detecting entanglement, in the form of non-causal or “intrinsic” context dependence [45,46,47], in the presence of classical, causal, context dependence that prompted the development of the contextuality by default (CbD) methodology for statistical analysis of entanglement studies [48,49]. Entanglement effects in human cognition have been demonstrated with high reliability using this latter methodology [50,51].
Here, we describe a search for detectable entanglement effects between brain- or body-scale bioelectric states of a human subject and bioelectric or biochemical states of a population of cultured human cancer cells in vitro. The human subject in these experiments was a biofield therapist [52] practicing the Bengston image-cycling method [53] of biofield therapy (BT). The cells were human PANC-1 pancreatic cancer cells. Our experimental design implemented a standard Clauser–Horne–Shimony–Holt (CHSH) statistical test for entanglement [54], and hence, was insensitive to underlying mechanisms. The entanglement search was motivated by preliminary data [55,56] demonstrating statistically significant effects of BT on cancer cell proliferation, motility, invasiveness, bioelectric state, and protein expression, consistent with previous results examining the effects of BT on lung cancer in mice in vitro and in vivo [57,58], and by the purported distance-independence of BT methods. While entanglement effects were not observed in this study, numerous low-level but statistically significant classical correlations were observed. Here, we report the experimental design, procedures used, and lessons learned from this negative entanglement-search result; a full classical analysis of the data obtained will be reported elsewhere.
2. Materials and Methods
We first describe the general structure of CHSH tests for entanglement [54], which derive from the pioneering work of Bell [59] on the mathematical analysis of thought experiments first proposed by Einstein, Podolsky, and Rosen [60]. We then describe the design and specific methods used in the present experiments.
2.1. General Structure of CHSH Tests
The “gold standard” experimental test for entanglement is, effectively, a test for the existence of a joint probability distribution satisfying the Kolmogorov axioms over a set of outcomes of measurements of two systems, conventionally called A and B. In the CHSH formulation, the test is derived by considering pairs of observables , and , that characterize the systems A and B, respectively, where each of these observables can have either +1 or −1 as an outcome value on each of a large number of independent trials. One then considers the quantity:
where for any variables x and y, the notation denotes the expectation value of a joint measurement of x and y and denotes the absolute value of x. If the A and B observables are mutually independent and perfectly pairwise ( with and with ) classically correlated or anticorrelated, the maximum value is obtained; if they are less than perfectly correlated, . For classical observables, therefore, we have the CHSH inequality:
see [61,62] for formal proof.
In a standard “Bell/EPR” experiment, e.g., as performed by Aspect et al. [1] and as replicated many times thereafter, e.g., [63,64,65,66,67,68,69,70], a source emits pairs of “particles” that can each occupy one of two states or that are or can be conceptualized as “spin” states and . The states are measured at locations A and B using detectors that each have an adjustable “setting” that is, or can be conceptualized as, a polarization angle. For classically correlated, but unentangled, spins, the expectation value for pairs of outcomes obtained at the two locations is proportional to the difference between the polarization angles. For pairs of spins in opposite directions, the usual situation for CHSH tests, the outcomes at A and B will be perfectly anticorrelated at 0° and 360° angular separation, perfectly correlated at 180° angular separation, and perfectly uncorrelated at 90° and 270° angular separation, as shown in Figure 1. Entangled photons, however, interfere with each other, replacing the linear dependence on angle with:
where a and b are the polarizer angles. This correlation function differs maximally from the classical correlation at 45°, 135°, 225°, and 315° as shown in Figure 1. These are the optimal angles for a CHSH experiment, and are those chosen in practice. Two of these angles are employed at each location, allowing the choice of angle at each site to be coded as +1 or −1. While the maximal violation of Equation (2) is Tsirelson’s bound [71], , the actual values obtained experimentally are typically significantly less; e.g., Rowe et al. [65] achieved values of S between 2.2 and 2.3 in an experiment using atomic states as entangled “spin” pairs, while Cervantes and Dzhafarov [50] achieved S∼2.4 with human subjects using binary-choice questions.
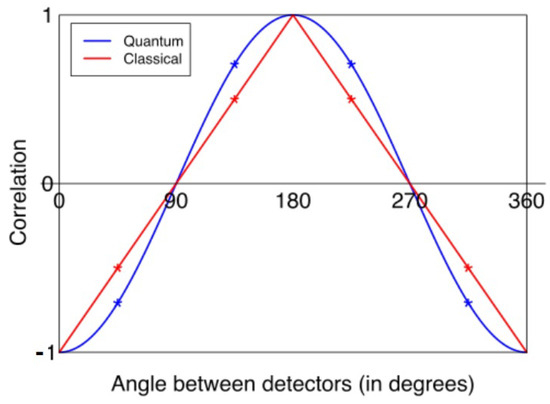
Figure 1.
Expected outcome values for joint measurements of photon pairs at A and B as a function of difference in polarizer angles, assuming perfect classical correlation (red) and entanglement (blue). Optimal angles are indicated by asterisks. From [72], CC-BY license.
Physical systems can exhibit apparent violations of the CHSH inequality, and hence, apparent entanglement effects, if the time resolution of measurements is sufficiently low that alterations of the “settings” at one measurement site can causally affect the outcomes obtained at the other site. “Causal” here means via some mechanism that transfers information at less than or equal to the speed of light; hence, such effects are often referred to as “signaling” effects. Such confounding causal mechanisms can be avoided by manipulating the “settings” in times much shorter than the light travel time between instruments, i.e., in nanoseconds to microseconds for instruments located meters to kilometers apart.
Avoiding confounding causal effects in experiments on biological systems has so far not been feasible. This has motivated a search for extensions of the CHSH inequality that account for any such causal effects. The CbD framework [48,49] accomplishes this by associating each individual measurement with a context—effectively, a collection of additional “settings” variables—and tests for classical effects of the choice of measurement context on the outcomes. As noted earlier, this methodology allowed the experimental demonstration of entanglement effects in human decision making even in the presence of signaling [50,51].
Following the notation of [62], the CbD extension of the CHSH inequality can be written, in the absence of classical causal effects, as ([62], Equation (36)):
where the notation indicates that observable has been measured in context j. Classical causal effects are accounted for by including a measure of the effects of context changes on individual variables that can be written ([62], Equations (32), (34) and (35)):
where and . Any physically meaningful measure of signaling effects must be non-negative; since the context labels are arbitrary, they can be chosen to assure that . Including this term yields a final test statistic that is more stringent, by , than the bare CHSH inequality ([62], Equation (41)):
Note that the values of all observables are, as above, restricted to +1 or −1.
In principle, any set of measurements that violates the CHSH inequality, and in which classical causal effects cannot be ruled out, must also pass the above, more stringent, statistical test before it can be considered to indicate entanglement. Conversely, no set of measurements that does not violate the CHSH inequality will indicate entanglement under this more stringent test. Hence, the CHSH inequality given by Equation (2) can be regarded as a “first-pass” test for entanglement, after which the more stringent test able to rule out classical causal artifacts, i.e., Equation (6), can be employed.
To summarize, using violations of the CHSH inequality to detect entanglement requires (1) a source of pairs of states (the “spins”) yielding highly correlated outcomes when subjected to identical measurements, (2) a source of independently variable pairs of states (the “settings”) that affect the correlation values in some reproducible way, (3) sufficiently low noise to detect the difference between classical and quantum correlations, and (4) quantum correlations in excess of any required corrections for classical causal signaling. These requirements guided our experiment design for the current entanglement search.
2.2. Design of the Present Experiment
The present experiment faced two challenges that are likely to characterize any implementation of a CHSH test that employs physiological degrees of freedom. First, it was not known in advance what observables would exhibit the needed correlations; hence, suitable observables had to be identified from among those that were experimentally accessible. Second, real-time control of the available observables was not feasible. Observables that exhibited at least quasi-periodic variations over the course of the experiment would, therefore, be required for the role of “settings” variables.
On the therapist (“A”) side, a large number of mutually conditionally independent variables could be accessed by measuring scalp electro-encephalography (EEG), heart-rate variability (HRV), and distal galvanic skin response (GSR). Choices were much more limited on the cell (“B”) side due to the requirement that any measurement be minimally physiologically disruptive over the course of the experiment. Three measures accessible with fluorescence labels were chosen: measures of polymerized tubulin (“tubulin”), polymerized actin (“actin”), and uptake (“”). Equipment limitations prevented simultaneous measurements of actin and ; therefore, the B observables were limited to the pairs (tubulin, actin) and (tubulin, ).
Preliminary trials of BT on PANC-1 cells showed no significant differences in measured effects of 15 versus 30 min treatment sessions [55,56]. Given this result, the above limitations on B side observables, and consideration of the therapist’s tolerance of the EEG headset, we chose a block design with six 15 min treatment sessions per day over 10 days, for a total of 60 treatment sessions. Live PANC-1 cells were treated in a total of 40 sessions, with the (tubulin, actin) and (tubulin, ) observable pairs measured in 20 sessions each. Dead PANC-1 cells and cell-culture medium without cells were each treated in 10 sessions each, as controls to assess whether the results obtained from the A-side measurements were dependent on the nature of the B-side target. Each day, live PANC-1 cells were presented for treatment sessions one, two, five, and six, with sessions one and two containing the tubulin and observable pair, and sessions five and six containing the tubulin and actin observable pair. Treatment sessions three and four contained the dead PANC-1 cells and cell-culture medium without cells, respectively, with a semi-random order each successive day. Replicate plates of live PANC-1 cells were maintained in a separate room and exposed to a sham therapy procedure during all trials as B-side controls; outcome values otained from these sham control cells were subtracted from the respective BT treated cell outcomes. A separate positive control invasion assay was set up on 2 of the 10 treatment days. PANC-1 cells were exposed to 15 min of BT or 15 min sham control on two separate days of the experiment and assayed 48 h later.
Therapist EEG, HRV, and GSR were measured for two minutes prior to, during, and two minutes following each 15 min treatment session. Treatment was initiated by a signal from an experimenter, which also served as a time-synchronization marker on all data sources. The therapist was instructed to remain sitting still, approximately 1 m from the cells or control plates being treated, for the first and last five minutes of each session. The therapist was allowed to move during the middle five minutes of each session to relieve discomfort; this motion introduced artifacts in the EEG data but prevented fatigue. These data corresponding to these middle five minutes of each session were removed from subsequent analyses as necessary to avoid artifacts. The therapist was unable to see the plates being treated during the treatment sessions, as they were contained at all times either within an incubator or within an enclosed microscope stage. The therapist was given a short questionnaire at the end of eash session to report any subjective experiences during the treatment session. Treatment sessions were separated by sufficient time to collect the treated plates, position fresh plates for treatment, and make any needed adjustments to the instruments, with a minimum interval between sessions of five minutes.
This design was preregistered with the Open Science Foundation, study y8sdn (https://osf.io/y8sdn/ (accessed on 4 March 2024)).
2.3. Cell Biology Methods
Human pancreatic cancer (PANC-1) cells were purchased from the American Type Culture Collection (Manassas, VA, USA). They were maintained in a humidified atmosphere with 5% carbon dioxide at 37 °C. Cells were routinely cultured in Dulbecco modified Eagle medium with high glucose (Invitrogen Corp., Grand Island, NY, USA) containing 10% fetal bovine serum (Hyclone Laboratories Inc., Logan, UT, USA) supplemented with 50 IU/mL penicillin, 50 g/mL streptomycin, and 2 mM L-glutamine from GIBCO (Invitrogen).
RFP-Actin PANC-1 cells were developed using RFP-Actin (Puro) Lentiviral particles expressing a fusion target of RFP-Actin (GenTarget, San Diego, CA, USA). The Lentiviral particles were transduced to PANC-1 cells in the presence of Polybrene (Sigma, St. Louis, MO, USA) in 6-well cell-culture plates as per the manufacturer’s protocol. After 72 h, selection antibiotic Puromycin was added to the wells and the cells were allowed to grow.
Dynamic changes in the microtubule cytoskeleton of PANC-1 cells were monitored by staining the cells with ViaFluor® Live Cell Microtubule-488 dye (Biotium, Fremont, CA, USA), a cell-permeant probe for staining the microtubule cytoskeleton in live cells. PANC-1 cells () were seeded to 12-well plates the day prior to the treatment day. Before the treatment, a 2X solution of ViaFluo-488 was made by diluting 2 L dye with 1 mL medium followed by addition of 1 L of verapamil to obtain a working solution. The cells were washed with Calcium/Magnesium-free Dulbecco’s PBS, then replaced with ViaFluo-488 working solution and incubated at 37 °C for 30 min. The staining solution was replaced with fresh medium Fluorobrite DMEM for imaging during the treatment. Fluorescence images of PANC-1 cells were taken every minute during the treatment with CytoSmart Lux FL (Axion Biosystems, Atlanta, GA, USA) using Fluorescence Green imaging function. The fluorescence intensity per cell was analyzed by FiJi (ImageJ 2.14.0/1.54f).
Dynamic changes in -actin protein was monitored in the RFP-Actin PANC-1 cells during treatment. Stably expressing RFP-Actin PANC-1 cells () were plated in 12-well cell-culture plates and allowed to attach overnight prior to treatment. The red fluorescence images were captured every minute in PANC-1 RFP-Actin cells using the EVOSTM M7000 Imaging System (Thermo Fisher, Waltham, MA, USA). Fluorescence intensity was quantified by CellesteTM 6.0 Imaging Analysis Software (Invitrogen).
Fluo-4-AM cell-permeable dye (Invitrogen) was used to measure calcium mobilization following the manufacturer’s instructions. Cells were also plated in 12-well plates as in the cell microtubule cytoskeleton staining assay the day prior to treatment. On the treatment day, cells were washed with PBS and then incubated in Fluorobrite DMEM containing 5 M Fluo-4-AM dye, organic anion-transport inhibitors probenecid (2 mM), and NucBlueTM Live ReadyProbesTM Reagent (Invitrogen, Waltham, MA, USA) for 30 min at 37 °C followed by 15 min incubation at room temperature. During the treatment, the green fluorescent and DAPI images of the cells were captured every minute by the EVOSTM M7000 Imaging System (Thermo Fisher). Fluorescence intensity was quantified by CellesteTM 6.0 Imaging Analysis Software (Invitrogen).
Invasiveness of PANC-1 cells was measured using Cytoselect cell Invasion Assay kits (Cell Biolabs, San Diego, CA, USA) in 24-well plate format. A total of cells in 300 L medium were plated in basement membrane-coated inserts (6 inserts/group), which is used to assay the invasive properties of tumor cells. The endpoint was monitored 48 h after each 15 min treatment, either BT or sham. The fluorescence intensity was measured with a microplate reader at 480 nm/520 nm (Molecular Devices, San Jose, CA, USA). This assay was not part of the entanglement study per se, but added as a positive control to ensure that the experiment affected cell properties as previously found [56].
2.4. EEG Methods
Therapist EEG data were recorded using a BrainVision (Morrisville, NC, USA) actiCHamp Plus 64 System with a 64-Channel actiCAP Snap cap and two 32-channel slim electrode bundle kits. We used BrainVision Recorder version 1.25.0101 to record the EEG, ECG, and GSR physiological measures.
Raw EEG data were processed to identify and remove sensor artifacts using the methods and EEGLAB software (version 2024.0, https://github.com/sccn/eeglab, accessed 28 March 2024) pipeline previously described [73,74]. Briefly, data were high-pass-filtered 0.5 Hz, and the EEGLAB implementation of the Artifact Subspace Reconstruction (ASR) method was used to identify and remove bad data segments. The EEGLAB implementation of Independent Component Analysis (ICA) was then used to detect and remove artifacts due to eye and muscle movements. Fast Fourier Transform with one-second windows was used for spectral analysis. Spectral power in each of the 4–8 Hz (theta), 8–12 Hz (alpha), 18–22 Hz (beta), and 30–45 Hz (gamma) bands were averaged over successive one-minute intervals for comparison with the cell-response data. The EEG data for minutes 6 to 10 in each 15 min treatment session, which contain artifacts due to the therapist being allowed to move during this period, were ignored in the subsequent analysis.
2.5. HRV and GSR Methods
Therapist GSR data were recorded using the BrainVision GSR Sensor kit; ECG data were recorded using MindWare (Westerville, OH, USA) leads and disposable electrodes.
Raw electrocardiogram data were processed using the BrainBeats EEGLAB plugin [75]. Raw GSR data were processed using the Convex Optimization Approach to Electrodermal Activity Processing [76] to derive the mean normal-to-normal sinus-node depolarization interval (NN_mean), the standard deviation of the NN interval (SDNN), the square root of the mean squared differences of successive NN intervals (RMSSD), the fraction of NN intervals greater than 50 ms (pNN50), and the spectral power in the high-frequency (>0.2 Hz) component (HF-HRV) [77].
2.6. Statistical Methods
Therapist EEG, HRV, and GSR data were divided into four segments: pre-treatment baseline (“Pre-Baseline”), treatment minutes 1–5 (“Treatment-1”), treatment minutes 11–15 (“Treatment-3”), and post-treatment baseline (“Post-Baseline”). Control sessions using dead cells and cell-free media were combined, yielding a comparison of live-cell treatments and control treatments. The following five analyses were run to distinguish these data sets:
- ANOVA over four periods (1 × 4 design): Pre-Baseline, Post-Baseline, Treatment 1, and Treatment 3;
- Paired t-test (1 × 2 design): Treatment 1 and 3 combined versus Pre- and Post-Baselines combined;
- Paired t-test (1 × 2 design): Treatment 1 versus Pre- and Post-periods combined (1 × 2 design);
- Paired t-test (1 × 2 design): Treatment 1 versus Treatment 2;
- Two-way ANOVA (2 × 2 design): Treatment 1 and 3 combined versus Pre- and Post-Baseline combined and cells of type 5 vs. cells of type 4 and 6 combined (cell types 4, 5, and 6 are blinded indices for live cells, cell-free media, and dead cells, in this or a permuted order).
Because we are taking a mass-univariate approach, we controlled for type 1 errors (also called family-wise error) using the spatiotemporal cluster correction [78] for parametric analyses (i.e., one-way ANOVA or paired t-test). Because this correction method could not be applied with the two-way ANOVA [73], a surrogate method with false discovery rate (FDR) correction was used in this case. Results of the above statistical analyses will be presented in a separate manuscript.
Real-time tubulin, actin, and responses of sham-treated control cells were subtracted from the corresponding responses of BT-treated cells to obtain real-time, sham-control-corrected live-cell measures. Pearson correlation coefficients were computed between (1) scalp EEG power for each EEG electrode, in each of four frequency bands (4–8 Hz [theta], 8–12 Hz [alpha], 18–22 Hz [beta], 30–45 Hz [gamma]), versus each real-time, sham-control corrected live cell measure; (2) connectivity for each pair of EEG electrodes, in each of the same four frequency bands, versus each real-time, sham-control corrected live cell measure; (3) each of the five derived HRV measures NN_mean, SDNN, RMSSD, pNN50, and HF-HRV [77] versus each real-time, sham-control-corrected live-cell measure; and (4) tonic and phasic GSR measures versus each real-time, sham-control-corrected live-cell measure. Correlation coefficients were corrected for multiple comparisons.
3. Results
As shown in Figure 2, the 48 h post-treatment invasiveness of BT-treated PANC-1 cells was significantly reduced compared to sham control cells, consistent with expectations based on prior work [56]. This reduction in invasiveness suggests that one or more cellular processes undergo significant changes post-treatment. During the 15 min treatment periods, however, only activity showed a significant difference between BT treatment relative to the sham control cells, with little difference between BT and sham controls for tubulin and -actin (relatively flat lines), as shown in Figure 3. The activity went up over time in both groups, but significantly less in the BT group relative to sham. These results suggest that cytoskeletal changes involved in the 48 h invasiveness response, if any, occur after the 15 min treatment period.
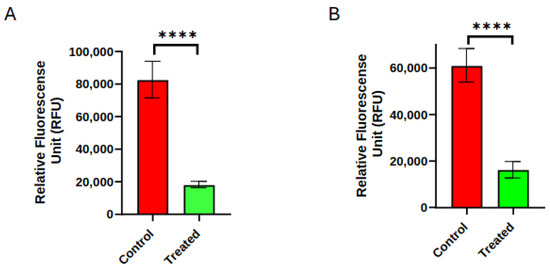
Figure 2.
Biofield therapy (BT) markedly inhibited invasiveness of PANC-1 cells. Invasive potential of PANC-1 cells 48 h after 15 min BT treatment (Treated) or 15 min sham control (Control) for (A) experimental series one and (B) experimental series two. Data are presented as mean ± SD (**** p < 0.0001).
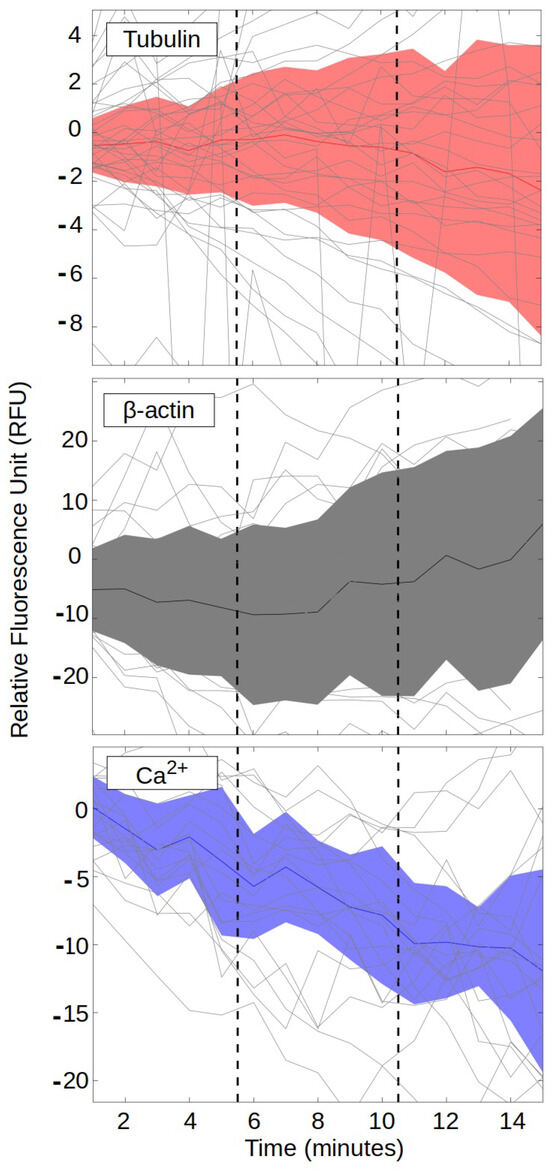
Figure 3.
Real-time responses of tubulin (top), -actin (middle), and measures to 15 min BT treatments. Light-gray lines indicate differences between BT-treated PANC-1 cells and sham-treated PANC-1 controls for 40 (tubulin) or 20 (-actin and ) individual BT sessions. Orange (tubulin), gray (-actin), and blue () shaded areas indicate 95% confidence intervals around the minute-to-minute average values (orange, gray, and blue lines, respectively). Results for each assay were normalized to the average baseline value, obtained in the one minute prior to initiation of treatment, for that assay and treatment group. Vertical dashed lines indicate the 5 min central period when the BT therapist was allowed to move to relieve discomfort during the treatments.
The results of this study that can be interpreted in purely classical terms, including differential EEG responses to live versus dead PANC-1 cells and bidirectional Granger causality analysis, will be reported elsewhere. Here, we report only a summary of the EEG, HRV, and GSR classical correlation results as they pertain to the entanglement search. We were unable in this study to demonstrate a violation of the CHSH inequality, Equation (2), and hence, unable to demonstrate evidence for entanglement between therapist and cell degrees of freedom. The primary reason for this was our inability to identify A and B observables meeting the classical correlation requirements for a meaningful CHSH test.
Let us first consider the choice of “spin” observables, i.e., the observables that are to be tested for entanglement. In a conventional experiment, these would be perfectly classically correlated, positively or negatively, when jointly subjected to any fixed measurement, i.e., when the values of all other relevant variables (in the conventional case, the settings) are fixed. We cannot, in the present design, fix the values of the other relevant variables, which potentially include all other variables that have been measured. Hence, we must examine correlations between candidate spin observables against some assumed background of values of all the other observables.
The vast majority of pairwise classical (Pearson) correlations, both between A observables and between A and B observables, have correlation coefficients and hence, , i.e., can be considered negligible [79]; see https://osf.io/y8sdn/files/osfstorage/, filename Appendix_A_all_correlations.xlsx (accessed on 4 March 2024) for the full Pearson correlation table. It is, therefore, reasonable to assume that background values of other observables are random when evaluating candidates for spin observables. Against a random background, spin observables for an entangled state would have and hence, . If we consider now the “settings” observables, the situation is exactly the same: for any given measurement, the values of the two settings observables in a conventional design are perfectly correlated, i.e., separated by exactly 90°. Hence, an informative experiment requires one “spin” A-B combination with and a second “settings” A-B combination with , with lower correlations in the second A-B combination rapidly leading to a lower probability of detecting entanglement.
Although the results of the invasiveness test confirm that the treatment was as effective in changing the states of PANC-1 cells as in previous trials [56], the Pearson correlations obtained from the current data do not satisfy the informativeness criteria needed for a CHSH test. Tubulin activity is the only cell measure recorded in all runs, so must be chosen as a B observable, but shows no correlations with A observables above (). Indeed, as shown in Figure 3 above, tubulin activity did not show any significant change, on average, between BT treatment and sham control sessions. The best EEG correlations are with -actin, but even after correction for the 6–10 min movement artifacts in the EEG data, these have (). While activity shows the strongest average response during the 15 min treatments, it has only weak real-time correlation with therapist EEG. The HRV and GSR results do not show any better correlations with the cell response data than do the EEG results. Although these correlation levels are insufficient for the CHSH test, they are in some cases statistically significant even after FDR correction, revealing classical correlations between EEG and cell outcomes. A Granger causality analysis of these data will be reported elsewhere.
4. Discussion
Indirect evidence for entanglement effects in human brains [34,50,51] and in individual human cells [29] have been reported by other groups. To our knowledge, no other experiments to date have detected entanglement between human brains and spatially distant human cells. The results presented here fail to resolve the question of whether such entanglement is possible.
A straightforward, but logically flawed, interpretation of our results is to claim that environmental decoherence renders the states of both therapist and cells—and indeed, all of their internal processes above the molecular scale—effectively classical and hence, able to interact only via classical, causal processes. Environmental decoherence models [80,81], even in their more sophisticated “quantum Darwinist” form [82,83], all assume a Hilbert-space decomposition that distinguishes the “system” of interest from its surrounding “environment.” In any entanglement study, the boundary and hence, the state space of the “system”, is precisely what is in question. Applying a decoherence model to the therapist and the cells separately, as is required to represent them as distinct, effectively classical systems, simply begs the question against the possibility of entanglement [84,85,86,87,88]. Decoherence models that rely on spatial separation also clearly beg the question against quantum-gravity models such as ER = EPR.
In critiquing our design, we assume that therapist–cell entanglement is possible, even though it may be undetectable in practice. We can ask, therefore, whether improvements to the design or methods could yield the correlated observables required for a meaningful CHSH test. As noted, a feature of our data that may prevent a meaningful CHSH test is lack of time synchrony between the relatively high (ms) time resolution EEG measures and the relative low (1 min) time resolution cellular-response measures. Such lack of time synchrony between signals can manifest as phase noise. Conventional CHSH tests rely on phase locking between both the “spin” and “settings” observables at high time resolution to be informative. Hence, an inability to align the outcome results precisely in time prevents an informative test.
Time synchrony between therapist and cell observables may be improved by increasing the time resolution of the cell measurements. Ion channels function in the tens of ms range, so could exhibit synchronous behavior in the tens of Hz range. Plating cells on high-resolution micro-electrode arrays may allow access to bioelectric signals from individual cells that can be correlated with therapist brain signals accessible with EEG or MEG. Advances in brain–computer interface (BCI) technology could enhance the measurement of therapist neural activity in the future; in the nearer term, use of MEG instead of or as a supplement to EEG may yield better results. Greater sensory isolation of the therapist may also yield improvements, though perhaps at the cost of lower therapist tolerance for the experimental protocol.
The statistically significant yet low-level correlations observed here are in themselves a novel and positive result for this experimental setting. In some domains of investigation, e.g., in genome-wide association studies [89], large numbers of low, but statistically significant, correlations can be given a mechanistic interpretation in the context of an independently well-confirmed mechanistic model. This is not the case in the present BT domain, where no such model yet exists.
Alternatives to CHSH tests that could be suggestive of entanglement include comparisons of cellular effects of BT with proximal or distal (e.g., separated by hundreds of km) therapists, or searches for effects on therapist observables of unexpected manipulations of the cells being treated. Any observed effect in such cases could, clearly, be due to classical signaling effects, but strong results in either test would strongly constrain the kinds of classical signaling that would be required to explain the results.
5. Conclusions
The present results do not resolve the question of the nature of the therapist–subject interaction during BT; indeed, they leave the question of mechanism in such settings entirely open. By working in a carefully controlled in vitro setting, we have, however, developed a methodology that can be applied using different sets of observables to establish meaningful empirical constraints on this mechanism.
We have not, moreover, succeeded in demonstrating entanglement between spatially separated living systems. We hope that our work will encourage others to employ high-resolution biophysical methods to probe for entanglement effects in other model systems.
Author Contributions
Conceptualization, C.F., L.C., A.D. and P.Y.; methodology, C.F., L.C., A.D. and P.Y.; software, A.D.; investigation, All authors; resources, P.Y.; data curation, A.C. and P.Y.; writing—original draft preparation, C.F., A.D. and P.Y.; writing—review and editing, C.F., L.C., A.C., A.D. and P.Y.; project administration, L.C.; funding acquisition, L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Emerald Gate Charitable Trust, grant number RCTS LS2022-00061373-LK. The APC was funded by this same grant.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board (or Ethics Committee) of The University of Texas MD Anderson Cancer Center (protocol code 2020-1210, most recent approval date 23 November 2022).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Full classical correlation data are available at https://osf.io/y8sdn/files/osfstorage/, filename Appendix_A_all_correlations.xlsx (accessed on 4 March 2024). Other data may be requested from L.C.; IRB approval may be required.
Acknowledgments
We thank John Lavack for participating in these experiments.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BT | Biofield Therapy |
| CHSH | Clauser–Horne–Shimony-Holt |
| EEG | Electro-Encephalography |
| ER | Einstein–Rosen |
| EPR | Einstein–Podolsky–Rosen |
| GSR | Galvanic Skin Response |
| HRV | Heart Rate Variability |
| MEG | Magneto-Encephalography |
| NMR | Nuclear Magnetic Resonance |
| OR | Objective Reduction |
References
- Aspect, A.; Dalibard, J.; Roger, G. Experimental test of Bell’s inequaties using time-varying analyzers. Phys. Rev. Lett. 1982, 49, 1804–1807. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
- Georgescu, I. How the Bell tests changed quantum physics. Nat. Phys. 2021, 3, 374–376. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Dowling, J.P.; Milburn, G.J. Quantum technology: The second quantum revolution. Phil. Trans. R. Soc. Lond. A 2003, 361, 1655–1674. [Google Scholar] [CrossRef]
- Ladd, T.D.; Jelezko, F.; Laflamme, R.; Nakamura, Y.; Monroe, C.; O’Brien, J.L. Quantum computers. Nature 2010, 464, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Gyongyosi, L.; Imre, S. A survey on quantum computing technology. Comput. Sci. Rev. 2019, 31, 51–71. [Google Scholar] [CrossRef]
- Zanardi, P. Virtual quantum subsystems. Phys. Rev. Lett. 2001, 87, 077901. [Google Scholar] [CrossRef]
- Zanardi, P.; Lidar, D.A.; Lloyd, S. Quantum tensor product structures are observable-induced. Phys. Rev. Lett. 2004, 92, 060402. [Google Scholar] [CrossRef]
- de la Torre, A.C.; Goyeneche, D.; Leitao, L. Entanglement for all quantum states. Eur. J. Phys. 2010, 31, 325–332. [Google Scholar] [CrossRef]
- Harshman, N.L.; Ranade, K.S. Observables can be tailored to change the entanglement of any pure state. Phys. Rev. A 2011, 84, 012303. [Google Scholar] [CrossRef]
- Thirring, W.; Bertlmann, R.A.; Köhler, P.; Narnhofer, H. Entanglement or separability: The choice of how to factorize the algebra of a density matrix. Eur. Phys. J. D 2011, 64, 181–196. [Google Scholar] [CrossRef]
- van Raamsdonk, M. Building up spacetime with quantum entanglement. Gen. Relativ. Grav. 2011, 42, 23232329. [Google Scholar] [CrossRef]
- Almheiri, A.; Dong, X.; Harlow, D. Bulk locality and quantum error correction in AdS/CFT. J. High Energy Phys. 2015, 4, 133. [Google Scholar] [CrossRef]
- Swingle, B. Spacetime from entanglement. Annu. Rev. Condens. Matter Phys. 2018, 9, 345–358. [Google Scholar] [CrossRef]
- Bain, J. Spacetime as a quantum error correcting code? Stud. Hist. Phil. Sci. B 2020, 71, 26–36. [Google Scholar] [CrossRef]
- Addazi, A.; Chen, P.; Fabrocini, F.; Fields, C.; Greco, E.; Lulli, M.; Marcianò, A.; Pasechnik, R. Generalized holographic principle, gauge invariance and the emergence of gravity à la Wilczek. Front. Astron. Space Sci. 2021, 8, 563450. [Google Scholar] [CrossRef]
- Fields, C.; Glazebrook, J.F.; Marcianò, A. Communication protocols and quantum error-correcting codes from the perspective of topological quantum field theory. arXiv 2023, arXiv:2303.16461. [Google Scholar]
- Maldacena, J.; Susskind, L. Cool horizons for entangled black holes. Forschr. Physik 2013, 61, 781–811. [Google Scholar] [CrossRef]
- Dai, D.-C.; Minic, D.; Stojkovic, D.; Fu, C. Testing the ER = EPR conjecture. Phys. Rev. D 2022, 102, 066004. [Google Scholar] [CrossRef]
- Schrödinger, E. What Is Life? Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
- Tegmark, M. Importance of quantum decoherence in brain processes. Phys. Rev. E 2000, 61, 4194–4206. [Google Scholar] [CrossRef]
- Arndt, M.; Juffmann, T.; Vedral, V. Quantum physics meets biology. HFSP J. 2009, 3, 386–400. [Google Scholar] [CrossRef] [PubMed]
- Lambert, N.; Chen, Y.-N.; Cheng, Y.-C.; Li, C.-M.; Chen, G.-Y.; Nori, F. Quantum biology. Nat. Phys. 2012, 9, 10–18. [Google Scholar] [CrossRef]
- Melkikh, A.V.; Khrennikov, A. Nontrivial quantum and quantum-like effects in biosystems: Unsolved questions and paradoxes. Prog. Biophys. Mol. Biol. 2015, 119, 137–161. [Google Scholar] [CrossRef] [PubMed]
- Nordén, B. Quantum entanglement: Facts and fiction–how wrong was Einstein after all? Quart. Rev. Biophys. 2016, 49, e17. [Google Scholar] [CrossRef] [PubMed]
- Marais, A.; Adams, B.; Ringsmuth, A.K.; Ferretti, M.; Gruber, J.M.; Hendrikx, R.; Schuld, M.; Smith, S.L.; Sinaykiy, I.; Krüger, T.P.J.; et al. The future of quantum biology. J. R. Soc. Interface 2018, 15, 20180640. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Cogdell, R.J.; Coker, D.F.; Duan, H.-G.; Hauer, J.; Kleinekathöfer, U.; Jansen, T.L.C.; Mančal, T.; Miiller, R.J.D.; Ogilvie, J.P.; et al. Quantum biology revisited. Sci. Adv. 2020, 6, eaaz4888. [Google Scholar] [CrossRef] [PubMed]
- Fields, C.; Levin, M. Metabolic limits on classical information processing by biological cells. BioSystems 2021, 209, 104513. [Google Scholar] [CrossRef] [PubMed]
- Lechelon, M.; Meriguet, Y.; Gori, M.; Ruffenach, S.; Nardecchia, I.; Floriani, E.; Coquillat, D.; Teppe, F.; Mailfert, S.; Marguet, D.; et al. Experimental evidence for long-distance electrodynamic intermolecular forces. Sci. Adv. 2022, 8, eabl5855. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.S.; Tan, Y.P.; Nguyen, L.H.; Budoyo, R.P.; Park, K.H.; Hufnagel, C.; Yap, Y.S.; Møbjerg, N.; Vedral, V.; Paterek, T.; et al. Entanglement in a qubit-qubit-tardigrade system. New J. Phys. 2022, 24, 123024. [Google Scholar] [CrossRef]
- Hameroff, S.; Penrose, R. Orchestrated reduction of quantum coherence in brain microtubules: A model for consciousness. Math. Comput. Simul. 1996, 40, 453–480. [Google Scholar] [CrossRef]
- Hameroff, S.; Penrose, R. Consciousness in the universe: A review of the ‘OrchOR’ theory. Phys. Life Rev. 2014, 11, 39–78. [Google Scholar] [CrossRef]
- Kerskens, C.M.; López Pérez, D. Experimental indications of non-classical brain functions. J. Phys. Comms. 2022, 6, 105001. [Google Scholar] [CrossRef]
- von Neumann, J. Mathematische Grundlagen der Quantenmechanik; Springer: Berlin/Heidelberg, Germany, 1932. [Google Scholar]
- Bohr, N. Atomic Physics and Human Knowledge; Wiley: New York, NY, USA, 1958. [Google Scholar]
- Wigner, E.P. Remarks on the mind-body question. In The Scientist Speculates; Good, I.J., Ed.; Basic Books: New York, NY, USA, 1962; pp. 284–302. [Google Scholar]
- Penrose, R. The Emperor’s New Mind; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Stapp, H.P. Quantum theory and the role of mind in nature. Found. Phys. 2001, 31, 1465–1499. [Google Scholar] [CrossRef]
- Orlov, Y.F. The wave logic of consciousness: A hypothesis. Int. J. Theor. Phys. 1982, 21, 37–53. [Google Scholar] [CrossRef]
- Yukalov, V.I.; Sornette, D. Scheme of thinking quantum systems. Laser Phys. Lett. 2009, 6, 833–839. [Google Scholar] [CrossRef][Green Version]
- Khrennikov, A. Quantum Bayesianism as the basis of general theory of decision-making. Phil. Trans. R. Soc. A 2016, 374, 20150245. [Google Scholar] [CrossRef] [PubMed]
- Pothos, E.M.; Busemeyer, J.R. Can quantum probability provide a new direction for cognitive modeling? Behav. Brain Sci. 2013, 36, 255–327. [Google Scholar] [CrossRef] [PubMed]
- Dzhafarov, E.N.; Zhang, R.; Kujala, J. Is there contextuality in behavioural and social systems? Phil. Trans. R. Soc. A 2016, 374, 20150099. [Google Scholar] [CrossRef] [PubMed]
- Bell, J.S. On the problem of hidden variables in quantum mechanics. Rev. Mod. Phys. 1966, 38, 447–452. [Google Scholar] [CrossRef]
- Kochen, S.; Specker, E.P. The problem of hidden variables in quantum mechanics. J. Math. Mech. 1967, 17, 59–87. [Google Scholar] [CrossRef]
- Mermin, N.D. Hidden variables and the two theorems of John Bell. Rev. Mod. Phys. 1993, 65, 803–815. [Google Scholar] [CrossRef]
- Dzhafarov, E.N.; Kujala, J.V. Context-content systems of random variables: The contextuality-by-default theory. J. Math. Psych. 2016, 74, 11–33. [Google Scholar] [CrossRef]
- Dzhafarov, E.N.; Kon, M. On universality of classical probability with contextually labeled random variables. J. Math. Psych. 2018, 85, 17–24. [Google Scholar] [CrossRef]
- Cervantes, V.H.; Dzhafarov, E.N. Snow Queen is evil and beautiful: Experimental evidence for probabilistic contextuality in human choices. Decision 2018, 5, 193–204. [Google Scholar] [CrossRef]
- Basieva, I.; Cervantes, V.H.; Dzhafarov, E.N.; Khrennikov, A. True contextuality beats direct influences in human decision making. J. Exp. Psych. 2019, 148, 1925–1937. [Google Scholar] [CrossRef]
- Jain, S.; Hammerschlag, R.; Mills, P.; Cohen, L.; Krieger, R.; Vietan, C.; Lutgendorf, S. Clinical studies of biofield therapies: Summary, methodological challenges, and recommendations. Glob. Adv. Health Med. 2015, 4, 58–66. [Google Scholar] [CrossRef]
- Bengston, W. A method used to train skeptical volunteers to heal in an experimental setting. J. Altern. Compl. Med. 2007, 13, 329–331. [Google Scholar] [CrossRef]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 1969, 23, 880–884. [Google Scholar] [CrossRef]
- Yang, P.; Chakraborty, S.; Nguyen, P.; Cui, M.; Cusimano, A.; Wei, D.; Prinsloo, S.; Cohen, L. Biofield therapy suppressed the growth of human pancreatic cancer cells by modulation of cell cycle and cell voltage potentials (abstract). Cancer Res. 2022, 82 (Suppl. S12), 5382. [Google Scholar] [CrossRef]
- Yang, P.; Chakraborty, S.; Nguyen, P.; Deng, D.; Cusimano, A.; Wei, D.; Cohen, L. Biofield therapy suppressed invasion and metastases of human pancreatic cancer (abstract). Cancer Res. 2024, 84 (Suppl. S6), 4128. [Google Scholar] [CrossRef]
- Yang, P.; Jiang, Y.; Rhea, P.R.; Conway, T.; Chen, D.; Gagea, M.; Harribance, S.L.; Cohen, L. Human biofield therapy and the growth of mouse lung carcinoma. Integr. Cancer Ther. 2019, 18, 1534735419840797. [Google Scholar] [CrossRef]
- Yang, P.; Rhea, P.R.; Conway, T.; Nookala, S.; Hegde, V.; Gagea, M.; Ajami, N.J.; Harribance, S.L.; Ochoa, J.; Sastry, J.K.; et al. Human biofield therapy modulates tumor microenvironment and cancer stemness in mouse lung carcinoma. Integr. Cancer Ther. 2020, 19, 1534735420940398. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein–Podolsky-Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Fine, A. Joint distributions, quantum correlations, and commuting observables. J. Math. Phys. 1982, 23, 1306–1310. [Google Scholar] [CrossRef]
- Khrennikov, A. Contextuality, complementarity, signaling, and Bell tests. Entropy 2022, 24, 1380. [Google Scholar] [CrossRef]
- Tapster, P.R.; Rarity, J.G.; Owens, P.C.M. Violation of Bell’s inequality over 4 km of optical fiber. Phys. Rev. Lett. 1994, 73, 1923–1926. [Google Scholar] [CrossRef] [PubMed]
- Tittel, W.; Brendel, J.; Zbinden, H.; Gisin, N. Violation of Bell inequalities by photons more than 10 km apart. Phys. Rev. Lett. 1998, 81, 3563–3566. [Google Scholar] [CrossRef]
- Rowe, M.A.; Kielpinski, D.; Meyer, V.; Sackett, C.A.; Itano, W.M.; Monroe, C.; Winel, D.J. Experimental violation of a Bell’s inequality with efficient detection. Nature 2001, 409, 791–794. [Google Scholar] [CrossRef]
- Giustina, M.; Versteegh, M.A.; Wengerowsky, S.; Handsteiner, J.; Hochrainer, A.; Phelan, K.; Steinlechner, F.; Kofler, J.; Larsson, J.-Å.; Abellán, C.; et al. A significant-loophole-free test of Bells theorem with entangled photons. Phys. Rev. Lett. 2015, 115, 250401. [Google Scholar] [CrossRef]
- Hensen, B.; Bernien, H.; Dreau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.L.; Schouten, R.N.; Abellán, C.; et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, 526, 682–686. [Google Scholar] [CrossRef]
- Shalm, L.K.; Meyer-Scott, E.; Christensen, B.G.; Bierhorst, P.; Wayne, M.A.; Stevens, M.J.; Gerrits, T.; Glancy, S.; Hamel, D.R.; Allman, M.S.; et al. A strong loophole-free test of local realism. Phys. Rev. Lett. 2015, 115, 250402. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Paesani, S.; Ding, Y.; Santagati, R.; Skrzypczyk, P.; Salavrakos, A.; Tura, J.; Augusiak, R.; Mančinska, L.; Bacco, D.; et al. Multidimensional quantum entanglement with large-scale integrated optics. Science 2018, 360, 285–291. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.-M.; Zhang, C.; Liu, B.-H.; Guo, Y.; Xing, W.-B.; Huang, C.-X.; Huang, Y.-F.; Li, C.-F.; Guo, G.-C. High-dimensional Bell test without detection loophole. Phys. Rev. Lett. 2022, 129, 060402. [Google Scholar] [CrossRef]
- Cirel’son, B.S. Quantum generalizations of Bell’s inequality. Lett. Math. Phys. 1980, 4, 93–100. [Google Scholar] [CrossRef]
- Gill, R.S. Gull’s theorem revisited. Entropy 2022, 24, 679. [Google Scholar] [CrossRef]
- Pernet, C.R.; Martinez-Cancino, R.; Truong, D.; Makeig, S.; Delorme, A. From BIDS-formatted EEG data to sensor-space group results: A fully reproducible workflow with EEGLAB and LIMO EEG. Front. Neurosci. 2021, 14, 610388. [Google Scholar] [CrossRef]
- Delorme, A. EEG is better left alone. Sci. Rep. 2023, 13, 2372. [Google Scholar] [CrossRef]
- Cannard, C.; Wahbeh, H.; Delorme, A. BrainBeats: An open-source EEGLAB plugin to jointly analyze EEG and cardiovascular (ECG/PPG) signals. bioRxiv 2023. [Google Scholar] [CrossRef]
- Greco, A.; Valenza, G.; Lanata, A.; Scilingo, E.P.; Citi, L. cvxEDA: A convex optimization approach to electrodermal activity processing. IEEE Trans. Biomed. Eng. 2016, 63, 797–804. [Google Scholar] [CrossRef]
- Shaffer, F.; Ginsberg, J.P. An overview of Heart Rate Variability metrics and norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef]
- Pernet, C.R.; Latinus, M.; Nichols, T.E.; Rousselet, G.A. Cluster-based computational methods for mass univariate analyses of event-related brain potentials/fields: A simulation study. J. Neurosci. Meth. 2015, 250, 85–93. [Google Scholar] [CrossRef]
- Mukaka, M.M. A guide to appropriate use of correlation coefficient in medical research. Malawi Med. J. 2012, 24, 69–71. [Google Scholar]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar] [CrossRef]
- Schlosshauer, M. Decoherence and the Quantum to Classical Transition; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Blume-Kohout, R.; Zurek, W.H. Quantum Darwinism: Entanglement, branches, and the emergent classicality of redundantly stored quantum information. Phys. Rev. A 2006, 73, 062310. [Google Scholar] [CrossRef]
- Zurek, W.H. Quantum Darwinism. Nat. Phys. 2009, 5, 181–188. [Google Scholar] [CrossRef]
- Dugić, M.; Jeknić, J. What is “system”: Some decoherence-theory arguments. Int. J. Theor. Phys. 2006, 45, 2249–2259. [Google Scholar] [CrossRef]
- Dugić, M.; Jeknić-Dugić, J. What is “system”: The information-theoretic arguments. Int. J. Theor. Phys. 2008, 47, 805–813. [Google Scholar] [CrossRef]
- Fields, C. Quantum Darwinism requires an extra-theoretical assumption of encoding redundancy. Int. J. Theor. Phys. 2010, 49, 2523–2527. [Google Scholar] [CrossRef]
- Fields, C. On the Ollivier-Poulin-Zurek definition of objectivity. Axiomathes 2014, 24, 137–156. [Google Scholar] [CrossRef]
- Kastner, R. ‘Einselection’ of pointer observables: The new H-theorem? Stud. Hist. Phil. Mod. Phys. 2014, 48, 56–58. [Google Scholar] [CrossRef]
- Visscher, P.M.; Brown, M.A.; McCarthy, M.I.; Yang, J. Five years of GWAS discovery. Am. J. Hum. Genet. 2012, 90, 7–24. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).