Optical Tweezers to Force Information out of Biological and Synthetic Systems One Molecule at a Time
Abstract
1. Introduction
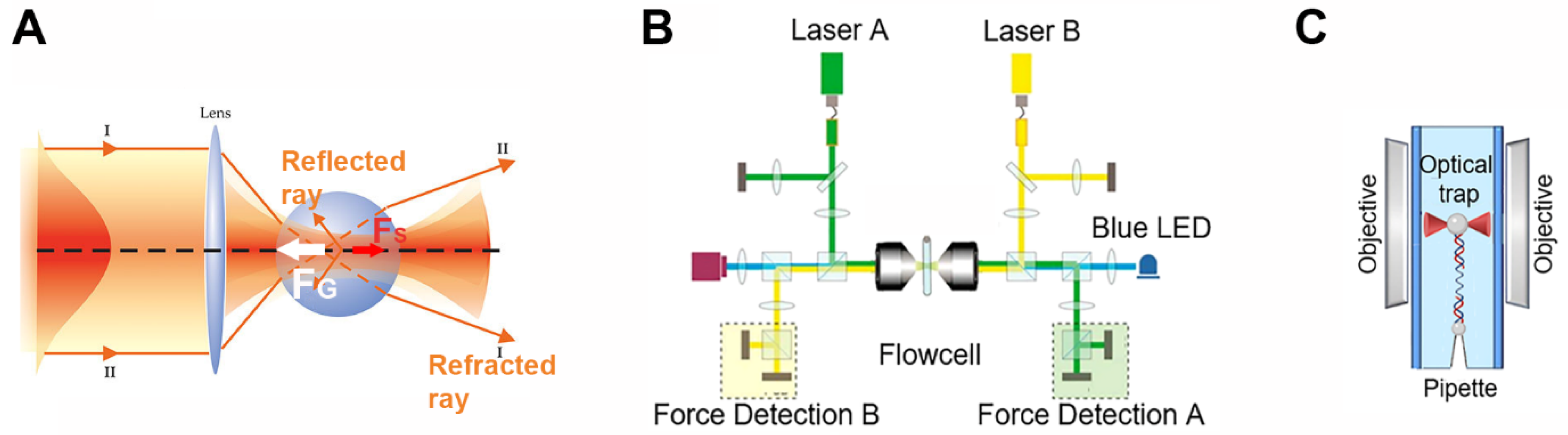
2. Optical Tweezers to Interrogate the Elastic Properties of DNA
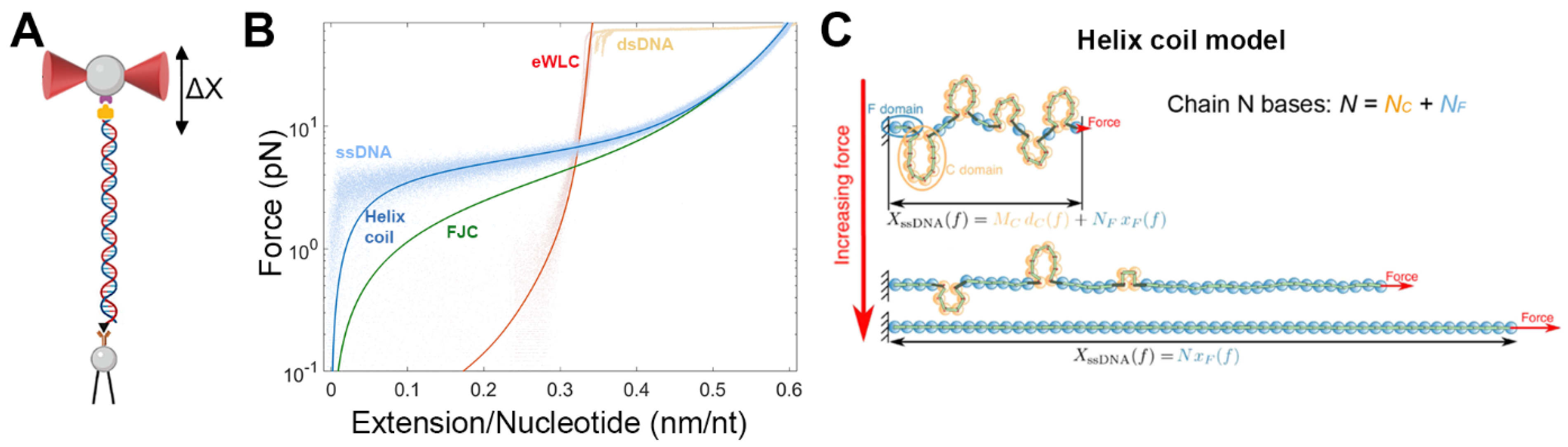
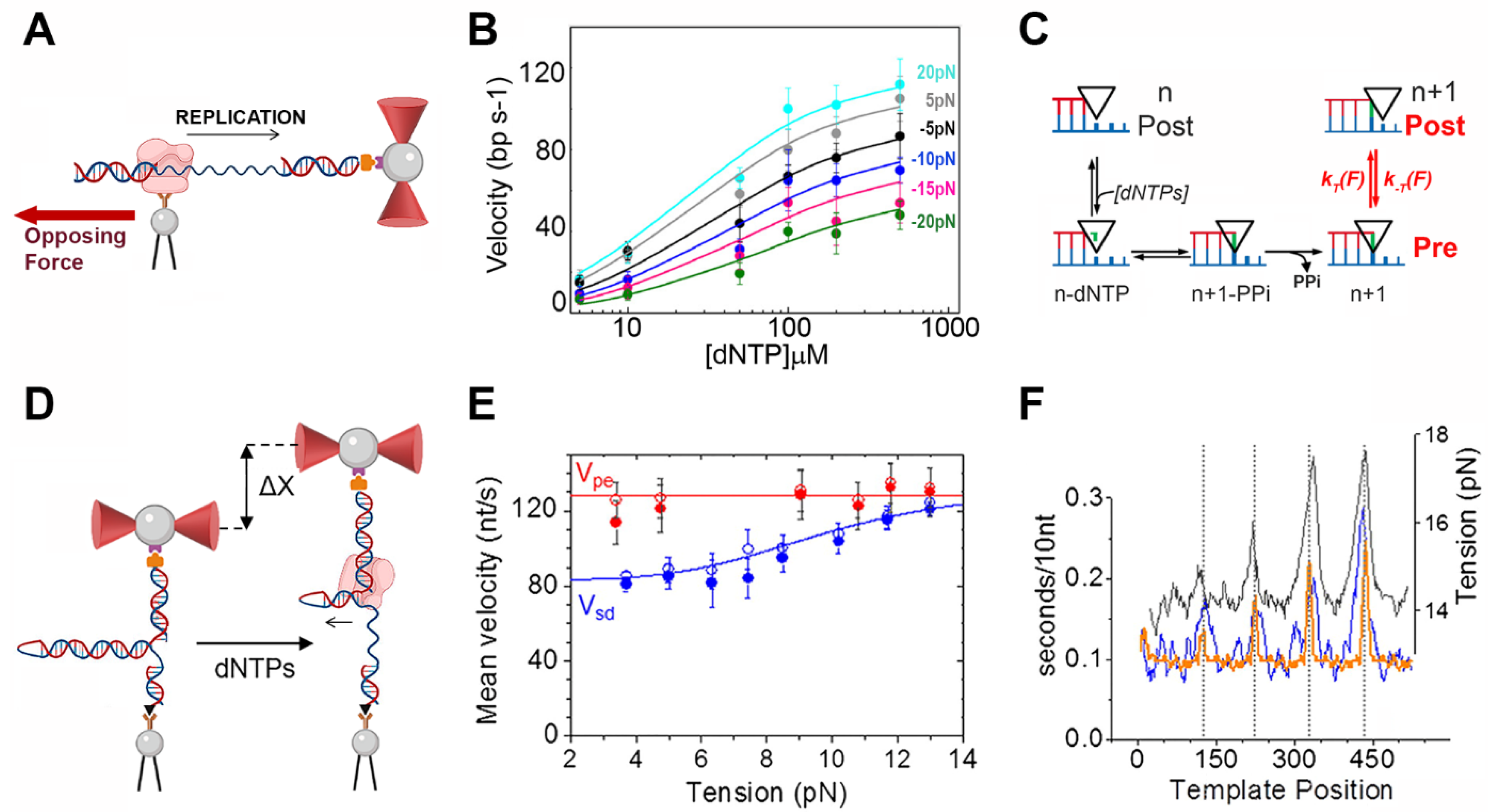
3. Optical Tweezers Assays to Study the Operation of Replicative DNA Polymerases
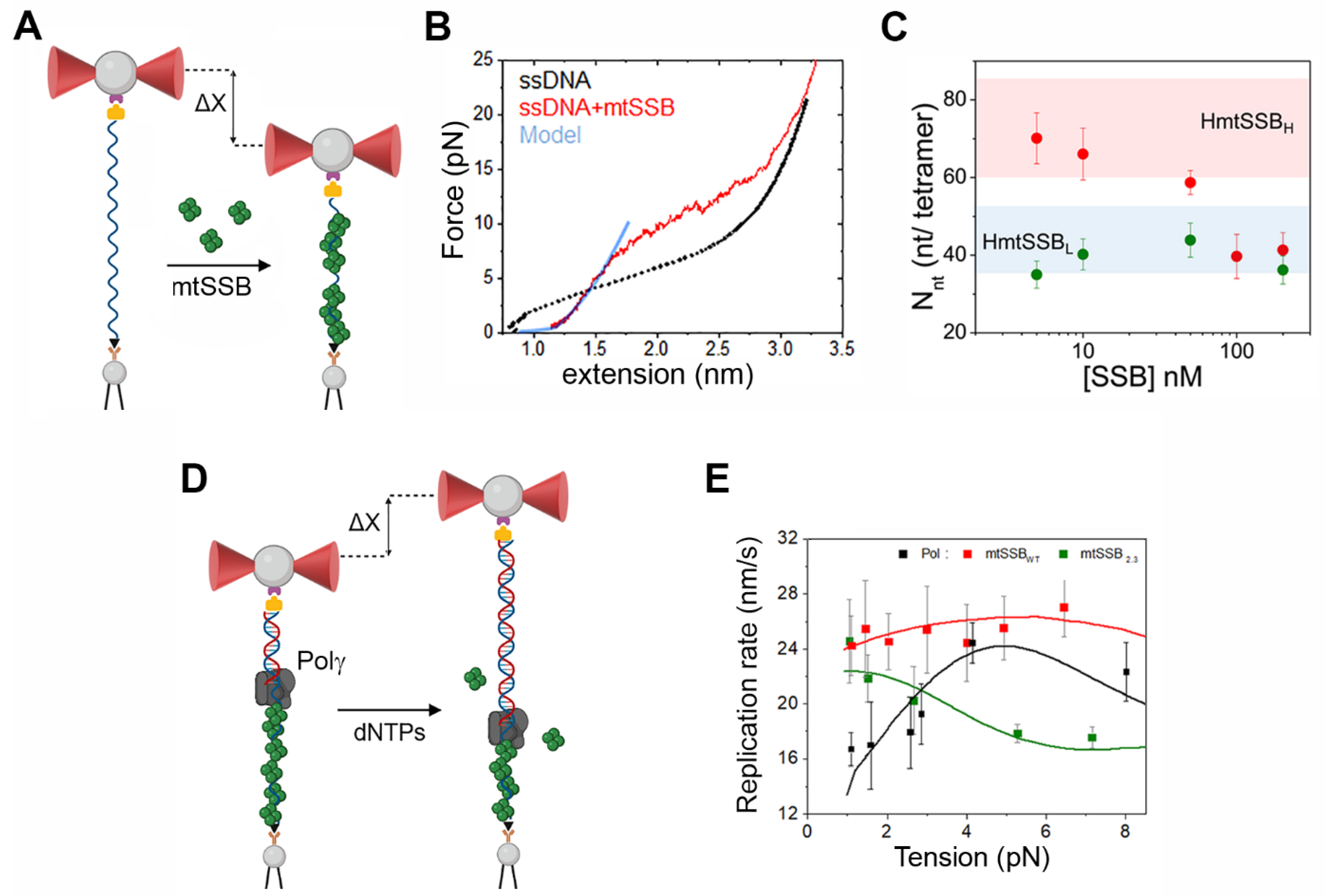
4. Optical Tweezers Assays to Study the Activity of the Human Mitochondrial Replisome
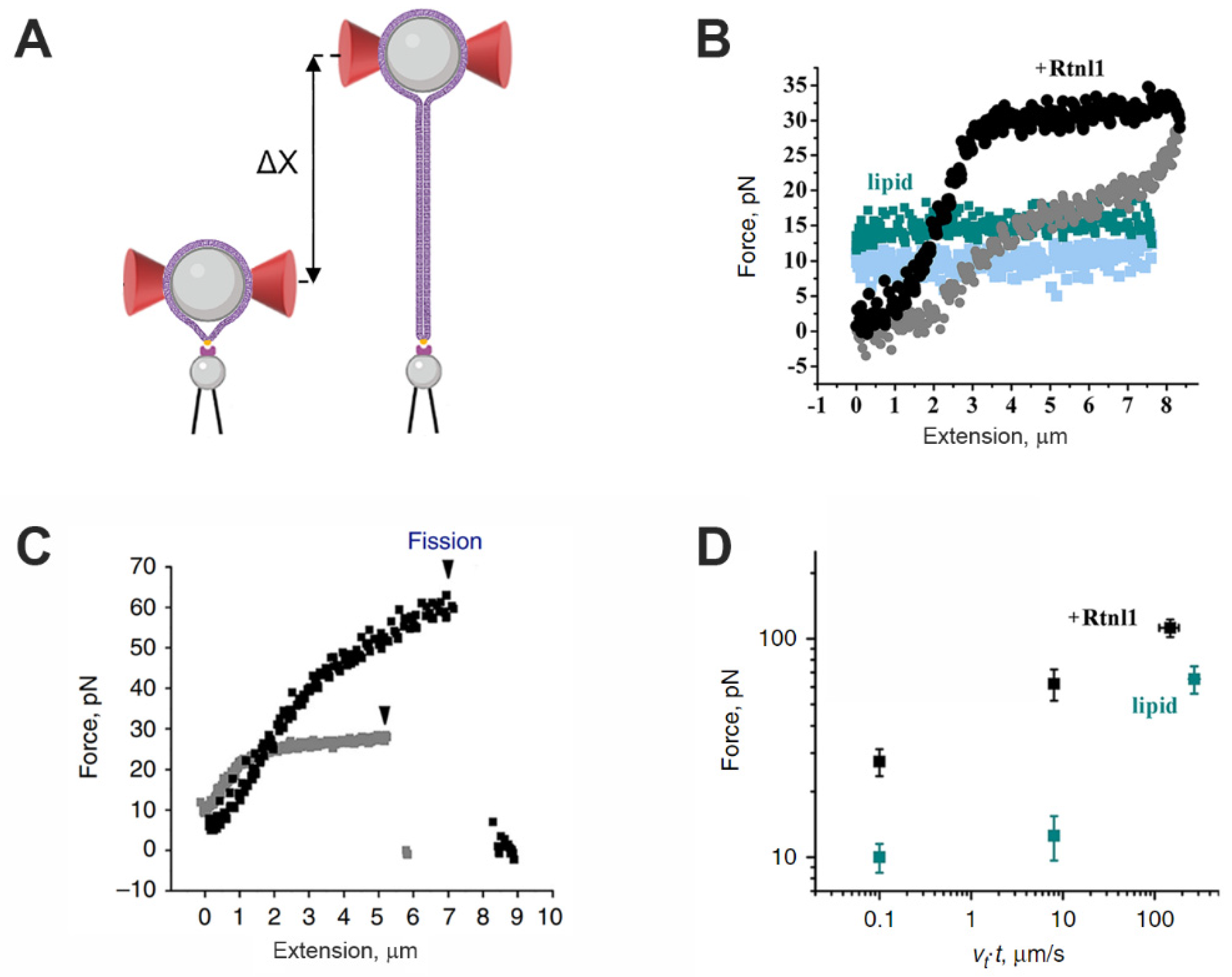
5. Optical Tweezers Studies of Membrane Remodeling Reactions
6. Optical Tweezers to Explore Noncovalent Interactions in Supramolecular Chemistry
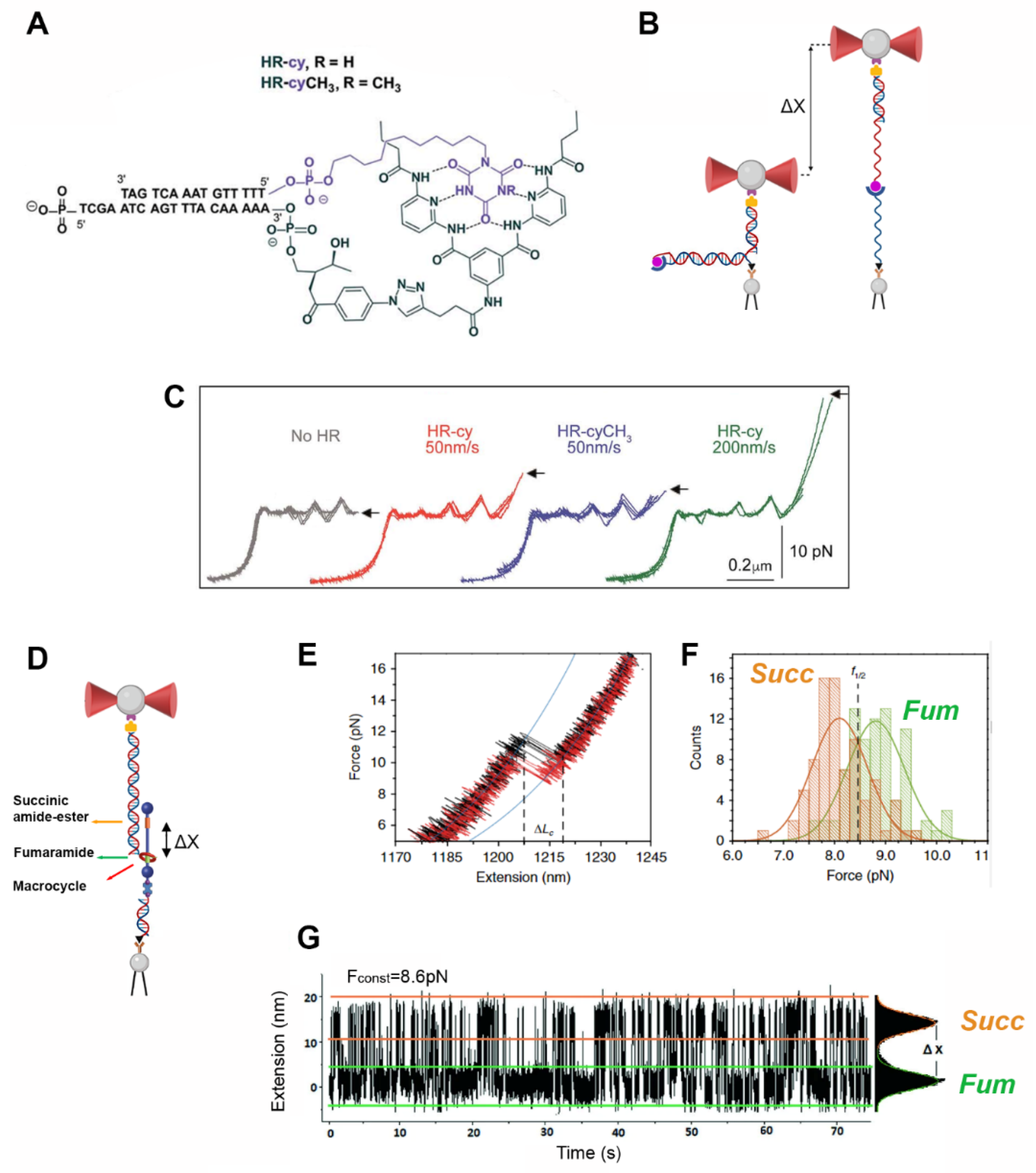
7. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bustamante, C. In singulo Biochemistry: When Less Is More. Annu. Rev. Biochem. 2008, 77, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Bustamante, C.; Chemla, Y.R.; Forde, N.R.; Izhaky, D. Mechanical Processes in Biochemistry. Annu. Rev. Biochem. 2004, 73, 705–748. [Google Scholar] [CrossRef] [PubMed]
- Van Mameren, J.; Wuite, G.J.L.; Heller, I. Introduction to Optical Tweezers: Background, System Designs, and Commercial Solutions. In Methods in Molecular Biology; Humana Press: Totowa, NJ, USA, 2011; Volume 783. [Google Scholar] [CrossRef]
- Bustamante, C.J.; Chemla, Y.R.; Liu, S.; Wang, M.D. Optical tweezers in single-molecule biophysics. Nat. Rev. Prim. 2021, 1, 25. [Google Scholar] [CrossRef] [PubMed]
- Moffitt, J.R.; Chemla, Y.R.; Smith, S.B.; Bustamante, C. Recent Advances in Optical Tweezers. Annu. Rev. Biochem. 2008, 77, 205–228. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef]
- Smith, S.B.; Cui, Y.; Bustamante, C. [7] Optical-trap force transducer that operates by direct measurement of light momentum. In Methods in Enzymology; Academic Press: New York, NY, USA, 2003; Volume 361. [Google Scholar] [CrossRef]
- De Lorenzo, S.; Ribezzi-Crivellari, M.; Arias-Gonzalez, J.R.; Smith, S.B.; Ritort, F. A Temperature-Jump Optical Trap for Single-Molecule Manipulation. Biophys. J. 2015, 108, 2854–2864. [Google Scholar] [CrossRef]
- Bocanegra, R.; Plaza, G.I.; Pulido, C.R.; Ibarra, B. DNA replication machinery: Insights from in vitro single-molecule approaches. Comput. Struct. Biotechnol. J. 2021, 19, 2057–2069. [Google Scholar] [CrossRef]
- Cheppali, S.K.; Dharan, R.; Sorkin, R. Forces of Change: Optical Tweezers in Membrane Remodeling Studies. J. Membr. Biol. 2022, 255, 677–690. [Google Scholar] [CrossRef]
- Rissone, P.; Ritort, F. Nucleic Acid Thermodynamics Derived from Mechanical Unzipping Experiments. Life 2022, 12, 1089. [Google Scholar] [CrossRef]
- Bustamante, C.; Alexander, L.; Maciuba, K.; Kaiser, C.M. Single-Molecule Studies of Protein Folding with Optical Tweezers. Annu. Rev. Biochem. 2020, 89, 443–470. [Google Scholar] [CrossRef]
- Morin, J.A.; Cao, F.J.; Lázaro, J.M.; Arias-Gonzalez, J.R.; Valpuesta, J.M.; Carrascosa, J.L.; Salas, M.; Ibarra, B. Mechano-chemical kinetics of DNA replication: Identification of the translocation step of a replicative DNA polymerase. Nucleic Acids Res. 2015, 43, 3643–3652. [Google Scholar] [CrossRef] [PubMed]
- Castillo, J.P.; Tong, A.B.; Tafoya, S.; Jardine, P.J.; Bustamante, C. A DNA packaging motor inchworms along one strand allowing it to adapt to alternative double-helical structures. Nat. Commun. 2021, 12, 3439. [Google Scholar] [CrossRef] [PubMed]
- Gittes, F.; Schmidt, C. Interference model for back-focal-plane displacement detection in optical tweezers. Opt. Lett. 1998, 23, 7–9. [Google Scholar] [CrossRef]
- Allersma, M.W.; Gittes, F.; Decastro, M.J.; Stewart, R.J.; Schmidt, C.F. Two-Dimensional Tracking of ncd Motility by Back Focal Plane Interferometry. Biophys. J. 1998, 74, 1074–1085. [Google Scholar] [CrossRef] [PubMed]
- Kassem, S.; van Leeuwen, T.; Lubbe, A.S.; Wilson, M.R.; Feringa, B.L.; Leigh, D.A. Artificial molecular motors. Chem. Soc. Rev. 2017, 46, 2592–2621. [Google Scholar] [CrossRef] [PubMed]
- Kay, E.R.; Leigh, D.A.; Zerbetto, F. Synthetic Molecular Motors and Mechanical Machines. Angew. Chem. Int. Ed. 2006, 46, 72–191. [Google Scholar] [CrossRef]
- Smith, S.B.; Cui, Y.; Bustamante, C. Overstretching B-DNA: The Elastic Response of Individual Double-Stranded and Single-Stranded DNA Molecules. Science 1996, 271, 795–799. [Google Scholar] [CrossRef]
- Bosco, A.; Camunas-Soler, J.; Ritort, F. Elastic properties and secondary structure formation of single-stranded DNA at monovalent and divalent salt conditions. Nucleic Acids Res. 2014, 42, 2064–2074. [Google Scholar] [CrossRef]
- Wang, M.D.; Yin, H.; Landick, R.; Gelles, J.; Block, S.M. Stretching DNA with optical tweezers. Biophys. J. 1997, 72, 1335–1346. [Google Scholar] [CrossRef]
- Shon, M.J.; Rah, S.-H.; Yoon, T.-Y. Submicrometer elasticity of double-stranded DNA revealed by precision force-extension measurements with magnetic tweezers. Sci. Adv. 2019, 5, eaav1697. [Google Scholar] [CrossRef]
- Smith, S.B.; Finzi, L.; Bustamante, C. Direct Mechanical Measurements of the Elasticity of Single DNA Molecules by Using Magnetic Beads. Science 1992, 258, 1122–1126. [Google Scholar] [CrossRef]
- Camunas-Soler, J.; Ribezzi-Crivellari, M.; Ritort, F. Elastic Properties of Nucleic Acids by Single-Molecule Force Spectroscopy. Annu. Rev. Biophys. 2016, 45, 65–84. [Google Scholar] [CrossRef] [PubMed]
- Kratky, O.; Porod, G. Röntgenuntersuchung gelöster Fadenmoleküle. Recl. Trav. Chim. Pays-Bas 1949, 68, 1106–1122. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics. Pt. 1, Pt. 2. In Course of Theoretical Physics; Elsevier: Amsterdam, The Netherlands, 1980. [Google Scholar]
- Bustamante, C.; Marko, J.F.; Siggia, E.D.; Smith, S. Entropic Elasticity of Lambda-Phage DNA. Science 1994, 265, 1599–1600. [Google Scholar] [CrossRef] [PubMed]
- Bustamante, C.; Yan, S. The development of single molecule force spectroscopy: From polymer biophysics to molecular machines. Q. Rev. Biophys. 2022, 55, E9. [Google Scholar] [CrossRef]
- Marko, J.F.; Siggia, E.D. Stretching DNA. Macromolecules 1995, 28, 8759–8770. [Google Scholar] [CrossRef]
- Baumann, C.G.; Smith, S.B.; Bloomfield, V.A.; Bustamante, C. Ionic effects on the elasticity of single DNA molecules. Proc. Natl. Acad. Sci. USA 1997, 94, 6185–6190. [Google Scholar] [CrossRef]
- Odijk, T. Stiff Chains and Filaments under Tension. Macromolecules 1995, 28, 7016–7018. [Google Scholar] [CrossRef]
- Herrero-Galán, E.; Fuentes-Perez, M.E.; Carrasco, C.; Valpuesta, J.M.; Carrascosa, J.L.; Moreno-Herrero, F.; Arias-Gonzalez, J.R. Mechanical Identities of RNA and DNA Double Helices Unveiled at the Single-Molecule Level. J. Am. Chem. Soc. 2013, 135, 122–131. [Google Scholar] [CrossRef]
- Gross, P.; Laurens, N.; Oddershede, L.B.; Bockelmann, U.; Peterman, E.; Wuite, G.J.L. Quantifying how DNA stretches, melts and changes twist under tension. Nat. Phys. 2011, 7, 731–736. [Google Scholar] [CrossRef]
- Vafabakhsh, R.; Ha, T. Extreme Bendability of DNA Less than 100 Base Pairs Long Revealed by Single-Molecule Cyclization. Science 2012, 337, 1097–1101. [Google Scholar] [CrossRef] [PubMed]
- Rivetti, C.; Walker, C.; Bustamante, C. Polymer chain statistics and conformational analysis of DNA molecules with bends or sections of different flexibility. J. Mol. Biol. 1998, 280, 41–59. [Google Scholar] [CrossRef] [PubMed]
- Hogan, M.; LeGrange, J.; Austin, B. Dependence of DNA helix flexibility on base composition. Nature 1983, 304, 752–754. [Google Scholar] [CrossRef] [PubMed]
- Marin-Gonzalez, A.; Vilhena, J.G.; Moreno-Herrero, F.; Perez, R. DNA Crookedness Regulates DNA Mechanical Properties at Short Length Scales. Phys. Rev. Lett. 2019, 122, 048102. [Google Scholar] [CrossRef]
- Lankaš, F.; Sponer, J.; Hobza, P.; Langowski, J. Sequence-dependent elastic properties of DNA. J. Mol. Biol. 2000, 299, 695–709. [Google Scholar] [CrossRef]
- Marin-Gonzalez, A.; Pastrana, C.L.; Bocanegra, R.; Martín-González, A.; Vilhena, J.G.; Pérez, R.; Ibarra, B.; Aicart-Ramos, C.; Moreno-Herrero, F. Understanding the paradoxical mechanical response of in-phase A-tracts at different force regimes. Nucleic Acids Res. 2020, 48, 5024–5036. [Google Scholar] [CrossRef]
- Segal, E.; Widom, J. Poly(dA:dT) tracts: Major determinants of nucleosome organization. Curr. Opin. Struct. Biol. 2009, 19, 65–71. [Google Scholar] [CrossRef]
- Viader-Godoy, X.; Pulido, C.R.; Ibarra, B.; Manosas, M.; Ritort, F. Cooperativity-Dependent Folding of Single-Stranded DNA. Phys. Rev. X 2021, 11, 031037. [Google Scholar] [CrossRef]
- Montanari, A.; Mézard, M. Hairpin Formation and Elongation of Biomolecules. Phys. Rev. Lett. 2001, 86, 2178–2181. [Google Scholar] [CrossRef]
- Bocanegra, R.; Plaza, G.A.I.; Ibarra, B. In vitro single-molecule manipulation studies of viral DNA replication. In The Enzymes; Academic Press: Essen, Germany, 2021. [Google Scholar] [CrossRef]
- Joyce, C.M.; Steitz, T.A. Function and structure relationships in dna polymerases. Annu. Rev. Biochem. 1994, 63, 777–822. [Google Scholar] [CrossRef]
- Wuite, G.J.; Smith, S.B.; Young, M.; Keller, D.; Bustamante, C. Single-molecule studies of the effect of template tension on T7 DNA polymerase activity. Nature 2000, 404, 103–106. [Google Scholar] [CrossRef]
- Ibarra, B.; Chemla, Y.R.; Plyasunov, S.; Smith, S.B.; Lázaro, J.M.; Salas, M.; Bustamante, C. Proofreading dynamics of a processive DNA polymerase. EMBO J. 2009, 28, 2794–2802. [Google Scholar] [CrossRef] [PubMed]
- Morin, J.A.; Cao, F.J.; Lázaro, J.M.; Arias-Gonzalez, J.R.; Valpuesta, J.M.; Carrascosa, J.L.; Salas, M.; Ibarra, B. Active DNA unwinding dynamics during processive DNA replication. Proc. Natl. Acad. Sci. USA 2012, 109, 8115–8120. [Google Scholar] [CrossRef] [PubMed]
- Maier, B.; Bensimon, D.; Croquette, V. Replication by a single DNA polymerase of a stretched single-stranded DNA. Proc. Natl. Acad. Sci. USA 2000, 97, 12002–12007. [Google Scholar] [CrossRef]
- Manosas, M.; Spiering, M.M.; Ding, F.; Bensimon, D.; Allemand, J.-F.; Benkovic, S.J.; Croquette, V. Mechanism of strand displacement synthesis by DNA replicative polymerases. Nucleic Acids Res. 2012, 40, 6174–6186. [Google Scholar] [CrossRef] [PubMed]
- Hoekstra, T.P.; Depken, M.; Lin, S.-N.; Cabanas-Danés, J.; Gross, P.; Dame, R.T.; Peterman, E.J.; Wuite, G.J. Switching between Exonucleolysis and Replication by T7 DNA Polymerase Ensures High Fidelity. Biophys. J. 2017, 112, 575–583. [Google Scholar] [CrossRef]
- Naufer, M.N.; Murison, D.A.; Rouzina, I.; Beuning, P.J.; Williams, M.C. Single-molecule mechanochemical characterization of E. coli pol III core catalytic activity. Protein Sci. 2017, 26, 1413–1426. [Google Scholar] [CrossRef]
- Cerrón, F.; de Lorenzo, S.; Lemishko, K.M.; Ciesielski, G.L.; Kaguni, L.S.; Cao, F.J.; Ibarra, B. Replicative DNA polymerases promote active displacement of SSB proteins during lagging strand synthesis. Nucleic Acids Res. 2019, 47, 5723–5734. [Google Scholar] [CrossRef]
- Steitz, T.A. Visualizing polynucleotide polymerase machines at work. EMBO J. 2006, 25, 3458–3468. [Google Scholar] [CrossRef]
- Blanco, L.; Bernad, A.; Lazaro, J.M.; Martin, G.; Garmendia, C.; Salas, M. Highly efficient DNA synthesis by the phage Φ29 DNA polymerase. Symmetrical mode of DNA replication. J. Biol. Chem. 1989, 264, 8935–8940. [Google Scholar] [CrossRef]
- Kamtekar, S.; Richardson, C.; Salas, M.; Berman, A.; Rodríguez, I.; Steitz, T.; Blanco, L.; de Vega, M.; Lázaro, J. A specific subdomain in φ29 DNA polymerase confers both processivity and strand-displacement capacity. Proc. Natl. Acad. Sci. USA 2005, 102, 6407–6412. [Google Scholar]
- Morin, J.A.; Cao, F.J.; Valpuesta, J.M.; Carrascosa, J.L.; Salas, M.; Ibarra, B. Manipulation of single polymerase-DNA complexes: A mechanical view of DNA unwinding during replication. Cell Cycle 2012, 11, 2967–2968. [Google Scholar] [CrossRef] [PubMed]
- Nass, M.M.K.; Nass, S. Intramitochondrial fibers with dna characteristics. J. Cell Biol. 1963, 19, 593–611. [Google Scholar] [CrossRef] [PubMed]
- Wallace, D.C.; Zheng, X.; Lott, M.T.; Shoffner, J.M.; Hodge, J.A.; Kelley, R.I.; Epstein, C.M.; Hopkins, L.C. Familial mitochondrial encephalomyopathy (MERRF): Genetic, pathophysiological, and biochemical characterization of a mitochondrial DNA disease. Cell 1988, 55, 601–610. [Google Scholar] [CrossRef]
- Wallace, D.C.; Singh, G.; Lott, M.T.; Hodge, J.A.; Schurr, T.G.; Lezza, A.M.; Elsas, L.J., II; Nikoskelainen, E.K. Mitochondrial DNA mutation associated with Leber’s hereditary optic neuropathy. Science 1988, 242, 1427–1430. [Google Scholar] [CrossRef]
- Holt, I.; Harding, A.E.; Morgan-Hughes, J.A. Mitochondrial DNA polymorphism in mitochondrial myopathy. Qual. Life Res. 1988, 79, 53–57. [Google Scholar] [CrossRef]
- Morin, J.A.; Cerrón, F.; Jarillo, J.; Beltran-Heredia, E.; Ciesielski, G.L.; Arias-Gonzalez, J.R.; Kaguni, L.S.; Cao, F.J.; Ibarra, B. DNA synthesis determines the binding mode of the human mitochondrial single-stranded DNA-binding protein. Nucleic Acids Res. 2017, 45, 7237–7248. [Google Scholar] [CrossRef]
- Robberson, D.L.; Clayton, D.A. Replication of Mitochondrial DNA in Mouse L Cells and Their Thymidine Kinase-Derivatives: Displacement Replication on a Covalently-Closed Circular Template. Proc. Natl. Acad. Sci. USA 1972, 69, 3810–3814. [Google Scholar] [CrossRef]
- Fusté, J.M.; Shi, Y.; Wanrooij, S.; Zhu, X.; Jemt, E.; Persson, Ö.; Sabouri, N.; Gustafsson, C.M.; Falkenberg, M. In Vivo Occupancy of Mitochondrial Single-Stranded DNA Binding Protein Supports the Strand Displacement Mode of DNA Replication. PLoS Genet. 2014, 10, e1004832. [Google Scholar] [CrossRef]
- Jarillo, J.; Morín, J.A.; Beltrán-Heredia, E.; Villaluenga, J.P.G.; Ibarra, B.; Cao, F.J. Mechanics, thermodynamics, and kinetics of ligand binding to biopolymers. PLoS ONE 2017, 12, e0174830. [Google Scholar] [CrossRef]
- Lohman, T.M.; Ferrari, M.E. Escherichia coli single-stranded DNA-binding protein: Multiple DNA-Binding Modes and Cooperativities. Annu. Rev. Biochem. 1994, 63, 527–570. [Google Scholar] [CrossRef] [PubMed]
- Ciesielski, G.L.; Bermek, O.; Rosado-Ruiz, F.A.; Hovde, S.L.; Neitzke, O.J.; Griffith, J.D.; Kaguni, L.S. Mitochondrial Single-stranded DNA-binding Proteins Stimulate the Activity of DNA Polymerase γ by Organization of the Template DNA. J. Biol. Chem. 2015, 290, 28697–28707. [Google Scholar] [CrossRef] [PubMed]
- Farr, C.L.; Wang, Y.; Kaguni, L.S. Functional Interactions of Mitochondrial DNA Polymerase and Single-stranded DNA-binding Protein. J. Biol. Chem. 1999, 274, 14779–14785. [Google Scholar] [CrossRef] [PubMed]
- Cerrón, F.; Ibarra, B. Measurements of Replication Kinetics of DNA Polymerases on ssDNA Templates Coated with Single-Stranded DNA-Binding Proteins. In Methods in Molecular Biology; Humana Press: Totowa, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Dols-Perez, A.; Marin, V.; Amador, G.J.; Kieffer, R.; Tam, D.; Aubin-Tam, M.-E. Artificial Cell Membranes Interfaced with Optical Tweezers: A Versatile Microfluidics Platform for Nanomanipulation and Mechanical Characterization. ACS Appl. Mater. Interfaces 2019, 11, 33620–33627. [Google Scholar] [CrossRef] [PubMed]
- Moreno-Pescador, G.; Florentsen, C.D.; Østbye, H.; Sønder, S.L.; Boye, T.L.; Veje, E.L.; Sonne, A.K.; Semsey, S.; Nylandsted, J.; Daniels, R.; et al. Curvature- and Phase-Induced Protein Sorting Quantified in Transfected Cell-Derived Giant Vesicles. ACS Nano 2019, 13, 6689–6701. [Google Scholar] [CrossRef]
- Beltrán-Heredia, E.; Tsai, F.-C.; Salinas-Almaguer, S.; Cao, F.J.; Bassereau, P.; Monroy, F. Membrane curvature induces cardiolipin sorting. Commun. Biol. 2019, 2, 225. [Google Scholar] [CrossRef]
- Dasgupta, R.; Miettinen, M.S.; Fricke, N.; Lipowsky, R.; Dimova, R. The glycolipid GM1 reshapes asymmetric biomembranes and giant vesicles by curvature generation. Proc. Natl. Acad. Sci. USA 2018, 115, 5756–5761. [Google Scholar] [CrossRef]
- Neumann, S.; Pucadyil, T.J.; Schmid, S.L. Analyzing membrane remodeling and fission using supported bilayers with excess membrane reservoir. Nat. Protoc. 2013, 8, 213–222. [Google Scholar] [CrossRef]
- Sorkin, R.; Marchetti, M.; Logtenberg, E.; Piontek, M.C.; Kerklingh, E.; Brand, G.; Voleti, R.; Rizo, J.; Roos, W.H.; Groffen, A.J.; et al. Synaptotagmin-1 and Doc2b Exhibit Distinct Membrane-Remodeling Mechanisms. Biophys. J. 2020, 118, 643–656. [Google Scholar] [CrossRef]
- Brouwer, I.; Giniatullina, A.; Laurens, N.; van Weering, J.R.T.; Bald, D.; Wuite, G.J.L.; Groffen, A.J. Direct quantitative detection of Doc2b-induced hemifusion in optically trapped membranes. Nat. Commun. 2015, 6, 8387. [Google Scholar] [CrossRef]
- Ge, J.; Bian, X.; Ma, L.; Cai, Y.; Li, Y.; Yang, J.; Karatekin, E.; De Camilli, P.; Zhang, Y. Stepwise membrane binding of extended synaptotagmins revealed by optical tweezers. Nat. Chem. Biol. 2022, 18, 313–320. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Cai, Y.; Li, Y.; Jiao, J.; Wu, Z.; O’Shaughnessy, B.; De Camilli, P.; Karatekin, E.; Zhang, Y. Single-molecule force spectroscopy of protein-membrane interactions. eLife 2017, 6, e30493. [Google Scholar] [CrossRef] [PubMed]
- Westrate, L.M.; Lee, J.E.; Prinz, W.A.; Voeltz, G.K. Form Follows Function: The Importance of Endoplasmic Reticulum Shape. Annu. Rev. Biochem. 2015, 84, 791–811. [Google Scholar] [CrossRef] [PubMed]
- Orso, G.; Pendin, D.; Liu, S.; Tosetto, J.; Moss, T.J.; Faust, J.E.; Micaroni, M.; Egorova, A.; Martinuzzi, A.; McNew, J.A.; et al. Homotypic fusion of ER membranes requires the dynamin-like GTPase Atlastin. Nature 2009, 460, 978–983. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Tukachinsky, H.; Romano, F.B.; Rapoport, T.A. Cooperation of the ER-shaping proteins atlastin, lunapark, and reticulons to generate a tubular membrane network. eLife 2016, 5, e18605. [Google Scholar] [CrossRef]
- Grumati, P.; Morozzi, G.; Hölper, S.; Mari, M.; Harwardt, M.-L.I.; Yan, R.; Müller, S.; Reggiori, F.; Heilemann, M.; Dikic, I. Full length RTN3 regulates turnover of tubular endoplasmic reticulum via selective autophagy. eLife 2017, 6, e25555. [Google Scholar] [CrossRef]
- Khaminets, A.; Heinrich, T.; Mari, M.; Grumati, P.; Huebner, A.K.; Akutsu, M.; Liebmann, L.; Stolz, A.; Nietzsche, S.; Koch, N.; et al. Regulation of endoplasmic reticulum turnover by selective autophagy. Nature 2015, 522, 354–358. [Google Scholar] [CrossRef]
- Waugh, R.; Hochmuth, R. Mechanical equilibrium of thick, hollow, liquid membrane cylinders. Biophys. J. 1987, 52, 391–400. [Google Scholar] [CrossRef]
- Espadas, J.; Pendin, D.; Bocanegra, R.; Escalada, A.; Misticoni, G.; Trevisan, T.; Del Olmo, A.V.; Montagna, A.; Bova, S.; Ibarra, B.; et al. Dynamic constriction and fission of endoplasmic reticulum membranes by reticulon. Nat. Commun. 2019, 10, 5327. [Google Scholar] [CrossRef]
- Ferguson, S.M.; De Camilli, P. Dynamin, a membrane-remodelling GTPase. Nat. Rev. Mol. Cell Biol. 2012, 13, 75–88. [Google Scholar] [CrossRef]
- Roux, A.; Koster, G.; Lenz, M.; Sorre, B.; Manneville, J.-B.; Nassoy, P.; Bassereau, P. Membrane curvature controls dynamin polymerization. Proc. Natl. Acad. Sci. USA 2010, 107, 4141–4146. [Google Scholar] [CrossRef] [PubMed]
- Vögtle, F.; Stoddart, J.F.; Shibasaki, M. Stimulating Concepts in Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar] [CrossRef]
- Lussis, P.; Svaldo-Lanero, T.; Bertocco, A.; Fustin, C.-A.; Leigh, D.A.; Duwez, A.-S. A single synthetic small molecule that generates force against a load. Nat. Nanotechnol. 2011, 6, 553–557. [Google Scholar] [CrossRef] [PubMed]
- Van Quaethem, A.; Lussis, P.; Leigh, D.A.; Duwez, A.-S.; Fustin, C.-A. Probing the mobility of catenane rings in single molecules. Chem. Sci. 2014, 5, 1449–1452. [Google Scholar] [CrossRef]
- Brough, B.; Northrop, B.H.; Schmidt, J.J.; Tseng, H.-R.; Houk, K.N.; Stoddart, J.F.; Ho, C.-M. Evaluation of synthetic linear motor-molecule actuation energetics. Proc. Natl. Acad. Sci. USA 2006, 103, 8583–8588. [Google Scholar] [CrossRef] [PubMed]
- Chang, S.K.; Hamilton, A.D. Molecular recognition of biologically interesting substrates: Synthesis of an artificial receptor for barbiturates employing six hydrogen bonds. J. Am. Chem. Soc. 1988, 110, 1318–1319. [Google Scholar] [CrossRef]
- Naranjo, T.; Cerrón, F.; Nieto-Ortega, B.; Latorre, A.; Somoza, A.; Ibarra, B.; Pérez, E.M. Mechanical measurement of hydrogen bonded host–guest systems under non-equilibrium, near-physiological conditions. Chem. Sci. 2017, 8, 6037–6041. [Google Scholar] [CrossRef] [PubMed]
- Essevaz-Roulet, B.; Bockelmann, U.; Heslot, F. Mechanical separation of the complementary strands of DNA. Proc. Natl. Acad. Sci. USA 1997, 94, 11935–11940. [Google Scholar] [CrossRef]
- Wang, J.; Kouznetsova, T.B.; Craig, S.L. Single-Molecule Observation of a Mechanically Activated Cis-to-Trans Cyclopropane Isomerization. J. Am. Chem. Soc. 2016, 138, 10410–10412. [Google Scholar] [CrossRef]
- Naranjo, T.; Lemishko, K.M.; De Lorenzo, S.; Somoza, A.; Ritort, F.; Pérez, E.M.; Ibarra, B. Dynamics of individual molecular shuttles under mechanical force. Nat. Commun. 2018, 9, 4512. [Google Scholar] [CrossRef]
- Lemishko, K.M.; Naranjo, T.; Pérez, E.M.; Ibarra, B. Five Minutes in the Life of a Molecular Shuttle: Near-Equilibrium Measurements of Shuttling Dynamics Using Optical Tweezers. In Building and Probing Small for Mechanics. Advances in Atom and Single Molecule Machines; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Berná, J.; Bottari, G.; Leigh, D.A.; Pérez, E.M. Amide-based molecular shuttles (2001–2006). Pure Appl. Chem. 2007, 79, 39–54. [Google Scholar] [CrossRef]
- Yang, W.; Li, Y.; Liu, H.; Chi, L.; Li, Y. Design and Assembly of Rotaxane-Based Molecular Switches and Machines. Small 2012, 8, 504–516. [Google Scholar] [CrossRef] [PubMed]
- Credi, A.; Silvi, S.; Venturi, M. Light-Operated Machines Based on Threaded Molecular Structures. In Topics in Current Chemistry; Springer: Berlin, Germany, 2014; Volume 354. [Google Scholar] [CrossRef]
- Dvornikovs, V.; House, B.E.; Kaetzel, M.; Dedman, J.R.; Smithrud, D.B. Host−[2] Rotaxanes as Cellular Transport Agents. J. Am. Chem. Soc. 2003, 125, 8290–8301. [Google Scholar] [CrossRef] [PubMed]
- Nishimura, D.; Takashima, Y.; Aoki, H.; Takahashi, T.; Yamaguchi, H.; Ito, S.; Harada, A. Single-Molecule Imaging of Rotaxanes Immobilized on Glass Substrates: Observation of Rotary Movement. Angew. Chem. Int. Ed. 2008, 47, 6077–6079. [Google Scholar] [CrossRef]
- Van Dongen, S.F.M.; Cantekin, S.; Elemans, J.A.A.W.; Rowan, A.E.; Nolte, R.J.M. Functional interlocked systems. Chem. Soc. Rev. 2014, 43, 99–122. [Google Scholar] [CrossRef] [PubMed]
- Sitters, G.; Kamsma, D.; Thalhammer, G.; Ritsch-Marte, M.; Peterman, E.J.G.; Wuite, G.J.L. Acoustic force spectroscopy. Nat. Methods 2014, 12, 47–50. [Google Scholar] [CrossRef] [PubMed]
- Kriegel, F.; Vanderlinden, W.; Nicolaus, T.; Kardinal, A.; Lipfert, J. Measuring Single-Molecule Twist and Torque in Multiplexed Magnetic Tweezers. In Methods in Molecular Biology; Humana Press: Totowa, NJ, USA, 2018. [Google Scholar] [CrossRef]
- Agarwal, R.; Duderstadt, K.E. Multiplex flow magnetic tweezers reveal rare enzymatic events with single molecule precision. Nat. Commun. 2020, 11, 4714. [Google Scholar] [CrossRef]
- Granéli, A.; Yeykal, C.C.; Prasad, T.K.; Greene, E.C. Organized Arrays of Individual DNA Molecules Tethered to Supported Lipid Bilayers. Langmuir 2006, 22, 292–299. [Google Scholar] [CrossRef]
- Whitley, K.; Comstock, M.; Chemla, Y. High-Resolution Optical Tweezers Combined with Single-Molecule Confocal Microscopy. In Methods in Enzymology; Academic Press: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Whitley, K.D.; Comstock, M.J.; Chemla, Y.R. High-Resolution “Fleezers”: Dual-Trap Optical Tweezers Combined with Single-Molecule Fluorescence Detection. In Methods in Molecular Biology; Humana Press: Totowa, NJ, USA, 2017; Volume 1486. [Google Scholar] [CrossRef]
- Long, X.; Parks, J.W.; Stone, M.D. Integrated magnetic tweezers and single-molecule FRET for investigating the mechanical properties of nucleic acid. Methods 2016, 105, 16–25. [Google Scholar] [CrossRef]
- Heller, I.; Sitters, G.; Broekmans, O.D.; Farge, G.; Menges, C.; Wende, W.; Hell, S.W.; Peterman, E.; Wuite, G.J.L. STED nanoscopy combined with optical tweezers reveals protein dynamics on densely covered DNA. Nat. Methods 2013, 10, 910–916. [Google Scholar] [CrossRef]
- Heller, I.; Laurens, N.; Vorselen, D.; Broekmans, O.D.; Biebricher, A.S.; King, G.A.; Brouwer, I.; Wuite, G.J.L.; Peterman, E.J.G. Versatile quadruple-trap optical tweezers for dual DNA experiments. In Methods in Molecular Biology; Humana Press: Totowa, NJ, USA, 2017; Volume 1486, pp. 257–272. [Google Scholar] [CrossRef]
- Rico-Pasto, M.; Zaltron, A.; Davis, S.J.; Frutos, S.; Ritort, F. Molten globule–like transition state of protein barnase measured with calorimetric force spectroscopy. Proc. Natl. Acad. Sci. USA 2022, 119, e2112382119. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Galior, K.; Ma, V.P.-Y.; Salaita, K. Molecular Tension Probes for Imaging Forces at the Cell Surface. Acc. Chem. Res. 2017, 50, 2915–2924. [Google Scholar] [CrossRef]
- Wang, X.; Ha, T. Defining Single Molecular Forces Required to Activate Integrin and Notch Signaling. Science 2013, 340, 991–994. [Google Scholar] [CrossRef]
- Dufrêne, Y.F.; Evans, E.; Engel, A.; Helenius, J.; Gaub, H.E.; Müller, D.J. Five challenges to bringing single-molecule force spectroscopy into living cells. Nat. Methods 2011, 8, 123–127. [Google Scholar] [CrossRef]
- Oddershede, L.B. Force probing of individual molecules inside the living cell is now a reality. Nat. Chem. Biol. 2012, 8, 879–886. [Google Scholar] [CrossRef] [PubMed]
- Feringa, B.L. The Art of Building Small: From Molecular Switches to Molecular Motors. J. Org. Chem. 2007, 72, 6635–6652. [Google Scholar] [CrossRef] [PubMed]
- Cheng, B.; Cui, S. Supramolecular Chemistry and Mechanochemistry of Macromolecules: Recent Advances by Single-Molecule Force Spectroscopy. In Topics in Current Chemistry; Springer: Berlin, Germany, 2015. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bocanegra, R.; Ortiz-Rodríguez, M.; Garcia-Abadillo, I.P.; R-Pulido, C.; Ibarra, B. Optical Tweezers to Force Information out of Biological and Synthetic Systems One Molecule at a Time. Biophysica 2022, 2, 564-580. https://doi.org/10.3390/biophysica2040047
Bocanegra R, Ortiz-Rodríguez M, Garcia-Abadillo IP, R-Pulido C, Ibarra B. Optical Tweezers to Force Information out of Biological and Synthetic Systems One Molecule at a Time. Biophysica. 2022; 2(4):564-580. https://doi.org/10.3390/biophysica2040047
Chicago/Turabian StyleBocanegra, Rebeca, María Ortiz-Rodríguez, Ismael Plaza Garcia-Abadillo, Carlos R-Pulido, and Borja Ibarra. 2022. "Optical Tweezers to Force Information out of Biological and Synthetic Systems One Molecule at a Time" Biophysica 2, no. 4: 564-580. https://doi.org/10.3390/biophysica2040047
APA StyleBocanegra, R., Ortiz-Rodríguez, M., Garcia-Abadillo, I. P., R-Pulido, C., & Ibarra, B. (2022). Optical Tweezers to Force Information out of Biological and Synthetic Systems One Molecule at a Time. Biophysica, 2(4), 564-580. https://doi.org/10.3390/biophysica2040047




