Abstract
Directed cell migration is an essential building block of life, present when an embryo develops, a dendritic cell migrates toward a lymphatic vessel, or a fibrotic organ fails to restore its normal parenchyma. Directed cell migration is often guided by spatial gradients in a physicochemical property of the cell microenvironment, such as a gradient in chemical factors dissolved in the medium or a gradient in the mechanical properties of the substrate. Single cells and tissues sense these gradients, establish a back-to-front polarity, and coordinate the migration machinery accordingly. Central to these steps we find physical forces. In some cases, these forces are integrated into the gradient sensing mechanism. Other times, they transmit information through cells and tissues to coordinate a collective response. At any time, they participate in the cellular migratory system. In this review, we explore the role of physical forces in gradient sensing, polarization, and coordinating movement from single cells to multicellular collectives. We use the framework proposed by the molecular clutch model and explore to what extent asymmetries in the different elements of the clutch can lead to directional migration.
1. Introduction
Much like ants self-organize to build living bridges [1], sheep herds coordinate their movements to escape from a predator [2], or emperor penguins rearrange within the huddle to survive the winter [3], cells in our body coordinate their movement to achieve many of their main physiological functions. Essential to this self-organization, we find the capacity of cells to migrate in a directed form. Directed cell migration is present in most biological processes. For example, in the early stages of neocortical development, many neurons and interneurons migrate radially in a directed form to build highly laminated structures in the central nervous system, including the cerebral and cerebellar cortices, as well as other structures such as the spinal cord, striatum, and thalamus [4,5]. During the early stages of an immune response, dendritic cells migrate directly toward the lymphatic vessels to present antigens collected to T cells [6]. Directed cell migration also has a crucial role in tissue repair. After establishing a temporary basement membrane composed of plasma proteins, cells at the periphery of the wound directly migrate toward the injured site. Only after the migration has restored a coherent monolayer, proliferation and differentiation begin, leading to a functional epithelium [7].
In the above examples of directed cell migration, cells are tightly coordinated. When coordination fails, directed cell migration backfires and mediates devastating diseases. This is the case with some birth defects during development. For example, insufficient directionality of neural crest cells in early development has been pinpointed as the cause of neurocristopathies, a family of diseases that comprise a broad spectrum of congenital malformations [8]. At other times, these diseases are caused by excessive cell directionality. This is the case with cancer, in which directed cell migration is associated with a poor prognosis. To colonize distant organs, carcinoma cells must invade the surrounding tissue, intravasate into blood vessels, and extravasate into healthy tissue. While cancer cells can move both randomly and directly, the above steps are more effective when cancer cells move with directionality [9,10].
Directed cell migration is usually guided by spatial gradients in a physicochemical property of the cellular microenvironment, such as gradients in chemical factors dissolved in the medium (chemotaxis), gradients in the stiffness of the extracellular matrix (durotaxis), gradients in the density of proteins immobilized on the substrate (haptotaxis), variations in substrate topology (contact guidance), or gradients in substrate curvature (curvotaxis) (Figure 1). To directly migrate, cells must first sense the gradient, establish a back-to-front polarity, and coordinate the migration machinery accordingly. Central to these steps we find physical forces. Sometimes, these forces are integrated into the gradient sensing mechanism. Other times, these forces transmit information through the cell to coordinate a collective response. At any time, they are involved in the cell migration machinery. There are many excellent reviews addressing the fundamental principles of directed cell migration [11,12,13,14,15,16]. While some of them address some aspects of force transmission and sensing, a review focusing on the global role of forces in directed cell migration is missing. We designed this review to fill this gap.
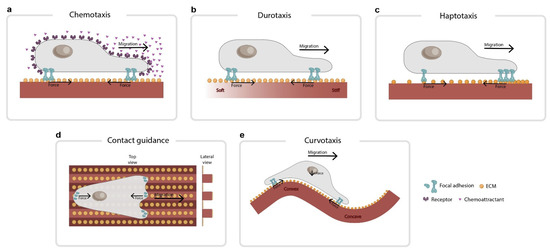
Figure 1.
Common types of directed cell migration. (a) In chemotaxis, cells follow gradients of chemical factors dissolved in the medium. (b) In durotaxis, cells follow gradients of stiffness in the extracellular matrix. (c) In haptotaxis, cells follow gradients of chemical factors immobilized in the matrix. These gradients can be made of ECM proteins such as fibronectin or collagen. (d) In contact guidance, cells orient to geometrical patterns such as grooves on the substrates. (e) In curvotaxis, cells avoid convex regions and position themselves in concave valleys. The force balance imposed by a curved cell–substrate interface could play a role in this migration. On a curved substrate, planar forces at both edges of the cell cannot cancel out vertically unless actin filaments press down on the nucleus (see arrows).
2. The Molecular Clutch Framework
To understand the role of forces in the diverse phenomenology displayed by migratory cells, we need to use the conceptual framework proposed by the molecular clutch model. The ideas behind this model were expressed as early as 1978 in a Croonian Lecture given by M. Abercrombie [17]. However, it was not until 1988 that Mitchison and Kirschner introduced the term ‘molecular clutch’ to explain the transmission of force between the cytoskeleton and the extracellular matrix (ECM) in analogy to a clutch that engages and disengages the power transfer between a shaft and an engine [18]. Twenty years after these early works, Chan, C.E. and Odde, D.J. adapted these ideas into a mathematical model and validated their predictions experimentally [19]. Later, A. Elosegui, P. Roca-Cusachs, and others complimented the model by introducing adhesion reinforcement [20,21]. In 2016, we used the molecular clutch model to explain collective durotaxis [22], and a year later Odde and colleagues generalized the molecular clutch to explain how cellular forces affected single-cell migration in substrates of different rigidities [23].
In the clutch model, cells exert forces on their ECM primarily by contracting the actin cytoskeleton through myosin molecular motors (Figure 2a and inset). Force is transmitted from the actin cytoskeleton to the ECM through integrins and through a series of adaptor proteins that link integrins to actin [24,25]. The amount of force transmitted to the substrate is controlled by a key parameter, the loading rate, which is defined as the speed at which force in the clutches builds up when they are engaged [24]. The loading rate depends on the substrate stiffness; the number of myosin motors pulling on actin; the molecular properties and quantity; and the distribution of adaptor proteins, integrins, and ECM ligands [25]. The myosin-powered contractility produces an actin retrograde flow that moves from the cell edge (where cell–ECM adhesions form) toward the cell center. The direction of this retrograde flow opposes that of actin polymerization (also referred to as cell protrusive activity), which pushes the cell membrane outward (Figure 2a and inset).
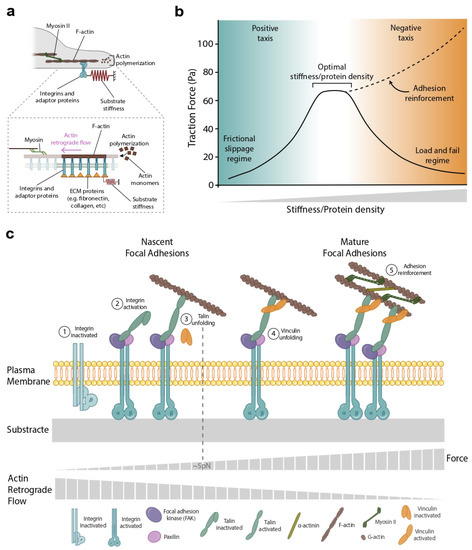
Figure 2.
The molecular clutch model provides a framework to understand the role of forces in directed cell migration. (a) Cells exert forces on their ECM largely through the contraction of the actin cytoskeleton by myosin molecular motors. (inset) Representative scheme of the clutch model. Substrate deformation is represented as a spring. The integrins/accessory proteins at each edge of the cell/cluster are modeled as clutches with given binding and unbinding rates. Myosin-driven contraction creates a retrograde flow from the cell edge toward the cell center. The direction of this retrograde flow opposes that of actin polymerization, which pushes the cell membrane outwards. (b) The clutch model predicts the existence of an optimal stiffness/protein density in which cells’ force and migration are maximal (solid line). This optimal stiffness/protein density, however, is frequently eclipsed by talin/vinculin-mediated reinforcing (dashed line). Adhesion reinforcement has been measured as a function of stiffness [20,21,23] but, as far as we know, not as a function of protein density. (c) Reinforcement takes place above a certain stiffness threshold, when the actin–integrin adaptor protein talin unfolds, exposing binding sites to vinculin. After reinforcement, focal adhesions grow, and the rate of clutch binding increases simply because there are more integrins to be bound to.
In the clutch model, force transmission is maximized for a specific value of stiffness [25] and protein ECM density (Figure 2b). In this paragraph, we will focus on the optimal stiffness case, but most of this analysis is valid for different ECM densities. At low rigidities, force is minimal as clutch engagement is unable to significantly slow retrograde flow. This regime is known as ‘frictional slippage’ and is characterized by high retrograde flow and low forces (Figure 2b, blue zone). On the contrary, at high substrate rigidities, the simultaneous engagement of several clutches leads to repeated cycles of the progressive buildup of force, followed by catastrophic disengagement and force release. This regime is known as ‘load and fail’ or ‘stick-slip’ and is characterized by the failure of the cell to support large forces (Figure 2b, orange zone). In between these two regimes, the clutch model predicts the existence of an optimal stiffness in which the traction forces are maximal [20,25] (Figure 2b). Although this optimal stiffness is predicted, its experimental observation is often overshadowed by talin/vinculin-mediated reinforcement [20,24,26]. Reinforcement occurs above a certain stiffness threshold when the actin–integrin adaptor protein talin unfolds, exposing binding sites to vinculin. After reinforcement, focal adhesions grow and the clutch binding rate increases simply because there are more integrins to bind to (Figure 2c). Reinforcement dominates over the ‘load and fail’ regime, obscuring the observation of the predicted optimal stiffness (Figure 2b, dashed line). Using the conceptual framework proposed by the molecular clutch, we will explore the role of physical forces during the different steps of the directed cell migration: gradient sensing, integrating the sensing information, establishing the back-to-front polarity, and locomoting.
3. Forces during Gradient Sensing
The first step in undergoing directed cell migration is to sense differences in the magnitude of the stimuli across the cell body or tissue. For most forms of directed cell migration, physical forces have a minor role in gradient sensing. This is the case of single-cell chemotaxis (Figure 1a), in which signal detection is achieved through specific receptors such as G-protein-coupled receptors in neutrophils and Dictyostelium cells [27] or by tyrosine kinase receptors in breast cancer cells [28]. However, when directed cell migration is driven by mechanical cues such as stiffness, topology, or substrate–ligand density, physical forces have a major role in signal detection. In such cases, the same structures that allow the cells to transmit forces to the substrate also allow the cells to detect variations in the properties of the ECM.
An example of force-driven sensing is observed during durotaxis (Figure 1b) [29], in which gradient detection is impaired by disrupting the activity of some proteins that mediate force transmission within the clutch. These proteins include integrins, the two isoforms of myosin II (A and B) [30], focal adhesion kinase (FAK) [31], and actin [32]. There is conflicting evidence about the role of the Arp2/3 complex in durotaxis. Arp2/3 inhibition impairs single-cell durotaxis in cancer cells [33] but not in human retinal pigment epithelial cells [34]. Intriguingly, recent studies show that durotaxis requires Zyxin [35,36] but is independent of Rho kinase, Arp2/3, and fascin; yet, the dual inhibition of Arp2/3 and fascin impairs it [35]. While the molecular details of durotaxis remain elusive, the molecular clutch framework can be used to shed some light on the stiffness detection mechanism. In its simplest form, durotaxis can be understood as two sets of identical clutches, one attached to a stiff region and the other attached to a soft one (Figure 3). A critical aspect of this model is how the force balance is imposed across these two clutches. There are two alternatives. In the first one, the force generated by actomyosin motors in each clutch is transmitted from one clutch to another (global force balance, Figure 3a). In the second one, the force generated in each clutch is balanced at the cell center (local force balance, Figure 3b). The stiffness gradient is detected because each clutch pulls a substrate with a different rigidity. Both clutches, therefore, will display unequal dynamics. How cells and tissues integrate these unequal dynamics will depend on whether the forces are balanced locally or globally, and this will be explored later in the review.
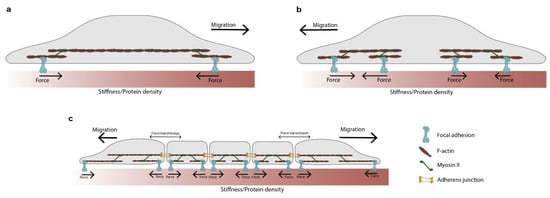
Figure 3.
A minimal conceptual model to detect gradients in the mechanochemical properties of the ECM. This model is useful to understand the role of forces behind the detection of stiffness and protein gradients. (a) In a global force balance scheme, the force is fully transmitted from one clutch to another. Therefore, both clutches are subjected to the same force loading rate, and their dynamics are identical. Durotaxis occurs because at every contraction step the soft clutch deforms the substrate more than the stiff one, shifting the cell towards the stiffer side. Similar principles can be applied to explain haptotaxis. The forces in the low- and high-protein clutches are identical. However, the force per adhesion will be greater in the low-protein part. Therefore, the clutch will collapse more frequently in low-protein regions compared to the high ones, biasing the movement of the cell. Under the global force balance scheme, the actin reward flow will be faster at the softer/low-protein side compared to the stiffer/high-protein one. (b) In a local force balance scheme, each extreme of the cell is independent. The side that transfers more force to the substrate has more stable protrusions and guides cell migration. Therefore, rather than necessarily favoring the stiffer edge, the movement will be biased towards that portion of the matrix. This concept has been explored in durotaxis [37] but not in haptotaxis. (c) The global force balance scheme depicted in panel (a) has been applied to clusters of cells to explain collective durotaxis. The panels in this figure have been adapted from references [38,39].
The framework we have applied to understand the mechanical forces at play during gradient sensing in durotaxis can be readily applied to other forms of directed cell migration. A convenient one is haptotaxis when it is mediated via density gradients of ECM ligands (Figure 1c) [40]. Haptotaxis is impaired by disrupting different elements of the clutch, such as actin polymerization [41], FAK [42], and Arp2/3 [42]. However, there is conflicting evidence for the role of Rho-kinase. Rho-kinase inhibition impairs single-cell haptotaxis in fibroblasts migrating on discrete haptotactic matrices, but not in fibroblasts migrating on continuous ones. In addition to differences in cell lines, this discrepancy could reflect differences in the experimental settings. Although the molecular details of haptotaxis have not yet been elucidated, the molecular clutch framework can provide insight into the role of forces in the detection of ECM gradients. As in durotaxis, a minimal model consists of two sets of identical clutches (Figure 3). This time, however, one of these clutches will be attached to a lower protein density region, while the other to a higher density one. The gradient is detected because each clutch pulls a substrate with a different ECM density, and this leads to unequal dynamics in both clutches. Again, the transmission of force within the cell (global or local) will be critical in integrating the information sensed by both clutches.
Physical forces are also thought to play a role during contact guidance, a form of directed cell migration in which cells and tissues are guided by topological features in the substrate (Figure 1d) [15,43]. These features can be straight or curved, reflecting the fact that healthy stromal tissue has wavy extracellular fibers, while metastasis-prone tissue has more linear ones [44]. Although the detection mechanisms for this type of directed cell migration are not fully understood, several studies point out that substrate topology may provide a template in which focal adhesion orient and actin-rich protrusions push the cell membrane outward along a privileged axis. Consistent with this view, cells polarize independently of myosin II [45], while Arp 2/3 inhibition increased topological detection, presumably by decreasing the protrusion area and improving the localization of protrusions along the lines [46]. In addition to protrusive activity, a recent study suggests that cortical tension at the cell–substrate interface could also play a role in contact guidance, at least in the ameboid migration of T cells [47]. In that study, T cells had their ability to follow grooves increased by seeding them on soft-grooved substrates or disrupting their microtubules with nocodazole [47]: treatments that decreased cortical tension at the cell–substrate interface. Contrariwise, other studies report an opposing effect of nocodazole and stiffness [48], suggesting intriguing differences in contact guidance between ameboid and mesenchymal migration.
Cells respond not only to grooved topological features but also to smooth sinusoidal substrates that present modulations of curvature in all directions (Figure 1e). Cells on these substrates avoid convex regions and position themselves in concave valleys [49,50,51]. This form of directed cell migration is called ‘curvotaxis’ and is currently the focus of intense study [52,53]. Substrate curvature affects focal adhesion organization and dynamics, nuclear shape, and gene expression [49,51]. Curvotaxis depends on actin dynamics, increases with Lamin A expression, and requires nucleoskeleton to cytoskeleton (LINC) complexes, but not microtubules [51]. There are at least two models to explain curvotaxis, both backed up by numerical simulations. In the first, the curvature of the substrate favors the extension of the lamellipodium towards concave regions [54]. In the second, the curvature of the substrate induces a pressure gradient inside the cell that triggers the internal motion of the nucleus, leading the cell toward concave curvatures [55]. A central part of both models is the role of the actin cortex and the membrane, which drive the cytoskeleton’s pressure gradient, polarizing either actin polymerization or nucleus movement. In addition to the actin cortex and the membrane, the force balance imposed by a curved cell–substrate interface could also play a role. On a curved substrate, planar forces at both edges of the cell cannot cancel out vertically unless actin filaments press down on the nucleus (Figure 1e). This mechanism could amplify the effect of the pressure gradient proposed in [55]. Future quantification of traction forces in curved substrates might clarify the contribution of force balance in this form of directed cell migration.
4. Forces during the Integration of Gradient Sensing Information
So far, we have discussed signal detection in various forms of directed cell migration in which force plays a role. More generally, in any directed cell migration mode, a gradient is detected by specialized proteins at the front and the back of the cell or tissue. After this detection, cells and tissues must integrate the information gathered across the body to establish polarity. The way this information is integrated will depend on the cell type, mode of directed migration, and whether the cell is migrating individually or collectively. Sometimes this information is integrated chemically. This is the case of single-cell chemotaxis, in which the response to a chemoattractant is mediated by the activation of second messenger pathways that eventually lead to polarization. Apart from these chemical strategies, we will argue that in certain conditions, forces are also relevant forms to transmit and integrate this information.
Perhaps the clearest evidence of the role of force in integrating gradient information takes place during collective migration. In such systems, blocking force transmission by perturbing cell–cell adhesions often compromises the collective ability to follow signals. This is the case for plithotaxis [56,57], collective chemotaxis [58], and collective durotaxis [22], in which disrupting cell–cell adhesions reduces directed migration and polarization. To understand how force transmission integrates the signal information gathered across the tissue, we will focus on collective durotaxis. In its simplest form, collective durotaxis has been modeled by the two-clutch framework with the global force balance described above (Figure 3c). Under these circumstances, both clutches are subjected to the same loading rate as the forces in the system are balanced. Since the loading rate determines the behavior of the clutch [24], the dynamics of the two clutches will be identical with just one crucial difference: for the same force, the soft clutch will deform the substrate more than the stiff one, shifting the cluster towards the stiffer side. A simple analogy captures this idea. Consider a skateboarder holding two springs, one stiff and one soft. If she contracts her arms, the stiff spring will deform less than the soft one, and she will move toward it [38]. The idea that forces integrate gradient sensing information was tested by disrupting force transmission using siRNA against α-catenin (an adaptor protein of the cell–cell adhesion complex). On α-catenin depleted clusters, traction forces at the edges declined, together with the capacity of the cluster to follow stiffness gradients [22]. Alternatively, physically cutting the cell cluster with a laser also impaired durotaxis, providing further proof that collective durotaxis requires force transmission within the cluster.
Collective durotaxis is an example of collective guidance in which each cell makes a measurement of the signal magnitude, and the cluster estimates the overall gradient by comparing the resulting single-cell measurements in a tug-of-war. In addition to this form of integration of signal information, collectives use other sensing strategies, such as collective susceptibility, in which a few informed cells sense the gradient while the majority only follow, or ‘many wrongs make right’, in which each cell makes a noisy but independent estimate of the gradient [59]. In these alternative strategies, force appears again as an effective way to transmit information across the cluster and integrate both chemical and mechanical information [60].
Although in most collective systems force transmission within the cluster is necessary to integrate sensing information, its role within single cells is more elusive. Part of this lack of knowledge is due to the difficulty of specifically blocking mechanical communication within different parts of the cell. In collective systems, force transmission is often impaired by disrupting cell–cell adhesions or cutting the tissue with laser ablation. These strategies are no longer available in single cells, as pharmacological interventions targeting the cytoskeleton are likely to disrupt not only force transmission, but also basic migratory structures. The evidence that single cells need long-range forces to integrate the mechanical information of the environment—let alone other types of information—is still controversial. There is evidence of rigidity sensing on both scales, either locally, by contractile filaments operating at the micrometer scale [61,62], or globally, by actin stress fibers operating at the whole cell scale [63,64,65]. Studies on single-cell-directed migration emphasize both. For example, haptotaxis has been suggested to be caused by the global balance of traction forces [66] or by the local protrusive activity of actin-rich lamellipodia [42]. Future work will establish a more comprehensive picture of how the cytoskeleton balances forces.
Perhaps the most surprising results of this local versus global controversy have been provided by applying the molecular clutch framework to single cell durotaxis. In a recent study, A. Isomursu and co-workers challenged the well-established notion that cell migration in durotaxis always moves from soft to stiff regions on the matrix. The molecular clutch framework predicts an optimal stiffness peak in which the cell traction forces are maximal [21,25] (Figure 2b). However, this peak is often overshadowed by adhesion reinforcement. Isomursu et al. then used U-251MG cells, a cell type lacking adhesion reinforcement [37]. They found that when these cells were seeded in a softer region than their optimal stiffness, they migrated towards stiffer regions (Figure 2b, blue zone). On the contrary, when they were seeded in a stiffer region than their optimal stiffness, they migrated to softer regions in what authors called ‘negative durotaxis’ (Figure 2b, orange zone). When modeling this behavior using the clutch framework, a critical detail emerged. For the molecular clutch to explain the data, forces needed to be balanced locally, as in Figure 3b. If forces are balanced globally at the cell periphery, force balance implies that substrate deformation will always be higher on the soft (rather than the stiff) clutch and the cell will always move towards the stiff [39]. Prior studies had reported evidence of axon guidance towards softer environments [67] and adurotactic cells [68]. The new data on negative durotaxis explain such observations and suggest that the interpretation of stiffness patterns may be more complicated than initially thought.
5. Establishing Polarity
The integration of the sensing information culminates in the establishment of a polarity that will bias movement along a particular axis. This polarity involves an asymmetric distribution of signaling molecules between the front and the back of the cell [69]. At the front, the small GTPases Rac and Cdc42 promote actin branching by nucleation-promoting factors (NPF) that activate the complex Arp2/3 [70,71,72,73,74] and trigger lamellipodia protrusions. At the back, the small GTPase Rho triggers ROCK, which phosphorylates the myosin light chain and causes the contraction of the actomyosin and the retraction of the back [72,75,76,77,78]. Rho and Rac are often considered antagonists of each other. Besides Rac and Rho, other proteins such as PI3K and PTEN are also distinctly distributed at the front and the back of the cell and participate in the polarization process [79,80,81,82]. In this section, we will explore how this remarkable asymmetric distribution of signaling proteins is often achieved by a combination of biochemical pathways and forces.
During neutrophil and Dictyostelium polarization, this asymmetric protein distribution is achieved by local excitation/global inhibition (LEGI) mechanisms [83]. LEGI mechanisms can be explained by Alan Turing’s seminal work on patterns [84], and consist of two elements: a local excitation signal that tends to induce polarization and a diffusive inhibitory signal that tends to oppose it [85]. Because the inhibitory signal rapidly diffuses across the cell, only the areas with the highest chemotactic stimulus create a large enough excitation signal to overcome global inhibition, leading to polarization. While LEGI mechanisms were initially conceived in the context of diffusive species interacting chemically, it is becoming clear that mechanical forces may play a role as well. In neutrophil cells, the membrane tension generated by actin polymerization at the leading edge acts as an inhibitory element for Rac activity [86]. The precise mechanism has not yet been fully elucidated, but it may be related to tension-gated ion channels [87] or intermediary proteins that sense membrane curvature [88]. Such as in neutrophils, membrane tension appears to antagonize protrusion in other cell lines such as fibroblasts [86], keratocytes [89], and Dictyostelium [90], suggesting an increasing role of membrane tension in cell polarization.
Together with LEGI schemes, the asymmetric distribution of signaling proteins that cause cell polarization has also been attributed to imbalances in actin rearward flow. This flow, caused by myosin-powered contractility, moves from the cell edge toward the cell center and pulls on focal adhesions anchored in the ECM. Therefore, differences in substrate stiffness or focal adhesion density inevitably cause a speed difference between actin flow at opposing sides of the cell. As such, this would direct the migration of cells to the side with the slowest rearward flow, assuming equal actin polymerization on both sides [91]. Moreover, given that actin flows can also transport actin-binding proteins, flow imbalances could reinforce an asymmetric accumulation of polarity cues across the cell. In cells already polarized, the accumulation of proteins such as myosin and utrophin at the back of the cell was correlated with the retrograde flow speed of the advancing front [92]. This reinforcement mechanism has been modeled to explain persistence patterns in 1D cell motility [93].
6. Forces during Migration
Once the polarization process assembles an asymmetric cellular architecture (Figure 4), the underlying migratory machinery is ultimately responsible for the cellular motion. Mesenchymal migration is usually modeled as a continuous process that involves the steps of protrusion (i), attachment (ii), contraction (iii), release (iv), and recycling (v) [94,95]. In the molecular clutch framework, these steps take place simultaneously as the cell converts a part of its traction forces into net cell displacements. Following the most basic molecular clutch framework for migration—the conceptual model depicted in Figure 3a polarized cell will advance due to asymmetries in actin retrograde flows, the front/back polarization rates, or both. Cell advancement is ultimately caused by actin polymerization, which pushes the cell edge forward. For a particular actin polymerization rate, the cells that exhibit the slowest retrograde flow—and a maximal force transmitted to the substrate—should migrate faster. Using this approach, Bangasser et al. [23] demonstrated that a generalized clutch model predicts biphasic migratory behavior with an optimal stiffness that depends on the number of clutches and motors. These predictions were effectively tested on neurons and glioma cells, which lack adhesion reinforcement. For most cell lines, however, adhesion reinforcement obscures this optimal stiffness, and the speed of migration monotonically increases with rigidity [96,97].
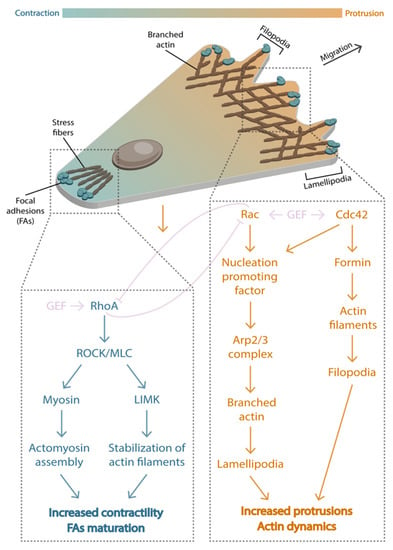
Figure 4.
Front-rear polarization. During cell migration, a front-rear gradient is defined by Rho GTPases activity. At the front, active Rac1 and Cdc42 (orange zone) promote actin polymerization via Arp2/3 complex and formin to generate protrusions, such as lamellipodia or filopodia. At the rear, active RhoA (blue zone) mediates cell contractility by stimulating focal adhesion maturation and the formation of stress fibers.
7. Forces beyond the Clutch Model
We have used the molecular clutch model as a framework to understand the forces that take place during directed cell migration, from detecting environmental cues to the actual cytoskeletal forces that propel the cells. In addition to these clutch-induced forces, other forces might contribute to the various steps of directed cell migration. The most conspicuous ones are the forces regulated by membrane tension. In recent years, whether cell membranes permit or resist membrane tension propagation has been a subject of debate. A first study employed membrane tethers to simultaneously perturb and measure tension with optical tweezers. They found that membrane tension was not propagated across the membrane, compromising the role of membrane tension as long-range intracellular signaling [98]. A recent study puts this controversy to rest by showing that when forces are applied to the membrane alone, tension is poorly propagated [99]. However, when forces are applied to both the plasma membrane and the actin cortex—for example, during cellular protrusions—the membrane tension rapidly propagates undampened across the cell.
The forces that deform cellular membranes are sensed by mechanosensitive ion channels. The activation of these channels induces a change in intracellular calcium levels. Acting as a secondary messenger, calcium directly affects cell migration through calcium-dependent proteins. The mechanosensitive ion channels are divided into two broad families: the Piezo and the transient potential receptor (TRP) [100]. In general, channels from the Piezo family are larger and respond faster to mechanical stimuli than the TRP family channels. Numerous studies point out that both families participate in the detection of mechanical signals, as well as in the migratory process. For example, during the retinal ganglion of the development of the Xenopus optic pathway, cell axons grow towards softer tissue. This negative durotaxis is mediated by Piezo channels [67]. In mesenchymal cell migration, the local influx of calcium triggered by mechanosensitive ion channels can promote the extension of actin protrusions, such as lamellipodia and filopodia, through calcium-induced activation of Rac1 [101,102]. Even chemotaxis is blocked when mechanosensitive ion channels are chemically or genetically inhibited [103,104]. The mechanisms of action seem to involve the re-localization of mechanosensitive ion channels to the direction of the chemoattractant signal. Localized calcium regulates actin remodeling at the leading edge of the cell, promoting directional cell migration [105]. More work needs to be conducted to integrate mechanosensitive ion channels into a general molecular clutch model.
8. Concluding Remarks
Numerous studies acknowledge that the molecular clutch is one of the most useful frameworks for understanding the underlying forces that drive cell migration. However, motor-clutch models fail to incorporate several features present in directed cell migration. First, models assume in-plane forces, even though three-dimensional traction force microscopy has shown that cellular adhesions display out-of-plane forces [106,107,108]. In addition, most physiological environments are three-dimensional (3D), non-linear, and structurally heterogeneous. Early work has shown that fibroblasts in such environments do not show a continuous rearward flow, suggesting that the molecular clutch framework should be adapted to such conditions [109]. Second, while the molecular clutch is largely based on actomyosin activity, other cytoskeleton elements such as microtubules [110], intermediate filaments [111], or membrane tension interact with the elements of the clutch. For example, keratin has been shown to stiffen the cytosol network and shield the nucleus from actomyosin-mediated mechanical deformation, altering the force pattern for different stiffnesses [112]. Third, recent evidence shows that durotaxis and chemotaxis cooperate to guide the Xenopus neural crest in vivo [113]. So far, it is unknown whether this cooperation is synergistic or additive and whether other forms of directed cell migration utilize a similar cooperation in vivo. Finally, recent results show that single cells are guided toward soft environments (negative durotaxis). We do not know if negative durotaxis is restricted to single cells or if it is a more general phenomenon affecting cell collectives. Addressing these limitations and comprehending the force-induced molecular events will allow clutch models to be refined to anticipate cell response in a much more comprehensive fashion.
In this review, we have explored the forces behind directed cell migration using the molecular clutch framework. Now, we speculate that the clutch itself could be elevated to a general mechanism of taxis. Most forms of directed cell migration commonly explained by motor-clutch mechanisms, such as durotaxis or contact guidance, are referred to as mechanotaxis. More generally, mechanotaxis refers to cell movement guided by mechanical cues [114]. Here we propose that mechanotaxis could explicitly encompass all forms of directed cell migration in which force participates in gradient sensing, integrating the sensing information, establishing the back-to-front polarity, and locomoting. Defined this way, mechanotaxis would rely on three ingredients: (i) a clutch or clutches at both sides of the cell/cluster, (ii) a force transmission scheme (global or local) across the cell or a cluster of cells, and (iii) an asymmetry in one of the elements of the clutch. Examples of these asymmetries include a stiffness difference, a difference in protein density, or even geometrical constraints that affect the number of focal adhesions at both sides of the cell/cluster. Through these asymmetries, force applied at the clutches will create a difference in the cytoskeleton’s dynamics. Sometimes this will bias the movement toward the increasing cue, for example, high stiffness or high protein density; sometimes, it will bias toward the decreasing cue, for example, in negative durotaxis. A unique feature of the mechanotaxis mechanism is that sensors and actuators are mechanically coupled. In addition to the robustness that this kind of coupling implies, it might be a sign that mechanotaxis could be one of the most rudimentary forms of gradient sensing. Although mechanotaxis has not been defined in this way, it would be reasonable to use this term to define how asymmetries in the molecular clutch bias the movement of single cells and groups.
Author Contributions
Conceptualization, R.S. and I.C.F.; Writing—original draft preparation, R.S.; Writing—review and editing, I.C.F. and R.S; Figure preparation, I.C.F. All authors have read and agreed to the published version of the manuscript.
Funding
This review was funded, in part, by the Spanish Ministry for Science and Innovation (PID2021-128674OB-I00).
Acknowledgments
We thank insightful conversations with X. Trepat, P. Roca-Cusachs, P. Guillamat, M. Matejcic, J.F. Abenza, and D.J. Odde. I.C. Fortunato is supported by the European Foundation for Study of Chronic Liver Failure (EF-Clif). R. Sunyer is a Serra-Hunter fellow.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Reid, C.R.; Lutz, M.J.; Powell, S.; Kao, A.B.; Couzin, I.D.; Garnier, S. Army ants dynamically adjust living bridges in response to a cost–benefit trade-off. Proc. Natl. Acad. Sci. USA 2015, 112, 15113–15118. [Google Scholar] [CrossRef]
- Ginelli, F.; Peruani, F.; Pillot, M.-H.; Chaté, H.; Theraulaz, G.; Bon, R. Intermittent collective dynamics emerge from conflicting imperatives in sheep herds. Proc. Natl. Acad. Sci. USA 2015, 112, 12729–12734. [Google Scholar] [CrossRef]
- Zitterbart, D.P.; Wienecke, B.; Butler, J.P.; Fabry, B. Coordinated Movements Prevent Jamming in an Emperor Penguin Huddle. PLoS ONE 2011, 6, e20260. [Google Scholar] [CrossRef]
- Ayala, R.; Shu, T.; Tsai, L.-H. Trekking across the Brain: The Journey of Neuronal Migration. Cell 2007, 128, 29–43. [Google Scholar] [CrossRef]
- Kriegstein, A.R.; Noctor, S.C. Patterns of neuronal migration in the embryonic cortex. Trends Neurosci. 2004, 27, 392–399. [Google Scholar] [CrossRef]
- Weber, M.; Hauschild, R.; Schwarz, J.; Moussion, C.; de Vries, I.; Legler, D.F.; Luther, S.A.; Bollenbach, T.; Sixt, M. Interstitial Dendritic Cell Guidance by Haptotactic Chemokine Gradients. Science 2013, 339, 328–332. [Google Scholar] [CrossRef]
- Eming, S.A.; Martin, P.; Tomic-Canic, M. Wound repair and regeneration: Mechanisms, signaling, and translation. Sci. Transl. Med. 2014, 6, 265sr6. [Google Scholar] [CrossRef]
- Watt, K.E.N.; Trainor, P.A. Chapter 17—Neurocristopathies: The Etiology and Pathogenesis of Disorders Arising from Defects in Neural Crest Cell Development. In Neural Crest Cells; Trainor, P.A., Ed.; Academic Press: Boston, MA, USA, 2014; pp. 361–394. ISBN 978-0-12-401730-6. [Google Scholar]
- Roussos, E.T.; Condeelis, J.S.; Patsialou, A. Chemotaxis in cancer. Nat. Rev. Cancer 2011, 11, 573–587. [Google Scholar] [CrossRef]
- Bravo-Cordero, J.J.; Hodgson, L.; Condeelis, J. Directed Cell Invasion and Migration during Metastasis. Curr. Opin. Cell Biol. 2012, 24, 277–283. [Google Scholar] [CrossRef]
- Petrie, R.J.; Doyle, A.D.; Yamada, K.M. Random versus directionally persistent cell migration. Nat. Publ. Group 2009, 10, 538–549. [Google Scholar] [CrossRef]
- Friedl, P.; Gilmour, D. Collective cell migration in morphogenesis, regeneration and cancer. Nat. Rev. Mol. Cell Biol. 2009, 10, 445–457. [Google Scholar] [CrossRef] [PubMed]
- Haeger, A.; Wolf, K.; Zegers, M.M.; Friedl, P. Collective cell migration: Guidance principles and hierarchies. Trends Cell Biol. 2015, 25, 556–566. [Google Scholar] [CrossRef] [PubMed]
- Shellard, A.; Mayor, R. All Roads Lead to Directional Cell Migration. Trends Cell Biol. 2020, 30, 852–868. [Google Scholar] [CrossRef] [PubMed]
- SenGupta, S.; Parent, C.A.; Bear, J.E. The principles of directed cell migration. Nat. Rev. Mol. Cell Biol. 2021, 22, 529–547. [Google Scholar] [CrossRef] [PubMed]
- Espina, J.A.; Marchant, C.L.; Barriga, E.H. Durotaxis: The mechanical control of directed cell migration. FEBS J. 2022, 289, 2736–2754. [Google Scholar] [CrossRef]
- Abercrombie, M. The Croonian Lecture, 1978—The crawling movement of metazoan cells. Proc. R. Soc. Lond. B Biol. Sci. 1980, 207, 129–147. [Google Scholar] [CrossRef]
- Mitchison, T.; Kirschner, M. Cytoskeletal dynamics and nerve growth. Neuron 1988, 1, 761–772. [Google Scholar] [CrossRef]
- Chan, C.E.; Odde, D.J. Traction Dynamics of Filopodia on Compliant Substrates. Science 2008, 322, 1687–1691. [Google Scholar] [CrossRef]
- Elosegui-Artola, A.; Bazellières, E.; Allen, M.D.; Andreu, I.; Oria, R.; Sunyer, R.; Gomm, J.J.; Marshall, J.F.; Jones, J.L.; Trepat, X.; et al. Rigidity sensing and adaptation through regulation of integrin types. Nat. Mater. 2014, 13, 631–637. [Google Scholar] [CrossRef]
- Elosegui-Artola, A.; Oria, R.; Chen, Y.; Kosmalska, A.; Pérez-González, C.; Castro, N.; Zhu, C.; Trepat, X.; Roca-Cusachs, P. Mechanical regulation of a molecular clutch defines force transmission and transduction in response to matrix rigidity. Nat. Cell Biol. 2016, 18, 540–548. [Google Scholar] [CrossRef]
- Sunyer, R.; Conte, V.; Escribano, J.; Elosegui-Artola, A.; Labernadie, A.; Valon, L.; Navajas, D.; García-Aznar, J.M.; Muñoz, J.J.; Roca-Cusachs, P.; et al. Collective cell durotaxis emerges from long-range intercellular force transmission. Science 2016, 353, 1157–1161. [Google Scholar] [CrossRef]
- Bangasser, B.L.; Shamsan, G.A.; Chan, C.E.; Opoku, K.N.; Tüzel, E.; Schlichtmann, B.W.; Kasim, J.A.; Fuller, B.J.; McCullough, B.R.; Rosenfeld, S.S.; et al. Shifting the optimal stiffness for cell migration. Nat. Commun. 2017, 8, 15313. [Google Scholar] [CrossRef]
- Elosegui-Artola, A.; Trepat, X.; Roca-Cusachs, P. Control of Mechanotransduction by Molecular Clutch Dynamics. Trends Cell Biol. 2018, 28, 356–367. [Google Scholar] [CrossRef]
- Bangasser, B.L.; Rosenfeld, S.S.; Odde, D.J. Determinants of Maximal Force Transmission in a Motor-Clutch Model of Cell Traction in a Compliant Microenvironment. Biophys. J. 2013, 105, 581–592. [Google Scholar] [CrossRef]
- Kechagia, J.Z.; Ivaska, J.; Roca-Cusachs, P. Integrins as biomechanical sensors of the microenvironment. Nat. Rev. Mol. Cell Biol. 2019, 20, 457–473. [Google Scholar] [CrossRef]
- Bagorda, A.; Parent, C.A. Eukaryotic chemotaxis at a glance. J. Cell Sci. 2008, 121, 2621–2624. [Google Scholar] [CrossRef]
- DesMarais, V.; Yamaguchi, H.; Oser, M.; Soon, L.; Mouneimne, G.; Sarmiento, C.; Eddy, R.; Condeelis, J. N-WASP and cortactin are involved in invadopodium-dependent chemotaxis to EGF in breast tumor cells. Cell Motil. Cytoskelet. 2009, 66, 303–316. [Google Scholar] [CrossRef]
- Lo, C.-M.; Wang, H.-B.; Dembo, M.; Wang, Y. Cell Movement Is Guided by the Rigidity of the Substrate. Biophys. J. 2000, 79, 144–152. [Google Scholar] [CrossRef] [PubMed]
- Raab, M.; Swift, J.; Dingal, P.C.D.P.; Shah, P.; Shin, J.W.; Discher, D.E. Crawling from soft to stiff matrix polarizes the cytoskeleton and phosphoregulates myosin-II heavy chain. J. Cell Biol. 2012, 199, 669–683. [Google Scholar] [CrossRef]
- Wang, H.B.; Dembo, M.; Hanks, S.K.; Wang, Y. Focal adhesion kinase is involved in mechanosensing during fibroblast migration. Proc. Natl. Acad. Sci. USA 2001, 98, 11295. [Google Scholar] [CrossRef]
- Vincent, L.G.; Choi, Y.S.; Alonso-Latorre, B.; del Álamo, J.C.; Engler, A.J. Mesenchymal stem cell durotaxis depends on substrate stiffness gradient strength. Biotechnol. J. 2013, 8, 472–484. [Google Scholar] [CrossRef] [PubMed]
- DuChez, B. The Response of Cancer Cells to Local Changes in Extracellular Stiffness—ProQuest; Georgetown University: Washington, DC, USA, 2017. [Google Scholar]
- Rong, Y.; Yang, W.; Hao, H.; Wang, W.; Lin, S.; Shi, P.; Huang, Y.; Li, B.; Sun, Y.; Liu, Z.; et al. The Golgi microtubules regulate single cell durotaxis. EMBO Rep. 2021, 22, e51094. [Google Scholar] [CrossRef] [PubMed]
- Hakeem, R.M.; Subramanian, B.C.; Hockenberry, M.A.; King, Z.T.; Butler, M.T.; Legant, W.R.; Bear, J.E. Zyxin and non-muscle myosin are required for single fibroblast durotaxis, but Rho-kinase activity and the Arp2/3 complex are dispensable. bioRxiv 2022, 2022.06.03.494725. [Google Scholar] [CrossRef]
- Yip, A.K.; Zhang, S.; Chong, L.H.; Cheruba, E.; Woon, J.Y.X.; Chua, T.X.; Goh, C.J.H.; Yang, H.; Tay, C.Y.; Koh, C.-G.; et al. Zyxin Is Involved in Fibroblast Rigidity Sensing and Durotaxis. Front. Cell Dev. Biol. 2021, 9, 735298. [Google Scholar] [CrossRef]
- Isomursu, A.; Park, K.-Y.; Hou, J.; Cheng, B.; Mathieu, M.; Shamsan, G.A.; Fuller, B.; Kasim, J.; Mahmoodi, M.M.; Lu, T.J.; et al. Directed cell migration towards softer environments. Nat. Mater. 2022, 21, 1081–1090. [Google Scholar] [CrossRef]
- Sunyer, R.; Trepat, X. Durotaxis. Curr. Biol. 2020, 30, R383–R387. [Google Scholar] [CrossRef]
- Beedle, A.E.M.; Roca-Cusachs, P. In search of a softer environment. Nat. Mater. 2022, 21, 995–996. [Google Scholar] [CrossRef]
- Carter, S.B. Haptotaxis and the Mechanism of Cell Motility. Nature 1967, 213, 256. [Google Scholar] [CrossRef]
- Wen, J.H.; Choi, O.; Taylor-Weiner, H.; Fuhrmann, A.; Karpiak, J.V.; Almutairi, A.; Engler, A.J. Haptotaxis is Cell Type Specific and Limited by Substrate Adhesiveness. Cell. Mol. Bioeng. 2015, 8, 530–542. [Google Scholar] [CrossRef]
- King, S.J.; Asokan, S.B.; Haynes, E.M.; Zimmerman, S.P.; Rotty, J.D.; Alb, J.G.; Tagliatela, A.; Blake, D.R.; Lebedeva, I.P.; Marston, D.; et al. Lamellipodia are crucial for haptotactic sensing and response. J. Cell Sci. 2016, 129, 2329–2342. [Google Scholar] [CrossRef]
- Leclech, C.; Villard, C. Cellular and Subcellular Contact Guidance on Microfabricated Substrates. Front. Bioeng. Biotechnol. 2020, 8, 1198. [Google Scholar] [CrossRef] [PubMed]
- Fischer, R.S.; Sun, X.; Baird, M.A.; Hourwitz, M.J.; Seo, B.R.; Pasapera, A.M.; Mehta, S.B.; Losert, W.; Fischbach, C.; Fourkas, J.T.; et al. Contractility, focal adhesion orientation, and stress fiber orientation drive cancer cell polarity and migration along wavy ECM substrates. Proc. Natl. Acad. Sci. USA 2021, 118, e2021135118. [Google Scholar] [CrossRef]
- Kubow, K.E.; Shuklis, V.D.; Sales, D.J.; Horwitz, A.R. Contact guidance persists under myosin inhibition due to the local alignment of adhesions and individual protrusions. Sci. Rep. 2017, 7, 14380. [Google Scholar] [CrossRef]
- Juan, G.R.R.-S.; Oakes, P.W.; Gardel, M.L. Contact guidance requires spatial control of leading-edge protrusion. Mol. Biol. Cell 2017, 28, 1043–1053. [Google Scholar] [CrossRef]
- Tabdanov, E.D.; Rodríguez-Merced, N.J.; Cartagena-Rivera, A.X.; Puram, V.V.; Callaway, M.K.; Ensminger, E.A.; Pomeroy, E.J.; Yamamoto, K.; Lahr, W.S.; Webber, B.R.; et al. Engineering T cells to enhance 3D migration through structurally and mechanically complex tumor microenvironments. Nat. Commun. 2021, 12, 2815. [Google Scholar] [CrossRef]
- Comelles, J.; Fernández-Majada, V.; Acevedo, V.; Rebollo-Calderon, B.; Martínez, E. Soft topographical patterns trigger a stiffness-dependent cellular response to contact guidance. bioRxiv 2022, 2022.01.25.477731. [Google Scholar] [CrossRef]
- Park, J.Y.; Lee, D.H.; Lee, E.J.; Lee, S.-H. Study of cellular behaviors on concave and convex microstructures fabricated from elastic PDMS membranes. Lab. Chip 2009, 9, 2043–2049. [Google Scholar] [CrossRef]
- Song, K.H.; Park, S.J.; Kim, D.S.; Doh, J. Sinusoidal wavy surfaces for curvature-guided migration of T lymphocytes. Biomaterials 2015, 51, 151–160. [Google Scholar] [CrossRef]
- Pieuchot, L.; Marteau, J.; Guignandon, A.; Dos Santos, T.; Brigaud, I.; Chauvy, P.-F.; Cloatre, T.; Ponche, A.; Petithory, T.; Rougerie, P.; et al. Curvotaxis directs cell migration through cell-scale curvature landscapes. Nat. Commun. 2018, 9, 3995. [Google Scholar] [CrossRef]
- Baptista, D.; Teixeira, L.; van Blitterswijk, C.; Giselbrecht, S.; Truckenmüller, R. Overlooked? Underestimated? Effects of Substrate Curvature on Cell Behavior. Trends Biotechnol. 2019, 37, 838–854. [Google Scholar] [CrossRef]
- Vassaux, M.; Pieuchot, L.; Anselme, K.; Bigerelle, M.; Milan, J.-L. Designing Optimal Scaffold Topographies to Promote Nucleus-Guided Mechanosensitive Cell Migration Using In Silico Models. In Developments and Novel Approaches in Biomechanics and Metamaterials; Abali, B.E., Giorgio, I., Eds.; Advanced Structured Materials; Springer International Publishing: Cham, Switzerland, 2020; pp. 199–216. ISBN 978-3-030-50464-9. [Google Scholar]
- Winkler, B.; Aranson, I.S.; Ziebert, F. Confinement and substrate topography control cell migration in a 3D computational model. Commun. Phys. 2019, 2, 82. [Google Scholar] [CrossRef]
- Vassaux, M.; Pieuchot, L.; Anselme, K.; Bigerelle, M.; Milan, J.-L. A Biophysical Model for Curvature-Guided Cell Migration. Biophys. J. 2019, 117, 1136–1144. [Google Scholar] [CrossRef]
- Tambe, D.T. Collective cell guidance by cooperative intercellular forces. Nat. Mater. 2011, 10, 469–475. [Google Scholar] [CrossRef]
- Trepat, X.; Fredberg, J.J. Plithotaxis and emergent dynamics in collective cellular migration. Trends Cell Biol. 2011, 21, 638–646. [Google Scholar] [CrossRef]
- Malet-Engra, G.; Yu, W.; Oldani, A.; Rey-Barroso, J.; Gov, N.S.; Scita, G.; Dupré, L. Collective Cell Motility Promotes Chemotactic Prowess and Resistance to Chemorepulsion. Curr. Biol. 2015, 25, 242–250. [Google Scholar] [CrossRef]
- Camley, B.A. Collective gradient sensing and chemotaxis: Modeling and recent developments. J. Phys. Condens. Matter Inst. Phys. J. 2018, 30, 223001. [Google Scholar] [CrossRef]
- Wang, N.; Tytell, J.D.; Ingber, D.E. Mechanotransduction at a distance: Mechanically coupling the extracellular matrix with the nucleus. Nat. Rev. Mol. Cell Biol. 2009, 10, 75–82. [Google Scholar] [CrossRef]
- Ghassemi, S.; Meacci, G.; Liu, S.; Gondarenko, A.A.; Mathur, A.; Roca-Cusachs, P.; Sheetz, M.P.; Hone, J. Cells test substrate rigidity by local contractions on submicrometer pillars. Proc. Natl. Acad. Sci. USA 2012, 109, 5328–5333. [Google Scholar] [CrossRef]
- Plotnikov, S.V.; Pasapera, A.M.; Sabass, B.; Waterman, C.M. Force Fluctuations within Focal Adhesions Mediate ECM-Rigidity Sensing to Guide Directed Cell Migration. Cell 2012, 151, 1513–1527. [Google Scholar] [CrossRef]
- Trichet, L.; le Digabel, J.; Hawkins, R.J.; Vedula, S.R.K.; Gupta, M.; Ribrault, C.; Hersen, P.; Voituriez, R.; Ladoux, B. Evidence of a large-scale mechanosensing mechanism for cellular adaptation to substrate stiffness. Proc. Natl. Acad. Sci. USA 2012, 109, 6933–6938. [Google Scholar] [CrossRef]
- Hoffecker, I.T.; Guo, W.; Wang, Y. Assessing the spatial resolution of cellular rigidity sensing using a micropatterned hydrogel–photoresist composite. Lab Chip 2011, 11, 3538–3544. [Google Scholar] [CrossRef]
- Hu, S.; Chen, J.; Fabry, B.; Numaguchi, Y.; Gouldstone, A.; Ingber, D.E.; Fredberg, J.J.; Butler, J.P.; Wang, N. Intracellular stress tomography reveals stress focusing and structural anisotropy in cytoskeleton of living cells. Am. J. Physiol.-Cell Physiol. 2003, 285, C1082–C1090. [Google Scholar] [CrossRef] [PubMed]
- Autenrieth, T.J.; Frank, S.C.; Greiner, A.M.; Klumpp, D.; Richter, B.; Hauser, M.; Lee, S.; Levine, J.; Bastmeyer, M. Actomyosin contractility and RhoGTPases affect cell-polarity and directional migration during haptotaxis. Integr. Biol. 2016, 8, 1067–1078. [Google Scholar] [CrossRef] [PubMed]
- Koser, D.E.; Thompson, A.J.; Foster, S.K.; Dwivedy, A.; Pillai, E.K.; Sheridan, G.K.; Svoboda, H.; Viana, M.; da Costa, L.F.; Guck, J.; et al. Mechanosensing is critical for axon growth in the developing brain. Nat. Neurosci. 2016, 19, 1592–1598. [Google Scholar] [CrossRef]
- Yeoman, B.; Shatkin, G.; Beri, P.; Banisadr, A.; Katira, P.; Engler, A.J. Adhesion strength and contractility enable metastatic cells to become adurotactic. Cell Rep. 2021, 34, 108816. [Google Scholar] [CrossRef]
- Rappel, W.-J.; Edelstein-Keshet, L. Mechanisms of Cell Polarization. Curr. Opin. Syst. Biol. 2017, 3, 43–53. [Google Scholar] [CrossRef]
- Ridley, A.J.; Hall, A. The small GTP-binding protein rho regulates the assembly of focal adhesions and actin stress fibers in response to growth factors. Cell 1992, 70, 389–399. [Google Scholar] [CrossRef]
- Rohatgi, R.; Nollau, P.; Ho, H.Y.; Kirschner, M.W.; Mayer, B.J. Nck and phosphatidylinositol 4,5-bisphosphate synergistically activate actin polymerization through the N-WASP-Arp2/3 pathway. J. Biol. Chem. 2001, 276, 26448–26452. [Google Scholar] [CrossRef]
- Burridge, K.; Wennerberg, K. Rho and Rac take center stage. Cell 2004, 116, 167–179. [Google Scholar] [CrossRef]
- Rottner, K.; Schaks, M. Assembling actin filaments for protrusion. Curr. Opin. Cell Biol. 2019, 56, 53–63. [Google Scholar] [CrossRef]
- Møller, L.L.V.; Klip, A.; Sylow, L. Rho GTPases-Emerging Regulators of Glucose Homeostasis and Metabolic Health. Cells 2019, 8, E434. [Google Scholar] [CrossRef] [PubMed]
- Ridley, A.J. Life at the leading edge. Cell 2011, 145, 1012–1022. [Google Scholar] [CrossRef] [PubMed]
- Chrzanowska-Wodnicka, M.; Burridge, K. Rho-stimulated contractility drives the formation of stress fibers and focal adhesions. J. Cell Biol. 1996, 133, 1403–1415. [Google Scholar] [CrossRef] [PubMed]
- Worthylake, R.A.; Burridge, K. RhoA and ROCK promote migration by limiting membrane protrusions. J. Biol. Chem. 2003, 278, 13578–13584. [Google Scholar] [CrossRef]
- Mayor, R.; Carmona-Fontaine, C. Keeping in touch with contact inhibition of locomotion. Trends Cell Biol. 2010, 20, 319–328. [Google Scholar] [CrossRef]
- Li, Z.; Dong, X.; Dong, X.; Wang, Z.; Liu, W.; Deng, N.; Ding, Y.; Tang, L.; Hla, T.; Zeng, R.; et al. Regulation of PTEN by Rho small GTPases. Nat. Cell Biol. 2005, 7, 399–404. [Google Scholar] [CrossRef]
- Vemula, S.; Shi, J.; Hanneman, P.; Wei, L.; Kapur, R. ROCK1 functions as a suppressor of inflammatory cell migration by regulating PTEN phosphorylation and stability. Blood 2010, 115, 1785–1796. [Google Scholar] [CrossRef]
- Yang, S.; Kim, H.-M. The RhoA-ROCK-PTEN pathway as a molecular switch for anchorage dependent cell behavior. Biomaterials 2012, 33, 2902–2915. [Google Scholar] [CrossRef] [PubMed]
- Lawson, C.D.; Ridley, A.J. Rho GTPase signaling complexes in cell migration and invasion. J. Cell Biol. 2018, 217, 447–457. [Google Scholar] [CrossRef]
- Parent, C.A.; Devreotes, P.N. A Cell’s Sense of Direction. Science 1999, 284, 765–770. [Google Scholar] [CrossRef]
- Turing, A.M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1952, 237, 37–72. [Google Scholar] [CrossRef]
- Bailles, A.; Gehrels, E.W.; Lecuit, T. Mechanochemical Principles of Spatial and Temporal Patterns in Cells and Tissues. Annu. Rev. Cell Dev. Biol. 2022, 38, 321–347. [Google Scholar] [CrossRef] [PubMed]
- Houk, A.R.; Jilkine, A.; Mejean, C.O.; Boltyanskiy, R.; Dufresne, E.R.; Angenent, S.B.; Altschuler, S.J.; Wu, L.F.; Weiner, O.D. Membrane Tension Maintains Cell Polarity by Confining Signals to the Leading Edge during Neutrophil Migration. Cell 2012, 148, 175–188. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Xie, K.; Jiang, H. Durotaxis Index of 3T3 Fibroblast Cells Scales with Stiff-to-Soft Membrane Tension Polarity. Biophys. J. 2020, 119, 1427–1438. [Google Scholar] [CrossRef] [PubMed]
- Tsujita, K.; Takenawa, T.; Itoh, T. Feedback regulation between plasma membrane tension and membrane-bending proteins organizes cell polarity during leading edge formation. Nat. Cell Biol. 2015, 17, 749–758. [Google Scholar] [CrossRef] [PubMed]
- Keren, K.; Pincus, Z.; Allen, G.M.; Barnhart, E.L.; Marriott, G.; Mogilner, A.; Theriot, J.A. Mechanism of shape determination in motile cells. Nature 2008, 453, 475–480. [Google Scholar] [CrossRef]
- Meili, R.; Alonso-Latorre, B.; del Álamo, J.C.; Firtel, R.A.; Lasheras, J.C. Myosin II Is Essential for the Spatiotemporal Organization of Traction Forces during Cell Motility. Mol. Biol. Cell 2010, 21, 405–417. [Google Scholar] [CrossRef]
- Escribano, J.; Sánchez, M.T.; García-Aznar, J.M. Modeling the formation of cell-matrix adhesions on a single 3D matrix fiber. J. Theor. Biol. 2015, 384, 84–94. [Google Scholar] [CrossRef]
- Maiuri, P.; Rupprecht, J.-F.; Wieser, S.; Ruprecht, V.; Bénichou, O.; Carpi, N.; Coppey, M.; De Beco, S.; Gov, N.; Heisenberg, C.-P.; et al. Actin Flows Mediate a Universal Coupling between Cell Speed and Cell Persistence. Cell 2015, 161, 374–386. [Google Scholar] [CrossRef]
- Ron, J.E.; Monzo, P.; Gauthier, N.C.; Voituriez, R.; Gov, N.S. One-dimensional cell motility patterns. Phys. Rev. Res. 2020, 2, 033237. [Google Scholar] [CrossRef]
- Vedula, S.R.K.; Ravasio, A.; Lim, C.T.; Ladoux, B. Collective Cell Migration: A Mechanistic Perspective. Physiology 2013, 28, 370–379. [Google Scholar] [CrossRef] [PubMed]
- Sheetz, M.P.; Felsenfeld, D.; Galbraith, C.G.; Choquet, D. Cell migration as a five-step cycle. Biochem. Soc. Symp. 1999, 65, 233–243. [Google Scholar]
- Ulrich, T.A.; de Juan Pardo, E.M.; Kumar, S. The Mechanical Rigidity of the Extracellular Matrix Regulates the Structure, Motility, and Proliferation of Glioma Cells. Cancer Res. 2009, 69, 4167–4174. [Google Scholar] [CrossRef]
- Discher, D.E. Tissue Cells Feel and Respond to the Stiffness of Their Substrate. Science 2005, 310, 1139–1143. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Graber, Z.T.; Baumgart, T.; Stone, H.A.; Cohen, A.E. Cell membranes resist flow. bioRxiv 2018, 175, 1769–1779. [Google Scholar] [CrossRef] [PubMed]
- Belly, H.D.; Yan, S.; da Rocha, H.B.; Ichbiah, S.; Town, J.P.; Turlier, H.; Bustamante, C.J.; Weiner, O.D. Actin-driven protrusions generate rapid long-range membrane tension propagation in cells. bioRxiv 2022, 2022.09.07.507005. [Google Scholar] [CrossRef]
- Canales Coutiño, B.; Mayor, R. Mechanosensitive ion channels in cell migration. Cells Dev. 2021, 166, 203683. [Google Scholar] [CrossRef]
- Becker, D.; Bereiter-Hahn, J.; Jendrach, M. Functional interaction of the cation channel transient receptor potential vanilloid 4 (TRPV4) and actin in volume regulation. Eur. J. Cell Biol. 2009, 88, 141–152. [Google Scholar] [CrossRef]
- Fiorio Pla, A.; Ong, H.L.; Cheng, K.T.; Brossa, A.; Bussolati, B.; Lockwich, T.; Paria, B.; Munaron, L.; Ambudkar, I.S. TRPV4 mediates tumor-derived endothelial cell migration via arachidonic acid-activated actin remodeling. Oncogene 2012, 31, 200–212. [Google Scholar] [CrossRef]
- Fabian, A.; Bertrand, J.; Lindemann, O.; Pap, T.; Schwab, A. Transient receptor potential canonical channel 1 impacts on mechanosignaling during cell migration. Pflugers Arch. 2012, 464, 623–630. [Google Scholar] [CrossRef]
- Damann, N.; Owsianik, G.; Li, S.; Poll, C.; Nilius, B. The calcium-conducting ion channel transient receptor potential canonical 6 is involved in macrophage inflammatory protein-2-induced migration of mouse neutrophils. Acta Physiol. Oxf. Engl. 2009, 195, 3–11. [Google Scholar] [CrossRef]
- Lepannetier, S.; Zanou, N.; Yerna, X.; Emeriau, N.; Dufour, I.; Masquelier, J.; Muccioli, G.; Tajeddine, N.; Gailly, P. Sphingosine-1-phosphate-activated TRPC1 channel controls chemotaxis of glioblastoma cells. Cell Calcium 2016, 60, 373–383. [Google Scholar] [CrossRef] [PubMed]
- Legant, W.R.; Choi, C.K.; Miller, J.S.; Shao, L.; Gao, L.; Betzig, E.; Chen, C.S. Multidimensional traction force microscopy reveals out-of-plane rotational moments about focal adhesions. Proc. Natl. Acad. Sci. USA 2013, 110, 881–886. [Google Scholar] [CrossRef] [PubMed]
- Dalaka, E.; Kronenberg, N.M.; Liehm, P.; Segall, J.E.; Prystowsky, M.B.; Gather, M.C. Direct measurement of vertical forces shows correlation between mechanical activity and proteolytic ability of invadopodia. Sci. Adv. 2020, 6, eaax6912. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Colin-York, H.; Barbieri, L.; Javanmardi, Y.; Guo, Y.; Korobchevskaya, K.; Moeendarbary, E.; Li, D.; Fritzsche, M. Astigmatic traction force microscopy (aTFM). Nat. Commun. 2021, 12, 2168. [Google Scholar] [CrossRef]
- Owen, L.M.; Adhikari, A.S.; Patel, M.; Grimmer, P.; Leijnse, N.; Kim, M.C.; Notbohm, J.; Franck, C.; Dunn, A.R. A cytoskeletal clutch mediates cellular force transmission in a soft, three-dimensional extracellular matrix. Mol. Biol. Cell 2017, 28, 1959–1974. [Google Scholar] [CrossRef]
- Garcin, C.; Straube, A. Microtubules in cell migration. Essays Biochem. 2019, 63, 509–520. [Google Scholar] [CrossRef]
- Guo, M.; Ehrlicher, A.J.; Mahammad, S.; Fabich, H.; Jensen, M.H.; Moore, J.R.; Fredberg, J.J.; Goldman, R.D.; Weitz, D.A. The Role of Vimentin Intermediate Filaments in Cortical and Cytoplasmic Mechanics. Biophys. J. 2013, 105, 1562–1568. [Google Scholar] [CrossRef]
- Kechagia, Z.; Sáez, P.; Gómez-González, M.; Zamarbide, M.; Andreu, I.; Koorman, T.; Beedle, A.E.M.; Derksen, P.W.B.; Trepat, X.; Arroyo, M.; et al. The laminin-keratin link shields the nucleus from mechanical deformation and signalling. bioRxiv 2022, 2022.03.01.482474. [Google Scholar] [CrossRef]
- Shellard, A.; Mayor, R. Collective durotaxis along a self-generated stiffness gradient in vivo. Nature 2021, 600, 690–694. [Google Scholar] [CrossRef]
- Roca-Cusachs, P.; Sunyer, R.; Trepat, X. Mechanical guidance of cell migration: Lessons from chemotaxis. Curr. Opin. Cell Biol. 2013, 25, 543–549. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).