A Python-Based Thermodynamic Equilibrium Library for Gibbs Energy Minimization: A Case Study on Supercritical Water Gasification of Ethanol and Methanol
Abstract
1. Introduction
1.1. Current Status of Thermodynamic Equilibrium Software
1.2. Current Status of Thermodynamics of SCWG of Methanol and Ethanol
- I
- Methanol decomposition:
- II
- Water–gas shift reaction:
- III
- CO methanation:
1.3. Research Gap and Objectives
2. Methodology
2.1. Thermodynamic Approach for Process Evaluation
2.1.1. Calculation of Equilibrium Compositions in an Isothermal Reactor: Problem Represented as Gibbs Energy Minimization
2.1.2. Considerations on the Non-Idealities of the Reactive System
2.2. Strategies for Solving Nonlinear Problems
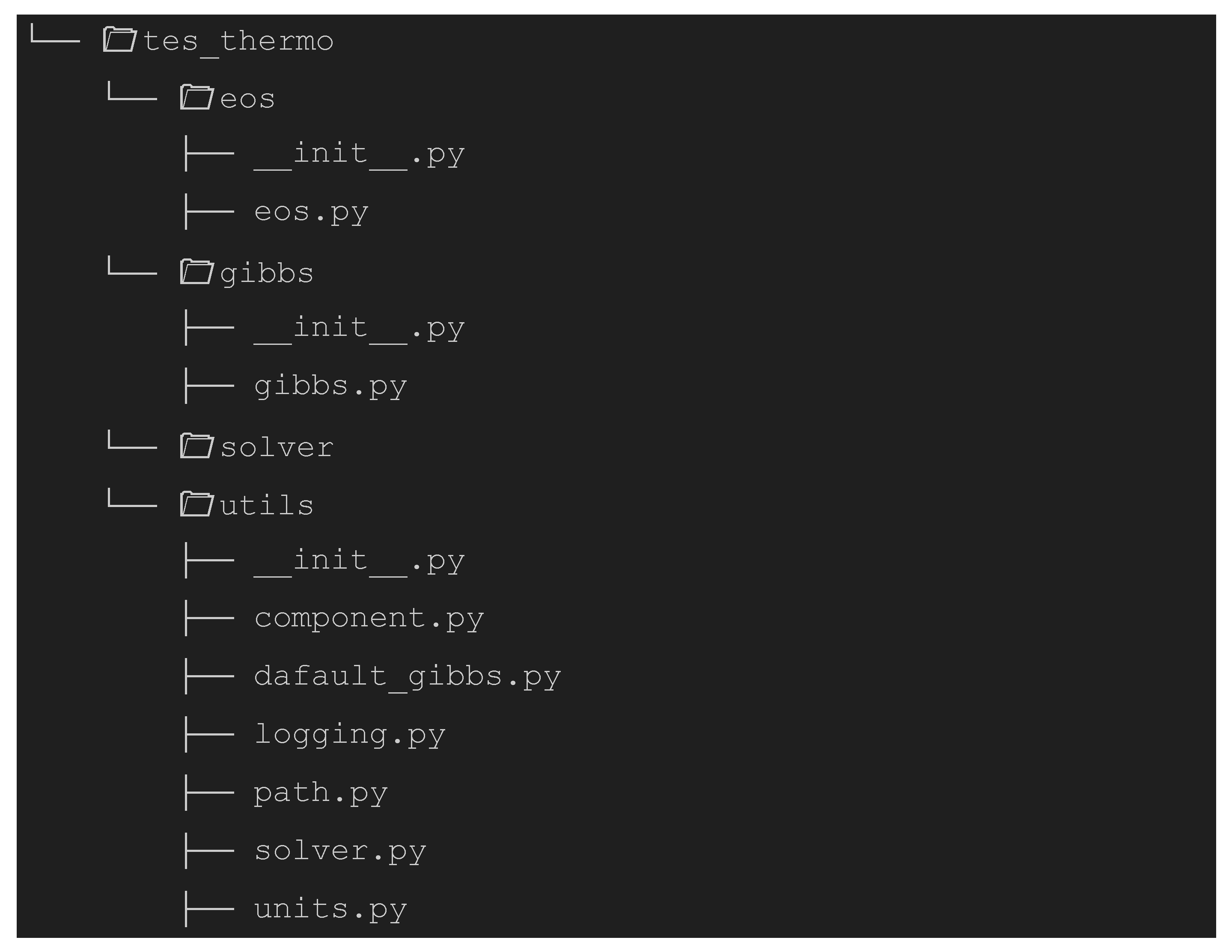
2.3. Simulator Development in the Form of a Python Library
 eos Python module contains functions for calculating fugacity coefficients in the vapor phase. The
eos Python module contains functions for calculating fugacity coefficients in the vapor phase. The  utils module includes all resources used for solving the Gibbs free energy minimization problem, as well as additional utilities to enhance the user experience. Finally, the
utils module includes all resources used for solving the Gibbs free energy minimization problem, as well as additional utilities to enhance the user experience. Finally, the  gibbs module contains the core optimization problem, the Gibbs energy minimization formulated using Pyomo and solved with IPOPT, which is stored in the
gibbs module contains the core optimization problem, the Gibbs energy minimization formulated using Pyomo and solved with IPOPT, which is stored in the  solver module.
solver module. gibbs module, must be initialized with the component data relevant to the reactive system. The solve_gibbs method of the Gibbs class requires as parameters the feed stream composition and the operating temperature and pressure conditions. The output of this method is the equilibrium composition of the components considered in the reactive process under the specified temperature and pressure conditions.
gibbs module, must be initialized with the component data relevant to the reactive system. The solve_gibbs method of the Gibbs class requires as parameters the feed stream composition and the operating temperature and pressure conditions. The output of this method is the equilibrium composition of the components considered in the reactive process under the specified temperature and pressure conditions.3. Results
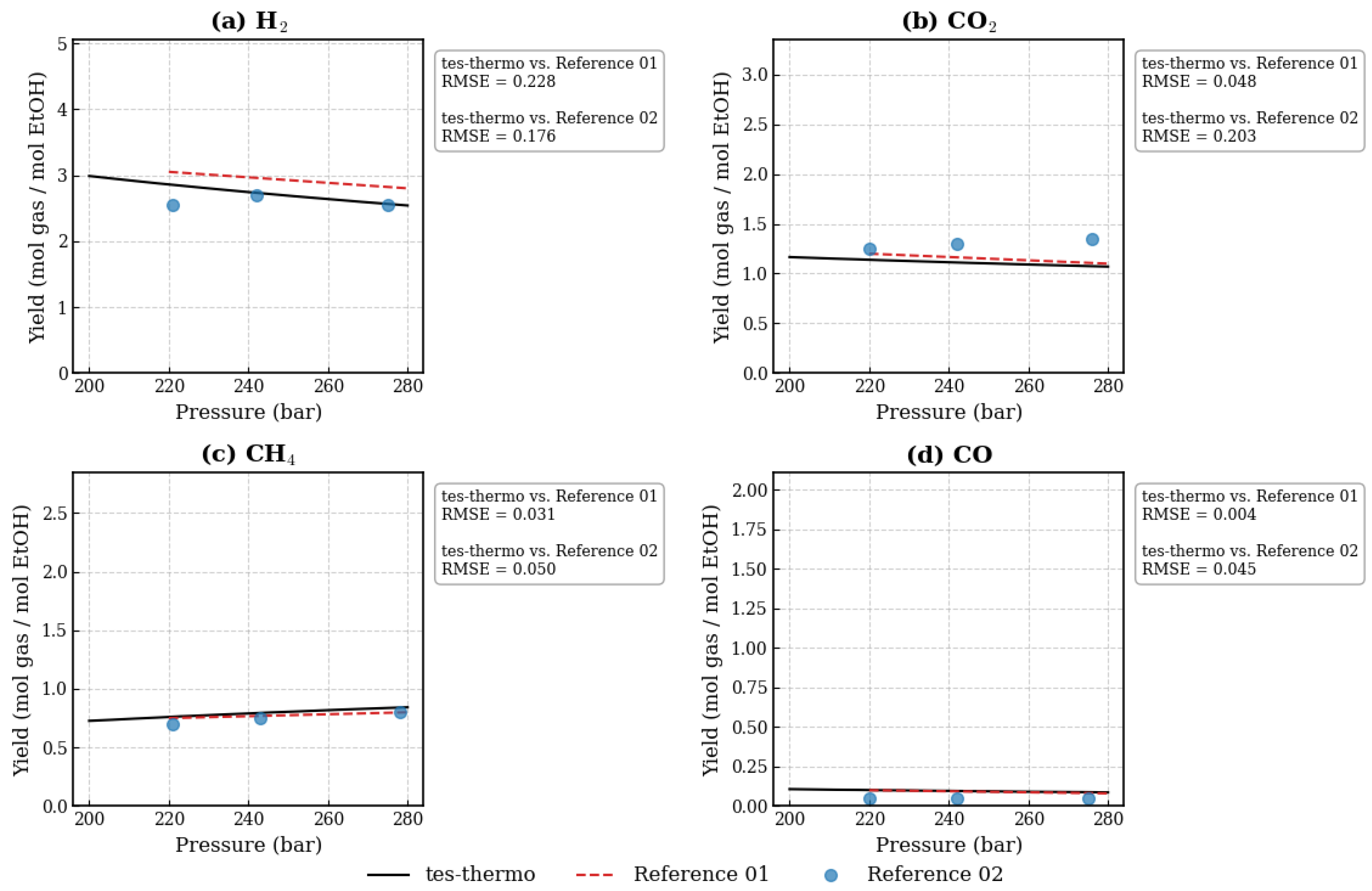
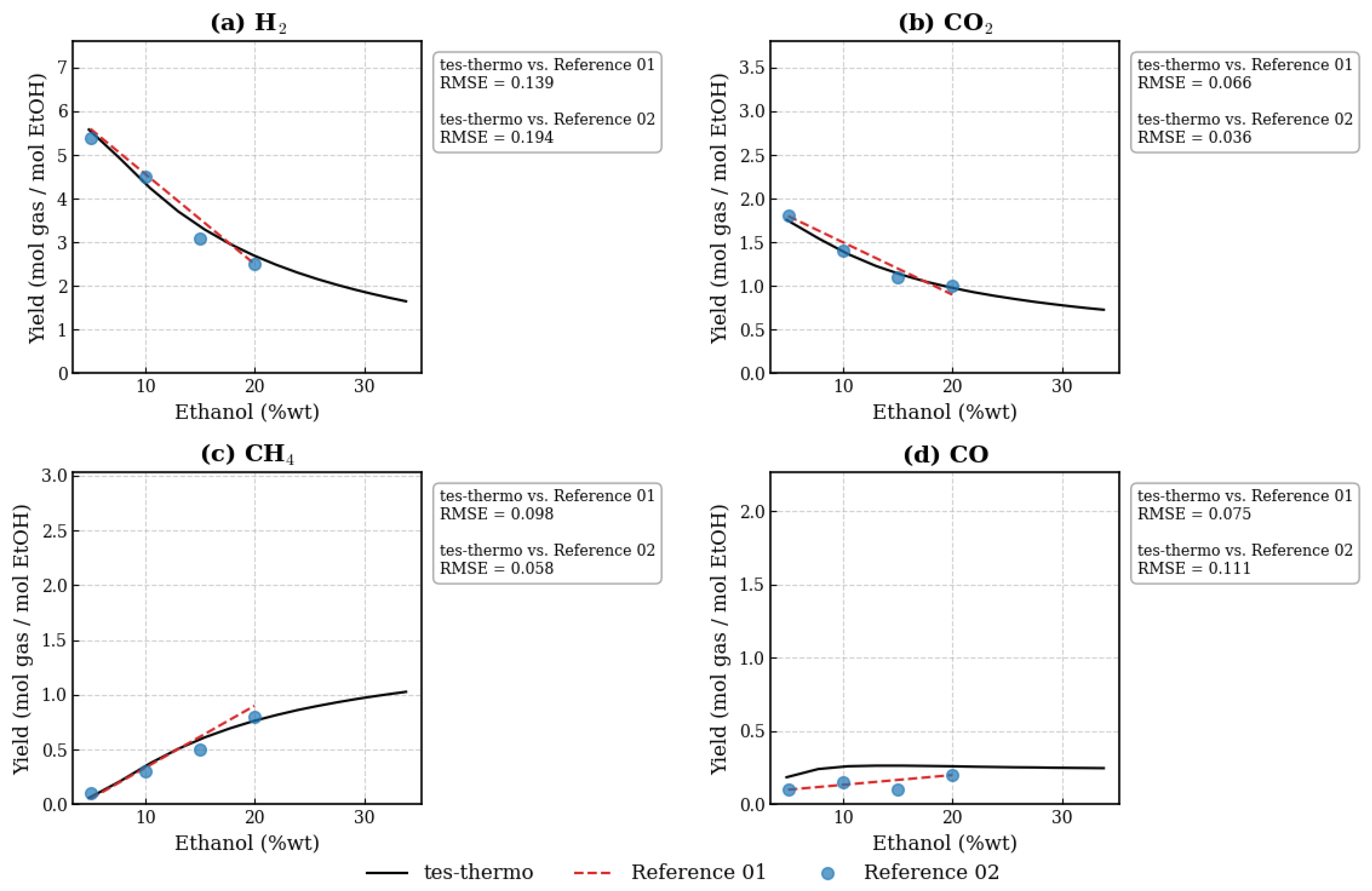
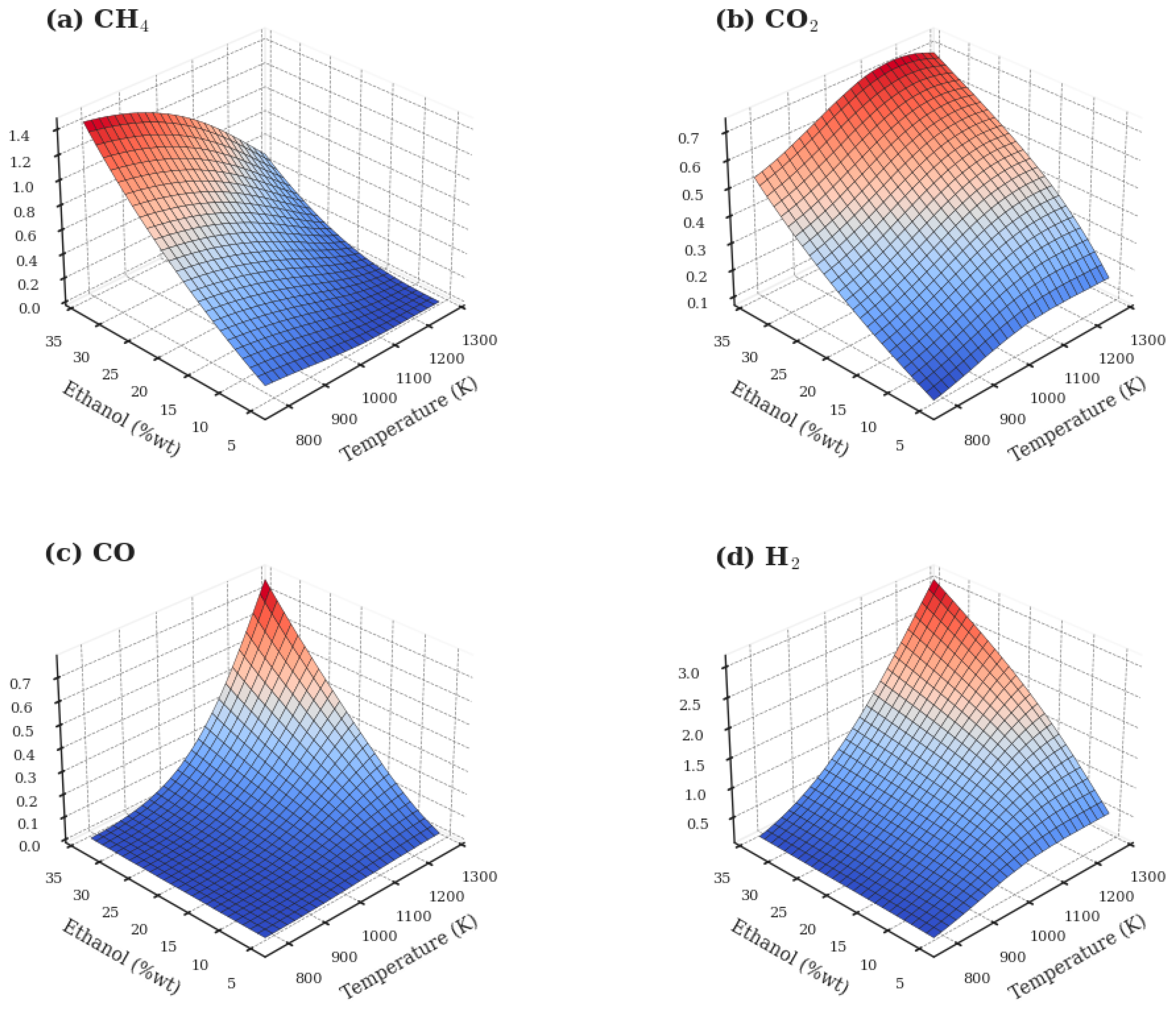
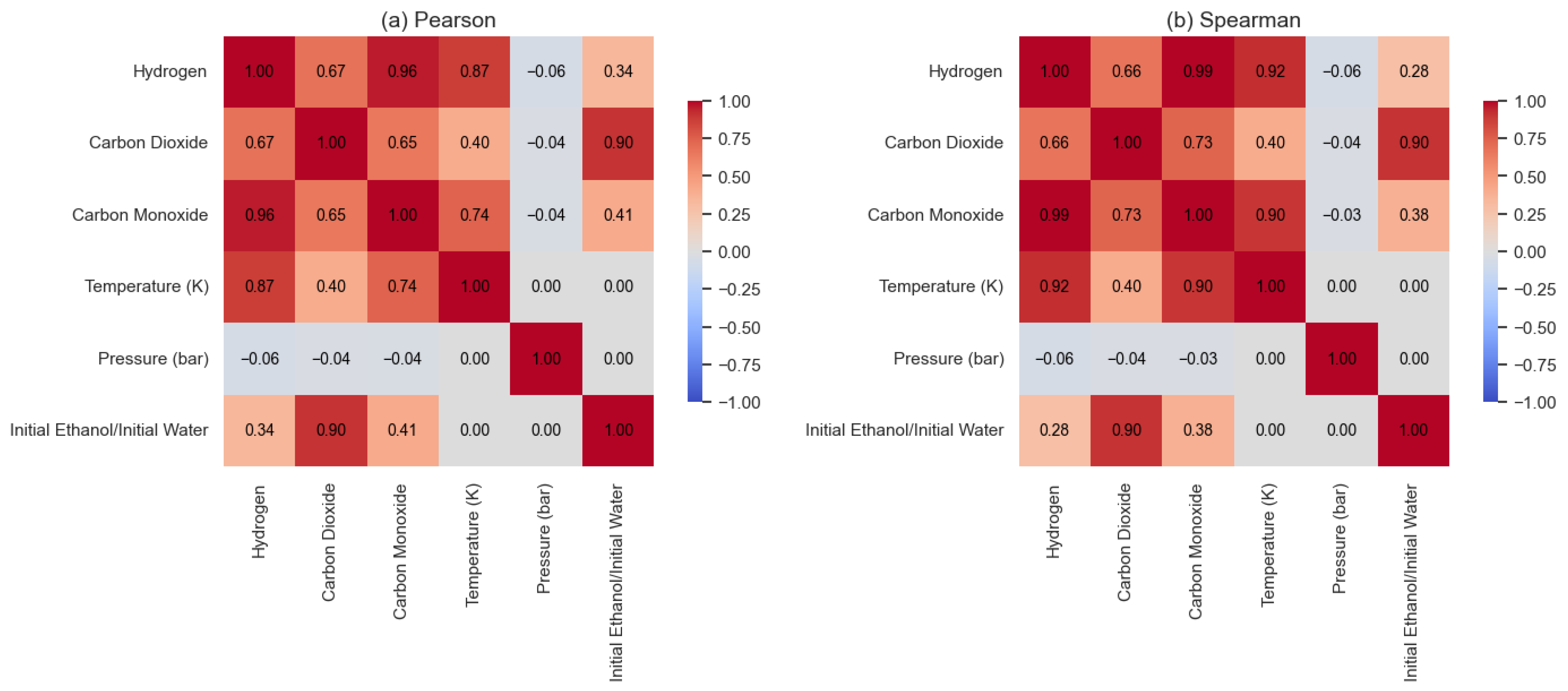
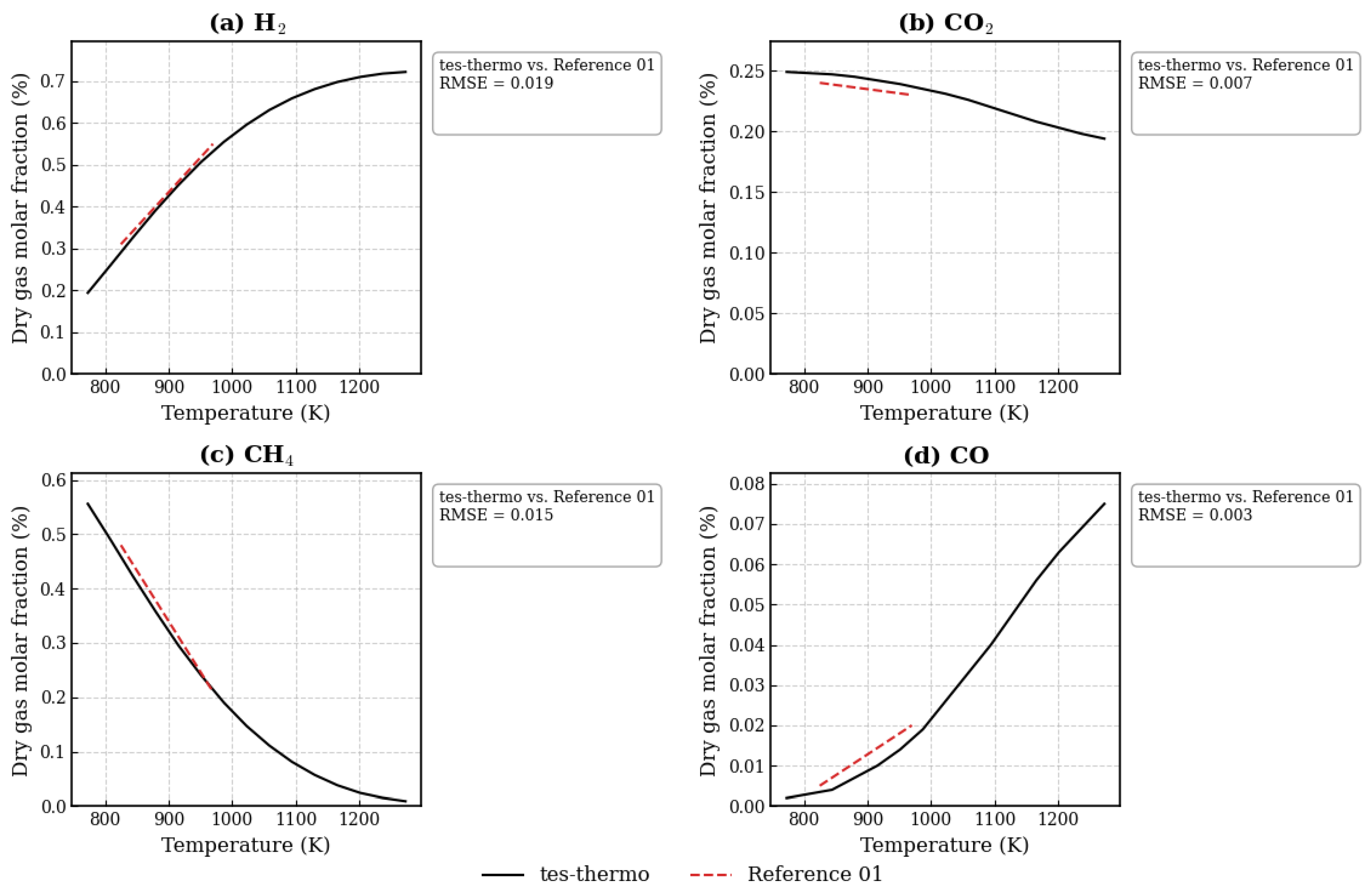
3.1. Evaluation of the Ethanol SCWG Process
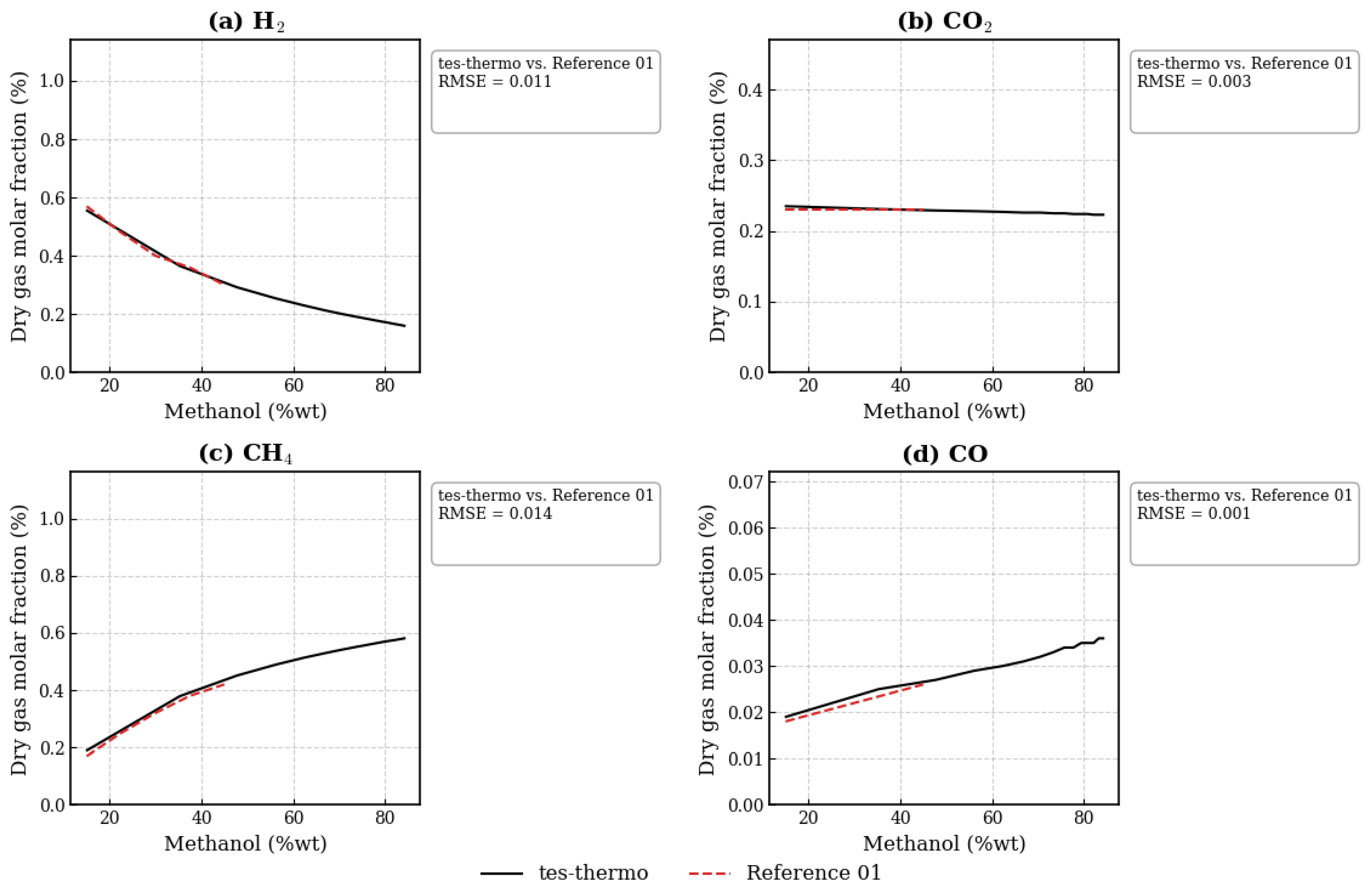
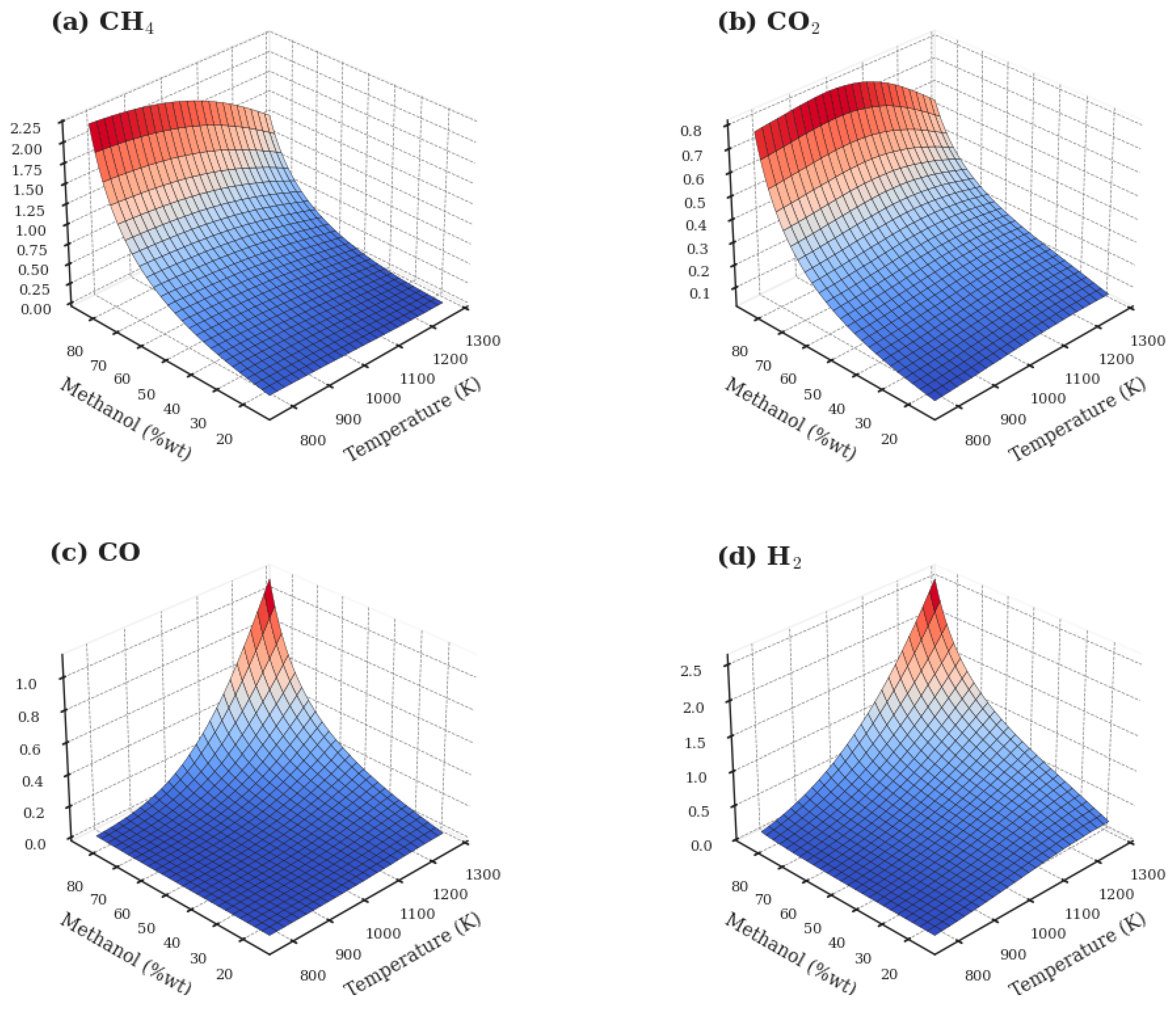
3.2. Evaluation of the Methanol SCWG Process
4. Conclusions
5. Patents
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclatures
| G | Total Gibbs energy. |
| l | Liquid phase. |
| s | Solid phase. |
| v | Vapor phase. |
| NC | Number of components. |
| NF | Number of phases. |
| Number of moles of component i in phase k; i = [1, 2, 3, …, NC]; k = [v, l, s]. | |
| R | Universal gas constant. |
| T | Temperature. |
| P | Pressure. |
| µik | Chemical potential of component i in phase k; i = [1, 2, 3, …, NC]; k = [v, l, s]. |
| Fugacity of component i in phase k. | |
| Fugacity of pure species i in a standard reference state. | |
| Number of atoms of element i in component m. | |
| Number of moles in standard state. | |
| Enthalpy of component i in phase k. | |
| Enthalpy of component i in the standard state. | |
| H0 | Total enthalpy. |
| Chemical potential of component i in a standard reference state. | |
| Coefficient of fugacity of component i in phase k; i = [1, 2, 3, …, NC]; k = [v, l]. | |
| Mole fraction of component i in the vapor phase. | |
| Molar fraction of component i in the liquid phase. | |
| Component saturation pressure i. | |
| Zi | Compressibility factor. |
| A, B, u, w | Parameters of the cubic equation of state. |
| am | Attraction parameter for mixtures. |
| bm | Repulsion parameter for mixtures. |
| kij | Binary interaction parameter. |
| Tc,i | Critical component temperature i. |
| Pc,i | Critical component pressure i. |
| wi | Acentric factor. |
| n | Number of moles. |
References
- Seider, W.D.; Lewin, D.R.; Seader, J.D.; Widagdo, S.; Gani, R.; Ng, K.M. Product and Process Design Principles: Synthesis, Analysis and Evaluation; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Seborg, D.E.; Edgar, T.F.; Mellichamp, D.A.; Doyle, F.J., III. Process Dynamics and Control; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Biegler, L.T. Nonlinear Programming: Concepts, Algorithms, and Applications to Chemical Processes; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- Turton, R.; Bailie, R.C.; Whiting, W.B.; Shaeiwitz, J.A. Analysis, Synthesis and Design of Chemical Processes; Pearson Education: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Al-Malah, K.I.M. Aspen Plus: Chemical Engineering Applications; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Hantoko, D.; Yan, M.; Prabowo, B.; Susanto, H.; Li, X.; Chen, C. Aspen Plus Modeling Approach in Solid Waste Gasification. In Current Developments in Biotechnology and Bioengineering; Elsevier: Amsterdam, The Netherlands, 2019; pp. 259–281. [Google Scholar] [CrossRef]
- Alqaheem, Y.; Alobaid, M. Development of a membrane process in CAPE-OPEN to CAPE-OPEN (COCO) simulator for carbon dioxide separation. Results Eng. 2024, 22, 102239. [Google Scholar] [CrossRef]
- Sandrock, C.; de Vaal, P.L. Dynamic simulation of Chemical Engineering systems using OpenModelica and CAPE-OPEN. Comput. Aided Chem. Eng. 2009, 26, 859–864. [Google Scholar] [CrossRef]
- Andreadou, C.; Martinopoulos, G. CAPE-OPEN simulation of waste-to-energy technologies for urban cities. Int. J. Sustain. Energy 2018, 37, 96–104. [Google Scholar] [CrossRef]
- Sreemahadevan, S.; Sivakumar, K.V.; Palanisamy, M. Evaluation of the Open Source Process Simulator DWSIM for Bioprocess Simulation. Period. Polytech. Chem. Eng. 2024, 68, 195–202. [Google Scholar] [CrossRef]
- Ullah, K.; Asaad, S.M.; Inayat, A. Process modelling and optimization of hydrogen production from biogas by integrating DWSIM with response surface methodology. Digit. Chem. Eng. 2025, 14, 100205. [Google Scholar] [CrossRef]
- Hassan, T.N.; Manji, S.T. Simulating Combined Cycle and Gas Turbine Power Plant under Design Condition using Open-Source Software DWSIM. ARO-Sci. J. KOYA Univ. 2023, 11, 60–71. [Google Scholar] [CrossRef]
- Tangsriwong, K.; Lapchit, P.; Kittijungjit, T.; Klamrassamee, T.; Sukjai, Y.; Laoonual, Y. Modeling of chemical processes using commercial and open-source software: A comparison between Aspen Plus and DWSIM. IOP Conf. Ser. Earth Environ. Sci. 2020, 463, 012057. [Google Scholar] [CrossRef]
- Goodwin, D.G.; Moffat, H.; Speth, R.L. Cantera: An Object-Oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes. Version 2.2.1. 2016. Available online: https://api.semanticscholar.org/CorpusID:86382900 (accessed on 25 August 2025).
- Leader, M.; McTague, M.; Lavelle, T.; Wang, X.; Dickens, K.; Hill, J. NASA Chemical Equilibrium with Applications (CEA) Tutorial. In Proceedings of the AIAA SciTech Forum, Orlando, FL, USA, 6–10 January 2025. [Google Scholar]
- Rossum, V. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- McKinney, W. Data structures for statistical computing in Python. SciPy 2010, 445, 51–56. [Google Scholar]
- Dechamps, P. The IEA World Energy Outlook 2022—A brief analysis and implications. Eur. Energy Clim. J. 2023, 11, 100–103. [Google Scholar] [CrossRef]
- Peterson, A.A.; Vogel, F.; Lachance, R.P.; Fröling, M., Jr.; Antal, M.J.; Tester, J.W. Thermochemical biofuel production in hydrothermal media: A review of sub- and supercritical water technologies. Energy Environ. Sci. 2008, 1, 32. [Google Scholar] [CrossRef]
- Matsumura, Y.; Minowa, T.; Potic, B.; Kersten, S.; Prins, W.; Vanswaaij, W.; Vandebeld, B.; Elliott, D.; Neuenschwander, G.; Kruse, A. Biomass gasification in near- and super-critical water: Status and prospects. Biomass Bioenergy 2005, 29, 269–292. [Google Scholar] [CrossRef]
- Dincer, I.; Acar, C. Review and evaluation of hydrogen production methods for better sustainability. Int. J. Hydrogen Energy 2015, 40, 11094–11111. [Google Scholar] [CrossRef]
- Tang, H.; Kitagawa, K. Supercritical water gasification of biomass: Thermodynamic analysis with direct Gibbs free energy minimization. Chem. Eng. J. 2005, 106, 261–267. [Google Scholar] [CrossRef]
- Ciuffi, B.; Chiaramonti, D.; Rizzo, A.M.; Frediani, M.; Rosi, L. A critical review of SCWG in the context of available gasification technologies for plastic waste. Appl. Sci. 2020, 10, 6307. [Google Scholar] [CrossRef]
- De Blasio, C.; Järvinen, M. Supercritical Water Gasification of Biomass. In Encyclopedia of Sustainable Technologies; Elsevier: Amsterdam, The Netherlands, 2017; pp. 171–195. [Google Scholar] [CrossRef]
- Castello, D.; Fiori, L. Supercritical water gasification of biomass: Thermodynamic constraints. Bioresour. Technol. 2011, 102, 7574–7582. [Google Scholar] [CrossRef]
- Basu, P.; Mettanant, V. Biomass Gasification in Supercritical Water—A Review. Int. J. Chem. React. Eng. 2009, 7. [Google Scholar] [CrossRef]
- Reddy, S.N.; Nanda, S.; Dalai, A.K.; Kozinski, J.A. Supercritical water gasification of biomass for hydrogen production. Int. J. Hydrogen Energy 2014, 39, 6912–6926. [Google Scholar] [CrossRef]
- Voll, F.A.P.; Rossi, C.C.R.S.; Silva, C.; Guirardello, R.; Souza, R.O.M.A.; Cabral, V.F.; Cardozo-Filho, L. Thermodynamic analysis of supercritical water gasification of methanol, ethanol, glycerol, glucose and cellulose. Int. J. Hydrogen Energy 2009, 34, 9737–9744. [Google Scholar] [CrossRef]
- Junior, J.M.D.S.; de Freitas, A.C.D.; Mariano, A.P. An AI-Assisted Thermodynamic Equilibrium Simulator: A Case Study on Steam Methane Reforming in Isothermal and Adiabatic Reactors. Processes 2025, 13, 2508. [Google Scholar] [CrossRef]
- Castillo, J.; Grossmann, I.E. Computation of phase and chemical equilibria. Comput. Chem. Eng. 1981, 5, 99–108. [Google Scholar] [CrossRef]
- Smith, J.M.; Van Ness, H.C.; Abbott, M.M.; Swihart, M.T. Introduction to Chemical Engineering Thermodynamics; McGraw-Hill: Singapore, 2018. [Google Scholar]
- Robinson, D.B.; Peng, D.-Y.; Ng, H.-J. Applications of the Peng-Robinson Equation of State; American Chemical Society: Washington, DC, USA, 1977; pp. 200–220. [Google Scholar] [CrossRef]
- Ghanbari, M.; Ahmadi, M.; Lashanizadegan, A. A comparison between Peng-Robinson and Soave-Redlich-Kwong cubic equations of state from modification perspective. Cryogenics 2017, 84, 13–19. [Google Scholar] [CrossRef]
- Soave, G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Tsonopoulos, C. An empirical correlation of second virial coefficients. AIChE J. 1974, 20, 263–272. [Google Scholar] [CrossRef]
- Gomes, J.G.; Mitoura, J.; Guirardello, R. Thermodynamic analysis for hydrogen production from the reaction of subcritical and supercritical gasification of the C. Vulgaris microalgae. Energy 2022, 260, 125030. [Google Scholar] [CrossRef]
- Junior, J.M.D.S.; Mariano, A.P. Gasification of Lignocellulosic Waste in Supercritical Water: Study of Thermodynamic Equilibrium as a Nonlinear Programming Problem. Eng 2024, 5, 1096–1111. [Google Scholar] [CrossRef]
- Freitas, A.C.D.; Guirardello, R. Use of CO2 as a co-reactant to promote syngas production in supercritical water gasification of sugarcane bagasse. J. CO2 Util. 2015, 9, 66–73. [Google Scholar] [CrossRef]
- Barros, T.V.; Carregosa, J.D.C.; Jr, A.W.; Freitas, A.C.D.; Guirardello, R.; Ferreira-Pinto, L.; Bonfim-Rocha, L.; Jegatheesan, V.; Cardozo-Filho, L. Assessment of black liquor hydrothermal treatment under sub- and supercritical conditions: Products distribution and economic perspectives. Chemosphere 2022, 286, 131774. [Google Scholar] [CrossRef]
- Freitas, A.C.D.; Guirardello, R. Oxidative reforming of methane for hydrogen and synthesis gas production: Thermodynamic equilibrium analysis. J. Nat. Gas Chem. 2012, 21, 571–580. [Google Scholar] [CrossRef]
- Yan, Q.; Guo, L.; Lu, Y. Thermodynamic analysis of hydrogen production from biomass gasification in supercritical water. Energy Convers. Manag. 2006, 47, 1515–1528. [Google Scholar] [CrossRef]
- Feng, W.; van der Kooi, H.J.; de Swaan Arons, J. Biomass conversions in subcritical and supercritical water: Driving force, phase equilibria, and thermodynamic analysis. Chem. Eng. Process. Process Intensif. 2004, 43, 1459–1467. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’connell, J.P. Properties of Gases and Liquids; McGraw-Hill Education: New York, NY, USA, 2001. [Google Scholar]
- Hart, W.E.; Laird, C.D.; Watson, J.-P.; Woodruff, D.L.; Hackebeil, G.A.; Nicholson, B.L.; Siirola, J.D. Pyomo-Optimization Modeling in Python; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math Program 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Santos, J.J.M.; Zelioli, Í.A.M.; Guimarães, F.E.É.X.; Freitas, A.C.D.; Mariano, A.P. Supercritical water gasification thermodynamic study and hybrid modeling of machine learning with the ideal gas model: Application to gasification of microalgae biomass. Energy 2024, 291, 130287. [Google Scholar] [CrossRef]
- Byrd, A.J.; Pant, K.K.; Gupta, R.B. Hydrogen Production from Ethanol by Reforming in Supercritical Water Using Ru/Al2O3 Catalyst. Energy Fuels 2007, 21, 3541–3547. [Google Scholar] [CrossRef]
- Freitas, A.C.D.; Guirardello, R. Comparison of several glycerol reforming methods for hydrogen and syngas production using Gibbs energy minimization. Int. J. Hydrogen Energy 2014, 39, 17969–17984. [Google Scholar] [CrossRef]
- Savage, P.E. Organic Chemical Reactions in Supercritical Water. Chem. Rev. 1999, 99, 603–622. [Google Scholar] [CrossRef]
- Guan, Q.; Wei, C.; Savage, P.E. Kinetic model for supercritical water gasification of algae. Phys. Chem. Chem. Phys. 2012, 14, 3140. [Google Scholar] [CrossRef]
- Correa, C.R.; Kruse, A. Supercritical water gasification of biomass for hydrogen production—Review. J. Supercrit. Fluids 2018, 133, 573–590. [Google Scholar] [CrossRef]
- Santos, J.M.D.; De Sousa, G.F.B.; Vidotti, A.D.S.; De Freitas, A.C.D.; Guirardello, R. Optimization of glycerol gasification process in supercritical water using thermodynamic approach. Chem. Eng. Trans. 2021, 86, 847–852. [Google Scholar] [CrossRef]
- Freitas, A.C.D.; Guirardello, R. Supercritical Water Gasification of Glucose and Cellulose for Hydrogen and Syngas Production. Chem. Eng. Trans. 2012, 27, 361–366. [Google Scholar] [CrossRef]

| Components | Tc (K) | Pc (bar) | ω | ∆Hf (cal/mol) | ∆Gf (cal/mol) |
|---|---|---|---|---|---|
| H2O | 647.140 | 220.640 | 0.344 | −5.78 × 104 | −5.46 × 104 |
| H2 | 32.980 | 12.930 | −0.217 | 0 | 0 |
| CH4 | 190.560 | 45.990 | 0.011 | −1.78 × 104 | −1.21 × 104 |
| CO2 | 304.150 | 73.740 | 0.225 | −9.41 × 104 | −9.43 × 104 |
| CO | 132.850 | 34.940 | 0.045 | −2.64 × 104 | −3.28 × 104 |
| O2 | 154.580 | 50.430 | 0.022 | 0 | 0 |
| CH4O | 512.640 | 80.970 | 0.565 | −4.80 × 104 | −3.88 × 104 |
| C2H6 | 305.320 | 48.720 | 0.099 | −2.00 × 104 | −7.61 × 103 |
| C3H8 | 369.830 | 42.480 | 0.152 | −2.50 × 104 | −5.81 × 103 |
| C2H4 | 282.340 | 50.410 | 0.087 | 1.250 × 104 | 1.64 × 104 |
| CH3OH | 512.600 | 87.970 | 0.564 | −2.351 × 104 | −1.684 × 104 |
| C2H6O | 513.900 | 61.480 | 0.645 | −2.006 × 104 | −1.619 × 104 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
dos Santos Junior, J.M.; Daltro de Freitas, A.C.; Mariano, A.P. A Python-Based Thermodynamic Equilibrium Library for Gibbs Energy Minimization: A Case Study on Supercritical Water Gasification of Ethanol and Methanol. Eng 2025, 6, 208. https://doi.org/10.3390/eng6090208
dos Santos Junior JM, Daltro de Freitas AC, Mariano AP. A Python-Based Thermodynamic Equilibrium Library for Gibbs Energy Minimization: A Case Study on Supercritical Water Gasification of Ethanol and Methanol. Eng. 2025; 6(9):208. https://doi.org/10.3390/eng6090208
Chicago/Turabian Styledos Santos Junior, Julles Mitoura, Antonio Carlos Daltro de Freitas, and Adriano Pinto Mariano. 2025. "A Python-Based Thermodynamic Equilibrium Library for Gibbs Energy Minimization: A Case Study on Supercritical Water Gasification of Ethanol and Methanol" Eng 6, no. 9: 208. https://doi.org/10.3390/eng6090208
APA Styledos Santos Junior, J. M., Daltro de Freitas, A. C., & Mariano, A. P. (2025). A Python-Based Thermodynamic Equilibrium Library for Gibbs Energy Minimization: A Case Study on Supercritical Water Gasification of Ethanol and Methanol. Eng, 6(9), 208. https://doi.org/10.3390/eng6090208






