Simplifying Data Processing in AFM Nanoindentation Experiments on Thin Samples
Abstract
1. Introduction
2. Materials and Methods
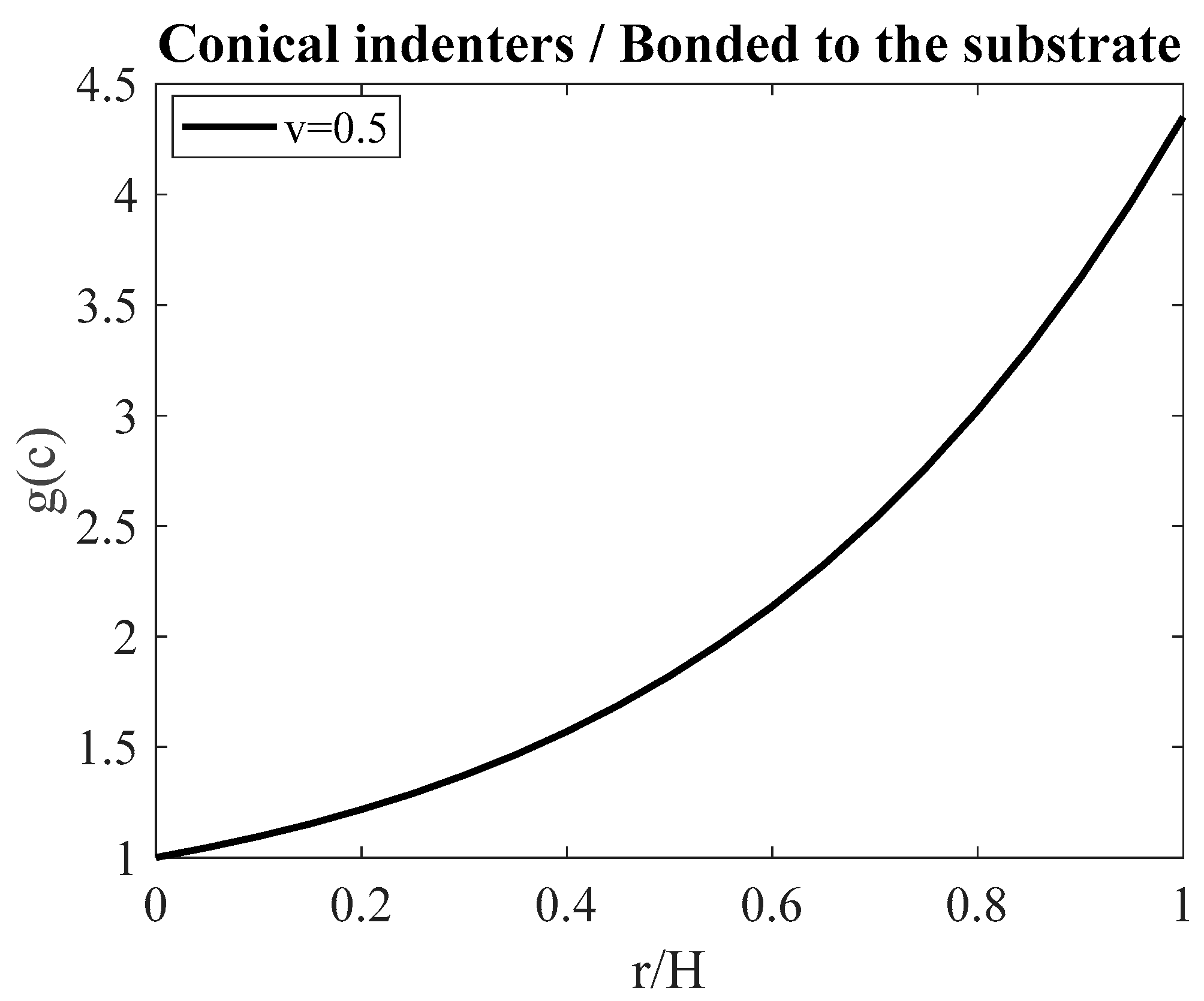
2.1. Simplifying Data Processing Using Classic Mathematical Tools
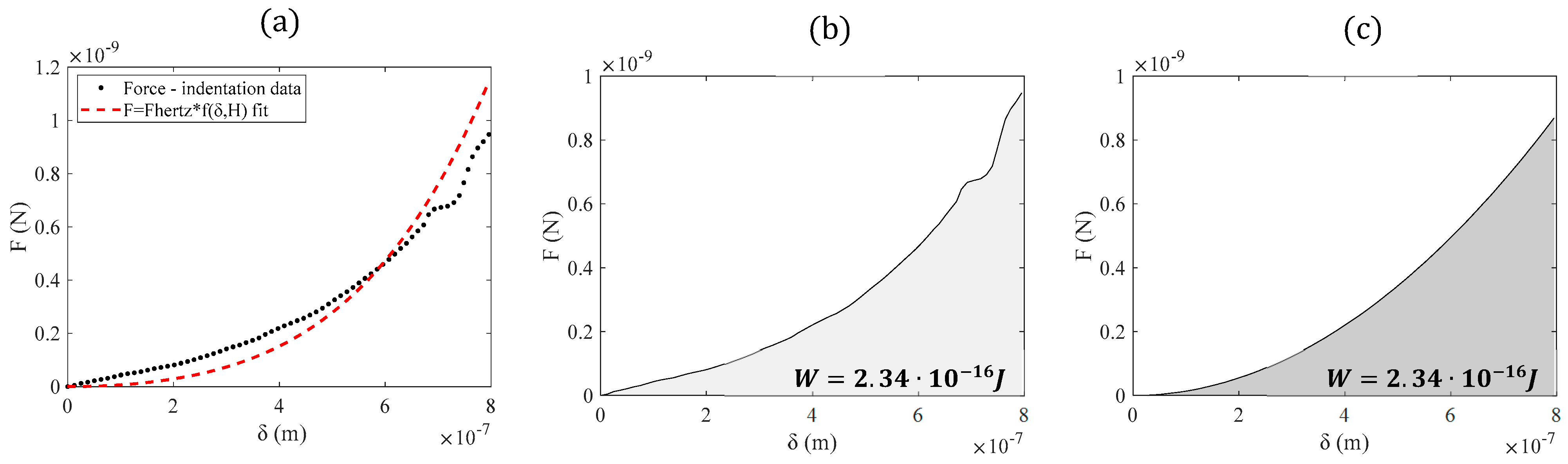
2.2. AFM Data from Fibroblasts (Open-Access Data from Reference [37])
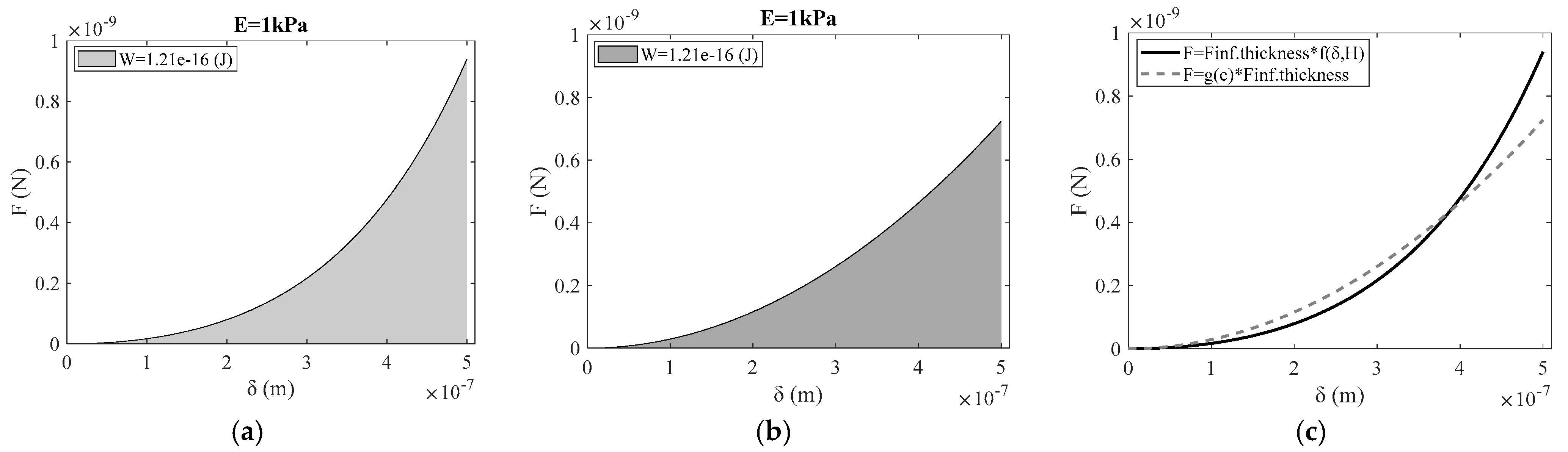
2.3. Simulated Data (Open-Access Data from Reference [37])
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Thin samples bonded to the substrate with v = 0.5 (conical indenters) | |||||||
| 0.005 | 1 | 0.255 | 1.30 | 0.505 | 1.84 | 0.755 | 2.79 |
| 0.010 | 1.01 | 0.260 | 1.31 | 0.510 | 1.85 | 0.760 | 2.83 |
| 0.015 | 1.01 | 0.265 | 1.32 | 0.515 | 1.87 | 0.765 | 2.84 |
| 0.020 | 1.02 | 0.270 | 1.32 | 0.520 | 1.87 | 0.770 | 2.86 |
| 0.025 | 1.02 | 0.275 | 1.32 | 0.525 | 1.90 | 0.775 | 2.89 |
| 0.030 | 1.03 | 0.280 | 1.34 | 0.530 | 1.91 | 0.780 | 2.92 |
| 0.035 | 1.03 | 0.285 | 1.34 | 0.535 | 1.93 | 0.785 | 2.94 |
| 0.040 | 1.03 | 0.290 | 1.35 | 0.540 | 1.94 | 0.790 | 2.97 |
| 0.045 | 1.04 | 0.295 | 1.35 | 0.545 | 1.95 | 0.795 | 3.00 |
| 0.050 | 1.04 | 0.300 | 1.37 | 0.550 | 1.97 | 0.800 | 3.03 |
| 0.055 | 1.05 | 0.305 | 1.39 | 0.555 | 1.99 | 0.805 | 3.05 |
| 0.060 | 1.05 | 0.310 | 1.39 | 0.560 | 2.01 | 0.810 | 3.08 |
| 0.065 | 1.06 | 0.315 | 1.41 | 0.565 | 2.02 | 0.815 | 3.11 |
| 0.070 | 1.06 | 0.320 | 1.41 | 0.570 | 2.03 | 0.820 | 3.14 |
| 0.075 | 1.07 | 0.325 | 1.42 | 0.575 | 2.05 | 0.825 | 3.15 |
| 0.080 | 1.08 | 0.330 | 1.42 | 0.580 | 2.07 | 0.830 | 3.19 |
| 0.085 | 1.08 | 0.335 | 1.44 | 0.585 | 2.09 | 0.835 | 3.22 |
| 0.090 | 1.09 | 0.340 | 1.45 | 0.590 | 2.10 | 0.840 | 3.24 |
| 0.095 | 1.09 | 0.345 | 1.45 | 0.595 | 2.12 | 0.845 | 3.28 |
| 0.100 | 1.09 | 0.350 | 1.47 | 0.600 | 2.15 | 0.850 | 3.31 |
| 0.105 | 1.10 | 0.355 | 1.47 | 0.605 | 2.15 | 0.855 | 3.33 |
| 0.110 | 1.10 | 0.360 | 1.48 | 0.610 | 2.18 | 0.860 | 3.37 |
| 0.115 | 1.11 | 0.365 | 1.50 | 0.615 | 2.18 | 0.865 | 3.40 |
| 0.120 | 1.11 | 0.370 | 1.50 | 0.620 | 2.22 | 0.870 | 3.44 |
| 0.125 | 1.13 | 0.375 | 1.52 | 0.625 | 2.23 | 0.875 | 3.46 |
| 0.130 | 1.13 | 0.380 | 1.52 | 0.630 | 2.25 | 0.880 | 3.50 |
| 0.135 | 1.13 | 0.385 | 1.53 | 0.635 | 2.27 | 0.885 | 3.52 |
| 0.140 | 1.14 | 0.390 | 1.55 | 0.640 | 2.28 | 0.890 | 3.56 |
| 0.145 | 1.14 | 0.395 | 1.56 | 0.645 | 2.31 | 0.895 | 3.59 |
| 0.150 | 1.15 | 0.400 | 1.57 | 0.650 | 2.32 | 0.900 | 3.62 |
| 0.155 | 1.15 | 0.405 | 1.58 | 0.655 | 2.35 | 0.905 | 3.66 |
| 0.160 | 1.16 | 0.410 | 1.60 | 0.660 | 2.36 | 0.910 | 3.69 |
| 0.165 | 1.17 | 0.415 | 1.61 | 0.665 | 2.38 | 0.915 | 3.73 |
| 0.170 | 1.17 | 0.420 | 1.62 | 0.670 | 2.41 | 0.920 | 3.75 |
| 0.175 | 1.19 | 0.425 | 1.62 | 0.675 | 2.42 | 0.925 | 3.79 |
| 0.180 | 1.19 | 0.430 | 1.65 | 0.680 | 2.45 | 0.930 | 3.83 |
| 0.185 | 1.20 | 0.435 | 1.65 | 0.685 | 2.47 | 0.935 | 3.86 |
| 0.190 | 1.20 | 0.440 | 1.66 | 0.690 | 2.49 | 0.940 | 3.90 |
| 0.195 | 1.22 | 0.445 | 1.67 | 0.695 | 2.51 | 0.945 | 3.93 |
| 0.200 | 1.22 | 0.450 | 1.68 | 0.700 | 2.53 | 0.950 | 3.98 |
| 0.205 | 1.22 | 0.455 | 1.71 | 0.705 | 2.56 | 0.955 | 4.01 |
| 0.210 | 1.23 | 0.460 | 1.71 | 0.710 | 2.58 | 0.960 | 4.05 |
| 0.215 | 1.23 | 0.465 | 1.73 | 0.715 | 2.60 | 0.965 | 4.09 |
| 0.220 | 1.25 | 0.470 | 1.74 | 0.720 | 2.63 | 0.970 | 4.12 |
| 0.225 | 1.25 | 0.475 | 1.75 | 0.725 | 2.65 | 0.975 | 4.15 |
| 0.230 | 1.26 | 0.480 | 1.77 | 0.730 | 2.67 | 0.980 | 4.19 |
| 0.235 | 1.26 | 0.485 | 1.78 | 0.735 | 2.69 | 0.985 | 4.23 |
| 0.240 | 1.27 | 0.490 | 1.79 | 0.740 | 2.73 | 0.990 | 4.26 |
| 0.245 | 1.28 | 0.495 | 1.82 | 0.745 | 2.73 | 0.995 | 4.32 |
| 0.250 | 1.28 | 0.500 | 1.82 | 0.750 | 2.77 | 1.000 | 4.35 |
| Thin samples bonded to the substrate with v = 0.5 (conical indenters) | |||||||
| 0.005 | 1.00 | 0.255 | 1.31 | 0.505 | 1.78 | 0.755 | 2.46 |
| 0.010 | 1.01 | 0.260 | 1.32 | 0.510 | 1.79 | 0.760 | 2.48 |
| 0.015 | 1.01 | 0.265 | 1.32 | 0.515 | 1.80 | 0.765 | 2.49 |
| 0.020 | 1.02 | 0.270 | 1.33 | 0.520 | 1.81 | 0.770 | 2.51 |
| 0.025 | 1.02 | 0.275 | 1.34 | 0.525 | 1.82 | 0.775 | 2.53 |
| 0.030 | 1.03 | 0.280 | 1.35 | 0.530 | 1.83 | 0.780 | 2.54 |
| 0.035 | 1.03 | 0.285 | 1.36 | 0.535 | 1.85 | 0.785 | 2.56 |
| 0.040 | 1.04 | 0.290 | 1.36 | 0.540 | 1.86 | 0.790 | 2.58 |
| 0.045 | 1.04 | 0.295 | 1.37 | 0.545 | 1.87 | 0.795 | 2.59 |
| 0.050 | 1.05 | 0.300 | 1.38 | 0.550 | 1.88 | 0.800 | 2.61 |
| 0.055 | 1.05 | 0.305 | 1.39 | 0.555 | 1.89 | 0.805 | 2.63 |
| 0.060 | 1.06 | 0.310 | 1.40 | 0.560 | 1.91 | 0.810 | 2.64 |
| 0.065 | 1.07 | 0.315 | 1.40 | 0.565 | 1.92 | 0.815 | 2.66 |
| 0.070 | 1.07 | 0.320 | 1.41 | 0.570 | 1.93 | 0.820 | 2.68 |
| 0.075 | 1.08 | 0.325 | 1.42 | 0.575 | 1.94 | 0.825 | 2.70 |
| 0.080 | 1.08 | 0.330 | 1.43 | 0.580 | 1.96 | 0.830 | 2.72 |
| 0.085 | 1.09 | 0.335 | 1.44 | 0.585 | 1.97 | 0.835 | 2.73 |
| 0.090 | 1.09 | 0.340 | 1.45 | 0.590 | 1.98 | 0.840 | 2.75 |
| 0.095 | 1.10 | 0.345 | 1.46 | 0.595 | 1.99 | 0.845 | 2.77 |
| 0.100 | 1.10 | 0.350 | 1.46 | 0.600 | 2.01 | 0.850 | 2.79 |
| 0.105 | 1.11 | 0.355 | 1.47 | 0.605 | 2.02 | 0.855 | 2.81 |
| 0.110 | 1.12 | 0.360 | 1.48 | 0.610 | 2.03 | 0.860 | 2.83 |
| 0.115 | 1.12 | 0.365 | 1.49 | 0.615 | 2.05 | 0.865 | 2.84 |
| 0.120 | 1.13 | 0.370 | 1.50 | 0.620 | 2.06 | 0.870 | 2.86 |
| 0.125 | 1.13 | 0.375 | 1.51 | 0.625 | 2.07 | 0.875 | 2.88 |
| 0.130 | 1.14 | 0.380 | 1.52 | 0.630 | 2.09 | 0.880 | 2.90 |
| 0.135 | 1.15 | 0.385 | 1.53 | 0.635 | 2.10 | 0.885 | 2.92 |
| 0.140 | 1.15 | 0.390 | 1.54 | 0.640 | 2.11 | 0.890 | 2.94 |
| 0.145 | 1.16 | 0.395 | 1.55 | 0.645 | 2.13 | 0.895 | 2.96 |
| 0.150 | 1.16 | 0.400 | 1.56 | 0.650 | 2.14 | 0.900 | 2.98 |
| 0.155 | 1.17 | 0.405 | 1.57 | 0.655 | 2.16 | 0.905 | 3.00 |
| 0.160 | 1.18 | 0.410 | 1.58 | 0.660 | 2.17 | 0.910 | 3.02 |
| 0.165 | 1.18 | 0.415 | 1.59 | 0.665 | 2.19 | 0.915 | 3.04 |
| 0.170 | 1.19 | 0.420 | 1.60 | 0.670 | 2.20 | 0.920 | 3.06 |
| 0.175 | 1.20 | 0.425 | 1.61 | 0.675 | 2.21 | 0.925 | 3.08 |
| 0.180 | 1.20 | 0.430 | 1.62 | 0.680 | 2.23 | 0.930 | 3.10 |
| 0.185 | 1.21 | 0.435 | 1.63 | 0.685 | 2.24 | 0.935 | 3.12 |
| 0.190 | 1.22 | 0.440 | 1.64 | 0.690 | 2.26 | 0.940 | 3.14 |
| 0.195 | 1.22 | 0.445 | 1.65 | 0.695 | 2.27 | 0.945 | 3.16 |
| 0.200 | 1.23 | 0.450 | 1.66 | 0.700 | 2.29 | 0.950 | 3.18 |
| 0.205 | 1.24 | 0.455 | 1.67 | 0.705 | 2.30 | 0.955 | 3.20 |
| 0.210 | 1.24 | 0.460 | 1.68 | 0.710 | 2.32 | 0.960 | 3.22 |
| 0.215 | 1.25 | 0.465 | 1.69 | 0.715 | 2.33 | 0.965 | 3.24 |
| 0.220 | 1.26 | 0.470 | 1.70 | 0.720 | 2.35 | 0.970 | 3.26 |
| 0.225 | 1.26 | 0.475 | 1.71 | 0.725 | 2.36 | 0.975 | 3.29 |
| 0.230 | 1.27 | 0.480 | 1.72 | 0.730 | 2.38 | 0.980 | 3.31 |
| 0.235 | 1.28 | 0.485 | 1.73 | 0.735 | 2.40 | 0.985 | 3.33 |
| 0.240 | 1.29 | 0.490 | 1.74 | 0.740 | 2.41 | 0.990 | 3.35 |
| 0.245 | 1.29 | 0.495 | 1.75 | 0.745 | 2.43 | 0.995 | 3.37 |
| 0.250 | 1.30 | 0.500 | 1.76 | 0.750 | 2.44 | 1.000 | 3.40 |
References
- Lekka, M.; Laidler, P. Applicability of AFM in cancer detection. Nat. Nanotechnol. 2009, 4, 72. [Google Scholar] [CrossRef]
- Plodinec, M.; Loparic, M.; Monnier, C.A.; Obermann, E.C.; Zanetti-Dallenbach, R.; Oertle, P.; Hyotyla, J.T.; Aebi, U.; Bentires-Alj, M.; Lim, R.Y.H.; et al. The nanomechanical signature of breast cancer. Nat. Nanotechnol. 2012, 7, 757–765. [Google Scholar] [CrossRef] [PubMed]
- Stylianou, A.; Lekka, M.; Stylianopoulos, T. AFM assessment of nanomechanical fingerprints for cancer early diagnosis and classification: From single cell to tissue level. Nanoscale 2018, 10, 20930–20945. [Google Scholar] [CrossRef] [PubMed]
- Stylianou, A.; Gkretsi, V.; Stylianopoulos, T. TGF-β modulates pancreatic cancer-associated fibroblasts cell shape, stiffness, and invasion. Biochim. Biophys. Acta 2018, 1862, 1537–1546. [Google Scholar] [CrossRef]
- Stylianou, A.; Kontomaris, S.V.; Alexandratou, E.; Grant, C. AFM on biological materials related to pathological conditions. Scanning 2019, 45, 8452851. [Google Scholar]
- Lekka, M.; Gil, D.; Pogoda, K.; Dulińska-Litewka, J.; Jach, R.; Gostek, J.; Laidler, P. Cancer cell detection in tissue sections using AFM. Arch. Biochem. Biophys. 2012, 518, 151–156. [Google Scholar] [CrossRef]
- Lekka, M. Discrimination between normal and cancerous cells using AFM. BioNanoScience 2016, 6, 65–80. [Google Scholar] [CrossRef] [PubMed]
- Zemła, J.; Danilkiewicz, J.; Orzechowska, B.; Pabijan, J.; Seweryn, S.; Lekka, M. AFM as a tool for assessing cellular elasticity and adhesiveness to identify cancer cells and tissues. Semin. Cell Dev. Biol. 2018, 73, 115–124. [Google Scholar] [CrossRef] [PubMed]
- Cross, S.E.; Jin, Y.-S.; Tondre, J.; Wong, R.; Rao, J.; Gimzewski, J.K. AFM-based analysis of human metastatic cancer cells. Nanotechnology 2008, 19, 384003. [Google Scholar] [CrossRef] [PubMed]
- Holuigue, H.; Lorenc, E.; Chighizola, M.; Schulte, C.; Varinelli, L.; Deraco, M.; Guaglio, M.; Gariboldi, M.; Podestà, A. Force sensing on cells and tissues by AFM. Sensors 2022, 22, 2197. [Google Scholar] [CrossRef]
- Ludwig, T.; Kirmse, R.; Poole, K.; Schwarz, U.S. Probing cellular microenvironments and tissue remodeling by AFM. Pflug. Arch. Eur. J. Physiol. 2008, 456, 29–49. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, K.; Iwata, M. Stiffness of cancer cells measured with AFM indentation method. J. Mech. Behav. Biomed. Mater. 2015, 49, 105–111. [Google Scholar] [CrossRef]
- Sokolov, I.; Dokukin, M.E.; Guz, N.V. Method for quantitative measurements of elastic modulus of biological cells in AFM indentation experiments. Methods 2013, 60, 202–213. [Google Scholar] [CrossRef]
- Viji Babu, P.K.; Radmacher, M. Mechanics of brain tissues studied by AFM: A perspective. Front. Neurosci. 2019, 13, 600. [Google Scholar] [CrossRef] [PubMed]
- Jorba, I.; Uriarte, J.J.; Campillo, N.; Farré, R.; Navajas, D. Probing micromechanical properties of ECM of soft tissues by AFM. J. Cell. Physiol. 2017, 232, 19–26. [Google Scholar] [CrossRef]
- Gautier, H.O.B.; Thompson, A.J.; Achouri, S.; Koser, D.E.; Holtzmann, K.; Moeendarbary, E.; Franze, K. AFM-based force measurements on animal cells and tissues. Biophys. Methods Cell Biol. 2015, 125, 211–235. [Google Scholar]
- Abidine, Y.; Constantinescu, A.; Laurent, V.M.; Rajan, V.S.; Michel, R.; Laplaud, V.; Duperray, A.; Verdier, C. Mechanosensitivity of cancer cells in contact with soft substrates using AFM. Biophys. J. 2018, 114, 1165–1175. [Google Scholar] [PubMed]
- Liu, S.; Han, Y.; Kong, L.; Wang, G.; Ye, Z. AFM in disease-related studies: Exploring tissue and cell mechanics. Microsc. Res. Tech. 2023, 87, 660–684. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, B.; Tang, G.; Yu, X.F.; Galluzzi, M. Cells nanomechanics by AFM: Focus on interactions at the nanoscale. Adv. Phys. X 2021, 6. [Google Scholar] [CrossRef]
- Liang, W.; Shi, H.; Yang, X.; Wang, J.; Yang, W.; Zhang, H.; Liu, L. Recent advances in AFM-based biological characterizations and applications at multiple levels. Soft Matter 2020, 16, 8962–8984. [Google Scholar]
- Kiio, T.M.; Park, S. Nano-scientific application of AFM in pathology: From molecules to tissues. Int. J. Med. Sci. 2020, 17, 844–858. [Google Scholar] [CrossRef]
- Calò, A.; Romin, Y.; Srouji, R.; Zambirinis, C.P.; Fan, F.; Santella, A.; Feng, E.; Fujisawa, S.; Turkekul, M.; Huang, S.; et al. Spatial mapping of collagen distribution in human and mouse tissues by force volume AFM. Sci. Rep. 2020, 10, 15664. [Google Scholar] [CrossRef] [PubMed]
- Ihnatouski, M.; Pauk, J.; Karev, D.; Karev, B. AFM-based method for measurement of normal and osteoarthritic human articular cartilage surface roughness. Materials 2020, 13, 2302. [Google Scholar] [CrossRef]
- Stolz, M.; Gottardi, R.; Raiteri, R.; Miot, S.; Martin, I.; Imer, R.; Staufer, U.; Raducanu, A.; Düggelin, M.; Baschong, W.; et al. Early detection of aging cartilage and osteoarthritis in mice and patient samples using AFM. Nat. Nanotechnol. 2009, 4, 186–192. [Google Scholar] [CrossRef]
- Loparic, M.; Wirz, D.; Daniels, A.U.; Raiteri, R.; Vanlandingham, M.R.; Guex, G.; Martin, I.; Aebi, U.; Stolz, M. Micro- and nanomechanical analysis of articular cartilage by indentation-type AFM: Validation with gel-microfiber composite. Biophys. J. 2010, 98, 2731–2740. [Google Scholar] [CrossRef] [PubMed]
- Dimitriadis, E.K.; Horkay, F.; Maresca, J.; Kachar, B.; Chadwick, R.S. Determination of elastic moduli of thin layers of soft material using AFM. Biophys. J. 2002, 82, 2798–2810. [Google Scholar] [CrossRef]
- Santos, J.A.C.; Rebêlo, L.M.; Araujo, A.C.; Barros, E.B.; de Sousa, J.S. Thickness-corrected model for nanoindentation of thin films with conical indenters. Soft Matter 2012, 8, 4441. [Google Scholar] [CrossRef]
- Gavara, N.; Chadwick, R.S. Determination of elastic moduli of thin samples and adherent cells using conical AFM tips. Nat. Nanotechnol. 2012, 7, 733–736. [Google Scholar] [CrossRef] [PubMed]
- Garcia, P.D.; Garcia, R. Determination of elastic moduli of a single cell cultured on a rigid support by force microscopy. Biophys. J. 2018, 114, 2923–2932. [Google Scholar] [CrossRef]
- Chiodini, S.; Ruiz-Rincón, S.; Garcia, P.D.; Martin, S.; Kettelhoit, K.; Armenia, I.; Werz, D.B.; Cea, P. Bottom Effect in Atomic Force Microscopy Nanomechanics. Small 2020, 16, 2000269. [Google Scholar] [CrossRef] [PubMed]
- Argatov, I.; Jin, X. Self-Consistent Approximations for the Frictionless Paraboloidal and Conical Depth-Sensing Indentation: The Generalized Bottom Effect. Int. J. Solids Struct. 2024, 291, 112713. [Google Scholar] [CrossRef]
- Hermanowicz, P. Determination of Young’s Modulus of Samples of Arbitrary Thickness from Force Distance Curves: Numerical Investigations and Simple Approximate Formulae. Int. J. Mech. Sci. 2021, 193, 106138. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Stylianou, A.; Malamou, A.; Nikita, K.S. An Alternative Approach for the Young’s Modulus Determination of Biological Samples Regarding AFM Indentation Experiments. Mater. Res. Express 2018, 6, 025407. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Stylianou, A.; Chliveros, G.; Malamou, A. Determining Spatial Variability of Elastic Properties for Biological Samples Using AFM. Micromachines 2023, 14, 182. [Google Scholar] [CrossRef] [PubMed]
- Polezzi, M. On the Weighted Mean Value Theorem for Integrals. Int. J. Math. Educ. Sci. Technol. 2006, 37, 868–870. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Stylianou, A.; Georgakopoulos, A.; Malamou, A. Is It Mathematically Correct to Fit AFM Data (Obtained on Biological Materials) to Equations Arising from Hertzian Mechanics? Micron 2023, 164, 103384. [Google Scholar] [CrossRef]
- Hermanowicz, P.; Sarna, M.; Burda, K.; Gabryś, H. An Open Source Software for Analysis of Force Curves. Rev. Sci. Instrum. 2014, 85, 063703. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Malamou, A. Hertz Model or Oliver & Pharr Analysis? Tutorial Regarding AFM Nanoindentation Experiments on Biological Samples. Mater. Res. Express 2020, 7, 033001. [Google Scholar]
- Baldwin, S.J.; Sampson, J.; Peacock, C.J.; Martin, M.L.; Veres, S.P.; Lee, J.M.; Kreplak, L. A New Longitudinal Variation in the Structure of Collagen Fibrils and Its Relationship to Locations of Mechanical Damage Susceptibility. J. Mech. Behav. Biomed. Mater. 2020, 110, 103849. [Google Scholar] [CrossRef] [PubMed]
- Persch, G.; Born, C.; Utesch, B. Nano-Hardness Investigations of Thin Films by an Atomic Force Microscope. Microelectron. Eng. 1994, 24, 113–121. [Google Scholar] [CrossRef]
- Stolz, M.; Raiteri, R.; Daniels, A.U.; VanLandingham, M.R.; Baschong, W.; Aebi, U. Dynamic Elastic Modulus of Porcine Articular Cartilage Determined at Two Different Levels of Tissue Organization by Indentation-Type Atomic Force Microscopy. Biophys. J. 2004, 86, 3269–3283. [Google Scholar] [CrossRef]
- Managuli, V.; Roy, S. Asymptotical Correction to Bottom Substrate Effect Arising in AFM Indentation of Thin Samples and Adherent Cells Using Conical Tips. Exp. Mech. 2018, 58, 733–741. [Google Scholar] [CrossRef]
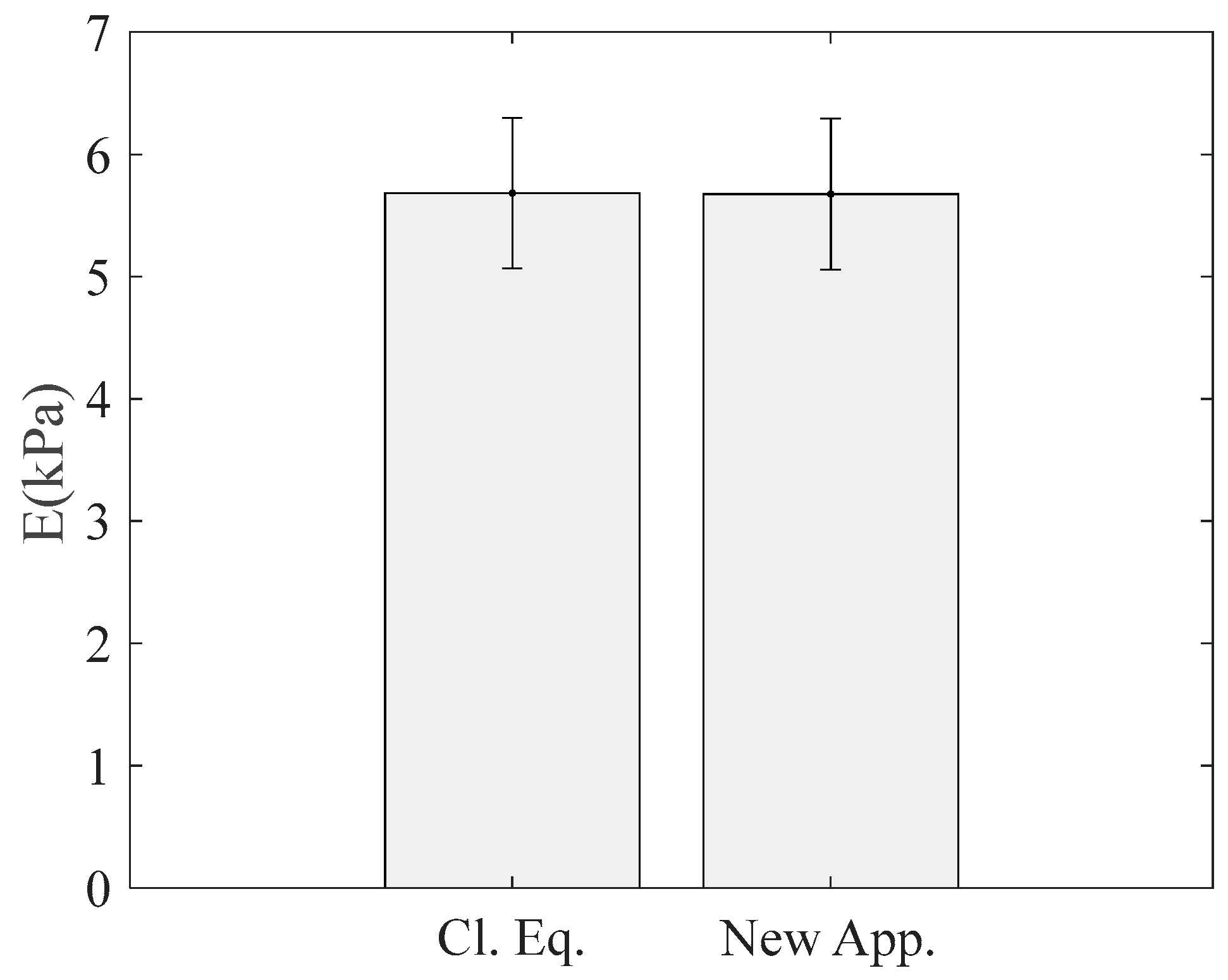
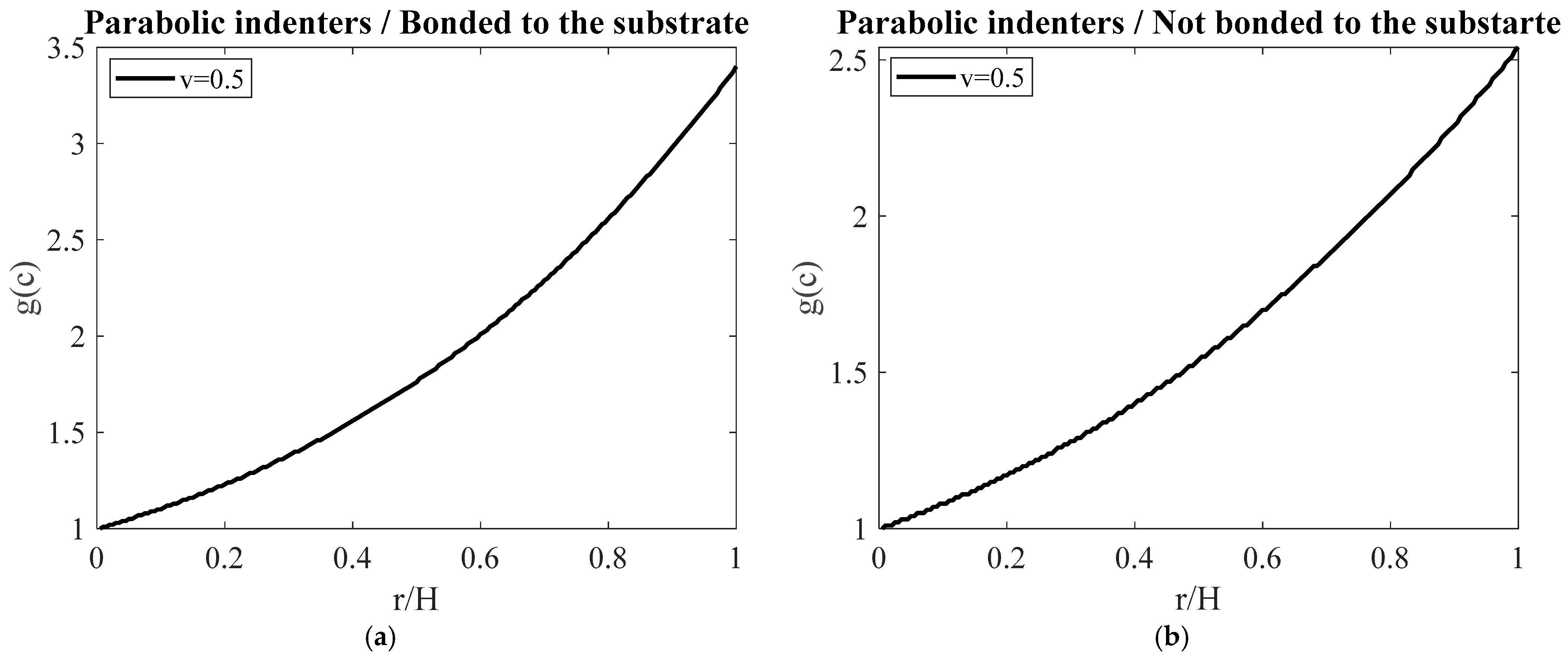
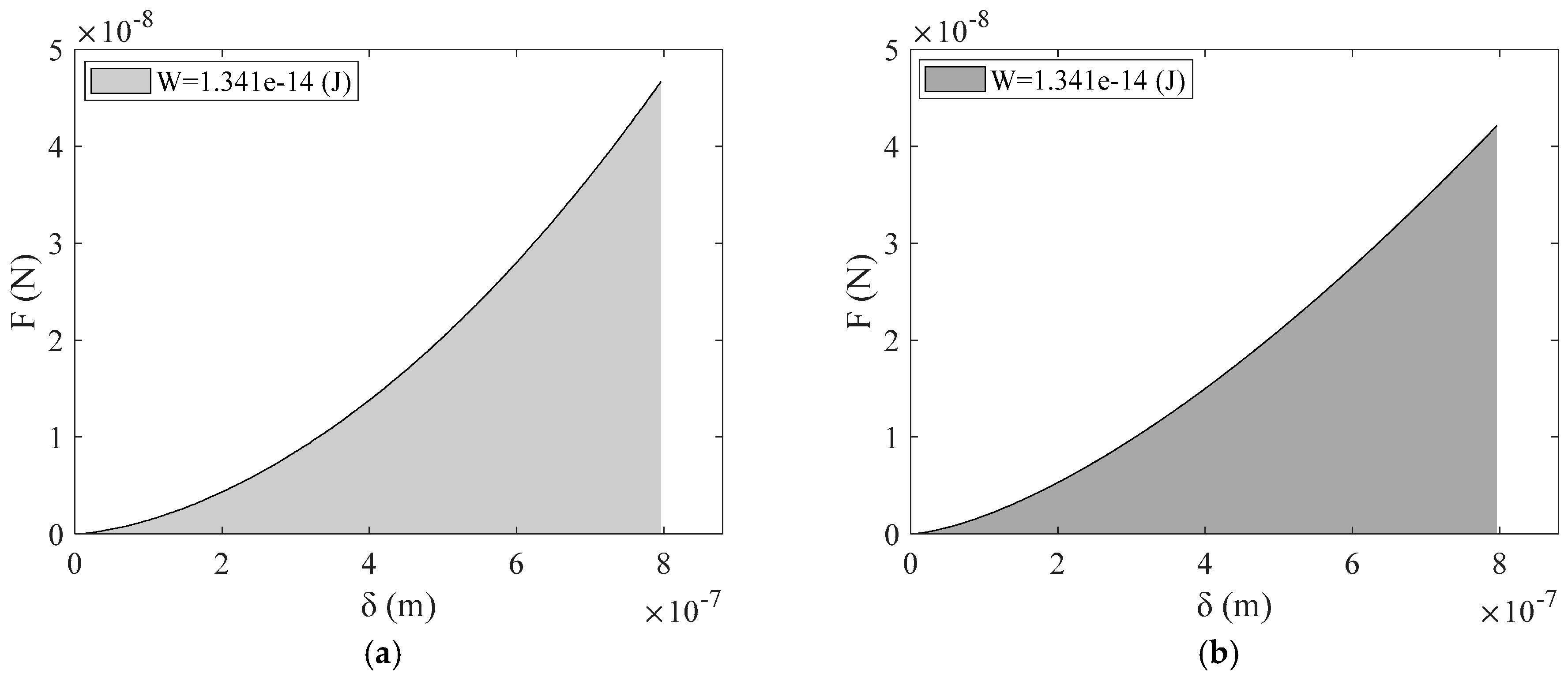
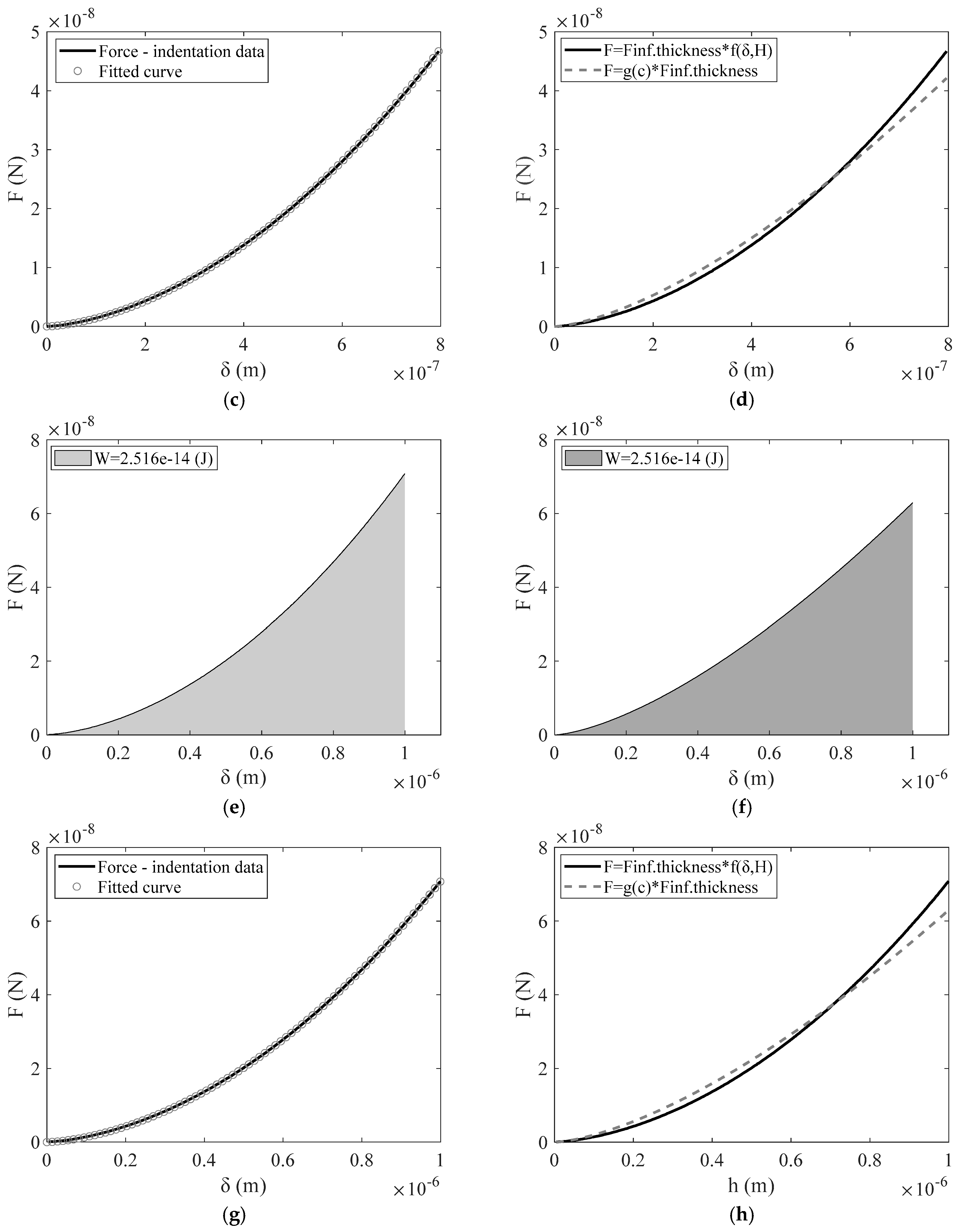

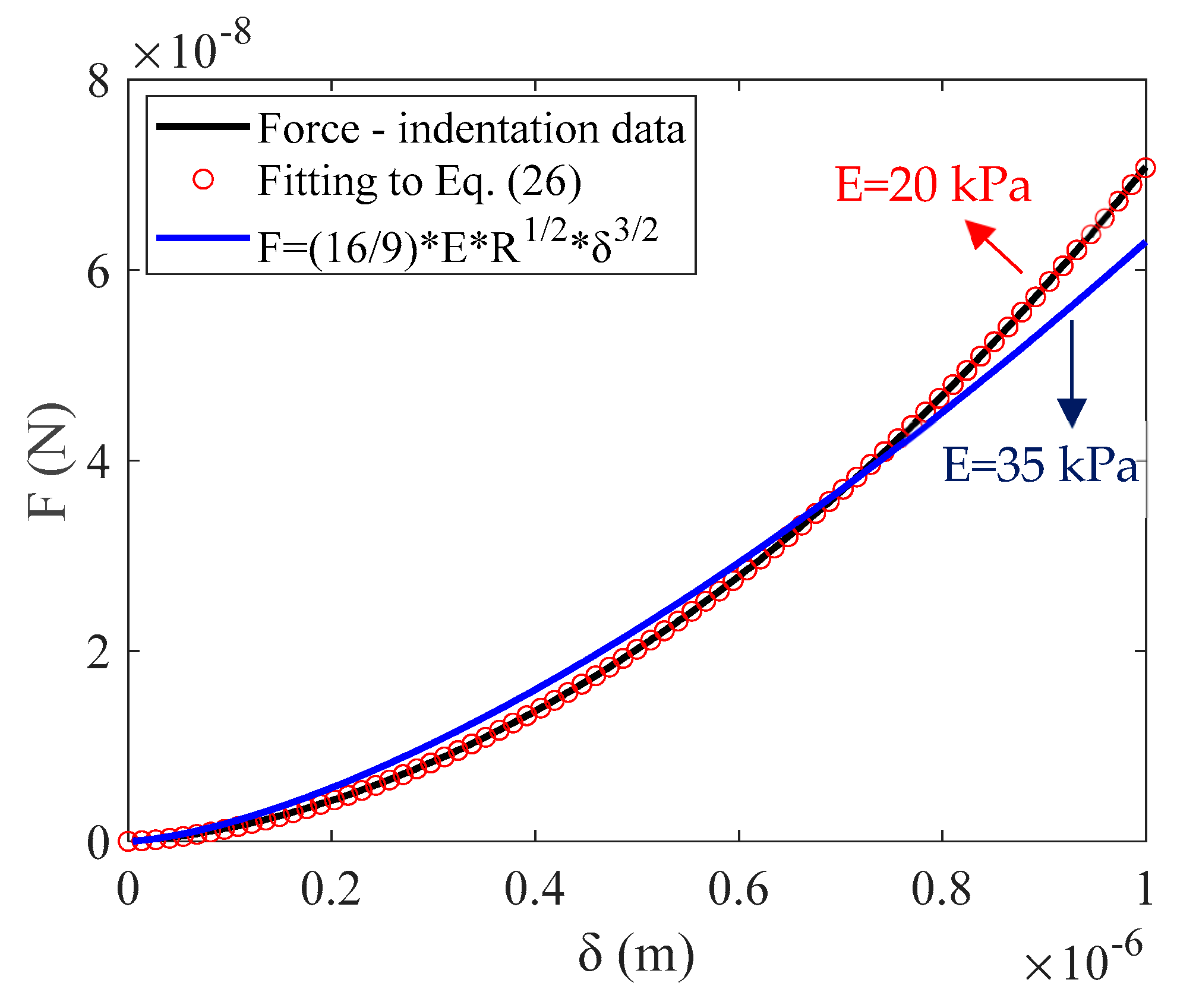
| r/H | (c) | Young’s Mod. (kPa) (Equation (6)) | Young’s Mod. (kPa) (Equation (16)) |
|---|---|---|---|
| 0.126 | 1.13 | 6.04 | 6.00 |
| 0.132 | 1.13 | 5.13 | 5.14 |
| 0.129 | 1.13 | 5.76 | 5.75 |
| 0.128 | 1.13 | 5.87 | 5.85 |
| 0.139 | 1.14 | 4.79 | 4.79 |
| 0.125 | 1.13 | 5.61 | 5.57 |
| 0.139 | 1.14 | 4.74 | 4.73 |
| 0.137 | 1.14 | 5.05 | 5.04 |
| 0.121 | 1.11 | 6.32 | 6.37 |
| 0.112 | 1.11 | 6.75 | 6.74 |
| 0.131 | 1.13 | 5.63 | 5.63 |
| 0.130 | 1.13 | 5.50 | 5.49 |
| 0.117 | 1.11 | 6.49 | 6.51 |
| 0.126 | 1.13 | 5.30 | 5.26 |
| 0.125 | 1.13 | 6.29 | 6.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kontomaris, S.V.; Malamou, A.; Stylianou, A. Simplifying Data Processing in AFM Nanoindentation Experiments on Thin Samples. Eng 2025, 6, 32. https://doi.org/10.3390/eng6020032
Kontomaris SV, Malamou A, Stylianou A. Simplifying Data Processing in AFM Nanoindentation Experiments on Thin Samples. Eng. 2025; 6(2):32. https://doi.org/10.3390/eng6020032
Chicago/Turabian StyleKontomaris, Stylianos Vasileios, Anna Malamou, and Andreas Stylianou. 2025. "Simplifying Data Processing in AFM Nanoindentation Experiments on Thin Samples" Eng 6, no. 2: 32. https://doi.org/10.3390/eng6020032
APA StyleKontomaris, S. V., Malamou, A., & Stylianou, A. (2025). Simplifying Data Processing in AFM Nanoindentation Experiments on Thin Samples. Eng, 6(2), 32. https://doi.org/10.3390/eng6020032








