Abstract
Soil electrical resistivity is a fundamental parameter in various geotechnical, agricultural, environmental, and engineering applications, as it directly depends on the soil’s moisture content and physical properties. Understanding this relationship is crucial for improving the safety and efficiency of electrical installations. This study analyzes the relationship between soil electrical resistivity and gravimetric moisture content in three soil types, sandy, clayey, and silty, with the aim of comparing the performance of different predictive models under controlled laboratory conditions. Seven fitting models were evaluated, Logarithmic Spline, Radial Basis Function (RBF), Locally Estimated Scatterplot Smoothing (LOESS), Least Absolute Shrinkage and Selection Operator (LASSO), Ridge Regression (RIDGE), Power Law and a segmented equation, using metrics such as Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE) and coefficient of determination
. The Spline and RBF models showed excellent accuracy and near-zero errors in all soils, although their applicability is limited by the lack of an explicit formulation and by the fact that, as interpolation methods, they do not guarantee predictive capacity outside the experimental dataset. Therefore, their use should be restricted to controlled laboratory conditions, as field variability factors can significantly alter soil resistivity responses. Among the explicit models, the Segmented Equation obtained a MAPE of 6.14% (sandy), 15.1% (clayey), and 13.16% (silty), with
values of 0.91, 0.93, and 0.89, respectively, demonstrating good performance and functionality. The Power Law model, although showing an
close to 0.96, presented significant overestimations, especially in silty soils (MAPE > 187%). The LASSO model yielded inconsistent predictions with percentage errors exceeding 120% in silty soils. In conclusion, nonparametric models provide excellent accuracy, while the segmented equation stands out as the best explicit alternative for estimating resistivity with reasonable precision.
Keywords:
predictive modeling; electrical resistivity; soils; sandy; clay; silty; gravimetric moisture 1. Introduction
Soil electrical resistivity is a fundamental parameter in various geotechnical, agricultural and environmental applications, from grounding system design to geophysical exploration [1,2,3,4]. This property is influenced by multiple factors, the most important of which are soil texture, compaction, salinity, temperature and, particularly, moisture content [5,6,7]. In addition to these factors, the electrochemical interactions between water and soil particles play a decisive role, especially in fine-grained soils. In clay particle-water interactions, the formation of the diffuse double layer (DDL) around charged clay minerals strongly affects ion mobility and, consequently, the bulk electrical resistivity of soils [8,9]. The thickness and behavior of the DDL depend on mineralogy, cation exchange capacity, pore water salinity and the degree of saturation [10,11,12].
Furthermore, soil electrical resistivity is influenced by mineralogical composition, particle size distribution, void ratio, and pore connectivity, which together determine porosity and current flow paths. These factors explain why clay-rich soils often have a lower resistivity than sandy soils with similar moisture contents [13,14,15,16,17].
Among these, gravimetric moisture content plays a determining role by modifying the contact between soil particles, particularly between clay minerals and the surrounding silt and sand grains, and consequently the soil’s ability to conduct electric current [18,19,20]. Understanding the relationship between soil moisture and its electrical resistivity allows for the development of useful predictive models to optimize systems dependent on the electrical properties of the ground.
Several theoretical frameworks have been developed to explain the relationship between soil moisture and electrical resistivity. One of the most widely recognized is Archie’s Law [21,22], originally formulated for porous media, which expresses resistivity as a function of porosity, degree of saturation, and pore water resistivity. Although initially applied to saturated rocks, this law has been adapted to soils, showing that resistivity decreases as water content and pore connectivity increase [23,24,25]. Complementary models emphasize thin-film conduction mechanisms, where continuous water films surrounding soil particles provide pathways for ionic conduction, especially under low moisture conditions [26,27]. In addition, capillary water retention theories suggest that the distribution of bound and free water strongly modulates the electrical response of soils [28]. These theories, together with the diffuse double layer concept, highlight that the moisture–resistivity relationship is nonlinear and highly dependent on soil texture, porosity, and pore fluid chemistry.
Previous studies have shown that soil resistivity decreases with increasing moisture content, due to increased ionic mobility and improved continuity in the liquid phase of the soil [29,30]. However, this relationship is neither linear nor uniform, as it also depends on the soil’s texture and its ability to retain and distribute water. In this context, granulometric classification allows for the precise identification of the soil textural categories (sandy, silty, or clayey), which is essential for establishing models that explain its electrical behavior [31].
The prediction of electrical resistivity from moisture is of great scientific and practical interest, since it can improve soil characterization models in applications such as irrigation management, environmental monitoring and geotechnical sensor design [32]. In moist soils, the increased presence of free water between pores facilitates current flow, significantly decreasing resistivity. This effect is especially pronounced in soils with a higher water-holding capacity, such as clay-rich soils like bentonite, where particle interactions and ionic conduction dominate the resistivity response [33,34]. This effect is more noticeable in soils with a higher water-holding capacity, although it may also depend on pore connectivity and water distribution in the soil matrix. In dry soil, on the other hand, resistivity increases dramatically due to the interruption of the conductive path formed by water. This condition affects each soil type differently [35].
Despite advances, there are still discrepancies regarding which soil types are most sensitive to moisture changes and how to accurately model this relationship under controlled experimental conditions [36,37,38,39]. For example, while some authors suggest that sandy soils respond more abruptly due to their low water-holding capacity, others emphasize the dominant ionic conduction in clayey soils as the main driving factor behind the decrease in resistivity [40,41,42]. Furthermore, there is no consensus on the mathematical form of the moisture–resistivity relationship, with models ranging from simple exponential or power laws to more complex empirical and machine learning approaches.
For example, ref. [38] observed an average resistivity decrease of 13.8 in compacted clay samples as moisture content increased from 10 to 20, while [15] identified a two-stage exponential decay pattern in Locally Estimated Scatterplot Smoothing (LOESS), with resistivity decreasing from 420 at 10 saturation to 90 at 40. Similarly, ref. [6] reported that in loamy soils, resistivity decreased markedly with compaction and low moisture content (<25), confirming the strong influence of surface conduction effects.
Beyond laboratory-scale analyses, several studies have attempted to model resistivity behavior using empirical or machine learning approaches. For example, ref. [5] applied Artificial Neural Networks (ANNs), achieving high accuracy ( = 0.99), while [16] reported even higher predictive reliability using a hybrid ANN-AG model ( = 0.99, RMSE = 0.0041). Despite these excellent numerical performances, these models often lack physical transparency and remain restricted to specific datasets. In contrast, analytical and semi-empirical formulations such as Archie’s generalized model [22] achieved reasonable prediction errors (relative error = 0.7–29.8) but are generally limited to specific soil textures or moisture ranges.
Similarly, Refs. [39,41] identified significant but inconsistent correlations between resistivity and parameters such as friction angle, plasticity index, and porosity, with regression analyses showing a stronger dependence on moisture and a weaker or negligible association with other soil properties. Experimental differences, including electrode configuration and testing frequency, have also led to variability in reported power-law relationships, as shown by [40], who found frequency-dependent resistivity behavior and abrupt changes around 0 .
Furthermore, recent investigations have highlighted the significant influence of dry-wet cycles on the mechanical and electrical responses of soils, especially under varying environmental conditions. Reference [43] demonstrated that the hydro-mechanical coupling in expansive soils during wetting–drying cycles critically affects pore water pressure distribution. Similarly, Ref. [44] applied advanced machine learning algorithms to model the hydraulic conductivity of sandy soils, showing that changes in gradation and compaction directly impact their hydraulic and conductive behavior. These studies underscore the complex interaction between soil moisture variation and electrical or hydraulic properties, supporting the need for predictive resistivity models that account for nonlinearity and moisture-dependent behavior in different soil types.
Another source of inconsistency is the reliability with which controlled laboratory measurements can be extrapolated to field conditions, where heterogeneity and stratification prevail. These discrepancies define the research gap addressed in this study, which aims to provide a systematic evaluation of predictive models through controlled experiments in different soil textures and moisture regimes.
These limitations reflect the need for experimental approaches that consider both particle size classification and rigorous moisture control to establish applicable predictive models.
Previous studies on soil electrical resistivity have employed a variety of modeling approaches, ranging from linear and power-law regression models to more flexible nonparametric techniques [7]. Simple linear or parametric models often fail to capture the complex nonlinear relationship between moisture content and resistivity, particularly in heterogeneous soils. For example, studies employing hyperspectral modeling approaches [45,46] have achieved moderate predictive performance ( ≈ 0.57–0.74) but often suffer from high data dimensionality, limited interpretability, and a lack of physical transparency. In contrast, nonparametric models such as Spline-Log, Radial Basis Function (RBF), LOESS, Least Absolute Shrinkage and Selection Operator (LASSO), and Ridge Regression (RIDGE) provide greater flexibility, accurately fitting experimental data and capturing nonlinear trends [47,48,49,50].
Furthermore, combining these models with explicit empirical equations enables practical field applications in contexts where computational tools may not be available [50].
Based on previous studies, we hypothesize that nonparametric machine learning models such as Spline-Log, RBF, LOESS, LASSO, and RIDGE will exhibit superior predictive performance (higher R2 and lower RMSE and MAE values) compared to explicit empirical equations and segmented functional models when describing the moisture–resistivity relationship under controlled laboratory conditions. Furthermore, the predictive accuracy of all models is expected to vary depending on the soil type (sandy, silty, and clayey), reflecting the influence of soil texture and fines content on electrical resistivity behavior.
The objective of this study is to establish predictive electrical resistivity models for each of the sandy, silty, and clayey soils as a function of gravimetric moisture content (expressed as a percentage of the soil’s dry mass), integrating particle size analysis for accurate soil classification, and comparing the models to determine which one is more accurate. Unlike previous research, which focused solely on homogeneous soils, this study evaluates how textural variability affects the moisture–resistivity relationship, providing a more robust approach for future applications.
This work presents a series of empirical models based on laboratory data obtained under controlled conditions from sandy, silty, and clayey soils. Particle size analyses were performed to properly classify the samples, and electrical resistivity was measured using a tellurometer coupled to a soil box, along with gravimetric moisture measurements. The results allow for the establishment of a quantitative correlation between soil moisture and electrical resistivity, which is relevant for future research.
The possible contributions of the study are briefly mentioned below:
- (a)
- It is determined how moisture modifies the electrical resistivity of sandy, silty and clayey soils.
- (b)
- Specific predictive models are proposed for each soil texture category (sandy, silty, and clayey), incorporating particle size distribution and Atterberg limits to account for differences in texture and plasticity. This approach has not been addressed in previous studies and allows for a more precise assessment of the moisture–resistivity relationship in various soil types.
- (c)
- The study provides a comparative evaluation between explicit empirical models, segmented functional models, and nonparametric machine learning methods (Log-Spline, RBF, LOESS, LASSO, and RIDGE), under the same controlled laboratory framework. This parallel analysis offers new insights into the suitability, advantages, and limitations of each modeling approach for different soil textures.
2. Materials and Methods
2.1. Research Proposal
This study examined the relationship between electrical resistivity and gravimetric moisture content in sandy, silty, and clayey soils. The literature review presented in the introduction guided the selection of soil samples, followed by particle size analysis to classify the soils. Laboratory tests were conducted to measure moisture content and electrical resistivity. Empirical models were developed to correlate these variables, and their accuracy was assessed by calculating model errors. The results were then interpreted, and recommendations were formulated accordingly.
Figure 1 shows the flowchart describing the research steps in this article.
Figure 1.
Flowchart showing the steps of the study.
2.2. Granulometric Analysis–Particle Size Analysis
Soil samples were collected directly from field sites selected for their predominant textural characteristics (sandy, clayey, or silty). The sampling procedure was designed to ensure representativeness of natural soil conditions in each category. No preconditioning or artificial treatment was applied to the samples prior to laboratory testing in order to preserve their natural composition and structure as closely as possible.
The particle size distribution of the samples was determined according to the standardized procedures of ASTM D422 [51] and ASTM D6913-04 [52]. For coarse soils (mainly sandy), the dry sieving method was employed using a series of standard sieves with openings ranging from 4.75 mm to 0.075 mm. The samples were oven-dried at 110 °C for 24 h, and the weight of each fraction retained on the sieves was recorded to construct the granulometric curve (% passing vs. particle size).
For soils with particles smaller than 0.075 mm (silt and clay), the hydrometer method of ASTM D7928-21e1 [53] was used to determine the fine fraction. Organic matter was removed using hydrogen peroxide from Contyquim (Querétaro, Mexico). A suspension was then prepared with the sample and distilled water, and readings were taken with the hydrometer at defined time intervals. Stokes’ law was applied to calculate the particle size. These data were used to classify the soils texturally and establish the basis for correlating their composition with electrical resistivity. At the same time, it is important to note that the use of hydrogen peroxide () for removing organic matter can alter the surface charge distribution of clay and silt particles, thereby affecting their water-holding capacity and electrical response.
2.3. Gravimetric Moisture Measurement
To ensure measurement consistency and reproducibility, all soil samples were compacted according to ASTM D698-12 [54]. The target dry density for each soil type was determined from preliminary compaction curves, and the samples were prepared by compacting them in three equal layers within the test container. This procedure allowed for porosity conditions to be controlled, minimizing variability due to differences in soil structure.
The samples were completely dried in an oven at 105 °C until they reached a constant weight, thus determining the initial gravimetric moisture content (0%), in accordance with ASTM D2216-19 [55]. Distilled water from Contyquim (Querétaro, Mexico) was then added in controlled increments, increasing the moisture content by 5% per mass until the samples approached full saturation. To ensure homogeneous moisture distribution, especially in sandy soils where rapid drainage and uneven absorption can occur, water was gradually added using a fine mist sprayer.
For each moisture level, the samples were continuously mixed manually for approximately five minutes after each increment, until visually uniform, following the recommendations of ASTM D2216-19 [55]. The corresponding resistivity measurements were then taken immediately after. For each moisture increment, a single measurement of soil resistivity was performed.
Humidity measurements were taken using a sensor HydroSense II (Campbell Scientific Inc., Logan, UT, USA) with a range of 0.1% to 99.9% and an accuracy of ±2%, to verify the water content at each stage. The moisture sensor was calibrated using oven-dried soil samples with known water content before each measurement session. While this calibration improves measurement reliability, the ±2% accuracy introduces quantifiable uncertainty that can be propagated to empirical and nonparametric models.
To verify uniformity, gravimetric moisture samples were taken from the upper and lower thirds of the test containers, showing variations below ±1.5% for all tested moisture levels, confirming adequate homogeneity before resistivity measurement.
While this procedure allowed covering the full range of gravimetric moisture contents, it did not include replicate measurements. This aspect is recognized as a limitation regarding experimental variability.
2.4. Measurement of Soil Electrical Resistivity
The electrical resistivity of each sample was measured using the Wenner method in a Soil Box-type container, with a high-precision digital tellurometer Fluke 1623 Earth (Fluke Corporation, Everett, WA, USA), in accordance with ASTM G57-20 [56] and ASTM G187-18 [57]. This method involves injecting an electric current through two outer electrodes (C1 and C2) and measuring the potential difference between two inner electrodes (P1 and P2), arranged at equal distances in a 4-pin Wenner configuration, as shown in Figure 2. The electrodes were placed at a depth not exceeding 5% of the minimum electrode spacing, ensuring that the geometric factor is properly accounted for in the resistivity calculation. Although the soil box contains integrated electrodes connected to the tellurometer, a conductive paste was applied to minimize contact resistance. This paste is a commercially available, non-toxic, water-based conductive gel with high ionic conductivity, designed to maintain stable electrical contact and reduce measurement variability.
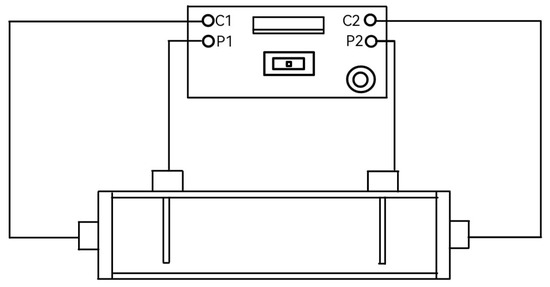
Figure 2.
Four-pin soil box configuration.
It should be noted that soil electrical resistivity depends on factors such as temperature, as variations in temperature affect the mobility of ions in the pore water. All measurements in this study were performed under controlled laboratory conditions at room temperature (25 °C), and no explicit temperature correction was applied. The dimensions of the soil box were as follows:
Width: 4.00
Height: 3.20
Cross-sectional area: 12.80
Pin spacing: 12.80
Based on the configuration and dimensions of the container, the soil resistivity () was calculated using Equation (1), adapted from the Wenner method for the Soil Box:
where is the resistivity (), is the cross-sectional area of the electrode with the sample , is the distance between the potential electrodes and is the measured resistance .
2.5. Predictive Models
To model the relationship between soil electrical resistivity and gravimetric moisture content, numerical analysis and empirical model fitting techniques were employed using the Python 3.10 programming language and machine learning. The experimental data consisted of electrical resistivity (ohm-m) measurements associated with different soil moisture contents (0–100%) for three soil types: sandy, clayey, and silty. A representative sample was used for each soil type, from which multiple moisture content and resistivity measurements were obtained. Furthermore, two complementary modeling strategies were employed: (1) nonparametric models were applied to identify underlying patterns without imposing a predefined functional form, and (2) explicit empirical equations were developed in parallel to provide simple formulas.
To ensure model robustness and avoid overfitting, leave-one-out cross-validation (LOOCV) was applied to all models. In this approach, each data point is sequentially removed from the dataset, the model is trained with the remaining points, and the excluded point is used for testing. This procedure provides rigorous internal validation without the need for additional physical samples. Although independent physical samples were not available for external validation, the LOOCV approach simulates an independent test for each measurement, ensuring that the models generalize correctly within the observed range of moisture content.
To ensure the robustness of the models, extreme values that acted as outliers in the data series were excluded, specifically the value corresponding to 0% gravimetric moisture. This data point exhibited extremely high resistivity values that are not representative of practical soil conditions and could have unduly influenced model fitting. The removal of this point may limit the evaluation of model performance at extremely low moisture contents, which is acknowledged as a limitation of the present study.
The experimental data were processed using the following Python 3.10 libraries: NumPy, Pandas, CubicSpline, Rbf, Curve_fit, Lasso, Ridge, breaks_cusumolsresid, Lowess, Seaborn, mean_squared_error, r2_score, SciPy, and Matplotlib, along with Excel tools. For each soil type, empirical models describing the moisture–resistivity relationship were fitted. These models were evaluated using Spline-Log, RBF, LASSO, RIDGE, Power Law, LOESS, logarithmic, polynomial, and segmented models [45,46].
The selection of predictive models was based on both the expected physical behavior of soil resistivity as a function of gravity moisture and the need for statistical flexibility. The Spline-Log model was used to capture the initial steep decline in resistivity at low moisture contents and the stabilization trend at higher saturation levels [35,36,37,38]. The Power Law model represents the empirical nonlinear decay frequently reported in conductive soil systems [7]. The segmented model considers the existence of distinct resistivity regimes, such as transitions between dry and saturated states.
Nonparametric models, including Radial Basis Function (RBF) and LOESS, were adopted to model local nonlinearities and data curvature arising from textural variability and water distribution patterns, without assuming a fixed global function. Finally, LASSO and Ridge Regression were used to test the performance of the regularized linear models, providing robust parameter estimation while mitigating overfitting. This combined modeling framework ensures a balance between physical interpretability, flexibility, and predictive performance across different soil types [46,47,48].
To ensure reproducibility, each model was implemented using specific functions. CubicSpline (SciPy) was used to interpolate nonlinear behavior by generating piecewise smooth polynomials. The RBF (Radial Basis Function) module was employed to capture localized nonlinearities in the data, particularly suited to irregular moisture–resistivity distributions. Parametric models, such as power law, logarithmic, and polynomial equations, were fitted using SciPy’s curve_fit function, which is based on a least-squares optimization routine [47,48].
For regularization-based approaches, LASSO (Least Absolute Shrinkage and Selection Operator) and RIDGE regression from the scikit-learn library were employed. These methods apply penalty terms to the regression coefficients: LASSO promotes sparsity by reducing some coefficients to zero, and RIDGE reduces variance by penalizing large coefficients. Both methods aim to improve model generalization and reduce overfitting. Nonparametric smoothing was achieved using LOWESS (Locally Weighted Scatterplot Smoothing), implemented with the Lowess function, which generates a local regression around each observation to capture subtle nonlinear trends in the experimental data [49,50].
The LASSO, RIDGE, and LOESS models were included as flexible statistical approaches to capture complex nonlinear patterns in the moisture–resistivity data. Although these models do not have a direct physical basis related to soil physics, they provide a means for performance comparison with empirically derived models. This approach facilitates the evaluation of both predictive accuracy and applicability, while acknowledging that purely statistical models may lack direct interpretability in terms of underlying soil processes.
All models were evaluated using standard statistical performance metrics: Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and the coefficient of determination calculated using the mean_squared_error and r2_score functions from scikit-learn. Data management was performed using Pandas to structure the soil and moisture datasets, while NumPy supported numerical operations. Visualizations were generated using Matplotlib and Seaborn to compare fitted curves with experimental values.
The selection of the optimal model for each soil type was based on the coefficient of determination (), root mean square error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and cross-validation was also performed to avoid overfitting.
3. Results
Based on the tests described in the methodology for the three selected soil types: sandy, silty, and clayey, the results of the granulometric analysis and the variation in electrical resistivity as a function of gravimetric moisture were obtained, and predictive models specific to each soil type were developed.
The experimental data revealed the differential electrical behavior of each soil under controlled moisture conditions, which was essential for establishing empirical correlations. Each set of results is organized into separate subsections, including granulometric curves, resistivity versus moisture graphs and tables, and models.
Figure 3 shows the measurement of resistivity in soil using the tellurometer and the soil box.

Figure 3.
Four-pin soil box configuration.
3.1. Results of Particle Size Analysis
Granulometric analysis enabled the classification of the soils according to particle size distribution, in accordance with the Unified Soil Classification System (USCS). For each sample, the percentages of gravel, sand, silt, and clay were determined, along with the corresponding plasticity indices when applicable ASTM D2487-17 [58]. The results obtained for each soil type are detailed below.
3.1.1. Sandy Soil
From the granulometric analysis of the sandy soil, it was determined that the percentage passing through the #200 sieve (0.075 mm) was 6.93% (<50.00%), classifying it as granular soil according to the USCS. The percentage of fines (<0.075 mm) was 6.93%, with 0.044 mm representing 6.93% and 0.00% in particles <0.002 mm. The percentage of gravel (>4.75 mm) was 8.21%, resulting in a total sand percentage of 91.79% − 6.93% = 84.86%. This gives a USCS classification of SP (Poorly graded clean sand) due to the uniform distribution and low content of fines.
3.1.2. Clay Soil
The results of the granulometric analysis of the clayey soil show that the percentage of particles passing through the #200 sieve (0.075 mm) was 51.01% (>50.00%), classifying it as fine soil according to the USCS. The percentage of fines (<0.075 mm) was 18.13%, with 0.044 mm accounting for 18.13% and 0.00% in particles <0.002 mm, resulting in a total of 33.23%. The percentage of clay (<0.002 mm) was 15.10%. From the plasticity test (Atterberg), a plasticity index of 8.00 (>7.00) was obtained, resulting in a CL classification (Low plasticity clay).
3.1.3. Silty Soil
The results of the granulometric analysis of the silty soil show that the percentage of material passing through the #200 sieve (0.075 mm) was 50.35% (just above 50.00%), classifying it as fine soil according to the USCS. The percentage of fines (<0.075 mm) was 30.03%, with 0.044 mm accounting for 30.03% and 5.55% in particles <0.002 mm, resulting in a total of 35.58%. The percentage of clay (<0.002 mm) was 5.55% (<15.00%, non-dominant). The plasticity test (Atterberg) yielded a plasticity index of 3.80 (<4.00), resulting in an ML classification (non-plastic inorganic silt).
Table 1 summarizes the measured properties for all soil types, providing the foundation for the development of predictive models.

Table 1.
Properties and composition of sandy, clayey, and silty soils.
3.1.4. Granulometric Curves
Figure 4 presents the granulometric curves for the three types of soil analyzed (sandy, silty and clayey), showing the accumulated percentage passing (% passing) as a function of particle size (mm).
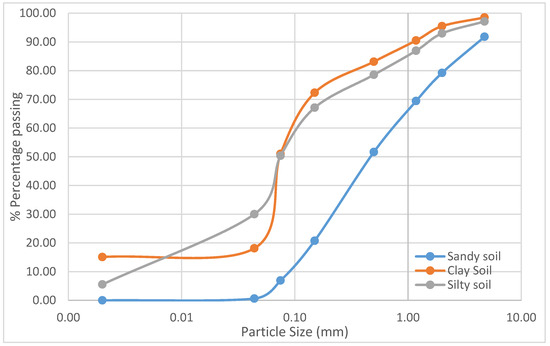
Figure 4.
Granulometric curves of soils.
3.2. Measurement of Moisture and Resistivity in Soils
Based on preliminary standard Proctor tests (ASTM D698-12), target dry densities were defined to ensure a reproducible soil structure during resistivity measurements. The densities adopted were sandy soil , silty soil , and clayey soil . These values correspond approximately to 98%, 96%, and 95% of the maximum dry densities obtained from the compaction curves (MDD ≈ 1.89, 1.71, and 1.63 for sand, silt, and clay, respectively) and were maintained within ±1% during specimen preparation. The selected ranges are representative of soils compacted under ASTM D698-12 and ensure that the observed resistivity response depends primarily on moisture content and not on compaction-induced variations in porosity.
Experimental results were obtained from gravimetric moisture content and resistivity measurements for the three soil types analyzed (sandy, silty, and clayey), evaluated under controlled laboratory conditions at an ambient temperature of 25 °C. The measurements were made using the Wenner method to determine the apparent resistivity () and electrical resistance () as a function of moisture content (0–100%).
Table 2, Table 3 and Table 4 shows the values obtained from the measurements carried out for each percentage of humidity and for each electrical resistivity.
3.2.1. Sandy Soil
The results obtained from the measurement of the percentage of humidity with respect to the electrical resistivity of sandy soil (SP) are shown in Table 2. The initial dry weight of the sample was 297.30 g, and in the dry condition (0% humidity), the resistivity was extremely high (138,404 ). The critical range (5–20% humidity) shows a drastic reduction in resistivity (from 555.04 to 77.40 ), indicating that small amounts of water significantly improve conductivity. When the soil becomes saturated (>30% humidity), the resistivity stabilizes around 26.8 , indicating a practical limit of improvement. Regarding its electrical behavior, the electrical resistance follows a similar trend, with values ranging from 13.59 (dry) to approximately 2.63 (saturated). The optimal zone occurred between 25% and 30% humidity, where the resistivity fell below 40 , complying with international regulations such as IEEE Std 80 [59]. In terms of granulometry, the low moisture retention of sandy soil (SP) explains the need for larger volumes of water to achieve low resistivities. The stabilization at values around 27 suggests that, once saturated, water fills the pores between particles, maximizing ionic conduction.
Sandy soil is highly dependent on moisture to achieve adequate resistivities (<100 ). Its use in electrical safety systems must be supported by maintenance strategies (such as periodic wetting or additives) to ensure electrical stability.

Table 2.
Humidity, resistivity and resistance in sandy soil.
Table 2.
Humidity, resistivity and resistance in sandy soil.
| Sandy Soil | ||||
|---|---|---|---|---|
| Humidity (%) | Added Water (mL) | Total Weight (gr) | Resistivity (Ωm) | Electrical Resistance (Ω) |
| 0 | 0.00 | 297.30 | 138,404.59 | 13,590,000.00 |
| 5 | 14.87 | 312.17 | 555.04 | 54,500.00 |
| 10 | 29.73 | 327.03 | 319.79 | 31,400.00 |
| 15 | 44.60 | 341.90 | 225.07 | 22,100.00 |
| 20 | 59.46 | 356.76 | 77.40 | 7600.00 |
| 25 | 74.33 | 371.63 | 39.52 | 3880.00 |
| 30 | 89.19 | 386.49 | 32.28 | 3170.00 |
| 35 | 104.06 | 401.36 | 30.55 | 3000.00 |
| 40 | 118.92 | 416.22 | 28.62 | 2810.00 |
| 45 | 133.79 | 431.09 | 27.90 | 2740.00 |
| 50 | 148.65 | 445.95 | 27.70 | 2720.00 |
| 55 | 163.52 | 460.82 | 26.89 | 2640.00 |
| 60 | 178.38 | 475.68 | 26.84 | 2635.00 |
| 65 | 193.25 | 490.55 | 26.79 | 2631.00 |
| 70 | 208.11 | 505.41 | 26.76 | 2628.00 |
| 75 | 222.98 | 520.28 | 26.73 | 2625.00 |
| 80 | 237.84 | 535.14 | 26.69 | 2621.00 |
| 85 | 252.71 | 550.01 | 26.67 | 2619.00 |
| 90 | 267.57 | 564.87 | 26.67 | 2619.00 |
| 95 | 282.44 | 579.74 | 26.64 | 2616.00 |
| 100 | 297.30 | 594.60 | 26.64 | 2616.00 |
3.2.2. Clay Soil
The clayey soil (CL) was evaluated under the same conditions as the sandy soil (25 °C, Wenner method) using a Soil Box with identical dimensions (Area: 12.80 , Pin spacing: 12.80 ). The results are shown in Table 3. In the dry condition, at 0% moisture content, the resistivity is extremely high (200,732 ), typical of compacted clays without water. Measurements were repeated under controlled laboratory conditions, yielding consistent results. Although no independent method was used for confirmation, these values are considered reproducible within the context of the experimental setup.
At the critical point (5–30% moisture content), the exponential reduction in resistivity is from 3340 to 30.15 , demonstrating the high sensitivity of clays to moisture. At the saturation stage (>35% moisture content), the resistivity reaches minimum values (≈6.3 ), thanks to the activation of ions in the clay. In terms of electrical behavior, the electrical resistance increases from 19.71 (dry) to ≈618 (saturated), with an optimal zone in the range of 30% to 35% humidity, where the resistivity falls below 30 . Regarding the relationship with granulometry, the 15.10% clay (<0.002 mm) and its high specific surface area explain the capacity to retain water and maintain conductivity even with low moisture volumes. The stabilization at ≈6.3 reflects the formation of a continuous ionic conductive network within the clay matrix.
Clay soil (CL) offers better electrical performance in humid conditions compared to sandy soil but requires maintenance strategies to prevent degradation in dry environments. Its use is recommended in projects where stable humidity is guaranteed or when combined with conductive additives.

Table 3.
Humidity, resistivity and resistance in clayey soil.
Table 3.
Humidity, resistivity and resistance in clayey soil.
| Clay Soil | ||||
|---|---|---|---|---|
| Humidity (%) | Added Water (mL) | Total Weight (gr) | Resistivity (Ωm) | Electrical Resistance (Ω) |
| 0 | 0 | 199.60 | 200,732.48 | 19,710,000.00 |
| 5 | 9.98 | 209.58 | 3340.45 | 328,000.00 |
| 10 | 19.96 | 219.56 | 665.03 | 65,300.00 |
| 15 | 29.94 | 229.54 | 211.83 | 20,800.00 |
| 20 | 39.92 | 239.52 | 147.47 | 14,480.00 |
| 25 | 49.90 | 249.50 | 102.66 | 10,080.00 |
| 30 | 59.88 | 259.48 | 30.15 | 2960.00 |
| 35 | 69.86 | 269.46 | 11.01 | 1081.00 |
| 40 | 79.84 | 279.44 | 8.23 | 808.00 |
| 45 | 89.82 | 289.42 | 8.12 | 797.00 |
| 50 | 99.80 | 299.40 | 8.02 | 787.00 |
| 55 | 109.78 | 309.38 | 7.69 | 755.00 |
| 60 | 119.76 | 319.36 | 7.04 | 691.00 |
| 65 | 129.74 | 329.34 | 6.98 | 685.00 |
| 70 | 139.72 | 339.32 | 6.90 | 678.00 |
| 75 | 149.70 | 349.30 | 6.48 | 636.00 |
| 80 | 159.68 | 359.28 | 6.39 | 627.00 |
| 85 | 169.66 | 369.26 | 6.32 | 621.00 |
| 90 | 179.64 | 379.24 | 6.29 | 618.00 |
| 95 | 189.62 | 389.22 | 6.29 | 618.00 |
| 100 | 199.60 | 399.20 | 6.29 | 618.00 |
3.2.3. Silty Soil
The silty soil (ML) was evaluated under the same conditions as the other soils. Table 4 shows the results obtained. In the dry condition, the soil at 0% moisture content had an initial resistivity of 9074 , which is significantly lower than that of dry sandy and clayey soils due to the moderate content of fines (35.58%). In the critical range from 5% to 30% moisture content, the progressive reduction in resistivity (from 734 to 14.05 ) showed a more stable transition than in clays. At saturation (>35% moisture content), the minimum resistivity values (≈6.0 ) are comparable to those of clayey soil but reached at lower moisture content. Regarding its electrical behavior, the electrical resistance decreased from 891 (dry) to ≈583 (saturated). The optimal zone ranges from 25% to 30% moisture, where resistivity falls below 50 , complying with regulations without the need for complete saturation. Regarding the relationship with particle size distribution, the 30.03% silt (0.075–0.002 mm) provides a balance between moisture retention and permeability, avoiding the extremes of sand (rapid drainage) and clay (low permeability). The minimum resistivity (5.94 ) reflects a homogeneous distribution of water in the soil matrix.
Silt soil (ML) offers the optimal balance between ease of installation, electrical stability and adaptability to variable environmental conditions.

Table 4.
Humidity, resistivity and resistance in silty soil.
Table 4.
Humidity, resistivity and resistance in silty soil.
| Silty Soil | ||||
|---|---|---|---|---|
| Humidity (%) | Added Water (mL) | Total Weight (gr) | Resistivity (Ωm) | Electrical Resistance (Ω) |
| 0 | 0 | 177.20 | 9074.21 | 891,000.00 |
| 5 | 8.86 | 186.06 | 734.29 | 72,100.00 |
| 10 | 17.72 | 194.92 | 359.51 | 35,300.00 |
| 15 | 26.58 | 203.78 | 266.83 | 26,200.00 |
| 20 | 35.44 | 212.64 | 134.23 | 13,180.00 |
| 25 | 44.30 | 221.50 | 46.03 | 4520.00 |
| 30 | 53.16 | 230.36 | 14.05 | 1380.00 |
| 35 | 62.02 | 239.22 | 13.80 | 1355.00 |
| 40 | 70.88 | 248.08 | 12.45 | 1222.00 |
| 45 | 79.74 | 256.94 | 12.07 | 1185.00 |
| 50 | 88.60 | 265.80 | 8.19 | 804.00 |
| 55 | 97.46 | 274.66 | 7.93 | 779.00 |
| 60 | 106.32 | 283.52 | 6.99 | 686.00 |
| 65 | 115.18 | 292.38 | 6.59 | 647.00 |
| 70 | 124.04 | 301.24 | 6.57 | 645.00 |
| 75 | 132.90 | 310.10 | 6.45 | 633.00 |
| 80 | 141.76 | 318.96 | 6.45 | 633.00 |
| 85 | 150.62 | 327.82 | 6.22 | 611.00 |
| 90 | 159.48 | 336.68 | 5.99 | 588.00 |
| 95 | 168.34 | 345.54 | 5.96 | 585.00 |
| 100 | 177.20 | 354.40 | 5.94 | 583.00 |
Considering the above results, Figure 5 compares the resistivity (Ω·m) of the three soil types as a function of moisture content, highlighting the patterns mentioned above.
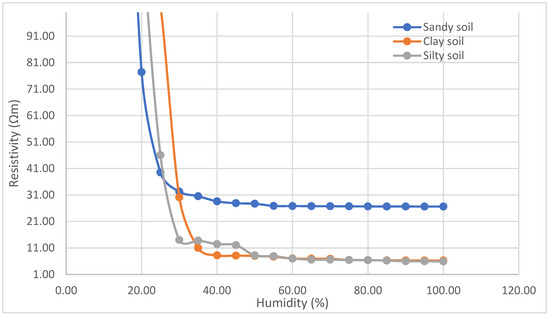
Figure 5.
Resistivity vs. Humidity in Soils.
In this study, distilled water was used both for the hydrometer procedure to determine the fine fraction of the soils and to adjust soil moisture during electrical resistivity measurements. The use of distilled water preserved the intrinsic ionic composition of the soil, avoiding external modifications that could affect resistivity readings. However, it should be noted that this method may not fully represent field conditions, where the ionic content of pore water varies, potentially influencing the measured resistivity.
3.3. Empirical Models for Soils
To predict the electrical resistivity behavior as a function of gravimetric moisture content, specific empirical models were developed for each of the three soil types analyzed: sandy (SP), clayey (CL), and silty (ML). The Python code used to build and adjust these models followed the methodology outlined in Section 2.5 of the Materials and Methods, corresponding to each soil type, respectively. The experimental data obtained in the laboratory were processed using advanced statistical and computational tools, including specialized Python libraries and complementary analysis tools in Microsoft Excel.
Different modeling approaches were applied for each soil type: logarithmic functions, polynomial models of varying degrees, power law fitting, cubic spline interpolation, radial basis functions (RBF), penalized regressions (LASSO and RIDGE), segmented models (breakpoints), and nonparametric smoothing using LOESS. The selection of the optimal model was based on goodness-of-fit criteria (coefficient of determination ), minimization of the root mean square error (RMSE), and cross-validation to avoid overfitting.
Each section presents the analysis and fitted models for each soil type. Scatter plots, fitted curves, derived equations, and evaluation metrics are included.
3.3.1. Sandy Soil
The experimental values and fitted models for the sandy soil are presented in Table 5. This table shows the measured electrical resistivity as a function of gravimetric moisture content, from 5% to 100% (excluding 0% due to its extreme value).

Table 5.
Comparison of numerical results by model for humidity levels from 5% to 100% in sandy soil.
Overall, the Spline-Log and RBF models accurately reproduce the actual values, matching each point exactly, reflecting a near-perfect fit. These models are particularly effective at capturing nonlinear behavior and the abrupt resistivity transition between 5% and 25% humidity, a critical zone where there is a sharp drop in resistivity (from 555.04 to 39.52 ).
The LASSO model tends to slightly underestimate values between 5% and 20% moisture content and overfit in intermediate ranges (30% to 60%), showing fluctuations that do not correspond to the experimentally observed pattern. On the other hand, the RIDGE model presents a good overall fit; however, it shows some significant deviations, especially between 15% and 25%, where it deviates notably from the actual values, with deviations of up to 100 . This suggests a low capacity to capture the nonlinear behavior of sandy soil under these conditions.
The Power Law model shows a good fit in the intermediate humidity ranges (25–60%), but overestimates resistivity under dry conditions and underestimates it under saturated conditions, with a progressive bias. Finally, the segmented equation shows good overall performance with small deviations, particularly in the critical zone between 15% and 20%, where it most faithfully replicates the inflection points in the humidity–resistivity curve.
Overall, the Spline-Log and RBF models are the most accurate and stable across the entire humidity range, making them suitable for representing the behavior of sandy soil, which is characterized by an exponential decrease in resistivity with increasing humidity until stabilizing at values close to 26.6 under saturation conditions (≥65%). On the other hand, the RIDGE, potential, and segmented models provide values for basic approximation.
Figure 6 illustrates the relationship between electrical resistivity and gravimetric moisture content for sandy soils, along with the fitted mathematical models. The black dotted curve represents the experimental values obtained in the laboratory. The fitting curves correspond to the following models: Logarithmic Spline, RBF, LASSO, RIDGE, and Power Law.
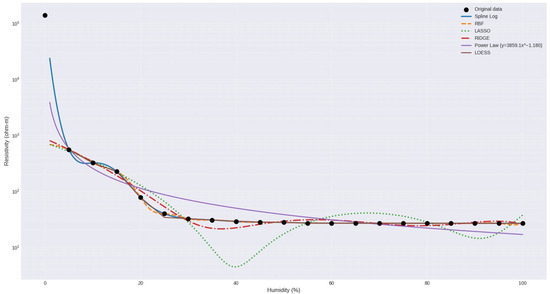
Figure 6.
Illustrates the relationship between electrical resistivity and gravimetric moisture for sandy soil along with the fitted mathematical models.
Models that present explicit equations include the Power Law model and the segmented equation model. These formulations allow the description of soil electrical resistivity as a direct function of gravimetric moisture content. The corresponding expressions are as follows:
Power Law Model:
Segmented Equation:
where and are indicator functions that equal 1 if the condition is met and 0 otherwise.
Table 6 shows the comparison of the fit metrics for each model, revealing the significant differences in accuracy and predictive capacity.

Table 6.
Comparison of metrics by model in sandy soil.
In the case of sandy soils, the Spline-Log and RBF models proved to be the most accurate, achieving an = 1.00 and zero error (RMSE = 0.00, MAE = 0.00, MA-PE = 0.00%), indicating a perfect fit to the experimental data. However, it should be noted that these models involve a higher degree of computational complexity, which may limit their applicability in scenarios where rapid or manual estimation is required.
In contrast, models with explicit expressions, such as Power Law and Segmented Equation showed inferior fit performance, = 0.95 and 0.91, respectively, and MAPE of 39.60% and 6.14%, implying a larger margin of relative error particularly for the Power Law model. Nevertheless, these formulations are valuable for their ease of use in manual calculations or quick applications.
Figure 7 presents the absolute error behavior of each model at different levels of gravimetric moisture content allowing us to identify its local accuracy. As can be seen, the Spline-Log and RBF models perform perfectly with an absolute error of zero at all points evaluated, confirming their excellent fit as previously noted.
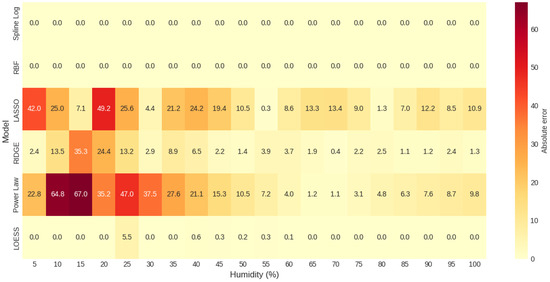
Figure 7.
Heat map of absolute error by model and gravimetric moisture level for sandy soil (SP).
The LOESS model also maintains minimal absolute errors (<1 ) at almost all levels with slight deviations only between 25% and 60% humidity, demonstrating a very robust adjustment capacity, although slightly lower than the two previous models.
In contrast, the Power Law model exhibits high errors especially between 10% and 30% moisture content with a maximum of 67.0 at 15%, representing a significant overestimation in low-moisture soil conditions. These errors decrease as moisture content increases but remain considerable.
The LASSO model exhibits erratic behavior with high errors ranging from 5% to 25% peaking at 49.2 at 20% humidity. Above 35% humidity the error tends to stabilize below 15 , although certain fluctuations persist, reducing its reliability.
For its part, the RIDGE model exhibits an intermediate pattern: errors lower than those of LASSO and Power Law, but still higher than LOESS with a maximum value of 35.3 at 15% humidity.
It is important to note that the predictive model for sandy soil is strictly valid within the experimentally determined gravimetric moisture range (5–100%). Within this interval, the model accurately reproduces the resistivity–moisture relationship, while extrapolation beyond these limits (especially under conditions of extreme dryness or saturation) can introduce uncertainty due to the nonlinear behavior of the soil. Therefore, predictions near or outside these limits should be interpreted with caution.
3.3.2. Clay Soil
The numerical results obtained for the clayey soil in a moisture content range between 5% and 100% are shown in Table 7. These results allow us to evaluate the predictive capacity of the different models used in the study. As can be seen in Table 7, the Logarithmic Spline and RBF models accurately reproduce the actual values at all moisture content levels. However, this accuracy may suggest overfitting or excessive dependence on the training set and should therefore be interpreted with caution when extrapolating results.

Table 7.
Comparison of numerical results by model for humidity levels from 5% to 100% in clay soil.
In contrast, the LASSO model shows significant deviation from actual values, especially at low and medium humidity levels, where even negative values are generated, which is physically meaningless in this context. This behavior indicates that the LASSO model has significant limitations in capturing the nonlinear behavior of resistivity with humidity, particularly in its critical transition zone.
The RIDGE model performs better than LASSO, although it also presents significant errors. While it more closely follows the decreasing trend in resistivity with increasing humidity, it experiences abrupt fluctuations with negative values starting at 20% humidity (e.g., −168.34 at 25%) and unexpectedly high values in the saturation zone (e.g., 151.77 at 45%).
The Power Law model offers predictions reasonably close to actual values in the initial humidity ranges (5–30%), but its accuracy decreases as the saturation zone increases. Above 30% humidity, the model tends to slightly overestimate values, although it always maintains physically valid results. This reinforces its usefulness as a generalizable explicit model, although it is not as accurate as other nonparametric approaches.
Finally, the segmented equation model exhibits adequate performance in both moisture content zones (hydration zone and saturation zone). Although it does not match the accuracy of Spline or RBF, it maintains contained errors and avoids extreme or inconsistent values. For example, it predicts 243.60 at 15% humidity (compared to a real 211.83 ) and 5.24 at 100% humidity (compared to a real 6.29 ), indicating a satisfactory fit within an explicit functional framework.
Taken together, these results reinforce that while nonparametric models offer superior accuracy for comprehensive datasets, explicit models, such as the Segmented Equation or Power Law, are valuable for their interpretability and general applicability.
Figure 8 shows the curve relating electrical resistivity and gravimetric moisture content for the clayey soil, along with the fitted mathematical models. The curve with black dots represents the experimental values obtained in the laboratory. The fitted curves correspond to the following models: Logarithmic Spline, RBF, LASSO, RIDGE, and Power Law.
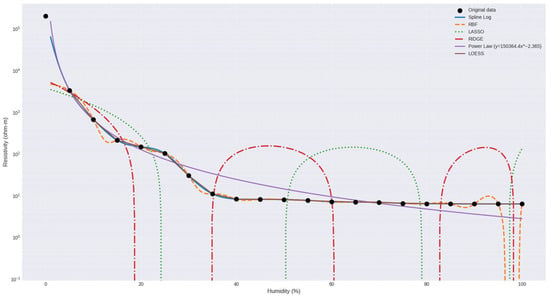
Figure 8.
Illustrates the relationship between electrical resistivity and gravimetric moisture content for clayey soil, along with the fitted mathematical models.
The models that present explicit equations are the power-law model and the segmented equation model. These formulations allow the electrical resistivity of the soil to be described as a direct function of gravimetric moisture content. The corresponding expressions are as follows:
Power Law Model:
According to the expression defined in Equation (3), the segmented equation is:
where and are indicator functions that equal 1 if the condition is met and 0 otherwise.
Table 8 shows the comparison of the fit metrics for each model, highlighting the significant differences in accuracy and predictive capacity.

Table 8.
Comparison of metrics by model in clay soil.
In the case of clayey soil, the fitting models show considerable variability in their ability to reproduce the actual electrical resistivity values as a function of gravimetric moisture content. The Spline-Log, RBF, and LOESS models show a perfect fit with a coefficient of determination () of 1.00 and practically zero errors (RMSE = 0.00 and MAE ≈ 0.00 for Spline-Log and RBF; RMSE = 0.07 and MAE = 0.04 for LOESS), demonstrating high fidelity to the experimental data. However, their use is limited to computational contexts due to the lack of explicit equations.
In contrast, models with explicit formulations, such as the Power Law model and the segmented equation model, show remarkably acceptable performance. The Power Law model stands out with an of 0.99, an RMSE of 14.49, and a MAPE of 52.7%, positioning it as a valuable tool for analytical calculations with low computational dependency. The segmented equation model, meanwhile, achieves an of 0.93 with a MAPE of 15.1%, improving in accuracy relative to the Power Law model, albeit with a slightly higher RMSE.
The LASSO and RIDGE models exhibit poorer fit, especially LASSO, with a MAPE of over 1000%, which limits their practical usefulness in this type of soil. This behavior is also reflected in their predictions, where at several points they present negative values or values far from the expected magnitude.
In summary, for clayey soils, models based on smoothing techniques such as Spline-Log, RBF, and LOESS offer the best predictive capacity, while the Power Law model and the segmented equation remain useful alternatives in contexts where an explicit mathematical expression is required.
Figure 9 presents a heat map depicting the absolute error as a function of moisture level for each of the models evaluated in the clayey soil. The Log-Spline and RBF models show zero absolute error at all moisture levels, reflecting an adequate fit. The LOESS model also exhibits negligible errors (≤0.2 ) across the entire moisture range, reinforcing its high accuracy, as reported in the global metrics.
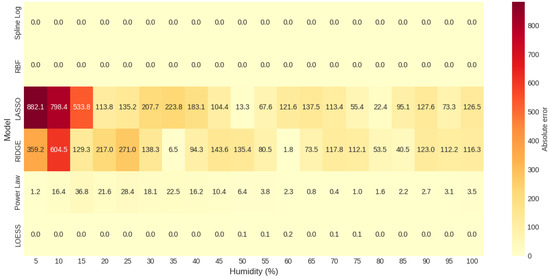
Figure 9.
Heat map of absolute error by model and gravimetric moisture level for clayey soil (CL).
In contrast, the LASSO and RIDGE models exhibit substantially higher errors across the entire humidity range, with maximum values of 882.1 and 604.5 , respectively, suggesting heightened sensitivity to low humidity conditions. As moisture content increases, the error decreases markedly in both models, although significant variability remains.
The Power Law model, while exhibiting larger errors than pure nonlinear models, offers acceptable performance, with errors below 40 at all humidity levels. The LOESS, Spline-Log, and RBF models offer superior and stable performance, while LASSO and RIDGE are less reliable.
It is important to note that the predictive model for clay soils is strictly valid within the experimentally determined gravimetric moisture range (5–100%). Within this interval, the model accurately reproduces the resistivity–moisture relationship, while extrapolation beyond these limits (especially under extremely dry or saturated conditions) can introduce uncertainty due to the nonlinear behavior of the soil. Therefore, predictions near or outside these limits should be interpreted with caution.
3.3.3. Silty Soil
The results for silty soils shown in Table 9 indicate that most of the analyzed models exhibit good predictive performance in the hydration zone (520) and in the saturation zone (moisture above 25). However, some models show considerable deviations from the actual values.

Table 9.
Comparison of numerical results by model for humidity levels ranging from 5% to 100% in silty soil.
The Spline-Log and RBF models again stand out for their accuracy, faithfully replicating actual values across the entire humidity range evaluated. This perfect match is due to the fact that both models directly interpolate the data and do not rely on an explicit equation, making them ideal benchmarks for comparison, although their applicability is limited in the absence of computational tools.
The RIDGE model maintains a good general approximation, with values close to the real ones, especially at humidity levels below 20%. However, it tends to overestimate resistivity at humidity levels above 30%, which is reflected in increasingly divergent predictions towards 100% humidity.
The Power Law model, while offering an explicit and easy-to-apply structure, exhibits significant overestimation at all humidity levels. Despite this deviation, its behavior is continuous and decreasing, maintaining its relative usefulness calculations with wide safety margins.
In contrast, the LASSO model presents inconsistent predictions with negative values in the range between 35% and 95% humidity, which shows a loss of predictive capacity and disqualifies it for application in this type of soil without reformulation.
For its part, the segmented equation maintains a more balanced performance, with low errors in the hydration zone and an acceptable fit in the saturation zone. Although it does not perfectly replicate real values, its predictions remain within physically reasonable ranges, and its explicit structure allows its use as an estimation tool.
Overall, the Spline-Log and RBF models stand out for their accuracy, while among the explicit models, the segmented equation offers the best relationship between accuracy and operational applicability in silty soils, followed by the Power Law model.
Figure 10 shows the relationship between electrical resistivity and gravimetric moisture content for the silty soil, along with the fitted mathematical models. The curve with black dots represents the experimental values obtained in the laboratory. The fitting curves correspond to the following models: Logarithmic Spline, RBF, LASSO, RIDGE, and Power Law.
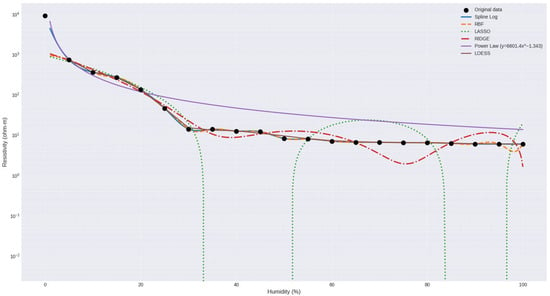
Figure 10.
Illustrates the relationship between electrical resistivity and gravimetric moisture content for silty soil along with the fitted mathematical models.
Models that present explicit equations include the power-law model and the segmented equation model. These formulations describe the electrical resistivity of the soil as a direct function of gravimetric moisture content. The corresponding expressions are as follows:
Power Law Model:
According to the expression defined in Equation (3), the segmented equation is:
where and are indicator functions that equal 1 if the condition is met and 0 otherwise.
Table 10 shows the comparison of the fit metrics for each model, highlighting the significant differences in accuracy and predictive capacity.

Table 10.
Comparison of metrics by model in silty soil.
The analysis of the metrics for the models applied to the silty soil confirms the findings observed in the numerical results. The Spline-Log and RBF models again achieved the best metrics (RMSE, MAE, and MAPE of 0, and equal to 1), indicating an exact fit to the input data. However, as mentioned above, their use may be limited by the need for specialized software when applied outside the modeling environment.
The LOESS model is among the methods that do not present explicit equations, showing minimal errors (RMSE = 0.48, MAE = 0.26, and MAPE = 2.60%) and an adequate coefficient of determination.
On the other hand, among the models with explicit expressions, the segmented equation offers the most balanced performance, with an MAPE of 13.16% and an of 0.89. Although its errors are higher compared to LOESS, it maintains reasonable accuracy.
The RIDGE model, with a MAPE of 36.90%, also shows a good fit ( = 0.99), although its absolute errors (RMSE = 17.48, MAE = 9.86) are more pronounced than in clayey soils. Even so, it could be considered an alternative when a balance between accuracy and simplicity is required.
The LASSO model, despite having a high (0.97), records a very high MAPE (124.50%). This indicates that, although it generally follows the data trend, its individual predictions are highly dispersed and, in some cases, unreliable, making it the model with the poorest performance, as it even predicts negative values. The Power Law model, although it shows a good coefficient of determination (0.96), has a MAPE exceeding 187%, revealing a substantial overestimation relative to the actual values.
The segmented equation offers relatively acceptable performance given its explicit nature and its potential use in calculations without requiring advanced modeling tools. With an RMSE of 19.63, an MAE of 12.32, and an MAPE of 13.16%, this model demonstrates acceptable accuracy, particularly in the high-humidity range, where predictions are remarkably close to actual values. The coefficient of determination ( = 0.89), although lower than those obtained with more complex models, still indicates a strong correlation between the independent variable (gravimetric moisture) and the dependent variable (electrical resistivity).
Overall, for silty soils, the Spline-Log, RBF, and LOESS models offer high accuracy, while the segmented equation and RIDGE models stand out as the most viable options when seeking a balance between applicability and acceptable error margins. However, the LASSO and Power Law models have error percentages that are too high for calculations requiring high precision.
Figure 11 illustrates the absolute error behavior for each model as a function of moisture content in silty soil. As in the other cases, the Log-Spline and RBF models perform exceptionally well, suggesting a complete fit to the training data. The LOESS model exhibits minimal errors—less than 1.5 across the entire analyzed interval—consolidating its accuracy and stability.
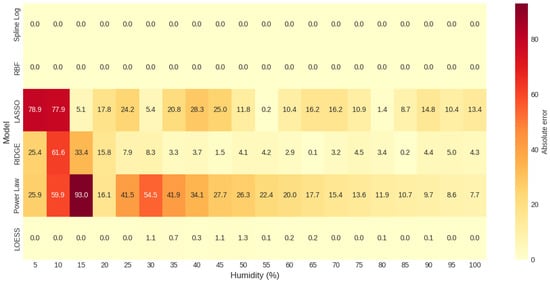
Figure 11.
Heat map of absolute error by model and gravimetric moisture level for silty soil (ML).
On the other hand, the Power Law model shows the largest errors at low humidity levels (10% to 30%), with a progressive decrease as humidity increases, eventually reaching near stabilization. The LASSO model displays an erratic pattern, with high errors (up to 78.9 ) at low humidity levels and intermediate error peaks, reflecting its sensitivity to the nonlinearity of the humidity–resistivity relationship.
In contrast, the RIDGE model exhibits more consistent behavior, with errors progressively decreasing to values below 5 at higher moisture levels. This analysis further demonstrates that models based on nonparametric and flexible techniques, such as LOESS, RBF, and Log-Spline, provide greater reliability for predicting electrical resistivity in silty soils, particularly under variable moisture conditions.
It is important to note that the predictive model for silty soils is strictly valid within the experimentally determined gravimetric moisture range (5–100%). Within this interval, the model accurately reproduces the resistivity–moisture relationship, while extrapolation beyond these limits (especially under extremely dry or saturated conditions) can introduce uncertainty due to the nonlinear behavior of the soil. Therefore, predictions near or outside these limits should be interpreted with caution.
The segmented equations were designed to consider two distinct humidity regimes observed in the experimental data: the hydration zone (low humidity) and the saturation zone (higher humidity). In the hydration zone, resistivity decreases sharply as water progressively fills the pore spaces, enhancing ionic mobility and electrical conduction. In contrast, the saturation zone represents a condition in which most conductive pathways are already established, resulting in a slower resistivity decline [13,14,15]. The transition point, identified at approximately 25% for sandy and silty soils and 30% for clayey soils, corresponds to the onset of continuous water films and percolation paths within the soil structure.
Logarithmic terms were applied in the hydration zone to capture the rapid decrease in resistivity with small increases in moisture, while power-law terms were employed in the saturation zone to represent the slower decrease. Breakpoints were determined from inflections in the measured resistivity curves, indicating transitions in the dominant driving mechanisms [17,28,34]. A limitation of the segmented equations is that, while empirically fitted and physically based, the choice of functional forms and breakpoints is specific to the soils studied. Extrapolation to other soil types or conditions should be undertaken with caution, and further validation is recommended.
In the segmented equations, moisture content is expressed directly as percentage units in logarithmic and power-law terms for convenience. Users should note that the models are validated only within the 5–100% moisture range, and numerical instability may arise if values outside this range are applied. Future work could explore normalization or dimensionless scaling to enhance numerical robustness.
Although LASSO and RIDGE regression models provide stability against overfitting and multicollinearity, their underlying linear structure limits their ability to capture the strong nonlinear dependencies between resistivity and moisture content. In soils, particularly clayey and silty types, electrical conduction mechanisms change nonlinearly with pore water distribution, ion mobility, and degree of saturation. The regularization terms (L1 for LASSO and L2 for RIDGE) enforce smooth and monotonic trends, which restricts the models’ responsiveness to abrupt resistivity variations across moisture regimes. Consequently, these models tend to underfit at extreme moisture levels and may yield physically unrealistic predictions. These anomalies result from overfitting in these nonparametric statistical models [47,49]. Consequently, caution should be exercised when interpreting these predictions. Future work could include constraints or physics-informed modeling to prevent such artifacts.
While the empirical equations derived from the explicit models in this study are strictly valid for the specific soil samples analyzed (classified as SP, CL, and ML according to the U.S. Soil Classification System), these models offer a computationally simple method for situations where advanced software and extensive databases are unavailable. Although site-specific calibration is recommended, these models could be used as reference curves to guide initial design considerations once validated through field studies.
It is important to note that although the Spline and RBF models yielded near-zero errors within the experimental dataset, their accuracy is a direct result of their interpolative nature. Consequently, they lack predictive capacity outside the tested range and should not be extrapolated to different soil conditions or moisture regimes without external validation. These limitations highlight the importance of developing and testing explicit models that can retain predictive reliability under variable field conditions.
Another limitation of this study is that, due to the use of a single sample per soil type, it was not possible to separate the data into independent training and test sets. While cross-validation techniques were applied to mitigate overfitting, the reported performance metrics (, RMSE, MAE) may be slightly optimistic. Therefore, the predictive models should be interpreted primarily within the context of the experimental data.
Another limitation is that MAPE can generate exaggerated errors at high humidity levels due to resistivity values close to zero, which may distort the model’s accuracy in this range. Future studies should consider alternative or complementary error metrics to avoid bias in performance assessment.
Although the Power Law model showed a high coefficient of determination, its error metrics revealed strong deviations in certain soil types, particularly silty soils. This discrepancy underscores that a high R2 alone is insufficient to establish predictive reliability. The segmented equation was prioritized because it offered a more consistent balance between accuracy, error distribution, and physical plausibility across soil types.
Another limitation of this study is that only one resistivity measurement was performed for each increment in gravimetric moisture content. While this procedure allowed for the characterization of the general relationship between soil moisture and resistivity, it limited the assessment of measurement variability and reproducibility. Consequently, it was not possible to report error bars or variability metrics. Therefore, future studies should incorporate replicate measurements to assess repeatability and improve the robustness of the data.
One limitation is that, although repeated measurements were performed to confirm the extremely high resistivity values observed in the 0% moisture samples, these results have not been validated using an independent measurement method. Future work should employ alternative instruments or field verification to further ensure the physical accuracy of these measurements.
Another limitation of this study is that the 0% gravimetric moisture measurement was excluded from the dataset, as it represented an extreme outlier with excessively high resistivity values, which could disproportionately affect model fitting. While this removal was necessary for the robustness of model development, it may limit the evaluation of model performance under very low moisture conditions.
A possible limitation of this study is that the manual homogenization of soil moisture, without mechanical mixing or a rest period, may have introduced minor non-uniformities in water distribution, potentially affecting the accuracy of resistivity measurements.
A limitation of this study is that the ±2% accuracy of the moisture sensor introduces uncertainty that may affect the precision of the predictive models, particularly at low moisture contents.
4. Discussion
A comparative analysis of prediction models applied to electrical resistivity as a function of gravimetric moisture content in sandy, clayey, and silty soils provides insight into the performance, accuracy, and applicability of various mathematical and statistical approaches. The Spline-Log, RBF, and LOESS models demonstrated outstanding performance across all three soil types, while linear models such as LASSO and RIDGE, as well as analytical models such as the Power Law and Segmented Equation, produced mixed results depending on the physical characteristics of the soil analyzed.
4.1. Sandy Soil
In the case of sandy soil, the Spline-Log and RBF models proved to be the most accurate, achieving an excellent fit ( = 1.00; RMSE, MAE and MAPE = 0.00), which demonstrates their high capacity to represent the nonlinear behavior of resistivity, especially in the critical zone between 5% and 25% moisture content, where a sharp drop in resistivity occurs. However, their computational complexity may limit their use in various applications.
Models such as the Power Law and the Segmented Equation, although less accurate ( = 0.95 and 0.91), offer explicit expressions at the cost of greater errors, particularly under low- or high-humidity conditions. The Segmented Equation provides values closest to the actual ones while also retaining an explicit formulation. The LOESS model demonstrated good performance with minimal errors, providing a balanced alternative between precision and interpretability. However, although in some aspects it is simpler than Spline-Log, LOESS still depends on computational parameters and is not analytical, which limits its use.
The LASSO and RIDGE models presented errors in the hydration zone; however, as humidity increases, the errors decreased drastically until they reach reasonable values.
4.2. Clay Soil
In clayey soil, the Logarithmic Spline, RBF, and LOESS models, similar to their performance in sandy soil, showed an excellent fit with practically zero errors, demonstrating their high precision.
In contrast, the Power Law model and the Segmented Equation offered acceptable performance with explicit formulations. The Power Law model stood out for its mathematical simplicity ( = 0.99), albeit with a high MAPE, while the Segmented Equation achieved greater relative accuracy (MAPE = 15.10%) and consistency across both humidity extremes.
4.3. Silty Soil
In silty soils, the Spline-Log, RBF, and LOESS models once again demonstrated outstanding accuracy, adequately replicating experimental data, although their use is restricted to computational environments. Among the models with explicit formulations, the Segmented Equation stood out for its balance between accuracy (MAPE = 13.16%) and applicability, remaining useful even without advanced tools. The RIDGE model also demonstrated a good overall fit ( = 0.99), although with more pronounced errors between 5% and 20% moisture content, making it suitable only in error-tolerant contexts.
The LOESS model, despite not having an analytical expression, exhibited minimal error (MAPE = 2.60%), positioning itself as a precise computational alternative. In contrast, the Power Law and LASSO models presented significant overestimations and negative values, respectively, which compromise their usefulness for this soil type. Overall, the Spline-Log, RBF, and LOESS models provide high accuracy, while the Segmented Equation and RIDGE models represent the most practical options.
In general, for all soils, nonlinear models such as Spline-Log, RBF and LOESS presented an excellent fit, indicating an exceptional capacity to model the nonlinear relationship between moisture and resistivity. This is consistent with previous studies that highlight the strong dependence of resistivity on small variations in moisture in high-retention materials [60].
Furthermore, previous studies have employed nonlinear regression and exponential models to relate soil resistivity to geotechnical parameters such as moisture, re-porting R2 values of 0.82, 0.77, and approximately 0.80 in others, demonstrating that exponential relationships can provide a robust predictive framework [1,2,3,4,10,11,12,13]. Compared to these works, the present study shows that both segmented equation models and nonparametric models (Spline-Log, RBF, LOESS) offer good accuracy, capturing complex nonlinear behavior in sandy, silty, and clayey soils.
Segmented equation and power-law models, while less accurate than more computationally complex methods, are particularly useful in field situations due to their explicit mathematical form, provided that these models have field validation.
It is worth mentioning that while the proposed empirical models captured the relationship between gravimetric moisture content and electrical resistivity for sandy, silty, and clayey soils, some limitations remain.
In particular, the resistivity–moisture relationship was analyzed separately for sandy, silty, and clayey soils, rather than using a unified model. This decision was based on the distinct nonlinear responses observed among soil types, and this methodological choice is directly supported by previous research demonstrating that soil texture significantly influences the resistivity–moisture relationship [13,18,32,42]. Combining these datasets into a single predictive framework would have obscured these differences, reducing the model’s accuracy and interpretability. Furthermore, the diffuse double layer (DDL) effect was not explicitly parameterized. While its influence is partially implied in the experimental measurements, more rigorous integration of DCD-related soil properties could improve the model’s generalizability.
It is important to note that the effects of ionic chemistry, such as temperature, ionic concentration, and pore fluid composition, were not explicitly incorporated into the predictive models. While our controlled laboratory measurements minimized the variability of these parameters, their influence on resistivity could be significant under field conditions. Additionally, laboratory-based resistivity measurements may not fully represent in situ conditions, where factors such as soil heterogeneity, stratification, and environmental variability can significantly affect resistivity. Therefore, while the models offer useful guidance, they must be validated under field conditions. Future research should consider these factors to improve the applicability and robustness of soil resistivity predictions. In addition, future studies could explicitly include saturation as a parameter to improve model accuracy, consider variations in water distribution within the soil matrix, strategies to determine whether generalized equations can adequately capture multi-soil variability while maintaining predictive reliability and mineralogical analyses to assess the role of specific clay minerals in conductivity behavior.
5. Conclusions
The comparative study of predictive models shows that nonparametric models, such as Spline-Log and RBF, offer the greatest accuracy for the three soil types analyzed, sandy, silty, and clayey, as demonstrated by the higher , RMSE, and MAE values; however, these models require the implementation of computational tools. On the other hand, segmented models also exhibited stable and interpretable behavior for all three soil types, representing a reliable intermediate approach between empirical simplicity and computational flexibility. Nevertheless, both nonparametric and explicit models should not be used without independent validation. The results reinforce the idea that soil texture and gravimetric moisture content play a decisive role in electrical behavior, with finer soils (silts and clays) showing a more pronounced decrease in resistivity with increasing moisture content. This influence dependent on texture and gravimetric moisture justifies the decision to develop and compare models independently for each soil type, thereby improving the accuracy and interpretability of the results. Future work should focus on field validation of the predictive models to assess their performance under naturally heterogeneous soil conditions. Furthermore, it is worthwhile to explore adaptations of the models to account for variations in salinity, temperature, and soil compaction, factors that can affect electrical resistivity. This will allow for more reliable application of these models in real-world contexts.
Author Contributions
C.A.N.R. and H.M.Á. conceived the research idea, collected the soils, manufactured the measuring device, and designed the models, under the supervision of J.G.R.M. and M.T.P. C.A.N.R. and H.M.Á. prepared the draft manuscript, supervised by M.T.P., J.G.R.M., R.V.C.-S. and S.O.-B. The authors contributed to all data analysis and interpretation in this manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request. All data generated or analyzed during this study are included in this published article.
Acknowledgments
We express our gratitude to all the authors who contributed to the development of this research, as well as to the Secretaria de Investigación, Innovación y Posgrado of the Universidad Autónoma de Querétaro, FONFIVE, and SECIHTI, for their valuable support in the development of the graduate studies.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kornkanok, S.; Avirut, P.; Shinya, I. Comprehensive analysis of correlations between soil electrical resistivity and index geotechnical properties. Results Eng. 2024, 23, 102696. [Google Scholar] [CrossRef]
- Alsharari, B.; Olenko, A.; Abuel-Naga, H. Modeling of electrical resistivity of soil based on geotechnical properties. Expert Syst. Appl. 2020, 141, 112966. [Google Scholar] [CrossRef]
- Sangprasat, K.; Puttiwongrak, A.; Inazumi, S. Review of Correlations Between Soil Electrical Resistivity and Geotechnical Properties. Geosciences 2025, 15, 166. [Google Scholar] [CrossRef]
- Kibria, A.G.; Hossain, A.M.S. Investigation of Geotechnical Parameters Affecting Electrical Resistivity of Compacted Clays. J. Geotech. Geoenviron. Eng. 2012, 138, 1520–1529. [Google Scholar] [CrossRef]
- Kundu, S.K.; Dey, A.K.; Sapkota, S.C.; Debnath, P.; Saha, P.; Ray, A.; Khandelwal, M. Advanced predictive modelling of electrical resistivity for geotechnical and geo-environmental applications using machine learning techniques. J. Appl. Geophys. 2024, 231, 105557. [Google Scholar] [CrossRef]
- Seladji, S.; Cosenza, P.; Tabbagh, A.; Ranger, J.; Richard, G. The effect of compaction on soil electrical resistivity: A laboratory investigation. Eur. J. Soil Sci. 2010, 61, 1043–1055. [Google Scholar] [CrossRef]
- de Jong, S.M.; Heijenk, R.A.; Nijland, W.; van der Meijde, M. Monitoring Soil Moisture Dynamics Using Electrical Resistivity Tomography under Homogeneous Field Conditions. Sensors 2020, 20, 5313. [Google Scholar] [CrossRef] [PubMed]
- Mojid, M.A.; Rose, D.A.; Wyseure, G.C.L. A model incorporating the diffuse double layer to predict the electrical conductivity of bulk soil. Eur. J. Soil Sci. 2007, 58, 560–572. [Google Scholar] [CrossRef]
- Mojid, M.A.; Cho, H. Estimating the fully developed diffuse double layer thickness from the bulk electrical conductivity in clay. Appl. Clay Sci. 2006, 33, 278–286. [Google Scholar] [CrossRef]
- Revil, A.; Coperey, A.; Shao, Z.; Florsch, N.; Fabricius, I.L. Complex conductivity of soils. Water Resour. Res. 2017, 53, 7121–7147. [Google Scholar] [CrossRef]
- Farhad, H.; Hossam, A.N.; Philip, B.; Leong, E.-C. Series-parallel structure-oriented electrical conductivity model of saturated clay. Appl. Clay Sci. 2018, 162, 239–251. [Google Scholar] [CrossRef]
- Hyojung, K.; Hyunwook, C.; Koochul, J. Effect of temperature on electrical conductivity of soils—Role of surface conduction. Eng. Geol. 2023, 321, 107147. [Google Scholar] [CrossRef]
- Wunderlich, T.; Petersen, H.; Attia al Hagrey, S.; Rabbel, W. Pedophysical Models for Resistivity and Permittivity of Partially Water-Saturated Soils. Vadose Zone J. 2013, 12, 1–14. [Google Scholar] [CrossRef]
- Sun, Z.; Mehmani, A.; Torres-Verdín, C. Pore-scale investigation of the electrical resistivity of saturated porous media: Flow patterns and porosity efficiency. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022608. [Google Scholar] [CrossRef]
- Zeng, H.; Zhang, Q.; Du, C.; Liu, J.; Li, Y. Quantitative Relationship Between Electrical Resistivity and Water Content in Unsaturated Loess: Theoretical Model and ERT Imaging Verification. Geosciences 2025, 15, 302. [Google Scholar] [CrossRef]
- Mustafa, R.; Ansari, A. Comprehensive analysis of soil electrical conductivity: An experimental and machine learning approach. Discov. Civ. Eng. 2024, 1, 82. [Google Scholar] [CrossRef]
- Jing, J.; Hou, J.; Sun, W.; Chen, G.; Ma, Y.; Ji, G. Study on Influencing Factors of Unsaturated Loess Slope Stability under Dry-Wet Cycle Conditions. J. Hydrol. 2022, 612, 128187. [Google Scholar] [CrossRef]
- Zamanian, M.; Asfaw, N.; Chavda, P.; Shahandashti, M. Deep Learning for Exploring the Relationship Between Geotechnical Properties and Electrical Resistivities. Transp. Res. Rec. 2024, 2678, 659–672. [Google Scholar] [CrossRef]
- Bhatt, S.; Jain, P.K. Correlation between electrical resistivity and water content of sand—A statistical approach. Am. Int. J. Res. Sci. The Technol. Eng. Math 2014, 6, 115–121. Available online: https://api.semanticscholar.org/CorpusID:140118130 (accessed on 13 March 2025).
- Pozdnyakov, A.I.; Pozdnyakova, L.A.; Karpachevskii, L.O. Relationship between water tension and electrical resistivity in soils. Eurasian Soil Sci. 2006, 39, S78–S83. [Google Scholar] [CrossRef]
- Paul, W.J.; Glover, M.J.; Hole, J.P. A modified Archie’s law for two conducting phases. Earth Planet. Sci. Lett. 2000, 180, 369–383. [Google Scholar] [CrossRef]
- Fu, Y.; Horton, R.; Ren, T.; Heitman, J.L. A general form of Archie’s model for estimating bulk soil electrical conductivity. J. Hydrol. 2021, 597, 126160. [Google Scholar] [CrossRef]
- Tso, C.H.; Binley, A. On the field estimation of moisture content using electrical geophysics: The impact of petrophysical model uncertainty. Water Resour. Res. 2019, 55, 7196–7211. [Google Scholar] [CrossRef]
- Chen, H.; Niu, Q. Improving moisture content estimation from field resistivity measurements with subsurface structure information. J. Hydrol. 2022, 613, 128343. [Google Scholar] [CrossRef]
- Michot, D.; Thomas, Z.; Adam, I. Nonstationarity of the electrical resistivity and soil moisture relationship in a heterogeneous soil system: A case study. Soil 2016, 2, 241–255. [Google Scholar] [CrossRef]
- Gerhard, F. On measuring the temperature coefficient of resistivity and the thermal expansion coefficient of conductive thin films. Thin Solid Film. 2025, 825, 140727. [Google Scholar] [CrossRef]
- Hazreek, Z.; Rosli, S.; Fauziah, A.; Wijeyesekera, D.; Ashraf, M.; Faizal, T.; Kamarudin, A.; Rais, Y.; Dan, M.; Azhar, A.; et al. Determination of Soil Moisture Content using Laboratory Experimental and Field Electrical Resistivity Values. J. Phys. Conf. Ser. 2018, 995, 012074. [Google Scholar] [CrossRef]
- Annan, Z.; Ruiqiu, H.; Daichao, S. Capillary water retention curve and shear strength of unsaturated soils. Can. Geotech. J. 2016, 53, 974–987. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, M.; Sun, P. Resistivity is used as a tool to evaluate the variability of soil water content. J. Mt. Sci. 2022, 19, 3533–3547. [Google Scholar] [CrossRef]
- Luca, B.; Benjamin, B.; Olivier, M.; Vincent, B.; Didier, M.; Jean, L. Monitoring soil volume wetness in heterogeneous soils by electrical resistivity. A field-based pedotransfer function. J. Hydrol. 2014, 516, 56–66. [Google Scholar] [CrossRef]
- Pascal, B.; Rémi, C.; Christophe, B. Monitoring soil water content and deficit using Electrical Resistivity Tomography (ERT)—A case study in the Cevennes area, France. J. Hydrol. 2020, 380, 146–153. [Google Scholar] [CrossRef]
- Friedman, S.P. Soil properties influencing apparent electrical conductivity: A review. Comput. Electron. Agriculture 2005, 46, 45–70. [Google Scholar] [CrossRef]
- Zheng, C.; Yuan, Y. Study on the effect of water content on physical properties of bentonite. PLoS ONE 2025, 20, e0303522. [Google Scholar] [CrossRef] [PubMed]
- Mao, J.; Yuan, D.; Jin, D.; Wang, B.; Wu, S. Experimental Study on Electrical Resistivity Characteristics of Saturated Sand Mixes with Bentonite Slurry. Appl. Sci. 2021, 11, 12126. [Google Scholar] [CrossRef]
- Salam, M.; Rahman, Q.; Ang, S.; Wen, F. Soil resistivity and ground resistance for dry and wet soil. J. Mod. Power Syst. Clean Energy 2015, 5, 290–297. [Google Scholar] [CrossRef]
- Abu-Hassanein, Z.; Benson, C.; Blotz, L. Electrical Resistivity of Compacted Clays. J. Geotech. Eng. 1996, 122, 397–406. [Google Scholar] [CrossRef]
- Hazreek, Z.A.M.; Azhar, S.; Madun, A.; Saad, R. Integral analysis of laboratory and field electrical resistivity for soil density prediction. In Green Building, Materials and Civil Engineering; CRC Press: Boca Raton, FL, USA, 2014; pp. 37–43. [Google Scholar] [CrossRef]
- Gerscovich, D.; Vipulanandan, C. Data Analyses to Correlate the Soil Properties to the Electrical Resistivity. Geotech. Geol. Eng. 2023, 41, 4507–4528. [Google Scholar] [CrossRef]
- Siddiqui, F.I.; Osman, S.B. Simple and multiple regression models for relationship between electrical resistivity and various soil properties for soil characterization. Environ. Earth Sci. 2013, 70, 259–267. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, J.; Cai, L.; Fan, Y.; Zheng, Z. Laboratory Investigations on Factors Affecting Soil Electrical Resistivity and the Measurement. IEEE Trans. Ind. Appl. 2015, 51, 5358–5365. [Google Scholar] [CrossRef]
- Jusoh, M.N.H.; Syamsunur, D.; Abd Rahman, N.; Olisa, E.; Rahim, A.; Md Yusoff, N.I. Soil Parameters Model Prediction via Resistivity Value Limit to Shallow Subsurface Areas. Shock. Vib. 2022, 2022, 3251250. [Google Scholar] [CrossRef]
- Merritt, A.J.; Chambers, J.E.; Wilkinson, P.B.; West, L.J.; Murphy, W.; Gunn, D.; Uhlemann, S. Measurement and modelling of moisture—Electrical resistivity relationship of fine-grained unsaturated soils and electrical anisotropy. J. Appl. Geophys. 2016, 124, 155–165. [Google Scholar] [CrossRef]
- Ijaz, N.; Ye, W.; ur Rehman, Z.; Dai, F.; Ijaz, Z. Numerical study on stability of lignosulphonate-based stabilized surficial layer of unsaturated expansive soil slope considering hydro-mechanical effect. Transp. Geotech. 2022, 32, 100697. [Google Scholar] [CrossRef]
- ur Rehman, Z.; Khalid, U.; Ijaz, N.; Mujtaba, H.; Haider, A.; Farooq, K.; Ijaz, Z. Machine learning-based intelligent modeling of hydraulic conductivity of sandy soils considering a wide range of grain sizes. Eng. Geol. 2022, 311, 106899. [Google Scholar] [CrossRef]
- Eirini, C.; Nikolaos, K.; Aspasia, E.; Erato, L.; Kalliopi, K.; Eleni, P.; Dimitrios, V.; Aikaterini, K. Estimation of soil properties using Hyperspectral imaging and Machine learning. Smart Agric. Technol. 2025, 10, 100790. [Google Scholar] [CrossRef]
- Datta, D.; Paul, M.; Murshed, M.; Teng, S.W.; Schmidtke, L. Comparative Analysis of Machine and Deep Learning Models for Soil Properties Prediction from Hyperspectral Visual Band. Environments 2023, 10, 77. [Google Scholar] [CrossRef]
- Fitzpatrick, B.R.; Lamb, D.W.; Mengersen, K. Ultrahigh Dimensional Variable Selection for Interpolation of Point Referenced Spatial Data: A Digital Soil Mapping Case Study. PLoS ONE 2016, 11, e0162489. [Google Scholar] [CrossRef] [PubMed]
- Smolik, M.; Skala, V.; Nedved, O. A Comparative Study of LOWESS and RBF Approximations for Visualization. In Computational Science and Its Applications—ICCSA 2016; Springer: Cham, Switzerland, 2016; pp. 405–419. [Google Scholar] [CrossRef]
- Melkumova, L.E.; Shatskikh, S.Y. Comparing Ridge and LASSO estimators for data analysis. Procedia Eng. 2017, 201, 746–755. [Google Scholar] [CrossRef]
- Zuzana, M.; Vaclav, S. Radial basis function approximations: Comparison and applications. Appl. Math. Model. 2017, 51, 728–743. [Google Scholar] [CrossRef]
- ASTM D422-63; Standard Test Method for Particle-Size Analysis of Soils. ASTM: West Conshohocken, PA, USA, 2007. [CrossRef]
- ASTM D6913-04(2009)e1; Standard Test Methods for Particle-Size Distribution (Gradation) of Soils Using Sieve Analysis. ASTM: West Conshohocken, PA, USA, 2017. [CrossRef]
- ASTM D7928-21e1; Standard Test Method for Particle-Size Distribution (Gradation) of Fine-Grained Soils Using the Sedimentation (Hydrometer) Analysis. ASTM: West Conshohocken, PA, USA, 2021. [CrossRef]
- ASTM D698-12; Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Standard Effort. ASTM: West Conshohocken, PA, USA, 2021. [CrossRef]
- ASTM D2216-19; Standard Test Methods for Laboratory Determination of Water (Moisture) Content of Soil and Rock by Mass. ASTM: West Conshohocken, PA, USA, 2019. [CrossRef]
- ASTM G57-20; Standard Test Method for Measurement of Soil Resistivity Using the Wenner Four-Electrode Method. ASTM: West Conshohocken, PA, USA, 2020. [CrossRef]
- ASTM G187-18; Standard Test Method for Measurement of Soil Resistivity Using the Two-Electrode Soil Box Method. ASTM: West Conshohocken, PA, USA, 2023. [CrossRef]
- ASTM D2487-17; Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). ASTM: West Conshohocken, PA, USA, 2020. [CrossRef]
- IEEE Std 80-2013; IEEE Guide for Safety in AC Substation Grounding. IEEE: New York, NY, USA, 2015. [CrossRef]
- Ángeles, H.M.; Moreno, J.G.R.; Rubio, C.A.N.; Castillo, R.R.V.; Ronquillo-Lomeli, G.; Carrillo-Serrano, R.V.; Perea, M.T. Effect of humidity incorporation on the development of a ground enhancement material. Sci. Rep. 2025, 15, 22049. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).