A Nonlinear Extended State Observer-Based Load Torque Estimation Method for Wind Turbine Generators
Abstract
1. Introduction
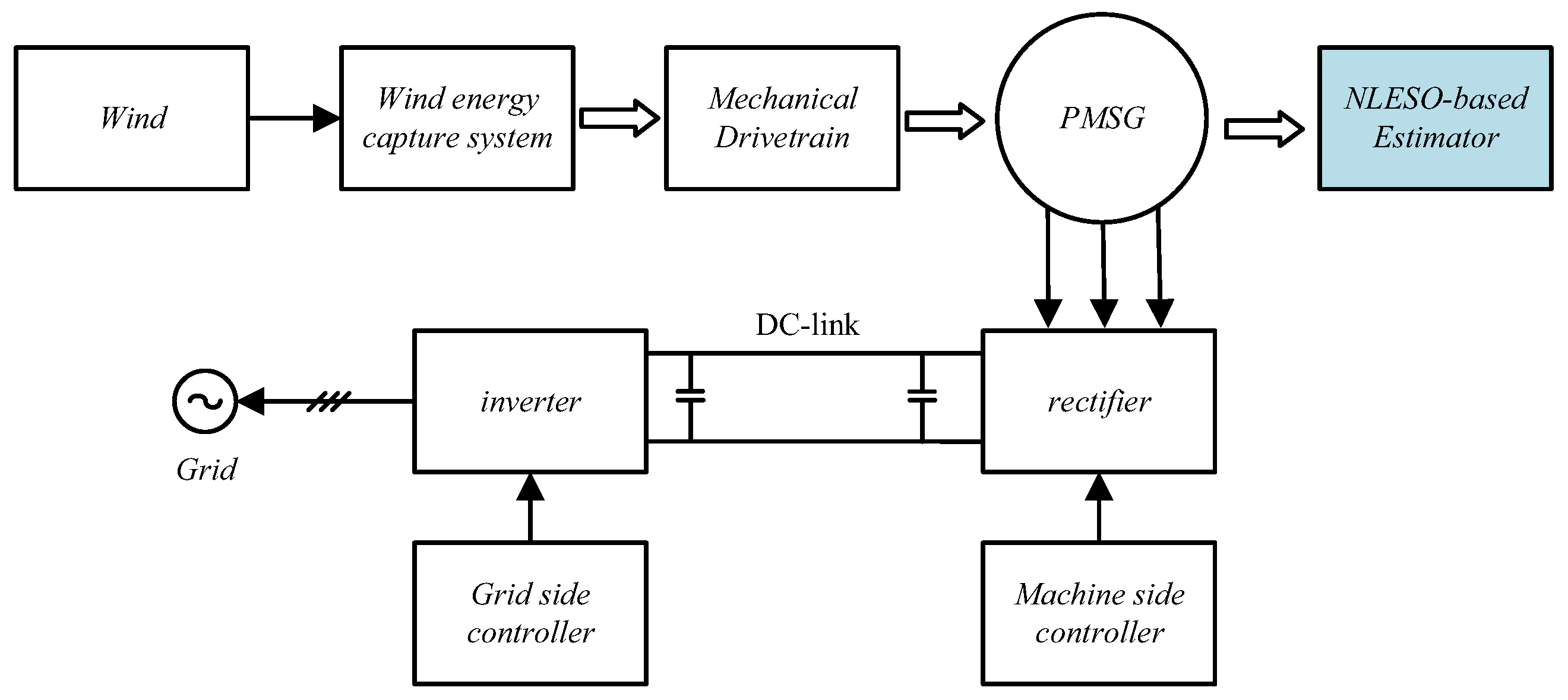
2. NLESO-Based Speed and Load Torque Estimation Method
2.1. Mathematical Model of Wind Turbine
2.2. NLESO-Based Speed and Acceleration Observer
2.3. Stability Analysis
2.4. Load Torque Estimation Method
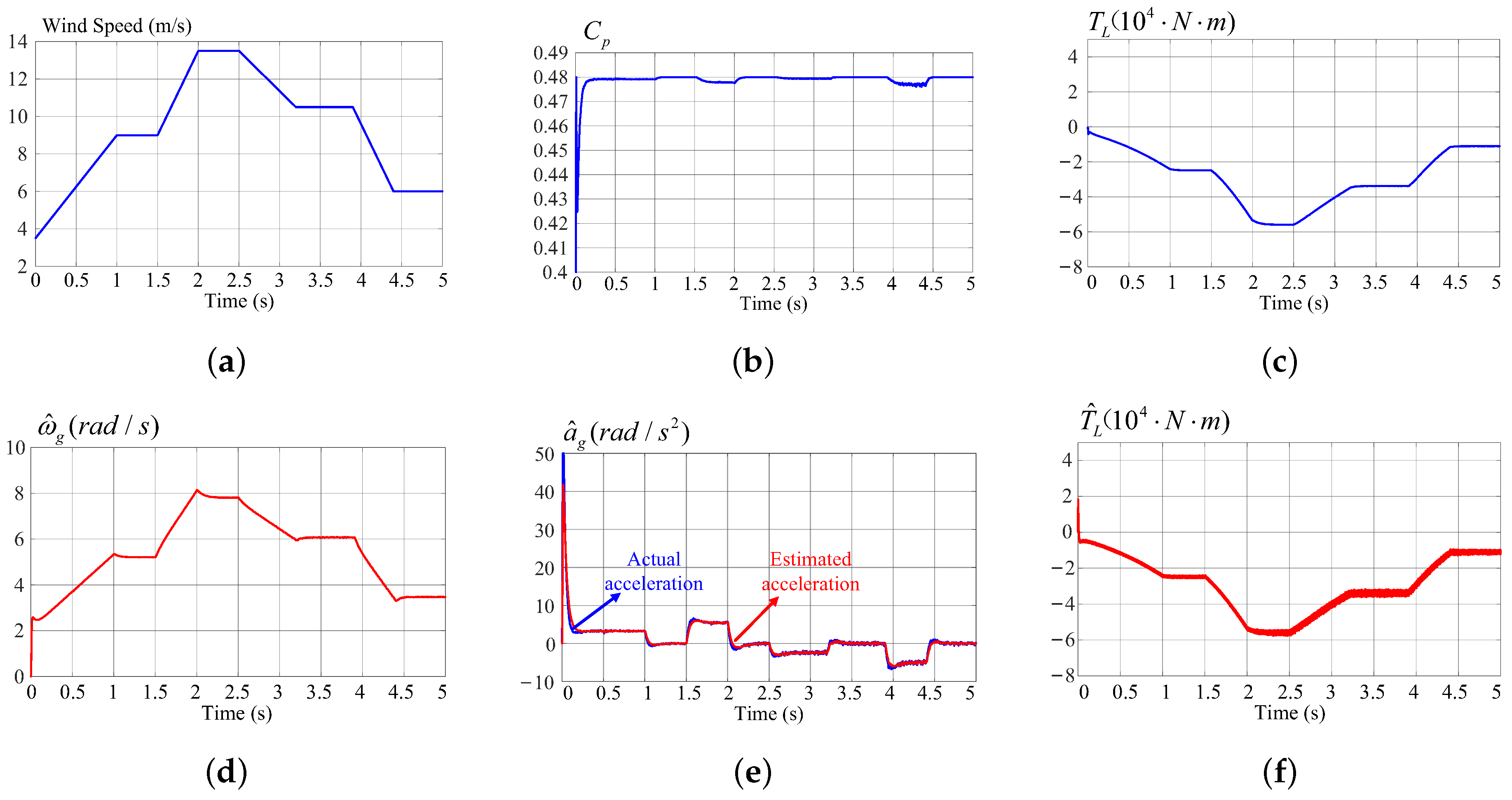
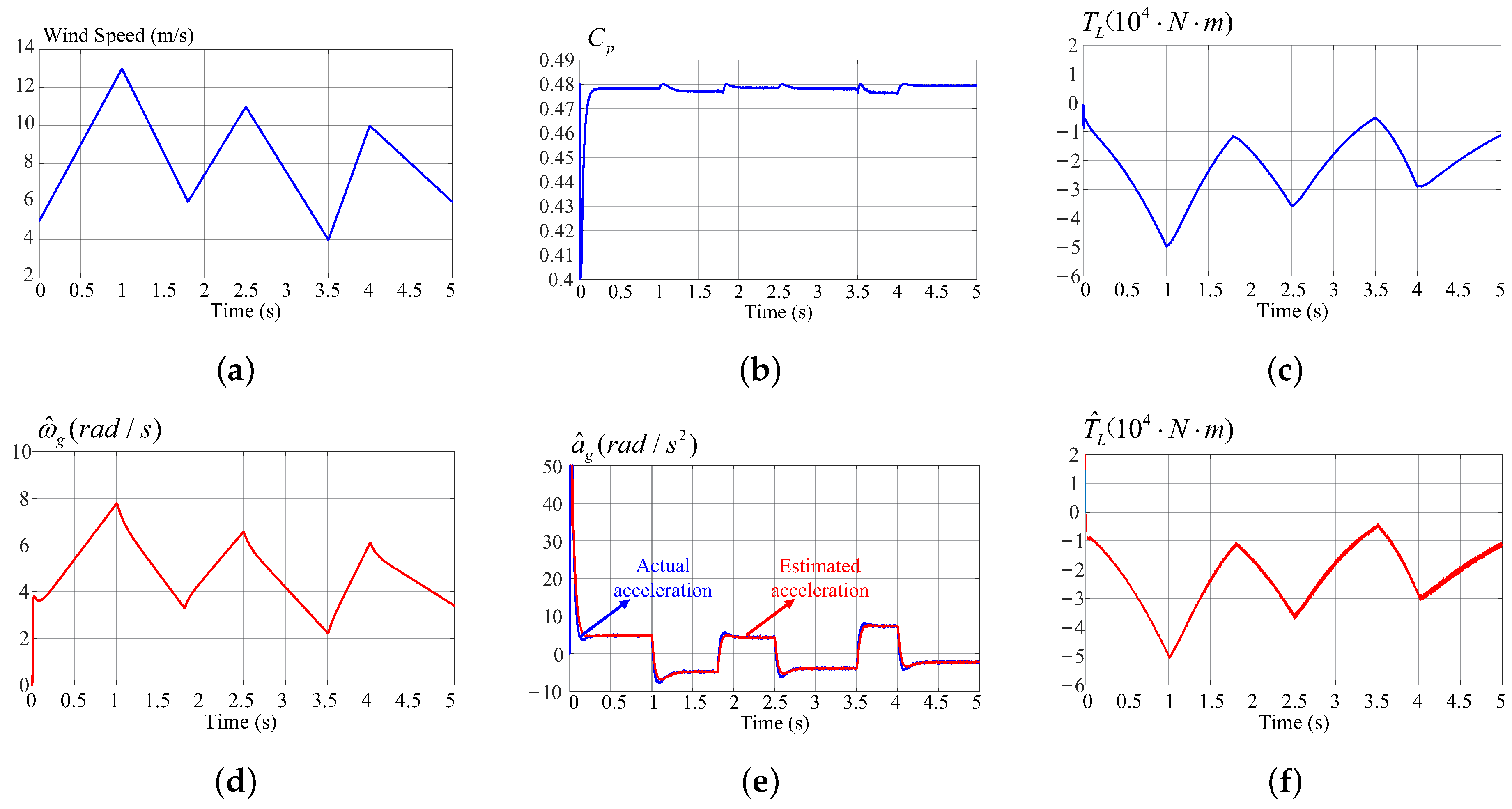
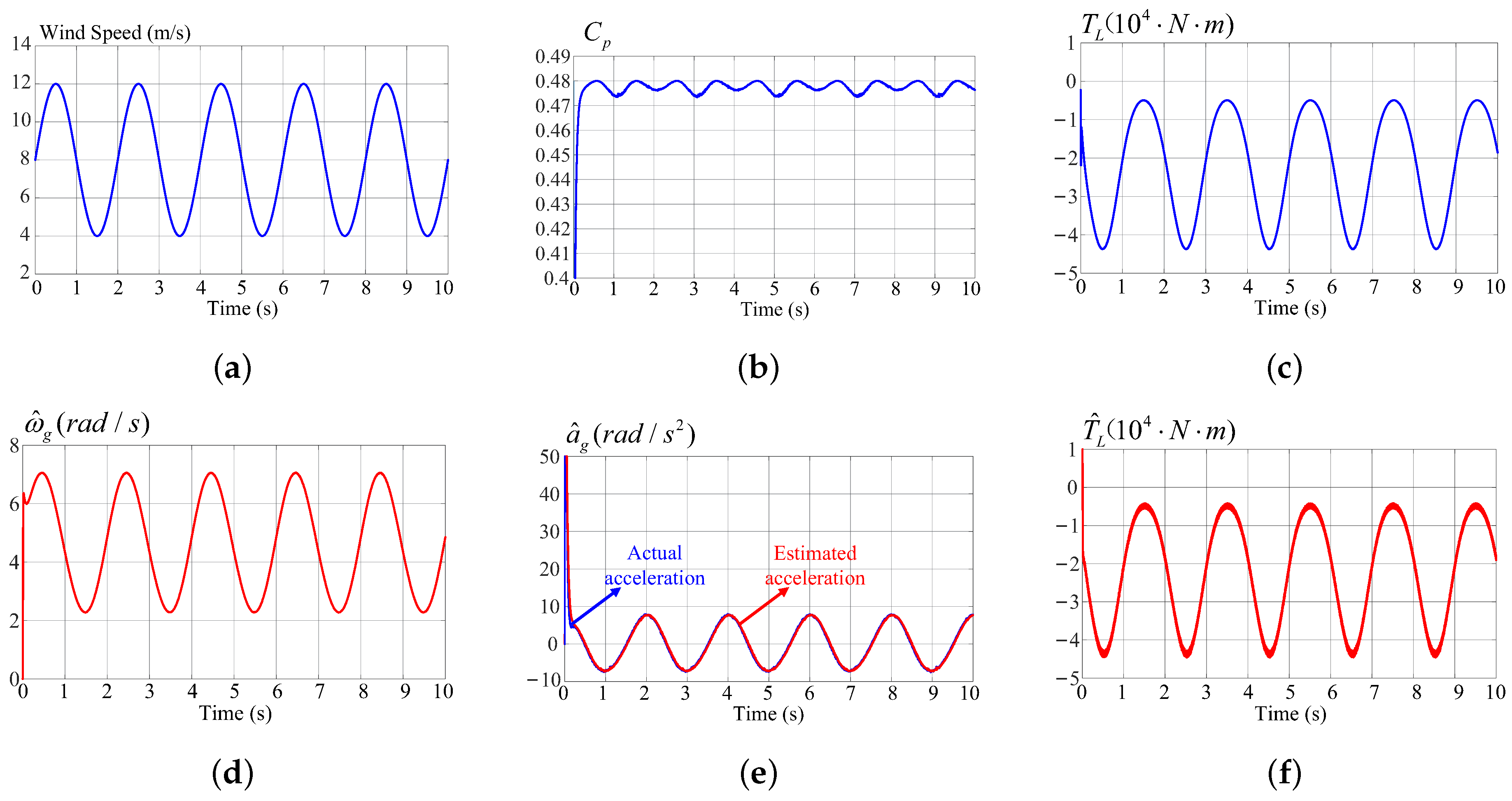
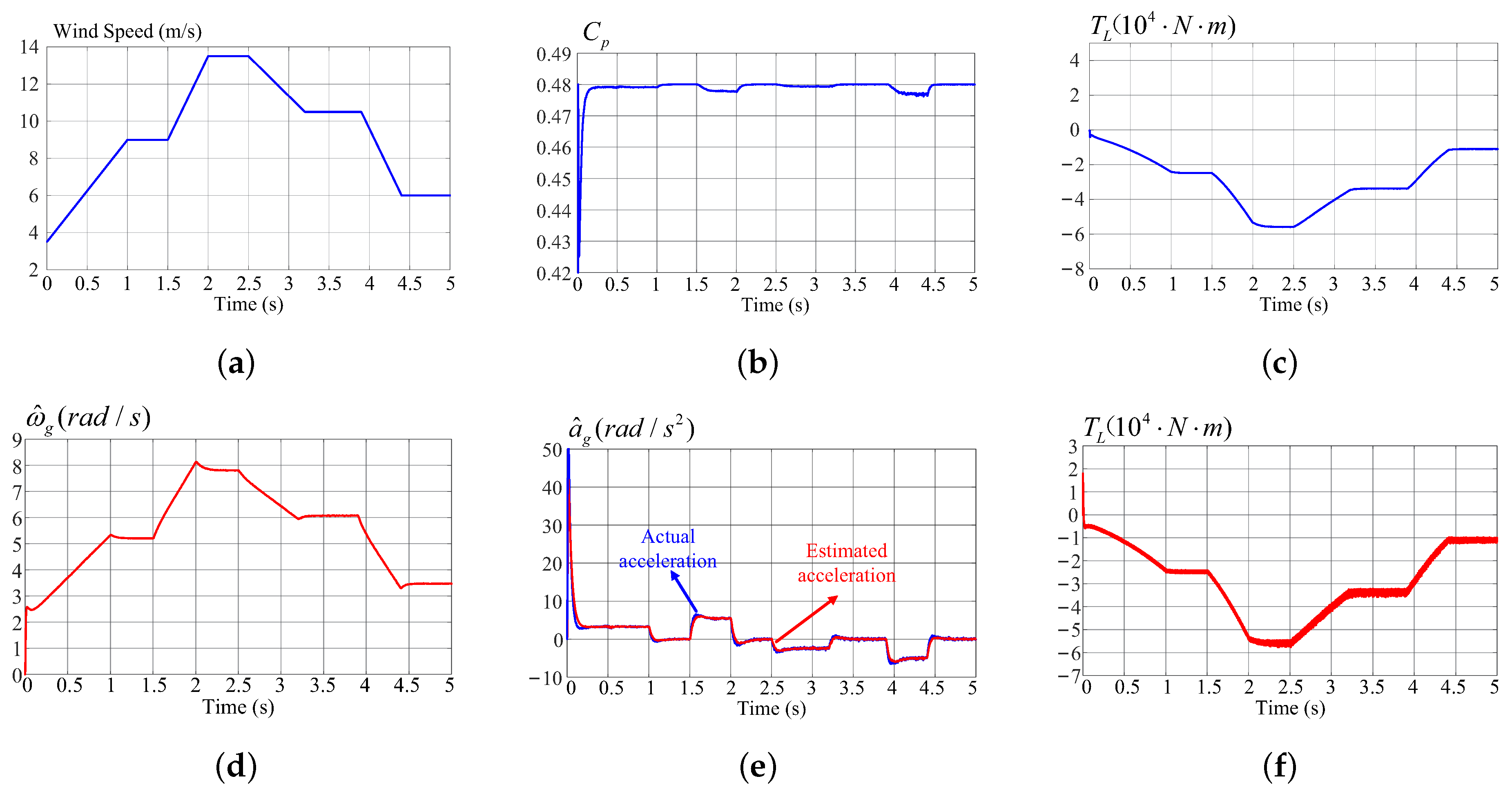
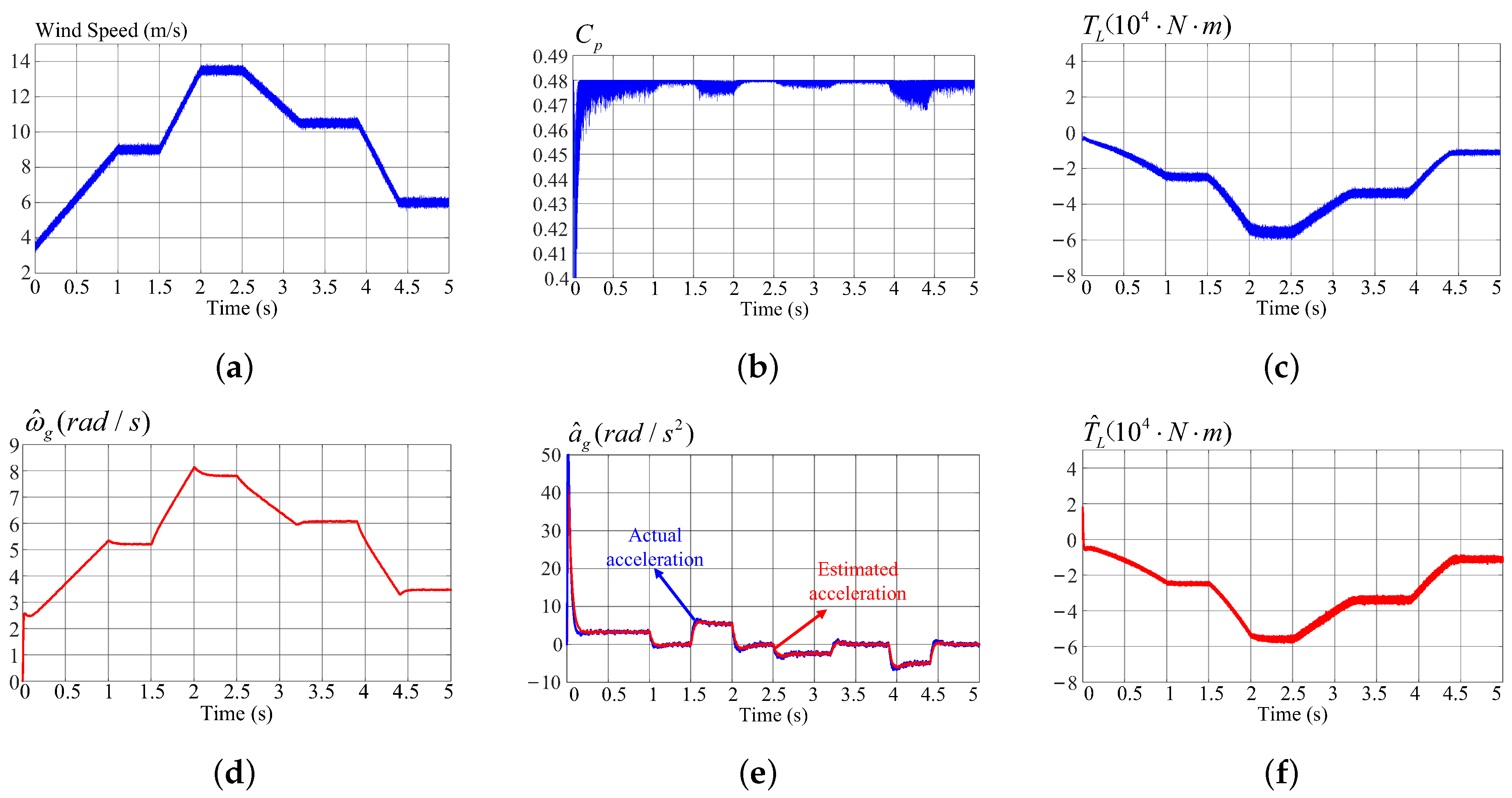
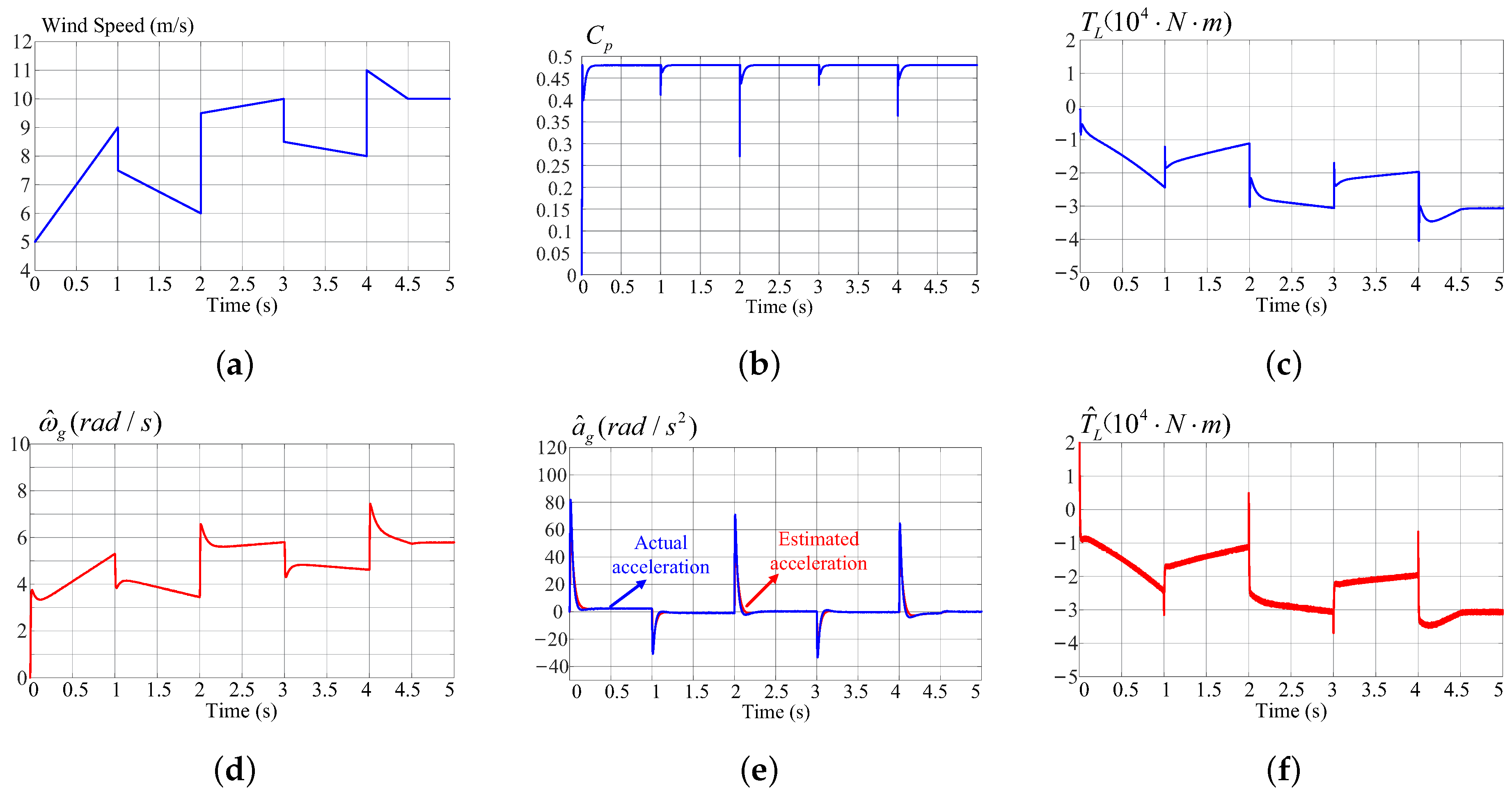
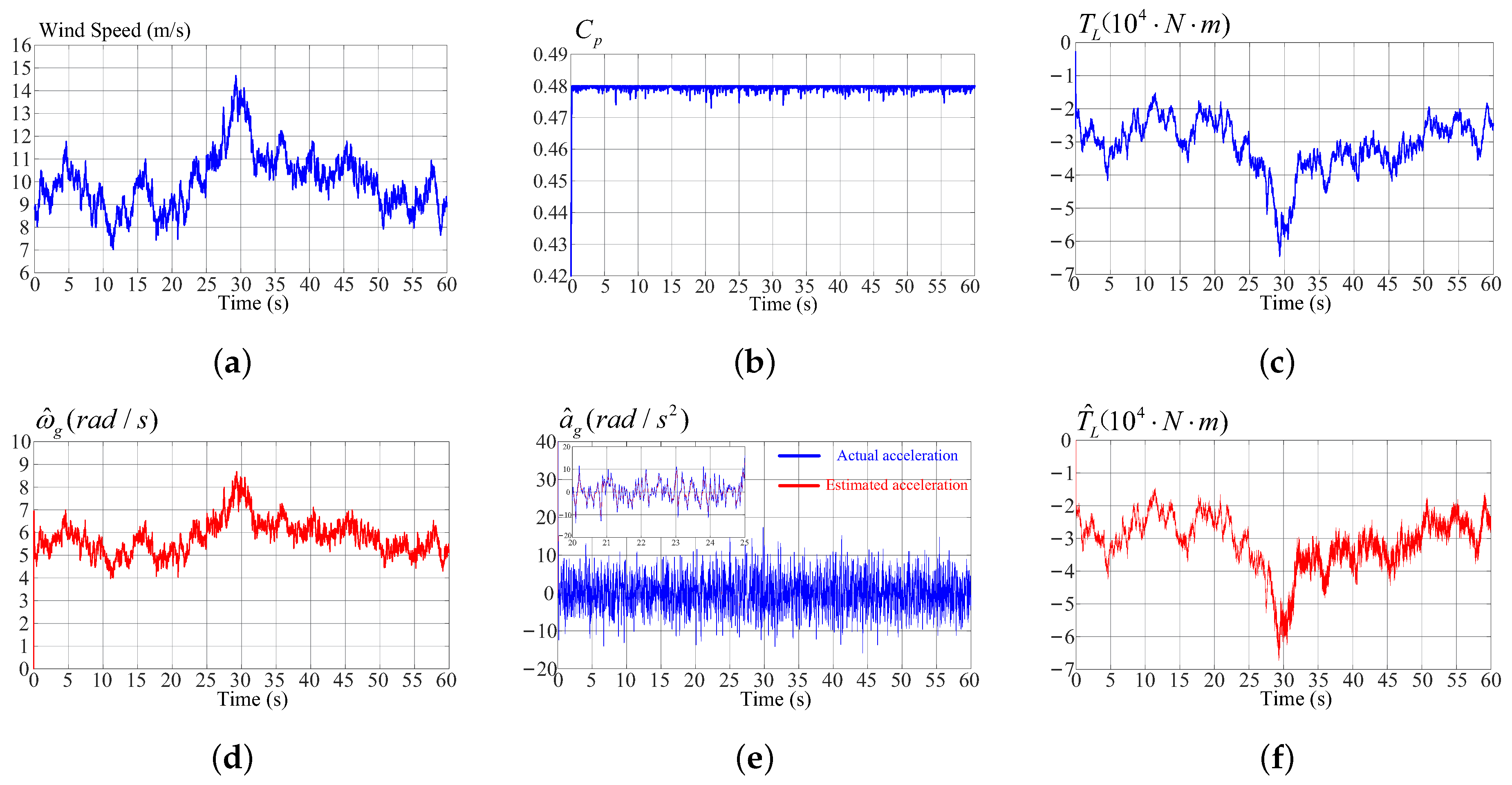
3. Simulation Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NLESO | Nonlinear extended state observer |
| TSR | Tip-speed ratio |
| SCADA | Supervisory control and data acquisition |
| CMSs | Condition monitoring systems |
| PMSG | Permanent magnet synchronous generator |
References
- Rahideh, A.; Korakianitis, T. Analytical magnetic field distribution of slotless brushless machines with inset permanent magnets. IEEE Trans. Magn. 2011, 47, 1763–1774. [Google Scholar] [CrossRef]
- Pastore, L.M.; Basso, G.L.; Ricciardi, G.; de Santoli, L. Synergies between Power-to-Heat and Power-to-Gas in renewable energy communities. Renew. Energy 2022, 198, 1383–1397. [Google Scholar] [CrossRef]
- Aissou, R.; Rekioua, T.; Rekioua, D.; Tounzi, A. Application of nonlinear predictive control for charging the battery using wind energy with permanent magnet synchronous generator. Int. J. Hydrogen Energy 2016, 41, 20964–20973. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Q.; Li, L.; Foley, A.M.; Srinivasan, D. Approaches to wind power curve modeling: A review and discussion. Renew. Sustain. Energy Rev. 2019, 116, 109422. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, X.; Wu, A.; Xu, B.; Lin, S. Turbulence intensity identification and load reduction of wind turbine under extreme turbulence. Ocean. Eng. 2022, 257, 111710. [Google Scholar] [CrossRef]
- Mérigaud, A.; Ringwood, J.V. Condition-based maintenance methods for marine renewable energy. Renew. Sustain. Energy Rev. 2016, 66, 53–78. [Google Scholar] [CrossRef]
- Liu, W.; Tang, B.; Han, J.; Lu, X.; Hu, N.; He, Z. The structure healthy condition monitoring and fault diagnosis methods in wind turbines: A review. Renew. Sustain. Energy Rev. 2015, 44, 466–472. [Google Scholar] [CrossRef]
- Salameh, J.P.; Cauet, S.; Etien, E.; Sakout, A.; Rambault, L. Gearbox condition monitoring in wind turbines: A review. Mech. Syst. Signal Process. 2018, 111, 251–264. [Google Scholar] [CrossRef]
- Valikhani, M.; Jahangiri, V.; Ebrahimian, H.; Moaveni, B.; Liberatore, S.; Hines, E. Inverse modeling of wind turbine drivetrain from numerical data using Bayesian inference. Renew. Sustain. Energy Rev. 2023, 171, 113007. [Google Scholar] [CrossRef]
- Hosseini, A.; Cannon, D.T.; Vasel-Be-Hagh, A. Wind farm active wake control via concurrent yaw and tip-speed ratio optimization. Appl. Energy 2025, 377, 124625. [Google Scholar] [CrossRef]
- Hosseini, A.; Cannon, D.T.; Vasel-Be-Hagh, A. Tip speed ratio optimization: More energy production with reduced rotor speed. Wind 2022, 2, 691–711. [Google Scholar] [CrossRef]
- Kamel, O.; Hauptmann, S.; Bottasso, C. Estimation of damage equivalent loads of Drivetrain of wind turbines using machine learning. J. Phys. Conf. Ser. 2022, 2265, 032075. [Google Scholar] [CrossRef]
- Yoon, Y.D.; Sul, S.K.; Morimoto, S.; Ide, K. High-bandwidth sensorless algorithm for AC machines based on square-wave-type voltage injection. IEEE Trans. Ind. Appl. 2011, 47, 1361–1370. [Google Scholar] [CrossRef]
- Wang, D.; Li, B.; Zhao, Y. An Adaptive SMO Approach for Low-Chattering Sensorless Control of PMSM. IEEE Trans. Power Electron. 2025, 2, 1–9. [Google Scholar] [CrossRef]
- Lee, J.; Hong, J.; Nam, K.; Ortega, R.; Praly, L.; Astolfi, A. Sensorless control of surface-mount permanent-magnet synchronous motors based on a nonlinear observer. IEEE Trans. Power Electron. 2009, 25, 290–297. [Google Scholar]
- Cooperman, A.; Martinez, M. Load monitoring for active control of wind turbines. Renew. Sustain. Energy Rev. 2015, 41, 189–201. [Google Scholar] [CrossRef]
- Liu, X.; Bo, L.; Luo, H. Dynamical measurement system for wind turbine fatigue load. Renew. Energy 2016, 86, 909–921. [Google Scholar] [CrossRef]
- Gambier, A.; Nazaruddin, Y.Y. Modelling the wind turbine by using the tip-speed ratio for estimation and control. Energies 2022, 15, 9454. [Google Scholar] [CrossRef]
- Tautz-Weinert, J.; Watson, S.J. Using SCADA data for wind turbine condition monitoring—A review. IET Renew. Power Gener. 2017, 11, 382–394. [Google Scholar] [CrossRef]
- Lee, S.; Churchfield, M.; Driscoll, F.; Sirnivas, S.; Jonkman, J.; Moriarty, P.; Skaare, B.; Nielsen, F.G.; Byklum, E. Load estimation of offshore wind turbines. Energies 2018, 11, 1895. [Google Scholar] [CrossRef]
- Loriemi, A.; Jacobs, G.; Bosse, D. Estimation of rotor and main bearing loads using artificial neural networks. J. Phys. 2022, 2151, 012002. [Google Scholar] [CrossRef]
- Klein, A.; Wintermeyer-Kallen, T.; Stegink, J.; Kösters, T.; Zierath, J.; Nelles, O.; Abel, D.; Vallery, H.; Basler, M. Control-oriented wind turbine load estimation based on local linear neuro-fuzzy models. J. Phys. Conf. Ser. 2024, 2767, 032016. [Google Scholar] [CrossRef]
- Meng, L.; Zhu, Y.; Xu, S.; Xu, S.; Yang, K. Torque Estimation Based on An Improved SOGI-FLL for IPMSM. In Proceedings of the 2024 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2024; pp. 1188–1193. [Google Scholar]
- Zhang, Y.; Yin, Z.; Tang, R.; Liu, J. Moment of Inertia and Load Torque Identification Based on Adaptive Extended Kalman Filter for Interior Permanent Magnet Synchronous Motors. IEEE Trans. Instrum. Meas. 2025, 74, 1–12. [Google Scholar] [CrossRef]
- Mohamed, Y.A.R.I. A Newly Designed Instantaneous-Torque Control of Direct-Drive PMSM Servo Actuator With Improved Torque Estimation and Control Characteristics. IEEE Trans. Ind. Electron. 2007, 54, 2864–2873. [Google Scholar] [CrossRef]
- Liu, L.; Song, H.; Liang, D. High Performance Sensorless Control of PMSM with Sliding Mode Load Torque Observer. In Proceedings of the 2020 4th International Conference on HVDC (HVDC), Xi’an, China, 6–9 November 2020; pp. 1060–1065. [Google Scholar]
- Wu, Z.; Wang, X.; Ren, N.; Li, G.; Dai, Z. An acceleration-observer-based position and load torque estimation method for wind turbine with sensor faults. Energies 2025, 18, 2787. [Google Scholar] [CrossRef]
- Watil, A.; El Magri, A.; Raihani, A.; Lajouad, R.; Giri, F. An adaptive nonlinear observer for sensorless wind energy conversion system with PMSG. Control. Eng. Pract. 2020, 98, 104356. [Google Scholar] [CrossRef]
- Niu, L.; Xu, D.; Yang, M.; Gui, X.; Liu, Z. On-line Inertia Identification Algorithm for PI Parameters Optimization in Speed Loop. IEEE Trans. Power Electron. 2015, 30, 849–859. [Google Scholar] [CrossRef]
- Beller, S. Torque estimation with artificial intelligence methods in a brushed geared DC motor. Çukurova Üniv. Mühendis. Fak. Derg. 2022, 37, 885–898. [Google Scholar] [CrossRef]
- Lončarek, T.; Lešić, V.; Vašak, M. Increasing accuracy of Kalman filter-based sensorless control of wind turbine PM synchronous generator. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 745–750. [Google Scholar]
- Zhao, Y.; Li, G.; Dai, Z.; Li, B.; Lin, H.; Yang, J. Integral-type half-tangent phase-locked loop for more electric aircraft grids. IET Power Electron. 2023, 16, 1472–1485. [Google Scholar] [CrossRef]

| Parameter | Description | Value |
|---|---|---|
| P | rated power | |
| J | Inertia | 60 kg·m2 |
| number of pole pairs | 12 | |
| permanent magnet flux linkage | ||
| R | PMSG resistance | 0.025 |
| L | PMSG inductance |
| Cases | Test Conditions |
|---|---|
| Case A | Wind speed with gradual variation |
| Case B | Continuously varying wind speed |
| Case C | sinusoidally varying wind speed profile |
| Case D | Wind speed with gradual variation along with a 10% change of the stator resistance and inductance in the PMSG |
| Case E | Wind speed with gradual variation with superimposed wind speed noise |
| Case F | Wind speed with step change |
| Case G | Mean wind speed 10 m/s and turbulence intensity 0.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Yu, J.; Tang, Y.; Hao, W.; Yang, Z.; Li, G.; Dai, Z. A Nonlinear Extended State Observer-Based Load Torque Estimation Method for Wind Turbine Generators. Eng 2025, 6, 264. https://doi.org/10.3390/eng6100264
Zhu Y, Yu J, Tang Y, Hao W, Yang Z, Li G, Dai Z. A Nonlinear Extended State Observer-Based Load Torque Estimation Method for Wind Turbine Generators. Eng. 2025; 6(10):264. https://doi.org/10.3390/eng6100264
Chicago/Turabian StyleZhu, Yihua, Jiawei Yu, Yujia Tang, Wenzhe Hao, Zhuocheng Yang, Guangqi Li, and Zhiyong Dai. 2025. "A Nonlinear Extended State Observer-Based Load Torque Estimation Method for Wind Turbine Generators" Eng 6, no. 10: 264. https://doi.org/10.3390/eng6100264
APA StyleZhu, Y., Yu, J., Tang, Y., Hao, W., Yang, Z., Li, G., & Dai, Z. (2025). A Nonlinear Extended State Observer-Based Load Torque Estimation Method for Wind Turbine Generators. Eng, 6(10), 264. https://doi.org/10.3390/eng6100264






