Abstract
A main topic in mass production of machine parts is how to increase the productivity to produce more parts in a given time while maintaining the prescribed surface quality on the machined surfaces. Novel machining procedures have been introduced to achieve this goal; however, the further development of already established and wide-spread procedures can offer simply accessible solutions. Tangential turning is a rediscovered variant of the traditional turning procedure, where a specially designed cutting tool ensures chip removal with a feed tangential to the workpiece. This process results in low surface roughness even at higher feed rates. In this paper, the achievable surface roughness is analyzed by analytical and experimental steps. In the mathematical analysis, the theoretical surface roughness is determined using the constructive geometric modelling method. The worked-out equations are validated in cutting experiments on 42CrMo4 grade steel workpieces. The theoretical and experimental analyses show that the strictly prescribed surface roughness can be achieved with high feed rates by the application of tangential turning.
1. Introduction
Surface roughness plays a pivotal role in the performance and durability of machined parts across various industries. It influences not only the aesthetic appeal of components but also the functional aspects such as friction, wear resistance, and fatigue strength [1,2,3,4]. In the context of finish machining, achieving the desired surface roughness is important, as it directly impacts the quality and reliability of the final product [5,6]. This importance spans all types of parts, from complex aerospace components to everyday mechanical parts, making the study and analytical determination of surface roughness a necessary area of research. Machining, particularly finish machining, involves precise operations that aim to achieve tight tolerances and high-quality surface finishes. Among the various parts manufactured, shafts are of significant interest due to their widespread use in mechanical systems. Shafts are critical components in automotive, aerospace, and industrial applications, where they often operate under high stress and in demanding environments. The surface roughness of shafts affects their performance, influencing factors such as rotational accuracy, load-bearing capacity, and resistance to wear and corrosion.
In finish machining, the surface roughness is determined by several parameters, including the cutting speed, feed rate, depth of cut, and the geometry of the cutting tool [7,8]. Each of these parameters must be optimized to achieve the desired surface finish without decreasing the efficiency of the machining process. Analytical determination of surface roughness involves the application of mathematical models to predict the roughness based on these machining parameters [9,10,11]. This approach allows for the optimization of machining conditions, leading to improved surface quality and reduced manufacturing costs [12]. The significance of surface roughness in machining is highlighted by its impact on component performance. For instance, rough surfaces can lead to increased friction and wear, reducing the lifetime of the part. In contrast, smoother surfaces enhance lubrication retention, reducing friction and wear [13,14]. Moreover, the surface roughness can affect the assembly of components, influencing the fit and function of mating parts. This is particularly critical in high-precision applications, where even minor deviations in surface finish can lead to significant performance issues [15]. In the machining of shafts, achieving an optimal surface finish is essential to ensure their proper functioning. Shafts typically operate under dynamic loads and require high surface integrity to withstand fatigue and wear. The analytical determination of surface roughness in shaft machining involves the use of theoretical models that account for the kinematic and geometric parameters of the cutting process. These models help in predicting the roughness and in setting the optimal machining conditions to achieve the desired surface quality [16,17]. Advanced analytical methods have been developed to predict surface roughness in finish machining. These methods involve the use of mathematical models that incorporate various machining parameters and their interactions. The models are based on empirical data and theoretical analyses, providing accurate predictions of surface roughness [18,19,20]. The analytical determination of surface roughness is not only limited to traditional machining processes but also extends to advanced manufacturing techniques. In traditional turning, the theoretical value of the Mean Roughness Depth can be easily calculated by the widespread equation, with which the sought roughness value can be calculated as feed squared divided by eight times the nose radius of the tool [7]. However, this method has some limitations. First, it takes into account the projection of the tool onto the base plane. Therefore, it works the best if the tool has no inclination. Secondly, it is accurate when the tool has an exact value for the nose radius. These considerations are showed by Klocke et al. in the analysis of rotational turning [19]. This procedure applies a helical cutting edge, which was projected onto the base plane as a cosine function. The surrounding of the surface generating point was approximated by a circle, thus a virtual nose radius was used for the calculation of the theoretical surface roughness. Martikáň et al. used an analytical approach based on the trigonometric function of the projection of the cutting edge [20]. These studies show that practically usable equations can be deduced, when the correct factors are considered. However, these determined equations are approximations. More accurate formulas can be determined when different mathematical methods are applied.
In this paper, the achievable surface roughness through tangential turning [21] is analyzed (Figure 1). This machining technique has gained attention due to its numerous beneficial properties.

Figure 1.
Tangential turning and its kinematic scheme [22].
Research by Leichner et al. demonstrated that tangential turning on sealing surfaces can reduce oil leakage, tool wear, and machining costs [23]. An effective alternative is a combined procedure that integrates turning and grinding on the same machine [24]. It can produce twist-free surfaces [25]. The different insert and feed motion involved in tangential turning enhance tool life compared to traditional turning methods [22]. When tangential turning is used for finish machining, the MQL (Minimum Quantity Lubrication) technique can also be applied. As with any machining process, machining accuracy in tangential turning depends on various factors [26], such as the inclination angle, tangential feed, and depth of cut. Machine tool manufacturers, such as EMAG [27], have developed the application of tangential turning. It should also be noted that this procedure has its limitations. A special machine tool is needed, which is capable in the realization of the tangential motion. Due to the high inclination of the cutting edge, burr formation can be expected. Since every point of the cutting edge takes part in the generation of the machined surface, the possible occurrence of local chipping in the tool material is an important factor in the decision of application.
The aim of this study is to analytically determine the surface roughness in tangential turning. Many methods are available to achieve this task. Geometrical and analytical tools have long been applied in mathematics to describe and determine complex interrelationships in both the design of machine parts and the planning of manufacturing processes. The work of Litvin is foundational in the international literature for defining workpiece surfaces [28]. Hsieh demonstrated that constructive geometric modeling can be used to analyze the cutting capability of tools [29]. This approach also facilitates the study of undercuts [30], such as those in helical drives with a circular profile in the axial section, by accounting for the mutual influence of interacting mathematical parameters [31]. Kinematic modeling enables the calculation and correction of geometric errors in 5D gear profile grinders [32] and machining centers [33]. Balajti created a novel mathematical method for positioning CCD cameras with precision, allowing the reconstruction of cutting edge curves from digitized images for wear measurement [34]. Perepelitsa further advanced the kinematic method, enhancing the mathematical apparatus for multiparameter mappings of affine space [35]. This advancement allows for the mathematical-analytical determination of shaped cutting tools [36] and the analysis of geometric relations during cutting [37]. The application of this method is suitable for the determination of the roughness parameters.
In summary, selected surface roughness parameters are studied theoretically and experimentally in this study. The calculation formulas of the Mean Roughness Depth and Arithmetical Mean Roughness were determined by the application of constructive geometrical modeling. Practical cutting experiments were also carried out to study the effect of the technological parameters and to validate the deducted equations.
2. Methods and Materials
The surface roughness in tangential turning was studied by the application of two methods: firstly, the equations that determine the analyzed roughness parameters were derived and secondly experiments were conducted to further analyze and validate the mathematical results. The determination of the equations was carried out using the constructive tool geometry methodology. The cutting experiments were executed using a machine tool, which is capable of achieving the tangential feed motion in turning of outer cylindrical surfaces. In this study, two surface roughness parameters quantifying the two-dimensional (2D, linear) profile were analyzed (ISO 21920:2021 [38]):
- •
- Ra—Arithmetic Mean Roughness, the arithmetic mean from all values of the roughness profile R within the measuring distance [μm],
- •
- Rz—Mean Roughness Depth, the average value from the individual roughness depths of five individuals measuring distances in sequence [μm].
The analytical determination of the roughness parameters was carried out using the constructive tool geometric methodology. In a previous study [39], the mathematical model of the tangential turning procedure was defined, consisting of the following parts: (1) geometrical and kinematical analysis, (2) definition of the needed coordinate systems, (3) characterization of the transformational equations, (4) specifying the vector equation of the cutting edge, and (5) determination of the equation of motion.
The geometrical and kinematical analysis showed that the parameters describing the tangential turning procedure can be categorized into two groups. The geometrical parameters determine the different dimensional connections between the tool and the workpiece, which are the following: radius of the machined surface (rw), radius of the surface to be machined (Rw), inclination angle (λs), length of the workpiece (Lw), and projected length of the tool (Lt). The kinematic parameters describe the relative motion of the tool and the workpiece, where the following are defined: tangential feed rate (vt,t), angular velocity of the workpiece (ωw), and number of revolutions of the workpiece (nw). After reviewing the relevant literature, it became evident that defining four coordinate systems (CS) is practical and beneficial for the determination. The first coordinate system, referred to as the “Tool Moving CS” (Kt,m), serves as the initial coordinate system where the vector equation of the cutting edge is specified. This system is attached to the tool, moving in parallel with it during the machining process. The second coordinate system is the “Tool Standing CS” (Kt,s). This system is linked to the machine itself, and the transformation between Kt,m and Kt,s represents the feeding movement of the tool. Thus, it effectively describes the movement of the tool reference point relative to the machine. The third coordinate system is identified as the “Workpiece Standing CS” (Kw,s). This system is also attached to the machine but is connected to the workpiece null point. The transformation between the Tool Standing CS and the Workpiece Standing CS represents the radial distance (aw) between the tool coordinate systems and the symmetry axis of the workpiece. The fourth coordinate system, termed the “Workpiece Moving CS” (Kw,m), is associated with the workpiece but rotates with it. The transformation between the Workpiece Standing CS and the Workpiece Moving CS accounts for the rotary motion of the machined part.
In summary, there are two coordinate systems linked to the workpiece and two linked to the tool. Among these, one for the tool and one for the workpiece are moving with their respective geometric objects, while the other pair remains stationary relative to the machine. Figure 2 illustrates these coordinate systems for tangential turning, which also illustrates the movements of the workpiece and the tool within the defined coordinate systems.
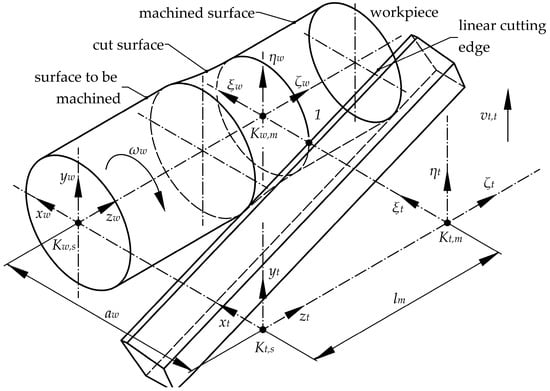
Figure 2.
Mathematical model of tangential turning [39].
The rotation of the workpiece is characterized by its angular speed (ωw) in all three cases due to its advantageous application in mathematical derivation. After establishing the correct starting points for the coordinate systems, additional considerations were also necessary for analytical determination and to facilitate mathematical derivation. Greek letters ξi, ηi, and ζi represent the axes of a moving coordinate system, whereas Latin letters xi, yi, and zi denote the axes of a standing coordinate system, where i = w for “workpiece” and t for “tool“. The ζi and zi axes are aligned with the symmetry axis of the workpiece. The base plane is described by the [xi; zi] and [ξi; ζi] planes. The axes within a given coordinate system should form a right-handed coordinate system, which defines the orientation of the ηi and yi axes. The ξi axis of the tool and workpiece moving coordinate systems passes through the surface-generating point, indicated as “1”.
The result of the mathematical determination [39] is the equation of the cut surface section in the base plane in one-variable function form, which is written as
and this equation is used in the following mathematical determination of the studied surface roughness parameters.
The cutting experiments were carried out on an EMAG VSC 400 DS (EMAG GmbH & Co. KG, Salach, Germany) hard machining center. This advanced machine tool is well-suited for precision machining tasks, especially the cutting of hard materials. The workpieces machined during the experiments were made of 42CrMo4 grade alloyed steels, which were hardened to a Rockwell hardness of 60 HRC, ensuring a consistent and challenging material for the experiments. The diameter of the machined workpieces was 70 mm, providing a substantial size for the thorough analysis. The tangential turning tool used in the experiments was manufactured by HORN Cutting Tools Ltd. This tool featured an inclination angle of 45°, with the specific holder coded as H117.2530.4132. The cutting insert used in conjunction with this holder was an uncoated carbide insert, coded as S117.0032.00, MG12 material type. The precise specifications of the tool and insert were critical in maintaining consistent cutting conditions throughout the experiments. The position and clamping of the workpiece and the tool are shown in Figure 3.

Figure 3.
Relative position of the tool and the workpiece during the experiments.
It should be noted that the inclination angle of the cutting edge is also a significant feature of the cutting system. The carried-out pre-experiments before this study showed that choosing a tool with relatively low inclination angle (λs < 30°) leads to chatter due to the small thickness of the removed chip. Furthermore, higher values of the inclination angle (λs > 55°) lead to increased roughness, thus the advantage of tangential turning cannot be exploited. The aim of this study is to analytically determine the procedure, which is supplemented by the validation of the results and the further analysis of the surface roughness. Therefore, one type of cutting tool was chosen for the practical cutting experiments with an inclination angle of 45°.
The objective was to investigate how variations in several key cutting parameters influenced the tangential turning process. Specifically, this study focused on the effects of altering the cutting speed (vc), the feed per workpiece revolution (f), and the depth of cut (a). By systematically varying the chosen parameters, a comprehensive identifying of their impact on the surface roughness and overall machining performance was characterized. It was expected that the feed would have more impact on the surface roughness, while the other two parameters would have a lower influence. Furthermore, due to the relatively high inclinational angle of the cutting edge, higher than usual in precision machining feeds needed to be selected, as previous pre-experiments also suggested. Therefore, four kinds of feed per workpiece revolution were chosen for the experiments, which were the following: 0.3 mm/rev, 0.6 mm/rev, 0.8 mm/rev, and 1.0 mm/rev. The cutting speed was varied between two levels: 200 m/min and 250 m/min. Since the tangential turning procedure is mainly used in finishing procedures, the depth of cut was chosen according to the usual finishing allowances. Therefore, 0.1 mm and 0.2 mm depths of cut were set. The experimental plan was designed to study the effect of changing one parameter. Hence, four experiments were initially carried out with 200 m/min cutting speed and 0.1 depth of cut on all four chosen level of the feed per workpiece revolution. In the next four experiments, the cutting speed was increased to 250 m/min, the depth of cut was unchanged, and the feed varied again. The last four experiments had 0.2 mm as depth of cut, while the cutting speed was changed back to 200 m/min, and the feed was set to the designed four values. This resulted in 12 experimental setups, the setup parameters of which are summarized in Table 1. To achieve the demanded cutting speeds, 909.45 1/min and 1136.82 1/min number of revolutions were set in the machine for the 200 m/min and 250 m/min cutting speeds, respectively. The cutting parameters were chosen according to the recommendations of the tool manufacturers, actual industrial practices, and the different experiments published in international high-ranking journals by other researchers.

Table 1.
Setup values of the varied technological parameters.
After completing the cutting experiments, accurate measurements were conducted on the machined workpieces. These measurements were performed using an advanced AltiSurf 520 (Altimet, Thonon-les-Bains, France) three-dimensional topography measuring instrument, equipped with a highly precise confocal chromatic probe. This instrument allowed for detailed surface characterization and ensured high accuracy in capturing the topographical features of the workpieces. To obtain comprehensive surface roughness data, roughness profiles were recorded along three generatrix lines on each machined cylindrical surface. These generatrix lines provided multiple cross-sectional views of the surface, offering a thorough representation of the surface roughness across different sections of the shaft. The collected roughness profiles were then processed and analyzed using the AltiMap Premium 6.2.7487 surface analysis software. This software is renowned for its robust analytical capabilities, enabling precise evaluation of the surface roughness data. The use of the AltiSurf 520, combined with the powerful analytical features of AltiMap Premium 6, ensured that the measurement process was both precise and thorough. This combination of instrumentation and software facilitated an in-depth understanding of the surface characteristics resulting from the tangential turning process.
3. Analytical Determination of the Studied Surface Roughness Parameters
This study continues with the analytical determination of the theoretical values of the Arithmetic Mean Roughness and the Mean Roughness Depth after the methods and materials are specified. To determine the calculation method of Ra and Rz, the theoretical profile of the machined surface intersecting with the base plane must be studied. In this section, the Mean Roughness Depth is determined firstly, which is followed by the deduction of the Arithmetical Mean Roughness. The investigation is based on the previously described mathematical model of the tangential turning. The mathematical calculations are confirmed by the Maplesoft Maple 16.0 software.
3.1. Mean Roughness Depth
The position of the tool edge in the base plane is determined with the help of the relations given earlier, which in tangential turning is influenced by the diameter of the machined surface of the workpiece and the inclination angle of the linear edge of the tool. It was shown [39] that the resulting profile will be periodical and has a hyperbolic-like shape. The degree of periodicity of the surface is determined by the resulting axial feed (f). The shape of the theoretical profile of the machined surface is illustrated in Figure 4.

Figure 4.
The shape of the theoretical machined surface in tangential turning.
The resultant axial feed is determined by the tangential feed rate, the angular velocity of the workpiece, and the inclination angle, and can be calculated as follows:
It can be seen in the theoretical profile that the valley depths and peak heights do not vary in the evaluated length; however, some degree of alteration is expected on real surfaces. The determination of the Rz parameter is based on this attribute of the theoretical profile. Due to this phenomenon, only one segment of the profile should be analyzed, which starts from the lowest point of one valley and goes until the peak point of the given curve. This is a segment of the cut surface, which is interested by the tool in the previous (or next) rotation. This curve is determined by Equation (1). The height of the roughness peak is determined by the substitution of its axial position into Equation (1). Due to the periodicity and symmetry, the axial position of the roughness peak will be equal to the half of the axial feed (Figure 4). This takes the following form:
Based on the above, the theoretical relationship of the Mean Roughness Depth is determined. The theoretical value depends on the tangential feed rate of the tool, the angular velocity of the workpiece, the inclination angle of the cutting edge, and the radius of the machined surface of the workpiece:
3.2. Arithmetic Mean Roughness
The section of the cut surface showed in Figure 5 must to be analyzed thoroughly in order to determine the Arithmetical Mean Roughness, due to the symmetry attribute of the periodically repeating surface.
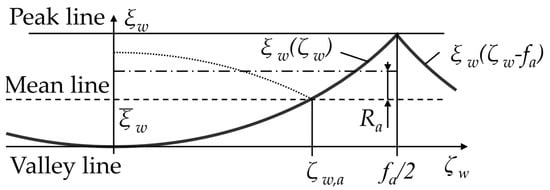
Figure 5.
Definition of the characteristic parameters of Ra in tangential turning.
The standard [40] defines the Ra roughness parameter as the solution of the following integral equation for the theoretical profile:
where
is the height of the Mean Line measured from the
axle. The definition states that the area (determined by the profile and the Mean Line) above and below the Mean Line should be the same. The
is determined by the ratio of the evaluated length and the integrand of the analyzed profile for the
axle.
In conclusion, the height of the Mean Line can be calculated as:
It can be concluded from the explanation above that Equation (5) can be transformed into a different form. On the one hand, due to the symmetry of the examined profile, the lower limit of the integration can be 0 instead of −f/2. On the other hand, it is advisable to divide the integration range into two parts, calculating the size of the area below and above the Mean Line separately. The coordinate
(interpreted on the horizontal axis) splits the range in two, where the Mean Line intersects the examined curve, as shown in the Figure 5. Therefore, the following relationship is fulfilled:
Accordingly, Equation (5) can be transformed, and the theoretical value of the Arithmetical Mean Height can be determined as:
To determine the theoretical value of Ra, the position of the base line of the analyzed profile must first be specified. Since the form of Equation 1 is complicated, an approximation is advisable to solve Equation 6 for this specified case. Due to the shape and properties of the function, a sixth-order Taylor expansion of Equation (1) is used. The approximation error is negligible according to the function analysis, and a 0.01 μm magnitude error can be expected in the realistic values of the geometric and kinematic parameters. The approximation of Equation (1) results in the following function of the roughness profile:
Performing the designated mathematical operations in Equation (6) by the substitution of Equation (9), the vertical position of the Mean Line can be determined:
The next step is the determination of
by the solution of Equation (7). If Equations (9) and (10) are substituted, Equation (7) takes the following form:
from which the horizontal coordinate of the intersecting point of the Mean Line and the machined surface profile can be determined, as follows:
Ultimately, the theoretical value of the Arithmetical Mean Roughness can be determined by the substitution of Equations (2), (10), and (12) into Equation (8). The result of the designated mathematical operations results in the following formula:
which can be simplified further by the application of mathematical deductions. The theoretical value of the Arithmetical Mean Roughness can be calculated as:
4. Results
In addition to the mathematical deduction of the theoretical values of the studied roughness parameters, the designed experiments were also carried out. Following the completion of the cutting experiments, as detailed in Section 2, measurements were carefully conducted on the machined workpieces. These measurements focused on assessing the two surface parameters. For each workpiece surface, three distinct profiles were measured to ensure a comprehensive evaluation of the surface characteristics. Once all the measurement results were collected, the average values of each parameter were calculated to provide a characteristic value for each setup. This averaging process helped in minimizing the influence of any localized anomalies and offered a more accurate depiction of the overall surface quality.
The detailed results of these measurements, along with the calculated average values, are systematically presented. Table 2 shows the measurement results and their averages for the Mean Roughness Depth, while Table 3 shows the same type of data for the Arithmetical Mean Roughness. These tables encapsulate the findings from the surface roughness measurements, offering a clear and organized view of the data obtained from the machining experiments.

Table 2.
Mean Roughness Depth measurement results and their averages.

Table 3.
Arithmetic Mean Roughness measurement results and their averages.
In the designed experimental setup, theoretical calculations were performed to determine the Arithmetical Mean Roughness (Ra) and Mean Roughness Depth (Rz). These calculations were essential to predict the surface quality expected from the machining process. The results revealed that the calculated values for both Ra and Rz were identical across three different experimental setups. This is caused by the fact that the theoretical values of the studied roughness parameters are not dependent on the cutting speed and depth of cut [7,41,42]. The results of the calculations are summarized in Table 4, with the setups also marked which have the same theoretical surface roughness.

Table 4.
Theoretical values of the analyzed roughness parameters.
5. Discussion
This study continues with the discussion and evaluation of the results of the cutting experiments and the above determined equations. It is important to analyze the effect of the different technological parameters on the practical values of Arithmetical Mean Roughness and Mean Roughness Depth, and to validate the calculation formulas given by this study by the comparison of the theoretical and experimental values.
The following statements can be made if the 12 setups are analyzed simultaneously. The lowest values of the roughness values were achieved when 0.3 mm feed, 0.1 mm depth of cut, and 250 m/min cutting speed were set (Setup 9), where 0.257 μm was measured for Ra and 1.751 μm was measured for Rz. The highest value of the Mean Roughness Depth was 4.525 μm, while the Arithmetical Mean Roughness had 0.997 μm as its highest value. These were achieved with the same settings: f = 1.0 mm, a = 0.1 mm, vc = 250 m/min. Overall it can be seen that by setting the feed low enough, the tangentially turned workpiece will resemble the properties of a surface machined by grinding procedure (Ra < 0.63, random topography), while when high feeds are applied, the procedure is still capable of generating surfaces with the characteristics of traditional finish turning. However, the feed in the latter is around five times lower than the values applied for tangential turning in this study. Therefore, a much higher productivity can be achieved by the application of the studied procedure, since the machining time can be significantly lowered compared to traditional turning (three- to five-fold decrease), while maintaining the same surface roughness on the machined surface. It can also be seen that increasing the feed has a negative effect on the values of the surface roughness. The lowest values of the roughness parameters are achieved, when 0.3 mm feed is set. Increasing f to 0.6 mm led to a 1.4–1.6-fold increase in the studied roughness parameter. When the feed is increased further, a nearly 60% increase is observed. When the feed is set to 1.0 mm from 0.8 mm, an around 1.3-fold increase is noted. These findings lead to the conclusion that when 0.3 mm feed is applied, the surface roughness is not affected mainly by the feed, but other phenomenon should affect the surface quality more. This will be explained further in a latter part of the paper.
Figure 6 compares the results of Setups 1–4 and 5–8. The first four experiments were designed to have a changing feed, while the second four experiments applied an increased depth of cut, with the value increased from 0.1 mm to 0.2 mm. In traditional turning, the former is usually used in finish machining, while the latter is rather utilized in semi-finishing operations. The increase of the depth of cut results mainly in two changes. Firstly, the width of the contact between the cutting edge and the workpiece, and therefore the chip width, increases. Secondly, the cross-sectional area of the removed chip increases, which results in higher cutting forces. Since the chip height is nearly unaffected by the change of the depth of cut, a two-fold increase in a results in an approximately two-fold increase in the cutting forces. However, these two factors play little role in the machined surface roughness. The former mainly increases the different loads on the cutting edge leading to an increased tool wear, whereas the latter results in a higher elastic deformation in the machining system, which has a bad effect on the shape and dimension accuracy of the machined part. The results of the cutting experiments prove that the expected results will be true in machining with tangential turning.
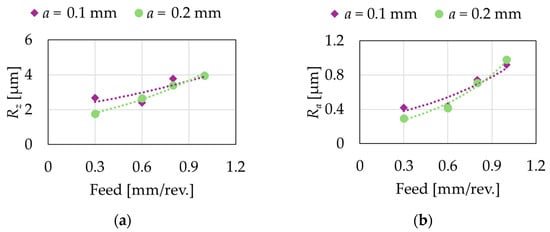
Figure 6.
Effect of increased depth of cut (a) as a function of feed on (a) Mean Roughness Depth and (b) Arithmetical Mean Roughness.
The Mean Roughness Depth shows a higher variation, where the difference decreases as the feed is increased (Figure 6a). The results of Setup 4 and 8 are practically the same. However, in the case of Arithmetical Mean Roughness (Figure 6b), an 0.6 mm feed is enough to achieve the same value. These results prove that in the point of view of the surface roughness, the depth of cut can be increased without affecting the roughness of the surface in tangential turning.
The effect of the cutting speed on the Mean Roughness Depth and Arithmetical Mean Roughness is evaluated by using Figure 7. In these diagrams, the measurement results after the cutting experiments are shown for Setup 1–4 and 9–12. The cutting speed was increased from 200 m/min to 250 m/min in the latter four setups, thus the effect of the cutting speed can be studied separately. In traditional turning, the cutting speed affects the quantity of workpiece material removed in a given time, the sum of the energy needed to do the machining, the rate of the surface generation, and the amount of material coming into contact with the tool in a given time. In technical terms, the value of vc mainly affects the following: the tool wear, the power requirement, and the strain rate in the chip root. The wear of the tool plays a great role in the quality of the machined workpiece; however, a sharp cutting edge was used in all of the experiments, so it can be neglected in this study. The power requirement mainly affects the load on the machine; thus, it is important in the machine tool design. However, the strain rate in the chip root is important in the point of view of the surface quality. If the cutting speed changes, the strain rate will be different according to the alteration in vc, which results in different plastic and elastic deformations in the machined surface, a phenomenon proved in many international studies in the analyses of different machining procedures [41,42,43,44,45]. Usually, there is an optimal cutting speed value, where the interactions in the chip root are ideal. The main task for process planners is to find this value. The above-described phenomenon can be seen in our experiments with tangential turning as well.
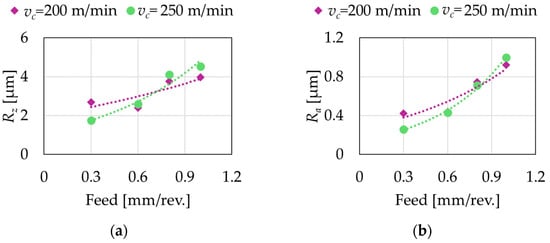
Figure 7.
Effect of increased cutting speed (vc) as a function of feed on (a) Mean Roughness Depth and (b) Arithmetical Mean Roughness.
Figure 7a presents the change in the Mean Roughness Depth if the cutting speed is increased on different feeds. It can be concluded that the effect of the cutting speed is not constant. In the range of low feed (f < 0.6 mm), increasing the cutting speed resulted in lower roughness. When 0.6 mm and 0.8 mm were set, vc had a slight increasing effect. If Setup 4 and 12 are compared, the increasing effect is a little higher. The same findings can be also said about the values of Arithmetical Mean Roughness. An important conclusion is the statement that the value of cutting speed should be chosen according to the other technological data, and not just the workpiece and tool material should be taken into consideration in the process planning of tangential turning.
It is interesting to note that the various roughness parameters could change differently, especially when the process parameters changed. It was found in a previously carried out study [46] that increasing the cutting speed and depth of cut can lead to lower core roughness. The different behavior could be explained by the different range of the cutting speed. It was found that 100 m/min cutting speed is too low for the applied workpiece and tool. The carried-out preliminary experiments showed that the ideal value for this pairing is between 200 m/min and 300 m/min. This study proved that in this range the roughness remains nearly the same. The lower significancy of the depth of cut on the surface roughness can be explained by the different effect of the chip width on the different roughness parameters, which is mainly affected by this process parameter.
The last section of this study is the validation of the mathematically deducted calculation formulas of the two roughness parameters. Figure 8 and Figure 9 present the results of the measurements after the 12 practical cutting experiments, and the calculated theoretical values of Rz and Ra, respectively. The setups were grouped in three groups according to the experimental design. The first group (purple diamond) contains the first four setups, which were the basis of this study. The second group (green circle) represents the second four setups, where the depth of cut was increased, and the third group (yellow triangle) includes the last four setups, where the cutting speed was changed. In the three groups, the increase of the feed can be observed. Observing Figure 8 and Figure 9, it can be seen that the theoretical values of the surface roughness parameters are usually lower than the characteristics of the measured surfaces. This is a common phenomenon in the theoretical description of the surface roughness, since when an analytical approach is applied, it can only take into account the geometry of the cutting tool in the base plane, and the kinematic movements of the tool and the workpiece. The surface roughness is also affected by other things, like grain size in the surface of the workpiece or material separation between and in the grains; however, the mathematically determined values of the roughness values show the same tendency if the feed is increased.
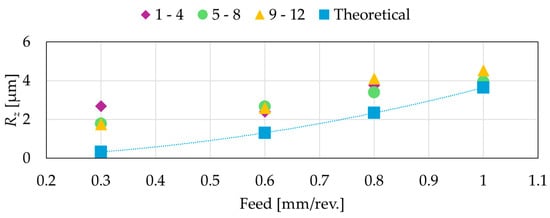
Figure 8.
Comparison of the experimental measurements with the theoretically calculated values of the Mean Roughness Depth. The setups are presented in the 3 groups according to the plan.
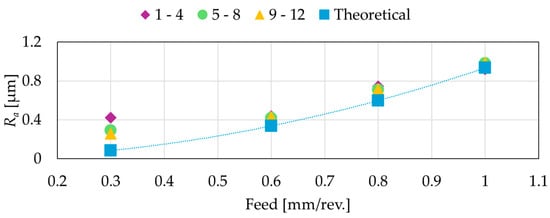
Figure 9.
Comparison of the experimental measurements with the theoretically calculated values of the Arithmetical Mean Roughness. The setups are presented in the 3 groups according to the plan.
Another important finding is the different deviation of the experimental and theoretical values on different feeds. When a 0.3 mm feed is applied, the practical values of Rz are around six times higher and the values of Ra are around 3.8 times higher than the theoretical value. This is caused by the fact that for every procedure which applies geometrically defined cutting edges (turning, drilling, milling, etc.), there is a limit in the feed. Below that limit, the effect of the cutting edge geometry is not so significant, but the other factors affect more the roughness of the generated surface. However, if the feed is increased above a given value, the cutting edge geometry becomes more and more significant. This can also be observed in our study. When a 0.6 mm feed is set, the difference decreases: the practical values of Rz are around 1.9 times higher and the values of Ra are around 1.26 times higher. The deviation of the Mean Roughness Depth values is 60% and the deviation of the Arithmetical Mean Roughness values is 20%, when a 0.8 mm feed is applied. If the feed is 1.0 mm, the lowest deviations are achieved in this study: 14% for Rz and 3% for Ra. It can be clearly seen that as the feed increases, and as the geometry of the cutting edge becomes more and more significant, the calculated values of the roughness parameters became more accurate. Overall, the results have a lower deviation in the prediction of the Arithmetical Mean Roughness, while in case of the Mean Roughness Depth, higher feeds must be set to reliably predict the machined surface roughness.
6. Conclusions
This paper examines the impact of feed, depth of cut, and cutting speed changes in tangential turning by comparing theoretical and experimental values of the Mean Roughness Depth (Rz) and Arithmetic Mean Roughness (Ra). A method was elaborated to determine the theoretical roughness values by deriving an equation based on the geometry of the cutting tool. This equation calculates Rz and Ra as a function of the significant kinematic and geometric parameters. Actual cutting experiments were also carried out to show the effect of the three technological parameters on the surface roughness. Using the selected technological parameters within the studied range, the theoretical values were computed and validated through practical cutting experiments.
Analyzing the 12 experimental setups, this study reveals significant insights into the surface roughness outcomes of tangential turning. The optimal roughness values were observed with a 0.3 mm feed, 0.1 mm depth of cut, and 250 m/min cutting speed (Setup 9), achieving an Ra of 0.257 μm and Rz of 1.751 μm. The highest roughness values, with Ra reaching 0.997 μm and Rz 4.525 μm, were noted in the setup with a 1.0 mm feed, 0.1 mm depth of cut, and the same cutting speed. It is evident that lower feeds can produce surfaces which are similar to those which are finished by grinding, while higher feeds, although still effective, exhibit roughness typical of traditional finish turning. This method significantly boosts productivity compared to conventional turning. Increasing the feed generally worsens surface roughness, with a marked rise when moving from 0.3 mm to higher feeds. This study also shows that increasing the depth of cut does not notably affect surface roughness. Variations in cutting speed influence roughness, particularly at lower feeds, where higher speeds reduce roughness. Theoretical calculations, while generally lower than practical measurements, align well at higher feeds, demonstrating the importance of feed in determining surface quality.
The most important findings of this study are the following:
- •
- Accurate calculation formulas were determined for the theoretical investigation of the Arithmetic Mean Roughness and the Mean Roughness Depth by the application of constructive tool geometry.
- •
- The carried-out experiments proved the hypothesis that the feed has an increasing effect on the surface roughness.
- •
- Due to the applied inclination angle, the achievable surface roughness was very low; therefore, surfaces with low roughness values can be produced with high feeds.
- •
- The comparison of the experimental and theoretical results showed that the deducted equations are capable of predicting the Arithmetic Mean Roughness and Mean Roughness Depth, which is essential in the production planning of a machining procedure.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the author.
Acknowledgments
The author fully acknowledges and greatly appreciates the support of the University of Miskolc in the preparation of this work.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Sedlaček, M.; Podgornik, B.; Vižintin, J. Influence of surface preparation on roughness parameters, friction and wear. Wear 2009, 266, 482–487. [Google Scholar] [CrossRef]
- Svahn, F.; Kassman-Rudolphi, A.; Wallén, E. The influence of surface roughness on friction and wear of machine element coatings. Wear 2003, 254, 1092–1098. [Google Scholar] [CrossRef]
- Kovács, G. Optimization of a new composite multicellular plate structure in order to reduce weight. Polymers 2022, 14, 3121. [Google Scholar] [CrossRef]
- Georgakopoulos-Soares, I.; Papazoglou, E.L.; Karmiris-Obratański, P.; Karkalos, N.E.; Markopoulos, A.P. Surface antibacterial properties enhanced through engineered textures and surface roughness: A review. Colloids Surfaces B Biointerfaces 2023, 231, 113584. [Google Scholar] [CrossRef]
- Abellán-Nebot, J.V.; Pastor, C.V.; Siller, H.R. A Review of the Factors Influencing Surface Roughness in Machining and Their Impact on Sustainability. Sustainability 2024, 16, 1917. [Google Scholar] [CrossRef]
- M’Saoubi, R.; Outeiro, J.C.; Chandrasekaran, H.; Dillon, O.W., Jr.; Jawahir, I.S. A review of surface integrity in machining and its impact on functional performance and life of machined products. Int. J. Sustain. Manuf. 2008, 1, 203–236. [Google Scholar] [CrossRef]
- Shaw, M.C. Metal Cutting Principles; Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
- Khorasani, A.M.; Yazdi, M.R.S.; Safizadeh, M.S. Analysis of machining parameters effects on surface roughness: A review. Int. J. Comput. Mater. Sci. Surf. Eng. 2012, 5, 68. [Google Scholar] [CrossRef]
- Kundrák, J.; Felhő, C.; Nagy, A. Analysis and Prediction of Roughness of Face Milled Surfaces using CAD Model. Manuf. Technol. 2022, 22, 558–572. [Google Scholar] [CrossRef]
- Dimopoulos, C.; Karkalos, N.E.; Kundrák, J.; Markopoulos, A.P. Combination of an improved 3D geometry and coupled eulerian-lagrangian formulation for turning simulation. Mater. Sci. Forum 2020, 994, 240–247. [Google Scholar] [CrossRef]
- Ferencsik, V.; Varga, G. The influence of diamond burnishing process parameters on surface roughness of Low-Alloyed aluminium workpieces. Machines 2022, 10, 564. [Google Scholar] [CrossRef]
- Lopes, L.G.D.; Gomes, J.H.d.F.; de Paiva, A.P.; Barca, L.F.; Ferreira, J.R.; Balestrassi, P.P. A multivariate surface roughness modeling and optimization under conditions of uncertainty. Measurement 2013, 46, 2555–2568. [Google Scholar] [CrossRef]
- Liu, L.; Yang, C.; Sheng, Y. Wear model based on real-time surface roughness and its effect on lubrication regimes. Tribol. Int. 2018, 126, 16–20. [Google Scholar] [CrossRef]
- Kuti, R.; Szabó, Á.I.; Tóth, Á.D. Experimental Investigation of Tribological Properties of Two Fully Formulated Engine Oils with Additional Nanoscale Spherical Zirconia Particles. Lubricants 2022, 10, 246. [Google Scholar] [CrossRef]
- Tuzun, U. Load-dependent contact mechanics of particulate assemblies: Multi-variant particle size, shape and surface roughness in advanced materials and process applications. Chem. Eng. Res. Des. 2018, 137, 101–112. [Google Scholar] [CrossRef]
- Felho, C.; Varga, G. Theoretical roughness modeling of hard turned surfaces considering tool wear. Machines 2022, 10, 188. [Google Scholar] [CrossRef]
- Vrabeľ, M.; Maňková, I.; Paľo, M.; Lattner, R. The Effect of Artificial Neural Network Architecture on Surface Roughness Parameter Prediction Capability when Turning Inconel 718. Manuf. Technol. 2016, 16, 834–839. [Google Scholar] [CrossRef]
- Benardos, P.; Vosniakos, G.-C. Predicting surface roughness in machining: A review. Int. J. Mach. Tools Manuf. 2003, 43, 833–844. [Google Scholar] [CrossRef]
- Klocke, F.; Bergs, T.; Degen, F.; Ganser, P. Presentation of a novel cutting technology for precision machining of hardened, rotationally symmetric parts. Prod. Eng. 2012, 7, 177–184. [Google Scholar] [CrossRef]
- Martikan, P.; Holubjak, J.; Czanova, T.; Pustay, J.; Joch, R. Identification of roughness parameter when turning process with helical cutting edge for machining of automotive transmission parts. Transp. Res. Procedia 2019, 40, 362–366. [Google Scholar] [CrossRef]
- Schreiber, L.; Trott, K. Verfahren zur Drallfreien Spanenden Bearbeitung von Rotationssymmetrischen Flächen. Patent DE19963897A1, 28 April 1999. [Google Scholar]
- Schneider, J.; Schreiber, L. Maschinen Und Anlagen-Mit dem Tangentialdrehen zu drallfreien Oberflachen. Werkstatt Und Betrieb. 2002, 135, 40–45. [Google Scholar]
- Leichner, T.; Franke, V.; Sauer, B.; Aurich, J.C. Investigation of the tribological behavior of radial shaft rings and soft turned shafts under the influence of abrasive particles. Prod. Eng. 2011, 5, 531–538. [Google Scholar] [CrossRef]
- Kundrák, J.; Molnár, V.; Markopoulos, A.P. Joint Machining: Hard Turning and Grinding. Rezan. I Instrum. V Tehnol. Sist. 2019, 34–41. [Google Scholar] [CrossRef]
- Schubert, A.; Zhang, R.; Steinert, P. Manufacturing of twist-free surfaces by hard turning. Procedia CIRP 2013, 7, 294–298. [Google Scholar] [CrossRef]
- Nee, A.; Venkatesh, V. Form accuracy of tangentially skived workpieces. CIRP Ann. 1985, 34, 121–124. [Google Scholar] [CrossRef]
- EMAG. Scroll-Free Turning from EMAG: Fast, Precise, Reliable; EMAG GmbH & Co., KG: Salach, Germany; Available online: https://www.emag.com/technologies/scroll-free-turning.html (accessed on 16 February 2021).
- Litvin, F.L.; Fuentes, A.; Curti, G. Gear Geometry and Applied Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Hsieh, J.-F. Mathematical modeling of interrelationships among cutting angles, setting angles and working angles of single-point cutting tools. Appl. Math. Model. 2010, 34, 2738–2748. [Google Scholar] [CrossRef]
- Máté, M.; Hollanda, D.; Tolvaly-Roşca, F.; Forgó, Z.; Egyed-Faluvégi, E. Synthesis of a Profile Errorless Involute Shaper Cutter with Cylindrical Rake Face. In Proceedings of the 2019 IEEE 19th International Symposium on Computational Intelligence and Informatics and 7th IEEE International Conference on Recent Achievements in Mechatronics, Automation, Computer Sciences and Robotics (CINTI-MACRo), Szeged, Hungary, 14–16 November 2019; pp. 71–78. [Google Scholar]
- Balajti, Z. Determination of Undercutting Avoidance for Designing the Production Technology of Worm Gear Drives with a Curved Profile. Machines 2023, 11, 56. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, S.; Fang, C.; Sun, S.; Dai, H. Geometric error modeling and compensation for five-axis CNC gear profile grinding machine tools. Int. J. Adv. Manuf. Technol. 2017, 92, 2639–2652. [Google Scholar] [CrossRef]
- Li, Z.; Yang, J.; Fan, K.; Zhang, Y. Integrated geometric and thermal error modeling and compensation for vertical machining centers. Int. J. Adv. Manuf. Technol. 2014, 76, 1139–1150. [Google Scholar] [CrossRef]
- Balajti, Z. Challenges of engineering applications of descriptive geometry. Symmetry 2023, 16, 50. [Google Scholar] [CrossRef]
- Perepelitsa, B.A. Mapping of Affine Space in the Theory of Shaping of Surfaces by Cutting [Otobrazhenija affinnogo prostranstva v teorii formoobrazovanija poverhnostej rezaniem]; Vyshcha Shkola: Kharkiv, Ukraine, 1981; p. 107. (In Russian) [Google Scholar]
- Perepelitsa, B.A. Development of the Theory of Shaping and Design of Cutting Tools Based on Multi-Parameter Mappings. Ph.D. Thesis, Kharkov, Ukraine, 1982. (In Russian). [Google Scholar]
- Vasilko, K. Kinematics Analysis of the movement of cutting tool against the workpiece and creation of new schemes. Manu-Facturing Ind. Eng. Kosice 2010, 9, 8–15. [Google Scholar]
- ISO 21920-1:2021; Geometrical Product Specifications (GPS)—Surface Texture: Profile. ISO: Geneva, Switzerland, 2021.
- Sztankovics, I. Analytical determination of high-feed turning procedures by the application of constructive geometric modeling. FME Trans. 2024, 52, 173–185. [Google Scholar] [CrossRef]
- ISO 4287:1997; Geometrical Product Specifications (GPS)—Surface Texture: Profile Method—Terms, Definitions and Surface Texture Parameters. International Organization for Standardization: Geneva, Switzerland, 1997.
- Sun, Z.; Geng, D.; Guo, H.; Zhang, Q.; Liu, Y.; Liu, L.; Jiang, X.; Zhang, D. Introducing transversal vibration in twist drilling: Material removal mechanisms and surface integrity. J. Mech. Work. Technol. 2024, 325, 118296. [Google Scholar] [CrossRef]
- Geng, D.; Sun, Z.; Liu, Y.; Liu, L.; Ying, E.; Cai, J.; Jiang, X.; Zhang, D. Unravelling the influence of vibration on material removal and microstructure evolution in ultrasonic transversal vibration-assisted helical milling of Ti-6Al-4V holes. J. Mater. Process. Technol. 2024, 326, 118320. [Google Scholar] [CrossRef]
- Bordin, A.; Bruschi, S.; Ghiotti, A. The effect of cutting speed and feed rate on the surface integrity in dry turning of CoCrMo Alloy. Procedia CIRP 2014, 13, 219–224. [Google Scholar] [CrossRef]
- Bedi, S.S.; Sahoo, S.P.; Vikas, B.; Datta, S. Influence of cutting speed on dry machinability of AISI 304 stainless steel. Mater. Today Proc. 2020, 38, 2174–2180. [Google Scholar] [CrossRef]
- Sun, Z.; Geng, D.; Guo, H.; Ge, E.; Zhou, E.; Fan, Z.; Meng, F.; Jiang, X.; Zhang, D. Influence of transversal vibration on cutting performance and surface integrity during ultrasonic peening drilling of Al-Li alloys. Chin. J. Aeronaut. 2024. [Google Scholar] [CrossRef]
- Sztankovics, I. Analysis of Selected Function-Defining 2D Surface Roughness Parameters in Tangential Turning. Rezan. I Instrum. V Tehnol. Sist. 2023, 109–115. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).